Free-space optical communications over imperfect ${\mathcal {F}}$ turbulence channels with pointing errors

Abstract

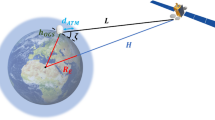
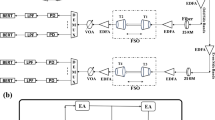
In this paper, we examine the performance of a free-space optical (FSO) communication system under imperfect Fisher-Snedecor ${\mathcal {F}}$ atmospheric turbulence channels. Taking into consideration the atmospheric turbulence, channel estimation errors, and pointing errors, simple and accurate analytical expressions for the probability density function and cumulative density function under intensity modulation direct detection (IM/DD) and heterodyne detection techniques are derived. Consequently, new analytical expressions for useful performance metrics such as outage probability, average bit error rate, and ergodic capacity are derived. To get more insight into the system diversity gain, asymptotic analytical expressions, in the high signal-to-noise ratio regime, for the outage probability and average BER are obtained. Our analysis is validated by means of numerically and Monte-Carlo simulations under various turbulence conditions and system parameters. The numerical results demonstrate that the derived analytical expressions are very accurate and provide precise evaluations for the proposed performance analyses. In addition, the results show that imperfect CSI seriously affects the FSO communication systems. However, the performance of heterodyne detection outperforms its counterpart the intensity modulation/direct-detection under all scenarios.

APPENDIX

Proof of Lemma 1

To find the PDF of $\gamma$, we need first to find the PDF of $\hat{h}=h+\epsilon$. To this end, the PDF of $\hat{h}$ can be found via

$$\begin{aligned} {f}_{\hat{h}}(\omega )={f}_X(x)\circledast f_Y(y) =\int _{0}^{\infty }{f}_X(x)f_Y(\omega -x)dx \end{aligned}$$

(47)

where $x = \rho h$ and $y =\sqrt{1-\rho ^2}\epsilon$. Using (3), (4) and after performing transformation of RVs, (47) can be rewritten as (48), at the top of the next page. Using [23, Eq. (1.211.1)] and [22, Eq. (8.4.3.1)], the integral in (48) can be rewritten as in (49), which can be solved with the help of [22, Eq. (2.24.1.1)] and after some algebraic manipulations as in (10).

$$\begin{aligned} {f}_{\hat{h}}(\omega )&=\frac{a^a\bigg (-\frac{\omega ^2}{2(1-\rho ^2)} \bigg )}{\rho ^a(b-1)^a\Gamma (a)\Gamma (b)\sqrt{2\pi (1-\rho ^2)}}\nonumber \\&\quad \times \int _{0}^{\infty }x^{a-1}{\textrm{G}}_{1,1}^{1,1} \left( \frac{a}{\rho (b-1)}x \bigg |\begin{array}{c} 1-(a+b) \\ 0 \end{array}\right) \nonumber \\&\quad \times \exp \bigg (\frac{\omega x}{(1-\rho ^2)}\bigg ) \exp \bigg (-\frac{x^2}{2(1-\rho ^2)}\bigg )dx, \end{aligned}$$

(48)

$$\begin{aligned} {f}_{\hat{h}}(\omega )&=\frac{a^a\text {exp} \bigg (-\frac{\omega ^2}{2(1-\rho ^2)}\bigg )}{\rho ^a(b-1)^a \Gamma (a)\Gamma (b)\sqrt{2\pi (1-\rho ^2)}}\nonumber \\&\quad \sum _{k=0}^{\infty }\frac{\omega ^k}{k!(1-\rho ^2)^k} \int _{0}^{\infty }x^{a+k-1}{\textrm{G}}_{0,1}^{1,0} \left( \frac{x^2}{2(1-\rho ^2)}\bigg |\begin{array}{c} - \\ 0 \end{array}\right) \nonumber \\&\quad {\textrm{G}}_{1,1}^{1,1} \left( \frac{a}{\rho (b-1)}x \bigg |\begin{array}{c} 1-(a+b) \\ 0 \end{array}\right) dx, \end{aligned}$$

(49)

The CDF of $\hat{h}$ can be obtained by integrating (10) along with using [22, Eq. (2.24.2.2)] and [22, Eq. (8.4.16.1)], it can be expressed as in (11). This ends the proof of Lemma. 1. $\square$

Proof of Lemma 2

The proof of the turbulence misalignment scenario is similar to that in turbulence scenario only. Thus, using (3), (7), and after performing transformation of RVs, (47) can be rewritten as in (50). Using [23, Eq. (1.211.1)] and [22, Eq. (8.4.3.1)], the integral in (50) can be rewritten as in (51), which can be solved with the help of [22, Eq. (2.24.1.1)] and after some algebraic manipulations as in (14). Thereafter, the CDF of $\gamma$ can be obtained by integrating (14), using [22, Eq. (2.24.2.2)], and [22, Eq. (8.4.16.1)]. This completes the proof of Lemma. 2. $\square$

$$\begin{aligned} {f}_{\hat{h}}^{pe}(\omega )&=\frac{az^2\bigg (-\frac{\omega ^2}{2(1-\rho ^2)} \bigg )}{\sqrt{2\pi (1-\rho ^2)}\rho (b-1)h_lA_o\Gamma (a)\Gamma (b)}\nonumber \\&\quad \int _{0}^{\infty }{\textrm{G}}_{2,2}^{2,1} \left( \frac{a}{\rho (b-1) h_lA_o}x \bigg |\begin{array}{c} -b,z^2 \\ a-1,z^2-1 \end{array}\right) \nonumber \\&\quad \exp \bigg (\frac{\omega x}{(1-\rho ^2)}\bigg ) \exp \bigg (-\frac{x^2}{2(1-\rho ^2)}\bigg )dx, \end{aligned}$$

(50)

$$\begin{aligned} {f}_{\hat{h}}^{pe}(\omega )&=\frac{az^2\bigg (-\frac{\omega ^2}{2(1-\rho ^2)} \bigg )}{\sqrt{2\pi (1-\rho ^2)}\rho (b-1)h_lA_o \Gamma (a)\Gamma (b)}\nonumber \\&\quad \sum _{k=0}^{\infty }\frac{\omega ^k}{k!(1-\rho ^2)^k} \int _{0}^{\infty }x^k{\textrm{G}}_{0,1}^{1,0} \left( \frac{x^2}{2(1-\rho ^2)}\bigg |\begin{array}{c} - \\ 0 \end{array}\right) \nonumber \\&\quad {\textrm{G}}_{2,2}^{2,1} \left( \frac{a}{\rho (b-1) h_lA_o}x \bigg |\begin{array}{c} -b,z^2 \\ a-1,z^2-1 \end{array}\right) dx, \end{aligned}$$

(51)

Proof of Lemma 3

Based on (1), the received electrical SNR and the average electrical SNR for the FSO systems under consideration can be respectively expressed as $\gamma =(\frac{\epsilon \omega }{N_o})^r$ and $\mu _r=\frac{\epsilon ^r E^r[\omega ]}{N_o}$, where $N_o$ refers to the Gaussian noise power spectral density, v characterizes the detection type. Note that $r=1$ for heterodyne detection while $r=2$ for IM/DD. Here, $E[\cdot ]$ refers to the expectation operator, where the n-th moment is defined as

$$\begin{aligned} E[x^n]=\int _{0}^{\infty }x^nf_{x}(x)dx. \end{aligned}$$

(52)

Substituting (10) into (52), using [23, Eq. (3.326.2)] and after some mathematical manipulation, the n-th moment in (18) is obtained. $\square$

Proof of Lemma 4

With the aid of (10), (11), and (18), the PDF and CDF of the received SNRs, for both detection techniques, can be respectively obtained as in (19) and (20). $\square$

Proof of Lemma 5

Substituting (14) into (52), then using [23, Eq. (3.326.2)] and after some mathematical manipulation, the n-th moment of the ${\mathcal {F}}$ turbulence channel with imperfect CSI and in the presence of pointing errors can be obtained as in (21). $\square$

Proof of Lemma 6

With the help of (14), (15), and (21), the PDF and CDF of the received SNRs for both detection techniques under the ${\mathcal {F}}$ turbulence channel model with imperfect CSI and in the presence of pointing errors can be respectively obtained as in (22) and (23). $\square$