1 Introduction

The total cost of operating a network has been significantly decreased owing to introduction of Dense Wavelength Division Multiplexing (DWDM) and other new technologies. However, power consumption of such networks is remarkable. Optical-Electrical-Optical (OEO) conversions along the used paths are known to be one of the highest power consumers. These conversions are performed not only at source/destination nodes, but are also used for the purpose of re-amplifying, re-shaping, and re-timing of the signal (called 3R), every several tens of kilometers. In order to minimize the number of performed OEO conversions—i.e., to migrate to all-optical network [5]—two solutions have been proposed: optical regeneration, and physical impairment aware routing (especially its variant called Physical Impairment Constrained Routing (PICR) which concentrates on the fine tuning of the power levels of the wavelengths).

Even though utilization of optical regenerators was the subject of extensive research presented in many papers (see e.g., [6]), such solutions are not frequently used in practice. Physical impairment aware routing is a quite new concept, and some approaches are already available in the literature. These methods differ in their physical impairment models and in the way they handle the three main problems of physical impairment aware routing—i.e., routing, wavelength assignment, and physical impairments issue [3, 19]. A detailed summary of physical layer impairment aware routing issues are given in [2].

In the history of modern telecommunications, expectations of users have grown rapidly, which was mostly compensated with newly introduced technologies, and with the increase of the reliability of network elements. Lots of services, like Virtual Private Network (VPN), Video on Demand (VoD), certainly need protection against unpredictable events. Protection methods can be classified based on the offered protection level. For example, the concept of Shared Risk Groups (SRG) was introduced to handle problems that may affect not only a single component, but a set of resources [11, 13, 23]. However, in optical networks, probability of multiple failures is low. Therefore, in this paper we will consider failures of single network elements. In particular, protection against single link failures will be investigated, since in wide-area networks, random failures refer almost always to network links.

Naturally, since all demands should be routed, if it is not feasible to serve a demand in all-optical way, then electrical regeneration of the signal must take place along the path. We are sure that such duality—i.e., serving demands either in all-optical way, or with electrical regeneration applied along the paths—will coexist for a long time, since any transition to a newer technology should be done in a step-by-step way. Our opinion is that it would be cost-efficient for operators to apply the idea of partial migration. For instance, they may reserve a given amount of their power budget and available wavelengths for Physical Impairment Constrained Routing (PICR)—i.e., the amount of power and wavelengths that can be solely used for transporting data over the links with all-optical routing—while utilizing the remaining part of the budget, as it was used in the past. The budget reserved for PICR may be then increased in a step-by-step manner until all or nearly all demands can be routed in all-optical way. However, during the transition process, operators have to choose, which newly arrived demands should be routed with PICR, and which one should not.

In one of our previous papers [10], we introduced a work-flow for routing demands with protection utilizing PICR approach. Since one of the key issues refers to minimizing the operational complexity, for demands requiring protection, it makes sense to route both primary and backup paths using the same assumptions (e.g., in all-optical way). As a consequence, we will assume that PICR is used either for both the primary and the backup path, or for none of them.

The main achievement of this paper is a novel step-by-step transition approach to the all-optical survivable routing under path length limitations imposed by physical impairments of PICR. In particular, we present a new work-flow providing a smooth transition to PICR, as well as methods that can be applied in a continuous way to maximize the number of dynamic traffic demands routed in all-optical way with protection.

The paper is organized as follows: Sect. 2 gives the description of the investigated problem and the applied network model. Details of our model and presentation of physical background can be found in Sect. 2.1. In Sect. 2.2 we summarize basic protection schemes. The proposed heuristics are given in Sect. 3. Simulation results are studied in Sect. 4, conclusion is given in Sect. 5.

2 Problem formulation and the goal of research

In this paper, a two-layer network is considered, where the upper (electronic) layer is time-switching capable, while the lower (optical) layer is wavelength-switching capable. The control plane is assumed to have information on both interconnected layers. Both layers are utilized in accommodating demands.

We assume that characteristics of analyzed networks, including their topology, physical constraints, the number of fibers, capacity, number of wavelength channels per link, as well as link lengths, are given. The case of dynamic traffic consisting of unicast demands with protection is analyzed. Another assumption is that the network operator has to reserve a given amount of power for PICR that is smaller than what is required to route all demands in all-optical way. In our approach, we are interested in routing as many demands as possible with protection using PICR technique.

The Wavelength Graph (WG) model is used for routing in two-layer networks [26]. This graph corresponds to the logical network, and is derived from the physical network considering its topology, and capabilities of physical devices.

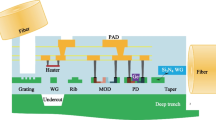
A subgraph of a versatile equipment is depicted in Fig. 1. The equipment originates, terminates and electrically splits the traffic. This is illustrated by an electronic node in the subgraph—the single node on the top of the figure. Figure 1 assumes two fibers being connected to the device and two WLs per fiber.

Fig. 1
figure 1

Representation of an Optical-Cross-Connects node (OXC), connecting two fibers with two WLs in each

Full size image

2.1 Physical impairment constrained routing

It is natural that operators try to maximize their profit. This goal can be achieved by introducing technologies helping to reduce the operational expenditures (OPEX), e.g., by a separate fine-tuning of the power level of every single wavelength in the network. As a precondition, wavelength controlling, and monitoring functionalities are needed. OPEX can be also decreased by avoiding manual maintenance with the utilization of remote configuration capabilities, including power tuning. Such options are available in new-technology equipment, like reconfigurable optical add/drop multiplexers (ROADM). Other desired features like power measurement, and special settings per wavelength are included in the majority of commercially available products [1, 7].

Nowadays, in nearly all types of ROADMs, signal power can be tuned with variable optical attenuators (VOA) by the management system. In metro WDM networks, signal power of optical channels is determined by Cross-Phase Modulation (XPM) and Raman scattering, but not by the Brillouin threshold. Therefore, only the maximum of the power inserted into the fiber is limited (not the power level of a single channel). As a consequence, it is possible to increase the power of some channels up to the Brillouin threshold, while other channel powers are tuned down to fulfill the XPM, and Raman scattering constraints. This idea allows the use of PICR for lightpath configuration [21] (this also holds for core networks).

Figure 2 shows example configurations for two wavelengths: ϕ 1 and ϕ 2. In Case A, PICR is not used. Therefore, due to physical constraints, data from node A can be transferred only to node C in all-optical way. However, for a demand between nodes A and D the signal transmitted along the respective path has to be electrically regenerated in one of the transit nodes: in B or in C. Case B refers to the same example, but this time for PICR. This technique allows to increase the signal power of ϕ 2 to fulfill the Optical Signal-To-Noise Ratio (OSNR) request at node D, providing that the summarized power load does not exceed the physically affordable limits on each link. This way it is possible to establish an all-optical connection between nodes A, and D.

Fig. 2
figure 2

Base idea of PICR

Full size image

In our PICR scheme, maximum length of all-optical path is upper bounded by Quality of Service (QoS)—i.e., with the increase of the input power over a limit non-linear impairments and cross-talk significantly decreases the quality of the received signal—and power constraints of links. If there are enough resources, by tuning the signal power without electric signal regeneration, routing can be done entirely in all-optical way.

Under PICR, different channel powers are utilized for every wavelength within the same optical fiber. In general, the used power is the function of the distance the ligthpath has to pass through. This in turn raises new problems that have to be addressed before (see.e.g. [21]).

In order to determine the relation between signal power and the maximum allowed distance, we consider a noise-limited system where physical effects can be taken into account as power-penalties. As proved in [18] by means of analytical calculations, the channel power and the maximum allowed distance of a lightpath is in a linear relation: L=L c ×P mW , where L is the maximum allowed distance, P mW is the input power in mW and L c is the linear factor between them. For typical constant values used in telecommunications, L c is between 500, and 2000. The impact of a node is in turn modeled with an edge of a certain length—len PhyNode . In this paper, we consider that L c is 1000, len PhyNode is 90 km, the maximum power over a link should not exceed 20 mW.

2.2 Protection methods

In most cases, calculation of backup paths providing protection against single link failures is done by means of utilizing variants of the two following methods. The first approach, called dedicated protection, is utilized if Quality of Service (QoS) features and other related properties are required. In this case, a dedicated backup path is calculated which is link-disjoint with the respective primary path. This protection path, reserved for a single demand only, is utilized only if the demand cannot be routed according to its primary path. In other cases—i.e., low QoS needs, reliable network components, high network load, etc.—shared protection may be used. Shared protection allows resource sharing between backup paths protecting mutually disjoint primary paths. This is because resource sharing is possible only between backup paths that do not provide protection against any common failures. The issue of sharing the backup path resources (mostly bandwidth) was addressed many times (see e.g., [15]). Since in our paper, the main resource is power level, we will concentrate on shared protection as the mean of power sharing—but of course in our simulations we also allowed bandwidth sharing.

In the next three sections we will summarize the most important algorithms used to calculate primary and backup paths in general.

2.2.1 Segment protection

In case of segment protection, the primary path is divided into smaller segments. Here the backup path is not calculated for the whole path but for each segment separately (see [20]). This method is known for its resource saving properties in general. In our case, the input power is in strong connection with the length of the path it should take. To make the investigated proposition (i.e., PICR with protection) compatible with segment protection, the input power should be calculated from the path length of the longest possible path after a link failure. This is the consequence of the fact that the OSNR should be good enough to retrieve the data even if the working path is switched onto the backup without violating the power constraints at any link. This would significantly increase the power consumption of the overall network, which is in contradiction with the main aim of PICR.

2.2.2 Optimal solution

The problem to provide routing of one or more static demands with and without protection has been addressed many times, and the respective methods have been proposed in the literature to find optimal [8], or quasi optimal solutions [24]. We are convinced that solution to the PICR problem can be found using these methods with only a few minor modifications. However, the disadvantage is that, the time needed to find an optimal solutions with these methods makes it hardly possible to apply them for dynamic problems (even the static version of the problem without PICR is known to be NP-hard [16]).

2.2.3 Heuristic approaches

The problem of finding primary and backup paths for a single demand is a very well analyzed one, and several important heuristic approaches are available. The most important methods include: Shortest Pair of Link Disjoint Paths (SPLP) [14], k-Disjoint Paths method (KDPM) [4, 25], and k-Penalty algorithm [22] as follows.

Shortest Pair of Link-Disjoint Paths: Under SPLP, primary and backup paths are calculated sequentially. When the first route is identified from the source to the destination, direction of its edges is reversed, while their cost is multiplied by minus one. These edges can be further used during the search for the backup path. The result—i.e., a pair of link-disjoint paths—is obtained from edges traversed only once.

k-Disjoint Paths Method: When using KDPM method, any backup path is calculated after the respective primary one has been found using the modified graph of a network topology obtained from the original one by excluding all the links utilized by the primary path. Advantages of KDPM include speed and easiness of adjusting to our problem. However, under KDPM, there is a risk that the algorithm may enter into the trap problem, i.e., it may fail to find the next path, even though the requested number of disjoint paths exist.

k-Penalty: works in a similar way to the KDPM method. However, in order to avoid the mentioned trap problem, before finding the next disjoint path, the links traversed by the recently found path are not removed from the graph. Instead, their cost is increased by a large value. k-Penalty allows the next path of a demand to temporarily use the common links with the former paths. However, if such a situation occurs, finding the set of paths starts from the beginning with new (i.e., permanently increased) initial costs of links. After possible several iterations, the most critical links in the network are identified (their cost becomes high), that should be traversed by paths only when there is no other way. After several possible conflicting situations, the algorithm finally manages to find the required set of disjoint paths for a demand. Unlike KDPM, this algorithm may be also used when differentiated costs of links are utilized to find working and backup paths, respectively.

In case of WG, a simple physical link is modeled by means of multiple edges. Link disjointness can be achieved, only if for every edge from the primary path, there is no edge in the backup path that is part of the same physical link. As a result, the set of edges that can be used by the backup path is the function of the primary path and the current candidate for the backup path. Computational complexity of SPLP and k-Penalty is higher than of KDPM. Additionally, SPLP typically does not provide significantly better solutions than KDPM. Therefore, methods proposed in the next sections are based on KDPM.

3 Proposed selection methods

3.1 Used method

Decision concerning the utilization of PICR technique should be made between the moment the demand enters the network, and the time just before the bandwidth and power is allocated for it. In particular, if decision is done in the very beginning (at the time of entering), the solution is based only on location of the source and the destination nodes, the distance between them, as well as on the current state of the network. In our paper, we will not consider this, since the same decision can be made later, as all these and even more information will be still available until resources are reserved for the demand.

In our proposal, the decision is made at the time of finding the paths for demands. In particular, we have extended here our algorithm originally presented in [10]—with a few additional steps (see Algorithm 1).

Algorithm 1
figure 3

Algorithm to find the primary and the backup path utilizing PICR

Full size image

In Algorithm 1, any path is found as the cheapest one using any shortest path method (e.g. Dijkstra’s algorithm [12]). If the path cannot be found, routing of a given demand fails. Otherwise, the graph is temporally updated by removing the links used by the primary path. This is the first point in time when, based on the primary path details, the decision can be made about the routing. In case of shared protection, before finding the backup path, the free power load should be modified on edges where power sharing can be introduced (i.e., sharing the resources of the backup path currently to be established, and of the backup paths of previously established demands). After that, backup path is searched from the source to the destination node using the modified graph. If the backup path can be found, then we have all needed information to either choose routing of the demand in all-optical way (i.e., with PICR), or without it. However, if there is no possibility to find the backup path, or the decision is such that the demand should not be routed with PICR, all the previous modifications should be reverted. If a path exists and the demand should be routed according to it, the power and bandwidth are allocated accordingly.

In case the backup path cannot be found, another option would be to select a longer primary path, and then try again to find the corresponding backup path. However, this would increase the total used power, and, owing to the greater length of the primary path, also increase the possibility of a failure. Therefore, such an option is not considered in this paper.

In Algorithm 1, we assume the existence of a method to generate a path that complies with PICR rules. Details of this method are further explained in Algorithm 2 presenting an additional search loop to the Dijkstra’s method. According to Algorithm 1, the first task is to find the shortest possible path between a given pair of nodes. If network resources are sufficient to find the path, the loop terminates and the respective result is returned. However, violation of any existing power constraint implies the need to find another path in a network with one of the edges removed (i.e., for which the total power exceeds the maximum allowed limit). The search loop is terminated when a feasible solution is found, or there is no further possibility to find a proper path. Since at the end of every iteration the search is either finished with success, or an edge is removed from the graph, in the worst possible case, execution of Algorithm 2 ends after all the edges are removed.

Algorithm 2
figure 4

Steps to find a path with PICR

Full size image

3.2 Proposed filtering methods

In Sect. 3.1, we assumed that the decision whether to route a given demand with PICR or without it, can be made by the network operator when either the primary, or when both the primary and the backup paths are calculated. For this purpose, the following information can be considered:

  • distance between source and destination nodes,

  • path,

  • power,

  • length of the paths.

It is worth noting that the distance between the source and the target is always smaller or equal to the length of the shortest possible path. In case of our PICR technique, power is the function of the length of the path. Thus, in this paper we will not consider the distance between the source and the target, and the power as filtering options.

In [9], we have demonstrated that in case of PICR, Traffic Engineering resulting in modifications of the path based on the already reserved power, should not be used. This is because the method may increase the path length of the demand, which in turn increases the power consumption, as well as decreases the number of routeable demands. Therefore, direct interaction of paths of different demands will be not analyzed in this paper. Instead, only the following aspects of primary and backup paths are considered here:

  • path lengths themselves,

  • ratio of the backup and the primary path length.

The maximum path length is limited in case of PICR by default. This length can be obtained based on the properties of the network and the needed level of Quality of Service (QoS). In our simulations, we assumed the maximum path length of 1000 km, see Sect. 2.1. According to our proposition, operators should not route any demand in all-optical way if the length of its backup or primary path exceeds a given value.

Figure 3 shows the idea behind our second proposition—i.e., limitation of ratio of the backup and primary paths length. Usually, when finding paths of a demand between distant nodes, the length of a backup path is similar to the length of the primary path. However, this is not true, if end nodes of a demand are located close to each other. In such scenario, backup paths are much longer than the corresponding primary paths. To include these characteristics into our proposal, we introduced another condition: if the ratio of backup and primary path length is smaller than a given value, the demand should not be routed with PICR—this way we tried to introduce an indirect path length limitation. To investigate this idea in our simulations we tried out three different numbers as limitations of the backup path and the primary path: 1.0625, 1.125, 1.25.

Fig. 3
figure 5

Behavior of the ratio of the length of the backup path and the primary path. Primary paths are shown with solid lines, while backup paths are in broken lines. Length of every edge is 1. Demand D1 goes from N1 to N3. Ratio of the length of the backup and the primary path is 1.5. Demand D2 goes from N4 to N5. Ratio of the length of the backup and the primary path is 2

Full size image

4 Results

A simulator was implemented including both filtering methods to perform extensive simulations of characteristics of the two proposed methods. We supposed that P mW was set to 20 mW, while L max was equal to 1000 km (see Sect. 2.1). Heavy dynamic traffic was inserted into the Cost266BT [17] network (average link length: 426 km, diameter: 5061 km), while its size was scaled down using multiplier values from range (0, 1]. During simulations, we observed that if the network is scaled down by 0.0625, around 80 random demands could be routed with protection without blocking. Thus, in our simulations, the size of a demand set was each time a multiple of 80 on average. For each demand, its end nodes were chosen randomly. We assumed that each demand requires full capacity of a wavelength. During simulations, we cyclically analyzed the number of demands routed with PICR. In each simulation window, at least 10000 demands entered and left the network. The sources and the destinations of these demands were generated with uniform distribution, the holding time followed exponential distribution.

4.1 Routing results for ratio-based selection approach

Simulation results prove that path length ratio based limitations should not be applied with dedicated protection, see Figs. 4(a), 4(c), and 4(e). This remark complies with our former observations presented in [10], showing the performance comparison of pure dedicated and shared protection for PICR. In particular, in that paper we noticed that shared protection technique obtains the worst results, since it allows routing of long demands. Therefore, the ratio-based selection approach is not able to improve the performance of dedicated protection significantly by eliminating demands with relatively short backup paths.

Fig. 4
figure 6

Results for backup and primary path length ratio-based selection if the number of demands is significantly higher than the number of demands routeable by PICR. The average results are presented together with 95 % confidence intervals

Full size image

Figures 5(b), 5(d), and 5(f) show that the ratio-based selection can be useful for medium-sized networks. In this case, by using the proposed filtering algorithm, the number of routeable demands is improved by 3 % on average. However, with the decrease of the network load, the beneficial properties of this method slowly disappear.

Fig. 5
figure 7

Results for path length based selection if the number of demands is significantly higher than the number of demands routeable by PICR. The average results are presented together with 95 % confidence intervals

Full size image

To conclude, we suggest to use ratio-based limitation approach only with shared protection and quite large traffic compared to the amount of traffic routable only with PICR.

4.2 Routing results for path length based approach

Length-based filtering method performs well for small- or medium-sized networks if the number of inserted demands is higher than what is routeable exclusively with PICR, see Fig. 5. In case of dedicated protection and relatively low traffic, path length based filtering does not improve the number of routeable demands significantly for the same reason the ratio-based approach failed, see Figs. 5(a), 5(c), and 5(e). Our method performs quite well in case of shared protection. Results show that in some cases, the number of routed demands was increased by up to 10 %.

4.3 Dynamic analyses

In Fig. 6, we show how the number of routeable demands varies with time. It can be observed that the amplitude of the number of routed demands is significantly higher for shared protection. This suggests that in case of shared protection there is a ‘building up’ phase, when nearly all demands are routed, including even a few demands between distant nodes. After this period the routed demands with distant source and target nodes block the routing of newly arrived demands, which generates a significant decrease phase. This phase ends after the long demands exit. This behavior confirms our previous observation that utilization of shared protection allows routing of longer demands and lowers the number of routeable demands in average as a consequence.

Fig. 6
figure 8

Change of the number of routed demands with time with different technologies if the number of demands is significantly higher than the number of demands routable by PICR

Full size image

Both methods are more stable (i.e., the difference between the highest and lowest number of demands is relatively smaller) in case of dedicated protection than in case of shared protection.

4.4 Summary of results

Simulation results showed that none of the proposed methods could increase the number of routed demands in case of large networks. This can be explained with the fact that in large networks, a few nodes can be traversed by a path without signal regeneration. Thus, in case of large networks, operators should route all the demands in all-optical way where a suitable path can be found, without utilizing any filtering method.

In most cases, path length limitation based approach outperforms the path length ratio-based one. The only case where path length ratio-based approach gives better solution refers to medium-size networks with shared protection. However, path length ratio-based approach is less sensitive to the misconfiguration of the parameters than the length based one—i.e. the difference between two significantly different settings within the same method is not that big in case of ratio based approach. The reason for this behavior is that path length based selection creates direct limitation, while the other one gives only a soft constraint.

It is clear that if edge power constraints of PICR are the dominant factor of the system—i.e., in small networks with dedicated protection applied—path length based limitation is a good choice. However, for demands with huge distances between nodes, it is better to avoid using any selection method. Lastly, if the network is of medium size, the use of path length ratio-based approach can be the most efficient.

Simulations also showed that in case of PICR, shared protection should not be used.

5 Conclusion

In this paper, we proposed two new strategies for selecting demands requiring protection for routing with PICR—based on the path lengths, and on the ratio of the backup and the primary path length, accordingly. Extensive simulations were made to evaluate our propositions considering shared and dedicated protection scenarios. They showed that in the case of PICR, dedicated protection should be used.

The general conclusion is that for small networks, selection of demands to be routed with PICR should be based on path lengths, and dedicated protection should be applied. However, for medium-sized networks, path length ratio with dedicated protection is the best choice. We have confirmed by simulations that the proposed methods are able to increase the number of demands with protection routed in all-optical way. However, none of the methods should be used if the traffic is not significantly higher than what can be routed solely with PICR.