Abstract
Alonzo Church proposed a powerful and elegant theory of sequences of functions and their arguments as surrogates for Russellian singular propositions and singular concepts. Church’s proposed theory accords with his Alternative (0), the strictest of his three competing criteria for strict synonymy. The currently popular objection to strict criteria like (0) on the basis of the Russell–Myhill antinomy is here rebutted. Russell–Myhill is not a problem specifically for Alternative (0); it is a refutation of unrestrained concept comprehension. Unrestricted comprehension is also inconsistent with facts about sets of properties. Criteria more lax than (0) are philosophically inadequate. In particular, the rival conception of propositions as classes of possible worlds is subject to a fatal philosophical collapse. It follows on that conception, given that each of us is fallible, that everyone believes everything. It is shown, however, that Church’s proposed theory is vulnerable under (0) to a version of Russell’s notorious Gray’s Elegy objection. Some amendments to Church’s proposal are proffered, including an amendment, first proposed in the author’s Frege’s Puzzle (1986), that addresses Russell’s objection. Church’s response (personal correspondence) is considered.
Avoid common mistakes on your manuscript.
1 I
A Russellian singular proposition is a proposition that concerns an object (at least one) by including that object itself as a component rather than a proxy or representation.Footnote 1 The singular proposition that three is odd is composed of three and the concept of being odd. Analogously, and more generally, a singular concept is a concept that is intrinsically relational with respect to a particular by including that particular as a component.Footnote 2 The concept the successor of two is a singular concept of three that is intrinsically relational with respect to two. A Russellian singular proposition may be regarded as a singular concept of one of the two truth-values, truth and falsehood. A Russellian propositional function is a function that assigns to a given particular object a singular proposition concerning that object. The propositional function of being odd assigns to an object x the singular proposition that x is odd. (The value of the function incorporates the concept of being odd rather than the propositional function itself.)
No one has shed more light on the theory of propositions, as the semantic contents of declarative sentences and the cognitive contents of belief and various other attitudes, than Alonzo Church. We here investigate Church’s underappreciated theory of surrogates for Russellian singular propositions and singular concepts. In the present section and the next two, we present significant considerations favoring the representation of singular propositions by means of ordered n-tuple avatars.
A property, concept, or proposition is impredicative iff it is defined by abstraction involving quantification over a totality of which it itself is a member. For example, the property of having at least one of Bertrand Russell’s most notable qualities is itself one of Russell’s most notable qualities. As is well known, impredicatively defined properties and concepts give rise to antinomies (paradoxes). Russell presented such an antinomy, now known as ‘the Russell–Myhill paradox’, in appendix B of his brilliant book Principles of Mathematics (1903). He there also suggested but dismissed a resolution, arguably by means of what is now known as ‘the ramified theory of types’, which invokes a stratification of propositions, of propositional functions, and of related intensional entities. Later in the first edition of their monumental masterpiece Principia Mathematica, Whitehead and Russell (1910, 1927, at *12) would endorse the ramified-type-theoretic resolution. Later still, Alfred Tarski employed stratification, albeit only of semantic predicates for a fixed formal language, to resolve semantic antinomies, like those of the Liar sentence and Kurt Grelling and Leonard Nelson’s deeply puzzling adjective ‘heterological’.
In his Logic of Sense and Denotation (LSD), Church developed rigorously a theory of propositions and of concepts more generally.Footnote 3 John Myhill demonstrated that Church’s initial formulation was open to Russell’s Principles appendix B antinomy (which Myhill discovered independently).Footnote 4 Church modified his initial formulation using stratification to obtain a consistent formulation of LSD. He later wrote:
If, following the early Russell, we hold that the object of an assertion or a belief is a proposition and then impose on propositions the strong conditions of identity which this requires, while at the same time undertaking to formulate a logic that will suffice for classical mathematics, we therefore find no alternative except ramified type theory with axioms of reducibility and with [appropriate additional] axioms. (Church, 1984, p. 521; cf. Church 1974, at pp. 149–151 and Church, 1993, p. 152.)
In LSD, Church proposed three principal rival criteria for strict synonymy, i.e., for sameness of semantic content: Alternatives (0), (1), and (2), numbered in order of decreasing strictness, or decreasing fine granularity of concepts and propositions—and not coincidentally, in order of decreasing plausibility.Footnote 5 According to Church’s intended understanding of Alternative (2), and his heuristic explication, on Alternative (2) expressions are strictly synonymous if they have the same free variables and are logically equivalent. In the special case of sentences and the propositions they express, according to Alternative (2), p = q iff ⊧(p ↔ q).Footnote 6 As intended, Alternative (2) effectively identifies the proposition expressed by a sentence ϕ with the class of logically possible worlds with respect to which ϕ is true. According to Alternative (1), expressions are strictly synonymous iff they have the same free variables and one is obtainable from the other by a sequence of applications of λ-conversion and replacement of a component by a strict synonym of the same type. Although an improvement over (2), like (2) this criterion deems the conjunction ‘Fa & Ga’ to be strictly synonymous with the subject-predicate sentence ‘(λx[Fx & Gx])a’. If proper names are Millian designators or “logically proper names” (I deem it all but certain that they are), then according to Alternative (1) ‘Hesperus is brighter than Phosphorus’, which might capture the content of someone’s rational belief, is strictly synonymous with ‘Venus is a thing brighter than itself’.Footnote 7
According to the strictest of the three competing criteria, Alternative (0), expressions are strictly synonymous iff they are “synonymously isomorphic”. A pair of expressions are synonymously isomorphic if they have the same free variables and one is obtainable from the other by a sequence of applications of: (i) alphabetic change of bound variable; (ii) replacements of a component expression of a given type (e.g., a predicate) by a strictly synonymous simple (non-compound) constant of that same type; and (iii) replacements of a component simple constant of a given type by a strictly synonymous expression (simple or compound) of that same type. According to Alternative (0), even sentences as close in meaning as ‘Romeo loves Juliet’ and ‘Juliet is loved by Romeo’ are not strictly synonymous.Footnote 8
2 II
Numerous prominent philosophers—including David Chalmers, M. J. Cresswell, Jaakko Hintikka, Frank Jackson, David Lewis, Richard Montague, Robert Stalnaker, and Timothy Williamson—conceive of a proposition quite differently: as a class of metaphysically possible worlds. On this conception, p = q iff □(p ↔ q) (See Footnote 6). This yields a fourth criterion for strict synonymy, according to which there is nothing more to the semantic content of an expression than its semantic intension, i.e., its associated function from metaphysically possible worlds to semantic extensions (e.g., to truth-values). Setting aside as irrelevant for the present purpose subtle issues about the logic of indexicals, the fourth criterion is even more lax than Alternative (2). Using Church’s system of classification in order of increasing laxness, the conception of content as mere semantic intension may be labelled ‘Alternative (3)’. On Alternative (3), expressions are strictly synonymous iff they are semantically co-intensional, i.e., iff they have the same free variables and under any assignment of values to variables they have the same semantic intension. Alternative (3) effectively replaces Alternative (2)’s classes of logically possible worlds with their subclasses of metaphysically possible worlds.Footnote 9
A goodly number of philosophers and logicians—including Harry Deutsch, Cian Dorr, Peter Fritz, Harvey Lederman, Gabriel Uzquiano, Timothy Williamson, and others—have urged rejection of a conception of propositions as composite entities structured in something like the manner of an ordered n-tuple of proposition-components.Footnote 10 They hold that antinomies of impredicativity like Russell–Myhill refute or otherwise discredit structured propositions. I deem this a quantum leap backward.
Impredicative definition of concepts, in contrast to extensions, is dubious business.Footnote 11 The Russell–Myhill test of a theory of propositions is consequently a deeply flawed tool. A facile resolution of the Russell–Myhill antinomy blames the contradiction on the fine granularity of propositions on conceptions like Church’s Alternative (0). That antinomies of impredicativity can be resolved instead by means of stratification has been known at least since Russell (1908). Both Russell and Church took propositions to be structured (at least sometimes). Both were well aware of Russell–Myhill. (Russell invented it. Church was stung by it.) Both resolved the antinomy through ramified type theory with axioms of reducibility. Dorr (2016, p. 64) summarily dismisses the ramified-type-theoretic option, claiming a “widespread consensus that this would be a major cost.” Echoing Dorr, Williamson dismisses Alternative (0), asserting that Alternative (3) “is the simpler and stronger framework.” Williamson goes further and provides an argument for the sake of heaven against the ramified-type-theoretic resolution.Footnote 12 He says,
the best view [of propositions] is the very coarse-grained one that propositions are simply sets of metaphysically possible worlds … All the other views introduce massive complications for very meagre rewards. … Russellian theories project the syntactic structure of sentences onto the language-independent entities they are supposed to express. As for a full-bloodedly fine-grained approach to individuating propositions, it turns out to be inconsistent, by what is known as the Russell–Myhill paradox. The best strategy is to work with simple, coarse-grained contents but, when merely cognitive differences matter, to deal with them openly, by explicitly referring to the vehicles of content, such as sentences, or sentences in contexts.Footnote 13
It must be noted in response that the facts about some things are complicated, sometimes very complicated. Seeking the truth and sorting through complications is laborious, to be sure, but for those who value truth the reward of having gotten things right is never meager, and the benefits of having avoided complexity, when they come at the cost of falsity, are ill-gotten gains. The Russellian holds that the proposition that three is odd has as its component elements three and oddness (including whatever components the latter has). In the name of theoretic elegance and simplicity, Williamson advocates exchanging three and oddness in the proposition with an uncountable infinity of unimaginably complex entities, possible worlds (See Footnote 9). He sees this move as furthering theoretic simplicity because it supposedly obviates the need for the sort of stratification that is characteristic of ramified type theory. Of course, equating propositions with classes of possible worlds does not eliminate antinomies of impredicativity. At a minimum one would need to replace properties and concepts, wherever antinomies threaten, with corresponding functions from uncountably many unimaginably complex entities to extensions. It is far from clear that this wholesale replacement follows the dictates of theoretic simplicity.
By contrast, the resources needed to resolve the Russell–Myhill antinomy are fairly meager. Much more importantly, they are plausible. An intuitively appropriate restriction on naïve concept comprehension in a suitable free higher-order intensional logic suffices without stratification to throw out the bath water without the baby.Footnote 14 Those who urge rejecting structured-proposition theory on the basis of Russell–Myhill hold that any restriction on naïve comprehension of concepts or properties is ad hoc.Footnote 15 On the contrary, unrestricted comprehension principles are routinely inconsistent, or inconsistent with the facts, often by way of theorems of first-order logic. As the case of ZF set theory illustrates, jettisoning naïve comprehension is not ad hoc. It is acknowledgment of reality. One must eschew whatever is logically inconsistent. That inconsistent comprehension principles must be weakened or replaced is equally true of such principles for sets and for properties, for propositions and for concepts.Footnote 16
Obliterating the internal structure of all intensional entities still does not eliminate the perils of impredicativity. Any entities that encode properties or concepts in the right way are fertile ground for antinomy if properties and concepts are proliferated impredicatively. Consider the antinomy about sets of properties. (Cf. Salmón, 2021.) Contradiction arises from the property R of being a set at least one element of which is a property that the set itself lacks. Its unit set, {R}, if it exists, both has and lacks R. Aside from principles of logic and set theory, the only assumptions involved in the antinomy are that R is a property and that every property has a unit set. The objection to structured-proposition theory on the basis of Russell–Myhill embraces the former assumption. The Russell–Myhill test of structured-proposition theory thereby involves a commitment to the existence of peculiar properties that are curiously barred by logic from membership in sets. Such is the way of the Russell–Myhill-test trap.
The case of sets provides for a telling rebuttal to objections to the theory of structured propositions on the basis of its supposed inconsistency owing to fine-granularity. Suppose one were to argue analogously that the orthodox rejection of unrestricted comprehension of naïve set theory is ad hoc. Instead it is held that for any class (or kind) F, without exception, {x | Fx}—the set of Fs—exists.Footnote 17 But the orthodox position is rejected that the membership of the set of Fs is comprised by all and only the Fs. The set of penguins exists, but penguins, it is held, are not the sort of thing that can be elements of sets. Instead the elements of the set of Fs are (let us suppose) exactly the possible worlds in which all of the actual Fs exist.Footnote 18 Here sets are the analogs of propositions, and phrases of the form ⌜the set of νs⌝, where ν is an English count noun, are the analogs of ‘that’-clauses (e.g., ‘that three is odd’). In particular, it may be claimed, just as the proposition that 2 + 3 = 5 does not have five as an immediate component—the proposition is as much about seventeen million or the Church-Turing thesis as it is about five—so the elements of the set of odd integers, since all integers exist necessarily, are all the possible worlds. Similarly, the elements of the set of even integers are all the possible worlds. By Extensionality, it is argued, the set of odd integers and the set of even integers are the same set. This fact is routinely missed but, it is held, only because people are misled by their adherence to the orthodox position that the elements of the set of Fs are the Fs.
In fact, the argument continues, it turns out that a full-bloodedly fine-grained approach to individuating sets in accordance with the orthodoxy is inconsistent! This is shown by the antinomy of sets of properties. According to the myth that the elements of the set of Fs are the Fs, R is the only element of the set of properties that are identical with R. This leads directly to the contradiction that {X | X = R} both has and lacks R. This antinomy, it is argued, constitutes a disproof of the orthodox position. The best strategy is to scrap the orthodoxy and to acknowledge that the set of odd integers and the set of even integers are the same set. That no odd integer is even is a merely mathematical fact. Such non-set facts are to be accounted for in terms of words like ‘odd’ and ‘even’, which differ in their application. Despite the two words having very same worlds in their semantic extension, it is argued, we apply ‘odd’ to three and not to two, ‘even’ to two and not to three. (Explanation of this curious fact is left as an exercise.) Disabused of the myth that the set of Fs has the Fs as its elements, Russell’s antinomy disappears. Contrary to popular opinion, it is argued, the set of sets that are not elements of themselves exists. But its elements are not the non-self-membered sets; instead they are possible worlds (at least the actual world). In particular, Russell’s set is a set of the very kind that it is the set of: not an element of itself. Thus, it is argued, naïve set comprehension is vindicated.
The most glaring weakness in this analog of the objection to structured propositions from Russell–Myhill is its spectacularly erroneous denial that the elements of the set of Fs include all and only the Fs. Far from being inconsistent, it is in fact analytic that the elements of the set of Fs (if such a set exists) are exactly the Fs. It is completely trivial that the set of Fs is the set whose elements are the Fs. The set of Fs is by definition or by stipulation the set whose elements are the Fs.Footnote 19 That very triviality is a highly relevant point of disanalogy. As the antinomy of property sets demonstrates, antinomies of impredicativity arise, and require resolution, with regard to entities that encode properties or concepts and for which resolution by coarse-grained individuation is foreclosed. However it is that the antinomy of property sets is correctly resolved, it is not by rejecting the orthodoxy that the set of Fs has the Fs as its elements. That is not a genuine option. Antinomies invoking impredicative properties or concepts thus do not provide a basis on which to challenge or to question the fine-grainedness of entities that encode properties and concepts as components or elements. The source of the relevant contradiction, and the antinomies’ correct resolution, lie elsewhere, viz., with unrestrained comprehension of properties or concepts. Any entities that appropriately encode properties or concepts—including sets of properties and including propositions that incorporate concepts (if any do)—will give rise to antinomies of impredicativity if suitable precautions are not taken in regard to comprehension. The mere presence of impredicativity antinomies presents no more challenge to the thesis that two, three, and five are all the numeric components of the proposition that 2 + 3 = 5 than they do to the truism that two, three, and five are all the elements of {2, 3, 5}. The alleged inelegance of stratification as a remedy does not militate against structured propositions any more than it militates against the stipulation that the set of penguins has penguins rather than possible worlds as elements. The alternative conception is not so much an alternate account of sets as it is a radical re-interpretation of the word ‘set’ and of the phrase ‘the set of Fs’. Something similar is true of Alternative (3) with regard to the word ‘proposition’ and ‘that’-clauses: (3) seriously misinterprets them.
The rejection of propositional structure because of Russell–Myhill is analogous to a purported refutation that invokes unrestricted set-theoretic comprehension to derive a contradiction from a contested hypothesis. Reliance on the inconsistent principle invalidates the purported refutation. The culprit responsible for Russell–Myhill is something that is common to both Russell–Myhill and the antinomy of property sets—something other than the composite structure of sets, which is certainly utterly guiltless.Footnote 20 Russell–Myhill is a genuine problem, but it is not a problem specifically for structured-proposition theory. It is a problem for a general theory of concepts, especially for an excessively permissive theory that places no constraint on concept comprehension in simple type theory. Stratification of such entities as properties and concepts is neither ad hoc nor inelegant nor massively complicated. Ramified type theory is intuitive, even satisfying. In fact, refusal to stratify is at best decidedly questionable (See Footnotes 4 and 11). As Russell (1910) and Whitehead and Russell (1910, introduction, chapter II, p. 56) astutely observed, Napoleon’s property of having all of the qualities of a great general is intuitively a further property of a great general, on a different level from first-level properties like those of being strategically brilliant, calculating, tactically ingenious, etc. Having all of the first-level qualities of a great general is a legitimate property, but it is not itself first-level; it is second-level. As Russell (1910) notes, the example of the second-level property of having all of the first-level qualities of a great general also supports at least some axioms of reducibility. Defining a second-level property by abstracting over first-level properties is clearly a legitimate operation. By contrast, the attempt to define a first-level property by abstracting over the very first-level properties of which it is supposed to be an instance smacks of the most vicious kind of circularity: circularity that inexorably leads to contradiction. To insist that having all of the qualities of a great general is just another property, exactly on a par with being tactically ingenious and the rest, is to be philosophically tone deaf, if not indeed stubborn. There is similarly something obviously suspicious about the putative unleveled property R. Not to put too fine a point on it, there is no such property. By contrast, there is nothing particularly fishy about the property of being a set of first-level properties at least one of which the set itself lacks. It is a second-level property, as kosher as any other. If the stratification resolution is deemed undesirable, that is not a legitimate reason to deny the composite structure of propositions, or of sets. It is a reason to seek an alternative account of concept comprehension.
3 III
Where one’s concerns are restricted to metaphysical modality, a concept’s modal intension—its associated function from metaphysically possible worlds to extensions—is the only aspect of the concept that matters. (A proposition’s modal intension is the characteristic or indicator function of the class of possible worlds in which the proposition is true.) However, the nature of propositions and concepts is in no way exhausted by their metaphysically modal characteristics. Propositions are the semantic contents of sentences. They are the objects we assert, deny, declare, announce, suggest, proclaim, insist upon, and the like. They are also objects to which we bear an array of attitudes: belief, disbelief, confidence, doubt, hope, fear, disgust, surprise, delight, resentment, wishing, and much more. (Some of these attitudes can also be directed non-propositionally.) Propositions are thus central to our mental life. Though they have modal attributes, they are not fundamentally metaphysically modal in nature. They are conceptual and cognitive.
Williamson says that strategically it is best to deal with “merely cognitive” differences (Williamson presumably means non-modal differences) among co-intensional sentences by explicitly referring to the sentences themselves instead of their semantic contents. Church’s arguments invoking the famous Church–Langford translation test demonstrate that the cognitive properties of propositions cannot be relegated in any straightforward manner to relations borne to the sentences that semantically express those propositions. The attribution ‘Jones believes that water is an element’ is not correctly analyzable or replaceable by ‘Jones acceptsL ‘Water is an element’’, for any of an extremely wide range of interpretations of ‘acceptsL’. In particular, it cannot be recast as ‘Jones takes ‘Water is an element’ to be trueL’ nor even as ‘ Jones believes the proposition expressed in L by ‘Water is an element’’.
The philosophical drawbacks of Alternative (3) by comparison with any of the more discriminating alternatives are genuinely massive, on the order of a supermassive black hole. Since Alternative (3) identifies distinct concepts that share exactly the same metaphysically modal characteristics, it should come as no surprise that the criterion has a number of unpalatable consequences in connection with non-modal aspects of expressions and propositions.Footnote 21 On that criterion’s conception of semantic content, any co-intensional expressions are ipso facto strictly synonymous. This includes expressions as unalike in meaning as ‘theorem of first-order logic’ and ‘valid formula of first-order logic’. In fact, on Alternative (3) proving theorems like Gödel’s completeness and incompleteness theorems would degenerate, without exception, into an exercise in merely demonstrating utter trivialities. On (3), there is only one necessary truth, so that the proposition that water is a chemical compound is the same thing as the proposition that arithmetic is not complete. According to this criterion, the sentence ‘Water is a compound’ expresses in English that gold is an element, and equally that eπi = −1.
The sentence ‘Water covers most of the Earth’s surface’ clearly differs in semantic content from the significantly stronger conjunction ‘Water covers most of the Earth’s surface and water is a chemical compound’. The differences in content are many: The latter is (propositionally) conjunctive in content; its left-hand conjunct alone is not. The latter specifies the chemical nature of water; the former does not. There is much more. Perhaps most telling, the latter entails that most of Earth’s surface is covered by a chemical compound; the former does not have this consequence. Yet each sentence is true with respect to the very same class of metaphysically possible worlds. Alternative (3) consequently deems the two sentences strictly synonymous, and thereby flies in the face of semantic reality. Even Alternative (2) respects the dictates of common sense on this score far better than Alternative (3) does.
Alternative (2) is entirely inadequate as a criterion for identity of propositions. In lectures on open problems in intensional logic at UCLA, Winter 1977, Church observed that Alternative (2) makes nonsense of the notion of logical proof, which is supposed to bring about and justify belief of q by demonstrating that it is a logical consequence of one’s prior beliefs p. For on Alternative (2), if p ⊧ q, then p = (p & q) = (q & p). Assuming that belief is closed under classical conjunction elimination—so that as a general principle, if a believes (q & p) then a believes q—it follows that on Alternative (2) belief is already closed under logical consequence.Footnote 22 As Scott Soames showed independently, assuming closure of belief under conjunction elimination, and assuming further that proper names are Millian designators, it follows on Alternative (3) that one who believes that ‘Hesperus’ designates Hesperus (in English) and that ‘Phosphorus’ designates Phosphorus thereby believes that ‘Hesperus’ and ‘Phosphorus’ co-designate.Footnote 23 Even without assuming Millianism, Church’s devastating objection to Alternative (2) generalizes into a fatal collapse of Alternative (3). On Alternative (3), if ◻(p → q) then p = (p & q), so that if a believes p, then a believes (p & q). Assuming that belief is closed under conjunction elimination, according to (3) the beliefs of each of us are also closed under metaphysical-modal entailment, i.e., if ◻(p → q) and a believes p, then a believes q. It follows that on (3), one who believes any contingent proposition thereby also believes every necessary truth (that water is a compound, that eπi = -1, that arithmetic is incomplete, etc.). Furthermore, on (3) there is also only one necessary falsehood, so that the propositions that water is an element and that arithmetic is complete are one and the same. According to (3), one who believes anything impossible—that water is an element, or that 1 + eπi ≥ 1, or that arithmetic is complete, or that London and Londres are different cities, etc.—thereby believes every proposition without exception, whether necessary, contingent, or impossible. Each of us who is fallible believes some impossible things of the form: Actually p. The steadfast advocate of Alternative (3) ultimately must deny the principle, which seems fundamental to the nature of belief, that if a believes (p & q) then a believes p.
It should be acknowledged that there are attitude-like relations toward classes of metaphysically possible worlds. For example, there is a notion of intension-belief, whereby a intension-believes a class of worlds K iff a believes some proposition p whose intension is K. This in turn yields an attenuated belief-like relation toward genuine propositions: a (3)-believes p iff a intension-believes the intension of p, i.e., iff a believes some proposition co-intensional with p. One who believes any necessary truth thereby (3)-believes every necessary truth; one who believes any necessary falsehood thereby (3)-believes every necessary falsehood. Unlike genuine belief, (3)-belief is not closed under conjunction elimination.
It is natural to suspect that the Alternative (3) theorist confuses the propositional attitudes with one or another of their attenuated counterparts.Footnote 24 More to the point, rejection of closure under conjunction elimination is tantamount to raising the price on proven defective goods. Alternative (3) entails that if ◻(p ↔ q) then one who believes p thereby believes q. It follows on (3) that Kripke’s Pierre (who believes that Londres is pretty but London is not) believes that pigs fly and London is not Londres. It also follows that one who believes that water is an element thereby believes that water is an element that runs uphill. It also follows that one who believes that water runs downhill thereby believes that water is a compound that runs downhill. Even in advance of invoking closure, these consequences are quite bad enough. Rather than making things better, adding in rejection of closure compounds the error, and to that extent makes matters worse.
Taking account of its various consequences, Alternative (3) is scarcely more credible than the obviously false claim that there are just two propositions—the Great Truth and the Great Falsehood—so that p = q iff (p ↔ q), and we all believe every proposition. (This is Alternative (5), as specified in Footnote 9.) Assuming closure under conjunction elimination, on (3) as well, everyone believes everything. Philosophical common sense demands a more reasonable conception of what we say and of how we process the world.
4 IV
As Church observed, it is evidently Alternative (0)—the strictest of his competing criteria—that comes closest to the facts about human cognition.Footnote 25 Alternative (0) is naturally fleshed out by representing propositions as ordered n-tuples. There have been multiple proposals (including one by the present author) for so representing Russellian singular propositions in particular. The most exact and elegant of these is one inspired by a proposal of Kazimierz Ajdukiewicz (1960) and (1967) as expounded by Church in a pair of unduly neglected papers, his “Intensionality and the Paradox of the Name Relation” (1989a) and its sequel “A Theory of the Meaning of Names” (1995).Footnote 26 Church’s principal proposal is designed to accord with Alternative (0). His systematic account of singular-proposition surrogates suggests a potential relative consistency proof for a variety of theories of singular propositions.Footnote 27 I propose here some amendments to Church’s proposed account.
Following Church, for illustration we shall consider a formal object language employing a standard notation in the simple theory of types, including the following:
the standard truth-functional sentential connectives: ‘~’, ‘→’, etc.
individual variables: ‘x’, ‘y’, ‘z’, etc.
individual constants: ‘a’, ‘b’, ‘c’, etc.
n-adic predicate constants: ‘F’, ‘G’, ‘H’, etc. (including the dyadic identity predicate ‘=’).
n-adic functor constants: ‘ƒ’, ‘ƒ′’, etc.
the operators ‘∀’ and ‘∃’.
the singulary-function-abstraction operator ‘λ’.
The operators ‘∀’ and ‘∃’ are treated not as variable-binding but as second-order predicate constants. Thus, each of ‘∀’ and ‘∃’ may be attached to the monadic predicate ‘F’ to form a well-formed formula (wff). The two second-order predicates are semantically correctly applied, respectively, to the characteristic (indicator) function of the class of all individuals, and to the characteristic functions of all and only non-empty classes of individuals. Aside from these second-order predicates, the object language is entirely first-order.
The language includes Church’s variable-binding operator, ‘λ’. Where ζα is a well-formed expression (wfe) of a type τ, the λ-abstract ⌜λαζα⌝ is a wfe of type (τ, ι), i.e., functions from individuals to objects of type τ. Its semantic extension, under an assignment σ of individuals as values for the variables, is the singulary function that assigns to any individual i the extension of ζα under the assignment σ′ that assigns i to α and is otherwise the same as σ. Aside from ‘λ’, the object language has no non-extensional operators. Compound expressions other than λ-abstracts result from application of function to argument. As in combinatory logic, juxtaposition between parentheses of a function expression and appropriate argument expressions indicates application of the function to those arguments, in that order. (Note that the parentheses enclose not only the argument expressions but the whole consisting of the function expression and its argument expressions, e.g. ‘(ƒxy)’ instead of ‘ƒ(xy)’. The reader is referred to Church’s “A Theory of the Meaning of Names” for further details.)
Lambda-abstraction provides the means to form compound predicates out of open formulas. Where ϕ is a wff and α is an individual variable, the construction ⌜∀αϕ⌝ abbreviates ⌜(∀λαϕ)⌝, and ⌜∃αϕ⌝ abbreviates ⌜(∃λαϕ)⌝. Every wfe is regarded as designating its semantic extension (where the extension of a predicate is a characteristic function of a class). The object language thus underwrites axioms of extensionality.Footnote 28
Each predicate, whether simple (non-compound) or a λ-abstract, is taken to be a function symbol. This makes for an elegant and highly systematic account of semantic-content surrogates, whereupon the content-surrogates of predicates are neither classes nor properties but functions. On the account Church considers, the semantic content-surrogate of a predicate of individuals is taken to be a Fregean Begriff, that is, a characteristic function from individuals to either truth or falsehood.Footnote 29 By contrast, and in accordance with semantic Russellianism, the semantic content (and the content-surrogate) of each simple (non-compound) individual constant (proper name), is taken to be simply the designatum.
Exploiting his notation for application of function to argument, Church succinctly summarizes his proposed account of the semantic content-surrogate of function application with the following words: “The method is simply that the notation ( ) for application of function to argument [i.e., any pair of parentheses] is replaced everywhere by the ordered-pair notation < > [angle brackets], without other change” (p. 72). Thus, for example, if ‘s’ is a functor for the successor function and ‘2’ is an individual constant for the number two, then the designatum of ‘(s2)’ is the number three, and whereas the semantic content-surrogate of ‘s’ is the successor function, and the semantic content-surrogate of ‘2’ is two, the semantic content-surrogate of ‘(s2)’ (and the semantic content-surrogate in English of ‘two’s successor’) is not three but the ordered pair of the successor function and two. The core idea of Church’s proposal for Alternative (0) is that the semantic content-surrogate of an expression consisting of an n-adic function symbol ξ together with its n attached argument expression-occurrences, is a concept surrogate, which is the ordered (n + 1)-tuple consisting of the semantic content-surrogate of ξ and the semantic content-surrogates of the argument expression-occurrences. The proposal extends straightforwardly to negations, conditionals, etc., and even to λ-abstracts.
The principal objective of the theory Church proposes is to construct concept surrogates (and as a special case, proposition surrogates) entirely out of semantic extensions in accordance with Alternative (0). Our objective here is somewhat different. It is to provide a systematic ontology of concept surrogates to underpin and support the philosophical insights of Millianism together with Alternative (0). From the present perspective, Church’s account has at least one very significant shortcoming. Supposing that every creature with a heart (“cordate”) is also a creature with a kidney (“renate”), and vice versa, Church’s account misrepresents the distinct propositions that Socrates is a cordate and that Socrates is a renate by means of the same proposition surrogate. In order to represent propositions by means of more discriminating surrogates, we shall depart from Church in a crucial respect. We retain the semantic Millianism/Russellianism of Church’s account in treating simple singular terms (proper names) differently from compound terms (definite descriptions), with the former functioning as what Russell called ‘logically proper names’. Church treats function symbols uniformly. We shall treat simple predicates somewhat differently from λ-abstracted predicates. We take the semantic content-surrogate of a simple predicate to be the relevant Russellian propositional function, i.e., the function from an appropriate sequence of one or more individuals to a singular proposition composed of those very individuals together with the concept actually semantically expressed by the predicate. The propositional functions corresponding to the concepts cordate and renate are distinct because the concepts themselves are distinct, despite their coincidence in extension.Footnote 30
This is a special case of a more general departure from Church. Following Church, and Frege before him, we postulate function concepts. A function concept is a conceptualization of a function. The successor function on the natural numbers can be conceptualized as that function which assigns to each natural number what comes immediately next in the progression of natural numbers. The same function can be conceptualized alternatively, e.g., as that function which assigns to each natural number the result of adding it to two, then subtracting one. These are two concepts of the same function. (In an alternative terminology, these are two functions-in-intension for the same function-in-extension.) We also postulate conceptual functions, on the model of a propositional function. A conceptual function is a function from suitable individuals to a singular concept composed of those individuals and a function concept. Propositional functions may be seen as conceptual functions to singular concepts of truth-values.
The semantic content-surrogate of any simple function symbol is its associated conceptual function. The content-surrogate with respect to an assignment σ of values to variables of a λ-abstract ⌜λαζα⌝, in contrast to a simple function symbol, is the function that assigns to any suitable value i for the variable α the content-surrogate of ζα under the value assignment σ′ that assigns i to α and is otherwise the same as σ. In this way, both simple function symbols and λ-abstracts take on conceptual-surrogate functions as their content-surrogate. In the case of a simple function symbol, the conceptual-surrogate function is a genuine conceptual function.
All other compound expressions are governed by a uniform rule of compositionality: The semantic content-surrogate of an expression consisting of an n-adic function symbol ξ, whether simple or a λ-abstract, together with its n attached argument expression-occurrences, is a Russellian concept surrogate, which is the ordered (n + 1)-tuple consisting of the semantic content-surrogate of ξ and the content-surrogates of the argument expression-occurrences. As a special case, the content-surrogate of a sentence is a proposition surrogate, which is a finite sequence of the content-surrogates of the component expressions. Singular concepts—and as a special case, atomic singular propositions—are thereby represented as ordered tuples.Footnote 31
As an illustration, if ‘s’ is a simple symbol for the successor function, then its semantic content-surrogate (and the content-surrogate of the English arithmetical functor ‘___’s successor’) is the particular conceptual function  that assigns to any natural number n, the singular concept n’s successor. The surrogate for two’s successor is then the ordered pair
that assigns to any natural number n, the singular concept n’s successor. The surrogate for two’s successor is then the ordered pair  . The surrogate captures the feature of the concept that it includes two as an immediate component. It nevertheless constitutes a significant departure from the account Church proposes. On that account, the semantic content-surrogate of ‘s’ is simply the successor function itself rather than a conceptual function. The conceptual function
. The surrogate captures the feature of the concept that it includes two as an immediate component. It nevertheless constitutes a significant departure from the account Church proposes. On that account, the semantic content-surrogate of ‘s’ is simply the successor function itself rather than a conceptual function. The conceptual function  is also distinct from the concept the successor of, just as the propositional function semantically assigned to the predicate ‘is odd’ is distinct from the concept of being odd. Let the English sentence ‘Two’s successor is odd’ be formalized by ‘(O(s2))’, where ‘O’ is a primitive predicate and ‘2’ a simple singular term. Its semantic content is then represented by the proposition surrogate
is also distinct from the concept the successor of, just as the propositional function semantically assigned to the predicate ‘is odd’ is distinct from the concept of being odd. Let the English sentence ‘Two’s successor is odd’ be formalized by ‘(O(s2))’, where ‘O’ is a primitive predicate and ‘2’ a simple singular term. Its semantic content is then represented by the proposition surrogate  where
where  is the propositional function associated with the predicate ‘O’ (and in English with ‘___ is odd’). The proposition surrogate captures the feature of the actual proposition that it includes two as a component (even if not an immediate component), by virtue of including the concept two’s successor.Footnote 32
is the propositional function associated with the predicate ‘O’ (and in English with ‘___ is odd’). The proposition surrogate captures the feature of the actual proposition that it includes two as a component (even if not an immediate component), by virtue of including the concept two’s successor.Footnote 32
Variable binding is restricted to function abstraction by means of ‘λ’. In conformity with the principle that each expression consisting of an n-adic function symbol attached to its n argument expression-occurrences is assigned the corresponding (n + 1)-tuple, the content-surrogate semantically assigned to the compound predicate ‘λx[(Fx) & (Gx)]’ is represented by the particular function  —where Κ is the propositional function expressed by the sentential connective ‘&’, ℱ is the propositional function expressed by ‘F’, and ℭ is the propositional function expressed by ‘G’. This is the propositional-surrogate function that assigns to any individual x the proposition surrogate
—where Κ is the propositional function expressed by the sentential connective ‘&’, ℱ is the propositional function expressed by ‘F’, and ℭ is the propositional function expressed by ‘G’. This is the propositional-surrogate function that assigns to any individual x the proposition surrogate  . The semantic content-surrogate assigned to ‘∀x[(Fx) → (Gx)]’ is < Π,
. The semantic content-surrogate assigned to ‘∀x[(Fx) → (Gx)]’ is < Π,  where Π is the second-order propositional function (function from first-order propositional functions to propositions) expressed by the universal quantifier ‘∀’ and C is the propositional function expressed by the connective ‘ → ’.Footnote 33
where Π is the second-order propositional function (function from first-order propositional functions to propositions) expressed by the universal quantifier ‘∀’ and C is the propositional function expressed by the connective ‘ → ’.Footnote 33
It is useful to contrast three things: the phenomena being represented; Church’s method of representation; and our present modification. The actual semantic content of any n-adic function symbol ξ, whether simple or a λ-abstract, is a function concept. Church takes the content-surrogate to be the n-ary function designated by ξ. In sharp contrast, we take it instead to be the associated n-ary conceptual-surrogate function. In general, our concept surrogates invoke conceptual-surrogate functions in lieu of function concepts and in lieu of the functions themselves. As a special case, proposition surrogates invoke propositional-surrogate functions. A predicate, whether simple or a λ-abstract, is simply a special case: Whereas its actual content is a Fregean characteristic-function concept, its content-surrogate is a Russellian propositional-surrogate function.
One very important feature of this theory of concept surrogates is that it distinguishes appropriately among the semantic contents of four logically equivalent sentences that express four different things according to Alternative (0) but all the same thing according to Alternatives (1) and (2):
-
i.
(Raa)
-
ii.
[λx(Rxa)a]
-
iii.
[λx(Rax)a]
-
iv.
[λx(Rxx)a].
Letting ‘a’ symbolize ‘Donald’ and ‘R’ symbolize ‘loves’ (of English), these sentences formalize, in turn: (i′) Donald loves Donald; (ii′) Donald is one who loves Donald; (iii′) Donald is one whom Donald loves; and (iv′) Donald is one who loves themself. Where L is the binary propositional function expressed in English by ‘loves’, the proposition surrogates assigned to these sentences are, respectively,: (i″) < L, Donald, Donald > ; (ii″) < λx < L, x, Donald > , Donald > ; (iii″) < λx < L, Donald, x > , Donald > ; and (iv″) < λx < L, x, x > , Donald > .Footnote 34
5 V
Notwithstanding its elegance, Church’s theory of concept surrogates under Alternative (0), both as here modified and without modification, might be vulnerable to a version of Russell’s infamous (albeit widely misunderstood) Gray’s Elegy objection.Footnote 35 The objection may be set out as follows.
Let English + be English supplemented with the caret ‘^’ as a mark of indirect-quotation. Indirect-quotation marks function like direct-quotation marks, except that whereas the result of enclosing an expression within direct-quotation marks designates (in the language in question) the enclosed expression itself, the result of enclosing an expression within indirect-quotation marks is a directly referential designator of the semantic content (in the relevant language) of the enclosed expression. The relationship between direct and indirect quotation is exhibited by the schema.
In English, ‘___’ semantically expresses ^___^.
For example, the English sentence ‘Snow is white’ semantically expresses the proposition ^Snow is white^. When enclosing a declarative sentence of English, indirect-quotation marks perform the same function in English as the ‘that’-clause forming operator: ‘Snow is white’ semantically expresses that snow is white. Indirect-quotation marks function exactly like the English ‘that’ operator, except that they are not restricted in their application to declarative English sentences and are instead applicable to any meaningful English expression.
We consider the following, which is a true sentence of both English and English+:
-
(1)
The Solar System’s center of mass is a point.
Where Σ is the Solar System, c is the conceptual function expressed in English by ‘the center of mass of’, and P is the propositional function expressed in English by ‘is a point’ (as applied to a point), the singular-concept surrogate that Church’s proposal as here modified assigns to ‘the Solar System’s center of mass’ under Alternative (0) is the ordered pair < c, Σ > , and the proposition surrogate that the proposal assigns to (1) is the ordered pair < P, < c, Σ > > .Footnote 36
We now contrast (1) with the following sentence of English+ :
-
(2)
^The Solar System’s center of mass^ is a point.
The English + sentences (1) and (2) are not synonymous. This is established by the fact that whereas (1) is true, (2) is false, since no concept (or concept surrogate) is a point. Yet on a Millian understanding of indirect quotation, (1) is the result of substituting a strict synonym for ‘^the Solar System’s center of mass^’ in (2). The singular proposition expressed by (2) thus appears to be the same ordered pair < P, < c, Σ > > . This is Russell’s Gray’s Elegy objection in a nutshell.
As Russell suggests, the point is also made by contrasting ‘Gray’s Elegy’s first line is a sentence’, which is true, with ‘^Gray’s Elegy’s first line^ is a sentence’, which is false.Footnote 37 Russell (who avoids a synthesis) concluded that any theory that assigns something—some unified thing like an ordered set—as semantic content to ‘the center of mass of the Solar System’ or to ‘the first line of Gray’s Elegy’ is incorrect.
A complication: The English words ‘is a point’ meaningfully attach to each of the terms ‘the Solar System’s center of mass’ and ‘^the Solar System’s center of mass^’—truly to the former, falsely to the latter. Church’s theory of types, together with his definition of angle-bracket notation (see Footnote 31), precludes an analogous situation in suitable formalizations of (1) and (2). Church’s proposal represents the otherwise univocal English predicate ‘is a point’ as ambiguous with regard to logical type. On Church’s type theory, there are different formalizations for the English predicate, a different one for each type of subject-term to which it is attached. One formalization is syntactically attachable to terms for individuals (including terms for points), i.e., to singular terms for things of type ι. That formalization is not syntactically attachable to terms like ‘ < c, Σ > ’. Another formalization is attachable (albeit falsely) to terms like ‘ < c, Σ > ’ but not to terms for individuals. This generates different propositional functions. There is first of all the propositional function P, which is defined for all and only individuals. Where κ is the type of the singular-concept surrogate < c, Σ > and τ is the type of the proposition surrogate about < c, Σ > that it is a point, there is another propositional function Pτκ, which is defined for all and only concept surrogates of type κ (and which yields a false proposition for each argument). The two formalizations of ‘is a point’ have different restricted ranges of meaningful application. Distinct proposition surrogates are thereby assigned to formalizations of (1) and (2), to wit, < P, < c, Σ > > and < Pτκ, < c, Σ > > , respectively. (Church’s original proposal unmodified does something exactly similar to this.)
While this appears to block the Gray’s Elegy objection, it does not entirely remove the problem. While Church’s type theory assigns distinct proposition surrogates to (1) and (2), the method still makes those sentences extremely close in semantic content. Notwithstanding their differing restricted ranges of meaningful application, each formalization of ‘is a point’ invokes a concept of being a point, and each is predicatively paired with the same concept surrogate (See Footnote 36). A strong trace of the Gray’s Elegy problem remains. The Gray’s Elegy objection does not point to any peculiarity with the philosopher’s (2). The singular-concept surrogate < c, Σ > hangs together because c is defined for Σ. Church’s formalized rendering of (2) combines its grammatical subject—an indirect quotation-name belonging to a particular type κ—with a predicate that meaningfully applies to objects of the very type κ. It thereby properly pairs the concept surrogate < c, Σ > with the propositional function Pτκ, yielding the falsehood about < c, Σ > that it is a point. The peculiarity is rather with the mundane and obviously true sentence (1). Church’s formalization of (1) combines its grammatical subject—a type ι formalization of ‘the Solar System’s center of mass’—with a predicate that meaningfully applies to things of the very type ι. It therewith pairs < c, Σ > with the propositional function P rather than with Pτκ. The resulting proposition surrogate < P, < c, Σ > > pairs < c, Σ > with the propositional function P rather than with Pτκ. This is a heterogeneous jumble. On Church’s usage, the propositional function P is defined for individuals, but not for concepts or their surrogates. It is defined for the Solar System’s center of mass, but not for < c, Σ > because of a clash of types. The difficulty is not that (2) expresses a falsehood. The difficulty rather is how it is that (1) manages to express a truth, given that the propositional function associated with its predicate is undefined for the concept surrogate associated with its subject-term.
Preempting the formulation of a problem is not the same thing as solving it. There are surely properties that differentiate between the center of mass of the Solar System and some concepts of it—properties like those of being a point and of being a concept. Just as surely there are properties that differentiate between the first line of Gray’s Elegy and some concepts of it. The first line of Gray’s Elegy is a sentence, not a concept; ^the first line of Gray’s Elegy^ is a concept, not a sentence. A suitably modified type theory will accommodate acknowledgment of this. Russell—one of the principal architects of type theory—evidently agreed, else he would not have seen his Gray’s Elegy objection as having any real force.
6 VI
I deem Russell’s Gray’s Elegy objection inconclusive. Church too was not persuaded. I sent him a letter (1989), dated October 17, 1989, setting out the problem and proposing my amendment to his theory to avoid the difficulty. He sent a response (1989c) handwritten in his unmistakable calligraphy.Footnote 38
Nov. 18, 1989
Dear Prof. Salmon,
In reply to your letter, and in consequence of my paper of which you have a manuscript copy, I think that advocates of direct denotation must now cut back their claims to the case of primitive names, including in particular all names introduced by what used to be called ostensive definition (or what some advocates of direct denotation now call dubbing). And indeed, at least some passages in your own writings seem to agree with this in advance.
…
Sincerely,
Alonzo Church
The paper to which Church refers is his “Intensionality and the Paradox of the Name Relation,” the last three paragraphs of which reject the theory of “direct denotation” (more commonly called direct reference) in light of the possibility of there being two individual constants with the same designatum but different senses. Church takes the pairs ‘Hesperus’/ ‘Phosphorus’ and ‘Dr. Jekyll’/’Mr. Hyde’ to be such cases.Footnote 39 I do not agree with Church, and did not then agree, that a name with an associated definite description—‘Dartmouth’, ‘Cape Town’, ‘Hesperus’, ‘Phosphorus’, ‘π’—cannot be a Millian direct designator. Indeed, such a name, since it is a name, must be Millian. I take Church to assert in his letter that the indirect quotations ‘^the Solar System’s the center of mass^’ and ‘^Gray’s Elegy’s first line^’ are not “primitive”—that is, they are verbally defined—and therefore they cannot be Millian designators. In Russell’s words, Church holds that concepts (and their surrogates) “cannot be got at except by means of denoting phrases,” i.e., they cannot be designated except by description. In effect, Church denies that there can be such a thing as a singular proposition about a concept.
Russell anticipated this reaction; indeed he correctly argued that the Fregean theory of sense and designation is committed to it. Russell also argued against this reaction—not completely successfully, but I think not completely unsuccessfully.Footnote 40 Still, a resolution is desirable that admits singular propositions about the contents of such expressions as ‘the center of mass of the Solar System’ and ‘the first line of Gray’s Elegy’ (See Footnote 33). I advocated such an alternative in Frege’s Puzzle (1986),Footnote 41 and I urged it upon Church in my 1989 letter. Church had read my book, but he did not accept the account I proposed for sentences like (1). I continue to believe that he should have.
The remedy I propose begins with a simple observation. The semantic content of a definite description interacts with the content of a predicate to form a proposition in a distinctive and significantly different way from a Millian designator. The content of a predicate combines with the designatum of a Millian designator as function to argument. Though there is not a significant grammatical difference in the case where the grammatical subject to the predicate is instead a definite description, the content of a predicate combines in a unique and special manner with that of a definite description occurring in subject position. In particular, the content of the description does not occur as an element or component (“constituent”) of the resulting proposition. The two contents occur not as function and argument but symbiotically, as mutual and co-equal sub-concepts of the proposition.
Consider the following sentences of supplemented English:
-
(3)
Two is prime
-
(4)
Two’s successor is prime
-
(5)
^Two’s successor^ is prime.
In (3) the semantic content of the predicate ‘is prime’ is in a certain sense attributed to the semantic content of a Millian designator ‘two’. Likewise in (5), the content of ‘is prime’ is attributed (falsely) to the content of the putative Millian designator ‘^two’s successor^’. By contrast, in (4) the content of ‘is prime’ instead collaborates with the content of the description ‘two’s successor’ to represent, in tandem, and is not in addition attributed to the description’s content.
Recall that we take the semantic content-surrogate of ‘two’s successor’ to be the concept surrogate  where
where  is the conceptual function expressed in English by the functor ‘___’s successor’. This concept surrogate is not a component of the English semantic content-surrogate of (4) in the way that two itself is a component of the semantic content-surrogate of (3). Whereas two is a concept-component of the proposition that two is prime, the concept two’s successor is instead a sub-concept of the proposition that two’s successor is prime—by analogy with the distinction between an element of a sequence and a sub-sequence. Employing concept surrogates, the distinction is not merely an analogy.
is the conceptual function expressed in English by the functor ‘___’s successor’. This concept surrogate is not a component of the English semantic content-surrogate of (4) in the way that two itself is a component of the semantic content-surrogate of (3). Whereas two is a concept-component of the proposition that two is prime, the concept two’s successor is instead a sub-concept of the proposition that two’s successor is prime—by analogy with the distinction between an element of a sequence and a sub-sequence. Employing concept surrogates, the distinction is not merely an analogy.
Whereas the proposition surrogate that is taken to be expressed by (3) is the ordered pair  where
where  is the propositional function expressed in English by ‘is prime’, the content-surrogate of (4) should be taken to be the ordered triple
is the propositional function expressed in English by ‘is prime’, the content-surrogate of (4) should be taken to be the ordered triple  as proposition surrogate rather than the ordered pair
as proposition surrogate rather than the ordered pair  . The latter is also a proposition surrogate. It is semantically expressed not by (4) but by (5). The immediate components of the latter are
. The latter is also a proposition surrogate. It is semantically expressed not by (4) but by (5). The immediate components of the latter are  whereas
whereas  are all three co-equal components of the former.Footnote 42
are all three co-equal components of the former.Footnote 42
Notes
Throughout, in calling a theory or idea ‘Russellian’ I mean that it is inspired by Russell’s writings or is often associated with Russell, not necessarily that it is faithful to the historical Russell.
Cf. my (1981), at pp. 17–21, 54–55.
Myhill (1958). Myhill (1951) and (1979) also debunked the still widespread misconception—which Russell had already addressed (1908c, pp. 243–244)—that Whitehead and Russell’s version of ramified type theory, which incorporates axioms of reducibility, reinstates the very antinomies (like Russel–Myhill) that the theory was designed to resolve. Uzquiano (2022) purports to demonstrate that the combination of structured-proposition theory and ramified type theory together with axioms of reducibility is inconsistent. However, the proof relies (as Uzquiano recognizes) on a questionable logical tenet which structured-proposition theory with ramified type theory and reducibility per se does not include: roughly, that a predicate may be attached to an argument of a level different from the level for which the predicate is tailored. Uzquiano acknowledges (p. 1672) that the supposed refutation of structured-proposition theory “collapses if we impose the further requirement that the level of an allowable argument for a [predicate] variable should invariably be strictly lower than the level of that very variable.” This reasonable requirement constrains the logic—as ramified type theory is designed to do—and is intended in Whitehead and Russell’s logic. Importantly, the core theory survives unscathed even if liberalization of the logic leads to inconsistency. It is the permissive logic, rather than propositional structure, that is the most dubious element of the targeted package.
Church’s alternatives concern “strict synonymy” in the sense of sameness of semantic content, as distinct from sameness of meaning in a sense of ‘meaning’ on which the same semantic content may be expressed in different contexts by expressions that differ in meaning (e.g., ‘I’ and ‘he’). For some illuminating work on Church’s LSD, see Kaplan (1964) and Anderson (2001), at pp. 421–22. There is a valuable discussion of LSD and Church’s three alternative criteria for strict synonymy in Anderson (1998). I thank Anderson for bibliographical references.
Here the variables ‘p’ and ‘q’ range over propositions, ↔ is the relation of material equivalence between propositions, and ⊧ is a logical property of contents (rather than of their expressions). Cf. Frege’s letter of December 9, 1906 to Edmund Husserl, in Frege (1980), at pp. 70–71. See also Frege (1979) , pp. 143, 197.
See Salmón (2010).
Church (1954).
Church would have regarded Alternative (3) as a variant of (2). He writes, “(2) leads to notions of necessity and strict implication akin to those of [C. I.] Lewis.” There are even more lax criteria. According to one, which may be called ‘Alternative (4)’, expressions are strictly synonymous iff they are co-designative, so that designation is all there is to semantic content. This was Russell’s conception of “meaning” from “On Denoting” onward. Church considered an extreme criterion, which may be called ‘Alternative (5)’, on which expressions are strictly synonymous iff they are co-extensional. On this criterion, materially equivalent sentences are strictly synonymous. I know of no one who has endorsed this, although given Timothy Williamson’s arguments supporting Alternative (3) it is unclear why he does not instead endorse (5).
Alternative (3)’s conception of propositions as classes of possible worlds evidently precludes the competing conception, which is more natural, of possible worlds as classes of propositions. Alternative (3) thus needs an alternative account of possible worlds. It is difficult to envision a viable account that does not invoke entities like propositions under Alternative (0) or (1) (e.g., states of affairs).
See Dorr (2016), at pp. 63–64; Fairchild (2017), Fritz et al. (2021), Goodman (2017), McGee and Rayo (2000), Uzquiano (2015) and (2022), Williamson (2021a, 2021b, 2021c, 2021d). Hodes (2015) acknowledges that genuine antinomies of impredicativity potentially provide a legitimate basis for ramified type theory. Bacon (2023) proposes an alternative theory of structured propositions that evades Russel–Myhill.
Insofar as mathematical analysis employs impredicative definition of extensional entities (sets, classes, truth-values, functions-in-extension from such entities to such entities), but not of the corresponding properties or concepts, simple type theory suffices. (Whitehead & Russell, 1910, 1927, p. 14, credit Wittgenstein with a closely related observation.) See Footnote 4 above.
Williamson (2021b). The important work of Church and others on LSD (see especially notes 3 and 5 above) belies Williamson’s claim that “the intensionalist approach [Alternative (3)] has been far more systematically and fully developed than hyperintensionalist accounts [Alternatives (0)–(2)]”.
This is already strongly suggested (although not required) by Russell's avoidance of impredicatively defined propositional functions. The Russell–Myhill antinomy is not fully resolved by denying that there is a set of all propositions. There are variants of Russell–Myhill that do not require the purported universal set of propositions, at least not directly. Cf. Robertson Ishii and` Salmón (2020), Salmón (2021), and Salmón (forthcoming). The principal antinomy discussed there invokes a purported property defined by impredicative abstraction over propositions but does not straightforwardly invoke classes of propositions. (Hodes 2015 presents, at p. 386, what is effectively the same variant of Russell–Myhill).
Dorr (2016, p. 64) and Williamson (2021a, p. 315) also give a cardinality argument, misidentified with the Russell–Myhill antinomy, against (in effect) Alternative (0) with naïve unrestricted property comprehension. Church’s mature version of Alternative (0) is vulnerable neither to Russell–Myhill nor to the cardinality variant. The cardinality argument makes the false claim that “on such a plenitudinous theory of properties, there are more properties of propositions than propositions, for Cantorian reasons” (Williamson). Like the universe of all sets, the universe of all propositions is not a set. (Even on Alternative (3), the one necessary “proposition” is not a set.).
Cf. Robertson Ishii and Salmón at pp. 1558–1559, and Salmón (2024).
We here consider naïve comprehension in the form.
∃y[ y = {x|ϕx}],
where ϕx is any well-formed formula in which ‘y’ does not occur free and ‘{x | φx}’ designates the set of individuals (if such exists) that satisfy φx. The idea is that for any open formula φx, including the formula ‘x ∉ x’, the set of individuals that satisfy φx exists.
Other choices are possible. The envisaged position is quite radical.
The notation ⌜{α| ϕα}⌝ may be taken as shorthand for ⌜℩β[β is a set &∀α (α ∈ β↔ϕα)]⌝, where ‘℩’ is the definite-description operator and is the first variable other than that does not occur free in ϕα.
Compare Kripke (1979), at pp. 253–254.
While some of the untoward consequences to be noted are commonly known, most have not been noted before.
There are likewise notions of (0)-belief, (1)-belief, etc. toward propositions. See Footnote 9 above. We define ⌜(n)-believe⌝ so that if ⌜α believes that φ⌝ is true and φ is deemed synonymous with ψ on Alternative (n), then ⌜α (n)-believes that ψ⌝ is true. In particular, one (5)-believes a proposition p by believing some proposition q that is materially equivalent to p. Everyone who is fallible (5)-believes every proposition.
Church (1993), at p. 156n2. See also Salmón (2010), especially at p. 461. In (2021a) Williamson says of Alternative (0) that it judges it to be an error to describe someone who concludes that ‘∀x(Fx → Gx) as concluding that every F is G (p. 316). But ‘∀x(Fx → Gx)’ and ‘Every F is G’ are trivially equivalent. Even if the propositions that if something is F it is G and that every F is G are deemed distinct, someone who draws one of these conclusions normally also draws the other. It is a virtue of Alternative (0) that it distinguishes contents among logically equivalent but non-synonymous expressions. By contrast, Alternatives (2) and (3) are blind to differences of content among classically equivalent expressions.
More precisely, the theory to be amended Church proposes succinctly in a Footnote of (1989a), at p. 163n29.
Cf.Church (1989a), p. 158n21. Church also notes (p. 164n30) that using a language based on a set-theoretic instead of a type-theoretic approach requires restricting Russell’s comprehension principle for propositional functions. Some such restriction seems correct in any case. Not every open well-formed formula in one free variable determines a corresponding property. See Footnote 14. (In contrast to Williamson’s apparent claim that “a full-bloodedly fine-grained approach” is inconsistent, Whitehead and Russell’s ramified type theory with axioms of reducibility apparently yields a consistent fine-grained approach.).
With axioms of extensionality, there is no need to impose further restrictions on λ-conversion such as might otherwise be required to ensure validity and consistency. For a higher-order language in which sentences are regarded as designating propositions and predicates as designating properties or similar intensional entities, ramified type theory together with axioms of reducibility may be employed. Alternatively, the rule of λ-expansion could be restricted to abstracts ⌜(λαζα)⌝ that do not involve impredicative abstraction. Such a language requires a free higher-order logic insofar as some of its impredicative λ-abstracts fail to designate. See Footnote 14 above.
As Frege taught us, a proposition is a concept of a truth-value, in Church’s sense of ‘concept of’. A Fregean Begriff is effectively the characteristic function of a class.
It should be noted that a monadic-predication singular proposition is composed of an individual together with a concept, rather than the individual together with the relevant propositional function. Proposition surrogates are not propositions; they are surrogates.
In “A Theory of the Meaning of Names,” Church refers to the semantic values of monadic predicates as “propositional functions” (pp. 72–73). This is misleading. On the preceding page, he stipulates that those semantic values are singulary functions from individuals to truth-values—that is, Fregean characteristic functions rather than Russellian functions to propositions.
Church’s notation replaces ordered n-tuples with particular characteristic functions, with the result that a metalinguistic expression of the form ⌜ < α1, α2,…, αn > ⌝ (and therefore its designatum) is of a type that is uniquely determined by, and varies with, the types of the particular expressions α1, α2,…, αn, respectively. Thus, <α, β > and < γ, δ > are of the same type iff α and γ are of the same type and β and δ are of the same type. See “Intensionality,” at p. 159n22. Church’s usage deviates from the standard set-theoretic understanding of ordered pairs as individuals, i.e., as things of type ι. Church evidently sees the deviation as unimportant. Cf. p. 164n30.
Adding to the language a simple sentential operator ‘□’ for necessity is straightforward. Its semantic content-surrogate is the propositional function that assigns to any proposition p the proposition that p is a necessary truth. The proposition that p is necessary, in turn, is composed of the concept of necessity and p. However, adding operators on concept surrogates gives rise to known complications. If one wishes to add a simple sentential operator for being a surrogate of a necessary truth, while also allowing for iteration, the most straightforward extension of the present method utilizes a ramified type theory by introducing a hierarchy of operators: one for being a first-level proposition surrogate, one for being a second-level proposition surrogate, and so on.
The reader should consult Church’s papers cited in Footnote 26 for further details. The semantic content of ‘two’s successor’, represented here by the surrogate
 might be more accurately represented by < ι, λx < ℘, 2, x > > as concept surrogate, where ι is the conceptual function expressed in English by the definite article ‘the’ in the sense of ‘the sole ___’, and ℘ is the binary propositional function expressed in English by ‘___ immediately precedes ___’. The former is the function that assigns to any singulary propositional function the corresponding descriptive individual concept of the form the such-and-such. This alternative has the advantage that it represents the definite article, which is a determiner, as categorematic. (This involves a significant departure from the account Church proposes. On that account the English semantic content of ‘the’ is taken to be a function from extensional entities to individuals. See Footnote 30.).
might be more accurately represented by < ι, λx < ℘, 2, x > > as concept surrogate, where ι is the conceptual function expressed in English by the definite article ‘the’ in the sense of ‘the sole ___’, and ℘ is the binary propositional function expressed in English by ‘___ immediately precedes ___’. The former is the function that assigns to any singulary propositional function the corresponding descriptive individual concept of the form the such-and-such. This alternative has the advantage that it represents the definite article, which is a determiner, as categorematic. (This involves a significant departure from the account Church proposes. On that account the English semantic content of ‘the’ is taken to be a function from extensional entities to individuals. See Footnote 30.).Kit Fine (2007) argues that (i) is semantically ambiguous in English between the coordinated reading and the (allegedly less likely) uncoordinated reading. The alleged coordinated reading is very closely related to (iv). Interpreted in accordance with Alternative (0), however, (i) does not express the same thing in English as (iv). I critique Fine’s theory in (2012). See especially p. 411 and Sect. 4, at pp. 437–438. In particular the Church-Langford translation test establishes that (i) is not synonymous in English with (iv). See also the sequels (2015) and (2018).
I offer an interpretation and assessment of Russell’s Gray’s Elegy objection in (2005).
Cf. Church, “A Theory of the Meaning of Names,” at p. 73. Recall that Church’s use of angle-bracket notation deviates from the standard set-theoretic understanding. See Footnote 31 above.
The first line of Thomas Gray’s Elegy Written in a Country Churchyard is ‘The curfew tolls the knell of parting day’.
In my letter to Church, I pointed out that his type theory prevents a univocal formalization for the relevant English predicate, and that he could rely on this consideration in addressing the objection. In his reply Church made nothing of the consideration.
I maintain that ‘Jekyll’ and ‘Hyde’ are designative but not co-designative.
See “On Designating,” especially pp. 1102ff.
Frege’s Puzzle, Appendix C, pp. 143–151. Cf. semantic clauses 23, 24, 32, and 33, pp. 145–146. See also “On Designating,” Sect. 7, pp. 1116–1124, especially p. 1122.
For further details see the passages listed in the preceding footnote. The proposition surrogate expressed by (4) might be more accurately represented by
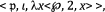 and the proposition surrogate expressed by (5) represented by
and the proposition surrogate expressed by (5) represented by 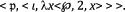 . Whereas the concept surrogate < ι, λx < ℘, 2, x>> is a concept-component of the latter, it is instead a sub-concept of the former.
. Whereas the concept surrogate < ι, λx < ℘, 2, x>> is a concept-component of the latter, it is instead a sub-concept of the former.
References
Ajdukiewicz, A. (1960). A Method of Eliminating Sentential Sentences and Sentential Formulae. Atti del XII Pongresso Internazionale di Filosofia: 5 Logica, Gonseologica, Filosofia della Scienza, Filosofia del Linguaggio (Sansoni Editor, Florence), pp. 17–24.
Ajdukiewicz K. (1967). Intensional expressions. David Pearce, trans, Studia Logica, 20, pp. 63–86. https://doi.org/10.1007/BF02340029; reprinted in Jerzy Giedymin, ed, The Scientific World-Perspective and Other Essays, 1931–1963, Synthese Library (Monographs on Epistemology, Logic, Methodology, Philosophy of Science, Sociology of Science and of Knowlegde, and on the Mathematical Methods of Social and Behavioral Sciences), 108 (Springer), pp. 320–361.
Anderson, C. A. (1998). Alonzo Church’s contributions to philosophy and intensional logic. The Bulletin of Symbolic Logic, IV, 2, 129–171.
Anderson, C. A. (2001). “Alternative (I*): A Criterion of Identity for Intensional Entities. In Anderson and Michael Zelëny, eds., Logic, Meaning and Computation: Essays in Memory of Alonzo Church (Kluwer), pp. 395–427.
Bacon, A. (2023). A theory of structured propositions. Philosophical Review, 132, 173–238.
Church, A. (1946). Abstract of a formulation of the logic of sense and denotation. Journal of Symbolic Logic, 1, 31.
Church, A. (1951). A formulation of the logic of sense and denotation. In P. Henle, H. Kallen, & S. Langer (Eds.), Structure, method and meaning: Essays in Honor of Henry M (pp. 3–24). Liberal Arts Press.
Church, A. (1954). Intensional Isomorphism and Identity of belief. Philosophical Studies, 5, 65–73.
Church, A. (1973). Outline of a revised formulation of the logic of sense and denotation. Part I, Noûs, VII, 1 (March 1973), pp. 24–33; Part II, Noûs, VIII, 2 (May 1974), pp. 135–56.
Church, A. (1977). Lectures on Open Problems in Intensional Logic, UCLA, Winter Quarter (January–March), unpublished, recorded by Nathan Salmón
Church, A. (1984). Russell’s theory of identity of propositions. Philosophia Naturalis, 21, 513–522.
Church, A. (1989a). Intensionality and the paradox of the name relation. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan (pp. 151–165). Oxford University Press.
Church, A. (1989b). Letter to Nathan Salmón, May 1
Church, A. (1989c). Letter to Nathan Salmón, November 18.
Church, A. (1993). A revised formulation of the logic of sense and denotation, alternative (1). Noûs, 2, 141–157.
Church, A. (1995). A theory of the meaning of names. In V. Sinisi & J. Woleński (Eds.), The heritage of Kazimierz Ajdukiewicz (pp. 69–74). Rodopi.
Church, A. (2019). The collected works of Alonzo Church, In T. Burge and H. Enderton (eds.) MIT Press.
Dorr, C. (2016). To be F is to be G. Philosophical Perspectives, 30(1), 39–134.
Fairchild, M. (2017). A paradox of matter and form. Thought, 6(1), 33–42.
Fine, K. (2007). Semantic relationism. Blackwell.
Frege, G. (1979). Posthumous writings, In H. Hermes, F. Kambartel, and F. Kaulbach, (eds.) University of Chicago Press.
Frege, G. (1980). Philosophical and mathematical correspondence, In Gabriel, H. Hermes, F. Kambartel, C. Thiel, and A. Veraart, (eds.) University of Chicago Press
Fritz, P., Lederman, H., & Uzquiano, G. (2021). Closed structure. Journal of Philosophical Logic, 50(6), 1249–1291.
Goodman, J. (2017). Reality is not structured. Analysis, 77(1), 43–53.
Hodes, H. (2015). Why ramify? Notre Dame Journal of Formal Logic, 56(2), 379–415.
Kaplan, D. (1964). Foundations of intensional logic, doctoral dissertation, University of California at Los Angeles
Kripke, S. (1979). A puzzle about belief. In A. Margalit (Ed.), Meaning and use (pp. 239–283). D. Reidel.
McGee, V., & Rayo, A. (2000). A puzzle about De Rebus belief. Analysis, 60(4), 297–299.
Myhill, J. (1951). Report on some investigations concerning the consistency of the axiom of reducibility. The Journal of Symbolic Logic, 16(1), 35–42.
Myhill, J. (1958). problems arising in the formalization of intensional logic. Logique Et Analyse Nouvelle Serie, 1(2), 74–83.
Myhill, J. (1979). A refutation of an unjustified attack on the axiom of reducibility. In G. W. Roberts (Ed.), Bertrand Russell memorial volume (pp. 81–90). Humanities Press Inc.
Robertson Ishii, T., & Salmon, N. (2020). Some highs and lows of hylomorphism: On a paradox about property abstraction. Philosophical Studies, 177(6), 1549–1563. https://doi.org/10.1007/s11098-019-01274-4
Russell, B. (1903). The principles of mathematics (pp. 523–528). Cambridge University Press.
Russell, B. (1908). Mathematical logic as based on the theory of types. American Journal of Mathematics, 30(3), 222–262. https://doi.org/10.2307/2369948
Russell, B. (1910). La théorie des types logiques. Revue De Métaphysique Et De Morale, 18, 263–301.
Salmón, N. (1981). Reference and essence. Prometheus Publishing.
Salmón, N. (1986). Frege’s puzzle. Ridgeview.
Salmón. N. (1989). Letter to Alonzo Church.
Salmón, N. (2010). Lambda in sentences with designators: An ode to complex predication. The Journal of Philosophy, CVII, 9, 445–468.
Salmón, N. (2012). Recurrence. Philosophical Studies, 159(3), 407–441.
Salmón, N. (2015). Recurrence again. Philosophical Studies, 172(2), 445–457.
Salmón, N. (2018). Cognition and recognition. Intercultural Pragmatics, 15(2), 213–235.
Salmón, N. (2021). A paradox about sets of properties. Synthese, 199, 12777–12793. https://doi.org/10.1007/s11229-021-03353-8
Salmón, N. (2014). Russell’s Law: An Ode to a Logical Theorem. In J. Almog and J. Pepp, (eds.) festschrift for David Kaplan. (Written in 2009, this item has been forthcoming since 2014).
Smith, P. (1972). Review of Kazimierz Ajdukiewicz, A method of eliminating sentential sentences and sentential formulae. Journal of Symbolic Logic, 37(1), 179–180.
Soames, S. (1985). Innocence lost. Linguistics and Philosophy, 8, 59–71.
Uzquiano, G. (2015). A neglected resolution of russell’s paradox of propositions. Review of Symbolic Logic, 8(2), 328–344.
Uzquiano, G. (2022). Ramified structure. Philosophical Studies, 180(5–6), 1651–1674.
Whitehead, A. N. Russell, B. (1910). Principia mathematica. Cambridge University Press.
Williamson, T. (2021a). Epistemological consequences of frege puzzles. Philosophical Topics, 49(2), 287–320.
Williamson, T. (2021b). Interview by Hasen Khudairi. Accessible online at https://www.academia.edu/48971322/Interview_with_Timothy_Williamson.
Williamson, T. (2021c). Metametaphysics and semantics. Talk presented to Università della Svizzera italiana, June 10, Accessible at https://fb.watch/63BNlcGiSO/.
Williamson, T. (2021d). Is hyperintensionalism good science?” Abstract of a talk presented to the University of St. Andrews Workshop on Hyperintensional Metaphysics (June 17). Accessible at https://www.st-andrews.ac.uk/arche/event/7288/.
Whitehead, A. N. Russell, B. (1927). Principia mathematica, second edition. Cambridge University Press.
Acknowledgements
This essay is dedicated to the memory of the great philosopher and logician, Alonzo Church. I had the good fortune to study under Prof. Church through the 1970s. Years later he read my Frege’s Puzzle (1986), in which I defend what is now called a Millian theory of semantic content. In May 1989, Prof. Church sent me a pair of manuscripts, then not yet published, in which he independently proposed similar ways of developing a theory of n–tuple surrogates for singular propositions. Church’s cover letter (1989b) began “Just to prove that great minds run in the same channel.” Although his throwaway remark did not reflect a genuine assessment—of me or of himself—it was exceedingly generous, and the memory of it can still cause me to blush. The present essay is in part a much delayed result of careful study of Church’s excellent papers. I am profoundly in his debt. The present essay encountered considerable intellectually improper resistance over several years. I am grateful to Otávio Bueno for his editorial integrity. I thank C. Anthony Anderson, David Braun, and especially Teresa Robertson Ishii for discussion, and anonymous reviewers for their helpful suggestions. Portions of this material were presented to the Pragmasofia International Conference in Pragmatics and Philosophy in Noto, Sicily in 2021 and to the National Autonomous University of Mexico (UNAM) in 2023. I thank my audiences for their participation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Salmón, N. Singular concepts. Synthese 204, 20 (2024). https://doi.org/10.1007/s11229-024-04624-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-024-04624-w


 might be more accurately represented by < ι, λx < ℘, 2, x > > as concept surrogate, where ι is the conceptual function expressed in English by the definite article ‘the’ in the sense of ‘the sole ___’, and ℘ is the binary propositional function expressed in English by ‘___ immediately precedes ___’. The former is the function that assigns to any singulary propositional function the corresponding descriptive individual concept of the form the such-and-such. This alternative has the advantage that it represents the definite article, which is a determiner, as categorematic. (This involves a significant departure from the account Church proposes. On that account the English semantic content of ‘the’ is taken to be a function from extensional entities to individuals. See Footnote
might be more accurately represented by < ι, λx < ℘, 2, x > > as concept surrogate, where ι is the conceptual function expressed in English by the definite article ‘the’ in the sense of ‘the sole ___’, and ℘ is the binary propositional function expressed in English by ‘___ immediately precedes ___’. The former is the function that assigns to any singulary propositional function the corresponding descriptive individual concept of the form the such-and-such. This alternative has the advantage that it represents the definite article, which is a determiner, as categorematic. (This involves a significant departure from the account Church proposes. On that account the English semantic content of ‘the’ is taken to be a function from extensional entities to individuals. See Footnote 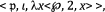 and the proposition surrogate expressed by (5) represented by
and the proposition surrogate expressed by (5) represented by 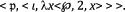 . Whereas the concept surrogate < ι, λx < ℘, 2, x>> is a concept-component of the latter, it is instead a sub-concept of the former.
. Whereas the concept surrogate < ι, λx < ℘, 2, x>> is a concept-component of the latter, it is instead a sub-concept of the former.