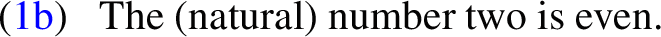Restricted nominalism about number and its problems

Abstract

Hofweber (Ontology and the ambitions of metaphysics, Oxford University Press, 2016) argues for a thesis he calls “internalism” with respect to natural number discourse: no expressions purporting to refer to natural numbers in fact refer, and no apparent quantification over natural numbers actually involves quantification over natural numbers as objects. He argues that while internalism leaves open the question of whether other kinds of abstracta exist, it precludes the existence of natural numbers, thus establishing what he calls “restricted nominalism” about natural numbers. We argue that Hofweber’s internalism fails to establish restricted nominalism. Not only is his primary argument for restricted nominalism invalid, the analysis of quantification proposed threatens to collapse internalism into either a traditional form of error theory or realism.

1 Introduction

What, if anything, do our linguistic practices tell us about the ontology of number?¹ In particular, do they support realism (numbers exist) or nominalism (numbers do not exist)?

There is a venerable philosophical tradition of providing semantic arguments for realism, tracing back to Frege (1884). Consider (1a,b):

A semantic argument for realism may be formulated as follows:

• (R1) If (1a,b) are true, then the underlined expressions in (1a,b) function referentially, referring to a number.

• (R2) (1a,b) are true.

• (RC) So, a number exists.

To be sure, the mere fact that the underlined expressions in (1a,b) function so as to refer does not ensure that they do so successfully. After all, the sentences may be false. But if (1a,b) are true, then the underlined expressions must refer, presumably to a number. In that case, realism follows.

A similar argument can be formulated involving non-referential expressions. Consider (2):

A variant of the original argument may be formulated as:

• (Q1) If (2) is true, then the underlined expression in (2) functions quantificationally, quantifying over a number.

• (Q2) (2) is true.

• (QC) So, a number exists.

Again, the mere fact that ‘some number’ functions so as to quantify over numbers does not ensure that it does so successfully. But if (2) is true, then it must quantify over a number. In which case, realism follows.

Of course, there are well-known nominalist responses to these arguments. Fictionalism maintains that apparent singular terms like those underlined in (1a,b) really are singular terms, and that quantificational expressions like those underlined in (2) really do quantify over numbers, but since there are no numbers, none of these sentences are true.² This imputes a general error theory to our numerical talk. From the nominalist’s vantage, this has the virtue of blocking the above arguments. However, it comes at an obvious prima facie cost: (1a,b) and (2) are paradigmatic truths. As such, it is at least prima facie undesirable to endorse a view that denies their truth.

An interesting alternative would be to hold that ordinary arithmetic statements like (1a,b) are true, and yet they do not commit speakers to the existence of numbers. The thesis is that (1a,b) and (2) are true despite surface semantic appearances, i.e. the underlined expressions in (1a,b) do not actually function referentially, and (2) does not actually quantify over numbers as objects. Following Hofweber (2016), we call this view internalism.

For a nominalist, internalism seems to have the virtues of blocking the semantic arguments for realism while maintaining consistency with the truth of (1) and (2). To that extent, internalism appears preferable to error theory. But it is one thing to assert internalism, quite another to substantiate it. The latter requires providing an empirically plausible semantics on which the underlined expressions function in the manner claimed, and that the resulting view is internally coherent.

To our knowledge, by far the most sustained, sophisticated attempt to develop internalism is that of (Hofweber, 2005, 2007, 2016, 2023). In view of this, we are inclined to treat Hofweber’s internalism as a kind of bellwether: reflection upon it can help in the assessment of internalism more generally.

Hofweber (2016) distinguishes two kinds of nominalist theses: unrestricted nominalism is the strong view that no abstracta whatsoever exist, while restricted nominalism proclaims only that putative abstract entities of a certain kind do not exist. He provides a sustained defense of restricted nominalism with respect to natural numbers, maintaining that his discussion leaves the status of unrestricted nominalism open.

As Hofweber notes, this combination of restricted nominalism and neutrality about unrestricted nominalism may seem strange, since the philosophical problems traditionally motivating nominalism seemingly apply to all abstracta. However, Hofweber’s case for restricted nominalism is different. It is to be established on the basis of empirical, linguistic considerations: “What matters primarily is to understand what we do when we talk about various things, and what is required for what we say to be true” (Hofweber, 2016, p. 290). Since, according to Hofweber, the best available semantics has it that we never successfully refer to numbers, numbers are not required to explain the truth of (2) and (2). In Hofweber’s words, such talk “is not about any objects, and consequently no objects are natural numbers” (Hofweber, 2016, p. 289).

We are skeptical of Hofweber’s pronouncements regarding the best available semantics for number talk.³ However, our primary focus here is on Hofweber’s internalism, and whether it succeeds in establishing restricted nominalism. We will argue that it does not, for two reasons. First, Hofweber’s primary argument for restricted nominalism, based on internalism, fails to establish its intended conclusion (Sect. 2). Not only is it invalid, with Hofweber’s attempts to preserve its validity falling short, one of its key premises is ambiguous, with neither available disambiguation supporting restricted nominalism. Secondly, the account of quantification underlying Hofweber’s internalism is problematic (Sect. 3). Specifically, it renders innumerable arithmetic statements, such as (1a,b) and (2), untrue, thus threatening a collapse into error theory. It also implies a commitment to an extensive array of abstract entities, including those which many realists identify with numbers, thus threatening a collapse into realism. After elucidating these problems for Hofweber’s internalism, we conclude by considering what lessons they may have for internalism more broadly (Sect. 4).

2 Internalism and the Simple Argument

In this section, we explain how Hofweber’s primary argument for internalism purports to establish restricted nominalism, and why it fails to do so. We begin by elaborating internalism, highlighting its two primary subtheses and explaining why, if correct, they would support restricted nominalism, without error (Sect. 2.1). We then articulate the primary argument for restricted nominalism in Hofweber (2016), namely what we call “the Simple Argument” (Sect. 2.2). After this, we formulate two kinds of challenges to the validity of the Simple Argument (Sect. 2.3). First, arguments of this form are generally invalid, and Hofweber’s attempt to exempt the Simple Argument from this charge is unsuccessful (Sects. 2.3.1, 2.3.2). Secondly, one of its key premises is ambiguous, and neither disambiguation of that premise ultimately supports restricted nominalism (Sect. 2.3.3).

2.1 Internalism

Internalism is the conjunction of two theses, the first of which is:

Non-referentiality: There are no expressions whose semantic function is to refer to numbers.⁴

Consider again the underlined expressions in (1a, b).

If Non-Referentiality is correct, then the truth of (1a,b) has no obvious implications for whether numbers exist. Thus, the main advantage of Non-Referentiality is that it may render the truth of arithmetic statements like (1a,b) consistent with restricted nominalism about numbers, without error.

However, there is also a significant theoretical cost. Very plausibly, the underlined expressions in (1a,b) belong to the same lexical category as those underlined in (3a,b) (Moltmann, 2013; Snyder, 2017).

Furthermore, on a standard formulation, compositionality requires a mapping from lexical categories to (a range of) semantic types (Partee, 1986). What’s more, the expressions in (3a,b) are paradigmatic singular terms, whose express semantic purpose is to refer (Partee, 1986). In which case, the expressions in (1a,b) are also singular terms, by compositionality. Thus, Non-Referentiality requires rejecting linguistic appearances, in at least one of three ways: (i) despite lexical appearances, the underlined expressions in (1) and (3) belong to different categories; (ii) despite semantic appearances, the underlined expressions in (3a,b) are not singular terms; or (iii) despite theoretical orthodoxy, natural language is not compositional, in this standard sense.⁵

The second thesis of internalism concerns determiners, such as ‘some’ in (2):

Non-Objectualism: Natural language determiners figuring in number discourse are generally interpreted substitutionally.⁶

In articulating Non-Objectualism, Hofweber (2016, Chap. 3) assumes a more general linguistic thesis concerning the interpretation of natural language determiners, namely:

Underspecification: All natural language determiners are semantically “underspecified” between two “readings”: an internal reading, and an external reading.⁷

These two “readings” correspond, respectively, to a familiar distinction between objectual and substitutional quantification. Roughly, on the former, ‘Something is F’ is true in a model if the domain contains at least one object satisfying F, while on the latter, it is true in a model if there is at least one term ‘t’ in the language such that ‘F(t)’ is true in that model. Hofweber’s view, then, is that natural language quantifiers are generally “underspecified” between these two interpretations. Or, quoting Hofweber (2016, p. 70):

I thus hold that quantifiers are polysemous, they have at least two different readings: one is the domain conditions reading, where they make a claim about the domain of objects in the world; the other is the inferential role reading, where they are inferentially related to their instances.

Of course, while it follows from Underspecification that quantifiers featuring in arithmetic discourse can be interpreted in these two ways, it does not follow that they should generally be interpreted substitutionally. Rather, this is due to the general failure of number words to refer, as Hofweber (2016, pp. 106–107) explains.

If number words in general are referring expressions, that is, if they are used by a speaker with the intention to pick out an object, then quantifiers in general can be expected to be used in their external reading. After all, if uses of number words like “five” are intended to pick out an object, then quantifiers like “every number” should be used to range over the domain of objects that the uses of number words aim to pick out. But on the other hand, if number words in general are not referring expressions, if they are not used with the aim to pick out an object, then quantifiers in general should not be expected to be used in their external reading.

Thus, Non-Objectualism is a natural consequence of Non-Referentialism, according to Hofweber.

Clearly, if Non-Objectualism is correct, then the truth of (2) does not imply the existence of a number.

Rather, that would follow only if (2) were objectually true. The proposed alternative is that (2) is substitutionally true in virtue of substituting English numerals, such as ‘two’ in (1a), for the predicates involved. Since these numerals fail to refer, by Non-Referentiality (1a) and (2) are both consistent with restricted nominalism about numbers, without error.

2.2 The Simple Argument

Suppose internalism is correct. This leads to Hofweber’s primary argument for restricted nominalism: the Simple Argument (Hofweber, 2016, p. 111).

The simple argument for a negative answer to the external question from the assumption of internalism is the following. If internalism is true about talk about natural numbers, then number words are non-referring expressions. Thus expressions like “2” or “the number 2” do not refer, in the broad sense, to anything. Thus none of the objects in the domain of our external quantifiers are referred to by these expressions. And thus none of them is the number 2. Since “the number 2” does not pick out or denote any object, whatever objects there may be, none of them is the number 2. So among all the objects, none of them is the number 2.

Let’s spell out the Simple Argument in more detail. By Non-Referentiality, no expressions purporting to refer to natural numbers actually refer, including those like ‘the number two’. Now, let ‘d’ be a name for an object in the domain of English quantifiers, interpreted objectually. Since identity statements equate the referents of singular terms, none of the sentences in (4) are true:

So, d is not the number one, or the number two, or ... However, the equivalence in (5) holds:

So (6) is thus true:

Generalizing, no object in the domain of English quantifiers is a natural number. Put differently, (7) is true, on an objectual interpretation:

And this is just a restatement of restricted nominalism: no objects are natural numbers.

As Hofweber (2016, p. 289) emphasizes, the Simple Argument has limited scope. Because the argument is formulated specifically for merely apparent singular terms like those in (1a,b), it implies nothing about the ontological status of other abstracta, including real numbers, sets, properties, etc. Indeed, according to Hofweber (2016, p. 113), the argument implies nothing about the ontological status of abstract objects which others have identified with natural numbers, such as sets or positions within an $\omega$-sequence.

To illustrate, suppose the domain of our quantifiers contains certain sets, and let ‘d’ in (4a) be a name of the singleton of the empty set: $\{\varnothing \}$. Since ‘the number one’ is non-referential, this instance of (4a) is not true. Likewise for every other sentence in (4) attempting to identify natural numbers with sets, or any other objects for that matter. Simply put, no such attempted identification of numbers can succeed, since the expressions purporting to pick out natural numbers do not refer, even if those purporting to pick out sets, positions within an $\omega$-sequence, etc. do.

In sum, the Simple Argument purports to establish restricted nominalism with respect to the natural numbers, while leaving the status of unrestricted nominalism unsettled. But does it succeed in this regard?

2.3 Problems for the Simple Argument

The Simple Argument is rather incredible, in that it purports to show that in virtue of our alleged failure to achieve genuine reference to numbers in natural language, we may infer a highly controversial ontological conclusion, namely that natural numbers do not exist. In this section, we argue that the Simple Argument fails to establish its intended conclusion, for two reasons. First, as Hofweber recognizes, arguments of this form are not generally valid—just because natural language fails to contain expressions successfully referring to some Fs, it does not follow that Fs do not exist. However, Hofweber’s attempt to “bridge the gap” between the Simple Argument and restricted nominalism is highly problematic. Secondly, one of the cornerstone theses of the Simple Argument—Non-Objectualism—is ambiguous, and neither potential disambiguation of the thesis supports restricted nominalism.

2.3.1 The non-sequitur objection

To appreciate the first problem, it suffices to observe that, plausibly, there are entities for which natural language cannot achieve successful reference to via singular terms, but whose existence we may otherwise have good reasons to accept. Within contemporary semantic theory, reference to particular individuals through paradigmatic singular terms, such as names (‘Mars’, ‘New York’), definite singular noun phrases (‘the planet Mars’, ‘that city’), or singular pronouns (‘(s)he’, ‘it’) (Partee, 1986), presupposes a notion of individuation (Grimm, 2018; Landman, 2020; Rothstein, 2017). The basic idea is that singular terms achieve reference to distinguishable entities, as exemplified in English by contrasts like (8a-c), involving count nouns such as ‘planet’ or ‘city’, and mass nouns such as ‘snow’ or ‘knowledge’.⁸

Within philosophical parlance, count nouns roughly correspond to what Frege (1884) calls sortal concepts, mass nouns to non-sortal concepts (Koslicki, 1997). On one influential characterization of this distinction, due to Hale and Wright (2001, Chap. 14), whereas sortal concepts have definite identity conditions, non-sortal concepts do not. The presumption is that only with sortal concepts can we say whether things falling under them are definitely identical or distinct.

With this in mind, consider subatomic particles, according to prevailing quantum theory. These fail to have definite identity conditions, in a fairly straightforward sense: as soon as we think we have picked out a particular subatomic particle having a definitive set of properties by using a singular term, there is no such thing having those properties. Accordingly, French and Krause (2006, p. 10) describe subatomic particles as non-individuals, since the notion of self-identity is apparently not well-defined for them:

[W]hat renders an object an individual object, what confers its fundamental ‘thisness’, is its identity with itself. We shall then defend the claim that the notion of non-individuality can be captured in the quantum context by formal systems in which self-identity is not always well defined.

Despite this, we are surely warranted in thinking that subatomic particles exist, as Hofweber (2016, p. 198) himself acknowledges.

Now consider entities residing outside our light cone. According to prevailing physical theory, at any point in time, we cannot causally interact with such an entity, at that time. Moreover, on the influential causal theory of reference, often associated with Kripke (1980), successful reference requires a causal connection between singular terms and their referents. If so, then at any point in time, we cannot successfully refer to entities outside our light cone, at that time, using singular terms. Yet, again, we are surely warranted in thinking such things exist. There are stars residing light years away, and have yet to be named, but could be named, for instance.

Finally, consider the case of mathematical entities. Certain (apparent) domains of some mathematical theories are too homogeneous for there to be reference to individual objects in them. For example, in Euclidean geometry, there is no way to refer to an individual point, since anything we might say about any given point holds of every other point.⁹ In other words, points fail to have definitive identity conditions. Accordingly, even if we augmented natural language with technical vocabulary and axioms of Euclidean geometry, successful reference to points, via singular terms, would not be achievable. Yet, it would surely beg the underlying metaphysical question to conclude, on this basis, that points in Euclidean space, or other geometric objects, do not exist.

Something similar may be said about basic arithmetic, regardless of the empirical viability of Non-Referentiality. Specifically, it is possible to formulate basic arithmetic without singular terms. One can just use a successor relation (or a predecessor relation), via the following axiomatization, which is equivalent to ordinary second-order Dedekind-Peano arithmetic:

• (A1) There is a number that is not a successor of any number.

• (A2) The successor relation is one-to-one in both arguments: every number has a unique successor (so that the successor relation is a function) and different numbers have different successors.

• (A3) For any predicate or property P, if P holds of every number that has no predecessor, and if, for any number n, if P holds of n then P holds of every successor of n, then P holds of all numbers.

Again, however, it would surely beg the question in favor of restricted nominalism to reject this axiomatization based on the alleged failure of number words in natural language to refer.

The upshot for the Simple Argument should be evident: In general, if a failure to achieve reference to purported entities of a given domain within natural language is not sufficient to warrant the conclusion that such entities do not exist, then the (alleged) failure to achieve reference to natural numbers within natural language does not warrant restricted nominalism.

The point generalizes: Just because a certain natural language fails to have genuine singular terms successfully referring to some Fs, it does not follow that Fs do not exist. It has been argued that in some natural languages, forming a name requires using the definite article (Matushansky, 2006). Suppose so, and suppose for argument’s sake that the only speakers of such a language, for whatever reason, failed to use the definite article when attempting to form names. In that case, if names were the only referential devices available, all attempts at referring within that language would be unsuccessful. Yet it clearly would not follow that some form of nihilism is correct—that anything these speakers attempt to reference, such as people, tables, or the language itself, does not exist. Simply put, the Simple Argument appears to be a non-sequitur.

Hofweber (2016, p. 112) is aware of this potential objection, of course:

There is a general worry about how the above argument could possibly be any good. After all, internalism is a thesis about language and its use. It is a position about what people do when they say certain things and what the semantic function of various expressions is. But how could a semantic and linguistic thesis like internalism imply a metaphysical thesis like the thesis that there are no natural numbers? It would seem that one could never bridge the gap between language and the world and draw conclusions about the latter simply from results about the former.

In response, Hofweber invokes Non-Referentiality: since number words are non-referential, we can know in advance that there is nothing they refer to. The situation is analogous to ‘nothing’, as Hofweber (ibid) explains:

Quantifiers are not referring expressions, they do something else, for example range over a domain of objects. “nothing” is such a quantifier. But suppose someone wanted to find out what The Nothing is, which, by definition, just is whatever object our phrase “nothing” refers to... We can conclude from semantic considerations alone that The Nothing does not exist. Since it, by definition, is whatever “nothing” refers to, and since we know that “nothing” is not a referring expression at all, but a quantifier, we can conclude that there is no such thing as The Nothing. We don’t have to look at all the objects and figure out whether any one of them is The Nothing. We can tell in advance that for any object o, o can’t be The Nothing since “nothing” doesn’t refer to o.

As Hofweber sees it, then, the Simple Argument is exempt from the above generalization because number expressions in natural language, like ‘nothing’, don’t even purport to function referentially.

There are two immediate problems with this response, however. First, as an empirical thesis, Non-Referentiality is highly dubious. In fact, on virtually all extant accounts of number expressions within linguistic semantics, ‘two’ in (1a) is a numeral, i.e. a name of a number, not a quantifier, and as such its semantic function is to refer (Snyder, 2021).¹⁰

Furthermore, the view that all occurrences of apparent numerals are really quantificational determiners makes numerous false semantic predictions (Rothstein, 2017; Snyder et al., 2022b). For example, it wrongly predicts that the pairs in (9a,b) and (10a,b) should be equally acceptable.

It also wrongly predicts that (11a,b) should be truth-conditionally equivalent.

Surely, then, the primary case for restricted nominalism should not rely so importantly on such a controversial, if not untenable, thesis.

Secondly, even if we were to grant Non-Referentiality, this would, at most, support a rather toothless form of restricted nominalism. By Hofweber’s own admission, English has expressions which at least purport to function referentially, in the form of names. Speaking of sentences like (12),

Hofweber (2016, p. 205) writes:

[W]e are entitled to take names to be at least broadly referential, certainly in many of their uses where they are in subject position. Reference is thus paradigmatically the relationship that holds between (certain uses of) proper names and objects.

Furthermore, it is important to Hofweber’s defense of the Simple Argument that number words never occur as names, since otherwise they, unlike ‘nothing’, would at least purport to function referentially.

However, while it is difficult to see why Hofweber would maintain that ‘Mike’ (12) is a name while ‘two’ in (1a) is a “quantifier”—due in no small part to a failure to provide or cite empirical criteria for distinguishing names from other lexical categories—the fact remains that so long as some expressions of English or other natural languages purport to refer, presumably we could employ those expressions to at least attempt reference to numbers. Clearly, it would be a rather Pyrrhic victory for restricted nominalism if, by chance, English did not contain genuine singular terms purporting to refer to numbers, but some other natural language did, or if no natural natural languages happen to actually contain such singular terms, but could, by extending the referential resources already available. In either case, Hofweber’s defense of the Simple Argument, by analogy to ‘nothing’, would collapse. In order to avoid this untoward consequence, Hofweber would thus need to argue for a much stronger thesis, namely:

Modal Non-Referentiality: No natural language could contain expressions whose semantic function is to refer to numbers.

Yet nothing in the Simple Argument or Hofweber’s pronouncements regarding the semantics of natural language would purport to establish this.

2.3.2 A dilemma for the Simple Argument

The second problem for the Simple Argument concerns an ambiguity in the formulation of internalism, which Hofweber (2016, pp. 107–108) describes as follows:

Internalism about a domain of discourse is the view that in general the singular terms in that domain are not referential, and that the quantifiers are in general used internally.

This is echoed in the formulation of Non-Objectualism given above:

Non-Objectualism: Natural language determiners figuring in number discourse are generally interpreted substitutionally.

Notice, however, that Non-Objectualism can be interpreted in two ways, depending on how one understands ‘generally’ (or ‘in general’). Specifically, there is a universal interpretation,

Universal Non-Objectualism: Natural language determiners figuring in number discourse are always interpreted substitutionally.

as well as a generic interpretation:

Generic Non-Objectualism: Natural language determiners figuring in number discourse are typically interpreted substitutionally.

The important difference between these two formulations is that whereas Generic Non-Objectualism tolerates exceptions—it would remain true even if some determiners figuring in number discourse are not interpreted substitutionally—Universal Non-Objectualism does not.

The problem for the Simple Argument is that neither interpretation of Non-Objectualism supports restricted nominalism. Consider first Universal Non-Objectualism, and recall that (7) is a restatement of restricted nominalism:

Thus, under present assumptions, (7) is true just in case there is no substitution of English number words satisfying the predicate ‘is a natural number’. Furthermore, according to Hofweber’s proposed semantics, (1a) is true in virtue of ‘two’ satisfying the predicate ‘is an even (natural) number’.

This is important, of course, because otherwise internalism threatens to collapse into error theory. However, (1a) clearly entails (13),

and so it too ought to be true. However, since this is inconsistent with the truth of (7), Universal Non-Objectualism undermines restricted nominalism.

Thus, suppose Generic Non-Objectualism is adopted instead. In that case, quantificational determiners involved in arithmetic discourse are usually, but not necessarily always, interpreted substitutionally. This seems to be the interpretation suggested by Hofweber (2016, pp. 106–107), repeated from above.

If number words in general are referring expressions, that is, if they are used by a speaker with the intention to pick out an object, then quantifiers in general can be expected to be used in their external reading... But on the other hand, if number words in general are not referring expressions, if they are not used with the aim to pick out an object, then quantifiers in general should not be expected to be used in their external reading

Given Non-Referentialism, number words are indeed generally non-referential, thus suggesting that quantification involved in numerical discourse ought to be generally interpreted substitutionally.

The obvious advantage of this interpretation is that it affords a way of rendering Non-Objectualism consistent with restricted nominalism, while maintaining the truth of statements like (1a). Specifically, it allows for the possibility that statements like (1a) and (13) are interpreted substitutionally, while others like (7) are interpreted objectually. The problem, however, is that Generic Non-Objectualism will not by itself guarantee that this is the case. It merely tolerates exceptions; it does not entail that there are exceptions, let alone that (7) is one of them. Yet, as we’ve seen, Non-Objectualism non-vacuously implies restricted nominalism only if this is the case.

Perhaps the problem is that we are conflating different kinds of “quantifiers”. Specifically, perhaps there are “quantifiers” like ‘two’, which at least appear to function as numerals, and other, more general purpose “quantifiers” like ‘nothing’, which do not. Thus, we read in Hofweber (Hofweber, 2016, p. 152):

Even when they appear in singular term position they are not referring expressions... Number words instead are determiners, modifiers, or adjectives. Number quantifiers generalize over the instances, although in certain cases not over all possible instances, but over the paradigmatic instances exemplified by the number words. Putting all those together we can see that internalism about talk about natural numbers is correct.

Perhaps, then, Non-Referentiality is only meant to support a more restricted version of Generic Non-Objectualism:

Restricted Generic Non-Objectualism: Typically, “number quantifiers” figuring in number discourse are interpreted substitutionally.

The trouble with this suggestion, however, is that insofar as it is possible to distinguish “number quantifiers” from other quantificational expressions, we can easily reformulate (7) using only the former.

By Hofweber (2016, Sect. 3.7)’s own semantics (see also Sect. 3.1), (7) and (14) are truth-conditionally equivalent: both are true just in case the set of things satisfying ‘is a natural number’, construed either as objects or as equivalence classes of expressions, is empty. So, if “number quantifiers” are generally interpreted substitutionally in number discourse, thanks to Non-Referentiality, then so is (14). And, again, this is inconsistent with the truth of (1a).

In summary, Non-Objectualism gives rise to a dilemma. It can be interpreted universally, in which case it undermines restricted nominalism. Alternatively, it can be interpreted generically, in which case there is no guarantee that (7) is interpreted objectually. Rather, if anything, it’s equivalence with (14) seemingly suggests that it too should be interpreted substitutionally. In either case, however, Non-Objectualism fails to support restricted nominalism.

3 The threat of collapse

So far, we have argued that Hofweber’s primary argument for restricted nominalism—the Simple Argument—fails to establish its intended conclusion. In this section, we argue that Hofweber’s internalism faces two additional challenges, owing to Hofweber’s analysis of quantification. The first is that it threatens to collapse into error theory. Rather than ensuring that ordinary, uncontroversial statements of basic arithmetic are true, as intended, Hofweber’s internalism instead renders innumerable such statements false. Secondly, it threatens to collapse into familiar forms of realism. Indeed, it is committed to the existence of an extensive array of abstract objects, including those which many prominent realists have identified with natural numbers.

We begin by sketching Hofweber’s analysis of quantification (Sect. 3.1). We then show that this semantics renders countless arithmetic statements false, thus threatening error theory (Sect. 3.2). After that, we explain why Hofweber’s semantics is committed to infinitely many abstracta (Sect. 3.3). Finally, we argue that this ontology is one which many realists about numbers characteristically endorse, thus threatening a collapse into realism (Sect. 3.4).

3.1 Hofweber’s analysis of quantification

We begin with an overview of Hofweber’s analysis of quantification, as sketched in Hofweber (2016, Sect. 3.7). As mentioned, key to Hofweber’s internalism is:

Underspecification: All natural language determiners are semantically “underspecified” between two “readings”: an internal reading, and an external reading.

This is reflected in Hofweber’s semantics. Specifically, he provides two corresponding interpretations of quantificational determiners. The first provides objectual interpretations, and is the predominant theory of natural language quantification within linguistic semantics, namely Generalized Quantifier Theory (GQT; Barwise and Cooper (1981)). According to GQT, determiners denote relations between sets, or predicate extensions. Accordingly, determiners take two predicates as arguments, and return a truth-value. For example, ‘some/a’ and ‘no’ receive the following denotations, where ‘$\llbracket \alpha \rrbracket$’ signifies the denotation of ‘$\alpha$’ (relative to a context, index, etc.).

Accordingly, ‘Some/An F is G’ is objectually true if at least one object in the domain satisfies both F and G, while ‘No F is G’ is objectually true if there is no such object. Similarly, ‘Something is an F’ is objectually true if at least one object satisfies F, and ‘Nothing is an F’ if no objects do.

Hofweber’s analysis of substitutional quantification is structurally similar. He begins with an equivalence relation on terms of a given language: say that $t_1$ is equivalent to $t_2$, in a given model M, if the sentence ‘$t_1=t_2$’ is true in M. If P is a predicate, then let $\bar{P}$ be the set of equivalence classes of terms t such that P(t) is true in M. That is, $\bar{P}$ is a set of sets. Substitutional denotations mirroring (15a,b) are then provided as follows (Hofweber, 2016, p. 100):

As before, determiners take two predicates as arguments. However, these now receive substitutional interpretations. For example, ‘Some F is G’ is substitutionally true if at least one term t is such that F(t) and G(t) are both true, while ‘No F is G’ is substitutionally true if there is no such term.

As highlighted in Sect. 2.1, Non-Objectualism plays a critical role in Hofweber’s defense of restricted nominalism. According to Hofweber (2016, p. 113):

Although internalism about number talk implies that there are no numbers, it leaves completely open that there are other things, even other things that some people thought are what numbers are: certain sets, or positions in an $\omega$-sequence, or classes of possible inscriptions of numerals, or what have you. Internalism about number talk does not rule the existence of any of these out, but it guarantees that our number talk is not about any of them, and that none of them are numbers.

Hofweber is making three claims here. First, internalism establishes restricted nominalism. Second, internalism leaves the status of unrestricted nominalism open. Third, although internalism is neutral with respect to whether certain abstracta exist, it implies that none of these are natural numbers. We have already challenged the first claim, via the Simple Argument. In the next section, we challenge it in a different way, via Hofweber’s analysis of quantification. In subsequent sections, we challenge the second claim, while also considering the implications for the third.

3.2 The threat of error

Recall the conclusion of the Simple Argument,

along with the infinitary:

Two points about Hofweber’s assumptions regarding (5) and (7) bear emphasizing. First, because determiners take predicates as arguments, ‘is a natural number’ has the semantic type of a predicate. That is, on either analysis of quantification sketched in Sect. 3.1, (7) is equivalent to (17), where ‘thing’ and ‘is a natural number’ are both arguments of the determiner ‘no’.

Second, (5) furnishes application conditions for ‘is a natural number’, and thus the required bridge between Non-Objectualism and the alleged truth of (7).

Now, consider a sentence of the form in (18).

Given the semantics in Sect. 3.1, a substitutional interpretation of ‘some’ requires that there is at least one term t satisfying both ‘is a natural number’ and F. Furthermore, by (5), t satisfies the former just in case at least one of the following disjuncts is true: ‘t is the number one or t is the number two or...’. Crucially, however, each disjunct contains a non-referring term, thanks to Non-Referentiality: ‘the number one’, ‘the number two’, etc. Since none of the disjuncts are true, it follows that any sentence of the form in (18) is substitutionally false, including e.g. those in (19).¹¹

For the same reason, all sentences having the form in (20) are substitutionally false, where ‘n’ is any apparent numeral or other singular term.

Thus, (1a) and (2) are actually substitutionally false,

as are countless other arithmetic statements having similar forms.

The obvious alternative is that we interpret the various quantifiers involved here objectually, along the lines of GQT. In that case, however, natural numbers exist objectually if any of these statements are true, thus undermining restricted nominalism.

The implications for Hofweber’s internalism are clear. Its chief purported advantage over error theory is that it promises to preserve the truth of arithmetic discourse, including statements like (19), (1a), and (2). However, if one accepts both Hofweber’s analysis of quantification and Non-Objectualism, this apparent advantage is lost. Yet without Non-Objectualism, no case for restricted nominalism remains.

3.3 Undermining unrestricted nominalism

As noted, Hofweber takes his position to leave “completely open” the question of whether unrestricted nominalism is true. However, this isn’t the case. As we’ll argue presently, if the analysis of quantification sketched in Sect. 3.1 is correct, then infinitely many—indeed, uncountably many—abstracta exist, in the form of sets.

A substitutional reading of the quantifiers has, of course, been raised before, and there is a substantial disagreement concerning how viable it can be as part of a defense of nominalism (Hand, 2007). We know of no treatment of the truth-conditions for sentences with a substitutional reading as detailed as Hofweber’s, so perhaps that can serve as a kind of bellwether for the whole program.

If F is a predicate, then let ‘Some(F)’ be an abbreviation of a sentence in the form ‘Something is F’. Hofweber (2016, p. 73) writes:

(SomeF) in its [substitutional] reading is truth conditionally equivalent to the disjunction of all the instances “F(t)” which imply it:

• (114) $F(t_1) \vee F(t_2) \vee F(t_3) \vee \dots$

...[By] an instance of (SomeF), we [mean] a sentence of the form “F(t)” where “t” [is] any term.

This, in combination with the fact that the available terms for natural numbers are countably infinite, implies

that the truth conditions of a quantified statement in its [substitutional] reading are equivalent to a disjunction (in case of the particular quantifier) or conjunction (in case of the universal one) of infinitely many instances. [ibid, p. 75]

To illustrate, consider (20).

According to Hofweber (2016, p. 150), “This sentence is truth conditionally equivalent, on its internal reading, to an infinitary conjunction where each conjunct contains an infinitary disjunction”, namely:

Of course, no one could speak or write down a sentence with infinitely many terms. Such sentences are described in the background metatheory, the framework in which the truth-conditions for the English sentences in question are given. As suggested in Sect. 3.1, this metatheory is a version of set theory.

One may question what is involved in using such a language. The quantifiers range over an uncountable totality—as formulated, there are $2^{\aleph _0}$ sentences in the envisioned infinitary language. Yet as Hofweber (2016, pp. 74–75) notes, there are at most countably many expressions in natural language.¹²

The most paradigm cases of a term alone guarantee that it will be infinite. We have, for example, in our language a term for every natural number (just regular arabic numerals would count), and we have terms like Mary, the mother of Mary, the mother of the mother of Mary, etc. But since our instances [of a substitutionally interpreted quantifier] are tied to our language and our language has a finite basic vocabulary, only countably many instances can be constructed.

Consequently, the quantifiers in the background set theory—those used to state truth-conditions—cannot have substitutional interpretations.¹³

In Hofweber’s semantics, equivalence classes are sets of sets. Moreover, many of these are infinite. For example, the terms ‘4’, ‘5-1’, ‘6-2’, ‘7-3’ ... are all coreferential, and so are in the same equivalence class with respect to identity. And there are infinitely many such equivalence classes, at least one for each natural number. So the envisioned metatheory has infinite sets of infinite sets.

Extending the substitutional semantics sketched in Sect. 3.1, Hofweber (2016, p. 100) suggests the following substitutional denotations, analogous to objectual interpretations assumed within GQT.¹⁴

Note that the ontology of the background set theory contains all finite cardinal numbers and at least one infinite cardinal, namely $\aleph _0$.¹⁵ Note also that the expressions occurring on the right-hand sides of (23a,b) are singular terms, since ‘$\ge$’ denotes a relation between entities, namely cardinalities.

Now, suppose (16) and (23) are correct. It then follows that some objects are sets. There are different ways of establishing this. One is to appeal to a familiar Quinean dictum: entities invoked by true theories exist, i.e. there are objects which are those entities. Presumably, Hofweber takes his semantics to be true. So there are objects which are the sets invoked. Alternatively, consider (24), which paraphrases (16a) in English.

Since (16a) is true, by hypothesis, so is (24). Yet the quantifiers involved (e.g. ‘any’ and ‘two’) can only be interpreted objectually. Hence, these same sets must be within the domain of English quantifiers. Clearly, then, unrestricted nominalism cannot be correct, from Hofweber’s perspective, at least not if sets are abstract objects, as typically assumed.

3.4 The threat of realism

Finally, we turn to Hofweber’s claim that even though internalism does not rule out the existence of abstracta, such as sets, it “guarantees” that none of them are natural numbers. To the contrary, we argue here that certain abstracta entailed by Hofweber’s analysis of quantification just are numbers, at least according to familiar forms of realism. Thus, absent some argument to the effect that these are not numbers, Hofweber’s internalism threatens to collapse into realism.

We have seen that Hofweber’s analysis of quantification is committed to a powerful background ontology of sets. As Hofweber (2016, p. 113) notes, on familiar forms of realism, not to mention the practice of set theory and other branches of mathematics, some of these sets are identified with natural numbers, as with familiar set-theoretic reductions discussed by Benacerraf (1965), as well as several highly influential philosophers (Dummett, 1991; Frege, 1884; Gödel, 1947; Hale & Wright, 2001; Quine, 1948; Russell, 1919). For all of these realists, then, Hofweber’s internalism does not leave “completely open” whether numbers exist. Rather, it entails that numbers exist.

Thus, in order to maintain that internalism does really leave open the question of whether numbers exist, it would appear that Hofweber must make the case that numbers, if they exist at all, are not any of the sets found within his semantic metatheory. However, Hofweber offers no such argument to this effect, and understandably so. After all, why engage with the question of what numbers are if they don’t actually exist, in light of restricted nominalism?

However, this is not the only familiar form of realism evoked by Hofweber’s analysis of quantification. We can see this by considering the consequence relation for the language in which Hofweber’s semantics is situated. The consequence relation for a formal language with substitutional quantification is of a piece with $\omega$-logic, a formal system which presupposes a structure isomorphic to the natural numbers. It is not strongly complete, nor is it compact (Dunn & Belnap, 1968; Shapiro, 1991, §9.1.2, §9.1.4). In this respect, substitutional readings are similar to weak second-order languages which have a quantifier ranging over finite sets or properties, a language with a quantifier ‘finitely many’ or ‘infinitely many’, and a language with a Fregean ancestral operator. All of these languages can characterize the natural numbers, up to isomorphism.

Consider why this does not occur in a first-order language whose quantifiers are construed objectually. The compactness theorem entails that any consistent set of sentences (construed objectually) that satisfies the usual axioms of arithmetic has a model whose domain has a member that is distinct from the referents of ‘0’, ‘1’, ‘2’, ...The first-order language can guarantee the truth of ‘0 is a number’, ‘1 is a number’, etc., but it cannot guarantee that those are all of the numbers. The additional resources of $\omega$-logic, weak-second order logic, and the like, as well as those of an infinitary language like ${\mathcal {L}}\omega _1\omega$, can guarantee this by, in effect, including something isomorphic to the natural numbers, or the correct notion of finitude, into the expressive resources.¹⁶

Something similar happens with the substitutional reading of the quantifiers. Recall that Hofweber constructs an equivalence relation on the terms of a given language: $t_1$ is equivalent to $t_2$ in a given model if ‘$t_1=t_2$’ is true in that model. The equivalence classes of terms are isomorphic to the natural numbers. In fact, each Arabic numeral occurs in exactly one such equivalence class. So like the other languages mentioned, the model theory for the substitutional quantifiers presupposes a structure isomorphic to the natural numbers. In fact, if understood with a substitutional reading, every truth in the language of arithmetic is a logical consequence of any set of sentences that includes all identities and non-identities of terms, i.e. sentences like ‘$6=6$’ and ‘$3^2 \ne 15$’. Like in the other cases, the reason is that the relevant structure—an $\omega$-sequence—is explicitly built into the model theory, and is presupposed in the understanding of the consequence relation.

Now, the essence of structuralism about the natural numbers, i.e. the view that they are places or positions within the natural number structure (Resnik, 1997; Shapiro, 1997), is nicely summarized by Benacerraf (1996): “any old $\omega$-sequence would do”. Specifically, all $\omega$-sequences are equally good candidates to play the role of the natural numbers, independent of what sorts of objects form such a sequence. From this perspective, any theory employing an $\omega$-sequence might as well be employing natural numbers, even if the objects forming that sequence are not explicitly identified with those numbers. Once again, for these structuralists, Hofweber’s internalism does not leave the question of realism “completely open”. And, again, it is understandable that Hofweber offers no arguments to the effect that these are not numbers.

So, how might Hofweber resist the charge that internalism collapses into realism? The obvious reply would appeal to the Simple Argument: since this establishes restricted nominalism, no matter what entities his internalism may be committed to, none of them are natural numbers. On the other hand, we have seen that endorsing the Simple Argument requires adopting an error theory with respect to much of our basic arithmetic discourse. It would thus appear that Hofweber’s internalism ultimately enjoys no clear theoretical advantage over traditional forms of error theory.

4 Conclusion

We have argued that Hofweber’s internalism faces serious theoretical challenges. First, Hofweber’s primary argument for restricted nominalism—the Simple Argument—fails to establish its intended conclusion. Furthermore, the analysis of quantification proposed threatens to collapse Hofweber’s internalism into a form of error theory or realism. Thus, absent some guarantee against these threats, it offers no obvious theoretical advantage over its primary rivals.

As emphasized in Sect. 1, because Hofweber’s internalism is by far the most developed version available, it is tempting to view it as a kind of test case for internalism more generally. And while the arguments here clearly do not purport to undermine all potential forms of internalism, there are general lessons to be drawn. We end by considering what we take to be the most significant.

Although the philosophical literature has tended to focus heavily on apparent numerals featuring in overtly arithmetic discourse (Snyder, 2021),

the fact is that there are numerous ways in which we purport to achieve reference to numbers in natural language. For example, we can also use a variety of singular definite noun phrases, as well as adjectival nominalization (Rothstein, 2017; Snyder, 2017).

And while some have denied on linguistic grounds that certain occurrences of apparent numerals are not genuine singular terms in specific kinds of constructions, such as ‘two’ in (25b) (e.g. Felka, 2014; Moltmann, 2013), it should be evident that this alone will not suffice as a general defense of internalism. Rather, maintaining internalism in full generality requires showing that all apparent reference to numbers is merely that: apparent. Even this is not enough to establish restricted nominalism, however, due to apparently true quantificational statements like (2).

Thus, an account of quantification on which the truth of (2) does not imply the existence of numbers is also required. What’s more, all of this should ideally be done in an empirically respectable way, one at least consistent with our best current linguistic theory. This is a very tall order, of course, and it is precisely for this reason that Hofweber’s internalism is so theoretically intriguing. Again, as far as we’re aware, it is the only extant attempt to defend internalism approaching the level of generality required.

To be sure, some of the challenges highlighted here target aspects of Hofweber’s specific formulation. For example, the Simple Argument is, to our knowledge, uniquely Hofweber’s, as is the analysis of quantification sketched in Sect. 3.1. Still, the challenges arising from these aspects of Hofweber’s internalism are illuminating. After all, any form of internalism must apparently link reference to quantification, so that the alleged general failure to refer to numbers goes hand-in-hand with an alleged general failure to quantify over a domain of those entities. But it is hard to see how else this link could be established, while simultaneously retaining the truth of basic arithmetic discourse, without holding that the domain of the quantifiers contains those expressions we purportedly use to refer to numbers. After all, what better candidates would be available, consistent with restricted nominalism?

The trouble, of course, is that not all quantification can be understood this way, since otherwise it would appear impossible to coherently state the desired ontological thesis, namely that no numbers exist. What’s more, this holds quite generally, independent of any specific empirical claims regarding e.g. the lexical category of of number words, or their particular semantic type. It is tempting, therefore, to conclude that any formulation of internalism with the required level of generality will ultimately face challenges similar to those formulated here.