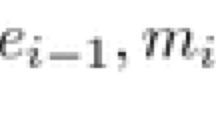An accuracy characterisation of approximate coherence

Abstract

Accuracy-first epistemologists argue that rational agents have probabilistically coherent credences. But why should we care, given that we can’t help being incoherent? A common answer: probabilistic coherence is an ideal to be approximated as best one can. De Bona (in: Philos Sci 84(2), 189–213, 2017) and Staffel (in: Unsettled thoughts: a theory of degrees of rationality, Oxford University Press, 2019) show how accuracy-firsters can spell out this answer by adopting an appropriate notion of approximate coherence. In this essay, I argue that De Bona and Staffel’s proposal is not entirely satisfactory, because it does not show whether, or why, it’s generally better to be more rather than less approximately coherent from an accuracy-first perspective. To address this point, I give a characterisation of their notion of approximate coherence in terms of accuracy. This shows that accuracy-firsters should maintain that more approximately coherent credences are better than less approximately coherent ones if and only if they accept that it’s better to miss out on less rather than more guaranteed accuracy.

1 Introduction

Accuracy-first epistemology is a philosophical programme which aims to justify principles of rationality by appealing to accuracy considerations. Philosophers working within this programme maintain that the primary epistemic value of credences is their accuracy, and seek to derive all other principles of rationality from this fundamental thesis. The centrepiece of the accuracy-first programme is its defence of Probabilism: the philosophical thesis that the credences of rational agents obey the probability axioms.

But Probabilism has long been criticised for being excessively idealised. For example, if an agent has any credence towards a logically true statement, the probability axioms require her to have maximal confidence in its truth, no matter how complex the statement. Clearly this goes well beyond the ability of any human reasoner. And if most humans, most of the time, cannot help being irrational according to Probabilism, why should we care about this standard of rationality?

One way to respond to this objection is to argue that, even for an agent who cannot have probabilistic credences, Probabilism serves as an ideal to be approximated as best one can. To build such a response, one needs to first specify a notion of approximate coherence, and then show that this notion is evaluatively meaningful, i.e. that there is some sense in which it is better to be more, rather than less, approximately coherent.

This essay looks at a recent proposal, due to De Bona and Staffel (2017), for a notion of approximate coherence that allows accuracy-firsters to pursue this response strategy. De Bona and Staffel introduce a measure of incoherence, and show that certain ways of reducing incoherence are epistemically beneficial. But it’s not clear whether, or why, accuracy-firsters should think it’s in general better to be less rather than more incoherent according to their notion.

To address this point, I will give a new characterisation of De Bona and Staffel’s incoherence measures in terms of accuracy. Informally, this shows that the degree of incoherence of a credence function is just the amount of guaranteed accuracy an agent misses out on by adopting that credence function. Therefore, accuracy-firsters should think that it is better to be more rather than less approximately coherent according to De Bona and Staffel’s measures if and only if they endorse the Graded Accuracy Dominance principle: the claim that agents who miss out on less guaranteed accuracy are in some sense epistemically better than those who miss out on more guaranteed accuracy.

I cannot provide a conclusive argument for or against Graded Accuracy Dominance in this essay. I will leave it for future work to determine whether this principle is justified, and thus, whether it is in general better to be more rather than less approximately coherent. However, I will at least sketch one possible way of motivating Graded Accuracy Dominance, showing that it can be derived by adapting an intuitive decision-theoretic assumption commonly made within the accuracy-first literature.

2 Ideal epistemology and non-ideal agents

This section introduces Probabilism and the accuracy argument used to support it. Then I look at the objection that Probabilism is inadequate as a norm or principle of rationality due to its excessively idealised nature. Finally, I outline one strategy for answering the objection, which motivates the introduction of a notion of approximate coherence.

2.1 Probabilism and the accuracy argument

Let’s start by introducing some notation. I will consider agents who have opinions towards some finite set ${\mathcal {F}}$ of sentences in a propositional language which includes all the usual connectives. We can capture these opinions by a credence function which assigns to each sentence in ${\mathcal {F}}$ a real number in [0, 1], representing the agent’s degree of belief in that sentence.¹ The set of all such functions is denoted by ${\mathcal {C}}_{\mathcal {F}}$. I will denote by ${\mathcal {W}}_{\mathcal {F}}$ the set of “possible worlds” corresponding to all the logically possible truth-value assignments for the sentences in ${\mathcal {F}}$. If $w \in {\mathcal {W}}_{\mathcal {F}}$ and $\phi \in {\mathcal {F}}$, then $w(\phi )$ is the truth-value of $\phi$ at w.²

Denote by ${\mathcal {F}}^*$ the smallest algebra containing ${\mathcal {F}}$. A credence function is coherent iff it can be extended to a probability function on ${\mathcal {F}}^*$. Many epistemologists maintain the following thesis:

• Probabilism: Rational agents have coherent credence functions.

Probabilism can be interpreted in two different ways. Some probabilists take coherence to be a norm of rationality, meaning that an agent with incoherent credences ought to have coherent ones instead. Others stop short of reading coherence as a norm, and instead take it to be merely a principle of rationality. According to this view, there is no general obligation for agents to have a coherent credence function. Instead, Probabilism is an evaluative claim: we can think of it as labelling all agents whose credence function is incoherent as irrational, because a rational agent would not have such credence function. In turn, this induces a labelling of credence functions: all incoherent credence functions are labelled as irrational, because they are not the kind of credence function a rational agent would have.³

One way to defend probabilism, first proposed by Joyce (1998), is known as the accuracy argument. While there are many variations of the argument, they all share the same structure.⁴ To run the argument, one starts by assuming that the only epistemic value of a credence function is its accuracy, a position known as veritism. The next step is to characterise a class of reasonable measures of inaccuracy for credence functions, which allow us to measure their epistemic value —intuitively, measuring how far a credence function is from the truth. Then one specifies an epistemic requirement of rationality, that is, a requirement of rationality for credence functions expressed in terms of their epistemic value. Because epistemic value is just accuracy, this will be equivalent to a requirement for credence functions expressed in terms of their accuracy. Finally, they prove an accuracy theorem: a mathematical theorem stating that, for any reasonable measure of inaccuracy, a credence function respects the accuracy requirement of rationality only if it is coherent.⁵

It’s worth going over these steps in some more detail, since some of these details will be relevant for my argument in later sections. Let’s start with a formulation of veritism:

• Veritism: The epistemic value of a credence function at a world w it its accuracy at world w.

To make this thesis precise, we need to specify a way to measure the inaccuracy of a credence function at a world. In this essay, I will consider the class of bounded, continuous, additive, and strictly proper measures of inaccuracy.⁶ To define them, first define a continuous, strictly proper scoring rule as a continuous function $s: [0,1] \times \{0,1\} \rightarrow {\mathbb {R}}$ such that, for any $p \in [0,1]$, the following function of x is uniquely maximised at $x = p$:

$$\begin{aligned} p s(x, 1) + (1-p) s(x, 0) \end{aligned}$$

(1)

Intuitively, the inaccuracy of having credence x in $\phi$ is given by s(x, 1) when $\phi$ is true, and by s(x, 0) when $\phi$ is false. Then, if p is your credence that $\phi$ is true and $(1 -p)$ your credence that $\phi$ is false, the expression in (1) is your expectation of the inaccuracy of having credence x in $\phi$. Thus, strict propriety requires that you expect your own credence to be the most accurate. The continuity assumption can be intuitively explained as requiring that, if we change a credence x by increasing it or decreasing it by some small amount $\epsilon$, the differences in inaccuracy $s(x + \epsilon , 0) - s(x, 0)$ and $s(x + \epsilon , 1) - s(x, 1)$ will also be small. Finally, s is bounded in the sense that for any $x \in [0,1]$ and $i \in \{0,1\}$, $s(x, i) \in {\mathbb {R}}$.

Continuous, additive, and strictly proper measures of inaccuracy are functions $S: {\mathcal {C}}_{\mathcal {F}}\times W_{\mathcal {F}}\rightarrow {\mathbb {R}}$ in the form:

$$\begin{aligned} S(c, w) = \sum _{\phi \in {\mathcal {F}}} s(c(\phi ), w(\phi )) \end{aligned}$$

(2)

where s is a (bounded) continuous, strictly proper scoring rule. So S(c, w) measures the inaccuracy of credence function c at world w by adding up all the scores $s(c(\theta ), w(\theta ))$ for $\theta \in {\mathcal {F}}$. These measures inherit the characteristic feature of proper scoring rules:

• Strict Propriety: If c is coherent, then for every $c' \ne c$, $\text {Exp}_c\left[ S(c, \cdot )\right] < \text {Exp}_{c}\left[ S(c', \cdot )\right]$. In other words, every coherent credence function expects itself to be the most accurate.

After specifying a class of reasonable measures of inaccuracy, we need to specify an epistemic requirement of rationality. Here is a popular candidate:

• No Dominance: A rational agent’s credence function is not guaranteed to be epistemically worse than some other credence function.

Since we are identifying the epistemic value of a credence function at a world with its accuracy at that world, c is guaranteed to be epistemically worse than $c'$ iff c is less accurate than $c'$ at every possible world. Using our measures of inaccuracy, c is guaranteed to be epistemically worse than $c'$ iff:

$$\begin{aligned} S(c, w) > S(c', w) \text { for every } w \in {\mathcal {W}}_{\mathcal {F}}. \end{aligned}$$

(3)

When this is the case, we say that c is accuracy-dominated by $c'$. So if we accept Veritism, No Dominance can be rewritten in accuracy terms as follows:

• No Accuracy Dominance: A rational agent’s credence function is not accuracy-dominated by some alternative credence function.

Finally, we give an accuracy theorem. It can be shown that, when inaccuracy is measured by a continuous, additive, and strictly proper measure, any incoherent credence function is accuracy-dominated by a coherent one, whereas no coherent credence function is accuracy-dominated.

• Accuracy Theorem⁷: Let S be a continuous, additive, strictly proper measure of inaccuracy, and let $c: {\mathcal {F}}\rightarrow [0,1]$ a credence function. If c is incoherent, then there is some coherent $c': {\mathcal {F}}\rightarrow [0,1]$ which accuracy-dominates c. If c is coherent, then it is not accuracy-dominated by any alternative credence function on the same domain.

Putting everything together, we get the following argument for Probabilism:

• 1. Veritism.

• 2. Continuous, additive, strictly proper inaccuracy measures.

• 3. No Dominance.

  • C1. No Accuracy Dominance (from 1 and 3).

• 4. Accuracy Theorem.

  • C2. Probabilism (from 2, C1, 5).

Although accuracy arguments like the one above can be used to establish coherence as a norm or principle of rationality, they don’t say much about agents who fail to be coherent, or their credences, besides that they fail to be rational. In particular, if you are routinely unable to be coherent, all that Probabilism has to say about you is that you are routinely unable to have rational credences. This has led some to question the value of Probabilism as a norm or principle of rationality.

2.2 The need for approximate coherence

Consider a large number of statements about the results of the next election (who wins, by how much, etc...), and a large number of statements about how various economic indicators (country’s GDP, price of oil, etc...) will change before the election. I have a degree of belief towards each individual statement, and in many cases, towards one statement conditional on another. Yet if I put all these opinions together, I do not get a coherent credence function. Up to this point, it seems, I have been irrational. Even worse: after realising this fact, though I might adjust some opinions here and there, I soon find that correcting all incoherences is impossibly difficult, and I give up. I remain irrational from this point onwards.

The upshot is that it often takes a perfect calculator, capable of working out arbitrarily complex logical and probabilistic relations, to ensure compliance with Probabilism. This gives rise to the objection that Probabilism is inappropriate as a norm for human-like agents (Foley, 1993; Savage, 1967). One way to spell out this criticism employs an ought-implies-can assumption (OIC): intuitively, a constraint has normative force over us only if we can comply with it. If this is the case, then the above example shows that Probabilism cannot be a rationality norm for human-like reasoners. I call this the OIC objection to Probabilism.⁸

One could answer the OIC objection by granting that Probabilism is not a norm of rationality. As mentioned earlier, some epistemologists take Probabilism to be merely a principle of rationality, which plays an evaluative role. According to their view, it’s not in general the case that agents ought to have coherent credences. But we can nonetheless evaluate an agent as irrational when her credences are incoherent.⁹

Although this deals with the OIC objection, it does not fully address the problem raised by the example above. Even if we interpret Probabilism as a principle of rationality, we are left with a theory of rationality that has little to say about agents like you and me. Most human-like agents and their credence functions will be labelled as “irrational” most of the time, while the label “rational” will be reserved to agents with superhuman computational power and their credence functions. This raises the worry that the notion of rationality characterised by Probabilism is too demanding, and too coarse, to be of any interest to beings like us. I call this the irrelevance objection to Probabilism.

A natural way to defend Probabilism against the irrelevance objection is to introduce a notion of approximate coherence.¹⁰ Those who are interested in Probabilism as a principle of rationality can use this notion to further refine their labelling of agents and their credence functions. Although all agents with incoherent credences are in some sense irrational, we can further distinguish between these agents depending on whether their credences are more or less approximately coherent. So even though human-like reasoners fall short of the probabilist ideal most of the time, we can still make interesting evaluative claims about them based on how closely they approximate this ideal.

A notion of approximate coherence can also be used to defend the normative status of Probabilism. Zynda (1996) develops this line of response, arguing that coherence does have an important normative role to play, even if we are routinely unable to satisfy its constraints. He gives the analogy of a machinist who works on a lathe, and receives a specification for a cylindrical component. Clearly, no matter how skilled the machinist and how technically advanced the lathe, the component will never be perfectly cylindrical. And yet, the specification is still normatively relevant for the machinist. This is because it allows us to determine that certain components are better than others, since they are more approximately cylindrical. As a consequence, the machinist is subject to a conditional obligation to produce more approximately cylindrical parts, conditional on the manufacturing technology improving. And approximating the ideal gives the manufacturing industry a reason to improve their technology. Coherence plays a similar role for us: although we are often unable to meet its requirements, we can distinguish between more and less approximately coherent credences. We have a conditional obligation to be more approximately coherent, conditional on our epistemic abilities improving, and approximating the ideal gives us a reason to improve our epistemic abilities.

For the above responses to be convincing, however, we need to say a bit more. First, we must specify what it means for a credence function to approximate coherence. Just like there are many ways in which a component can be said to have approximately cylindrical shape, there are many ways in which a credence function can be said to be approximately coherent. We need to specify which notion of approximate coherence is the relevant one.

Second, we need to show that this notion approximate coherence is evaluatively meaningful. In the machinist analogy, the component will be part of some larger mechanism. The more accurately it approximates the ideal shape and dimension, the better it will be at performing its intended function (by fitting in with the other pieces, by reducing attrition, etc...); in other words, judgements that one piece more closely approximates the ideal than another are evaluatively meaningful. Similarly, we need to show that more approximately coherent credences are at least in some sense epistemically better than less approximately coherent ones. If we subscribe to the thesis that accuracy is the fundamental epistemic value, this involves showing a connection between approximating coherence and accuracy improvements.¹¹

3 Approximate coherence for accuracy-firsters

This section looks at De Bona and Staffel’s (2017) proposal for a notion of approximate coherence for accuracy-firsters.¹² This proposal follows the two-step strategy discussed in the previous section: first define a notion of approximate coherence, and then show why it is better to be less rather than more incoherent.

However, De Bona and Staffel (2017; 2019) don’t show that it is generally better to be less rather than more incoherent. Rather, they show that some particular way of reducing incoherence leads to epistemic improvement. I will argue that this casts some doubt on whether their notion of approximate coherence gives us a fully satisfactory response to the irrelevance objection against Probabilism. Indeed, I will show that their results fail to vindicate some of our intuitions about how comparative incoherence judgements relate to judgements of comparative epistemic worth. This suggests that there is a tighter relationship between accuracy and incoherence than the one captured by De Bona and Staffel’s results.

These criticisms are not insurmountable, and they are not meant to show that De Bona and Staffel’s incoherence measures should be abandoned. Their purpose is to further motivate the (independently interesting) question of whether we can strengthen De Bona and Staffel’s results connecting incoherence and accuracy, showing that it is generally better to be less rather than more incoherent from an accuracy-first perspective.

3.1 How to approximate coherence

De Bona and Staffel (2017) define a quantitative notion of approximate coherence: they specify an incoherence measure, which assigns a real number to each credence functions. Then if c and $c'$ are credence functions defined on the same domain, c is more approximately coherent than $c'$ iff it has lower incoherence measure. They propose that we measure the incoherence of a credence function c as follows:

$$\begin{aligned} I_d(c) = \min \{d(c, y): y \quad \text {is a coherent credence function}\} \end{aligned}$$

(4)

where d is a continuous divergence. De Bona and Staffel (2017) focus on divergences derived from continuous, additive, and stricly proper inaccuracy measures. Recall that such measures can be defined as:

$$\begin{aligned} S(c, w) = \sum _{\phi \in {\mathcal {F}}} s(c(\phi ), w(\phi )) \end{aligned}$$

(5)

where s is a continuous, strictly proper scoring rule. To each measure of this kind, we can associate a corresponding divergence (defined for arbitrary c and coherent y):

$$\begin{aligned} d_{S}(c, y) = S(c, y) - S(y, y) \end{aligned}$$

(6)

where S(x, y) is a shorthand for $\text {Exp}_{y}[S(x, \cdot )]$, the expectation under y of the score of x. Because expectations are additive, $d_S(c, y) = \text {Exp}_{y}[S(c, \cdot ) - S(y, \cdot )]$ is just the expected value under y of the difference between the score of c and the score of y.

To each continuous, strictly proper, additive inaccuracy measure S, we can thus associate a corresponding incoherence measure $I_{d_S}$ defined from its divergence (I will slightly abuse the notation and write $I_S$ instead of $I_{d_S}$). Staffel (2019) shows that incoherence measures constructed in this way respect some plausible desiderata for a notion of approximate coherence.

After defining a reasonable notion of approximate coherence, we need to show that this notion is evaluatively meaningful. This involves showing that it is in some way epistemically better for agents to be less, rather than more, incoherent.

3.2 Why approximate coherence

The accuracy argument for Probabilism shows that incoherent credences have some fault which coherent credences are immune from: they are accuracy-dominated, which means they are not the kind of credence function a rational agent would have. However, this argument does not say anything about whether approximately coherent credences are any better than wildly incoherent ones.

De Bona and Staffel (2017) set out to address this point by arguing that “there is in fact a specific way of reducing incoherence in one’s credences that always constitutes an improvement of one’s epistemic situation” (p. 203, my emphasis), where the epistemic improvement amounts to a guarenteed increase in accuracy. Their argument is centered around the following result.

Proposition 1

(De Bona and Staffel, 2017, Proposition 1) Let S be a convex,¹³ continuous, strictly proper, additive inaccuracy measure. Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ be an incoherent credence function and let $c^*: {\mathcal {F}}\rightarrow {\mathbb {R}}$ be some $d_S$-closest coherent credence function to c, i.e. some coherent credence function which minimises $d_S(c, c^*)$. For any $\lambda \in (0, 1]$, define $c_{\lambda }: {\mathcal {F}}\rightarrow {\mathbb {R}}$ as $c_{\lambda }(\theta ) = (1-\lambda )c(\theta ) + \lambda c^*(\theta )$. Then:

• 1. $I_S(c_\lambda ) < I_S(c)$, and

• 2. $c_\lambda$ accuracy-dominates c under S.

This result shows that moving from an incoherent credence function c to some $c_\lambda$ on the path to its $d_S$-closest coherent credence function $c^*$ is guaranteed to increase accuracy, while also reducing incoherence as measured by $I_S$.¹⁴ Under the veritist theory of epistemic value, it establishes that, if $c'$ is on the direct path between c and its $d_S$-closest credence, then $c'$ is both less incoherent than c, and guaranteed to be epistemically better than c.¹⁵ And in turn, this gives us reason to consider an agent with credence function $c'$ as epistemically better than one with credence function c. We can thus derive the following extension of Probabilism:

• Weak Graded Probabilism

  • i Rational agents have coherent credence functions (Probabilism).

  • ii For a fixed measure of inaccuracy S, let $I_S$ its associated incoherence measure, and let $c, c'$ be two credence functions defined on the same domain. If $I_S(c') < I_S(c)$ and $c'$ is on the direct path between c and its $d_S$-closest credence function, then an agent with credence function $c'$ is epistemically better than one with credence function c.

The overall argument has the following structure:

• 1. Veritism.

• 2. Convex, continuous, strictly proper, additive measures of inaccuracy.

• 3. Definition of incoherence measures $I_S$.

• 4. No Dominance.

  • C1. No Accuracy Dominance (from 1 and 4).

• 5. Accuracy Theorem

• 6. Proposition 1.

  • C2. Weak Graded Probabilism (The first part follows from 2, C1 and 5. The second part follows from 1, 2, 3, and Proposition 1).

Note that Weak Graded Probabilism only shows that a small subset of the incoherence comparisons induced by the measure $I_S$ are evaluatively meaningful. To see this, suppose we measure incoherence by $I_S$, where S is our preferred convex measure of inaccuracy. Now pick two incoherent credence functions $c,c'$ such that $I_S(c') < I_S(c)$, i.e. $c'$ is less incoherent than c. How is this incoherence comparison reflected in our evaluative judgements? Well, if $c'$ happens to be on the direct path from c to its $d_S$-closest coherent credence function, then $c'$ accuracy-dominates c, and therefore $c'$ is guaranteed to be epistemically better than c. But if $c'$ is not along this path, the argument above gives us no reason to think it is epistemically better than c in any way.

In light of this, one might question whether De Bona and Staffel’s incoherence measures give us a fully satisfactory response to the irrelevance objection against Probabilism. Recall that we need a notion of approximate coherence that makes evaluatively meaningful comparisons in order to explain why Probabilism is normatively relevant for non-ideal agents. In the machinist analogy, the fact that more approximately cylindrical components are generally better at fulfilling their goals is a key part of our story about why the ideal cylinder specification, although unreachable, still has normative force over the machinist. Would it suffice to show that, starting from a non-cylindrical component, there is some way to make the component more cylindrical which also makes it more fit for the job? Maybe. But showing that all (or at least most) improvements in approximation produce improvement in performance would make for a more convincing story.

Similar considerations apply if we want to defend Probabilism as a principle of rationality. In this case, our notion of approximate coherence is supposed to help us refine our evaluations, so that we can make interesting evaluative judgements about non-ideal agents based on the degree to which they approximate the ideal. And while the evaluative judgements induced by Weak Graded Probabilism are certainly interesting, it would be better if we could compare the relative epistemic worth of agents whose credences are not aligned along a specific path.

Indeed, it seems that often we do judge incoherence comparisons between credence functions to be evaluatively meaningful, even when neither function is on the direct path between the other and its closest coherent credence function. As an example, consider the two credence functions in Fig. 1. Intuitively, $c'$ is doing a much better job at approximating coherence than c. And intuitively, this gives us reason to say that an agent with credence function $c'$ is in some sense epistemically better than one with credence function c.

For most reasonable measures of inaccuracy, De Bona and Staffel’s incoherence measures vindicate our intuitive incoherence comparison in this example, assigning lower incoherence measure to $c'$ than to c. But for most reasonable measures of inaccuracy, $c'$ is not on the path between c and its $d_S$-closest coherent credence, and so Weak Graded Probabilism has nothing to say about whether c is better than $c'$ in any way. This suggests that Weak Graded Probabilism does not capture the full extent to which our intuitive judgements of comparative incoherence are related to our intuitive judgements of relative epistemic worth.

Fig. 1

Here ${\mathcal {F}}= \{\phi , \psi \}$, where $\phi \equiv \lnot \psi$, so we can draw each credence function as a point in the plane. The x coordinate is the credence in $\phi$, and the y coordinate is the credence in $\psi$. The light gray region is that of coherent credence functions, for which $c(\phi ) = 1 - c(\psi )$

One might try to address this problem by extending Proposition 1. Perhaps we can show that there are ways of reducing incoherence other than moving towards the $d_S$-closest coherent credence function, which also guarantee increases in accuracy. However, for most reasonable measures of inaccuracy, there is no hope of such an extension giving evaluative meaning to all the incoherence comparisons induced by the measure $I_S$. This is because, as De Bona and Staffel (2017) also acknowledge, for any measure of inaccuracy S we can find a pair of credence functions $c, c'$ such that $I_S(c')< I_S(c)$, but $c'$ does not accuracy-dominate c.

What’s worse, there is no hope of such an extension giving evaluative meaning to all the incoherence comparisons that we find intuitively meaningful. As an example, consider again the two credence functions c and $c'$ defined as in Fig. 1, and let S be the Brier inaccuracy measure. This measure is convex, continuous, additive, and strictly proper. It is defined as follows:

$$\begin{aligned} S(c, w) = \sum _{\theta \in {\mathcal {F}}}(c(\theta ) - w(\theta ))^2 \end{aligned}$$

(7)

Under the Brier measure, the inaccuracy S(f, w) of credence function f at world w is just the square (Euclidean) distance between the point corresponding to f and the point corresponding w. Some calculation shows that the associated divergence $d_S(f, g)$ is also just the square (Euclidean) distance the between the two points corresponding to f and g. So in Fig. 1, $I_S(c)$ is the minimum square distance between c and a coherent credence function, i.e. the square distance between c and the light gray line. This is clearly greater than $I_S(c')$, the square distance between $c'$ and the gray line. And yet, $c'$ does not accuracy-dominate c under S. To see this, note that if c is closer to $w_2$ than $c'$ is. So the inaccuracy of c at $w_2$ is smaller than the inaccuracy of $c'$ at $w_2$. Therefore, no matter how we extend Proposition 1, we will never be able to show that $c'$ is guaranteed to be epistemically better than c under the Brier measure of inaccuracy.

Similar examples can be devised for any reasonable measure of inaccuracy. The upshot here is that, if we want to show that incoherence comparisons like the one in Fig. 1 are evaluatively meaningful, it won’t be enough to just extend Proposition 1. We also need to find a sense in which less incoherent credences can be epistemically better than more incoherent ones, even if the former don’t accuracy-dominate the latter.

Ultimately, even if one thinks that De Bona and Staffel’s results suffice to respond to the irrelevance objection against Probabilism, it remains an interesting question whether they can be strengthened. In this essay, I will be interested in the following two questions:

• 1. Is there a tighter connection between incoherence and accuracy than the one captured by De Bona and Staffel’s results?

• 2. Can accuracy-firsters use this connection to argue for something stronger than Weak Graded Probabilism? Specifically, can accuracy-firsters argue that all incoherence comparisons made by De Bona and Staffel’s measures are evaluatively meaningful?

Note that a positive answer to the second question requires a positive answer to the first. To argue that all incoherence comparisons are evaluatively meaningful, we need to show a sense in which less incoherent credences are epistemically better than more incoherent ones. And if we are committed to Veritism, any claim about the epistemic worth of credences is a claim about their accuracy profile. So we need show that incoherence comparisons entail some facts about the accuracy profile of the credence functions being compared, and then argue that these facts give us reason to consider less incoherent credences as epistemically better.

The next section will give a positive answer to the first question. I will show that incoherence comparisons under De Bona and Staffel’s measures can be fully characterised in terms of accuracy. Informally, c is less incoherent than $c'$ if and only if c misses out on less guaranteed accuracy than $c'$. However I will have little to offer, beyond an appeal to intuition, in defense of the claim that c should be considered epistemically better than $c'$ in virtue of its missing out on less guaranteed accuracy. Therefore, question 2 will remain open for debate.

4 Accuracy characterisation of approximate coherence

Although De Bona and Staffel (2017) define incoherence measures which can compare the degree of incoherence of any two credence functions, they only show that a small subset of these comparisons are evaluatively meaningful. In this section I give a new characterisation of De Bona and Staffel’s incoherence measures, which allows us to express every incoherence comparison in terms of accuracy. Then I use it to show what it would take to argue that all incoherence comparisons are evaluatively meaningful from the accuracy-first perspective.

The main formal result in this section will show that the incoherence measure $I_S(c)$ of a credence function c is equivalent to the amount of guaranteed accuracy, measured according to S, that an agent with credence function c misses out on.

Let’s make this more precise. Say $c'$ dominates c in accuracy according to S by amount t iff $c'$ is guaranteed to be more accurate than c of at least t, come what may. We are interested in the amount of accuracy that c leaves on the table, that is, the maximum amount by which some alternative credence $c'$ accuracy-dominates c. This is captured by the following measure:

$$\begin{aligned} A_S(c) = \sup \{ \min \{S(c, w) - S(f, w): w \in {\mathcal {W}}_{\mathcal {F}}\} \,: \, f \in {\mathcal {C}}_{\mathcal {F}}\} \end{aligned}$$

(8)

To see that $A_S(c)$ measures the largest amount by which c is accuracy-dominated, note that the quantity $m(c, f) = \min \{S(c, w) - S(f, w): w \in {\mathcal {W}}_{\mathcal {F}}\}$ is the minimum difference in inaccuracy between c and f across all possible worlds. If this quantity is negative, then there is at least one world where c is more accurate than f, so that $S(c, w) - S(f, w)$ is negative at that world. If this quantity is positive, then f is more accurate than c by at least this quantity at every possible world, i.e. f accuracy-dominates c by amount m(c, f). Finally, note that $m(c, f) = 0$ when $c = f$. So the supremum of m(c, f) over all credence functions f is the supremum of all the amounts by which c is accuracy-dominated, if c is accuracy-dominated by some alternative credence function, and will be equal to 0 if c is not accuracy-dominated by any alternative credence function. The following lemma shows that this supremum is actually a maximum: so for any c there is some credence f that accuracy-dominates c by the largest amount ($f=c$ if c is not accuracy-dominated); and furthermore, this maximum is always achieved by a coherent credence function f.

Lemma 1

Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ a credence function. Let $S: {\mathcal {C}}_{\mathcal {F}}\times W_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure. Then there is some coherent credence $g: {\mathcal {F}}\rightarrow {\mathbb {R}}$ and some $w_g \in {\mathcal {W}}_{\mathcal {F}}$ such that:

$$\begin{aligned} A_S(c) = S(c, w_g) - S(g, w_g) \end{aligned}$$

(9)

Proof

See Appendix. $\square$

The next result is an immediate consequence of the definition of $A_S$. It shows that, if $A_S(c) < A_S(c') = t$, then there is some credence function which is more accurate than $c'$ of at least t in every world, whereas no credence function can be more accurate than c of at least t in every world. In other words, $A_S(c) < A_S(c')$ if and only if the maximum amount by which c is accuracy-dominated is smaller than the maximum amount by which $c'$ is accuracy-dominated.

Proposition 2

Let $S: {\mathcal {C}}_{\mathcal {F}}\times W_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure, and let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ a credence function such that $A_S(c) = t$. Then:

• 1. For every $c': {\mathcal {F}}\rightarrow {\mathbb {R}}$, there is a $w \in {\mathcal {W}}_{\mathcal {F}}$ such that $S(c, w) - S(c', w) \le t$.

• 2. There is a $c': {\mathcal {F}}\rightarrow {\mathbb {R}}$ such that $S(c, w) - S(c', w) \ge t$ for every $w \in {\mathcal {W}}_{\mathcal {F}}$.

Proof

See Appendix. $\square$

The main formal result of this section shows that the incoherence measures $I_S$ defined by De Bona and Staffel are formally equivalent to the measures of accuracy-domination $A_S$ defined above.

Proposition 3

Let $S: {\mathcal {C}}_{\mathcal {F}}\times W_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure. Then for every credence function $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$, we have:

$$\begin{aligned} A_S(c) = I_S(c). \end{aligned}$$

(10)

where $I_S(c)$ is the incoherence measure defined from divergence $d_S$ as in (4).

Proof

See Appendix. $\square$

De Bona and Staffel’s incoherence measures capture the intuition that c approximates coherence to the extent that it is “close”, in a geometrical sense, to the set of coherent credence functions, whereas $A_S(c)$ is a measure of how much guaranteed accuracy an agent is leaving on the table by adopting credence function c. However, Proposition 3 shows that these two measures turn out to be equivalent.

We can use these results to express every incoherence comparison made by De Bona and Staffel’s measures in terms of the accuracy profiles of the two credence functions being compared. Let $c, c'$ be two credence functions defined on the same domain, and assume that $c'$ is more approximately coherent than c, i.e. $I_S(c') < I_S(c)$. By Proposition 3, this is the case if and only if $A_S(c') < A_S(c)$. And this latter comparison can be immediately expressed in terms of accuracy via Proposition 2: it means that the maximum amount by which $c'$ is accuracy-dominated is smaller than the maximum amount by which c is accuracy-dominated. So to show that all incoherence comparisons are evaluatively meaningful, accuracy-firsters just need to show that being accuracy-dominated by a smaller amount makes a credence function epistemically better, at least in some sense. That is, they need to establish the following variant of the No Accuracy Dominance principle:

• Graded Accuracy Dominance: For a fixed measure of inaccuracy S, an agent with credence function $c'$ is in some sense epistemically better than an agent with credence function c whenever the largest amount by which $c'$ is accuracy-dominated is smaller than the largest amount by which c is accuracy-dominated.

If Graded Accuracy Dominance is established, we can run a variant of the accuracy argument for Probabilism to derive the following principle:

• Strong Graded Probabilism:

  • i Rational agents have coherent credence functions (Probabilism).

  • ii For a fixed measure of inaccuracy S, let $I_S$ its corresponding incoherence measure. Then if $c'$ is more approximately coherent than c according to measure $I_S$, an agent with credence function $c'$ is in some sense epistemically better than one with credence function c.

Unlike Weak Graded Probabilism, the above principle shows that every incoherence comparison induced De Bona and Staffel’s scores is evaluatively meaningful. In particular, it will vindicate our intuitive evaluations in cases like Fig. 1. Note also that, unlike Proposition 1, none of the results given in this section assume that the inaccuracy measure S is convex. This is good news, since the status of convexity as a requirement on reasonable measures of inaccuracy is controversial (Joyce, 2009). Here is the full argument for Strong Graded Probabilism:

• 1. Veritism

• 2. Continuous, strictly proper, additive measures of inaccuracy.

• 3. Definition of incoherence measures $I_S$.

• 4. No Dominance.

  • C1. No Accuracy Dominance (from 1 and 4).

• 5. Graded Accuracy Dominance.

• 6. Accuracy Theorem.

• 7. Proposition 3.

  • C2. Strong Graded Probabilism (The first part follows from 2, C1, and 6. The second part follows from 2, 3, 5, and Proposition 3).

The above argument shows that, under the usual assumptions of the accuracy argument for Probabilism, Graded Accuracy Dominance entails that every incoherence comparison induced by De Bona and Staffel’s incoherence measures is evaluatively meaningful. And the converse is also true. For assume that Graded Accuracy Dominance is false. Then for some inaccuracy measure S, there are credence functions c and $c'$ defined on the same domain, such that the maximum amount by which c is accuracy-dominated is smaller than the maximum amount by which $c'$ is accuracy-dominated, and yet there is no sense in which an agent with credence function c is epistemically better than an agent with credence function $c'$. So by Proposition 3 we have that $I_S(c)<I_S(c')$, and yet there is no sense in which agent with credence function c is epistemically better than one with credence $c'$. In other words, some incoherence comparison induced by $I_S$ is not evaluatively meaningful.

Can we give some motivation for adopting Graded Accuracy Dominance as a premise? I do not know of any conclusive argument for or against this principle. The main contribution of this essay is to show that if an accuracy-firster can provide an argument for Graded Accuracy Dominance, they will be able to argue that every incoherence comparison made De Bona and Staffel’s incoherence measures is evaluatively meaningful. And conversely, any argument against Graded Accuracy Dominance will show that at least some incoherence comparisons induced by these measures is not evaluatively meaningful.

Although I can’t give a conclusive argument for Graded Accuracy Dominance here, I want to end this section by looking at what it would take to adapt the usual argument for No Accuracy Dominance to derive this new principle instead.

Recall that in the standard argument for Probabilism, No Accuracy Dominance is motivated by assuming an intuitive rationality principle, which I called No Dominance. No Dominance states that a rational agent’s credence function is not guaranteed to be epistemically worse than some other credence function. Under the assumption of Veritism, this is clearly equivalent to No Accuracy Dominance.

The intuition behind No Dominance is decision-theoretic in nature: imagine an agent having to choose between a set of options whose utility varies depending on which possible world is the actual one, in a way that the agent can know a priori. Then an ideally rational agent would never choose a dominated option, since there is an alternative option which can be known to be better a priori. In the epistemic case, the “options” are credence functions, and their utility at each world is their epistemic value at that world. Intuitively, an ideal rational agent interested in maximising epistemic value would not “choose” a credence function that she can a priori know to be worse than another credence function (Pettigrew, 2019).

One could try to appeal to a similar decision-theoretic intuition in support of Graded Accuracy Dominance. As an example, consider a binary set of possible worlds ${\mathcal {W}}= \{w_1, w_2\}$, and a decision-maker who has to pick between four options $o_1, o_2, o_1', o_2'$, whose utility at each world is described in Table 1.

Table 1 A simple decision problem with four options

Option $o_1'$ is guaranteed to be better than $o_1$ by at least 90 units of utility, and option $o_2'$ is guaranteed to be better than option $o_2$ by at least 1 unit. Even though both $o_1$ and $o_2$ are dominated in utility, and option $o_2$ is not guaranteed to be better than $o_1$, we might still find an an agent who chooses $o_1$ to be an intuitively worse decision maker than one who chooses $o_2$. After all, if missing out on some guaranteed utility is a rationality fault, it’s natural to think that an agent is more rationally faulty the larger the amount of guaranteed utility they miss out on.¹⁶

Those who share this decision-theoretic intuition can apply it to the epistemic case. Here the options are credence functions, and their utility at each world is their accuracy at that world. This leads to the following variant of No Dominance:

• Graded Dominance: Fix a measure of epistemic value. An agent with credence function $c'$ is in some sense epistemically better than an agent with credence function c whenever the largest amount by which $c'$ is dominated in epistemic value is smaller than the largest amount by which c is dominated in epistemic value.

Under the assumption of Veritism, it is easy to see that Graded Dominance is equivalent to Graded Accuracy Dominance. Thus if we assume Graded Dominance, we can derive Graded Accuracy Dominance as an intermediate conclusion in the argument for Strong Graded Probabilism given above.

5 Conclusion

Accuracy-first epistemologists defend Probabilism: the claim that rational agents have probabilistically coherent credences. Yet human-like agents are often unable to ensure their credences are coherent. This has led some to question whether Probabilism is appropriate as a norm or principle of rationality.

One way to respond to this objection is to argue that Probabilism is an ideal to be approximated as best one can. But this line of response only works if we can specify a notion of approximate coherence, and show that this notion is evaluatively meaningful, i.e. show that more approximately coherent agents are in some sense epistemically better than less approximately coherent ones.

In this essay, I looked at De Bona and Staffel’s (2017, 2019) proposal for a notion of approximate coherence suited for the accuracy-first programme. Their results only show that a small subset of incoherence comparisons are evaluatively meaningful from the accuracy-first perspective, leaving open the question of whether, or why, accuracy-firsters should think it is in general better to be more rather than less approximately coherent.

To address this point, I have shown that de Bona and Staffel’s notion of approximate coherence can be fully characterised in terms of accuracy. More precisely, for a fixed measure of inaccuracy, the degree of incoherence of a credence function c is the largest amount t such that some alternative credence function is guaranteed to be more accurate than c of at least t at every possible world. This characterisation allowed me to show that accuracy-firsters should maintain that it’s generally better to be more rather than less approximately coherent if and only if they endorse Graded Accuracy Dominance: the claim that agents who miss out on less guaranteed accuracy are in some sense epistemically better than those who miss out on more guaranteed accuracy.

Finally, I have pointed out that Graded Accuracy Dominance can be derived by assuming a variant of a principle, called No Dominance, which is commonly motivated on the basis of decision-theoretic intuitions. However, this variant of No Dominance is not as intuitively compelling as the original. So it remains an open question whether accuracy-firsters should endorse Graded Accuracy Dominance.

Appendix A: Proof of the results

Throughout this section, let ${\mathcal {F}}= \{\theta _1,\ldots , \theta _m\}$ be a finite set of sentences. A credence function is any function $c: {\mathcal {F}}\rightarrow [0,1]$ and can be identified with the $[0,1]^m$ vector ${\overline{c}} = (c(\theta _1),\ldots ,c(\theta _m))$. I will denote by ${\mathcal {C}}_{\mathcal {F}}$ the set of all credence functions on ${\mathcal {F}}$, which can be identified with the set $[0,1]^m$. I will denote by ${\mathcal {W}}_{\mathcal {F}}= \{w_1 , . . . ,w_n\}$ the set of “possible worlds” corresponding to all the logically possible truth-value assignments for the sentences in ${\mathcal {F}}$. If $w \in {\mathcal {W}}_{\mathcal {F}}$ and $\phi \in {\mathcal {F}}$, then $w(\phi )$ is the truth-value of $\phi$ at w.

Denote by ${\mathcal {F}}^*$ the smallest algebra containing ${\mathcal {F}}$. A credence function is coherent iff it can be extended to a probability function on ${\mathcal {F}}^*$. If y is a coherent credence on ${\mathcal {F}}$, then it can be written as the convex combination of the truth-value assignments corresponding to the worlds in ${\mathcal {W}}_{\mathcal {F}}$. I write $y^*_i$ to denote the weights of this convex combination, so that each coherent y can be written as:

$$\begin{aligned} y = \sum _{i=1}^n y^*_i w_i \end{aligned}$$

(A1)

where $\sum _{i=1}^n y^*_i = 1$ and $y^*_i \in [0,1]$ for every $i = 1,\ldots ,n$.

Recall that the measure of accuracy-domination I put forward in Sect. 4 was defined as:

(A2)

where S is a continuous, strictly proper additive inaccuracy measure, and ${\mathcal {C}}_{\mathcal {F}}$ is the set of all credence functions on ${\mathcal {F}}$. To prove results about this measure, it is helpful to show that the supremum in its definition is actually a maximum. That is, for every credence function c, there is some pair $(g, w_k)$ where $g \in {\mathcal {C}}_{\mathcal {F}}$, $w_g \in {\mathcal {W}}_{\mathcal {F}}$, and $A_S(c) = S(c, w_g) - S(g, w_g)$. Furthermore, we can show this maximum is always achieved by a coherent g.

Lemma 2

Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ a credence function. Let $S: {\mathcal {C}}_{\mathcal {F}}\times W_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure. Then there is some coherent credence $g: {\mathcal {F}}\rightarrow {\mathbb {R}}$ and some $w_g \in {\mathcal {W}}_{\mathcal {F}}$ such that:

$$\begin{aligned} A_S(c) = S(c, w_g) - S(g, w_g) \end{aligned}$$

(A3)

Proof

Fix a credence function c. For every $w \in {\mathcal {W}}_{\mathcal {F}}$, we know $S(c, w) - S(f, w)$ a continuous function of f for each $w \in {\mathcal {W}}_{{\mathcal {F}}}$. Consider the following function:

$$\begin{aligned} m_c(f) = \min _{w \in {\mathcal {W}}_{\mathcal {F}}}\{S(c, w) - S(f, w)\} \end{aligned}$$

(A4)

Seen as a function $m_c: [0,1]^m \rightarrow {\mathbb {R}}$, $m_c$ is continuous, as it is the minimum of finitely many continuous functions. The set $[0,1]^m$ of all credence functions over ${\mathcal {F}}$ is compact, and so its image under $m_c$ is a compact subset of ${\mathbb {R}}$, that is, a closed and bounded subset. Therefore there is some $g\in {\mathcal {C}}_{\mathcal {F}}$ such that:

$$\begin{aligned} m_c(g) = \sup \{m_c(f) \,: \, f \in {\mathcal {C}}_{\mathcal {F}}\} = A_S(c) \end{aligned}$$

(A5)

But then $m_c(g) = S(c, w_g) - S(g, w_g)$ for some $w_g \in {\mathcal {W}}_{\mathcal {F}}$. So the pair $(g, w_g)$ satisfies (A3).

Now assume by way of contradiction that g is incoherent. Then by the accuracy theorem in Predd et al. (2009), there is some coherent $g'$ such that $g'$ accuracy-dominates g. So for every $w_i \in {\mathcal {W}}_{\mathcal {F}}$, we have that $S(c, w_i) - S(g', w_i)$ is strictly greater than $S(c, w_i) - S(g, w_i)$. Therefore:

$$\begin{aligned} \min _{w \in {\mathcal {W}}_{\mathcal {F}}}\{S(c, w) - S(g', w)\} > \min _{w \in {\mathcal {W}}_{\mathcal {F}}}\{S(c, w) - S(g, w)\} \end{aligned}$$

(A6)

which contradicts the fact that $m_c(g) = \sup \{m_c(f): f \in {\mathcal {C}}_{\mathcal {F}}\}$. So g must be coherent. $\square$

The advantage of this measure is that it allows us to say something about what the inequality $A_S(c') < A_S(c)$ implies in terms of the epistemic utility of $c'$ and c.

Proposition 2

Let ${\mathcal {S}} : {\mathcal {C}}_{\mathcal {F}} \times {\mathcal {W}}_{\mathcal {F}} \rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure. Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ a credence function such that $A_S(c) = t$, for some $t > 0$. Then:

• (i) For every $c': {\mathcal {F}}\rightarrow {\mathbb {R}}$, there is a $w' \in {\mathcal {W}}_{\mathcal {F}}$ such that:

  $$\begin{aligned} S(c, w') - S(c', w') \le t \end{aligned}$$

  (A7)

• (ii) There is a $c': {\mathcal {F}}\rightarrow {\mathbb {R}}$ such that $S(c, w) - S(c', w) \ge t$ for every w.

Proof

(i): this is immediate from the definition of $A_S$. Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ such that $A_S(c) = t$. Assume by way of contradiction that for some $c': {\mathcal {F}}\rightarrow {\mathbb {R}}$ we have $S(c, w) - S(c', w) > t$ for every $w \in {\mathcal {W}}_{\mathcal {F}}$. Let $w' \in {\mathcal {W}}_{\mathcal {F}}$ a world which minimise this difference (it will always exist, since ${\mathcal {W}}_{\mathcal {F}}$ finite). Then:

$$\begin{aligned} A_S (c) \ge S(c, \omega ') - S(c', \omega ) > t \end{aligned}$$

(A8)

contradiction.

(ii) Let $(c', w')$ be the credence function-world pair of Lemma 2. Clearly the condition holds. $\square$

This shows that if $A_S(c') < A_S(c) = t$ then some credence function is more accurate than c of at least t in every world, whereas this cannot be the case for $c'$.

Before moving to the proof of Proposition 3, we need to introduce a few more definitions and results involving the class of divergences $d_S$ associated to the (bounded) continuous, additive, strictly proper measures of inaccuracy we have been considering. It will be particularly important for our proof of Proposition 3 that these are all Bregman divergences, which can be constructed as follows:

Definition 1

(Bregman Divergence, Predd et al., 2009) Let $\Phi : [0,1]^m \rightarrow {\mathbb {R}}$ be a strictly convex function, differentiable in the interior of $[0,1]^m$, whose gradient $\nabla \Phi$ extends to a bounded, continuous function on $[0,1]^m$. The Bregman divergence $\delta _\Phi : [0,1]^m \times [0,1]^m \rightarrow {\mathbb {R}}$ corresponding to $\Phi$ is given by:

$$\begin{aligned} \delta _\Phi (x, y) = \Phi (y) - \Phi (x) - \nabla \Phi (x) \cdot (y - x) \end{aligned}$$

(A9)

Predd et al. (2009) give us a way to associate a Bregman divergence to every (bounded) continuous, additive, strictly proper measure of inaccuracy S. Fix one such measure of inaccuracy S. Recall that it is defined from a continuous, strictly proper scoring rule $s: [0,1] \times [0,1] \rightarrow {\mathbb {R}}$ as follows:

$$\begin{aligned} S(c, w) = \sum _{\theta \in {\mathcal {F}}} s(c(\theta ), w(\theta )) \end{aligned}$$

(A10)

Using the scoring rule s, we can define a function $\varphi _s: [0,1] \rightarrow {\mathbb {R}}$ as follows:

$$\begin{aligned} \varphi (x) = -x s(1, x) - (1-x)s(0,x) \end{aligned}$$

(A11)

Predd et al. (2009, Proposition 2) show that $\varphi _s$ defined as above is a bounded, continuous, and strictly convex function, which is differentiable on (0, 1) and which satisfies the following equality for every $x \in [0,1]$:

$$\begin{aligned} s(i,x) = -\varphi _s(x) - \varphi _s'(x)(i-x) \end{aligned}$$

(A12)

where $\varphi _s'(x)$ denotes the derivative of $\varphi _s$ for $x \in (0,1)$, and the limits $\lim _{t \rightarrow 0^+} \varphi '_s(t)$ and $\lim _{t \rightarrow 1^-} \varphi '_s(t)$ for $x =0$ and $x=1$, respectively. Furthermore, $\varphi _s'$ is a bounded, continuous function on [0, 1].

Because $\varphi _s$ is strictly convex, differentiable in (0, 1), and its derivative extends to a bounded and continuous function in [0, 1], we can use it to define a function $\Phi _s$ that respects all the conditions of Definition 1 by simply letting $\Phi _s(x)$ be the sum of all $\varphi _s(x_j)$, for $j=1,\ldots , m$. If we think of the elements of $[0,1]^m$ as credence functions on ${\mathcal {F}}$, this is:

$$\begin{aligned} \Phi _s(c) = \sum _{j=1}^m \varphi _s(c_j) = \sum _{\theta \in {\mathcal {F}}} \varphi _s(c(\theta )) \end{aligned}$$

(A13)

Then, from $\Phi _s$, we can construct a Bregman divergence $\delta _{\Phi _s}$ as in Definition 1. All we need to do is show that the divergence $d_S$ which De Bona and Staffel (2017) associate to inaccuracy measure S is just the Bregman divergence $\delta _{\Phi _s}$ constructed as above. We can show this as follows:

$$\begin{aligned} d_{S}(c, p)&= \text {Exp}_p[S(c, \cdot ) - S(p, \cdot )] \quad (\text {from the definition of }d_S\text { in } (6))\\&= \sum _{j=1}^m p_js(c_j, 1) \!+\! (1\!-\!p_j)s(c_j, 0) \!-\! \sum _{j=1}^m p_js(p_j, 1) \!+\! (1\!-\!p_j)s(p_j, 0)\\&= \sum _{j=1}^m p_j(-\varphi _s(c_j) - \varphi _s'(c_j) (1-c_j)) + (1-p_j)(-\varphi _s(c_j) + c_j \varphi _s'(c_j))\\&\quad + \sum _{j=1}^m \varphi _s(p_j) \quad (\text {by }(\hbox {A}12)\text { and definition of }\varphi _s)\\&= \sum _{j=1}^m -\varphi _s(c_j) - \varphi _s'(c_j)(p_j-c_j) + \sum _{j=1}^m \varphi _s(p_j)\\&= - \Phi _s(c) - \nabla \Phi _s(c)\cdot (c - p) + \Phi _s(p) \quad (\text {from the definition of }\Phi _s)\\&= \delta _{\Phi _s}(c, p) \quad (\text {from Definition}~1). \end{aligned}$$

The fact that $d_S$ is a Bregman divergence gives us access to the following result, which is important for the proof of Proposition 3.

• Generalised Pythagorean Theorem (Predd et al. 2009, Prop. 3):

  Let $\delta _\Phi : [0,1]^m \times [0,1]^m \rightarrow {\mathbb {R}}$ be a Bregman divergence. For every credence function c there is a unique coherent credence function z which minimises $\delta _\Phi (c, f)$ among all coherent credence functions f. Moreover, for any coherent credence function f:

  $$\begin{aligned} \delta _\Phi (z, f) \le \delta _\Phi (c, f) - \delta _\Phi (c, z) \end{aligned}$$

  (I)

We can now introduce the following additional definitions:

Definition 2

($d_S$-projection, projection vertices) Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ be a credence function.

• 1. Let z be the coherent credence function which minimises $d_S(c, f)$ among all coherent credence functions f (z exists and is unique by the Generalised Pythagorean Theorem). We say that z is the $d_S$-projection of c onto the set of coherent credence functions.

• 2. Let z the $d_S$-projection of c onto the set of coherent credence functions. The projection vertices of c are the worlds $w_i \in {\mathcal {W}}_{\mathcal {F}}$ such that $z^*_i \ne 0$. Denote by ${\mathcal {K}}(c)$ the set of projection vertices of c.

With this in place, we can finally move to the proof of Proposition 3. The proof involves two lemmas:

Lemma 3

Let $S: {\mathcal {C}}_{\mathcal {F}}\times {\mathcal {W}}_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure, let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ an incoherent credence function, and let z be the $d_S$-projection of c onto the set of coherent credence functions. The difference in accuracy $S(c, w_i) - S(z, w_i)$ is constant for all projection vertices $w_i \in {\mathcal {K}}(c)$.

Proof

¹⁷ Let ${\mathcal {F}}= \{\theta _1,\ldots , \theta _m\}$ and ${\mathcal {W}}_{\mathcal {F}}= \{w_1,\ldots , w_n\}$. Let z be the $d_S$-projection of c onto the set of all coherent credence functions. For any $w_i \in {\mathcal {W}}_{\mathcal {F}}$, letting $y=w_i$ in the Pythagorean inequality (I) gives:

$$\begin{aligned}&d_S(z, w_i) \le d_S(c, w_i) - d_S(c, z) \end{aligned}$$

(A14)

$$\begin{aligned}&d_S(c, w_i) - d_S(z, w_i) \ge d_S(c, z) \end{aligned}$$

(A15)

which, from the definition of $d_S$, is equivalent to:

$$\begin{aligned} S(c, w_i) - S(z, w_i) \ge d_S(c, z) \end{aligned}$$

(A16)

Because z is coherent, we can write it as:

$$\begin{aligned} z = \sum _{i=1}^n z^*_i w_i \end{aligned}$$

(A17)

where $\sum _{i=1}^n z^*_i = 1$ and $z^*_i \in [0,1]$ for every $i = 1,\ldots ,n$. Using the definition of $d_S(c, z)$ we have:

$$\begin{aligned} d_S(c, z)&= \text {Exp}_z\left[ S(c, \cdot ) - S(z, \cdot )\right] \end{aligned}$$

(A18)

$$\begin{aligned}&= \sum _{i = 1}^n z^*_i (S(c, w_i) - S(z, w_i))\end{aligned}$$

(A19)

$$\begin{aligned}&= \sum _{w_i \in {\mathcal {K}}(c)} z^*_i (S(c, w_i) - S(z, w_i)) \end{aligned}$$

(A20)

But from equation (A16) we know that, for any $w_i \in {\mathcal {K}}(c)$, the difference $S(c, w_i) - S(z, w_i)$ is at least as great as $d_S(c, z)$. So if for some $w_j, w_i \in {\mathcal {K}}(c)$ we had that $S(c, w_j) - S(z, w_j) > S(c, w_i) - S(z, w_i)$, then the weighted sum in (A20) would be strictly greater than d(c, z), violating the equality. Thus the difference $S(c, w_i) - S(z, w_i)$ must be constant for every $w_i \in {\mathcal {K}}(c)$. $\square$

Lemma 4

Let $S: {\mathcal {C}}_{\mathcal {F}}\times {\mathcal {W}}_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure, let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ an incoherent credence, and let z be the $d_S$-projection of c onto the set of coherent credence functions. If $w_i \in {\mathcal {K}}(c)$ and $w_k \in {\mathcal {W}}_{\mathcal {F}}{\setminus } {\mathcal {K}}(c)$, then $S(c, w_k) - S(z, w_k) \ge S(c, w_i) - S(z, w_i)$.

Proof

Fix some $w_i \in {\mathcal {K}}(c)$ and $w_k \in {\mathcal {W}}_{\mathcal {F}}{\setminus } {\mathcal {K}}(c)$. From the generalised Pythagorean inequality (I), letting $y = w_k$ we have:

$$\begin{aligned}&d_S(z, w_k) \le d_S(c, w_k) - d_S(c, z) \end{aligned}$$

(A21)

$$\begin{aligned}&d_S(c, w_k) - d_S(z, w_k) \ge d_S(c, z) \end{aligned}$$

(A22)

Then, using the definition of $d_S(c, z)$:

$$\begin{aligned} d_S(c, w_k) - d_S(z, w_k)&\ge \text {Exp}_z\left[ S(c, \cdot ) - S(z, \cdot )\right] \end{aligned}$$

(A23)

$$\begin{aligned}&= \sum _{w_j \in {\mathcal {K}}(c)} z^*_j (S(c, w_j) - S(z, w_j))\end{aligned}$$

(A24)

$$\begin{aligned}&= S(c, w_i) - S(z, w_i) \end{aligned}$$

(A25)

where the last equality holds because, by Lemma 3, the difference $(S(c, w_j) - S(z, w_j))$ is constant for all $w_j \in {\mathcal {K}}(c)$. $\square$

Proposition 3

Let $S: {\mathcal {C}}_{\mathcal {F}}\times {\mathcal {W}}_{\mathcal {F}}\rightarrow {\mathbb {R}}$ be a continuous, additive, strictly proper inaccuracy measure. Then for every credence function $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$, we have $A_S(c) = I_S(c)$.

Proof

Let ${\mathcal {F}}= \{\theta _1,\ldots , \theta _m\}$ and ${\mathcal {W}}_{\mathcal {F}}= \{w_1,\ldots , w_n\}$. Denote by $d_S$ the Bregman divergence associated with the inaccuracy measure S. Let $c: {\mathcal {F}}\rightarrow {\mathbb {R}}$ an incoherent credence function, and let z be the $d_S$-projection of c onto the set of all coherent credence functions. Recall that De Bona and Staffel (2017) define their incoherence measure $I_S$ as:

$$\begin{aligned} I_S(c) = \min \{d_S(c, x): x \quad \text {is a coherent credence function}\} \end{aligned}$$

(A26)

so having defined z as the $d_S$-projection of c on the set of coherent functions, we will have $I_S(c) = d_S(c, z)$ by the Generalised Pythagorean Theorem.

Now let y be a coherent credence such that $A_S(c) = S(c, w_y) - S(y, w_y)$ for some $w_y \in {\mathcal {W}}_{\mathcal {F}}$ (we know it exists by Lemma 2). I start by showing that y and z are the same credence function, and then use this fact to show $A_S(c) = I_S(c)$.

From the definition of $A_S(c)$ we know that, for every $w \in {\mathcal {W}}_{\mathcal {F}}$:

$$\begin{aligned} S(c, w_y) - S(y, w_y) \le S(c, w) - S(y, w) \end{aligned}$$

(A27)

and also, because of the $\sup$ in the definition of $A_S$,

$$\begin{aligned} S(c, w_y) - S(y, w_y) \ge \min _{w \in {\mathcal {W}}_{\mathcal {F}}} \{S(c, w) - S(z, w)\} \end{aligned}$$

(A28)

We know by Lemma 4 that, if $w_i \in {\mathcal {K}}(c)$ and $w_k \in {\mathcal {W}}_{\mathcal {F}}{\setminus } {\mathcal {K}}(c)$, then $S(c, w_k) - S(z, w_k) \ge S(c, w_i) - S(z, w_i)$. Hence the minimum in (A28) is achieved at some $w_i \in {\mathcal {K}}(c)$. Combining this with (A27) and (A28), we obtain that whenever $w_i$ is a projection vertex the following inequality holds:

$$\begin{aligned} S(c, w_i) - S(y, w_i) \ge S(c, w_y)- S(y, w_y) \ge S(c, w_i) - S(z, w_i) \end{aligned}$$

(A29)

since $S(c, w_i) - S(z, w_i)$ is constant for all $w_i \in {\mathcal {K}}(c)$, by Lemma 3. Equation (A29) simplifies to $S(y, \omega _i) \le S(z, \omega _i)$. So for every $w_i \in {\mathcal {K}}(c)$, $S(y, \omega _i)$ is no greater than $S(z, \omega _i)$. But then:

$$\begin{aligned} \text {Exp}_z(S(y, \cdot ) - S(z, \cdot )) = \sum _{w_i \in {\mathcal {K}}(c)} z^*_i(S(y, w_i) - S(z, w_i)) \le 0 \end{aligned}$$

(A30)

since each addend in the sum is no greater than zero. And because S is strictly proper, this can only be the case (with equality) if $y = z$.

From the fact that $z = y$ it follows that $A_S(c) = I_S(c)$, because:

$$\begin{aligned} A_S(c)&= S(c, w_y) - S(y, w_y) \end{aligned}$$

(A31)

$$\begin{aligned}&= S(c, w_y) - S(z, w_y) \quad (\text {because }z = y)\end{aligned}$$

(A32)

$$\begin{aligned}&= S(c, w_i) - S(z, w_i) \quad \text {for some }w_i \in {\mathcal {K}}(c)\text { (by Lemma} ~4) \end{aligned}$$

(A33)

$$\begin{aligned}&= \sum _{w_i \in {\mathcal {K}}(c)} z^*_i (S(c, w_i) - S(z, w_i)) \quad \text {(by Lemma}~3)\end{aligned}$$

(A34)

$$\begin{aligned}&= \text {Exp}_z(S(c, \cdot ) - S(z, \cdot ))\end{aligned}$$

(A35)

$$\begin{aligned}&= d_S(c, z)\end{aligned}$$

(A36)

$$\begin{aligned}&= I_S(c) \quad \text {(by construction of }z). \end{aligned}$$

(A37)

$\square$