Abstract
This paper ties together three threads of discussion about the following question: in accepting a system of axioms S, what else are we thereby warranted in accepting, on the basis of accepting S? First, certain foundational positions in the philosophy of mathematics are said to be epistemically stable, in that there exists a coherent rationale for accepting a corresponding system of axioms of arithmetic, which does not entail or otherwise rationally oblige the foundationalist to accept statements beyond the logical consequences of those axioms. Second, epistemic stability is said to be incompatible with the implicit commitment thesis, according to which accepting a system of axioms implicitly commits the foundationalist to accept additional statements not immediately available in that theory. Third, epistemic stability stands in tension with the idea that in accepting a system of axioms S, one thereby also accepts soundness principles for S. We offer a framework for analysis of sets of implicit commitment which reconciles epistemic stability with the latter two notions, and argue that all three ideas are in fact compatible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Our overall goal in this paper is a philosophical investigation of the following question: in accepting a system of axioms S, what else are we thereby warranted in accepting, on the basis of accepting S? Three areas of discourse form the background to our investigation. (1) The implicit commitment thesis, which roughly states that accepting a system of axioms S implicitly commits one to accept additional statements beyond the logical consequences of S. (2) The idea, central to various foundational positions in the philosophy of mathematics, each with an associated system S, that it is rationally permissible to accept S and not thereby accept statements beyond the logical consequences of S. (3) The idea that we should like to accept various soundness assertions involving a notion of truth for a system S, on the basis of accepting S itself. The motivation for our investigation stems from the claims that (1) is incompatible with (2), and that (2) sits in tension with (3). Let us flesh out these claims.
First, the incompatibility between (1) and (2). The implicit commitment thesis (ICT) is introduced in Dean (2015), and states: anyone who accepts the axioms of a mathematical theory S is thereby also implicitly committed to accepting various additional statements \(\Gamma \) which are expressible in the language of S but which are formally independent of its axioms (Dean, 2015, p. 32). Dean argues the ICT is untenable for certain foundational positions and their corresponding philosophies of mathematics, specifically finitism, as articulated in Tait (1981), and first-orderism, as articulated in Isaacson (1996). The idea is that these foundational positions, along with their associated systems, are said to enjoy a kind of rational stability. In particular: a theory S is epistemically stable if there exists a coherent rationale for accepting S that does not entail or otherwise rationally oblige a theorist to accept statements which cannot be derived from the axioms of S (Dean, 2015, p. 53).Footnote 1 For our purposes, first-orderism is the more interesting of these two positions, and will be our central case of interest moving forward. To see why first-orderism is an epistemically stable foundational position, let us introduce its tenets.Footnote 2
First-orderism is the foundational standpoint that takes Peano Arithmetic (PA) to fully capture the notion of finitary mathematics, phrased as the claim that first-order PA “may be seen as complete for finite mathematics” (Isaacson, 1996, p. 204).Footnote 3 Here, PA is formulated in a first-order way, consisting of finitely many axioms together with the infinitely many axioms that comprise the first-order induction schema. In particular, first-orderism takes PA itself to be justified on the basis of a Dedekindian categorical conception of the natural numbers (Isaacson, 1996, p. 205). Consequently, the theorems of PA “consist of those truths that can be perceived as true directly from the purely arithmetical content of a categorical conceptual analysis of the notion of natural number” (Isaacson, 1996, p. 203). In this way, PA captures a conceptually well-defined region of arithmetical truth, justified by our grasp of the structure of the natural numbers. This is phrased as the claim that PA is “complete with respect to purely arithmetical truth” (Isaacson, 1996, p. 222).
The theorems of PA, then, form a subset of the class of mathematical truths. According to first-orderism, it is a proper subset. Since first-orderism holds that first-order PA is complete with respect to finitary, purely arithmetical truth, sentences that we perceive to be true that lie beyond the provable reach of PA are called either not first-order, not finitary, or not purely arithmetical. Accordingly, to perceive the truth of such sentences, we require higher-order, infinitary, or non-arithmetical concepts. Examples of such sentences are discussed, including: the canonical Gödel sentence for PA (\(\text {G}(\textsf {PA})\)), for which the justification is non-arithmetical (Isaacson, 1996, p. 214); Goodstein’s theorem, and Friedman’s finitization of Kruskal’s theorem, for which the justifications are infinitary (Isaacson, 1996, pp. 216, 219); and the Paris-Harrington sentence, for which the justification is higher-order (Isaacson, 1996, pp. 218–219).
So: the completeness of PA with respect to purely arithmetical truth marks the boundary of precisely which mathematical sentences \(\varphi \) receive first-order, finitary, or purely arithmetical justification. A consequence of the first-orderist’s acceptance of PA is that sentences \(\varphi \) such that \(\textsf {PA} \vdash \varphi \) are those truths one can perceive as directly true from the purely arithmetical content of the notion of natural number. Since PA is said to be complete with respect to purely arithmetical truth, such \(\varphi \) are the only truths one can perceive as directly true from the purely arithmetical content of the notion of natural number. Thus, acceptance of truths beyond the theorems of PA is not (even implicitly) justified by the first-orderist’s acceptance of PA. Rather, any such (higher-order, infinitary, or non-arithmetical) justification must come from somewhere else. In this sense, there exists a coherent rationale for accepting PA that does not entail or otherwise rationally oblige the first-orderist to accept statements beyond the logical consequences of PA itself. That is: first-orderism is an epistemically stable foundational position.
Dean’s (2015) claim is that the epistemic stability of PA makes first-orderism straightforwardly incompatible with the ICT, when the ICT is understood to include (for example) either of the following sentences among the resources \(\Gamma \): \(\text {G}(\textsf {PA})\), or the canonical consistency statement for PA (\(\text {Con}(\textsf {PA})\)). On one hand, epistemic stability decrees that accepting PA does not entail or otherwise thereby rationally oblige the first-orderist to accept \(\text {G}(\textsf {PA})\) or \(\text {Con}(\textsf {PA})\), since both lie beyond the provable reach of PA. On the other hand, the ICT decrees that the first-orderist is rationally obliged to count both \(\text {G}(\textsf {PA})\) and \(\text {Con}(\textsf {PA})\) among their implicit commitments on the basis of their acceptance of PA.Footnote 4 Thus, the corresponding version of the ICT is incompatible with the epistemic stability of first-orderism, and a generalized line of reasoning serves to show that the ICT is incompatible with the idea of epistemic stability, period.
This incompatibility motivates one specific goal of this paper. We propose nuanced understandings of epistemic stability and the implicit commitment thesis, and argue that on these understandings, the two notions are compatible after all.
Second, the tension between ideas (2) and (3) above. There are at least two obstacles inherent in (3), the idea that we should like to accept various soundness assertions involving a notion of truth for a system of axioms S, on the basis of accepting S itself. One: soundness assertions involving the notion of truth are not typically expressible in the language of S. Two: most truth-free surrogates of soundness assertions for S are not provable in S. Accounts attempting to overcome these problems typically appeal to the notion that in accepting S, one is thereby warranted in accepting reflection principles for S (Cieśliński, 2010, 2017; Feferman, 1962, 1991; Fischer, 2021; Fischer et al., 2021; Franzén, 2004; Horsten & Leigh, 2016; Ketland, 2005, 2010; Shapiro, 1998; Tennant, 2002, 2005; Turing, 1939).Footnote 5Footnote 6 But then the idea in (3) sits in tension with the idea of epistemic stability. For on one hand, a natural way to cash out the idea in (3) is to say that we should like to accept reflection principles involving a notion of truth for a theory S, on the basis of accepting S itself. But on the other hand, for a foundationalist who subscribes to the idea of epistemic stability, accepting S provides no epistemic obligation to accept corresponding reflection principles for S.
This tension motivates a second specific goal of this paper. We leverage our proposed understandings of epistemic stability and the implicit commitment thesis to formulate an account of arithmetic theory acceptance which accommodates certain reflection principles for an arithmetic base theory, and the epistemic stability of suitable foundational positions (thus dissolving the tension between (2) and (3) above). This account of theory acceptance draws on the account in Nicolai and Piazza (2019), and is comprised of two components, semantic and schematic. Our components of arithmetic theory acceptance reveal exactly the sets of principles such that, if acceptance of those sets of principles is warranted purely on the basis of accepting S, then the resulting picture is compatible with both a version of epistemic stability, and the implicit commitment thesis. Thus, overall, we aim to provide a conception of arithmetic theory acceptance according to which all three motivating ideas in existing discourse are compatible after all.
With our specific goals motivated, let us describe our approach. We address our first goal in Sect. 2. We make some observations on the notion of epistemic stability and the implicit commitment thesis, and tease apart two weaker versions of both of these notions. We adopt our weaker understandings of these notions going forward. To address our second goal, in Sect. 3 we survey a recent attempt to provide an account of arithmetic theory acceptance which accommodates certain reflection principles for an arithmetic base theory, and the epistemic stability of suitable foundational positions (Nicolai & Piazza, 2019). While this account has merits, we also believe it has problems. We use this account as a sort of diagnostic tool, and interleave our survey with our proposed framework for analyzing the idea of arithmetic theory acceptance. Our framework helps clarify what we think the essence of the problem is with the account in Nicolai and Piazza (2019) with respect to first-orderism, which we set out in Sect. 4. In Sect. 5, we provide the proof of a result, which yields a plausible alternative conception of the first-orderist’s implicit commitments to that proposed in Nicolai and Piazza (2019). In Sect. 6, we conclude.
2 Weak epistemic stability and the weak ICT
First, we propose weaker understandings of epistemic stability and the implicit commitment thesis, and argue that on these understandings, the two notions are compatible. To motivate our proposal, observe that the idea of epistemic stability as formulated in Dean (2015), and the implicit commitment thesis, are very close to being logically incompatible. Recall: a theory S is epistemically stable if there exists a coherent rationale for accepting S that does not entail or otherwise rationally oblige a theorist to accept statements which cannot be derived from the axioms of S. If we suppose that:
-
(1)
if there exists a coherent rationale for accepting S, then it is possible for one to accept S;
-
(2)
if the implicit commitment to accept featured in the ICT implies an entailment or otherwise rational obligation to accept; and
-
(3)
if accepting S implies accepting the axioms of S;
then epistemic stability is logically incompatible with the ICT. For if S is epistemically stable per Dean’s definition and (1)–(3) are true, then it follows that a theory S is epistemically stable if it is possible for one to accept the axioms of S but not be committed to accept statements which cannot be derived from the axioms of S. But the ICT then implies that anyone’s acceptance of the axioms of S entails or otherwise rationally obliges one to accept statements which cannot be derived from the axioms of S. Thus, it cannot be the case that S is both epistemically stable while the ICT holds for S.
These observations reveal at least three ways in which the notion of epistemic stability associated with first-orderism might be reconciled with the corresponding version of the ICT. One might try and argue that at least one of (1)–(3) are false, or at least that a first-orderist would think that at least one of (1)–(3) are false. However, we anticipate that any such argument would be difficult to make, and will not attempt to do so. Rather, the point of making these observations is to argue that the notion of epistemic stability defined in Dean (2015) is particularly strong; so strong that in fact it is very close to being logically incompatible with the ICT. Thus, we concede, that all things considered, the strong version of epistemic stability probably cannot be reconciled with this version of the ICT. However, rather than leaving things here, what we want to do is modify both this strong version of epistemic stability, and the articulation of the ICT, so that the modified versions are reconcilable in interesting ways. In particular, we want to tease apart the strong version of epistemic stability from a weaker version, offer a weaker version of the ICT, and subsequently argue that it is the weaker version of epistemic stability which can be reconciled with the weaker version of the ICT in interesting ways.
We make these modifications in a couple of stages. First consider epistemic stability. Recall this notion again: a theory S is epistemically stable if there exists a coherent rationale for accepting S that does not entail or otherwise rationally oblige a theorist to accept statements which cannot be derived from the axioms of S. “Statements” here is understood as any statements, and our first step in isolating the weaker notion of epistemic stability that we are interested in, is to relax that requirement. Instead of ruling out the availability of any statements which cannot be derived from the axioms of S, we require only that statements in the language of S which cannot be derived from the axioms of S are ruled out. Denoting the language of S by \({\mathcal {L}}_{\textsf {S}}\), we therefore propose the following, weaker notion of epistemic stability:
A theory S is epistemically stable for \({\mathcal {L}}_{\textsf {S}}\)-sentences, abbreviated as \({\mathcal {L}}_{\textsf {S}}\)-epistemically stable, if there exists a coherent rationale for accepting S that does not entail or otherwise rationally oblige a theorist to accept statements in the language of S which cannot be derived from the axioms of S.
To isolate the weaker version of the ICT we are interested in, we make an analogous move. Recall the ICT: anyone who accepts the axioms of a mathematical theory S is thereby also implicitly committed to accepting various additional statements \(\Gamma \) which are expressible in the language of S but which are formally independent of its axioms. Now, we are going to broaden the class of additional statements \(\Gamma \) the acceptor is implicitly committed to accepting to any statements, rather than merely statements expressible in the language of S. We therefore propose the following, weaker version of the ICT:
(Weak ICT): anyone who accepts the axioms of a mathematical theory S is thereby also implicitly committed to accepting various additional statements \(\Gamma \) which are formally independent of its axioms.
Weakening both the original notion of epistemic stability and the original version of the ICT in this way, we immediately have at our disposal new possible strategies for reconciling the notion of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability for first-orderism with the corresponding version of the weak ICT. For example, one might now try to argue that the first-orderist’s acceptance of PA entails or otherwise rationally obliges the first-orderist to accept sentences not in the language of PA. On one hand, this would serve to make the case that the first-orderist accepts the weak ICT. On the other hand, if one could show that the extension of PA by those sentences cannot derive anything in the language of PA that PA could not already derive – if the extension of PA by those sentences were syntactically conservative over PA – then the first-orderist’s position is compatible with the idea of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability.Footnote 7 This is the essence of the approach in Nicolai and Piazza (2019), so let us turn now to that account, and develop our proposed account of arithmetic theory acceptance.
3 A framework for resolution
In their (2019) paper, Nicolai and Piazza propose an account of theory acceptance which aims to reconcile the notions of what we have called \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability and the weak ICT. In Sect. 3.1 we survey this account. In Sect. 3.2 we propose our framework for analyzing candidate theories of implicit commitments with respect to \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability and the weak ICT.
3.1 The semantic core
The central thesis in Nicolai and Piazza (2019) is this:
when accepting a [mathematical] system S, we are bound to accept a fixed set of principles extending S and expressing minimal soundness requirements for S... there is also a variable component of implicit commitment that crucially depends on the justification given for our acceptance of S. (Nicolai & Piazza, 2019, p. 913)
The fixed set of principles extending S and expressing minimal soundness requirements for S is called the semantic core of S. These principles are formulated in the extension of the language of S by a new unary predicate T(x), intended as a truth predicate. The goal is to ensure that the semantic core of S is a conservative extension of S. However, whether or not the semantic core exhausts one’s implicit commitments depends on the particular foundational standpoint that leads one to accept a given theory S in the first place (Nicolai & Piazza, 2019, p. 929). In particular, in some cases, there are non-semantic considerations that feature in the justification for certain foundational standpoints. These considerations have to do with attitudes towards schematic reasoning, in particular, the extent to which one is implicitly committed to instances of induction schema in which predicates occur that are not part of the language of S. As a result, in addition to the semantic core, there is a variable component of theory acceptance, one that can be articulated in terms of implicit schematic commitments.
Thus, the general idea is this: on one hand, a foundationalist’s acceptance of a given base theory S implicitly commits that foundationalist to accept sentences not in the language of S (the semantic core of S). As a result, that foundationalist accepts the weak ICT. But for suitable theories S, the semantic core of S is conservative over S. This is the content of the following (Leigh, 2015, Theorem 1):
Theorem 1
(Leigh) Let \(\textsf {S}\) interpret \(\textsf {I}\Delta _0 + \text {exp}\). Then the semantic core of S is a conservative extension of S.
To prove Theorem 1 we formulate the semantic core of S, which we will denote by \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\),Footnote 8 as a sequent calculus which includes the following cut rule for truth:

Here, \(\Gamma , \Delta \) denote finite sets of formulas in the language of S expanded to include the truth predicate T.
Also, we consider a bounded version \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) of \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\), where the rule \((\text {Cut}_T)\) is replaced by the following schema of bounded cut rules, one for each \(k < \omega \):

Here,  reads: the logical depth of the \({\mathcal {L}}_{\textsf {S}}\)-sentence \(\varphi \) is \(< k\). Derivations in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) and \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) are defined in the usual way. The truth rank of a derivation is the least r such that for any rule \((\text {Cut}_T^k)\) occurring in the derivation, \(k < r\). A standard reduction argument is used to show that if the sequent \(\Gamma \Rightarrow \Delta \) is derivable in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) with truth rank \(r+1\), then there is a derivation of the same sequent with truth rank r, whence \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) is conservative over S. \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) is then embedded into \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) using the notion of approximations from Kotlarski et al. (1981). Derivations in \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) are replaced by approximations with bounded depth, and so can be carried out in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\). Since \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) is conservative over S, so is \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\).
reads: the logical depth of the \({\mathcal {L}}_{\textsf {S}}\)-sentence \(\varphi \) is \(< k\). Derivations in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) and \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) are defined in the usual way. The truth rank of a derivation is the least r such that for any rule \((\text {Cut}_T^k)\) occurring in the derivation, \(k < r\). A standard reduction argument is used to show that if the sequent \(\Gamma \Rightarrow \Delta \) is derivable in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) with truth rank \(r+1\), then there is a derivation of the same sequent with truth rank r, whence \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) is conservative over S. \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) is then embedded into \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) using the notion of approximations from Kotlarski et al. (1981). Derivations in \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) are replaced by approximations with bounded depth, and so can be carried out in \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\). Since \((\textsf {S}^T_{\text {Ax}_{\textsf {S}}})^{*}\) is conservative over S, so is \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\).
Thus, for suitable S, the foundationalist’s acceptance of S does not entail or otherwise rationally oblige that foundationalist to accept additional sentences in the language of S. The resulting picture is such that the foundationalist may come to accept a set of implicit commitments expressing minimal soundness requirements for S in such a way that these implicit commitments are also compatible with the idea of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability. In this way, for a range of foundational positions, the notion of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability and the weak ICT are reconciled after all, in such a way that minimal soundness requirements for S are also accommodated.
We think this account has merits. In particular, we broadly agree that the components of implicit commitment are plausible components for an account of theory acceptance. However, we think this account falls short in supposing that one component of theory acceptance is fixed, and that one is variable. In particular, we think the idea that the semantic core is a fixed component of theory acceptance is too strong. To say why, first we introduce a general framework for analyzing the two components of theory under consideration with respect to the following three goals: (1) isolating sets of implicit commitments for suitable theories S which express minimal soundness requirements for S, (2) isolating sets of implicit commitments for suitable theories S which meet the criteria for \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability, and (3) isolating sets of implicit commitments for suitable theories S which satisfy the weak ICT. We believe this framework offers a clear way of analyzing how these goals are to be met, and a clear way of drawing out what we think the problem is with the idea of a fixed semantic component and a variable schematic component.
3.2 Components of arithmetic theory acceptance
We offer a framework for analyzing two components of theory acceptance, for various choices of a suitable arithmetical base theory S. While we focus on the case where S = PA later on, by “suitable,” we take S to be any one of the following theories: Buss arithmetic \(\textsf {S}^1_2\),Footnote 9 the theory QF–IA,Footnote 10 or the fragments \(\textsf {I}\Sigma _n\) of PA (for \(n \in \omega \)).Footnote 11 For instance, we note that the framework of this paper (and the results in Sect. 5) cannot be applied uniformly to fully general choices of S; we require S at least be recursively axiomatizable, first-order schematically formulated, and contain suitable syntactic coding resources.
For definiteness, we take the (non-logical part of the) language of the fragments \(\textsf {I}\Sigma _n\) of PA, and the language of PA, to be the language of arithmetic \({\mathcal {L}}_A = \{0, 1, S, +, \cdot , \le \}\). The language of QF–IA is the quantifier-free version of \({\mathcal {L}}_A\). The language of \(\textsf {S}^1_2\) is \(\{0, S, +, \cdot , | \cdot |, \#, \llcorner \frac{\cdot }{2} \lrcorner \}\), where \(| \cdot |\) is the unary function such that |x| returns the number of symbols in the binary representation of x, \(\#\) is the binary function \(\#(x, y) = 2^{|x| \cdot |y|}\), and \(\llcorner \frac{\cdot }{2} \lrcorner \) is the unary function such that \(\llcorner \frac{x}{2} \lrcorner \) returns the lower integer part of \(\frac{x}{2}\).
For suitable S, we fix the following preliminaries and notational conventions.
-
1.
We denote the language of S by \({\mathcal {L}}_{\textsf {S}}\). We denote the language obtained by expanding \({\mathcal {L}}_{\textsf {S}}\) with a new unary predicate T(x) (intended as a truth predicate) by \({\mathcal {L}}_T\).Footnote 12
-
2.
We assume a fixed Gödel coding of \({\mathcal {L}}_{\textsf {S}}\) into \({\mathcal {L}}_A\), which extends to finite sequences of \({\mathcal {L}}_{\textsf {S}}\)-terms. In particular we have unary predicates \(\text {Sent}_{{\mathcal {L}}_{\textsf {S}}}(x)\) and \(\text {Ax}_{\textsf {S}}(x)\) representing the sets of Gödel codes of \({\mathcal {L}}_{\textsf {S}}\)-sentences and \({\mathcal {L}}_{\textsf {S}}\)-axioms respectively. We extend this notation in the natural way to languages \({\mathcal {L}}\) extending \({\mathcal {L}}_{\textsf {S}}\).
-
3.
Roman lower-case letters s, t, etc. range over (codes of) \({\mathcal {L}}_{\textsf {S}}\)-terms.
-
4.
Greek lower-case letters \(\varphi , \psi \) etc. from the end of the alphabet range over \({\mathcal {L}}_A\)-terms encoding \({\mathcal {L}}_{\textsf {S}}\)-formulas.
In what follows, we denote the xth numeral by \({\underline{x}}\) (i.e. the closed term resulting from x applications of the successor function). We denote the result of formally evaluating the (code of the) term t by \(t^{\circ }\). For readability, unless there is value in writing down Quine corners, we generally omit them when referring to Gödel codes of syntactic objects.
We denote the theory of a foundationalist’s implicit commitments on the basis of their acceptance of suitable S as an \({\mathcal {L}}_T\)-theory I(S) extending S. This aligns with the idea that the foundationalist’s implicit commitments in accepting S are sentences in the extended language.
Next, we axiomatize two components of theory acceptance. One of these components we call the semantic component of accepting S, intended to capture implicit commitments about (the behavior of) truth, along with minimal soundness principles for S. The second of these components we call the schematic component of accepting S, intended to capture implicit commitments about extending S’s induction schema to permit the occurrence of the truth predicate. These two components of accepting S align respectively with what Nicolai and Piazza (2019) call the fixed and variable components of accepting S. Our choice of titles for these two components of accepting S stems from our disagreement with the use of “fixed” and “variable” as they are used by Nicolai and Piazza (2019) to describe the two components.
The semantic component of accepting S is axiomatized by the following four \({\mathcal {L}}_T\)-theories extending S.
Definition 1
\(\textsf {S}^U\) is the \({\mathcal {L}}_T\) theory extending S with the schema of uniform Tarski biconditionals for \({\mathcal {L}}_{\textsf {S}}\); i.e. all sentences of the form:
for every \({\mathcal {L}}_{\textsf {S}}\)-formula \(\varphi (x_1, \dots , x_n)\).
Definition 2
\(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\) is the \({\mathcal {L}}_T\) theory \(\textsf {S}^U + \forall x (\text {Ax}_{\textsf {S}}(x) \rightarrow T(x))\). We call \(\forall x (\text {Ax}_{\textsf {S}}(x) \rightarrow T(x))\) the axiom soundness axiom for S.
In conjunction with minimal principles governing the behavior of the truth predicate (i.e., uniform Tarski biconditionals), which are really what license the name “truth” for the predicate T(x), the axiom soundness axiom for S says that all the axioms of S are true. The axiom soundness axiom for S is precisely the minimal soundness requirement for S aimed at in Nicolai and Piazza (2019).
Definition 3
\(\textsf {S}^T\) is the \({\mathcal {L}}_T\) theory extending S with the following fully compositional truth axioms:
-
1.
\(\forall x (T(x) \rightarrow \text {Sent}_{{\mathcal {L}}_{\textsf {S}}}(x))\).
-
2.
\(\forall s, t (T( \ulcorner s=t \urcorner ) \leftrightarrow (s^{\circ } = t^{\circ }))\).
-
3.
\(\forall \varphi (T(\ulcorner \lnot \varphi \urcorner ) \leftrightarrow \lnot T(\ulcorner \varphi \urcorner ))\).
-
4.
\(\forall \varphi , \psi (T(\ulcorner \varphi \vee \psi \urcorner ) \leftrightarrow (T( \ulcorner \varphi \urcorner ) \vee T(\ulcorner \psi \urcorner )))\).
-
5.
\(\forall v \forall \varphi (v) (T(\ulcorner \exists v \varphi ({\underline{v}}) \urcorner ) \leftrightarrow \exists x T( \ulcorner \varphi ({\underline{x}}) \urcorner ))\).
Definition 4
\(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) is the \({\mathcal {L}}_T\) theory \(\textsf {S}^T + \forall x (\text {Ax}_{\textsf {S}}(x) \rightarrow T(x))\).
We note that in a general setting, the axiom soundness axiom for S is a non-trivial addition to principles 1–5: theories that are not finitely axiomatizable cannot prove the corresponding axiom soundness axiom in the presence of principles 1–5.Footnote 13 However, finitely axiomatizable theories can.
The theory \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) is precisely the semantic core of S (Nicolai & Piazza, 2019, p. 928). As we noted, the axiom soundness axiom for S captures the idea of minimal soundness requirements for S. Fully compositional truth is motivated by the desiderata that the semantic core ought to be able to establish that instances of modus ponens preserve truth, and that the semantic core ought to capture a compositional notion of truth (Nicolai & Piazza, 2019, pp. 926–927). Crucially, in each of the four theories defined above, the predicate T(x) is not allowed to appear in instances of S’s induction schema. For a variety of arithmetical theories S, it is well-known that the result of expanding the language of S with a new unary predicate T(x) which is fully compositional and allowed to occur in formulas appearing in S’s induction schema is not conservative over S.Footnote 14
For suitable fixed S, the four theories above axiomatize four degrees of the semantic component of accepting S. They are four possible ways of capturing the foundationalist’s implicit semantic commitments in accepting S. Together with the trivial position, according to which the foundationalist has no implicit semantic commitments in accepting S, we may depict five degrees of the foundationalist’s implicit semantic commitment in accepting S in the following way.Footnote 15
This picture is more fine-grained than the picture in Nicolai and Piazza (2019). There, the semantic core \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) of S is a fixed component of implicit semantic commitment in accepting S. However, in what follows, we will be interested in what happens when we consider implicit commitments which do not contain the full resources of \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\). Thus, we take this finer approach.
To axiomatize degrees of implicit schematic commitment, we consider the case where the predicate T(x) is allowed into instances of the induction schema of each of the theories \(\textsf {S}^U\), \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\), \(\textsf {S}^T\), and \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\). Instances of induction schema are stratified according to the complexity of formulas appearing in them in the usual way. We say that a formula is \(\Delta _0\) if all quantifiers it contains are bounded. We say that a formula is \(\Sigma _1\) (resp. \(\Pi _1\)) if it is of the form \(\exists x \varphi \) (resp. \(\forall x \varphi \)) where \(\varphi \) is \(\Delta _0\). We say that a formula is \(\Sigma _n\) (resp. \(\Pi _n\)) if it is of the form \(\exists x \varphi \) (resp. \(\forall x \varphi \)) where \(\varphi \) is \(\Pi _{n-1}\) (resp. \(\Sigma _{n-1}\)). We say that a formula is \(\Delta _n\) if it is both \(\Sigma _n\) and \(\Pi _n\). The theory \(\textsf {I}\Gamma \) is Robinson Arithmetic Q plus induction for formulae in the class \(\Gamma \).
Definition 5
Let S be a suitable arithmetic theory and let \(\textsf {W}\) be any of \(\textsf {S}^U\), \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\), \(\textsf {S}^T\), or \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\). Then \((\textsf {W})_n\) is the \({\mathcal {L}}_T\)-theory axiomatized by \(\textsf {I}\Sigma _n({\mathcal {L}}_T)\), i.e., the \({\mathcal {L}}_T\)-theory extending W with instantiations of the induction scheme for \({\mathcal {L}}_T\)-formulas in the class \(\Sigma _n\). \((\textsf {W})_{\omega }\) is the \({\mathcal {L}}_T\)-theory axiomatized by \(\bigcup _{n \in \omega } \textsf {I}\Sigma _n({\mathcal {L}}_T)\).
When \(n = 0\), we write “\(\Delta _0(T)\)-induction” in place of “\(\Sigma _0(T)\)-induction.” Putting everything together, Fig. 2 below depicts the semantic and schematic components of implicit commitment in accepting a suitable arithmetic theory S. It will turn out that some of the theories of Fig. 2 coincide, but we address that further on.
Together, the semantic and schematic components of accepting S align respectively with what Nicolai and Piazza (2019) call the fixed and variable components of accepting S. According to their account, the semantic core of S is a fixed component of implicit semantic commitment in accepting S. On the other hand, whether or not the semantic core exhausts one’s implicit commitments depends on the particular foundational standpoint that leads one to accept a given theory S in the first place (Nicolai & Piazza, 2019, p. 929). In particular, if the S-foundationalist is implicitly committed to instances of induction in which the truth predicate occurs, then the S-foundationalist’s implicit commitments in accepting S may also include non-trivial schematic implicit commitments. Thus, this type of commitment may vary from foundationalist to foundationalist.
We are now in a position to draw out what we think the problem is with the idea that of a fixed semantic component of implicit commitment, and a variable schematic component of implicit commitment, in accepting S.
4 The problem with a fixed semantic core
To motivate the problem, let us first consider some remarks about what Nicolai and Piazza (2019) call the variable component of implicit commitment. The variable component of acceptance is introduced to us by way of several examples of different foundational standpoints which adopt different views on extending the induction schema of the arithmetical systems associated with them (Nicolai & Piazza, 2019, Section 4). Nicolai and Piazza argue that these views depend on the justification given for a particular foundational theory itself. Here are three examples.
First, consider the case in which one does not allow extensions of the induction schema to permit vocabulary beyond that of the base theory at all. A paradigmatic example of this sort is finitism as articulated by Tait (1981). We take the associated foundational theory to be QF–IA, a conservative extension by first-order quantifiers of Primitive Recursive Arithmetic.Footnote 16 The finitist is committed to instances of QF–IA’s induction schema on the basis of their acceptance of QF–IA insofar as those instances involve predicates that are expressible by a quantifier-free version of the language of arithmetic. By Tarski’s theorem on the undefinability of truth, a full truth predicate is not expressible by any formula in the language of arithmetic. Thus, for the finitist, the justification for claims about the totality of the natural numbers made via the extension of QF–IA’s induction schema to permit a (fully compositional) truth predicate is not implicit in the finitist’s acceptance of QF–IA. What’s more, the finitist is reluctant to admit that QF–IA’s induction schema even applies to predicates that are not expressible by formulas in the language of QF–IA. This is grounded in the justification the finitist gives for QF–IA itself. Such predicates are suspicious at best, and false at worst (Nicolai & Piazza, 2019, p. 930).
Second, consider the case in which one accepts instances of extended induction schema unrestrictedly, on the basis that one accepts an associated theory. The paradigmatic example of this sort is Feferman’s reflective closure of a theory S (1991). There are two versions of this. The first is the reflective closure \(\text {Ref}(\textsf {S})\) of a theory S. \(\text {Ref}(\textsf {S})\) captures statements in the base language \({\mathcal {L}}\) of S that ought to be accepted on the basis of accepting the basic axioms and rules of S. The second is the schematic reflective closure \(\text {Ref}^{*}(\textsf {S}(P))\) of a schematic version \(\textsf {S}(P)\) of a theory S. \(\text {Ref}^{*}(\textsf {S}(P))\) captures schemata in the language of \(\textsf {S}(P)\) that ought to be accepted on the basis of accepting the basic schematic axioms and rules of \(\textsf {S}(P)\). Where S is PA, in the case of the reflective closure of PA, one obtains the self-applicable theory of truth KF, and \(\text {Ref}(\textsf {PA})\) reaches the strength of ramified analysis up to \(\epsilon _0\). In the case of the schematic reflective closure of PA, one obtains a type-free theory of truth, and \(\text {Ref}(\textsf {PA})\) reaches the strength of ramified analysis up to the Feferman-Schütte ordinal \(\Gamma _0\) (Feferman, 1964; Schütte, 1964).Footnote 17
Third, consider the first-orderist. The two preceding positions hold different views about extending induction—views that roughly, are at either end of the extreme. According to Nicolai and Piazza, the first-orderist holds a third kind of view, which occupies what they call an intermediate position between the two preceding positions (Nicolai & Piazza, 2019, p. 931). On one hand, in the spirit of Feferman (and unlike the finitist), the first-orderist holds no particular reservations about the application of PA’s induction schema to predicates that are not expressible by formulas in the language of arithmetic. On the other hand, the first-orderist’s acceptance of instances of PA’s induction schema that involve a truth predicate, if the first-orderist accepts such instances at all, is essentially higher-order/infinitary/non-arithmetical.Footnote 18 The thought seems to be that this is more in keeping with the spirit of the finitist idea above: that the justification for claims about the totality of the natural numbers made via the extension of QF–IA’s induction schema to permit a (fully compositional) truth predicate is not implicit in the finitist’s acceptance of QF–IA.
Recall Fig. 2, and let S be PA. Using our framework, let us analyze which theory corresponds to the first-orderist’s implicit commitments I(PA) in accepting PA, based on the account in Nicolai and Piazza (2019). First, consider the semantic component. If the semantic core of PA is a fixed component of the first-orderist’s implicit commitments in accepting PA, then \(\textsf {I}(\textsf {PA})\) contains at least the theory \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\). Second, consider the schematic component. The theories PA, \((\textsf {PA})_n\), for each \(n \in \omega \), and \((\textsf {PA})_{\omega }\), are our formal representation of accepting various (sets of) instances of PA’s induction schema which permit the occurrence of the truth predicate on the basis of the first-orderist’s acceptance of PA.Footnote 19 In light of the remarks above, let us consider the following question: which of the theories PA, \((\textsf {PA})_n\), for each \(n \in \omega \), and \((\textsf {PA})_{\omega }\), correspond to what the first-orderist’s implicit commitments about extensions of PA’s induction schema are, on the basis of their acceptance of PA?
On the account in Nicolai and Piazza (2019), the answer cannot be any of the theories \((\textsf {PA})_n\), or the theory \((\textsf {PA})_{\omega }\). First consider \((\textsf {PA})_{\omega }\). If the semantic core of PA is a fixed component of the first-orderist’s implicit commitments in accepting PA, then \(\textsf {I}(\textsf {PA})\) contains at least the theory \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\). But if in addition \(\textsf {I}(\textsf {PA})\) contains \((\textsf {PA})_{\omega }\) we seem to be in some trouble. It is well-known that the result of extending PA by fully compositional truth and fully extended induction is not conservative over PA. For example, in the resulting theory, one easily derives the following global reflection principle:Footnote 20

Furthermore, from (\(\text {GRP}_{\textsf {PA}}\)), one can derive, for instance, \(\text {Con}(\textsf {PA})\) (by instantiating the falsity \(0 \ne 1\) in (\(\text {GRP}_{\textsf {PA}}\))). Thus, \(\text {Con}(\textsf {PA})\) is also part of \(\textsf {I}(\textsf {PA})\). So in fact, we are faced with the issue in Dean (2015) again. In any case, we have lost sight of one of the goals we set out to achieve: a set of implicit commitments on the basis of the first-orderist’s acceptance of PA compatible with the idea of \({\mathcal {L}}_{\textsf {PA}}\)-epistemic stability – the idea that in accepting PA, the first-orderist is not forced by entailment or rational obligation to accept statements in the language of PA not derivable from the axioms of PA.
Now consider any of the theories \((\textsf {PA})_n\), for some \(n \in \omega \). The situation is similar. Consider for example \((\textsf {PA})_0\), which corresponds to the very least non-trivial set of implicit commitments about extensions of PA’s induction schema the first-orderist may accept on the basis of their acceptance of PA. If the semantic core of PA is a fixed component of the first-orderist’s implicit commitments in accepting PA, and \((\textsf {PA})_0\) is also part of the first-orderist’s implicit commitments in accepting PA, then I(PA) contains at least the theory \((\textsf {PA}^T)_0\). And from \((\textsf {PA}^T)_0\), we can again obtain \(\text {Con}(\textsf {PA})\). The reason is that \((\textsf {PA}^T)_0\) plus the global reflection principle (\(\text {GRP}_{\textsf {PA}}\)) above is relatively interpretable in \((\textsf {PA}^T)_0\).Footnote 21 This is the content of the following:Footnote 22
Theorem 2
(Wcisło, Łełyk) \((\textsf {PA}^T)_0 + \forall \varphi (\text {Pr}_{\textsf {PA}}(\varphi ) \rightarrow T( \varphi ))\) is interpretable in \((\textsf {PA}^T)_0\) relative to PA.
The strategy is to recursively define a family of partial arithmetic truth predicates \(T_n(x)\), for \(n \in \omega \). This ensures that there is an arithmetical expression \(x = T_n(v)\) representing in PA the recursive function assigning to n the code of the formula \(T_n(v)\). For each \(n \in \omega \), we may then apply the truth predicate to the code of \(T_n(x)\) to obtain a family of predicates \(T(\ulcorner T_c(x) \urcorner )\), where the parameter c is possibly nonstandard. In the presence of \(\Delta _0(T)\)-induction, the predicates \(T(\ulcorner T_c(x) \urcorner )\) are like truth predicates in the sense that they are compositional for formulas with codes less than c. The defining formula \(T'(x)\) satisfying the axioms of \((\textsf {PA}^T)_0 + (\text {GRP}_{\textsf {PA}})\) is then constructed by taking the supremum of the predicates \(T(\ulcorner T_c(x) \urcorner )\). See Wcisło and Łełyk (2017) or Cieśliński (2017, Theorem 12.3.4) for a full proof.
Thus, again, we have lost sight of one of the goals we set out to achieve: a set of implicit commitments on the basis of the first-orderist’s acceptance of PA compatible with the idea of \({\mathcal {L}}_{\textsf {PA}}\)-epistemic stability.
So, the theories \((\textsf {PA})_n\), for each \(n \in \omega \), and the theory \((\textsf {PA})_{\omega }\), are off the table, and on the account in Nicolai and Piazza (2019), PA itself must correspond to the first-orderist’s implicit schematic commitments, on the basis of their acceptance of PA. But so far, so good: this looks consistent with Nicolai and Piazza’s remarks about the first-orderist’s variable schematic stance. For they say that if the first-orderist comes to accept instances of PA’s induction schema in which the truth predicate occurs, this acceptance does not follow merely from their acceptance of PA. That is: the first-orderist accepts no instances of PA’s induction schema in which the truth predicate occurs on the basis of their acceptance of PA.
But let us pause and reflect for a moment. At first glance, this might seem at odds with the idea that the first-orderist occupies an intermediate position between the finitist and foundationalists à la Feferman. For as far as truth in induction is concerned, the schematic implicit commitments of the first-orderist and the finitist are the same. Neither foundationalist accepts instances of their respective base theory’s induction schema in which the truth predicate occurs, on the basis of their acceptance of their respective base theory. But of course, there are still differences between the finitist’s and first-orderist’s attitudes towards extending induction. The finitist, for example, refuses to permit quantifiers into QF–IA’s induction schema. The first-orderist has no such qualms. So, if PA itself corresponds to the first-orderist’s implicit commitments about extensions of PA’s induction schema, then perhaps it is just that our acceptance framework fails to reveal any differences between the two foundationalists.
We think this is a hasty conclusion. We will return to it in Sect. 6. For now, let us reflect a little further. Consider the following dialogues. If one were to ask the finitist: “on the basis of accepting QF–IA, do you thereby accept instances of QF–IA’s induction schema in which the truth predicate occurs?” then we expect the answer to be something along the lines of: “no, I don’t think those instances of induction are acceptable at all.” But if one were to ask the first-orderist an analogous question, with PA in place of QF–IA, then we expect the answer to be something along the lines of: “no, but this is not to say that those instances of induction are unacceptable.” In other words: based on the tenets of both foundational positions, we really ought to be able to use attitudes towards truth in induction to distinguish the two. A natural follow up question to the first-orderist’s response is this: “if they are not unacceptable, then what reasons would you cite for accepting instances of PA’s induction schema in which the truth predicate occurs?” To which the first-orderist might reply by citing some higher-order, infinitary, or non-arithmetical justification.
Our key observation, is that one would expect to have a similar conversation with the first-orderist, about the fully compositional truth axioms for sentences of PA. If one were to ask the first-orderist: “on the basis of accepting PA, do you thereby accept the fully compositional truth axioms for sentences of PA?” then we expect the answer to be something along the lines of: “no, but this is not to say that those axioms are unacceptable.” And if we were to follow up by asking: “if they are not unacceptable, then what reasons would you cite for accepting those axioms?” then the first-orderist might reply by citing some higher-order, infinitary, or non-arithmetical justification.
Indeed, we claim that the problem with the idea of a fixed semantic core, is that it obscures the fact that one would expect to have this conversation with the first-orderist, about the fully compositional truth axioms for sentences of PA. If the first-orderist’s implicit commitments in accepting PA includes the theory \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\), then the first-orderist is forced to adopt a trivial position with regard their schematic implicit commitments. And notice in particular that it is the presence of the fully compositional truth axioms which forces the first-orderist into this position. (This by the observation above that \((\textsf {PA}^T)_0\) is not conservative over PA. So it does the first-orderist no good to give up on axiom soundness.) Rather than taking into account the idea that the first-orderist’s acceptance (if any) of the fully compositional truth axioms is grounded in higher-order/infinitary/non-arithmetical reasons, a fixed semantic core of implicit commitments simply decrees that the first-orderist accepts the fully compositional truth axioms by virtue of accepting PA.
To be clear, we do not think that the latter is necessarily a problem in itself: by weakening the ICT in the way that we did, and by pursuing the strategy of isolating a set of implicit commitments in the extended language \({\mathcal {L}}_T\), we cannot help but lose sight of the idea that we force the first-orderist into a position whereby they accept some statements beyond the logical reach of PA on the basis of their acceptance of PA. But this is true no matter which set of implicit commitments we opt for on our framework. To even attempt to articulate sets of implicit commitments on the basis of their acceptance of PA in the way that we have – in such a way to satisfy the weak ICT – we must go beyond the strict tenets of first-orderism.
Our complaint is that there is no reason at this stage to think that we ought to opt for fully compositional truth axioms at the expense of instances of PA’s induction schema in which the truth predicate occurs. For what reason do we have to think there is anything in the tenets of first-orderism, which would make the first-orderist prefer accepting a fully compositional theory of truth, over truth in induction, on the basis of their acceptance of PA? There is no evidence in the tenets of first-orderism itself that favors one of these sets of principles to the other in this respect. For according to the strict tenets of first-orderism, acceptance of either set of principles does not follow from the first-orderist’s acceptance of PA itself. Thus, we claim that the idea of a fixed semantic core is too strong. As far as first-orderism is concerned, there is no reason at this point to think we should adopt a conception of PA-acceptance which favors fully compositional truth over truth in induction.Footnote 23
However, we are not done yet. The stakes would change, if opting instead for instances of PA’s induction schema in which the truth predicate occurs, results in non-conservative extensions of PA. For this would violate epistemic stability, one of the principles we set out to respect, and so there might be reason to prefer the semantic core of PA after all.
But this is not the case. Of course, it is well-known that each of the theories \((\textsf {PA}^U)_n\), for each \(n \in \omega \), and \((\textsf {PA}^U)_{\omega }\), are conservative over PA.Footnote 24 However, those theories are poor candidates for the first-orderist’s implicit commitments, for in each of those cases we lose the minimal soundness requirement we set out to retain. Of the remaining theories in our framework which correspond to a non-trivial implicit schematic commitment, that leaves the following for investigation:
-
\((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_n\), for each \(n \in \omega \), and \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\).
-
\((\textsf {PA}^U)_n\), for each \(n \in \omega \), and \((\textsf {PA}^U)_{\omega }\).
-
\((\textsf {PA})_n\), for each \(n \in \omega \), and \((\textsf {PA})_{\omega }\).
To bolster our claim that the idea of a fixed semantic core is too strong, and draw our argument to a close, next we show that each of the theories above are conservative extensions of PA. Thus, in particular, the maximal theory among those above, the theory \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\), is a perfectly plausible candidate for the first-orderist’s implicit commitments in accepting PA.
5 Another resolution
Theorem 3 below shows that each of the theories \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_n\), for each \(n \in \omega \), and \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\), are conservative over PA. Thus, we provide a complete classification of the theories of Fig. 2, where S is PA, with respect to conservativity over PA.
Theorem 3 states that the theory obtained by adding to PA the uniform Tarski biconditionals, the full induction schema for \({\mathcal {L}}_T\)-formulas, and the following axiom:
is conservative over PA. Here D(x) is a PA-schema, defined below. The case of interest is where D(x) is \(\text {Ax}_{\textsf {PA}}(x)\), the formula expressing that x is the code of an axiom of PA.
Definition 6
Let p be a fresh unary predicate symbol not present in \({\mathcal {L}}_A\). An \({\mathcal {L}}_A\)-formula D is a PA-schema if
-
1.
\(\textsf {PA} \vdash D(\ulcorner \sigma \urcorner ) \rightarrow \sigma \) for every formula \(\sigma \in {\mathcal {L}}_A\), and
-
2.
there exists a finite set U of \({\mathcal {L}}_A \cup \{ p \}\)-formulas with at most x free such that
$$\begin{aligned} \textsf {PA} \vdash D(x) \rightarrow \exists \psi \bigvee _{\varphi \in U} (x = \ulcorner \varphi [\psi / p] \urcorner ). \end{aligned}$$
Theorem 3
Let D be a PA-schema. The theory \((\textsf {PA}^U)_{\omega } + \forall x (D(x) \rightarrow T(x))\) is a conservative extension of PA.
Let us first sketch our route towards the proof. We extend the strategy employed in Leigh (2015) to the theory \((\textsf {PA}^U)_{\omega }\). In what follows we focus on material relevant to our context different to that in Leigh (2015). We direct the reader to Leigh’s results where we use them.
We formulate the theory \((\textsf {PA}^U)_{\omega }\) as a sequent calculus with a cut rule and an induction rule for the truth predicate. Alongside \((\textsf {PA}^U)_{\omega }\) we consider \((\textsf {PA}^U)^{*}_{\omega }\), a version of \((\textsf {PA}^U)_{\omega }\) involving only bounded cuts. The main idea is to replace terms appearing in derivations involving cuts in \((\textsf {PA}^U)_{\omega }\) with new terms encoding formulas of bounded logical complexity. This is achieved via approximations, originally from Kotlarski et al. (1981); in particular, via a particular class of approximations, nth approximations. Defining the notion of nth approximations is slightly long and technical. With this in mind, but also for completeness’ sake, we include the details in Appendix A.
Using the notion of nth approximations, we show that \((\textsf {PA}^U)_{\omega }\) embeds into \((\textsf {PA}^U)^{*}_{\omega }\). Finally, derivations in \((\textsf {PA}^U)_{\omega }\) expanded by the rule

can be reduced to derivations in \((\textsf {PA}^U)^{*}_{\omega }\) expanded by a corresponding rule, denoted \((\text {D}_{{\varvec{w}}})\). In fact \((\textsf {PA}^U)_{\omega }\) interprets \((\text {D}_{{\varvec{w}}})\), whence derivations in \((\textsf {PA}^U)_{\omega } + (\text {D})\) can be carried out in \((\textsf {PA}^U)^{*}_{\omega }\). Since \((\textsf {PA}^U)^{*}_{\omega }\) conservatively extends PA, so does \((\textsf {PA}^U)_{\omega } + (\text {D})\).
We fix the following preliminaries and notational conventions for the proof of Theorem 3.
-
1.
We work with the language \({\mathcal {L}}_A^+ \supseteq {\mathcal {L}}_A\) which contains countably many new predicate symbols
$$\begin{aligned} {\mathcal {P}} = \{p^i_j : i, j < \omega \text{ and } p^i_j \text { is a predicate symbol with arity } i \}, \end{aligned}$$together with a new constant \(\epsilon \). (The new predicate symbols are introduced to facilitate the reduction of complexity of formulas appearing in the scope of the truth predicate in derivations in \((\textsf {PA}^U)_{\omega }\).)
-
2.
We assume a fixed Gödel coding of \({\mathcal {L}}_A^+\) into \({\mathcal {L}}_A\), which extends to finite sequences of \({\mathcal {L}}_A\)-terms. In particular we have the following:
-
(a)
Unary predicates, e.g., \(\text {Sent}_{{\mathcal {L}}_A}(x)\), representing the sets of Gödel codes of arithmetical sentences, terms, closed terms, etc. We extend this notation in the natural way to languages \({\mathcal {L}}\) extending \({\mathcal {L}}_A\).
-
(b)
The ternary substitution function sub(x, y, z) defining the operation that replaces each occurrence of the variable with code y in the term or formula coded by x by the term with code z. We abbreviate sub(x, y, z) by x[z/y].
-
(c)
A unary predicate \(\underset{\dot{}}{d}\) defining the following operation on codes of \({\mathcal {L}}_A^+\) formulas: \(\underset{\dot{}}{d}(\ulcorner \alpha \urcorner ) = x\) iff the logical complexity of \(\alpha \in {\mathcal {L}}_A^+\) is x.
-
(a)
-
3.
Greek lower-case letters \(\alpha , \beta , \gamma ,\) etc. from the start of the alphabet range over \({\mathcal {L}}_T\)-formulas.
-
4.
Greek lower-case letters \(\varphi , \chi ,\) etc. from the end of the alphabet range over \({\mathcal {L}}_A\)-terms encoding \({\mathcal {L}}^+_A\)-formulas. Greek lower-case letters in bold font \(\varvec{\varphi }, \varvec{\psi }\), etc. denote finite sequences of \({\mathcal {L}}_A\)-terms. If \(\varvec{\varphi } = \langle \varphi _0, \dots , \varphi _k \rangle \) is a sequence of \({\mathcal {L}}_A\)-terms, then \(T(\varvec{\varphi })\) denotes the set \(\{T(\varphi _i) : i \le k \}\).
-
5.
Roman lower-case letters s, t, etc. range over \({\mathcal {L}}_A\)-terms.
-
6.
Greek upper-case letters \(\Gamma , \Delta , \Sigma , \Pi \), etc. denote finite sets of \({\mathcal {L}}_T\)-formulas.
Next we present the axioms and rules of two sequent calculi: \((\textsf {PA}^U)_{\omega }\) and \((\textsf {PA}^U)^{*}_{\omega }\). They differ only in their cut rules. To obtain \((\textsf {PA}^U)^{*}_{\omega }\) from \((\textsf {PA}^U)_{\omega }\), we replace the cut rule for the truth predicate by a version that applies only when the formula to which the truth predicate is being applied is provably of some bounded logical complexity.
Axioms.
-
1.
\(\Gamma \Rightarrow \Delta , \varphi \) if \(\varphi \) is an axiom of Q.
-
2.
\(\Gamma , \varphi ({\underline{x}}) \Rightarrow \Delta , T( \varphi ({\underline{x}}) )\) where x is arbitrary and \(\varphi (v)\) is any \({\mathcal {L}}_A\)-formula.
-
3.
\(\Gamma , T( \varphi ({\underline{x}}) ) \Rightarrow \Delta , \varphi ({\underline{x}})\) where x is arbitrary and \(\varphi (v)\) is any \({\mathcal {L}}_A\)-formula.
Basic rules.



Induction rule.

where x is not free in the lower sequent, t is an arbitrary term, and \(\varphi (v)\) is any formula in the language \({\mathcal {L}}_T\). \((\textsf {PA}^U)_{\omega }\) and \((\textsf {PA}^U)^{*}_{\omega }\) each include the axioms, basic rules, and induction rule. The cut rules for each are the following.
Cut rules for \((\textsf {PA}^U)_{\omega }\).

In \((\text {Cut}_{{\mathcal {L}}_A})\) the cut formula \(\varphi \in {\mathcal {L}}_A\).

In \((\text {Cut}_{T})\) the formula under the truth predicate \(\varphi \in {\mathcal {L}}_A\).
Cut rules for \((\textsf {PA}^U)^{*}_{\omega }\).

For each \(k < \omega \):

where \(\Rightarrow ^{*}\) indicates that the sequent is derivable using only the axioms and arithmetical rules.
Towards the proof of Theorem 3, first we show that \((\textsf {PA}^U)^{*}_{\omega }\) is conservative over PA. The presence of truth in induction means that \((\textsf {PA}^U)^{*}_{\omega }\) does not, in general, admit cut elimination.Footnote 25 However, a result of Łełyk and Wcisło (2017) shows that \(\textsf {PA}^T\) interprets \((\textsf {PA}^U)_{\omega }\), whence the conservativity of \((\textsf {PA}^U)^{*}_{\omega }\) over PA follows from Theorem 1.
Lemma 1
\((\textsf {PA}^U)^{*}_{\omega }\) is a conservative extension of PA.
Proof
Suppose the truth-free sequent \(\Gamma \Rightarrow \Delta \) is derivable in \((\textsf {PA}^U)^{*}_{\omega }\). Then \(\Gamma \Rightarrow \Delta \) is derivable in \((\textsf {PA}^U)_{\omega }\). Let d denote this derivation. By Proposition 4.15 of Łełyk and Wcisło (2017), there exists an \({\mathcal {L}}_A\)-conservative relative interpretation of \((\textsf {PA}^U)_{\omega }\) in \(\textsf {PA}^T\). That is, there is a translation \(t: {\mathcal {L}}_T \rightarrow {\mathcal {L}}_T\) constant on arithmetical formulas such that for all \(\varphi \in {\mathcal {L}}_T\):
It follows that \(\textsf {PA}^T\) interprets d, whence \(\Gamma \Rightarrow \Delta \) is derivable in \(\textsf {PA}^T\), and the result follows from Leigh (2015, Theorem 1) (i.e. Theorem 1). \(\square \)
Next, using nth approximations, derivations in \((\textsf {PA}^U)_{\omega }\) are replaced by approximations with bounded depth. We note that the construction of nth approximations can be formalized within PA (in fact, in a much weaker theory, e.g., \(\textsf {I}\Delta _0 + \text {exp}\)). We refer the reader to Leigh (2015, §4.3). For the basic properties of nth approximations, see Leigh (2015, Lemmata 12,13). For a given sequence \(\varvec{\varphi }\) of \({\mathcal {L}}_A^+\)-formulas, we write \(lh(\varvec{\varphi })\) for the number of elements of \(\varvec{\varphi }\). We write H for the function \(H(k, n) = n \cdot 2^k\). By Lemma 7 of Leigh (2015), the nth approximation of \(\varvec{\varphi }\) has logical depth at most \(H(n, lh(\varvec{\varphi }))\).
We require the following definitions.
Definition 7
Let d be a derivation in \((\textsf {PA}^U)_{\omega }\) or \((\textsf {PA}^U)^{*}_{\omega }\).
-
1.
The truth depth of d is the maximum number of truth rules occurring in d.
-
2.
The truth rank of d is \(\sup \{k : (\text {Cut}^k_T) \text { occurs in } d\} + 1.\)
-
3.
The rank of d is any pair (n, r) such that n bounds the truth depth of d and r bounds the truth rank of d.
Lemma 18 of Leigh (2015) is one key ingredient for the proof of our version of the Bounding Lemma (Lemma 3), which we need for transforming derivations in \((\textsf {PA}^U)_{\omega }\) to derivations in \((\textsf {PA}^U)_{\omega }^{*}\). Lemma 18 of Leigh (2015) identifies a bound on the rank of derivations involving nth approximations. The presence of rule \((\text {Ind}_T)\) in our sequent calculus means that we need an analog of Lemma 18 for \((\text {Ind}_T)\).
Lemma 2
Let \(lh(\varvec{\varphi }) + lh(\varvec{\psi }) = n\). If the kth approximation to:
is derivable with rank (a, r), then the \(k+1\)th approximation of:
is derivable with rank \((a+1, r + H(k+1, n+2))\).
Proof
Suppose that:

is derivable with rank (a, r), where \({\varvec{w}} = \varvec{\varphi }^\frown \varvec{\psi }^\frown (\chi ({\underline{x}}))^\frown (\chi (\underline{x+1}))\). Let g(x, y, z) be the term given by Lemma 13 of Leigh (2015) and let:
By Lemma 15 of Leigh (2015), the sequent:

is derivable with rank \((a, r + H(k+1, n+2))\), where \({\varvec{w}}' = \varvec{\varphi }^\frown \varvec{\psi }^\frown (\chi ({\underline{0}}))^\frown (\chi (t))\). By Lemmata 12 and 13 of Leigh (2015), and using only arithmetical cuts, we obtain a derivation of the sequent:

with rank \((a, r + H(k+1, n+2))\). Lemma 12 of Leigh (2015) and \((\text {Ind}_T)\) then yield a derivation of the sequent:

with rank \((a+1, r + H(k+1, n+2))\). \(\square \)
The following Bounding Lemma provides a reduction of \((\textsf {PA}^U)_{\omega }\) to \((\textsf {PA}^U)^{*}_{\omega }\). We need only consider the case for the rule \((\text {Ind}_T)\); for the other cases, see Lemma 19 of Leigh (2015).
Lemma 3
(Bounding Lemma) There are recursive functions \(G_1\) and \(G_2\) such that for every \(a, n < \omega \), if \(lh(\varvec{\varphi }) + lh(\varvec{\psi }) \le n\) and the sequent:
is derivable in \((\textsf {PA}^U)_{\omega }\) with truth depth a, then its \(G_1(a, n)\)th approximation is derivable in \((\textsf {PA}^U)^{*}_{\omega }\) with rank \((a, G_2(a, n))\).
Proof
Define:
Notice that for all \(a, b, n, m < \omega \): if \(m < n\) then \(G_1(a, m) \le G_1(a, n)\); if \(a < b\) then \(G_1(a, n) \le G_1(b, n)\); and \(G_1(a, n+1) \le G_1(a+1, n)\). The proof proceeds by induction on a.
Suppose the sequent:
was obtained by \((\text {Ind}_T)\) applied to:
and that this derivation has height \(a+1\). Let \({\varvec{w}} = \varvec{\varphi }^\frown \varvec{\psi }^\frown \chi ({\underline{x}})^\frown \chi (\underline{x+1})\). The induction hypothesis is that the \(G_1(a, n+2)\)th approximation to the sequent:
is derivable in \((\textsf {PA}^U)^{*}_{\omega }\) with rank \((a, G_2(a, n+2))\). By Lemma 2 there is a derivation with height \(a+1\) of the \(G_1(a, n+2) + 1\)th approximation to the sequent:
This derivation has cut rank \(G_2(a, n+2) + H(G_1(a, n+2) + 1, n+2)\), so it’s enough to show that:
Consider \(G_2(a, n+2)\). For all \(a, n < \omega \) we have:
Now consider \(H(G_1(a, n+2) + 1, n+2)\). Notice that for all \(a, n < \omega \) we have:
Thus for all \(a, n < \omega \) we have:
whence adding \(G_2(a, n+2)\) and \(H(G_1(a, n+2) + 1, n+2)\) yields the desired inequality.Footnote 26\(\square \)
Theorem 3 now follows similarly as in Leigh (2015). We emphasize that uniform disquotational truth is sufficient; fully compositional truth is not necessary.
Proof of Theorem 3
Let D and U be as in the statement of the theorem. Let d be a derivation with truth depth a of the truth-free sequent \(\Gamma \Rightarrow \Delta \) in the system obtained from \((\textsf {PA}^U)_{\omega }\) by adding the following rule:

Redefine the functions \(G_1\) and \(G_2\) so that \(G_1(0, n)\) bounds the logical depth of the finitely many formulas in U for each n. Then the proof of Lemma 3 can be carried out to obtain a derivation with rank \((a, G_2(a, 0))\) of \(\Gamma \Rightarrow \Delta \) in the system obtained from \((\textsf {PA}^U)^{*}_{\omega }\) by adding the following rule:

where \(\Pi \) and \(\Sigma \) are truth-free, \(k = G_1(a, 0)\) and \({\varvec{w}} = \varvec{\varphi }^\frown \varvec{\psi }^\frown \sigma \). Notice that \(G_1(a, 0) \ge G_1(0, n)\) for all \(a, n < \omega \).
Call this derivation \(d^{*}\). Fix n such that for each instance of \((\text {D}_{{\varvec{w}}})\) occurring in \(d^{*}\), \(lh({\varvec{w}}) < n\). It is enough to show that \((\textsf {PA}^U)_{\omega }\) interprets \((\text {D}_{{\varvec{w}}})\).
Let:
Then the sequent:

is derivable in PA. Now, \(G_1(0, n)\) bounds the logical depth of the schematic formulas in D, and \(k = G_1(a, 0) \ge G_1(0, n)\) for all \(a, n < \omega \). Since every occurrence of a predicate symbol \(p_j^i\) in the kth approximation of x has depth at least k in x, it follows that if x is any instance of the schema D, then so is  . Moreover, this fact is derivable in PA. Since
. Moreover, this fact is derivable in PA. Since  is also derivable in PA, by \((*)\), the sequent:
is also derivable in PA, by \((*)\), the sequent:

is derivable in PA. Since the sequent \(D(\sigma ) \Rightarrow \sigma \) is derivable in PA for all arithmetical sentences \(\sigma \), and the sequent \(\sigma \Rightarrow T( \sigma )\) is derivable in \((\textsf {PA}^U)_{\omega }\) for all arithmetical sentences \(\sigma \) (this is where uniform disquotational truth is sufficient), the sequent:

is derivable in \((\textsf {PA}^U)_{\omega }\). Thus \((\textsf {PA}^U)_{\omega }\) interprets \((\text {D}_{{\varvec{w}}})\), and we obtain a derivation of the sequent \(\Gamma \Rightarrow \Delta \) in \((\textsf {PA}^U)^{*}_{\omega }\). By Lemma 1, \((\textsf {PA}^U)^{*}_{\omega }\) is conservative over PA, so \(\Gamma \Rightarrow \Delta \) is derivable in PA. \(\square \)
From Theorem 3 we immediately obtain:
Corollary 1
For each \(n \in \omega \), \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_n\) is conservative over PA. \(\square \)
6 Morals
With our points made, let us wrap things up. We understand the import of Theorem 3 to consist in revealing a different (and interesting) set of implicit commitments for the first-orderist than the semantic core of PA. We maintain our point from Sect. 4 that the general idea of a fixed semantic core of implicit commitments in accepting a given base theory S is too strong. In particular, the requirement that the first-orderist be implicitly committed to fully compositional axioms for the truth predicate on the basis of their acceptance of PA is too strong. For it is precisely the presence of fully compositional truth principles which forces the first-orderist to give up all (sets of) instances of extended induction to the language \({\mathcal {L}}_T\) as part of I(PA). Moreover, there is no principled reason why we should require fully compositional truth, rather than extended induction, to form part of the first-orderist’s implicit commitments on the basis of their acceptance of PA (or vice versa). All things considered, the theories \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\) and \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\) are equally plausible candidates for the first-orderist’s implicit commitments on the basis of their acceptance of PA.
To anticipate an objection, one might complain that the theory \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\) is not a plausible theory of truth precisely because it lacks full compositionality,Footnote 27 and that this is a reason to prefer to cash out the first-orderist’s implicit commitments on the basis of accepting PA as the theory \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\), rather than the theory \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\). Essentially, though, we think this misses the point. First, one still has a notion of uniform disquotational truth at play in the theory \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\), and since one of the underlying motivations for this project was to accommodate the assertion that all of the axioms of PA are true among the first-orderist’s implicit commitments on the basis of their acceptance of PA, we think uniform disquotational truth is enough to say we have achieved this much. But second, to say that the first-orderist’s implicit commitments on the basis of accepting PA amount to the principles of \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\) is not to say that the first-orderist thereby rejects a fully compositional notion of truth. All that follows is that if the first-orderist indeed accepts the idea that truth is fully compositional, then their acceptance of the corresponding principles is not grounded purely in their acceptance of PA. We maintain that there is no principled reason the first-orderist should prefer an implicit commitment to fully compositional truth at the expense of an implicit commitment to extended induction purely on the basis of accepting PA. If there are reasons why the first-orderist might prefer one of these theories of implicit commitments to the other, then those reasons are independent of the idea of the first-orderist’s acceptance of PA.
Let us also return to the hasty conclusion we pointed out in Sect. 4: that perhaps our acceptance framework fails to reveal any differences between the finitist and the first-orderist with respect to their attitudes towards truth in induction. On the contrary, Theorem 3 shows that our framework does reveal a difference between these two foundationalists in this respect.
On one hand, our acceptance framework: (1) shows that \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\) and \(\textsf {PA}^T_{\text {Ax}_{\textsf {PA}}}\) are both plausible candidate theories of the first-orderist’s implicit commitments on the basis of their acceptance of PA, yet (2) also has no preference about whether the fully compositional truth axioms, or instances of PA’s induction schema in which the truth predicate occurs, form part of the first-orderist’s implicit commitments. Moreover, this lack of preference is not a failure on the part of our acceptance framework. Rather, given our remarks in Sect. 4, it is exactly what we should expect of an account of theory acceptance.
On the other hand, our framework still accommodates the idea that the semantic core \(\textsf {QF}\text {--}\textsf {IA}^T_{\text {Ax}_{\textsf {QF}\text {--}\textsf {IA}}}\) of QF–IA is a plausible candidate theory of the finitist’s implicit commitments on the basis of their acceptance of QF–IA. But since truth in induction is off the table for finitist, the theory \((\textsf {QF}\text {--}\textsf {IA}^U_{\text {Ax}_{\textsf {QF}\text {--}\textsf {IA}}})_{\omega }\) is off the table as a plausible candidate theory for I(QF–IA). This is the difference revealed by our framework: \((\textsf {PA}^U_{\text {Ax}_{\textsf {PA}}})_{\omega }\) is available to the first-orderist, but \((\textsf {QF}\text {--}\textsf {IA}^U_{\text {Ax}_{\textsf {QF}\text {--}\textsf {IA}}})_{\omega }\) is not available to the finitist.
The overall moral of our story is that the relevant versions of the three ideas which formed the motivation for this project are reconcilable in different, equally interesting ways: (1) the weak ICT, (2) \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability, and (3) the idea that we should like to accept soundness assertions involving a notion of truth for S, on the basis of accepting S itself.
We have put forward a framework for analyzing implicit commitments in accepting a given suitable arithmetic theory S. There are two broad components of this framework: semantic and schematic, and each component admits fine-grained degrees. In general, neither component is fully fixed. If it makes sense to say that any of the principles we have considered are fixed implicit commitments in accepting a given theory S, we suggest that it is the common core of the theories \(\textsf {S}^T_{\text {Ax}_{\textsf {S}}}\) and \((\textsf {S}^U_{\text {Ax}_{\textsf {S}}})_{\omega }\); that is, the theory \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\). In any case, in general, sets of implicit commitments on the basis of accepting a given base theory S vary from foundationalist to foundationalist. This framework provides a general understanding of just what an epistemically-stable foundationalist’s implicit commitments can be.
By suitably modifying the original notions of epistemic stability and the implicit commitment thesis as in Dean (2015), we hope to have offered a clear way of understanding which sets of implicit commitments are compatible with weaker notions of epistemic stability and the implicit commitment thesis. In general, we do think that it is possible for epistemic stability to be compatible with the implicit commitment thesis: conservative extensions of S according to our framework reconcile weak epistemic stability with non-trivial versions of the weak implicit commitment thesis. In particular, for suitable arithmetic theories S, it is possible for (1) there to exist a coherent rationale for accepting a given arithmetical theory S that does not entail or otherwise rationally oblige a theorist to accept statements in the language of S, which cannot be derived from the axioms of S, and (2) anyone who accepts the axioms of S to be implicitly committed to accepting various additional statements which are formally independent of S. Cashing out theories of implicit commitments as theories of truth extending S makes this possible.
Indeed, it is not only possible to reconcile the notion of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability with the weak ICT for foundational positions that the compatibility of the original notions of epistemic stability and the ICT are said to be problematic for, but (depending upon the foundational position) this can be achieved with respect to a variety of implicit commitments, all of which contain desirable minimal soundness requirements for S. Finally, our framework is still compatible with the idea that one’s implicit commitments may also include strong reflection principles. Strong reflection principles occur among one’s implicit commitments just in case one’s implicit commitments include both the fully compositional truth principles for S-sentences, and the fully extended S-induction schema to the expanded language of truth. Nonetheless, the occurrence of the weak reflective axiom soundness principle among one’s implicit commitments is compatible with the idea of epistemic stability, in a variety of ways.
Data availability
Not applicable.
Code availability
Not applicable.
Notes
We equivocate between using the term epistemic stability as a property of both foundational positions and associated base theories.
Other characterizing theses of foundational positions said to be epistemically stable include: Dedekind’s thesis (Dedekind, 1888); the Feferman-Schütte thesis (Feferman, 1964; Kreisel, 1960; Schütte, 1965, 1964); and Nelson’s thesis (Nelson, 1986). For discussion of these various theses in the context of epistemic stability, see: Madison and Waxman (2021) (for Dedekind’s thesis, Isaacson’s thesis, Tait’s thesis, and the Feferman-Schütte thesis); Dean (2015) (for Isaacson’s thesis and Tait’s thesis); Nicolai and Piazza (2019) (for Isaacson’s thesis, Tait’s thesis, and Nelson’s thesis).
In case it is not clear, do not confuse “the first-orderist” with Isaacson himself. We are concerned with the idea of the epistemic stability of the position, and do not intend to claim that the author of this idea occupies this position.
To be clear, it does not follow from this incompatibility that the first-orderist does not accept the sentences \(\text {G}(\textsf {PA})\) or \(\text {Con}(\textsf {PA})\). Rather, the first-orderist does not accept these sentences purely on the basis of their acceptance of PA. Rather, if the first-orderist does accept \(\text {G}(\textsf {PA})\) or \(\text {Con}(\textsf {PA})\), then the justification for that acceptance is grounded in higher-order/infinitary/non-arithmetical concepts.
Statements which assert the truth of certain classes of logical consequences of S.
This aligns with the idea in Dean (2015) that \(\text {G}(\textsf {PA})\) and \(\text {Con}(\textsf {PA})\) are natural candidates to include among the resources \(\Gamma \). For instance, \(\text {Con}(\textsf {PA})\) is equivalent (over a weak theory) to the theory: all \(\Pi _1^0\)-theorems of PA are true. The latter is a weak reflection principle of just the sort we are interested in. Moreover, \(\text {G}(\textsf {PA})\) and \(\text {Con}(\textsf {PA})\) are equivalent over, e.g., PA.
A theory \(\textsf {T}_1\) is syntactically conservative over another theory \(\textsf {T}_2\) iff for every formula \(\varphi \) in the language of \(\textsf {T}_2\), if \(\textsf {T}_1 \vdash \varphi \), then \(\textsf {T}_2 \vdash \varphi \). We henceforth use “conservative”, rather than “syntactically conservative.”
We clarify this notation shortly.
We claim that nothing is lost by this minor restriction, since this collection of theories includes those which typically appear in existing literature on implicit commitments.
We note that \({\mathcal {L}}_T\) is not, strictly speaking, uniform, since \({\mathcal {L}}_{\textsf {S}}\) differs for different choices of S. But this is a technical distinction we ignore for our purposes.
See Nicolai and Piazza (2019, Lemma 1).
For the non-conservativity result where S is \(\textsf {S}^1_2\), see Nicolai and Piazza (2019, Proposition 3). Indeed, full compositionality of the truth predicate is not necessary; we may obtain non-conservativity even in the presence of uniform disquotational truth. The non-conservativity results where S is any of the theories \(\textsf {I}\Sigma _n\) for \(n \in \omega \), are obtained similarly. We discuss the non-conservativity result in the case where S is PA later on.
We note that the ordering of \(\textsf {S}^T\) and \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\) is somewhat arbitrary, since in general, \(\textsf {S}^T\) cannot derive the axiom soundness axiom, but can derive the uniform Tarski biconditionals for S, and \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\) cannot derive the fully compositional truth axioms. However, the ordering of \(\textsf {S}^T\) and \(\textsf {S}^U_{\text {Ax}_{\textsf {S}}}\) in Fig. 1 does not really matter for our purposes, so without loss of generality we opt for the above.
McGee also offers a reading of the position in which one extends induction unrestrictedly, arguing that induction schema are like the laws of logic, which we expect to persist through changes in language (1997, p. 58). Consequently acceptance of (for example) PA should commit one not only to instances of induction applied to extensions of one’s language, but also to instances of induction corresponding to any subset of the natural numbers. An analysis of this sort yields categorical theories. For further discussion of McGee’s position, see Pedersen and Rossberg (2010).
Cf. the outline of first-orderism in Sect. 1.
We acknowledge that the sense in which (for example) \((\textsf {PA})_{\omega }\) is a formal representation of accepting all instances of PA’s induction schema in which the truth predicate occurs may be a little artificial. Without at least the presence of the uniform disquotational principles, it doesn’t really make sense to call the predicate T occurring in instances of PA’s induction schema a truth predicate. Ultimately this won’t be a problem, since every interesting set of implicit commitments concerning instances of extended induction we consider in this paper also contain at least the uniform disquotational principles for the T predicate. In any case, artificial or not, we think the stratification of the schematic component of implicit commitment via the theories \((\textsf {PA})_n\), for each \(n \in \omega \), and \((\textsf {PA})_{\omega }\), adds at least some pedagogical value to our framework.
See e.g., Wcisło and Łełyk (2017).
See for example Lindström (1997, Ch. 12) for a definition of relative interpretation.
It is well-known that \((\textsf {PA}^T)_1\) proves (\(\text {GRP}_{\textsf {PA}}\)). See, e.g., Wcisło and Łełyk (2017, Theorem 12). A natural question is whether one can relax the assumption of \(\Pi _1\) T-induction, and ask whether \((\textsf {PA}^T)_0\) proves (\(\text {GRP}_{\textsf {PA}}\)). Kotlarski (1968) originally published an alleged proof of a similar result using a theory of satisfaction, rather than truth, before Albert Visser and Richard Heck independently identified a gap in the proof. Theorem 2 shows that (\(\text {GRP}_{\textsf {PA}}\)) is arithmetically conservative over \((\textsf {PA}^T)_0\). Wcisło and Łełyk (2017) also show that slightly modifying \((\textsf {PA}^T)_0\) actually proves (\(\text {GRP}_{\textsf {PA}}\)).
Perhaps instead all this serves to show is that first-orderism is simply an incoherent view after all. We think this would be a hasty conclusion. The goal all along has been to reconcile the idea of \({\mathcal {L}}_{\textsf {S}}\)-epistemic stability with the weak ICT for various foundational positions said to be epistemically stable in some sense. If all we are prepared to conclude at this stage is that one of these foundational positions was incoherent all along, this does not seem very in keeping with our original goal.
See e.g., Halbach (2014). Hence, so are the theories \((\textsf {PA})_n\), for each \(n \in \omega \), and \((\textsf {PA})_{\omega }\).
This differs from the context in Leigh (2015), since cut elimination is available for the bounded counterpart to \(\textsf {PA}^T\).
Notice that \(n+2 \le a+n+1\) whenever \(a \ge 1\), so we may invoke monotonicity whenever \(a \ge 1\); but the claimed inequality also holds whenever \(a=0\) and \(n < \omega \) is arbitrary.
References
Buss, S. R. (1986). Bounded arithmetic. Bibliopolis.
Cieśliński, C. (2010). Truth, conservativeness, and provability. Mind, 119(474), 409–422. https://doi.org/10.1093/mind/fzq034
Cieśliński, C. (2017). The epistemic lightness of truth: Deflationism and its logic. Cambridge University Press.
Dean, W. (2015). Arithmetical reflection and the provability of soundness. Philosophia Mathematica, 23(1), 31–64. https://doi.org/10.1093/philmat/nku026
Dedekind, R. (1888). Was sind und was sollen die Zahlen? In (1965) Was sind und was sollen die Zahlen? Stetigkeit und Irrationale Zahlen, (pp. 1–47). Vieweg+Teubner Verlag.
Feferman, S. (1962). Transfinite recursive progressions of axiomatic theories. Journal of Symbolic Logic, 27(3), 259–316. https://doi.org/10.2307/2964649
Feferman, S. (1964). Systems of predicative analysis. Journal of Symbolic Logic, 29(1), 1–30. https://doi.org/10.2307/2269764
Feferman, S. (1991). Reflecting on incompleteness. Journal of Symbolic Logic, 56(1), 1–49. https://doi.org/10.2307/2274902
Field, H. (1986). The deflationary conception of truth. In G. MacDonald & C. Wright (Eds.), Fact, science and morality: Essays on A. J. Ayer’s Language, truth and logic (pp. 55–117). Blackwell.
Field, H. (1999). Deflating the conservativeness argument. Journal of Philosophy, 96(10), 533–540. https://doi.org/10.2307/2564613
Fischer, M. (2021). Another look at reflection. Erkenntnis. https://doi.org/10.1007/s10670-020-00363-9
Fischer, M., Horsten, L., & Nicolai, C. (2021). Hypatia’s silence: Truth, justification, and entitlement. Noûs, 55(1), 62–85. https://doi.org/10.1111/nous.12292
Franzén, T. (2004). Inexhaustibility. A non-exhaustive treatment. Lecture Notes in Logic. Association for Symbolic Logic (Vol. 16). A. K. Peters.
Halbach, V. (2014). Axiomatic theories of truth. Cambridge University Press.
Hilbert, D., & Bernays, P. (1968). Grundlagen der Mathematik (2nd ed.). Springer.
Horsten, L., & Leigh, G. E. (2016). Truth is simple. Mind, 126(501), 195–232. https://doi.org/10.1093/mind/fzv184
Horwich, P. (1990). Truth. Blackwell.
Isaacson, D. (1996). Arithmetical truth and hidden higher-order concepts. In W. D. Hart (Ed.), The philosophy of mathematics (pp. 203–224). Oxford University Press.
Ketland, J. (2005). Deflationism and the Gödel phenomena: Reply to Tennant. Mind, 114(453), 75–88. https://doi.org/10.1093/mind/fzi075
Ketland, J. (2010). Truth, conservativeness, and provability: Reply to Cieśliński. Mind, 119(474), 423–436. https://doi.org/10.1093/mind/fzq039
Kotlarski, H. (1968). Bounded induction and satisfaction classes. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 32(31–34), 531–544. https://doi.org/10.1002/malq.19860323107
Kotlarski, H., Krajewski, A., & Lachlan, A. H. (1981). Construction of satisfaction classes for nonstandard models. Canadian Mathematical Bulletin, 24(3), 283–293. https://doi.org/10.4153/cmb-1981-045-3
Kreisel, G. (1960). La prédicativité. Bulletin de la Societété Mathématique de France, 88, 371–391.
Leigh, G. (2015). Conservativity for theories of compositional truth via cut-elimination. The Journal of Symbolic Logic, 80(3), 845–865. https://doi.org/10.1017/jsl.2015.27
Łełyk, M., & Wcisło, B. (2017). Models of weak theories of truth. Archive for Mathematical Logic, 56(5–6), 453–474. https://doi.org/10.1007/s00153-017-0531-1
Lindström, P. (1997). Aspects of incompleteness. Cambridge University Press.
Madison, B., & Waxman, D. (2021). Stable and unstable theories of truth and syntax. Mind, 130(518), 439–473. https://doi.org/10.1093/mind/fzaa034
McGee, V. (1997). How we learn mathematical language. The Philosophical Review, 106(1), 35–68. https://doi.org/10.2307/2998341
Nelson, E. (1986). Predicative arithmetic. Princeton University Press.
Nicolai, C., & Piazza, M. (2019). The implicit commitment of arithmetical theories and its semantic core. Erkenntnis, 84(4), 913–937. https://doi.org/10.1007/s10670-018-9987-6
Pedersen, N. J. L. L., & Rossberg, M. (2010). Open-endedness, schemas and ontological commitment. Noûs, 44(2), 329–339. https://doi.org/10.1111/j.1468-0068.2010.00742.x
Schütte, K. (1964). Eine Grenze für die Beweisbarkeit der Transfiniten Induktion in der verzweigten Typenlogik. Archiv für Mathematische Logik und Grundlagen-forschung, 7(1–2), 45–60. https://doi.org/10.1007/bf01972460
Schütte, K. (1965). Predicative well-orderings. In J. N. Crossley & M. Dummett (Eds.), Formal systems and Recursive Functions (pp. 280–303). North-Holland.
Shapiro, S. (1998). Proof and truth: Through thick and thin. The Journal of Philosophy, 95(10), 493–521. https://doi.org/10.2307/2564719
Simpson, S. G. (2009). Subsystems of second order arithmetic. Cambridge University Press.
Skolem, T. (1923). The foundations of elementary arithmetic established by means of the recursive mode of thought, without the use of apparent variables ranging over infinite domains. In J. Van. Heijenoort (Ed.), From Frege to Gödel: A source book in mathematical logic, 1879–1931 (pp. 303–333). Harvard University Press.
Tait, W. W. (1981). Finitism. The Journal of Philosophy, 78(9), 524–546. https://doi.org/10.2307/2026089
Tennant, N. (2002). Deflationism and the Gödel phenomena. Mind, 111(443), 551–582. https://doi.org/10.1093/mind/111.443.551
Tennant, N. (2005). Deflationism and the gödel phenomena: Reply to ketland. Mind, 114(453), 89–96. https://doi.org/10.1093/mind/fzi089
Turing, A. (1939). Systems of logic based on ordinals. Proceedings of the London Mathematical Society, S2–45, 161–228. https://doi.org/10.1112/plms/s2-45.1.161
Wcisło, B., & Łełyk, M. (2017). Notes on bounded induction for the compositional truth predicate. The Review of Symbolic Logic, 10(3), 455–480. https://doi.org/10.1017/s1755020316000368
Acknowledgements
I would like to thank Graham Leigh for many helpful comments on the approximations material and the proof of the main result.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
Not applicable.
Corresponding author
Ethics declarations
Conflict of interest
The author has no conflict of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Approximations
Appendix A: Approximations
Here we define approximations, and ultimately nth approximations. Recall that we are working with the language \({\mathcal {L}}_A^+\) that extends \({\mathcal {L}}_A\) by a new constant \(\epsilon \) and the set \({\mathcal {P}}\) of countably many new predicate symbols \(p^i_j\).
Definition 8
Let \(X \subseteq {\mathcal {P}}\) be a finite subset consisting of the predicates \(p^i_j\). An assignment is any function \(g: X \rightarrow {\mathcal {L}}_A^+\) such that for every i, j, if \(p^i_j \in X\) then \(g(p^i_j)\) is a formula with arity i.
If g is an assignment and \(\varphi \in {\mathcal {L}}_A^+\), then \(\varphi [g]\) denotes the result of replacing each predicate \(p^i_j(s_1, \dots , s_i)\) occurring in \(\varphi \) by \(g(p^i_j)(s_1, \dots , s_i)\) if \(g(p^i_j)\) is defined, and by \(\epsilon \) otherwise.
Definition 9
Let \(\varvec{\varphi } = \langle \varphi _0, \dots , \varphi _m \rangle \) and \(\varvec{\psi } = \langle \psi _0, \dots , \psi _m \rangle \) be two sequences of closed \({\mathcal {L}}_A^+\)-formulas. We say that \(\varvec{\varphi }\) approximates \(\varvec{\psi }\) if there exists an assignment g such that \(\psi _i = \varphi _i[g]\) for each \(0 \le i \le m\).
We are interested in defining a particular class of approximations; nth approximations. They are constructed in the following way. Let \(w, z, z_1, z_2, \dots \) be new variable symbols.
Definition 10
Let \(\varphi \in {\mathcal {L}}_A\). An occurrence in \(\varphi \) is any pair \(\langle \varphi ', t \rangle \) such that:
-
1.
\(\varphi ' \in {\mathcal {L}}_A \cup \{z\}\) such that z occurs in \(\varphi '\) exactly once;
-
2.
\(\text {Term}_{{\mathcal {L}}_A \cup \{w\}}(t)\);
-
3.
t is free for z in \(\varphi '\);
-
4.
\(\varphi = \varphi '[t/z]\).
We denote the set of occurences in \(\varphi \) by \({\mathcal {O}}(\varphi )\).
Definition 11
Let \(\varphi \in {\mathcal {L}}_A\). The w-free form of \(\varphi \) is the \({\mathcal {L}}_A \cup \{w\}\)-formula \({\overline{\varphi }}\) obtained from \(\varphi \) by:
-
1.
replacing all free variables in \(\varphi \) by the variable w;
-
2.
replacing all terms in the result of 1. above in which the only variable that occurs in w, by w.
If \(\langle \varphi ', t \rangle \) is an occurrence in \(\varphi \) where \(\varphi \) is in w-free form, then \(t = w\). We say that two \({\mathcal {L}}_A\)-formulas \(\varphi \) and \(\psi \) are weakly equivalent if their w-free forms are equal; i.e. if \({\overline{\varphi }} = {\overline{\psi }}\).
Each \({\mathcal {L}}_A\)-formula \(\varphi \) is associated with a unique function \(t_{\varphi }: {\mathcal {O}}(\varphi ) \rightarrow \text {Term}_{{\mathcal {L}}_A}\) such that replacing each occurrence of the variable w in the w-free form of \(\varphi \) by \(t_{\varphi }(w)\) results in \(\varphi \). We say that two \({\mathcal {L}}_A\)-formulas \(\varphi \) and \(\psi \) are strongly equivalent, which we write as \(\varphi \approx \psi \), if they are weakly equivalent and in addition there exists an equivalence relation E on \({\mathcal {O}}({\overline{\varphi }}) = {\mathcal {O}}({\overline{\psi }})\) such that \(t_{\varphi }, t_{\psi }\) are well-defined on  and disagree on at most finitely many E-equivalence classes.
and disagree on at most finitely many E-equivalence classes.
Let \(\Phi \) be a set of pairwise weakly equivalent \({\mathcal {L}}_A\)-formulas, such that each has only a finite number of free variables. There is a canonical way of defining an equivalence relation E on \({\mathcal {O}}(\Phi )\) as above, since \({\mathcal {O}}(\Phi )\) is the common value of \({\mathcal {O}}({\overline{\varphi }})\) for each \(\varphi \in \Phi \). The functions \(\{t_{\varphi } : \varphi \in \Phi \}\) induce an equivalence relation \(E_{\Phi }\) on \({\mathcal {O}}(\Phi )\) by setting:
For each \(\varphi \in \Phi \), let  be the map induced by \(t_{\varphi }\). If \(\varphi _0, \varphi _1 \in \Phi \) then there are at most finitely many \(E_{\Phi }\)-equivalence classes in
be the map induced by \(t_{\varphi }\). If \(\varphi _0, \varphi _1 \in \Phi \) then there are at most finitely many \(E_{\Phi }\)-equivalence classes in  on which \(t'_{\varphi _0}\) and \(t'_{\varphi _1}\) disagree.
on which \(t'_{\varphi _0}\) and \(t'_{\varphi _1}\) disagree.
We use the notion of strong equivalence to define the template of a set \(\Phi \) of \({\mathcal {L}}_A\)-formulas. Let \(\Phi \) be a set of pairwise strongly equivalent \({\mathcal {L}}_A\)-formulas. Let \({\mathcal {C}}_1, \dots , {\mathcal {C}}_l\) enumerate the finitely many \(E_{\Phi }\)-classes \({\mathcal {C}}\) in  such that there are \(\psi _0, \psi _1 \in \Phi \) with \(t'_{\psi _0}({\mathcal {C}}) \ne t'_{\psi _1}({\mathcal {C}})\), or \(t'_{\psi _0}({\mathcal {C}})\) is a variable. Let \(\varphi \in \Phi \) and consider its w-free form \({\overline{\varphi }}\). If \({\mathfrak {o}} \in {\mathcal {O}}({\overline{\varphi }})\) is such that \({\mathfrak {o}} \in {\mathcal {C}}_i\) for some \(1\le i \le l\), we replace \({\mathfrak {o}}\) by the new variable \(z_i\). Otherwise \({\mathfrak {o}} \in {\mathcal {O}}({\overline{\varphi }})\) is not in any \({\mathcal {C}}_i\), so we replace \({\mathfrak {o}}\) by \(t_{\varphi }({\mathfrak {o}})\). The resulting formula:
such that there are \(\psi _0, \psi _1 \in \Phi \) with \(t'_{\psi _0}({\mathcal {C}}) \ne t'_{\psi _1}({\mathcal {C}})\), or \(t'_{\psi _0}({\mathcal {C}})\) is a variable. Let \(\varphi \in \Phi \) and consider its w-free form \({\overline{\varphi }}\). If \({\mathfrak {o}} \in {\mathcal {O}}({\overline{\varphi }})\) is such that \({\mathfrak {o}} \in {\mathcal {C}}_i\) for some \(1\le i \le l\), we replace \({\mathfrak {o}}\) by the new variable \(z_i\). Otherwise \({\mathfrak {o}} \in {\mathcal {O}}({\overline{\varphi }})\) is not in any \({\mathcal {C}}_i\), so we replace \({\mathfrak {o}}\) by \(t_{\varphi }({\mathfrak {o}})\). The resulting formula:
is called the template of \(\Phi \). The template of \(\Phi \) is unique up to permutation of the variables \(z_1, \dots , z_l\), and does not depend on the choice of \(\varphi \). Also, for each \(\varphi \in \Phi \) there exist unique terms \(t_1, \dots , t_l\) such that \(\varphi = \Theta _{\Phi }(t_1, \dots , t_l)\).
The following sequence of definitions culminates in the definition of nth approximations.
Definition 12
Let \(\varvec{\varphi } = \langle \varphi _0, \dots , \varphi _m \rangle \) be a non-empty sequence of \({\mathcal {L}}_A\)-formulas. The set of parts of of \(\varvec{\varphi }\), denoted \(\Pi (\varvec{\varphi })\), is the set of pairs \(\langle \varphi ', \psi \rangle \) such that:
-
1.
\(\varphi ' \in {\mathcal {L}}_{A} \cup \{ \epsilon \}\) is such that \(\epsilon \) occurs in \(\varphi '\) exactly once;
-
2.
\(\psi \in {\mathcal {L}}_A\); and
-
3.
\(\varphi _i = \varphi '[\psi / \epsilon ]\) for some \(0 \le i \le m\).
We define an ordering \(\preceq \) on \(\Pi (\varvec{\varphi })\) such that:
iff there exists \(\chi \in {\mathcal {L}}_A \cup \{\epsilon \}\) with \(\varphi _0 = \varphi _1[\chi / \epsilon ]\) and \(\psi _1 = \chi [\psi _0 / \epsilon ]\).
Definition 13
Let \(\langle \varphi , \psi \rangle \in \Pi (\varvec{\varphi })\). The depth of \(\langle \varphi , \psi \rangle \), denoted \(d(\varphi , \psi )\), is the number of logical operators of \(\varphi \) within whose scope \(\epsilon \) falls under.
Using the notion of strong equivalence and the ordering \(\preceq \), we define the following sets recursively on k.
Intuitively, \(\Pi ^{(k+1)}(\varvec{\varphi }, n)\) consists of the parts of \(\varvec{\varphi }\) that are approximated by some \(\langle \varphi _1, \psi _1 \in \Pi ^{(k)}(\varvec{\varphi }, n)\), such that the template of \(\varphi _1\) occurs in \(\varvec{\varphi }\) with depth at most n.
For large enough \(k < \omega \), \(\Pi ^{(k)}(\varvec{\varphi }, n)\) is fixed; i.e. there exists j such that \(\Pi ^{(j)}(\varvec{\varphi }, n) = \Pi ^{(j+1)}(\varvec{\varphi }, n)\). Fix such a j and define:
Let \(\approx \) partition \(\Gamma _I(\varvec{\varphi }, n)\) into the set of equivalence classes  . Let \(\Phi _0, \dots , \Phi _l\) enumerate the elements of
. Let \(\Phi _0, \dots , \Phi _l\) enumerate the elements of  . For \(0 \le i \le l\), let \(\Theta _{\Phi _i}(z_1, \dots , z_{l_{\Phi _i}})\) be the template of \(\Phi _i\), with arity \(l_{\Phi _i}\). For each \(\varphi \in \Phi _i\), let \(t_1^{\varphi }, \dots , t_{l_{\Phi _i}}^{\varphi }\) be the terms such that \(\varphi = \Theta _{\Phi _i}(t_1^{\varphi }, \dots , t_{l_{\Phi _i}}^{\varphi })\).
. For \(0 \le i \le l\), let \(\Theta _{\Phi _i}(z_1, \dots , z_{l_{\Phi _i}})\) be the template of \(\Phi _i\), with arity \(l_{\Phi _i}\). For each \(\varphi \in \Phi _i\), let \(t_1^{\varphi }, \dots , t_{l_{\Phi _i}}^{\varphi }\) be the terms such that \(\varphi = \Theta _{\Phi _i}(t_1^{\varphi }, \dots , t_{l_{\Phi _i}}^{\varphi })\).
Definition 14
Define a function:
recursively by:
-
1.
\(F_{\varvec{\varphi }, n}(\psi ) = \psi \) if
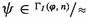 is atomic.
is atomic. -
2.
\(F_{\varvec{\varphi }, n}(\psi ) = p_i^{l_{\Phi _i}}(t_1^{\psi }, \dots , t_{l_{\Phi _i}}^{\psi })\) if
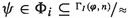 (for some \(0 \le i \le l\)) is not atomic.
(for some \(0 \le i \le l\)) is not atomic. -
3.
If \(\psi \in \Gamma (\varvec{\varphi }, n) \setminus \Gamma _I(\varvec{\varphi }, n)\), define:
-
(a)
\(F_{\varvec{\varphi }, n}(\psi _0 \vee \psi _1) = F_{\varvec{\varphi }, n}(\psi _0) \vee F_{\varvec{\varphi }, n}(\psi _1)\).
-
(b)
\(F_{\varvec{\varphi }, n}(\lnot \psi ) = \lnot F_{\varvec{\varphi }, n}(\psi ).\)
-
(c)
\(F_{\varvec{\varphi }, n}(\exists x \psi ) = \exists x F_{\varvec{\varphi }, n}(\psi )\).
-
(a)
Definition 15
Let \(\varvec{\varphi } = \langle \varphi _0, \dots , \varphi _m \rangle \) be a sequence of closed \({\mathcal {L}}_A^+\)-formulas. The n-th approximation of \(\varvec{\varphi }\) is the sequence:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Colclough, T.M. Components of arithmetic theory acceptance. Synthese 203, 32 (2024). https://doi.org/10.1007/s11229-023-04465-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04465-z







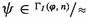 is atomic.
is atomic.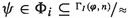 (for some
(for some