Abstract
This article investigates the connection and dependence between the definiteness of the totalities involved in mathematical structures and the determinateness of statements about that structure. From a logical perspective, we investigate whether logical principles expressing the definiteness of totalities license the use of classical logic. From a philosophical perspective, this article provides a reconstruction of Solomon Feferman’s claim that the definiteness of the natural number conception implies the determinateness of arithmetical statements and therefore justifies the adoption of classical logic for arithmetical theories.
Similar content being viewed by others
1 Introduction
One of the central questions in the philosophy of logic(s) is about the correctness or adequacy of logic. Similarly, a central issue in the philosophy of logic and mathematics is to provide principles and criteria for adopting a specific logic for a given mathematical subject matter. These questions are sometimes framed in terms of correctness or adequacy, as the question of providing the ‘correct’ logic of a given subject matter. Other times these questions are framed in epistemic terms: the issue of justifying the employment of a target logic for a given subject matter. Well-known instances of these questions in the philosophy of mathematics are for instance the following: Are we justified in adopting classical logic for the natural numbers? Are we justified in doing so when reasoning about sets?
Quite famously, Solomon Feferman claimed that, for any mathematical subject matter X, classical logic is licensed over X only if X is a definite subject matter.Footnote 1 In his well-known Is the Continuum Hypothesis a Definite Mathematical Problem? Feferman claims the following:
Since \(\textsf{LEM}\) is rejected in intuitionistic logic as a basic principle, that suggests the slogan “What’s definite is the domain of classical logic, what’s not is that of intuitionistic logic.” (Feferman, 2011, p. 23)
In this quote, Feferman suggests that there is in fact a relation between the so-called ‘definiteness’ of a domain and the adoption of LEM, the Law of Excluded Middle. Feferman argues rather informally in several places that an example of such a conception that licenses classical reasoning is ‘the’ natural number structure. Moreover, Feferman argued extensively that, in contrast to the natural numbers, the set-theoretic conception lacks definiteness and therefore, only intuitionistic reasoning is licensed for it at best.Footnote 2 Feferman’s work on this issue inspired a flourishing field of research, most notably, the work on semi-intuitionistic and semi-constructive theories.Footnote 3 Despite this burgeoning literature inspired by Feferman’s work, his own philosophical framework, Conceptual Structuralism, and his claims about the relation between classical logic, intuitionistic logic, and the notion of definiteness, have received little attention in the philosophical community.Footnote 4
This article investigates the philosophical question about the connection and dependence between the definiteness of the mathematical concepts involved in a structural conception and the determinateness of statements within that structural conception. This includes the question in what sense definite structural conceptions license the use of classical logic. With this, the article provides an analysis of the requirements and assumptions, in terms of definiteness, to secure classical logic for a specific conception. When investigating this issue, the article proposes a reconstruction of Feferman’s claim that the definiteness of the natural number conception implies the determinateness of arithmetical statements, and therefore, it justifies the adoption of classical logic for arithmetical theories.
The article has the following structure: Sect. 2 introduces Feferman’s conceptual structuralism together with the relevant concepts of definiteness and determinateness. It makes these notions more precise and presents Feferman’s claim that definiteness implies determinateness. Section 3 provides a rational reconstruction and investigation of Feferman’s argument that definiteness implies determinateness. More precisely, we focus on the ‘case study’ of the natural number conception and show ‘how much’ definiteness is needed to imply determinateness over that structural conception. After providing a philosophical analysis of some known dependencies between formal representations of definiteness and determinateness, we provide our own analysis using an axiomatic theory of truth and show explicitly what principles capturing the definiteness of the natural numbers give us the desired determinateness (Lemma 7). After that, Sect. 4 provides a philosophical discussion of our analysis. With this paper, we clarify Feferman’s rather informal claims about definiteness. Moreover, we hope to provide some insights into the current understanding of Feferman’s conceptual structuralism as a framework to evaluate these important issues in the philosophy of logic and over other mathematical conceptions different from the natural numbers. Finally, this article should (hopefully) be the beginning of a more general discussion of Feferman’s framework in the context of mathematical and logical pluralism.
2 Feferman’s philosophy of mathematics
Before providing an interpretation of Feferman’s understanding of the notions of definiteness of a property or totality and of determinateness of statements, it will be informative to consider briefly his broader view in philosophy of mathematics. Feferman’s position is called conceptual structuralism and, as the name suggests, it is a form of structuralism: mathematics is primarily about ‘structures’ and not about mathematical objects in isolation. More precisely, according to Feferman mathematics is about structural conceptions.Footnote 5 In contrast to other forms of structuralism, such as Shapiro’s ante rem structuralism, structures are not understood as entities independent of the mathematicians working with these conceptions.Footnote 6 Importantly, Feferman’s structuralism is explicitly an anti-realist position and these conceptions do only exist within the community of mathematicians. Although Feferman’s conceptual structuralism avoids the infamous access problem of realist conceptions, it faces the objectivity challenge: to explain the possibility of the objectivity of mathematical discourse. Feferman’s answer to the challenge is to argue that mathematical discourse, at least in some instances, is strongly intersubjective.Footnote 7 Feferman’s argument for the determinateness of arithmetical statements can be interpreted as one form of answering the objectivity challenge.
The most relevant example of a structural conception discussed by Feferman is the structure of the natural numbers, where 0 is some initial object, Sc is an operation, and < a relation. The natural numbers \({\mathbb {N}}\) are generated from 0 by closure under Sc and can be pictured as the following tuple:Footnote 8
Although this article focuses mainly on definiteness and determinateness, it is illustrative to provide more context by including Feferman’s view about the clarity and lack thereof of some mathematical conceptions. The notion of clarity employed by Feferman is informal and rather elusive.Footnote 9 Feferman ascribes a special clarity to the conception of the natural numbers:
The conception of the structure \((N^+, 1, Sc, <, +, \times )\) is so intuitively clear that (again implicitly, at least) there is no question in the minds of mathematicians as to the definite meaning of such statements and the assertion that they are true or false, independently of whether we can establish them in one way or the other. (Feferman, 2014, p. 6)
Despite ‘clarity’ being a rather informal notion, Feferman seems to take the fact that most mathematicians agree in their believes about arithmetic as a support for the claim that the natural number conception is clear. Moreover, most mathematicians seem to take the determinateness of arithmetical statements as a given. Such a form of agreement in the case of arithmetic is an indicator of a strong form of intersubjectivity, which is the base for answering the objectivity challenge.Footnote 10 Feferman’s analysis does not exclude the possibility of the same clarity (at some point) about other mathematical conceptions.
According to Feferman, set theory, in contrast, is a structural conception lacking clarity because its underlying totality, i.e. the universe of sets, \(\textsf{V}\), is inherently indefinite in the strong sense that any attempt to specify the concept is bound to fail. According to Feferman, the indefiniteness of the universe of sets implies the existence of indeterminate statements about sets: an important example of such an indeterminate statement is the Continuum Hypothesis, \(\textsf{CH}\). As we will see later in more detail, the indeterminateness of a statement is understood by Feferman as a failure of LEM for that statement. So in the case of CH, Feferman draws the conclusion that \(\textsf{CH} \vee \lnot \textsf{CH}\) does not hold.Footnote 11 It is important to keep in mind that this is a much stronger claim than the claim of the epistemic indeterminacy of \(\textsf{CH}\).
Following the idea that some set-theoretic statements do not satisfy LEM, Feferman rejects the use of unrestricted classical logical principles for a set-theoretic discourse. In cases of indefinite domains or indefinite concepts Feferman refrains from employing classical reasoning tout court but rather suggests the more cautious use of intuitionistic logic or so-called semi-intuitionistic systems, where classical quantification is permitted only for a restricted class of statements, whereas for unrestricted principles only intuitionistic logic is used.Footnote 12
Before discussing the notions of definiteness and determinateness in detail, we clarify our use of them. Feferman employs these notions in several places for different purposes. Despite the risk of simplification we propose a more uniform use by understanding Feferman as roughly providing a three-layered framework for his philosophy of mathematics: the top layer concerns structural conceptions and is about structures understood as complex conceptions. Feferman employs informal notions, such as clarity, to describe these structural conceptions. The middle layer concerns single concepts that are involved within the structural conceptions. This is on the one hand the underlying totality or in more familiar terms of structuralism the domain of the structure and on the other hand it includes the basic properties, relations and operations of the structure.Footnote 13 Feferman uses the notions of definiteness for the description of these concepts. Finally, for the bottom layer, which concerns the level of statements and theories, Feferman employs the notion of determinateness.Footnote 14
2.1 Definiteness of totalities and determinateness of statements
Feferman connects the definiteness of a given totality with the definiteness of quantification over this totality and Rathjen (2019, p. 3) provides the following interpretation of the connection:
(D1) A totality D is definite if and only if quantification over D is a definite logical operation, i.e., whenever \(R(y,\textbf{x})\) is definite over D, so are \(\forall y \in D \; R(y, \textbf{x} )\) and \(\exists y \in D \; R(y, \textbf{x})\).
A given totality D is considered definite just in case for any definite property or relation R over that totality, the definiteness of R is preserved when forming new relations by using existential or universal quantification over D.
In the case of concepts, properties and relations Feferman’s understanding of definiteness is different. Feferman takes a property to be definite if for all elements of the totality the property is true of those elements or it is not true of those elements. It is natural to use a deflationary reading of the notion ‘true’ here, as also suggested by Feferman himself:
One way of saying of a statement \(\varphi \) that it is definite is that it is true or false; on a deflationary account of truth that’s the same as saying that the Law of Excluded Middle (LEM) holds of \(\varphi \), i.e. one has \(\varphi \vee \lnot \varphi \). (Feferman, 2011, p. 23)
Therefore Rathjen’s interpretation of Feferman’s relevant notion of definiteness for concepts in Rathjen (2019, p. 3) appears appropriate:Footnote 15
(D2) A concept P is definite over a domain D iff LEM holds with regard to it, i.e.,
To sum up, a property or relation R is definite just in case LEM holds for R. On the other hand, a totality D is definite just in case, for any definite property or relation R, unrestricted quantification over D preserves LEM for R. This seems a very intuitive interpretation of Feferman’s claim, and for the purpose of this article we will follow Rathjen’s reconstruction in most cases and only slightly deviate when we focus on truth.
Finally, Feferman suggests that a statement or sentence \(\varphi \) is determinate if and only if either \(\varphi \) is true or the negation of \(\varphi \) is true. Formulas \(\varphi (x)\) are treated similarly and determinate if for all elements of the domain they are true of those elements or not true. Analogous remarks about the deflationary use of truth as in the previous case also suggest here a reading via LEM: a formula \(\varphi (x)\) is determinate iff \(\forall x (\varphi (x) \vee \lnot \varphi (x) )\) holds. This understanding of determinateness of a statement \(\varphi \), i.e., the fact that LEM holds for \(\varphi \), as equivalent to the fact that “classical truth” is applicable to \(\varphi \), i.e., that \(\varphi \) is true or its negation is, explains Feferman’s previously mentioned remark that ‘Since \(\textsf{LEM}\) is rejected in intuitionistic logic as a basic principle, that suggests the slogan “What’s definite is the domain of classical logic, what’s not is that of intuitionistic logic.”
2.2 The dependence between definiteness and determinateness
Feferman argues that the definiteness of a concept is necessary for the determinateness, or equivalently, for a classical notion of truth:
[T]he classical notion of truth in a structure need not be applicable unless we are dealing with a conception (such as that of the structure of natural numbers) for which the basic domains are definite totalities and the basic notions are definite operations, predicates and relations. (Feferman, 2014, p. 80)
Feferman claims that, in order for the classical notion of truth to be applicable to a conception C, the totality and operations, predicates and relations of that totality must be definite.
(\(\dag \)) For a conception P, the definiteness of the totality and its basic notions are a necessary condition for adopting a classical notion of truth in a structure.
This claim has some rationale, but also a sufficiency claim has some intuitive appeal. We are interested in Feferman’s informal claim that the acceptance of the natural number structure as definite ‘implies’ the acceptability of classical logic for the natural numbers. Our focus will be on reconstructing a possible argument from definiteness to determinateness and to show how the definiteness—as spelt out in this section—of the natural numbers with the definiteness of its properties and relations implies the determinateness of statements about the natural numbers. This is a non-trivial task: the very idea that definiteness implies LEM is in tension with the possibility of accepting the natural numbers as a definite totality whilst accepting LEM for restricted classes of formulas. In the case of Heyting Arithmetic HA, for example the decidability of identity is not sufficient to establish \(\textsf{LEM}\) for all the arithmetical sentences.
3 From definiteness to determinateness
This section reconstructs a possible argument from definiteness to determinateness. We analyse different possibilities of making the definiteness of the natural number structure precise and explicit by additional principles. Then we inquire whether these additional principles are sufficient to guarantee a unique truth value. With this we clarify in what sense and to what extent the definiteness of a totality implies determinateness.Footnote 16 More precisely, we consider how the definiteness of the totality of the natural numbers, implies LEM over that totality. Additionally, we provide a truth theoretic argument for a classical notion of truth in a natural number structure.
Following Feferman’s suggestion to employ an intuitionistic framework for the investigation of possibly indefinite domains or concepts we start with an intuitionistic version of arithmetic, the familiar Heyting arithmetic, \(\textrm{HA}\). With this we try not to trivialize the argument by presupposing too much determinacy from the start.
3.1 Hi and HA
We will use a Hilbert-style axiomatic version of intuitionistic logic, Hi. For details we refer the reader to Troelstra and Schwichtenberg (2000, p. 51). The intuitionistic theory of Heyting arithmetic \(\textrm{HA}\) has the same axioms as the classical counterpart Peano arithmetic \(\textrm{PA}\). Following standard presentations of \(\textrm{HA}\) we consider it to be formulated in the language of \(\textrm{PRA}\), i.e., it contains function symbols for all primitive recursive functions.Footnote 17
Identity for natural numbers is taken to be a definite basic concept and therefore classical. Also the numbers themselves are taken as definite in the sense of having decidable identity criteria. With this we do not presuppose that the natural numbers form a definite totality.
The quantifier free part of \(\textrm{HA}\) is given by the axioms of \(\textrm{PRA}\) with induction formulated as a rule for quantifier free formulas, also referred to as \(\textsf{QF}\). This intuitionistic subtheory of \(\textrm{HA}\) also referred to as \(\textrm{PRA}^i\) is based on an extensional conception of identity and the determinateness of identity is provable, i.e., \(\textrm{PRA}^i \vdash x = y \, \vee \, x \ne y\).Footnote 18 It is well-known that this \(\textrm{PRA}^i\) provable determinateness extends to all quantifier free formulas, i.e., for all \(A \in \textsf{QF}\)
The proof is carried out by induction on the logical complexity of quantifier free formulas and indicates that the logical connectives of intuitionistic logic are accepted as determinateness preserving.
This is a first version of the argument from definiteness to determinateness. Assuming the definiteness of identity and the primitive recursive terms as well as the definiteness of the logical connectives, we can establish the determinacy of the statements of the quantifier free fragment.
Since \(\textrm{HA}\) is a stronger theory the natural question arises whether it establishes more determinacy, i.e., determinacy for a larger class of formulae. There is a well-known upper bound for the question of determinacy connected with the constructiveness of \(\textrm{HA}\). One of the reasons for considering \(\textrm{HA}\) as a constructive theory is the fact that \(\textrm{HA}\) has both the disjunction property (\(\textsf{DP}\)) and the numerical existence property (\(\textsf{NEP}\)).
In connection with the question of provable determinacy the disjunction property implies in combination with Gödel’s second incompleteness theorem that we cannot expect for a \(\Pi ^0_1\)-statement A that \(\textrm{HA} \vdash A \vee \lnot A\).
Let us try to approach the question more systematically. For a class of formulas \(\Theta \) we let (\(\Theta \)-DET) be the principle \(A \vee \lnot A\) for all formulas \(A \in \Theta \).Footnote 19 Our previous remarks can then be stated as follows: \(\textrm{HA}\) proves (\(\Delta _0\)–DET), but does not prove (\(\Pi _1\)–DET). An investigation into more exact bounds would be interesting, but will not be pursued further here. Rather we will consider several additional general logical principles, understood as possible definiteness claims, and see how they impact on the question of determinacy.
3.2 Non-constructive principles
In the setting of intuitionistic logic a quite natural suggestion is to connect the assumption of the definiteness of the underlying domain with the so-called constant domain conception. From a semantic point of view, more concretely Kripke semantics, the motivation is to consider only models with the same domain. So for the classical models associated with the nodes of the frame we have a constant domain D in contrast to the more general intuitionistic picture that allows for growing domains along the accessibility relation.
From a syntactic point of view, more concretely a Hilbert-style axiomatic perspective, the assumption of constant domains corresponds to the following principle:

Adding the principle (CD) to \(\textbf{Hi}\) forms an intermediate logic. This logic has some special features. Although it has the disjunction property, a proof-theoretic presentation requires some extra work.Footnote 20
A first observation is that constant domains allow us to establish that for determinate predicates either everything satisfies the predicate or there exists a counterexample, a principle also called bounded omniscience principle:

The principle (\(\textsf{BOS}\)) is connected to determinateness claims for the quantifiers and is equivalent to a definiteness claim for the existential quantifierFootnote 21:

Since \(\vdash _{Hi} \exists x \lnot A(x) \rightarrow \lnot \forall x A(x)\) we also have that (\(\textsf{BOS}\)) implies that the universal quantifier preserves determinateness

Let us now see these principles’ impact on the question of determinacy. For our purposes it might appear interesting to consider \(\textrm{HA}\) over the intermediate logic of constant domains. However, as we will see in this case (\(\textsf{CD}\)) is a rather strong assumption. Whereas \(\textrm{HA}\) itself and the logic of constant domains have the disjunction property, \(\textrm{HA}^{cd}\), i.e., \(\textrm{HA}\) over the logic of constant domains, fails to retain this property.
Proposition 1
-
1.
\(\textrm{HA}^{cd}\) does not have the disjunction property;
-
2.
\(\textrm{HA}^{cd}\) does not have the numerical existence property.
There are several ways to establish this, but there is a simple reason. In combination with the arithmetical axioms, (\(\textsf{CD}\)) is strong enough to establish (\(\textsf{LEM}\)) for all arithmetical formulae.Footnote 22 Interpreting the definiteness of the quantifiers by (\(\textsf{CD}\)) and the definiteness of the basic concepts by the arithmetical axioms allows us to provide an inductive proof on the logical complexity of formulas. The arithmetical axioms guarantee the determinateness of the atomic formulas, intuitionistic logic establishes the closure under the logical connectives and (\(\textsf{CD}\)) the closure under quantifiers.
A similar reasoning is available if we have both \((\textsf{DET}_\exists )\) and \((\textsf{DET}_\forall )\). In the setting of arithmetic (BOS) is also called the numerical omniscience principle (NOS). With the equivalence of (\(\textsf{NOS}\)) and (\(\textsf{DET}_\exists \)) and the fact that (\(\textsf{NOS}\)) implies \((\textrm{DET}_\forall )\) we also have a collapse into classical reasoning in the case of \(\textrm{HA}\) over \(\textbf{Hi}\) plus (\(\textsf{NOS}\)). With this we would have in the three cases a simple argument from definiteness to determinateness and a reason for using classical logic for first-order arithmetic. All three principles that we considered to be ‘natural’ formalizations of definiteness, namely \((\textsf{CD})\), \((\textsf{NOS})\) and \((\textsf{DET}_\exists )\) and \((\textsf{DET}_\forall )\), therefore imply determinateness in a strong sense.
A remaining question is whether there are ‘natural’ versions of definiteness that only imply a partial form of determinateness. In order to have some interesting form of partial determinateness for arithmetical statements of low complexity, we seem to be forced to consider principles weaker than (\(\textsf{NOS}\)) and (\(\textsf{CD}\)).Footnote 23 Let \(\textrm{HA}^{D\forall }\) be \(\textrm{HA}\) over the intermediate logic \(\textbf{Hi} + (\textsf{DET}_\forall \)),Footnote 24 then
Lemma 1
Let A be a \(\Pi _1\) sentence, then \(\textrm{HA}^{D\forall } \vdash A \vee \lnot A\).
The argument is simple. If A is \(\Pi _1\), then it is of the form \(\forall x B(x)\) with B bounded. Since \(\textrm{HA} \vdash \forall x ( B(x) \vee \lnot B(x))\) we have \(\textrm{HA}^{D\forall } \vdash \forall x B(x) \vee \lnot \forall x B (x)\).
Since the proof only employs the principle (\(\textsf{DET}_\forall \)) we can use the Lemma to see that \(\textrm{HA}^{D\forall }\) does not have the disjunction property. Let \(\textsf{con}_{\mathrm{HA^{D\forall }}}\) be the \(\Pi ^0_1\) sentences stating the consistency of \(\textrm{HA}^{D\forall }\). Then by the Lemma we get \(\textrm{HA}^{D\forall } \vdash \textsf{con}_{\mathrm{HA^{D\forall }}} \vee \lnot \textsf{con}_\mathrm{HA^{D\forall }}\). By Gödel’s second incompleteness theorem we know that neither \(\textrm{HA}^{D\forall } \vdash \textsf{con}_{\textrm{HA}^{D\forall }}\) nor \(\textrm{HA}^{D\forall } \vdash \lnot \textsf{con}_{\textrm{HA}^{D\forall }}\).
It remains to establish that \(\textrm{HA}^{D\forall }\) is weaker than \(\textrm{PA}\). For this we can use a simple Kripke model of \(\textrm{HA}\) in which \((\textsf{DET}_\forall )\) holds but \((\textsf{DET}_\exists )\) does not. We can employ a frame with two worlds \(w_{\mathcal {N}}\), \(w_{\mathfrak {M}}\), where \(w_{\mathcal {N}}\) is associated with the standard model \({\mathcal {N}}\) and \(w_{\mathfrak {M}}\) with a nonstandard model \({\mathfrak {M}}\) of \(\textrm{PA}\), that contains a nonstandard element c witnessing a proof of \(0 = 1\). Since \({\mathfrak {M}} \models \textsf{proof}_{HA}(c, 0=1)\) we have \(w_{\mathfrak {M}} \Vdash \textsf{proof}_{HA}(c, 0=1)\) in the Kripke model. And since \(w_{\mathfrak {M}}\) is accessible from \(w_{\mathcal {N}}\), \(w_{\mathcal {N}} \not \Vdash \lnot \exists x {\, \mathsf proof}_{HA} (x, 0 =1)\) and also \(w_{\mathcal {N}} \not \Vdash \exists x \, \textsf{proof}_{HA} (x, 0 =1)\) since \(\textrm{HA}\) is consistent in the standard model. Since \(\textsf{proof}_{HA}\) is \(\Delta _0 (PR)\) this shows that \((\textsf{DET}_\exists )\) is not satisfied in this model. However, in \({\mathfrak {M}}\) as well as \({\mathcal {N}}\) there are nonproofs of \(0=1\) and so \(\lnot \forall x \, \textsf{proof}_{HA} (x, 0=1)\) is satisfied in the model.
A natural suggestion for a systematic investigation could be to define a hierarchy of determinateness principles along the arithmetical hierarchy, however, in the intuitionistic setting a suitable choice for an ‘arithmetical hierarchy’ is not as straightforward as in the classical case. We will not pursue such an investigation but rather switch to a truth theoretic setting.
Before continuing with our analysis using an axiomatic theory of truth, we should clarify the result of the present section. We showed how the definiteness of the conception of natural numbers, once made precise formally, implies the determinateness of arithmetical statements. However, our argument does not focus on (and does not determine) what must motivate the acceptance of the conception of natural numbers as definite. In the case of Feferman, the purported clarity of the natural numbers seems to motivate his acceptance of the definiteness of the conception of natural numbers and of the logical operators on it.Footnote 25
3.3 Truth over intuitionistic logic
In this subsection we consider the options of employing a truth predicate in order to analyze whether the determinacy given in \(\textrm{HA}\) can be expanded to a wider range of formulae. Here the basic motivation stems from Feferman’s remarks, as quoted in Sect. 2.2, that a notion of truth in a structure is only justified for a conception with a definite totality and definite basic concepts.Footnote 26
Again we assume that in the arithmetical setting we have the definiteness of the basic concepts and with it the determinateness of the quantifier free formulas. Additionally, we will now also use a primitive truth predicate for the arithmetical language.
We start by discussing some truth principles for an extension of \(\textrm{HA}\) by a typed truth predicate. Similar to the classical setting one of the natural desiderata is the derivability of all disquotation principles for arithmetical formulae \(\varphi \):
whereas in the classical setting the theory \(\textrm{CT}\) with classical truth principles is a natural theory, the situation for intuitionistic logic is not so obvious, especially since we do not intend a trivial collapse argument.
We still would like to employ compositional principles. One of the desiderata for our theory of truth should be symmetry, i.e., the inner logic should correspond to the outer intuitionistic logic, where the former is the logic inside the scope of the truth predicate, whereas the latter is the logic outside the scope of the truth predicate.
Without the interdefinabilities it might appear that we need truth principles for all the primitives \(\wedge , \vee , \rightarrow , \bot , \forall , \exists \). However, due to the observations in Burr (2004) we can simplify the picture: over \(\textrm{HA}\) we can define \(\bot \) by \(0 = \textsf{S} 0\) and \(A \vee B\) by \(\exists z [( z = 0 \rightarrow A ) \wedge (z \ne 0 \rightarrow B)]\), and moreover we can also define conjunctionsFootnote 27 and therefore one could simply use \(( \rightarrow , \forall , \exists )\) as primitives only.
We introduce a theory of intuitionistic truth \(\textrm{IT}\). Our arithmetical language \({\mathcal {L}}_A\) comprises the logical symbols \(\bot , \rightarrow , \wedge , \vee , \exists , \forall , =\), the arithmetical symbols \(+, \times , \textsf{S}, 0\) and additionally primitive function symbols for sufficiently many primitive recursive functions. The language \({\mathcal {L}}_\textsf{T}\) is the expansion of \({\mathcal {L}}_A\) by a one-place predicate \(\textsf{T}\).
Our base theory is a version of \(\textrm{HA}\) for the expanded language. Since coding works perfectly fine in \(\textrm{HA}\) we use common conventions. For an expression e, \(\# e\) is the Gödelnumber of e. The numeral for n is \({\overline{n}}\). We use s, t, .. as variables ranging over closed terms and \({\ulcorner \! \varphi \! \urcorner }\) for sentences of \({\mathcal {L}}_A\), i.e. \(\forall s ...\) is short for \(\forall x ( \textsf{ct}_A (x) \rightarrow ...)\); \(\exists s ...\) is short for \(\exists x ( \textsf{ct}_A (x) \wedge ...)\) and \(\forall {\ulcorner \! \varphi \! \urcorner }...\) is short for \(\forall x ( \textsf{sent}_A (x) \rightarrow ...)\); \(\exists {\ulcorner \! \varphi \! \urcorner }...\) is short for \(\exists x ( \textsf{sent}_A (x) \wedge ...)\), where \(\textsf{ct}_A (x)\) is the formula representing the primitive recursive set of (codes of) closed terms of \({\mathcal {L}}_A\) in \(\textrm{HA}\) and \(\textsf{sent}_A\), the set of (codes of) sentences in \({\mathcal {L}}_A\). We also use \(\ulcorner \! \varphi {\dot{x}} \! \urcorner \) as a shorthand for \(\textsf{sub} ({\ulcorner \! \varphi \! \urcorner }, \textsf{num} (x))\) as usual and the dot notation for the representation of the respective syntactic function, for example \(\mathop {\wedge }\limits _{.}\).Footnote 28
Our truth theoretic principles are the universal closures, in the sense of \(\forall \ulcorner \varphi \urcorner \rightarrow ...\), of the following:
We call the resulting theory \(\textrm{IT}\) for intuitionistic truth over intuitionistic logic with induction for \({\mathcal {L}}_\textsf{T}\).Footnote 29
A few clarifications about the plausibility of the axioms for truth are in order. (\(\textsf{IT1}\)) and (\(\textsf{IT2}\)) are unproblematic even from a weak, deflationary understanding of truth. The compositional principles guarantee that the inner and the outer logic agree. Additionally, logically equivalent formulas are intersubstitutable in truth-theoretic contexts. This follows from the following claim concerning a standard provability predicate \(\textsf{Pr}_{I \Delta _0}\) for the intuitionistic version of \(\textrm{I} \Delta _0\), the arithmetical theory with induction restricted to \(\Delta _0\)-formulae.
Lemma 2
In \(\textrm{IT}\) we can derive:
Proof
We can reformulate the theory \(\textrm{I} \Delta _0\) with axioms whose syntactic complexity is \(\Delta _0\). Then the disquotation principles \((\textsf{IT1})\) and \((\textsf{IT2})\) establish the truth of the axioms and \((\textsf{IT3})\) and \((\textsf{IT4})\) guarantees that modus ponens preserves truth. A cut-elimination argument establishes that generalisation is not used. \(\square \)
With this we can show that (i) disquotation for \(\bot \) is derivable, (ii) the commutation with negation holds and (iii) the internal logic of T is consistent.
Lemma 3
In \(\textrm{IT}\) we can derive:
-
(i)
\(\textsf{T}(\ulcorner \bot \urcorner ) \leftrightarrow \bot \);
-
(ii)
\(\lnot \textsf{T}(\ulcorner \varphi \urcorner ) \leftrightarrow \textsf{T}(\ulcorner \lnot \varphi \urcorner )\);
-
(iii)
\(\lnot \textsf{T}(\ulcorner \varphi \wedge \lnot \varphi \urcorner \)).
Proof
For (i) we use (\(\textsf{IT1}\)) and (\(\textsf{IT2}\)); for (ii) we use (\(\textsf{IT3}\)) and (\(\textsf{IT4}\)) as well as (i); for (iii) we formalize the proof of \(A \wedge \lnot A \rightarrow \bot \) in \(\textrm{I} \Delta _0\) and then use Lemma 2. \(\square \)
The aim of the following is to transfer the provable classicality of the \(\Delta _0\)-fragment to the full language of arithmetic. In contrast to classical arithmetic we do not have a prenex normal form for arithmetical formulas and with it the familiar arithmetical hierarchy of \(\Pi _n\)- and \(\Sigma _n\)-formulas. However, there is an alternative characterization–at least of the \(\Pi _n\)’s–via \(\Phi _n\) sets of formulas due to Burr (2004).
Following Burr (2004) one defines \(\Phi _n\) in the following manner:
-
(i)
\(\Phi _0 : \leftrightarrow \Delta _0\).
-
(ii)
\(\Phi _1 : \leftrightarrow \Pi _1\).
-
(iii)
Suppose that \( \Phi _{n-1} \) and \(\Phi _{n-2}\) are defined for \( n \ge 2.\) \(\Phi _n \) is the class of formulae of the form \(\forall x (\psi \rightarrow \exists z \chi ) \), where \(\psi \) is in \(\Phi _{n-1}\) and \(\chi \) is in \(\Phi _{n-2}\) and x may occur in both \(\psi \) and \(\chi \).
These \(\Phi _n\) correspond to the classical \(\Pi _n\), in fact they are classically equivalent to them.Footnote 30 Moreover, they exhaust the full language, i.e., for all \(\varphi \in {\mathcal {L}}_A\) there is an n and a \(\psi \in \Phi _n\) such that \(\textrm{HA}\) derives \(\varphi \leftrightarrow \psi \).Footnote 31 This means that we can reduce the arithmetical vocabulary to \(\{ \rightarrow , \forall , \exists , = \}\).
Since \(\Delta _0\) formulas are provably decidable and \(\Pi _1\) and \(\Phi _1\) coincide, we can define a partial truth predicate \(\textsf{T}_0\), such that \(\textrm{HA}\) proves the Tarski clauses for \(\Delta _0\) formulas. Then it is also possible to define partial truth predicates \(\textsf{T}_n\) for all finite stages of the intuitionistic arithmetical hierarchy, such that \(\textrm{HA} \vdash \textsf{T}_n (\ulcorner \! \varphi (\dot{\textbf{x}}) \! \urcorner ) \leftrightarrow \varphi (\textbf{x})\) for all \(\varphi \in \Phi _n\).Footnote 32 Our primitive truth predicate corresponds to these definable truth predicates on the relevant fragment, and therefore we have the uniform T-biconditionals for the full language.
Lemma 4
\(\textrm{IT} \vdash \textsf{T}(\ulcorner \! \varphi (\dot{\textbf{x}}) \! \urcorner )\leftrightarrow \varphi (\textbf{x})\) for all \(\varphi \in {\mathcal {L}}_A\).
In the next step, we consider the question of determinacy. Our starting point is the \(\textrm{HA}\)-provable determinacy of the \(\Delta _0\)-fragment. By formalizing the proof in \(\textrm{HA}\) we get the following:
Lemma 5
\(\textrm{HA} \vdash \forall {\ulcorner \! \varphi \! \urcorner }(\Delta _0 ({\ulcorner \! \varphi \! \urcorner }) \rightarrow \forall \textbf{x} ( \textsf{T}_0 (\ulcorner \! \varphi (\dot{\textbf{x}}) \! \urcorner ) \vee \textsf{T}_0 (\ulcorner \! \lnot \varphi (\dot{\textbf{x}}) \! \urcorner )))\).
Without further assumptions we cannot use Lemmas 4 and 5 directly to infer the determinacy of all arithmetical formulas. We consider again additional principles motivated by the assumption that the natural numbers form a definite totality. In the setting with a truth predicate we make this assumption explicit as the claim that if a formula is truth determinate then also all its universal, and existential generalizations are truth determinate. Since we can code finite sequences we will simplify notation in the following and only use a single free variable x instead of \(\textbf{x}\) and do not explicitly mention the additional parameters.


Moreover, we require that the determinacy of truth—as in Lemma 5—is preserved by implication, that is, that for any two formulas \(\varphi , \psi \) of \({\mathcal {L}}_A\) we have that if they are determinate, then the implication is also determinate. With our intuitionistic arithmetical hierarchy we need the conditional to be determinateness preserving:

Lemma 6
\(\textrm{IT}\) proves \((\mathsf{TDET_\rightarrow })\)
Proof
We argue in \(\textrm{IT }\).
Assume that
Then we can establish
We also have that all the disjuncts except the second imply \(\textsf{T}(\ulcorner \! \varphi \rightarrow \psi \! \urcorner )\), whereas the remaining disjunct implies \(\textsf{T}(\ulcorner \! \lnot (\varphi \rightarrow \psi ) \! \urcorner )\). \(\square \)
The resulting theory is called \(\textrm{DIT}\), i.e. \(\textrm{IT}\) plus \((\textsf{TDET}_\forall )\), \((\textsf{TDET}_\exists )\). In \(\textrm{DIT}\) we can show that all arithmetical statements are determinate.
Lemma 7
Proof
By internal induction.
For \(\Phi _0\)-formulas we use Lemma 5 and the fact that our primitive truth predicate \(\textsf{T}\) corresponds with \(\textsf{T}_0\) on \(\Delta _0\)-formulas. For \(\Phi _1\)-formulas we use \((\textsf{TDET}_\forall )\).
For \(n\ge 2\) we argue as follows: If \(\Phi _n ({\ulcorner \! \varphi \! \urcorner })\), then \({\ulcorner \! \varphi \! \urcorner }= \ulcorner \! \mathop {\forall }\limits _{.} x (\psi \mathop {\rightarrow }\limits _{.} \mathop {\exists }\limits _{.} z \chi ) \! \urcorner \) and \(\Phi _{n-1}(\ulcorner \! \psi \! \urcorner )\) and \(\Phi _{n-2}(\ulcorner \! \chi \! \urcorner )\). By induction hypothesis \(\psi \) and \(\chi \) are truth determinate. By \((\textsf{T DET}_\exists )\) also \(\exists z \chi \) is determinate. By \((\textsf{T DET}_\rightarrow )\) we have that \(\psi \rightarrow \exists z \chi \) is determinate and with \((\textsf{T DET}_\forall )\) \(\varphi \) itself is determinate. \(\square \)
Lemma 7 shows how the additional determinacy, in terms of \((\textsf{TDET}_\forall )\), \((\textsf{TDET}_\exists )\), implies the determinateness of the whole arithmetic language. In this sense, the truth-theoretic framework makes explicit how the definiteness of the natural numbers—modulo the truth-theoretic formulation—licences the adoption of classical logic for the natural numbers. The remainder of the paper offers a philosophical discussion of our results about definiteness and determinateness.
4 Philosophical discussion
In the previous sections, we investigated the claim that definiteness implies determinateness. We showed how one could extend Heyting Arithmetic with additional principles, which allow us to recover (either partial or total) determinateness, in the form of LEM. In the remainder of this article, we will make some important, initial philosophical remarks on the dependence between definiteness and determinateness. Moreover, we provide a philosophical analysis of the investigation provided in the previous section.
4.1 Definiteness and intrinsic justification
We saw that in an arithmetical context there are several ways to recover the principle of LEM from different principles of definiteness. Starting from the definiteness of basic concepts and an understanding of the definiteness of the totality of natural numbers as the definiteness of the logical operations of quantification one can establish the determinacy of all arithmetical statements. In more detail, we assume that identity and the primitive recursive operations are definite, the logical connectives as well as the quantifiers are determinacy preserving. The determinacy preservation of the quantifiers over the natural numbers is expressed by, following Rathjen, as: if P is a definite property, so that for all n, P(n) holds or \(\lnot P(n)\) holds, then also \(\forall x P(x)\) holds or \(\lnot \forall x P(x)\) holds as well as \(\exists x P(x)\) holds or \(\lnot \exists x P(x)\) holds.
We saw that the extension of Heyting Arithmetic with the definiteness of both quantifiers proves LEM for the full arithmetical language, recovering Peano Arithmetic PA. The same result holds if one extends HA either with the schema (CD) expressing that the first-order domain is constant or with the numerical omniscience schema (NOS). The fact that a variety of seemingly harmless principles of definiteness force a collapse into classical logic in the setting of arithmetic might be interpreted as an indication for the naturalness of accepting the determinacy of arithmetical statements as implied by a definite conception of the natural numbers.
It appears much more difficult to find interesting and natural principles of definiteness that do not provide a full collapse. For example the definiteness of universal quantification alone is not sufficient to recover LEM for the entire language. However, from the perspective of definiteness of the totality of natural numbers it appears more natural to accept both quantifier principles. Moreover, from the perspective of the natural numbers as a clear structural conception with a definite domain, the numerical omniscience principle appears to have some motivation. Of course, this is not intended as an argument against a fully constructive understanding of the natural numbers and the coherence and use of Heyting arithmetic.
For the discussion of Feferman’s idea that the definiteness of the natural number structure implies the determinateness of all arithmetical statements, we take these results as making explicit how much definiteness is needed to license the use of classical logic over the natural number structure. From Feferman’s perspective, who takes the natural numbers as given, not much definiteness is needed; it is only needed that, whenever LEM holds for a property P, LEM can be lifted to both \(\forall x P(x)\) and \(\exists x P(x)\).
Let us try to be a little bit more explicit on how to understand the connection between the structural conception of the natural numbers as a definite totality and the determinacy principles for the quantifiers by considering the notions of intrinsic and extrinsic justification. This terminology is used for example in the discussion about finding ‘new’ axioms of set theory. Maddy puts the issue quite clearly and succinctly:
It has become customary to describe these two rough categories of justification as ‘intrinsic’ – self-evident, intuitive, part of the ‘concept of set’, and such like – and ‘extrinsic’ – effective, fruitful, productive. (Maddy, 2011, p. 47)
In general, we can say that a principle is intrinsically justified by some mathematical conception just in case ‘it follows’ from that conception. The informal notion of ‘follows from’ needs some clarification. Although we do not attempt a substantial explanation here, we distinguish a conceptual or semantical reading from an epistemic reading of the connection.Footnote 33
Using these terms, we can reformulate the dependence between definiteness and LEM as follows: LEM is intrinsically justified by a structural conception of the natural numbers that takes it as a definite totality. Such a definite conception of natural numbers provides an intrinsic ground for NOS (and therefore for LEM). From this perspective, the scepticism about the truth of NOS would seem unreasonable and should be independently motivated, meaning that an argument for the indefiniteness is necessary. In the case of arithmetic, although it is not impossible to conceive of them as not forming a definite totality, strong convincing arguments for their indefiniteness are not to be expected.
In contrast to the conception of natural numbers, the conception of set is drastically different. According to Feferman, it lacks ‘clarity’. Feferman also argues extensively against the claim that the sets form a definite totality. For example, in his (Feferman (2011), p. 1) Feferman claims that “the concept of arbitrary set [...] is vague or underdetermined and there is no way to sharpen it without violating what it is supposed to be about”. This purported indefiniteness has implications on the determinateness of set-theoretical statements, as one can see from Feferman’s claim about the status of the Continuum’s Hypothesis:
My own view – as is widely known – is that the Continuum Hypothesis is what I have called an “inherently vague” statement, and that the continuum itself, or equivalently the power set of the natural numbers, is not a definite mathematical object. [...] On my view, it follows that the conception of the whole of the cumulative hierarchy, i.e., the transfinitely cumulatively iterated power set operation, is even more so inherently vague, and that one cannot in general speak of what is a fact of the matter under that conception. (Feferman et al., 2000, p. 405)
This quote suggests a reading of the implication from definiteness to determinateness as conceptual or semantic.Footnote 34 Feferman seems to suggest that the ‘unclarity’ of the conception of set—in term of its vagueness or underdetermination—implies the indeterminateness of some set-theoretical statements and thereby indefiniteness of unrestricted quantification in the context of set theories. The indefiniteness of set theory is for Feferman a reason to reject unrestricted principles of omniscience for the concept of set. This is motivated by the idea that—following Feferman—principles of omniscience are not meaningful when formulated unrestrictedly quantifying over the whole universe of sets. In the set-theoretic context, Feferman would only accept omniscience principles in a bounded formulation, where the quantifiers in the formulation of omniscience do not quantify unrestrictedly over the whole universe of sets.Footnote 35
4.2 Definiteness and implicit commitments
The second reading of the implication from definiteness to determinateness is epistemic in the following sense: if one accepts the concept of the natural number structure as definite, then one ought to accept LEM for the full language. An epistemic reading is motivated also given Feferman’s interest in implicit commitments: the acceptance of LEM can be interpreted as an implicit commitment of anyone accepting the natural numbers as definite. Most notably, Feferman considered the acceptance of so-called ‘reflection principles’ for arithmetic as implicit in the acceptance of theories of arithmetic.Footnote 36 Similarly, accepting logical principles such as LEM are implicit in accepting definite concepts. In this sense, the implication would express a conditional (rational) obligation: if the natural numbers are accepted to be a definite totality—as suggested by Feferman and reconstructed by Rathjen—rejecting classical logic is not rationally supported. The implication’s strong epistemic reading seems to be suggested by Feferman in his brief discussion of the structural conception given by the powerset of the natural numbers. He claims the following:
If S(N) [i.e., the powerset of the natural numbers] is considered as a definite totality, the classical notion of truth is applicable and the semantics of second-order logic must be accepted. (Feferman, 2014, p. 81) [our emphasis]Footnote 37
From the perspective of the epistemic reading, we also better understand the essential role of the notion of truth; without the notion of truth, the acceptance of the natural numbers as a definite conception only motivates a schematic or local acceptance of LEM. For any given sentence \(\varphi \) in the language of arithmetic, one would be implicitly committed to accept LEM for \(\varphi \). Importantly, one would not be able to claim one’s own acceptance of LEM; this is due to its schematic formulation. In contrast to this scenario, the notion of truth allows us to make the acceptance of LEM completely explicit. This is the content of Lemma 7, where the truth predicate allows us to quantify over all arithmetical sentences and state the acceptance or validity of LEM as a single sentence. Philosophically, we can take this as being an explicit articulation of an agent’s global acceptance of LEM for his structural conception of the natural numbers.
Despite the fact that truth allows us to express the acceptance of LEM globally, an additional argument would be required to draw the stronger conclusion that the structural conception of the natural numbers is unique. The uniqueness of the structural conception is a stronger notion of the determinacy of arithmetical truth. A standard structuralist understanding of the determinacy of arithmetical truth would require an ‘absolute’ truth as truth in ‘all’ arithmetical structures. One might wonder whether the definiteness of the natural numbers is strong enough to secure this form of determinacy of truth. However, definiteness and LEM are prima facie insufficient to secure truth in ‘all’ arithmetical structures. A possible strategy to argue for such a strong form of determinacy would be to employ categoricity theorems for arithmetical structures. In the setting of conceptual structuralism, such a categoricity theorem could then be used to establish the ‘uniqueness’ of the natural number conception.Footnote 38
4.3 Definiteness and pluralism
As we saw, Feferman’s framework based on the notion of definiteness can be used to evaluate important questions in the philosophy of logic and, in particular, questions about which logic should be adopted for a given mathematical subject matter. In his discussion in Feferman (2014), Feferman uses the notion of definiteness to distinguish between mathematical conceptions licensing classical logic and conceptions licensing intuitionistic logic at best. This seems to suggest a pluralist understanding of Feferman’s philosophy of logic. To our best knowledge, Feferman never explicitly proposed a pluralism about logic. However, the pluralist reading of his position seems quite natural. Different logics are best suited for different mathematical conceptions or subject matters: classical logic is the logic of definite conceptions, whereas intuitionistic logic is the logic of indefinite conceptions. For theories about definite and indefinite totalities, such as second-order arithmetic, some semi-intuitionistic logic will do.Footnote 39 Feferman’s position seems to carry traces of a relativist pluralist position about mathematical domains because it does not claim the existence of a single correct logic for all branches of mathematics.
Although a simple domain relativist position would still be consistent with logical monism, Feferman’s position is nevertheless compatible with a pluralist stance about logic as well. This is connected with Feferman’s antirealist philosophy of mathematics; since not all mathematical structures, qua abstract conceptions, are alike—some are definite, and some are not—different logics are appropriate for different mathematical conceptions. In contrast to a realist structuralist position, Feferman’s structuralism is compatible with the idea that there might be no fact of the matter as to whether a structural conception is definite. The notion of clarity and definiteness of conceptions would be central to such a pluralist position.
There is hope to find agreement on what the ‘correct’ logic is only for conceptions that are clear enough and guarantee sufficient intersubjectivity. This dependence on the clarity of the structural conceptions might appear problematic, but it also enables a form of logical pluralism that is not only a form of domain relativism. Since the notion of ‘clarity’ is rather imprecise and gradual it appears not counterintuitive to expect a variety of logics to be appropriate. There might be more possibilities besides classical or intuitionistic logic. This suggests a quite intuitive generalisation of Feferman’s framework to a more substantial form of pluralism.
There are several possible reasons for Feferman to focus primarily on classical and intuitionistic logic. One of these is his focus on the question of indefinite versus definite totalities. Connecting indefinite totalities with intuitionistic reasoning has a strong tradition, as Dummett and others exemplify.Footnote 40 Although the choice of intuitionistic logic is motivated it might not be the only reasonable candidate. Work on potentialism suggests that modal logics could play a reasonable alternative,Footnote 41 or even mixed variations of modal and intuitionistic logics.Footnote 42 Intuitionistic logic has some appeal in cases where we have open-ended conception with some intuition of possible extensions of the domain. However, one could also imagine abstract structures in which not only growing domains are an option but also a shrinking of the domain is a viable possibility.
By including other forms of underdetermination in the discussion other logics might be appropriate. Whereas Feferman makes use of free logics or logics of partial terms in his work on unfolding he famously critizised many-valued logics such as \(\textbf{K3}\) or \(\textbf{LP}\) in Feferman (1984) as not well-suited for ‘sustained ordinary reasoning’.Footnote 43 Despite Feferman’s criticism, we might want to consider mathematical conceptions that prima facie motivate alternative logics. One example is a Kripkean conception of type-free truth based on the fixed point models. In the four valued case the fixed points form a complete lattice and the internal logic is \(\textbf{FDE}\). Besides the fact that an intuitionistic conditional is too strong for a transparent version of the logic of truth there might be additional reasons to consider ‘weaker’ logics. It might be of interest to consider not only growing domains by considering ‘larger’ fixed-points but also to consider ‘smaller’ fixed-points. Analogously to Feferman’s semi-intuitionist systems one could then also consider mixed logics with classical principles for the number quantifiers and partial logics for the arithmetical subsets definable by partial predicates.
One could use Feferman’s framework to characterise all sorts of logic weaker than intuitionistic logic, as logics of particular mathematical conceptions. This suggests an interesting logical pluralism, claiming that different logics are best suited for different subject matters. And this pluralism would be motivated—modulo the notion of definiteness—by a pluralism about the definiteness of mathematical conceptions.
Data availability
Not applicable.
Notes
Here we take the word ‘subject matter’ to be informal. As we will see later, in his framework, Feferman calls such subject matters ‘structural conceptions’ or ‘structural concepts’. The notion of ‘definiteness’ is introduced and analysed later.
It is not clear whether Feferman in his 2014 uses the words ‘concept’ and ‘conceptions’ interchangeably, but we reserve the notion ‘conception’ for structures and ‘concept’ for properties.
Feferman’s use of this notion is critically discussed in Koellner (2017).
In this sense, Feferman’s argument based on agreement provides some empirical grounds for the informal thesis that arithmetic is ‘clear’. This consensus would, however, provide empirical grounds at most.
These concepts are intensional and not extensional as the more common related versions in relational structures. Feferman understands properties and operations as intensional objects—as he pointed out already in Feferman (1979).
We should remark that this layer is not purely formal: these are interpreted statements and mathematical theories.
In Scambler (2016, p. 556), Scambler agrees with Rathjen’s reconstruction of Feferman’s definiteness and also proposes to understand the definiteness of a given totality as being equivalent to the definiteness of quantification over that totality in the sense specified by Rathjen.
The motivation for these additional principles is taken from Feferman’s remarks on the clarity of the natural number structure and should be understood as an assumption in need of justification.
For details we refer the reader to Troelstra and Dalen (1988).
See Troelstra and Dalen (1988, p. 128).
This corresponds to (\(\Theta \)-LEM) as for example investigated in Akama et al. (2004) .
A rather complicated sequent system developed by Kashima and Shimura (1994) allows one to establish cut-elimination and the disjunction property (DP). For DP see Theorem 5.6 in Kashima and Shimura (1994) and compare Aschieri (2018). The extra complications arise because the straightforward multi-conclusion system does not allow for cut-elimination (nor interpolation) as explained in López-Escobar (1983) and Mints et al. (2013). The straightforward system is gained by replacing the rule: \(\frac{\Gamma \Rightarrow A}{\Gamma \Rightarrow \forall x A (x)}\) with a rule allowing contexts in the consequent \(\frac{\Gamma \Rightarrow \Delta , A}{\Gamma \Rightarrow \Delta , \forall x A (x)}\).
Compare Crosilla and Linnebo (2023, fn. 10). The determinateness of A implies the determinateness of \(\lnot A\) as well as the equivalence \(\lnot \lnot A \leftrightarrow A\). With the intuitionistic valid equivalence \(\forall x \lnot A \leftrightarrow \lnot \exists x A\) we get the desired equivalence.
Compare Troelstra (1973, p. 92).
Considering restricted forms of (\(\textsf{LEM}\)), i.e.,(\(\Theta \)-\(\textsf{LEM}\)) we have that \(\Pi _1\)-\(\textsf{LEM}\) does not imply \(\Sigma _1\)-\(\textsf{LEM}\) over \(\textrm{HA}\) whereas the converse is the case. Compare Akama et al. (2004).
Alternatively in the setting of \(\textrm{PRA}\) we could consider a limited principle of omniscience (\(\textsf{LPO}_{pr}\)):
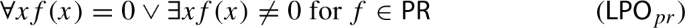
To determine precisely why arithmetic or other mathematical conceptions should be accepted as clear or definite to start with would involve an (probably empirical) investigation of the purported agreement mentioned by Feferman, and would exceed the scope of our theoretical investigation.
An alternative would be to work in a partial setting such as \(\textbf{FDE}\), for instance with the theory of truth \(\textrm{PKF}\). See for instance Halbach and Horsten (2006) for a presentation of the theory.
See Lemma 3 (iv) in Burr (2004).
For a standard reference for this convention, see Halbach (2014).
Compare Leigh and Rathjen (2012) for type-free theories of truth in an intuitionistic setting.
Compare Lemma 2 in Burr (2004).
Actually \(\textrm{I} \Delta _0\) is sufficient. Compare Corollary 4 in Burr (2004).
Compare Burr (2004, Theorem 7, p. 54).
Martin (2018) provides some more information.
As for Feferman’s reasons to think that the conception of set is vague, he also seems to have here (similarly to the arithmetical case) some empirical considerations. In his article Feferman (2011), he takes the purported disagreement about \(\textsf{CH}\) as an indicator that set theory lacks clarity. As Feferman recognises, this would only provide weak evidence for his claim, which seems mainly conceptual. In fact, he claims that “none of this by itself establishes that CH is not a definite mathematical problem, but it surely has to give one pause and ask if the concepts of arbitrary set and function that are essential to its formulation are indeed as definite as one thought, despite their ubiquity in modern mathematics” (Feferman, 2011, p. 8).
We should point out, however, that a more cautious reading of the epistemic implication is possible: definiteness can be understood as providing only a warrant to accept classical logic, without being an obligation. We think that both readings are possible and not exclusive. An investigation of these readings needs independent attention.
An interesting example of a mathematical conception prima facie definite but non-categorical is the conception of dense linear order without endpoints. See Martin (2018) for a brief discussion. To investigate the relation between definiteness and categoricity would exceed the scope of this article. For the discussion about the philosophical uses of categoricity, see Parsons (2008), Button and Walsh (2016, 2018), Maddy and Väänänen (2022), Fischer and Zicchetti (2023) and Picollo and Waxman (2023).
These are called ‘partially open-ended structures’ in Feferman (2014), as Feferman sometimes uses the word ‘open-ended’ as synonymous with ‘indefinite’.
Compare Rathjen (2019) for a connection between Feferman’s notion of indefinite totality and Dummett’s discussion of indefinite extensibility.
Compare the discussion in Linnebo and Shapiro (2021).
References
Akama, Y., Berardi, S., Hayashi, S., & Kohlenbach, U. (2004). An arithmetical hierarchy of the law of excluded middle and related principles. In Proceedings of the 19th annual IEEE symposium on logic in computer science, 2004. IEEE.
Aschieri, F. (2018). On natural deduction for Herbrand constructive logics III: The strange case of the intuitionistic logic of constant domains. Electronic Proceedings in Theoretical Computer Science, 281, 1–9.
Beeson, M. J. (1985). Foundations of constructive mathematics. Springer.
Burr, W. (2004). The intuitionistic arithmetical hierarchy. In J. V. Eijck, V. V. Oostrom, & A. Visser (Eds.), Logic colloquium ’99: Lecture notes in logic 17 (pp. 51–59).
Button, T., & Walsh, S. (2016). Structure and categoricity: Determinacy of reference and truth value in the philosophy of mathematics. Philosophia Mathematica, 24(3), 283–307.
Button, T., & Walsh, S. (2018). Philosophy and model theory. Oxford University Press.
Crosilla, L., & Linnebo, Ø. (2023). Weyl and two kinds of potential domains. Noûs, 1–23.
Feferman, S. (1962). Transfinite recursive progressions of axiomatic theories. The Journal of Symbolic Logic, 27(3), 259–316.
Feferman, S. (1964). Systems of predicative analysis. The Journal of Symbolic Logic, 29(1), 1–30.
Feferman, S. (1979). Constructive theories of functions and classes. In M. Boffa, D. Dalen, & K. McAloon (Eds.), Logic colloquium ’78, volume 97 of Studies in logic and the foundations of mathematics (pp. 159–224). Elsevier.
Feferman, S. (1984). Toward useful type-free theories. I. The Journal of Symbolic Logic, 49(1), 75–111.
Feferman, S. (1995). Definedness. Erkenntnis, 43(3), 295–320.
Feferman, S. (1996). Gödel’s program for new axioms: Why, where, how and what? In P. Hájek (Ed.), Gödel ’96: Logical foundations of mathematics, computer science and physics-Kurt Gödel’s legacy (pp. 3–22). Springer.
Feferman, S. (2009). Conceptions of the continuum. Intellectica, 51(1), 169–189.
Feferman, S. (2011). Is the continuum hypothesis a definite mathematical problem? In EFI workshop general background material.
Feferman, S. (2012). On the strength of some semi-constructive theories. In U. Berger, H. Diener, P. Schuster, & M. Seisenberger (Eds.), Logic, construction, computation (pp. 201–226). De Gruyter.
Feferman, S. (2014). Logic, mathematics and conceptual structuralism. In P. Rush (Ed.), The metaphysics of logic (pp. 72–92). Cambridge University Press.
Feferman, S., Friedman, H. M., Maddy, P., & Steel, J. R. (2000). Does mathematics need new axioms? Bulletin of Symbolic Logic, 6(4), 401–446.
Feferman, S., & Strahm, T. (2000). The unfolding of non-finitist arithmetic. Annals of Pure and Applied Logic, 104, 75–96.
Feferman, S., & Strahm, T. (2010). Unfolding finitist arithmetic. Review of Symbolic Logic, 3(4), 665–689.
Ferreirós, J. (2022). Conceptual structuralism. Journal for General Philosophy of Science, 54(1), 125–148.
Fischer, M., & Zicchetti, M. (2023). Internal categoricity, truth and determinacy. Journal of Philosophical Logic, 52(5), 1295–1325.
Halbach, V. (2014). Axiomatic theories of truth (revised edition). Cambridge University Press.
Halbach, V., & Horsten, L. (2006). Axiomatizing Kripke’s theory of truth. The Journal of Symbolic Logic, 71, 677–712.
Isaacson, D. (2011). The reality of mathematics and the case of set theory. In Z. Novák & A. Simonyi (Eds.), Truth, reference, and realism (pp. 1–75). Central European University Press.
Kashima, R., & Shimura, T. (1994). Cut-elimination theorem for the logic of constant domains. Mathematical Logic Quarterly, 40, 153–172.
Koellner, P. (2017). Feferman on set theory: Infinity up on trial. In G. Jäger & W. Sieg (Eds.), Feferman on Foundations. Outstanding contributions to logic. Springer.
Leigh, G., & Rathjen, M. (2012). The Friedman Sheard programme in intuitionistic logic. The Journal of Symbolic Logic, 77(3), 777–806.
Linnebo, O. (2013). The potential hierarchy of sets. Review of Symbolic Logic, 6(2), 205–228.
Linnebo, O., & Shapiro, S. (2021). Predicativism as a form of potentialism. The Review of Symbolic Logic, 16, 1–32.
López-Escobar, E. (1983). A second paper “On the interpolation theorem for the logic of constant domains’’. The Journal of Symbolic Logic, 48, 595–599.
Maddy, P. (2011). Defending the axioms: On the philosophical foundations of set theory. Oxford University Press.
Maddy, P., & Väänänen, J. (2022). Philosophical uses of categoricity arguments, arxiv preprint: 2204.13754.
Martin, D. A. (2018). Completeness or incompleteness of basic mathematical concepts. Retrieved 12 February 2018 from https://www.math.ucla.edu/~dam/booketc/efi.pdf
Mints, G., Olkhovikov, G., & Urquhart, A. (2013). Failure of interpolation in constant domain intuitionistic logic. The Journal of Symbolic Logic, 78(3), 4937–950.
Parsons, C. (1983). Sets and modality. In Mathematics in philosophy. Cornell University Press.
Parsons, C. (2008). Mathematical thought and its objects. Cambridge University Press.
Picollo, L., & Waxman, D. (2023). Internalism and the determinacy of mathematics. Mind, 132, 1028–1052.
Rathjen, M. (2016). Indefiniteness in semi-intuitionistic set theories: On a conjecture of Feferman. Journal of Symbolic Logic, 81(2), 742–754.
Rathjen, M. (2019). The scope of Feferman’s semi-intuitionistic set theories and his second conjecture. Indagationes Mathematicae, 30(3), 500–525.
Reck, E., & Schiemer, G. (2020). Structuralism in the philosophy of mathematics. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (spring 2020 edition). Metaphysics Research Lab, Stanford University.
Scambler, C. (2016). An indeterminate universe of sets. Synthese, 197(2), 545–573.
Troelstra, A. (1973). Metamathematical investigation of intuitionistic arithmetic and analysis. Springer.
Troelstra, A., & Dalen, D. v. (1988). Constructivism in mathematics (Vol. I). Elsevier.
Troelstra, A., & Schwichtenberg, H. (2000). Basic proof theory (2nd ed.). Cambridge University Press.
Acknowledgements
Thanks to Gianluca Grilletti, Luca Castaldo and others for helpful discussions on the topic. Martin Fischer thankfully acknowledges the financial support by the DFG-project Logic: from tolerance to pluralism, “Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) – Projektnummer 407312485”. Matteo Zicchetti is grateful to the National Science Centre, Poland (MAESTRO project number 2019/34/A/HS1/00399) for their financial support. Matteo Zicchetti’s funding is provided within the project Epistemic and Semantic Commitments of Foundational Theories (PI Cezary Cieśliński).
Author information
Authors and Affiliations
Contributions
All authors whose names appear on the submission (i) made substantial contributions to the conception of the work; (ii) drafted the work and revised it critically for important intellectual content; (iii) approved the version to be published; (iv) agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Corresponding author
Ethics declarations
Competing interests
No competing interests.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fischer, M., Zicchetti, M. Definite totalities and determinate truth in conceptual structuralism. Synthese 203, 26 (2024). https://doi.org/10.1007/s11229-023-04443-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04443-5