The import of hypodoxes for the Liar and Russell’s paradoxes

Abstract

Is the set of all self-membered sets, S, a member of itself? In naive set theory, this is Russell’s hypodox. By the Laws of Excluded Middle and Non-contradiction, S is a member of itself xor it is not, but no principle of classical logic or naive set theory determines which. (Herein, ‘xor’ extends English with a specifically exclusive disjunction.) As a hypodox, the Truth-teller is a sentence that says of itself simply that it is true; by the above mentioned principles, the Truth-teller is true xor not true, but no principle of classical logic or naive truth determines which. Many concepts that have paradoxes have related hypodoxes, although the focus here is on these two. I argue that the Truth-teller does not rely on a principle of truth, in particular it does not rely on the T-schema. I also argue that Russell’s hypodox does not rely on Comprehension. Yet I relate Russell’s paradox and hypodox based on involution functions. The Liar and the Truth-teller are also related by means of involutions. Relations based on these involution functions can be represented in duality squares. Although hypodoxes are not paradoxes, these involution functions and duality relations warrant some commonality in a correct solution to a paradox and its dual hypodox. Using this and some other premises, I provide novel arguments supporting non-classical solutions for the Liar paradox and the significance of Russell’s hypodox for solutions to Russell’s paradox.

1 Introduction

Russell’s hypodox concerns the set of all self-membered sets, S. By the Laws of Excluded Middle and Non-contradiction, S is a member of itself xor it is not, but no principle of classical logic or naive set theory determines which. (Herein, ‘xor’ extends English with a specifically exclusive disjunction.) As a hypodox, the Truth-teller is a sentence that says of itself simply that it is true. By the above mentioned principles, the Truth-teller is true xor not true, but no principle of classical logic or naive truth determines which. Many concepts that have paradoxes have related hypodoxes, although the focus here is initially on these two hypodoxes, particularly in relation to the Liar and Russell’s paradoxes.

The Liar and Russell’s paradoxes have multiple solutions. Classical solutions use classical logic and replace naive conceptual principles about truth and membership. A justification is necessary for a solution to be correct. A correct solution is justified by an analysis that warrants it. Solutions without justification are ad hoc. The Truth-teller and Russell’s hypodoxes also have multiple solutions. Examples include: granting some principle that determines whether the Truth-teller is true, or distinguishing S as a class and not a set. A classical solution to a hypodox will maintain classical logic. Again, justification is necessary for a solution to be correct.

The noun ‘hypodox’ (adj. ‘hypodoxical’) was coined by Peter Eldridge-Smith. Moreover, he distinguished a hypodox as underdetermined, whereas a paradox is inconsistently overdetermined. Furthermore, he conjectured that each paradoxical sentence has a hypodoxical dual (Eldridge-Smith 2007 esp. endnote 3; 2008). The concept is similar to a number of pre-existing concepts (see Billon 2019, footnote 3 for some brief comparisons). This was hardly the first time underdetermination or the like had been considered. (See for example Jaynes 1973, p. 490). There is also a duality between gluts and gaps that is well-known; however, that is a duality between some paraconsistent theories and some paracomplete theories. What that duality is about is that the same expressions are gluts in one theory as are gaps in some other theory. Cook (2004) proved duality between some paradoxical expressions, and separately proved duality between some indeterminate expressions; and Rabern et al. (2013) have generalised these theorems. However, the duality Eldridge-Smith is talking about is different; he is claiming that pairs of intuitively related paradoxes and hypodoxes are duals. The intellectual prior close relative of this claim is Mackie’s (1973, p. 298) listing of Truth-teller counterparts for many of the paradoxes of self-reference. Mackie does not, however, claim that each pair of paradox and hypodox are duals.

It will be convenient to begin with what Tarski (1944) called ‘ordinary laws of logic’ and label some explicitly in Sect. 2. Following Tarski, let a formulation of a paradox be an exhibited derivation in some object language. Even some semi-formalized fragment of natural language will do. A formulation of a hypodox involves a short exhibited derivation, and also reasoning in a meta-language (in our case natural language) about why it is underdetermined. A formulation of the Liar paradox uses a principle of truth, such as the T-schema,

(T-schema) T$<\phi>$ $\leftrightarrow$ $\phi$ where $\phi$ is a sentence, for which $<\phi>$ is a name, $\leftrightarrow$ is a biconditional, and ‘T’ represents the truth predicate.

A formula matching an instance of $\text {the T-schema}$ is called a ‘T-biconditional’. Our formulation of the Liar uses one. There is one for the $\text {Truth-teller}$ too, although that one can be derived without using $\text {the T-schema}$. A formulation of Russell’s paradox uses a principle of membership, such as Abstraction (Meyer et al. 1979, p. 124; Weber 2010, p. 88) or Naive Comprehension (Eldridge-Smith 2015, p. 111; Irvine and Deutsch (2021))

(Abstraction principle) $t \in \{x: \phi (x)\} \leftrightarrow \phi (t)$

for all terms t and predicates $\phi$.

Naive Comprehension (NC) $\exists y\forall x(x \in y \leftrightarrow \phi (x))$, where y is not free in the formula $\phi$.

The Truth-teller and Russell’s Hypodox still arise without granting such principles (Eldridge-Smith 2012; 2015, Appendix). I demonstrate and extend these results in Sect. 3.

Intuitions notoriously differ; and in a debate over whether a classical solution to the Liar paradox also solves the Truth-teller, the premises for one’s main argument need to be based on something other than intuitions. This article duly sets out part of a theory of hypodoxes and their relations with paradoxes. (I am using ‘theory’ here in the general scientific sense of the word, rather than its more specific meaning in formal logic.) Hence, where these arguments draw on this theory of hypodoxes for premises, those premises are maintained by inference to the best explanation rather than intuition. Aiming at this, Sect. 4 sets out part of a theory of hypodoxes: providing a working definition of a ‘hypodox’, arguing hypodoxes are not paradoxes, and listing ways to justify a correct solution to a hypodox.

Section 5 categorises the types of flaws that an analysis might find in a paradox and which, if found, can justify a solution that redresses those flaws. I then reference classical analyses of our paradoxes.

In Sect. 6, I provide novel arguments supporting non-classical solutions for the Liar paradox and the significance of Russell’s hypodox for solutions to Russell’s paradox. Is a classical solution to the Liar a correct solution to the Truth-teller? I present several arguments to the effect that it is not. Is a classical solution to Russell’s paradox a correct solution to its hypodox? I present arguments to the effect that this is not the case for the theory of types. Is another necessary condition for a solution to a paradox to be correct that it has something in common with a justified solution to its related hypodox? I argue that the relation between our paradoxes and hypodoxes warrants this. I relate Russell’s paradox and hypodox based on involution functions. The Liar and the Truth-teller are also related by means of involutions. Relations based on these involution functions can be represented in duality squares. Although hypodoxes are not paradoxes, these involution functions and duality relations warrant some commonality in a correct solution to a paradox and its dual hypodox. Let ‘$\alpha$’ abbreviate ‘an element of a correct solution of a given pair of a paradox and its dual hypodox is the revision of a classical logical principle’. The argument with the most contentious premises supports $\alpha$ for the Liar and Truth-teller.

2 Ordinary laws of logic and object languages

The Liar has its origins in informal reasoning, whereas $\text {Russell's paradox}$ arose from work on the formal foundations of mathematics. Formulations of these paradoxes rely on some logical principles, including the Law of Non-Contradiction (LNC) and the Law of Excluded Middle (LEM), as well as conceptual principles for truth and membership. I tacitly rely on the extensive literature for paraconsistent and paracomplete solutions to assume that LEM and LNC are relevant to all formulations of the Liar (Priest, 2006; Field, 2008). Russell’s paradox can be proven using Intuitionistic logic, so it does not rely on LEM. I will present two formulations of Russell’s paradox, one using sentential logic with Abstraction and the other using quantificational logic with $\text {Naive Comprehension}$. My formulation of the Liar also uses substitution of identicals (=E). Skyrms (1970) proposed that substitution of identicals was also at issue in the Liar. Moreover, Eldridge-Smith (2008, 2015, 2019, 2020) provides different arguments to the effect that the Liar depends on substitution of identicals (=E).¹

Our formulations also use the following connectives and axiom schemas, where $\phi$ and $\psi$ are sentences. The biconditional, ‘$\leftrightarrow$’, is one for which substitution of equivalences holds. There is an ‘xor’ connective in both the object language and meta-language.

Let a dilemma be a sentence of the form $`\phi$ xor $\psi$’ that has a designated value if, and only if, just one of its alternatives has a designated value.

The dilemmas used will generally be instances of ‘the Exclusive Law of Excluded Middle’² (ELEM):

ELEM: $\phi$ xor $\mathord {\sim }\phi$

In classical logic, ELEM is derivable from LEM and LNC. Slightly more generally, ELEM holds in a logic iff a dilemma satisfies the above definition and there is an operator ‘$\mathord {\sim }$’ that takes designated values to undesignated ones, and undesignated values to designated ones. Also, I will use an axiom schema which I will label ‘Sentential Self-Equivalence’ (SSE).

SSE: $\phi$ $\leftrightarrow$ $\phi$

SSE is a classical truth-functional equivalence of ELEM.

I construe ‘the ordinary laws of logic’ as including the above. They are basically a subset of the laws of classical logic used in some semi-formalised fragment of natural language. Connectives in the object language should be interpreted classically, except where the textual discussion indicates another interpretation is being considered. Also tacitly included in the ordinary laws of logic are the usual structural rules, particularly transitivity of entailment, and the classical consequence relation.³

My meta-language is a fragment of natural language extended with some formal vocabulary. Sentences about something being paradoxical or hypodoxical are made in the meta-language. However, formulations of hypodoxes and paradoxes are given in different object languages, because contradictions are derived in some. My object languages are underspecified. For hypodoxes, I could use either a fragment of natural language with the ordinary laws of logic or classical first order logic with identity. This language, whichever it is, is extended with names of expressions and names of sets, and with the truth predicate, T, and the membership relation, $\in$. However, it is left unspecified whether or not there are any principles governing the use of ‘T’ or ‘$\in$’. It is presumed the language is consistent unless proven otherwise. For the Liar paradox, that language is extended by granting $\text {the T-schema}$; for Russell’s paradox, it is instead extended by granting $\text {Abstraction}$ or $\text {Naive Comprehension}$. For the most part, I leave use of meta-language or object language understood.

Dealing with formulations helps isolate inconsistency. Inconsistencies are like a contagion in classical logic. Consequently, it may not be very helpful to define a paradoxical sentence in terms of being inconsistent. I will give a definition of ‘hypodoxical sentence’ but not ‘paradoxical sentence’. This is not a big issue, as there is little doubt that Liar sentences and certain sentences about Russell’s set are paradoxical. Nevertheless, as a partial remedy sufficient for present purposes, I map hypodoxical sentences to paradoxical sentences (in Sect. 6.2). Hence, at least for those that can be so mapped, one does not need to define ‘paradoxical sentence’.

3 A hypodox does not require a conceptual principle used by its dual paradox

A formulation of the Liar paradox uses a principle of truth, such as the T-schema. (For an example, see Sect. 5.2). A formulation of Russell’s paradox uses a principle of membership, such as Abstraction or Naive Comprehension (e.g. as in 5.4). Nevertheless, the Truth-teller and Russell’s Hypodox still arise without granting such principles (Eldridge-Smith 2012; 2015, Appendix). I extend these results in this section. I demonstrate that any argument for the hypodoxicality of the $\text {Truth-teller}$ would not rely on $\text {the T-schema}$. And I demonstrate that any argument for the hypodoxicality of $\text {Russell's hypodox}$ would not rely on $\text {Abstraction}$ nor on $\text {Naive Comprehension}$.

3.1 The Truth-teller does not require the T-schema

Although the Liar paradox requires a conceptual principle of truth like $\text {the T-schema}$:

(A) Given some ordinary laws of logic, the $\text {Truth-teller}$ does not require $\text {the T-schema}$ or any principle of truth to derive its T-biconditional (Eldridge-Smith 2012; 2015, Appendix).

(B) If the $\text {Truth-teller}$ requires a principle of truth to determine its truth-value, it is not $\text {the T-schema}$. A fortiori, the same results apply for any weakening of $\text {the T-schema}$. (A ‘weakening’ of $\text {the T-schema}$ validates a proper subset of formulas validated by $\text {the T-schema}$.)

Suppose towards a contradiction, that (A) is not the case. Then it would not be possible to derive an instance of the T-schema for the Truth-teller without using a principle of truth. But this is possible as per the proof below. This proof uses only an identity, some classically valid logical principles and naming conventions. The identity premise represents the Truth-teller as a self-referential sentence that says of itself simply that it is true. The angle bracket expression represents a name for the expression enclosed, for which it is perhaps simplest to use quote marks to name the expression but other names could be used. ‘e’ abbreviates some suitable term, such as ‘my second favourite sentence’. In that case, line (1) in the proof below represents ‘My second favourite sentence is “My second favourite sentence is true"’. Then (1) is a contingently true sentence. Alternatively, ‘e’ could also abbreviate a functional expression using a syntactic function, so that (1) would be true by definition of the function (Quine, 1995).

(1)	e $=$ < Te>
(2)	Te $\leftrightarrow$ Te	SSE
(3)	T< Te> $\leftrightarrow$ Te	(1), (2) =E

Line (3) in the derivation above is a T-biconditional, which is formally the same as an instance of the T-schema. The T-schema is not needed as line (3) is derived without it. Hence, (A). Assume now that the $\text {Truth-teller}$ requires a principle of truth to determine its truth-value. It cannot be $\text {the T-schema}$, because of result (A). Thus, (B).

The above results do not require any premise about whether the Truth-teller is a hypodox.

3.1.1 More Truth-tellers

I note that there are what might be called ‘contingent Truth-tellers’ which are like the Truth-teller given some circumstances. There are actually vast numbers of these (Kripke, 1975). At least some of these also do not require $\text {the T-schema}$. Here is a demonstration of one case, which is a Truth-teller contingent on some sentence Q.

(1)	f $=$ < Tf $\vee$ Q>
(2)	$\sim$Q	Premise
(3)	Tf $\leftrightarrow$ Tf	SSE
(4)	T< Tf $\vee$ Q> $\leftrightarrow$ Tf	(1), (3) =E
(5)	T< Tf $\vee$ Q> $\rightarrow$ (Tf $\vee$ Q)	(4) SL (Sentential Logic)
(6)	(Tf $\vee$ Q) $\rightarrow$ Tf	(2) SL
(7)	(Tf $\vee$ Q) $\rightarrow$ T< Tf $\vee$ Q>	(6), (1) =E
(8)	T< Tf $\vee$ Q> $\leftrightarrow$ (Tf $\vee$ Q)	(5), (7) SL

So this contingent Truth-teller does not require $\text {the T-schema}$.

3.2 Russell’s hypodox does not require abstraction or naive comprehension

Directly similar results hold for Russell’s hypodox with respect to $\text {Abstraction}$. Although $\text {Russell's paradox}$ requires a conceptual principle like $\text {Abstraction}$:

(C) Given some ordinary laws of logic, $\text {Russell's hypodox}$ does not require $\text {Abstraction}$ to derive its instances of that principle (Eldridge-Smith 2012; 2015, Appendix).

(D) If $\text {Russell's hypodox}$ requires a principle of membership to determine whether it is self-membered, it is not $\text {Abstraction}$. A fortiori, (D) applies for any weakening of $\text {Abstraction}$.

Now the proof of the instance of Abstraction for Russell’s hypodoxical set, S, using ordinary laws of logic is immediate. (1) has the form of the relevant instance of the Abstraction schema, but is derivable as a theorem using just classical logic.

(1)

{x: (x $\in$ x)} $\in$ {x: (x $\in$ x)} $\leftrightarrow$ {x: (x $\in$ x)} $\in$ {x: (x $\in$ x)}

SSE

Given (1) as a theorem of our logic, $\text {Abstraction}$ is not needed as line (1) is derived without it. Hence, (C). Assume now that $\text {Russell's hypodox}$ requires a principle of membership to determine whether it is self-membered. It cannot be $\text {Abstraction}$, because of result (C). Thus, (D).

The situation is much the same for $\text {Naive Comprehension}$, the relevant instance of which for $\text {Russell's hypodox}$ is (4) below. Using (4) with first-order inferences to derive anything relevant to whether the set of self-membered sets pertains to itself would proceed, so to speak, via (6). In such reasoning, (5) is used with (4) towards deriving something relevant by existential quantifier elimination ($\exists$E). Observe though that (3) and (6) are the same, and that (3) can be used with (2) to derive an equivalent statement without using $\text {Naive Comprehension}$. For example, (8) follows from (5) and (8) is relevant given (7), but then (8) can be derived instead from (3) and (7). Moreover, given (7), (8) is equivalent to (3). (1) is derived above as a theorem using just classical logic. (2) follows from the theorem (1). So, instead of using $\text {Naive Comprehension}$, (6) can be assumed and used with (2) to derive anything relevant to determine if Russell’s hypodoxical set pertains to itself.

(2)	$\exists$u({x: (x $\in$ x)} $\in$ u $\leftrightarrow$ {x: (x $\in$ x)} $\in$ {x: (x $\in$ x)})	(1) $\exists$I
(3)	{x: (x $\in$ x)} $\in$ c $\leftrightarrow$ {x: (x $\in$ x)} $\in$ {x: (x $\in$ x)}	(2) Assumption
(4)	$\exists$y$\forall$z(z $\in$ y $\leftrightarrow$ z $\in$ {x: (x $\in$ x)})	NC
(5)	$\forall$z(z $\in$ c $\leftrightarrow$ z $\in$ {x: (x $\in$ x)})	Assumption
(6)	{x: (x $\in$ x)} $\in$ c $\leftrightarrow$ ({x: (x $\in$ x)} $\in$ {x: (x $\in$ x)})	(5) $\forall$E
(7)	S = {x: (x $\in$ x)}	Stipulation
(8)	S $\in$ c $\leftrightarrow$ S $\in$ {x: (x $\in$ x)}	(5) $\forall$E; or (3), (7) =E

In this way, given that (1) is a theorem in our logic, $\text {Russell's hypodox}$ does not require $\text {Naive Comprehension}$. Hence, (E) and (F):

(E) Given some ordinary laws of logic, $\text {Russell's hypodox}$ does not require $\text {Naive Comprehension}$.

(F) If $\text {Russell's hypodox}$ requires a principle of membership to determine whether it is self-membered, it is not $\text {Naive Comprehension}$.

I note that the above results do not require any premise about whether our so-called ‘$\text {Russell's hypodox}$’ is really a hypodox.

4 Part of a theory of hypodoxes, including ways of resolving them

This section sets out part of a theory of hypodoxes. I set out a working definition of a ‘hypodox’. The $\text {Truth-teller}$ and $\text {Russell's hypodox}$ satisfy this definition. Recall that ‘$\alpha$’ abbreviates ‘an element of a correct solution of a given pair of a paradox and its dual hypodox is the revision of a classical logical principle’. Now, if hypodoxes were paradoxes such that the Truth-teller was a species of the Liar paradox, there would be a simple argument for $\alpha$. However, I argue that hypodoxes are not paradoxes. Also, I categorise the types of flaws that an analysis might find in a hypodox and which, if found, can justify a solution that redresses those flaws.

4.1 A working definition of ‘hypodox’

Eldridge-Smith (2007, endnote 3) distinguished hypodoxes as underdetermined whereas paradoxes (or at least a significant subset of them) are inconsistently overdetermined. Adding some caveats and generalities with reference to similar statements (Eldridge-Smith 2008; 2012; 2015, Appendix and 2022), we have the following contradistinction.

First feature distinguishing a hypodox from a paradox: Whereas a paradox of a certain class incompatibly overdetermines something or is itself incompatibly overdetermined by tacitly or explicitly granted principles (in some cases, given some apparently possible circumstances), a hypodox underdetermines something or is itself underdetermined for lack of a granted principle that determines the matter (in some cases, given some apparently possible circumstances). In classical reasoning the way in which a paradox is incompatibly overdetermined is by being inconsistently overdetermined.

From this contradistinction, it follows that the same thing cannot be both inconsistently overdetermined and underdetermined at the same time in the same circumstance by the same granted principles, although most things are neither. Thus, these are contrary concepts.

I add the following comments. The above distinction could be used as a definition if we knew the genus of paradoxes and hypodoxes. In the abstract, our hypodoxes were introduced as riddles. Different authorities define paradoxes as a species of various kinds of things, including riddles (Sorensen 2003, pp. 3-4), arguments (Mackie, 1973), and conclusions (Quine, 1976). Being granted is stronger than being assumed. What is paradoxical is relative to which principles are granted. Indeed, people may disagree whether something is paradoxical, hypodoxical or determined, if they disagree over which principles are granted. Such principles may be part of some standard grouping of principles into a logic or theory, such as classical logic, naive set theory, or a naive theory of truth. As an example, a theory of probability that includes the principle of indifference is appropriate for discussing Bertrand’s chord paradox.

For our present concerns we need a definition that discerns hypodoxical sentences. There is some difficulty in eliminating phrases like ‘for lack of a principle that determines the matter’ or ‘due to there being no principle...’ or ‘because there is no principle...’. Indeed, as per the First feature distinguishing a hypodox specified above, that is part of the problem posed by a hypodox.⁴

Working definition of ‘hypodoxical sentence’: A sentence $\phi$ is a hypodox iff there is a sentence $\psi$ such that ‘$\phi$ xor $\psi$’ has a designated value but which alternative is designated is not determined because there is no granted principle that conclusively determines which one of $\phi$ and $\psi$ has a designated value (in some cases, in some given apparently possible circumstances).⁵

In applying the above definition for the cases treated in this article, $\psi$ is simply $\sim \phi$. In general, from our working definition it is apparent that a hypodox could be solved by granting some principle that determines which alternative is the case, by arguing the dilemma is ill-formed or invalid, or even by accepting the hypodox. As mentioned in the Introduction, a correct solution needs a justification. I will explain how an analysis might justify a solution to a hypodox in 4.5.

The hypodoxes are almost as varied and large a class as the paradoxes. There are hypodoxes for almost all concepts that have paradoxes. There are hypodoxes of birthdays and time travel (Eldridge-Smith 2012, 2007). Here is an example. On the one hand, W. S. Gilbert’s paradox is about Frederic, born on 29th February, being indentured to a pirate until his 21st birthday; on the other hand, Frederica, who is Frederic’s twin sister, is trying to determine when she should celebrate her 21st birthday. She thinks it should be both 28th February and 1st March. Her orthodox parents disagree, maintaining her 21st birthday is either on 28th February xor 1st March. Her father argues she was born on the last day of February. Her mother distinctly remembers her being born the day after the 28th February (Eldridge-Smith 2012). There is some inconclusive reason for each date, but the date of her 21st birthday is underdetermined for lack of a principle that conclusively determines the matter. W. V. O. Quine, when consulted, says a birthday only occurs on the exact date (Quine, 1976). Quine maintains Frederica’s birthday occurs at most once every four years. However, Frederica respectfully points out that Professor Quine is an authority on logic rather than birthdays, and she quotes the Oxford English Dictionary entry to him.

I think there are paradoxes that do not have hypodoxes. I think the lottery paradox is an example (Kyburg, 1997). And I think Codman’s paradox is another example that does not have a dual hypodox for reasons beyond the scope of this article (Pearl et al., 1992).⁶

Given ELEM, then there are a couple of equivalences that will be useful later in mapping hypodoxes to paradoxes.

Hypodoxical Equivalence by External Negation (HEEN): Given ELEM, for any sentence $\phi$, $\phi$ is hypodoxical iff $\mathord {\sim }\phi$ is hypodoxical.

Paradoxical Equivalence by External Negation (PEEN): Given ELEM, for any sentence $\phi$, $\phi$ is paradoxical iff $\mathord {\sim }\phi$ is paradoxical.

(HEEN) may seem surprising if one thinks of the Truth-teller as (1) ‘This self-referential sentence is true’ and one thinks of its negation as (2) ‘This self-referential sentence is not true’. However, in the latter, the sentence referred to is not the former. (HEEN) presupposes that the sentence referred to is the same in both the self-referential sentence and its external negation. That being so, ‘(1) is not true’ is an external negation of (1).

4.2 The Truth-teller is a hypodox

Using our working definition of a ‘hypodoxical sentence’, consider whether the $\text {Truth-teller}$ is a hypodox. Remember that our Truth-teller is a sentence of the form ‘Te’ such that the following identity holds and its T-biconditional can be derived.

(1)	e $=$ < Te>
(2)	Te $\leftrightarrow$ Te	SSE
(3)	T< Te> $\leftrightarrow$ Te	(1), (2) =E

Hypodoxes are generally treated as less problematic than paradoxes. In one respect though, hypodoxes are harder than their corresponding paradoxes. It is easier to derive a contradiction about the Liar than to formally prove the Truth-teller is underdetermined. An argument that the Truth-teller is a hypodox is partly formal and partly informal. The formal part is a one line proof below by ELEM that there is a dilemma over whether the Truth-teller whose identity is given by (1) above, has a designated value or not.

(4)

Te xor $\sim$Te

ELEM (or (2) Classical equivalence)

The second informal part of the argument is reasoning in the meta-language that - even given (1) through (4) - no standard principle of classical logic or naive Truth theory determines the semantic value of the Truth-teller. It is evident that (2) cannot assist us in determining the matter. Eliminating the biconditional in (2) yields the same conditional ‘if Te then Te’, but to eliminate that conditional we would need to already have determined the value of Te. The situation with (3) is much the same. This is because e is self-referential, as per (1). If e referred to some merely contingent statement, then it would have the same semantic value as that contingent statement. (1) enables inferring (3) from (2) (and back again). (4) is classically logically equivalent to (2), and thus no more informative than (2). Any other classical logical principle could only help determine the matter if it could do so in combination with (1). But no other classical principle determines the value of a sentence unless that sentence is a tautology or a self-contradiction. However, ‘Te’ has neither the structure of a tautology nor a self-contradiction. Now from (B) from section 3.1 and what is granted about our object language at the end of Sect. 2, there is no granted principle of truth determining the truth-value of ‘Te’. Hence, in accord with our working definition, ‘Te’ is a hypodox. Moreover, by (HEEN), so is ‘$\mathord {\sim }$Te’.

4.3 “Russell’s hypodox” is really hypodoxical

Using similar reasoning to the previous section, I would argue sentences for $\text {Russell's hypodox}$ also satisfy our working definition of hypodoxical sentence. The argument for Russell’s hypodox would apply to the alternatives on either side of the ‘xor’ in (1) below.

(1)	({x: (x $\in$ x)} $\in$ {x: (x $\in$ x)}) xor ({x: (x $\in$ x)} $\notin$ {x: (x $\in$ x)})	ELEM
(2)	({x: (x $\in$ x)} $\in$ {x: (x $\notin$ x)}) xor ({x: (x $\in$ x)} $\notin$ {x: (x $\notin$ x)})	ELEM

Remembering the identity of S, it can be argued that:

‘S $\in$ S’ is hypodoxical and so is its negation.

But wait! There are two more hypodoxical sentences. We can also argue in much the same way with reference to each of the alternatives in (2) that:

‘({x: (x $\in$ x)} $\in$ {x: (x $\notin$ x)})’ is hypodoxical and so is its negation.⁷

4.4 The simplest argument on the import of hypodoxes is fallacious

What if (1) hypodoxes were paradoxes, such that (2) each hypodox was a variation of a paradox and (3) solving a hypodox required a rejection or restriction of some principle necessary for the paradox of which it is a variation? (2) in effect posits that the $\text {Truth-teller}$ is a species of the Liar paradox and $\text {Russell's hypodox}$ is a species of $\text {Russell's paradox}$. Then an argument for non-classical solutions to the Liar and Russell’s paradoxes would be simple.⁸ Given (1), (2) and (3), this would follow, because results (A) though (F) from Sects. 3.1 and 3.2 show that our particular hypodoxes are hypodoxical independently of $\text {the T-schema}$, and $\text {Abstraction}$ or $\text {Naive Comprehension}$. So $\text {the T-schema}$ would not be necessary for all variations of the Liar. Moreover, $\text {Abstraction}$ and $\text {Naive Comprehension}$ would not be necessary for all variations of $\text {Russell's paradox}$. Then it would follow by (3) above that some ordinary law of logic must be rejected or restricted.

However, the above argument is fallacious; although valid, it is unsound if our theory of hypodoxes is accepted. Eldridge-Smith (2012) would posit that (1) and (3) are false. Moreover, Eldridge-Smith (2007, 2008) would replace (2) by a dual relation between a paradox and a hypodox. That is, a hypodox is not another paradoxical variation; nevertheless, it is related to a paradox as a dual. (Duality will be justified later in Sect. 6.2, as it will only be required for our last arguments.) The next section justifies the idea that (1) is false and that there are more options for solving a hypodox than (3) considers.

4.5 The ways of hypodoxes

As per the working definition of ‘hypodox’, there are two parts to a hypodox, a dilemma and an alternative in that dilemma that is underdetermined. Accordingly, there are the following possible flaws in a hypodox. The hypodoxical sentence is ill-formed or meaningless, the dilemma is really undesignated, or there is a principle that conclusively determines the hypodox and granting it is justified, or the hypodox is somehow acceptable. A correct solution must justify itself by the flaw or flaws found through an analysis of the hypodox.

Because hypodoxes are underdetermined, one way they can be solved is by monotonically granting an additional principle that determines the matter. Obviously, the principle needs to be justified. Note that the effect of monotonically adding a principle is to assert more theorems while not retracting any theorems.

The option of granting an additional principle provides a:-

Second feature distinguishing a hypodox from a paradox: A Hypodox can be solved by monotonically adding a principle that determines the hypodox. In contrast, paradoxes cannot be solved by monotonically adding an additional principle.

This is because paradoxes are already incompatibly overdetermined so that monotonically adding a principle will not solve a paradox. Hence:-

Hypodoxes are not paradoxes since not only are hypodoxes underdetermined whereas paradoxes are incompatibly overdetermined but also hypodoxes can be solved in a way that paradoxes cannot be.

Accepting a hypodox may be a partial solution in a system that might be extended by granting an additional principle that determines the matter (e.g. Eldridge-Smith 2019; 2020). Alternatively, accepting the hypodox might lead to an indeterminate solution (e.g. Rabern et al. 2013).

5 What is a correct solution to the Liar or Russell’s paradox?

This section initially categorises the types of flaws that an analysis might find in a paradox and which, if found, can justify a solution that redresses those flaws. Then I give example formulations of the Liar and Russell’s paradoxes and refer to their classical analyses. And I argue that correct solutions do need to be distinguished.

5.1 Possible flaws of paradoxes

Sainsbury categorises the possible flaws in a paradox as follows.

This is what I understand by a paradox: an apparently unacceptable conclusion⁹ derived by apparently acceptable reasoning from apparently acceptable premises. Appearances have to deceive, since the acceptable cannot lead by acceptable steps to the unacceptable. So, generally, we have a choice: either the conclusion is not really unacceptable, or else the starting point, or the reasoning, has some non-obvious flaw.

An analysis of a paradox (or an analysis of a kind of paradox) must argue it has one or more of the above flaws and use that to justify one or more of the following possible options for a solution.

The possible options for a solution to a paradox are to accept the conclusion or reject the circumstances as impossible,¹⁰ reject some part of the paradox as ill-formed or meaningless, or restrict or reject a pattern of reasoning on which the paradox depends. That pattern of reasoning may have followed a conceptual principle or an ordinary law of logic. If a pattern of reasoning is rejected it may be replaced with a pattern of reasoning that implements some distinction. Replacement of conceptual principles by making a distinction has a noble history (James, 1907; Russell, 1908; Tarski, 1944).

5.2 A formulation of the Liar

Here is a formulation of the Liar paradox.

(1)	a = < $\sim$Ta>
(2)	T< $\sim$Ta> $\leftrightarrow$ $\sim$Ta	T-schema
(3)	Ta $\leftrightarrow$ $\sim$Ta	(1), (2) =E
(4)	Ta xor $\sim$Ta	ELEM
(5)	Ta xor Ta	(3), (4) substitution of equivalences

Remember that the definition of a dilemma is such that ‘$\phi$ xor $\phi$’ cannot take a designated value.¹¹ An identity of the form on line (1) can be assured using syntactic functions (Quine, 1995). The classical analysis accepts this; however, I will then argue that there is some issue about how the Tarskian solution is implemented. The classical analysis takes issue with line 2, its solution rejects, restricts or replaces the T-schema.

Eldridge-Smith (2019, 2020) takes issue with step 3, as he restricts the use of =E in the scope of the truth predicate. Nevertheless, many other formulations of the Liar avoid explicitly using substitution of identicals (=E) by using an instance of the Diagonal Lemma or appealing to meaning.¹²

Step (4) is derived as an instance of ELEM; its derivation does not rely on (1), (2) or (3). Classically, ELEM is equivalent to the conjunction of LEM and LNC. It may also be derived from an instance of SSE. Solutions based on rejecting or restricting LNC or LEM reject (4); in particular, a dialetheic solution (Priest, 2006) and a paracomplete solution (Field, 2008) reject (4).¹³

I am not aware of any solution that restricts substitution of equivalences to avoid (5); however, there are structural principles involved in the derivation, which may be restricted. Nevertheless, (5) is self-contradictory. Given a classical interpretation of ‘xor’, none of the above mentioned solutions would assert (5).

5.3 Tarski’s analysis of the Liar paradox

The classical analysis of the Liar paradox is essentially Tarski’s analysis.

If we analyse the assumptions which lead to the antinomy of the liar, we notice the following:

(I) We have implicitly assumed that the language in which the antinomy is constructed contains, in addition to its expressions, also the names of these expressions, as well as semantic terms such as the term “true” referring to sentences of this language; we have also assumed that all sentences which determine the adequate usage of this term can be asserted in the language. A language with these properties will be called “semantically closed.”

(II) We have assumed that in this language the ordinary laws of logic hold.

(III) We have assumed that we can formulate and assert in our language an empirical [identity] premise such as the statement [(1) in our formulation of the Liar].

It turns out that assumption (III) is not essential, for it is possible to reconstruct the antinomy of the liar without its help. (Tarski 1944, pp. 348–349)

It is important to our argument that the classical solution is not based on assumption (III) above. Tarski himself claims (III) is not an essential assumption, noting that an empirical identity premise can be replaced by a non-empirical premise using a syntactic function (Tarski 1944, Endnote 11). Tarski’s idea is similar to Quine’s use of a syntactic function for self-predication to formulate the Liar paradox (Quine, 1995).¹⁴

5.4 Two formulations of Russell’s paradox

Russell’s paradox is derived below using Abstraction

(1)	({x: (x $\notin$ x)} $\in$ {x: (x $\notin$ x)}) $\leftrightarrow$ ({x: (x $\notin$ x)} $\notin$ {x: (x $\notin$ x)})	Abstraction
(2)	({x: (x $\notin$ x)} $\in$ {x: (x $\notin$ x)}) xor ({x: (x $\notin$ x)} $\notin$ {x: (x $\notin$ x)})	ELEM
(3)	({x: (x $\notin$ x)} $\in$ {x: (x $\notin$ x)}) xor ({x: (x $\notin$ x)} $\in$ {x: (x $\notin$ x)})	(1), (2) substitution of equivalences

Here is a formulation using $\text {Naive Comprehension}$.

(1)	$\forall$x(x $\in$ c) $\leftrightarrow$ (x $\notin$ x)	NC
(2)	(c $\in$ c) $\leftrightarrow$ (c $\notin$ c)	(1) $\forall$E

5.5 A Russellian analysis of the contradiction and Russell’s and Fraenkel’s solutions

Russell gave a number of analyses for his contradiction. The following early analysis identifies two possible flaws.

The reason that a contradiction emerges here is that we have taken it as an axiom that any propositional function containing only one variable is equivalent to asserting membership of a class defined by the propositional function. Either this axiom, or the principle that every class can be taken as one term, is plainly false, and there is no fundamental objection to dropping either. But having dropped the former, the question arises: Which propositional functions define classes which are singular terms as well as many, and which do not? (Russell 1903, ch. 10, s. 101)

Hence, the classical analysis rejects an axiom equivalent to the Abstraction principle or the Naive Comprehension schema as flawed. But even having rejected that axiom, there is still some issue about which classes can be treated as individuals that are members of other classes.¹⁵

Russell’s solution was his theory of types in which ‘x $\in$ y’ is only well-formed or meaningful if the type of x is one lower than the type of y. Fraenkel’s solution, ZF set theory, addresses the first flaw by restricting comprehension in the Axiom of Separation. It addresses the second flaw by the Axiom of Regularity in such a way that no self-membered set exists.¹⁶

5.6 Why correct solutions must be distinguished

Classical solutions restrict naive principles, viz. the T-schema, $\text {Abstraction}$ and Naive Comprehension. The theory of types restricts Comprehension by distinguishing a hierarchy of types. Tarski stratifies languages and truth predicates and hence the T-schema. ZF set theory restricts Comprehension in the Axiom of Separation (Fraenkel, 1976). However, hypodoxes cannot be solved this way as they do not require these principles to pose a hypodox. So, classical solutions do not solve the hypodoxes. Yet, given that hypodoxes do not arise in classical solutions, there is some sense in which they are solved by classical solutions. Some distinction is required.

Accordingly, we have asserted that a necessary condition for a correct solution is that it is justified. A solution without justification is ad hoc. We have justified this assertion on the basis that an analysis of a paradox (or hypodox) aims to find flaws and then uses that to warrant a solution addressing that flaw or those flaws.

6 Arguments about the import of hypodoxes for the Liar and Russell’s paradoxes

Drawing on results from previous sections and progressively stronger premises about the relationship between our paradoxes and hypodoxes, I present arguments supporting a non-classical solution to the Liar and against the theory of types solution to Russell’s paradox. Given the results of previous sections, there is a good argument that the classical solution to the Liar cannot be extended to a correct solution for the $\text {Truth-teller}$, as set out in section 6.1. However, a similar argument is unsound for Russell’s paradox and hypodox. These arguments use only readily granted premises about any relation between the given paradox and hypodox. However, stronger premises may be used about the relations between our paradoxes and hypodoxes, given adequate justification. Section 6.2 accordingly explains and analyses Eldridge-Smith’s (2007; 2008; 2022) theory of duality relations between some paradoxes and hypodoxes, as well as defining some involution functions between versions of the particular paradoxes and hypodoxes that concern us. (Remember, an involution function is its own inverse function.) Sect. 6.3 then gives the final arguments concerning $\text {the import of a hypodox for its dual paradox}$ based on the above theory of relations and functions between hypodoxes and paradoxes.

6.1 Arguments from hypodoxes of truth and membership

Where a paradox, p, requires some conceptual principle for at least some of its formulations that some hypodox, h, that uses the same conceptual predicate or relation does not require for any of its formulations, then a correct solution of h is not a replacement, restriction or rejection of that conceptual principle. For a solution for h to be correct it must be justified as addressing some flaw found in h. However, if h did not require the conceptual principle, then it is not a flaw in h. (This is true even if that conceptual principle is fallacious.) If a solution is not a correct solution of h, it is not a correct solution of p and h together.

In fact, our hypodoxes do not require the conceptual principles our paradoxes require (Sect. 3), consequently possible flaws in our hypodoxes do not include the specific conceptual principles that our particular paradoxes require (as per Sect. 4.5). A Tarskian solution to the Liar rejects $\text {the T-schema}$ (Sect. 5.2). However, the $\text {Truth-teller}$ does not require $\text {the T-schema}$. Hence, this solution does not address a possible flaw in the $\text {Truth-teller}$. Thus, this is not a correct solution for the Liar paradox and the $\text {Truth-teller hypodox}$ together.

This solution cannot be extended by granting an additional principle of truth that will determine the $\text {Truth-teller}$, because the identity premise already cannot be true in a Tarskian hierarchy. Tarski’s analysis considers the identity premise and explicitly grants that such a premise can be true. However, the classical Tarskian solution either makes the identity premise of the $\text {Truth-teller}$ ill-formed or false. Indeed, it is ill-formed in the usual implementation of a Tarskian hierarchy. (An “unusual” implementation of the Tarskian hierarchy that denied the identity premise would be ad hoc.) The T-biconditional for the Truth-teller sentence cannot be formed in such a language. For the same reason, the identity premise cannot be asserted in such a language, despite it being possibly true according to Tarski’s analysis. Thus, this classical solution cannot be extended with a correct solution to the $\text {Truth-teller}$.

This argument does not apply, for example, to Bertrand’s chord paradox and the $\text {Truth-teller}$, because they do not concern the same predicates or relations. Nevertheless, this argument applies as much to Curry’s paradox using the truth predicate and the $\text {Truth-teller}$ as it does to the Liar and $\text {Truth-teller}$. The only relation between p and h that was used as a premise is that they both use the same predicate or relation. I think stronger conclusions follow if premises about a stronger relation between our paradoxes and hypodoxes are justified. I will attempt to provide some justification in the next section.

The above argument would apply mutatis mutandis for whether rejecting a conceptual principle to solve $\text {Russell's paradox}$ is also a correct solution for $\text {Russell's hypodox}$. That is, if a fallacious conceptual principle was the only flaw being addressed by that solution. However, Russell’s solution is intended to address both the flaws identified in his analysis. Moreover, he explicitly intends to make self-membership ill-formed in his solution. Thus, being unable to form sentences like $\text {Russell's hypodox}$ in the theory of types is intentional.

In ZF set theory, the matter stands a bit differently. Comprehension is restricted in the axiom of Separation to avoid the likes of Russell’s paradox. Self-membered sets do not exist, by the axiom of Regularity. These are intended solutions. However, because self-membership is not ill-formed, ‘S $\in$ S’ is expressible. However, this sentence is no longer hypodoxical in ZF, it is determined. It is not the case, by the axiom of Separation.

There is little more to argue here about the set-theoretic paradoxes and hypodoxes until I can justify stronger premises. I return to semantic considerations. Let ‘$\gamma$’ abbreviate ‘an element of a correct solution of the Liar paradox and the Truth-teller hypodox is a revision of an ordinary law of logic.’ (If the Truth-teller is the dual hypodox of the Liar, $\gamma$ is an instance of $\alpha$.)

We were precluded from adding a principle of truth to the Tarskian solution to correctly solve the Truth-teller. Nevertheless, Kripke (1975) added to Tarski’s analysis of the Liar and implemented a number of solutions that add a fixed-point semantics for a truth predicate within the language. Some of these, particularly those using a supervaluation semantics, could be thought classical, as they can validate classical theorems. For many sentences using the truth predicate, it is a contingent matter whether each is Liar-paradoxical or a Truth-teller. Kripke’s additions to the Tarskian analysis included that there is no intrinsic semantic or syntactic attribute of sentences using a truth predicate that can sieve out the Liar-paradoxical and Truth-teller sentences. Loosely put, Kripke’s solution sieves these out given a base model and using his jump function given either multi-valued truth-tables or a supervaluation semantics. Depending on details of the solution implemented, the Liar sentences and Truth-tellers either have a truth-value gap or are considered as having a different value. An advantage of the Kripke semantics for our present discussion is that it is possible to assert an identity sentence for a Truth-teller. (If the identity premise could not be true in a model, then an element of the solution is not correct, according to our analysis which was guided by Tarski’s on this point.)

So the question arises whether a fixed-point semantics can implement a classical and correct solution to both the Liar and the $\text {Truth-teller}$, and in particular, when their respective identity premises are made true in a model. The idea here would be that the fixed-point semantics in effect adds a principle of truth, which is a viable option for solving the $\text {Truth-teller}$ according to our analysis. So, the construction would use supervaluation to validate classical theorems. However, the first fixed-point does not actually determine the semantic status of the Truth-teller and being able to randomly add truth-tellers to the extension or anti-extension of truth after the first fixed-point is not the same as adding a principle that determines their value. The hypodoxes are not distinguished from paradoxes among the sentences that do not receive a truth-value at the first fixed point.¹⁷ It is part of Kripke’s analysis that there is no intrinsic syntactic or semantic feature that distinguishes Liar sentences. And this is also true of Truth-teller sentences in a fixed-point semantics. Thus it is contrary to Kripke’s analysis to resolve Truth-tellers by adding a principle that determines their value.

In summary, classical revisions of the T-schema are incompatible with a different principle of truth to determine the Truth-teller. A Tarskian stratification of the T-schema precludes the possibility. A Kripkean semantics, whether classical or not, is premised on there being no intrinsic syntactic or semantic sieve for Truth-tellers (as well as paradoxes), so an additional principle that determined their truth-value (or values) would be ad hoc. The premise for the Truth-teller is not impossible, so it is not correct to make such a premise ill-formed or always false. Leaving hypodoxes in a truth-value gap does not distinguish them from Liar paradoxes; so that is not a viable way of accepting the hypodoxes. Other ways of accepting the hypodoxes would result in a non-classical semantics, such as using an additional value or perhaps a relational semantics. Thus, the only correct solution to the Truth-teller modifies an ordinary law of logic. Thus, $\gamma$.

6.2 Paradox hypodox duals related by involutions

Eldridge-Smith (2007, endnote 3) conjectures that each paradox (of a class) has a hypodoxical dual. Our pairs are duals. That is, the Liar and Truth-teller are duals, and Russell’s paradox and hypodox are duals. On a straw poll, some people share this intuition and some do not. This section gives some justification for this use of ‘dual’. Partial analogies can be drawn with a Duality Theorem and some recent work on ‘duality relations’ that can be mapped in ‘Duality squares’. In both cases, involution functions can be specified that support the relations between paradoxical and hypodoxical sentences. That is actually all that is analogous with the Duality Theorem. That is, the use of the term ‘duality relation’ itself bears some analogy with its use in the literature on Duality squares (as will be explained shortly), and the relations in question can be based on a number of specifiable involution functions. The latter is true, whether or not there is a better term than ‘duality’ for these relations. I extend some of Eldridge-Smith’s (2022) account of these relations and functions.¹⁸

Prima facie there might appear to be some sort of opposition between pairs like (‘This self-referential sentence is not true’, ‘This self-referential sentence is true’) and (‘The set of non-self-membered sets is not a member of itself’, ‘The set of self-membered sets is a member of itself’). But, in the first pair, the subject terms do not refer to the same thing; and in the second pair, the subject terms are not the same. A slightly deeper issue is that opposition and negation do not “track" each other for paradoxical sentences in the same way they do for non-paradoxical sentences. For example, the following pair do not stand in a relation of contradiction given that they are both paradoxical, even though one is the negation of the other (‘The set of non-self-membered sets is a member of itself’, ‘The set of non-self-membered sets is not a member of itself’). The same point can be made for particular pairs of hypodoxes. As mentioned, our paradoxes and hypodoxes are examples for which the equivalences (PEEN) and (HEEN) hold.

There is a duality theorem in the meta-theory about sentential logic where $\delta$ is a syntactic involution function swapping conjunction and disjunction symbols. (Van Dalen 2008, p. 27)

Duality Theorem: $\models \phi \leftrightarrow \psi$ iff $\models \delta (\phi ) \leftrightarrow \delta (\psi )$,

Remember an involution function is its own inverse function. The details of $\delta$ depend on the object language.¹⁹

The use of such an involution function to map expressions is suggestive. Let ‘P’ stand for ‘is paradoxical’ and ‘H’ for ‘is hypodoxical’. (These are used as predicates in the meta-language about object language sentences. Remember the comments about our object languages at the end of Sect. 2. Then ‘H’ actually stands for ‘is a sentence that is hypodoxical in one of our object languages’.) I will show, at least for our paradoxes and hypodoxes, that there are a small number of involution functions that can take the place of g and f such that the following holds.

Paradox Hypodox Duality (PHD): if $\phi$ is a hypodoxical sentence, there are involution functions f and g such that g($<\phi>$) and f($<\phi>$) are paradoxical and where $\lnot$ is an external negation function taking a name of a sentence to a name of its external negation,

$<\phi>$ = g(g($<\phi>$)) = f(f($<\phi>$)),

g($<\phi>$) = f($\lnot <\phi>$),

$\lnot <\phi>$ = g(g($\lnot <\phi>$)) = f(f($\lnot <\phi>$)), and

g($\lnot <\phi>$) = f($<\phi>$).

It is easier to see what is being said by PHD in the following schematic diagram that uses functions g and f and where $\phi$ is a hypodoxical sentence:

Remember that given ELEM, if $\phi$ is a hypodoxical sentence, then $\sim \phi$ is also hypodoxical by HEEN. So if the expression named at the top right hand corner (TRHC) is hypodoxical, so is its negation, which is the expression named at the bottom left hand corner. PHD then states that if the expression named in the TRHC is hypodoxical, then given involution functions g and f, the expressions named on the other diagonal are paradoxical.

Indeed, there are multiple versions of Liar and Truth-teller sentences that can be mapped to each other in different pairings by a (small) number of different involution functions involving internal and external negation. In this way I would support the following conjecture for at least the class of hypodoxes of self-reference, and in particular the Truth-teller and Russell’s hypodoxes.

Paradox hypodox duality conjecture: Any hypodoxical sentence of a certain class has a paradoxical dual sentence to which it is mapped as per (PHD) by an involution function composed from one or more of internal negation, external negation, or replacing a predicate with one that has (at least conventionally) an opposite meaning, combined in certain cases with replacing a referential term or the reference of a term in a sentence with the effect of preserving self-reference. These certain cases are ones where the self-reference of the hypodoxical sentence itself depends on empirical premises or stipulations about the reference of a term.

Our application of this conjecture herein is only to the subclass of hypodoxes that presently concern us, which are themselves a subclass of the hypodoxes of self-reference. The only replacement of predicates that occurs in these cases is replacing ‘is true’ by ‘is false’. In some cases, this replacement is combined with replacing a term or the reference of a term to preserve self-reference.

Having multiple paradoxical and hypodoxical sentences paired in different combinations by different involution functions, as per PHD, suggests these could be depicted by more diagrams, analogous to the one above. It will be convenient to use what are called ‘duality squares’ in the literature (Demey and Smessaert 2016; 2017, Sect. 2.2). These squares represent four duality relations, viz. identity, internal negation, external negation and dual. The same arrangement can be set out relating pairs of our paradoxical and hypodoxical sentences. In examples of these squares each relation is symmetric and functional, which in our use means it can be based on an involution function. Our expressions use predicates where Smessaert and Demey use adverbials.

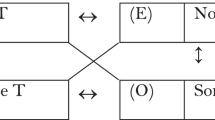
I present three examples using our paradoxical and hypodoxical sentences. After each, I specify the functions substituted for g and f in the instances of Paradox Hypodox Duality (PHD). First, duality relations between sentences expressing Russell’s paradox and hypodox and the negations of those sentences are represented in the following duality square.

The pair of sentences in the top right-hand corner (TRHC) and bottom left are hypodoxical, as per Sect. 4.3. The TRHC sentence is equivalent to ‘S $\in$ S’. For convenience let us use (A), (E), (I) and (O) to name the expressions at the left top, right top, left bottom and right bottom corners respectively. Then given that (E) is hypodoxical, HEEN assures (I) is hypodoxical. An instance of PHD then asserts:

P(A), P(O), (E) = Ineg1(Ineg1(E)) = Dual1(Dual1(E)), (A) = Ineg1(E) = Dual1($\lnot$(E)), (I) = $\lnot$(E) = Ineg1(Ineg1($\lnot$(E))) = Dual1(Dual1($\lnot$(E))), and (O) = Ineg1($\lnot$(E)) = Dual1(E).

Sect. 5.4 demonstrated (A) and (O) are paradoxical. The above listed identities represent mappings across the horizontals, from (E) to (A), and from (I) to (O), and mappings across the verticals, from (I) to (A), and from (E) to (O). These identities hold, given the functions defined below. Thus, there is a duality relation mapping these hypodoxical sentences to paradoxical sentences.

Let us define our functions.

For any relation, R, between two sets, where $\phi$ and $\psi$ are predicates, where the angle bracket expression represents a name of the expression exhibited between the brackets:

$ineg1(<$ $R(\{x$ $:\phi (x)\}, \{x:\psi (x)\})$ ) = $R(\{x:\mathord {\sim }\phi (x)\}, \{x:\mathord {\sim }\psi (x)\})$

and wherever the introduction of the negation sign results in a double negation, they are cancelled out. For example, if R were instantiated with $\notin$.

$Dual1(<$ $R(\{x$ $:\phi (x)\}, \{x$ $:\psi (x)\})$ ) = $\mathord {\sim }R(\{x:$ $\mathord {\sim }\phi (x)\}, \{x:$ $\mathord {\sim }\psi (x)\})$

and wherever the introduction of the negation sign results in a double negation, they are cancelled out.

Ineg1 and Dual1 are involution functions, as represented in the square. However, I have only used them from hypodoxes to paradoxes with PHD. PHD is mapped that way because I only defined ‘hypodoxical sentence’ (in Sect. 4.1). I did not define ‘paradoxical sentence’. Nevertheless, as above, PHD provides a way of finding paradoxical sentences that have a dual hypodox. Also, there are two more hypodoxical sentences for $\text {Russell's hypodox}$, as you may remember from Sect. 4.3. So, there are actually more pairs of paradoxical and hypodoxical sentences that can be mapped for Russell’s paradox and hypodox. Nevertheless, one can see how it is done. The existence of all these individual duality relations is the basis for saying that Russell’s hypodox and paradox are duals. That is, any of the sentential expressions for Russell’s hypodox can be mapped by an involution function to a sentential expression for Russell’s paradox as per PHD. Similar comments apply to Truth-teller and Liar sentences.

In accord with Tarski’s analysis of the Liar, there are formulations that do not need an empirical premise, as discussed in Sect. 5.3. As I mentioned there, Quine (1995) provides an example that uses a syntactic function. The following Quinean Truth-teller does not stipulate the reference of any individual term to achieve self-reference: ‘ “Yields a truth when appended to its own quotation” yields a truth when appended to its own quotation’. To demonstrate that a hypodox like this can be mapped syntactically to a Liar sentence, I will use a syntactic function devised by Quine (1995) for self-predication. (I note that I am using this function because it is suitable for this example, not because this function is commonly or standardly used in the literature.)

The self-predication of ‘x is green’ is “‘x is green” is green’.

The self-predication of ‘x is not true’ is “‘x is not true” is not true’.

Using angle brackets in place of quotation marks, Quine defines a function, sp, as follows.

$sp(<\phi (x)>) =<\phi (<\phi (x)>)>$, where angle bracket expressions are restricted to quotation-names for expressions.²⁰

Consider: The self-predication of ‘the self-predication of (x) is not true’. It is ‘The self-predication of “the self-predication of (x) is not true” is not true’. This has the form:

$sp(<\mathord {\sim }T(sp(x))>) =<\mathord {\sim }T(sp(<\mathord {\sim }T(sp(x))>))>$

Now, abbreviating the left-hand side by ‘a’, the above is of the form $a = <\mathord {\sim }Ta>$, which was our identity premise for the Liar in Sect. 5.2. Moreover,

$sp(<T(sp(x))>) =<T(sp(<T(sp(x))>))>$

Let e abbreviate ‘$sp(<T(sp(x))>)$’. Then this has the form $e = <Te>$, which was our identity premise for the Truth-teller.

Duality relations between this Truth-teller and this Liar are presented in the following square with labels for the corners.

(E) is our Truth-teller and (I) is its external negation. (I) is also hypodoxical. PHD then asserts:

P(A), P(O), (E) = Ineg2(Ineg2(E)) = Dual2(Dual2(E)), (A) = Dual2(E) = Ineg2($\lnot$(E)), (I) = $\lnot$(E) = Ineg2(Ineg2($\lnot$(E))) = Dual2(Dual2($\lnot$(E))), and (O) = Dual2($\lnot$(E)) = Ineg2(E).

Sect. 5.2 demonstrated (A) is paradoxical (as it has the same form as ‘$\mathord {\sim }Ta$’. So, by (PEEN), (O) is also paradoxical. The identities in this instance of PHD represent mappings across the horizontals, from (E) to (A), and from (I) to (O), and mappings across the verticals, from (I) to (A), and from (E) to (O). These identities hold, given the functions defined below. Thus, there is a duality relation mapping these hypodoxical sentences to paradoxical sentences.

Let us define our functions.

Dual2 toggles external and internal negations. For any predicate, $\phi$, where the angle bracket expression represents a name of the expression exhibited between the brackets such that $\phi (sp(x))$ has been predicated of itself:

$Dual2(<\phi (sp(<\phi (sp(x))>))>)$ = $<\mathord {\sim }\phi (sp(<\mathord {\sim }\phi (sp(x))>))>$

and wherever the introduction of the negation sign results in a double negation, they are cancelled out.

Ineg2 maps to an internal negation.

For any predicate, $\phi$, where the angle bracket expression represents a name of the expression exhibited between the brackets such that $\phi (sp(x))$ has been predicated of itself:

$Ineg2(<\phi (sp(<\phi (sp(x))>))>)$ = $<\phi (sp(<\mathord {\sim }\phi (sp(x))>))>$

and wherever the introduction of the negation sign results in a double negation, they are cancelled out.

The Simple Liar is a sentence that says of itself simply that it is false. Working through the same details, and allowing that an involution function can swap the truth and falsity predicate, the square below can be obtained for the simple Liar and the Truth-teller.

Again, (E) is our Truth-teller and (I) is its external negation. (I) is also hypodoxical by HEEN. (A) is a representation of the Simple Liar, which is well-known to be paradoxical. (O) is then paradoxical by PEEN. Given our functions below, PHD follows.

Let us describe these last functions.

Dual3 swaps ‘T’ with ‘F’, internally and externally.

Dual4 also swaps ‘T’ with ‘F’, internally and externally. As well, it adds an external negation, and if the introduction of the negation sign results in a double negation, they are cancelled out.

6.3 Arguments from dual hypodoxes

A sense in which our hypodoxes each have a ‘dual’ paradox has been justified. There are duality relations between at least some hypodoxical sentences and paradoxical sentences for the Liar and the Truth-teller, and between such sentences for Russell’s paradox and hypodox. Previous arguments about classical solutions were from more readily granted premises that did not rely on these relations. Those arguments were given in Sect. 6.1. I conclude with arguments from stronger premises. Remember ‘$\alpha$’ abbreviates ‘an element of a correct solution of a given pair of a paradox and its dual hypodox is the revision of a classical logical principle’. Let ‘$\beta$’ abbreviate ‘an element of a correct solution of a given pair of a paradox and its dual hypodox is either an additional conceptual principle or the revision of a classical logical principle’.

A hypodox and paradox being duals warrants some commonality in their correct solutions. The Liar and the Truth-teller are duals. So are Russell’s paradox and hypodox. Hence, correct solutions to these paradoxes will have some common element with a correct solution to their respective dual hypodoxes. Classical solutions to self-referential paradoxes revise conceptual principles, in effect rejecting or restricting the way they were used in the paradoxes (Sect. 5). However, their dual hypodoxes do not require those conceptual principles, so revising them does not solve those hypodoxes (Sects. 3 and 4).

Some classical solutions to self-referential paradoxes also restrict formation rules such that a formula in our formulations of the paradoxes would be ill-formed. However, our formulations of our hypodoxes need only rely on first-order logic with identity and naming conventions for their formation rules. That is, the syntax of using the truth predicate or the membership relation was not a flaw in our formulations of our hypodoxes, because they were introduced only as a first-order logic predicate and a relation and first-order logic with identity is consistent. So revision of formation rules would be an unjustified solution to either of our hypodoxes. However, Russell’s theory of types solves Russell’s hypodox by a restriction on formation rules that prevents expressing self-membership. Hence, the theory of types cannot be a correct solution to Russell’s hypodox. Thus, $\alpha$ would follow if the theory of types were the only classical solution to Russell’s paradox.

The remaining options for a correct solution to our hypodoxes are to add a justified conceptual principle that determines the hypodox, revise a classical logical principle (i.e. an ordinary law of logic) or accept the hypodox. At least one classical set theory, ZF, can give a principled solution to Russell’s hypodox. ZF set theory does add a principle, the Axiom of Regularity, that determines Russell’s hypodox. Hence, ZF set theory could be a correct solution to Russell’s hypodox. No classical set theory accepts $\text {Russell's hypodox}$. A classical semantics cannot accept the $\text {Truth-teller hypodox}$. The Tarskian hierarchical solution rejects it. Even leaving Truth-tellers in a truth-value gap in a fixed-point semantics does not distinguish hypodoxes from Liar paradoxes, which is not a way of accepting them. So, classical solutions cannot accept hypodoxes. Hence, a correct conjoint solution, if it is classical, must add a justified conceptual principle, or if it is non-classical, will revise a classical logical principle. Thus, $\beta$.

Although Tarski actually acknowledges that the premise of a formulation of the Liar paradox can be true, and ipso facto the premise of the $\text {Truth-teller}$ can be true, the formation rules of Tarski’s hierarchy of languages prevent expressing the premise for the Truth-teller. Hence, the classical semantic hierarchy of languages cannot be a correct solution to the Truth-teller. I do discuss options for Kripke’s theory of truth extending a classical solution with an additional principle in Sect. 6.1. It is contrary to Kripke’s analysis to resolve Truth-tellers in a principled way. I take Tarski’s solution and Kripke’s solution (when implemented to validate classical theorems) to be the classical solutions to the Liar, especially Tarski’s. However, these classical solutions to the Liar cannot determine a classical value for the Truth-teller by granting an additional principle of truth. Thus, the import of the Truth-teller for the Liar is that a non-classical solution is required. Thus, $\alpha$.