1 Introduction

A classical distinction within the multilevel selection literature is between multilevel selection 1 (MLS1) and multilevel selection 2 (MLS2) (e.g., Arnold & Fristrup, 1982; Sober, 1984; Damuth & Heisler, 1988; Mayo & Gilinsky, 1987; Okasha, 2006).Footnote 1 Suppose a population of lower-level entities (particles) nested into higher-level entities (collectives), as represented in Fig. 1: the distinction between the two types of multilevel selection boils down to the way fitness is defined at the collective level. Under the MLS1 approach, the fitness of a collective is measured as the number of offspring particles produced. Following Okasha (2006), I will refer to this as ‘collective fitness\(_{1}\).’ In contrast, under the MLS2 approach, collective fitness is defined as the number of offspring collectives produced. I will refer to this as ‘collective fitness\(_{2}\).’ Thus, from an MLS1 perspective, both particle and collective fitness are defined in terms of particles. By virtue of constituting a collective, the sum of the fitnesses of the collective’s particles amounts to its collective fitness\(_{1}\). In an MLS2 situation, particle and collective fitness are defined using different units, and it has been argued that particle fitness and collective fitness\(_{2}\) bear no necessary relation to one another (see Okasha, 2006, pp. 53–56).

Refining our understanding of the MLS1/MLS2 distinction is important because the distinction has been invoked in several subfields of philosophy of biology and evolutionary biology. Originally, the distinction was made to account for different ways of thinking about multilevel selection—in particular, but not exclusively, in the context of the group selection controversy and the context of species selection (Damuth & Heisler, 1988). Since, it has been invoked predominantly in the context of explaining evolutionary transitions in individuality (ETIs) (for classics in this literature, see Maynard Smith & Szathmary, 1995; Michod & Roze, 1999; Buss, 1987; Bourke, 2011). A prime example of an ETI is the transition to multicellularity from unicellularity, but several other transitions have also been proposed (see Bourke, 2011, for one way to classify them). Instances in the literature using this distinction in the context of ETIs include Michod, 2005; Okasha, 2006; Rainey & Kerr, 2010; Rainey & Kerr, 2011; Godfrey-Smith & Kerr, 2013. Additionally, the distinction (or equivalent distinctions) has been used in the context of the evolutionary dynamics of cancer (Lean & Plutynski, 2016; Okasha, 2021, fn. 19). Here, I will be primarily concerned with the literature on ETIs.

Following a model presented by Okasha (2006) based on the work of Michod et al. (see Michod, 2005), an ETI follows three stages. Each stage can be illustrated with the volvocine green algae, which is a well-suited taxonomic group for studying the evolution of multicellularity. This group comprises both unicellular and multicellular species that are closely related. Although these different species are not currently undergoing a transition, considering that the unicellular ancestors of the multicellular modern organisms (e.g., Volvox carteri) were similar to modern unicellular algae (e.g., Chlamydomonas reinhardtii) permits us to reconstruct what likely may have been the key steps of the ETIs undergone in this group. During the first stage, the particles of the population start cooperating. In the case of volvocine algae, it has been hypothesized and demonstrated experimentally that forming a group of cells leads to a lower rate of predation in this taxon (Michod, 2005; Herron et al., 2019). At that stage, the collective fitnesses in terms of particles (MLS1) and in terms of collectives (MLS2) are equal. During the second stage of an ETI, the interactions between the particles become more complex. Collectives become ‘entities in their own right’ (Okasha, 2006, p. 238), and a life cycle can be delineated at the collective level. In the case of volvocine algae, it has been hypothesized that a division of labor started to occur where some cells specialized in somatic function of the collective while others specialized in germ function (Michod, 2005). At that stage, the collective fitnesses measured in terms of particles and in terms of collectives are not equal but proportional. During the last stage of a transition, the collective fitnesses in terms of particles and in terms of collectives become independent of one another. At that point, according to Okasha, a transition to an MLS2 process has occurred. In the case of volvocine algae, at that stage, division of labor is extant, and genuine collective reproduction occurs. Following the view of Michod (2005), the fitness of the cells composing the collective is nil,Footnote 2 while that of the collective is positive, demonstrating genuine ‘decoupling’ between the two.

According to this three-part model, an ETI is fundamentally a transition from MLS1 to MLS2 where MLS1 and MLS2 are regarded as different processes of selection rather than different perspectives on a single evolutionary process. The view that MLS1 and MLS2 can represent different kinds of processes, as opposed to different perspectives on the same evolutionary process, is explicitly endorsed by Okasha when he claims that, according to his analysis, ‘MLS1 and MLS2 are causal processes which either do or do not occur’ (Okasha, 2006, p. 141). Elsewhere, when pressed on this exact point by Waters (2011, pp. 233–234) who highlights a possible ambiguity in Okasha’s claims about whether he regards the MLS1/MLS2 distinction as ways to model the same evolutionary process or as two distinct processes, Okasha (2011, p. 243) responds, ‘I insist that the difference is factual, while admitting that our explanatory interests may determine which process we study (if either), and thus which sorts of models we build.’

In this paper, I argue for the opposite conclusion to what has been classically admitted following Okasha’s analysis. Except in some degenerate cases, collective fitness\(_{2}\) and particle fitness bear some necessary relation if one is committed to the mereological supervenience (or constitutive dependence) of the collectives on particles and, by virtue of this, independence between MLS1 and MLS2 is not possible. This conclusion agrees with that of Gardner (2015, p. 310) who, relying on a notion of fitness in terms of expected long-term genetic contribution to future generations, claims that ‘because the reproductive value of any group is a simple sum of the reproductive values of its constituent individuals, the reproductive value of the mother group can be calculated either as the sum of the reproductive values of its daughter individuals or as the sum of the reproductive values of its daughter groups, and these two calculations will always yield the same answer.’ However, I show that, if understood in a pragmatic rather than factual way—that is, with practical considerations in mind—the distinction can nonetheless be useful. This reasoning leads me to propose an alternative interpretation of MLS1 and MLS2 that is pragmatic rather than factual, very much in line with the one proposed by Waters (2011).

Before doing this, it should be noted that when particles and collectives do not or only partly constitutively overlap (i.e., collectives do not fully mereologically supervene on particles), the relationship between the two collective fitnesses becomes contingent. However, in such cases, the conclusion that particle and collective fitness only bear a contingent relationship is unsurprising and, more importantly, due to some choice made by an observer to study different or, in some cases, partly overlapping bits of reality. In such cases, the claim that different processes of selection occur between entities described at different levels is no different from the claim that different selection processes occur in different populations at the same level since they do not concern the same physical entities.

The paper will run as follows. In the next section, I present in more detail why, in a multilevel setting, collective fitness\(_{1}\) and particle fitness are commensurable. I then present the case for collective fitness\(_{2}\) and why it might be argued that it does not bear any necessary relationship to particle fitness. Following Okasha (2006), I then formalize the problem in terms of the Price equation and present the argument that, from that perspective, MLS1 and MLS2 cannot be independent of one another. I then provide an interpretation of the problem using the Price equation, showing that MLS1 and MLS2 are two incomplete perspectives on the same process rather than two different types of process. Finally, in the last two sections, I discuss some of the constraints on modelling fitness in situations where the selective environment is heterogeneous and exhibits some path dependence between its different states. I then show why this matters in the context of ETIs and why, despite some important problems associated with the ontological interpretation of the MLS1/MLS2 distinction, some aspects of it are nevertheless valuable in a modelling context.

Fig. 1
figure 1

A population made of four collectives each containing ten particles of two types

Full size image

2 The MLS1/MLS2 distinction and the map between particle and collective fitness

One way to capture the distinction between MLS1 and MLS2 is to pay attention to what the concept entails with respect to the relationship or map between particle and collective fitness. In an MLS1 process, collective fitness\(_{1}\) represents the aggregative fitness contributions of this collective’s particles. Thus, in a collective k, substituting a particle i with another particle j with higher or lower particle fitness will lead the resulting collective fitness\(_{1}\) of k to change linearly. For example, assume that k comprises 10 particles, each having a particle fitness of two offspring. The collective fitness\(_{1}\) of k is two particles. If we now substitute one or more particles in this collective with a particle (which has either a higher or lower fitness), for each additional particle (not) produced, the collective fitness\(_{1}\) of k increases (decreases) by 0.1 (by virtue of the collective being constituted of 10 particles). This leads to the relationship between particle and collective fitness\(_{1}\) represented in Fig. 2. More formally, the mapping between the fitness of the particle j in the collective k (\(w_{kj}\)) and the fitness\(_{1}\) of the collective k (\(W_k\)) is .

In the case of MLS2, two types of situation can occur. In the first type, there is a known relationship between particle fitness and collective fitness\(_{2}\). To illustrate this, suppose that, following our previous example, the offspring collectives of k always have the same size as their parental collective and that reproduction at the collective level is asexual. With 20 particles produced by k, two collective offspring are produced, so that the collective fitness\(_{2}\) of k is 2, like its collective fitness\(_{1}\). The mapping between the fitness of particle j in collective k (\(w_{kj}\)) and the collective fitness\(_{2}\) of k (\(Y_k\)) is, once again, , so that \( W_k= Y_k\). It was stipulated in the example that collective offspring are produced with the same size as their parental collective. However, it could very well be the case that offspring collectives have different sizes to their parental collective. For instance, we could imagine that offspring collective size is completely or partly random, or that offspring collectives have a different but known size to their parent. In such cases, assuming a large population, although the relationship between \(w_{kj}\) and \(W_k\) may be different from that between \(w_{kj}\) and \(Y_k\), it would remain linear. For example, we could imagine a situation where the collective offspring of k are, on average, made of 3 particles and comprise between 2 and 10 particles, with most offspring collectives having a small size. Even in such a case, we would still be able to map the relationship between w and \(Y_k\) using a linear relationship. Consequently, while \(Y_k\) would be different from \(W_k\), the two collective fitnesses would be proportional to one another, so that .

Fig. 2
figure 2

Contribution of particle fitness to collective fitness\(_{1}\) in a collective comprising ten particles

Full size image

In the second situation, the relationship between particle fitness and collective fitness\(_{2}\) is unknown. This means either that it exists but is not known to the observer, or that there is no such relationship. More formally, either or . However, the second possibility can be eliminated in all situations where there is a complete (constitutive) overlap between the collective and the particles that constitute it—in other words, the collective is composed solely of particles. This is so by virtue of the collective mereologically supervening on the particles. Okasha (2006), who has developed the most sophisticated analysis of the MLS1/MLS2 distinction to date, is fully aware of the tension between the physicalist idea that higher-level processes supervene on (i.e., depend on) lower-level ones and the idea that particle-level and collective-level selection can be independent in an MLS2 setting. However, he does not see the supervenience assumption as a fatal blow to the view that the MLS1/MLS2 distinction is factual. While he recognizes that higher-level selection supervenes on lower-level processes, he denies that lower-level selection implies higher-level selection (Okasha, 2006, p. 105). In other words, the lower-level processes leading to higher-level selection are not necessarily lower-level selection processes.

I contend that to be successful, Okasha’s solution would have to suppose that some lower-level processes can have no impact on the particle fitness of a collective but have some impact on the collective fitness. However, fitness measured at any level is a property that tracks long-term evolutionary success (Fisher, 1930; Pence & Ramsey, 2013; Takacs and Bourrat, 2022; Doulcier et al., 2021; Gardner, 2015), potentially over an infinite number of generations. The only conditions where particle long-term evolutionary success does not go hand in hand with collective long-term evolutionary success in situations where there is mereological supervenience of collectives on particles are when collectives have an infinite or unlimited size and when smaller collective size does not negatively affect the number of offspring collectives produced, (or collectives produced in remote generations) Bourrat, (2021a, chap. 5).Footnote 3

To see this, suppose a simple case of two collectives of two different types reproducing asexually with perfect inheritance in discrete generations. One type always produces two collectives with a number of particles three times higher than the parental collective. The other type produces three collectives, but the number of particles produced is always two times higher than the number of particles constituting the parental collective. In such a scenario, the two ways to measure collective fitness would be genuinely decoupled.

There is clearly a limited number of biological situations relevant to this type of theoretical scenario. Species selection may be one of them (for an introduction to this literature, see Lloyd & Gould, 1993; Jablonski, 2008; Okasha, 2006, chap. 7). For instance, some species have a greater tendency to speciate than others. Since species are not typically defined by the number of members they comprise but by the existence of at least some members, one species could have a lower rate of speciation but over time accumulate a higher number of members. The fitness of a species measured in terms of number of members would be decoupled from its fitness in terms of daughter species produced, vindicating a factual interpretation of the collective fitness\(_{1}\) and collective fitness\(_{2}\) distinction. However, all else being equal, even in such situations, it might be reasoned that, in the long run, species comprising a lower number of members have a higher probability of extinction and speciate less (by virtue of having fewer members) than species comprising a higher number of members. If this was shown to be true, a recoupling of the two ways to measure collective fitness would occur. Whether this indeed is the case is an empirical matter that I will not pursue here.

Another general problem with this type of scenario is that it assumes that both population size and collective size can grow indefinitely. While the assumption of unlimited population size is often made in population genetics, in trying to understand the relationship between particle and collective fitness, this assumption has the implication that no matter the number of particles constituting a collective, the relationship between particle and collective fitness remains contingent. In other words, growing bigger or smaller does not make a systematic difference in the number of offspring collectives produced. While, as we have just seen, this assumption might have some a priori plausibility in situations of species selection, it is deeply implausible in most biological scenarios and, particularly, in light of life history theory, which emphasizes not only offspring number but also offspring quality (Gardner, 2015; Bourrat, 2021a).

Thus, in all situations where the collective size imposes some constraint on collective fitness\(_{2}\) understood as a measure of long-term evolutionary success, it will also de facto constrain the fitness of the particles that constitute a collective. All other cases that appear to lead to incongruent measures of particle and collective fitness are due to artifacts of the two fitnesses being compared when different sets of events are considered (i.e., different environments or different timescales) (Bourrat, 2015b, a; Black et al., 2020; Bourrat et al., 2022).

Excluding cases where the constitutive overlap between particles and collectives is not complete (for reasons given in the Introduction) or cases that would violate physicalism, these considerations leave us with the only viable explanation for the lack of a map between particle and collective fitness\(_{2}\)—namely, that the map exists but is unknown to the observer. In other words, particle and collective fitness are commensurable, but the reason this commensurability is not recognized is that the relationship between a particle trait and its long-term fitness is not known. In the next two sections, I substantiate my position using the Price equation.

3 MLS1 and MLS2 versions of the multilevel Price equation

In this section, I follow Okasha’s (2006) treatment of the multilevel Price equation (Price, 1972) for an MLS1 setting and the two single-level Price equations (Price, 1970) he derives for an MLS2 setting: one at the particle level and one at the collective level. I use a Price equation approach not because it is indispensable for my purpose but because it permits one to see clearly the point I want to make. Additionally, as expressed by (Rice 2004, p. 302) ‘because of its applicability to anything experiencing selection, Price’s theorem [read “the Price equation”] (see chapter 6) is particularly well suited to the study of multilevel selection (Price 1972, Wade 1985).’ Other approaches are obviously possible, but they are complementary to the Price equation rather than incompatible with it (e.g., Simon et al., 2013, p. 1562).

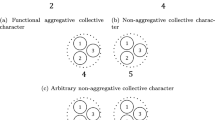
To begin with, suppose, as presented in Fig. 1, a population of n particles that reproduce perfectly and are nested in m non-overlapping collectives. We define the character z of a particle j in collective k as \(z_{kj}\). For simplicity, we will assume that the particles only vary with respect to character z and no other character. Similarly, we define the relative fitness of this particle as \(\omega _{kj}\), the latter of which is \(\frac{w_{kj}}{\overline{w}}\). From there, assuming collectives all have the same size N,Footnote 4 we define the character of collective k, \(Z_k\), as the average character of its constituent particles. Defined as such, Z is an aggregate character, an assumption I keep throughout (but see Footnote 14). Similarly, we define \(\Omega _k\), its relative collective fitness\(_{1}\), as the average relative fitness of its constituting particles. Formally, we have:

$$\begin{aligned} Z_k=\frac{1}{N}\sum _{j=1}^{N}z_{kj} \end{aligned}$$
(1)

and

$$\begin{aligned} \Omega _k=\frac{1}{N}\sum _{j=1}^{N}\omega _{kj}. \end{aligned}$$
(2)

Starting from the single-level version of the Price equation (Price, 1970; for derivations, see Okasha, 2006, chap. 1; Rice, 2004, chap. 6; Frank, 1998, 2012, chap.2), following the steps and assumptions described in Okasha (2006, chap. 1; see also Frank, 1998, 2012; Wade, 1985) using relative rather than absolute fitness as in Bourrat (2021a, appendix, Box 7) we can derive an MLS1 version of the Price equation, which describes the average change in mean collective character, \(\overline{Z}\), between two generations, assuming a simple model where generations are discrete and reproduction is asexual, asFootnote 5,Footnote 6

(3)

where, \({\text {Cov}}(\Omega _k,Z_k)\) represents the covariance between collective character and collective fitness, \({\text {E}}\) represents an expected value, and \({\text {Cov}}_{\textrm{k}}(\omega _{kj},z_{kj})\) represents the covariance between the particle character and relative growth of the particles within the collective k, compared to the entire population. The first term on the right-hand side of Eq. (3), which we can label ‘between-collective selection,’ is often interpreted as the selection occurring at the level of collectives. The second term on the right-hand side, which we can label ‘within-collective selection,’ is often interpreted as selection occurring at the particle level. This interpretation is questionable for a number of reasons that are detailed in Okasha (2006; see also Bourrat, 2021a); however, I will not consider them here. This version of the multilevel Price equation is an MLS1 version because, as we can see, collective fitness is an aggregative property of particle fitness.

Contrast Eq. (3) with the MLS2 version of the multilevel Price equation, in which collective fitness is defined not as the relative mean fitness of the collective’s particles but with a different metric that does not have a necessary relationship with \(\Omega \). Following Okasha’s analysis (2006, p. 74) in relative rather than absolute fitness terms, let us define \(\Upsilon _k\), the relative collective fitness\(_{2}\) of collective k.Footnote 7 We can write the mean change in collective character between two generations as:

(4)

where the first and second terms on the right-hand side, following a classical interpretation, represent the selection and transmission-bias terms, respectively, for the change in collective character.Footnote 8

In an MLS2 setting, particle-level selection is described using the classical single-level version of the Price equation (see Okasha, 2006, p. 74), which describes a change in mean particle character between two generations within a collective \(\overline{z_k}\). When particles are organized into collectives and indexed to collectives, we have:

(5)

where the first and second terms on the right-hand side, following a classical interpretation of the Price equation, represent the selection and transmission-bias terms in collective k, respectively, for the change in particle character. Thus, an MLS2 process involves two equations in which fitness defined at the particle level and at the collective level do not bear a necessary relationship.

As we can see, the components of Eqs. (3) and (4) are different. First, the second term on the right-hand side of Eq. (4) is interpreted as a transmission-bias whereas the second term on the right-hand side of Eq. (3) is interpreted as within-collective selection. This difference comes from the fact that the within-collective selection term of Eq. (3) is ‘coarse grained’ and represented as a transmission bias in Eq. (4). Second, the unit in which fitness at each level is defined is different. If a map between \(\omega \) and \(\Upsilon \) is not defined,Footnote 9 any relationship between the two is contingent. When this is the case, the two equations appear to be two incommensurable ways of accounting for the change in mean collective character between two generations. If we now assume that such a map, even though it is unknown, does exist—because supposing its nonexistence would violate the physicalist commitment—the gap between the two equations can be closed, as I show in the next section.

4 Closing the gap between the MLS1 and MLS2 versions of the Price equation

One implication of the assumption that a map between particle fitness and collective fitness\(_{2}\) is unknown but exists is that either \(\omega \) is only an imperfect estimate of the true particle-relative fitness, which would here be \(\upsilon \),Footnote 10 or that \(\Upsilon \) is an imperfect estimate of \(\Omega \). Recall that what grounds this reasoning is that fitness is a long-term measure of evolutionary success of the entities of a population and that, properly computed and compared, the fitnesses of a particle in a collective and that of the collective cannot come apart. Between the two possibilities, I will assume that \(\omega \) is an imperfect measure of \(\upsilon \) because, typically, collective fitness\(_{2}\) refers to evolutionary settings over longer timescales than MLS1 settings. Nonetheless, whether one chooses to regard \(\omega \) or \(\Upsilon \) as an imperfect estimate will have no impact on the reasoning presented below.

Thus, if this is correct, the difference between the two ways of defining particle and collective fitness can be viewed as measurement errors where one way to measure fitness (in this case, \(\omega \) or \(\Omega \)) is conducted in an environment that only partly overlaps with the environment in which the other way of measuring fitness is defined—that is, \(\Upsilon \) (\(\upsilon \) being only a theoretical possibility). Formally, we have:

$$\begin{aligned} \upsilon _{kj} = \omega _{kj} + \varepsilon _{kj}, \end{aligned}$$
(6)

where \(\varepsilon _{kj}\) represents the measurement error due to \(\omega \) only imperfectly estimating \(\upsilon \)—that is, assuming the environment in which collective fitness\(_{2}\) is the environment of reference. Here, we assume that \(\omega \) and \(\varepsilon \) are independent since there is no particular reason why measurement errors would be correlated with \(\omega \).Footnote 11

From there, we can define collective fitness\(_{2}\) as:

$$\begin{aligned} \Upsilon _k = \Omega _{k} + \mathcal {E}_k, \end{aligned}$$
(7)

where \(\mathcal {E}_k\) is the measurement error due to \(\Omega \) only imperfectly estimating \(\Upsilon \) and is defined as the sum of all particle fitness measurement errors in collective k: that is, \(\mathcal {E}_k=\frac{1}{N}\sum _{j=1}^{N}\varepsilon _{kj}\).

If we now plug these definitions of fitness into Eq. (4), we get the following:

(8)

Because we assume that particles reproduce perfectly and that collectives are composed of nothing more than particles varying solely for character z, we can consider that any change in collective character between two collective generations is necessarily due to particles with different character values reproducing differentially within the collective. Thus, we can define the change in character of the collective k between the two generations, following the single-level version of the Price equation as:

$$\begin{aligned} \Delta Z_k= {\text {Cov}}_{\textrm{k}}(\upsilon _{kj}, z_{kj})= {\text {Cov}}_{\textrm{k}}(\omega _{kj}, z_{kj}) + {\text {Cov}}_{\textrm{k}}(\varepsilon _{kj}, z_{kj}), \end{aligned}$$
(9)

where \({\text {Cov}}_{\textrm{k}}(\upsilon _{kj}, z_{kj})\) represents the covariance between the particle character and true particle fitness, and \({\text {Cov}}_{\textrm{k}}(\varepsilon _{kj}, z_{kj})\) the covariance between the particle character and the measurement error, both within collective k.

Inserting this decomposition into Eq. (8), developed following the properties of covariances and expected values, and rearranged, we get:

(10)

where the first and second terms on the right-hand side together form Eq. 3, the third term on the right-hand side is the covariance between \(\mathcal {E}\)—that is, the difference in measurement between \(\Omega \) and \(\Upsilon \)—and Z in the whole population and, thus, represents a between-collective component of selection; and the fourth, fifth, and sixth terms are measured within each collective and, thus, represent components of within-collective selection. The fourth term is the expected value of \(\Omega \) times the covariance between \(\varepsilon \)—that is, \(\omega - \upsilon \)—and z; the fifth is the expected values of \(\mathcal {E}\) times the covariance between \(\varepsilon \) and z; finally, the sixth term is the expected value of \(\mathcal {E}\) times the covariance between \(\varepsilon \) and z.

Equation (10) is a description of evolutionary change that starts from the MLS2 version of the Price equation. By assuming a necessary mapping between particle fitness and collective fitness\(_{2}\), but one that is different from that between particle fitness and collective fitness\(_{1}\) due to fitness measures being performed in different environments—or measurement errors when one environment is considered the reference environment—the equation contains the MLS1 version of the Price equation plus some terms that are due to measurement differences. As such, it creates a bridge between MLS1 and MLS2 and demonstrates that they do not represent two different processes of multilevel selection but rather two different approaches to the same process, where one is regarded as a truthful description of the process and the other an inaccurate estimate.

5 Why MLS2 is not superior to MLS1

From the above reasoning, one might be tempted to argue that MLS2 is a superior approach to multilevel selection (compared to MLS1) because the difference between the two is due to the fact that fitness in an MLS1 scenario is not adequately estimated. How should we answer this argument? The first thing to note is that the map between particle and collective fitness might simply be unknown, and the description of a system is only pragmatically possible at the collective level. In such cases, MLS2 would be the approach of choice—not because it is inherently superior to MLS1 but because it is the only possible one.

Second, recall that I conducted my demonstration by decomposing what I call the true particle fitness (\(\upsilon \)) into \(\omega \) and \(\varepsilon \) to recover the classical version of MLS1 with \(\omega \). Note, however, that one can use \(\upsilon \) in the MLS1 version of the equation and show that, through a simple coarse-graining where some details regarding within-collective context are lost, we can recover the MLS2 version of the equation. We have:

(11)

If we now coarse-grain the events of selection and transmission occurring within the collectives, we have \({\text {Cov}}_{\textrm{k}}(\upsilon _{kj},z_{kj})=\Delta Z_k\). Once replaced in Eq. (11), this leads to:

$$\begin{aligned} \Delta \overline{Z}= {\text {Cov}}(\Upsilon _{k},Z_{k})+{\text {E}}(\Upsilon _{k}\Delta Z_{k}),\qquad \qquad \qquad (4) \end{aligned}$$

which is Eq. (4). This demonstrates that MLS2 is not a superior approach to multilevel selection since the two approaches are congruent, provided that we start from the same quantity of information about the population. I claim that they are only ‘congruent’ rather than equivalent because it might be argued that MLS1 is, indeed, superior in situations where the collective transmission bias is explained both by within-collective selection and particle transmission bias because it will discriminate the relative part of each process. Recall that to recover Eq. (4) from Eq. (11), we had to coarse-grain the events occurring within collectives. Thus, if precision about the processes occurring within collectives is what matters, the MLS1 approach could be deemed superior to the MLS2 approach.

Finally, another reason why the MLS2 approach is not superior is illustrated well using ETIs. It could naively be reasoned that since \(\Upsilon \) rather than \(\Omega \) represents the most accurate measure of collective fitness once an ETI is complete, it should therefore be used throughout the ETI. However, this reasoning is mistaken. For this definition to be correct, we would need to assume that no state of the environment is precluded from being reachable, in principle, by any of the different types in the population at any point in time during an ETI. This assumption permits one to define an ergodic process, which then allows us to derive an accurate prediction about the long-term behavior of the population undergoing the evolutionary process (Doulcier et al., 2021). Unfortunately, ETIs, like many other evolutionary processes, are not ergodic processes once they have been conceived in their entirety. This is so because they exhibit some path dependence. Once a state is reached, the previous states cannot be reached again. Consequently, it does not follow that the use of MLS2—because it refers to \(\Upsilon \), which is more accurate in the last stage of an ETI—is unconditionally better. For this reasoning to be correct, the whole ETI would have to be an ergodic process—which it is not.

When an evolutionary process is not ergodic at the global scale, one approach to studying it is to partition the full sequence of events into parts, each of which satisfies the assumption of ergodicity. Then, the different partial or local explanations are woven together to obtain a global explanation. One prime example that uses this approach is adaptive dynamics, where the fitness of a new mutant is compared to that of the resident type with which it interacts (i.e., the environment) (Doulcier et al., 2021). The mutant and resident are assumed to be phenotypically close to each other. If the mutant type invades the population, it becomes the new resident population, and its fitness is then compared to a new mutant (again, phenotypically close to the new resident), which might, in turn, invade the population and become the new resident. Note here that mutation during each invasion is assumed to be impossible. This leads to a timescale separation between ecology and evolution. Only by weaving together these successive invasions can an adequate evolutionary explanation of the whole dynamics be obtained. Importantly, one could decide to define post ex facto a fitness value for all the variants and assign to the winner the highest value,Footnote 12 However, in doing so, one would lose track of the dynamics within each invasion and could assume incorrectly that the winner type would successfully invade any resident population. For instance, the winner type could fail to invade an environment where the resident type is quite different from it. As such, a successful variant at the beginning of the transition could turn out to be easily outcompeted at later stages of the transition when the resident population is very different. Therefore, such a measure of fitness would have no long-term predictive power for success in the past or the future where the future and the past involve different environments.

Once this reasoning is applied to ETIs, we could consider, broadly speaking, that each of the three phases of an ETI satisfies the assumption of ergodicityFootnote 13 but that, once taken together, they do not. Thus, it would be incorrect to consider that \(\Upsilon \), when computed in the third phase of a transition, represents a global correct measure of collective fitness. This is so because it would imply that the successful phenotypes in this phase of the transition are equally successful in the other phases, which they are clearly not. For example, phenotypes associated with germ function that are successful in the context of a multicellular organism would be outcompeted in a unicellular context.

6 Evolutionary transitions in individuality and the MLS1/MLS2 distinction

The previous section ended with a lesson—namely, that it is useful if not crucial to have collective fitness defined in different environments for the different stages of an ETI. Because the practicality of measuring collective character and collective fitness either as aggregates of particle properties or independently from them (i.e., without a map between particle and collective) will vary between the different stages of the transition, some way of measuring collective fitness will lend more naturally toward an MLS1 or MLS2 perspective. Although this point is well taken, my contention is that the interpretation of the MLS1/MLS2 distinction as resulting from two processes that occur in nature or as one resulting or transforming into another is not warranted, as Eq. (10) showed. Similarly, in the context of ETIs (and many other contexts beyond ETIs), assumptions of the nonexistence of a map between particle fitness and collective fitness or that collective fitness is measured by the number of collectives rather than particles produced are not factual but made for pragmatic (i.e., practical) reasons. With detailed knowledge, one would uncover the unavoidable map between particle and collective fitness and the fact that a higher number of collectives produced necessarily leads to a higher number of particles, once fitness at each level refers to the same environment. Pragmatic considerations should not be dismissed as unimportant; in fact, they are essential (Bourrat, in press). However, they should not be portrayed as what they are not—namely, objective facts.

Thus, how should we precisely interpret the three stages of an ETI in light of the analysis provided in the previous sections? Recall Okasha’s proposition that MLS1 is relevant at the beginning of a transition. In the second stage, both MLS1 and MLS2 can be applied with equal success. During this stage, collective fitness\(_{1}\) and collective fitness\(_{2}\) are claimed not to be equal but nevertheless proportional. In the third stage, according to the model, collective fitness\(_{1}\) and collective fitness\(_{2}\) have become independent, and any relationship between them is contingent.

The conclusion we reached in Sect. 4 is that MLS1 is reducible to MLS2 if one assumes that a map exists between particle and collective fitness (which itself follows from physicalism). However, in Sect. 5, we saw that to provide some details about the global evolutionary dynamics of a system where evolution exhibits some path dependence on the dynamics due in part to the selective environment being different in different phases of the transition, a global fitness estimator is not adequate to predict the dynamics during the three stages.

Taking these two conclusions together, we arrive at the following picture. During the first stage of the transition, the fitnesses of a collective measured in terms of particles produced (collective fitness\(_{1}\)) or in terms of collectives produced (collective fitness\(_{2}\)) can be tracked equally well since the maps between the particles and the collective offspring and character are simple. Thus, there is no need to follow collective offspring or characters. However, as the transition proceeds, this map and, more generally, the map between particle and collective characters become more complex. Initially, collective fitness can be recovered in terms of particles from the number of particles produced, and collective characters can be recovered from particle characters.Footnote 14 Alternatively, one can use the perspective of collectives, which is simpler but might lead to some loss of information about particle-level processes within collectives. Nevertheless, at that stage, a translation between the two perspectives is still possible. However, at some point, the mapping between particle fitness measured in the initial phase of the transition, \(\omega \), and collective fitness measured in the current phase is lost due to two factors. First, a change in the environment with which particles interact implies that predictions of the evolutionary dynamics made using \(\omega \) will be inaccurate. Second, knowledge about the maps between particle fitness and collective fitness, and between particle characters and particle fitness, becomes too costly to acquire. Thus, switching to a description at the collective level not only becomes the only practical option but also, even if a particle-level description were possible, a different measure of fitness at the particle level would have to be used to predict the dynamics in this phase of the transition. Note, once again, that using a different measure of fitness at a different level of description gives no traction to the objectivity of selection processes occurring at this level rather than other levels.

Before concluding, let us return to Eq. (10), which we will assume measures, in turn, the evolutionary change between two collective generations at the three different stages of the transition. Let us define three different true particle \(\hbox {fitnesses}_{\textrm{local}}\) (and their collective counterparts), \(\upsilon _1\) (\(\Upsilon _1\)), \(\upsilon _2\) (\(\Upsilon _2\)), and \(\upsilon _3\) (\(\Upsilon _3\)), where the index refers to the three stages of the transition, respectively—and permits an accurate explanation of the dynamics within each phase. \(\omega \) and \(\Omega \) are accurate estimates of fitness only at the initial stage (formation) of the transition.

At the beginning of a transition, \(\varepsilon \) and, consequently, \(\mathcal {E}\) are nil. This is because, during that phase, \(\omega \) tracks well \(\Upsilon _1\) defined for the dynamics observed during the first phase of the transition. All the terms of the equation that involve \(\varepsilon \) and \(\mathcal {E}\) in multiplicative and covariance terms are nil. Thus, the equation simplifies into:

$$\begin{aligned} \begin{aligned} \Delta \overline{Z}&= {\text {Cov}}(\Omega _{k},Z_{k})+{\text {E}}(\Omega _{k}{\text {Cov}}_{\textrm{k}}(\omega _{kj}, z_{kj})), \end{aligned} \end{aligned}$$

which is simply Eq. (3), the classical MLS1 version of the equation.

As the transition progresses, the exact mapping between particle fitness and collective fitness becomes more difficult to capture. Nonetheless, measures of \(\omega \) (and \(\Omega \)) track relatively well the dynamics observed during this stage of the transition, indicating that the differences between \(\omega \) (or \(\Omega \)) and \(\Upsilon _2\) are negligible. The evolutionary change can be described either as in the previous phase or, if the mappings between particle character or fitness and collective character or fitness are judged too unwieldy, by coarse-graining the within-selection term into a transmission-bias term at the collective level. In this latter case, the equation will refer to collectives only—the mark of MLS2—so that:

$$\begin{aligned} \begin{aligned} \Delta \overline{Z}&= {\text {Cov}}(\Omega _{k},Z_k)+{\text {E}}(\Omega _k\Delta Z_k). \end{aligned} \end{aligned}$$

Finally, in the last stage, measures of particle fitness (\(\omega \)) no longer track (\(\Upsilon _3\)); thus, projections of the evolutionary change of collective character based on \(\omega \) and \(\Omega \) are erroneous, in the sense that they do not yield an accurate prediction of the evolutionary change.Footnote 15 In such cases, the true MLS1 version of the change in collective character would be Eq. (11), where \(\upsilon _3\) and \(\Upsilon _3\) replace \(\upsilon \) and \(\Upsilon \), respectively, which would involve being able to compute \(\upsilon \). However, fitness measures are performed only at the collective level, and the map between particle and collective fitness is unknown (as is, for many characters, the map between particle and collective character), leaving only Eq. (4) as a way to describe evolutionary change at the collective level.

Taking stock, the main difference between Okasha’s analysis and the one presented here lies in the fact that Okasha considers the distinction between MLS1 and MLS2 to be factual, whereas I view it as pragmatic. In particular, my analysis makes explicit that collective fitness\(_{1}\) and collective fitness\(_{2}\) are estimates that are contingent upon specific environmental settings and not theoretical entities in the context of ETIs. When these characteristics are made explicit, it becomes clear why collective fitness\(_{1}\) and collective fitness\(_{2}\) cannot always be mapped onto one another. Further, my analysis reveals that if these two notions of fitness are regarded as theoretical entities, they are commensurable so long as one is committed to physicalism and finite collective sizes.

One possible response to these points could be that, ultimately, because there seems no single appropriate measure of fitness for all situations, there are no particular issues with treating each notion as a theoretical entity and instead using the appropriate measure for a particular setting or model without worrying about any metaphysical implications. Okasha’s more recent writings suggest that this might be the path he has taken (see Autzen & Okasha, 2022). However, this response would be at odds with Okasha’s response to Waters, quoted earlier. Additionally, it would make it hopelessly difficult to articulate an adequate explanation of phenomena involving different levels of organization, such as ETIs, with their specific models at different levels. I consider this too high a price to pay.

7 Conclusion: on the quasiontological status of the MLS1/MLS2 distinction

The idea that the distinction between MLS1 and MLS2 is fundamental has been pervasive in the literature on levels of selection (e.g., Arnold & Fristrup, 1982; Heisler & Damuth, 1987; Okasha, 2006; Calcott & Sterelny, 2011). Does the analysis provided here not contradict what many theoretical and experimental biologists have regarded as an important insight in their research? The answer is that it only contradicts a factual interpretation of the distinction between MLS1 and MLS2 in most of the contexts in which it has been invoked. As I showed, the distinction has some pragmatic utility. Ultimately, as I have argued in Bourrat (2021a), it is more tightly coupled with the question of whether, in a multilevel setting, collectives can be regarded as entities genuinely reproducing—that is, not as a reproductive by-product of their constituting particles. Okasha (2016) refers to this as situations in which ‘allocation mechanisms’ at the collective level exist.

An event of complex collective reproduction with allocation mechanisms seen from the perspective of a particle represents a sudden change in this particle’s environment. For example, in Dicotyostelium sp., the same cell could end up either in the fruiting body or in the stalk of the slime mold when it reproduces (Bonner, 2009). In the former case, its long-term fitness (ignoring any potential inclusive-fitness effects) might be positive, whereas, in the latter case, it would be nil. Without taking into account such abrupt changes in the selective environment of a particle, projecting particle fitness will be misleading. This implies that the emergence of collective-level reproduction during a transition is an important factor to consider and explain for articulating the relationship between particle and collective fitness. Further, for all practical purposes, distinguishing MLS1 from MLS2 as if they were two distinct processes—that is, giving a ‘quasi-ontological’ interpretation to the distinction—will pose no problem. However, in the context of a diachronic perspective, where the origins of collective-level entities is the phenomenon to be explained, or in the context of precise analysis of the relationship between particle and collective fitness during ETIs, the idea that the two perspectives track two distinct processes is misguided.