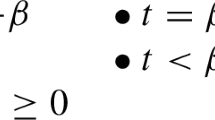Abstract
We explore the relationship between evidence and knowledge when knowledge is described by a standard partition over a finite state space, and evidence is represented by a state-dependent collection of finite sets of messages. When the collection is measurable with respect to the partition, there is evidence for an event only if the event is self-evident—i.e., known at every one of its states. Thus, an event is commonly known in and only if there is mutual evidence that implies that the event has occurred, and all knowledge can be proved only when the agent is informed about the state or knows nothing. The existence of partial provability outside these two extremes hinges on the non monotonic nature of provability.

Similar content being viewed by others
Notes
For studies on communication contexts, see., e.g., Forges and Koessler (2005), Hagenbach et al. (2014), Milgrom (1981a) and Okuno-Fujiwara et al. (1990). For mechanism design problems, see, e.g., Green and Laffont (1986), Ben-Porath and Lipman (2012), Kartik and Tercieux (2012), Hart et al. (2017) an Ben-Porath et al. (2019).
Intuitively, measurability—also imposed in Koessler (2004)—extends the meaning of verifiable information to situations in which agents are not necessarily informed about the state.
The meet is the finest common coarsening of \(\Pi \); namely, the finest partition X of S such that, for every i and s, \(\Pi _i(s)\subseteq {X(s)}\). That is, for every partition \(X'\) of S such that for every i and \(s \in S\), \(\Pi _i(s) \subseteq X'(s)\), \(X(s) \subseteq X'(s)\).
To our knowledge, the term “public” was coined by Milgrom (1981b). Notice that public events can be written as unions of elements of the meet of \(\Pi \).
Notice that we do not assume that there exists a state-independent message. We do, however, in Sect. 5.
Koessler (2004) also noticed that any evidence structure that is measurable with respect to an agent’s partition must be, state by state, a subset of the set of events that are self-evident for the agent. Yet he did not study the consequences of this result, which constitute the main goal of this paper.
Notice that the conclusion of Proposition 3 can be generalized: When an agent’s information is neither the finest nor the coarsest, there are events that are known but not provable or events that can be proven but cannot be known.
If \(\Pi _i\) is the coarsest partition, \(\mathcal {F}_i\) trivially satisfies both (M) and (SM).
Indeed, if both are singletons, the fact that the partition is not the finest one implies that there is some state \(\bar{s}\) such that \(\Pi _i(\bar{s})\) is non-singleton. Hence, \(\Pi _i(\bar{s})\cap {\Pi _i(s)}=\emptyset \). The argument that follows could then be carried out with \(\bar{s}\) and s.
References
Ben-Porath, E., Dekel, E., & Lipman, B. L. (2019). Mechanisms with evidence: Commitment and robustness. Econometrica, 87(2), 529–566.
Ben-Porath, E., & Lipman, B. L. (2012). Implementation with partial provability. Journal of Economic Theory, 147(5), 1689–1724.
Binmore, K., & Brandenburger, A. (1988). Common knowledge and game theory. Working Paper: Department of Economics, University of Michigan.
Crawford, V. P., & Sobel, J. (1982). Strategic information transmission. Econometrica, 50(6), 1431–1451.
Forges, F., & Koessler, F. (2005). Communication equilibria with partially verifiable types. Journal of Mathematical Economics, 41(7), 793–811.
Giovannoni, F., & Seidmann, D. J. (2007). Secrecy, two-sided bias and the value of evidence. Games and Economic Behavior, 59(2), 296–315.
Green, J. R., & Laffont, J. J. (1986). Partially verifiable information and mechanism design. Review of Economic Studies, 53(3), 447–456.
Hagenbach, J., & Koessler, F. (2017). Simple versus rich language in disclosure games. Review of Economic Design, 21(3), 163–175.
Hagenbach, J., Koessler, F., & Perez-Richet, E. (2014). Certifiable pre-play communication: Full disclosure. Econometrica, 82(3), 1093–1131.
Hart, S., Kremer, I., & Perry, M. (2017). Evidence games: Truth and commitment. American Economic Review, 107(3), 690–713.
Kartik, N., & Tercieux, O. (2012). Implementation with evidence. Theoretical Economics, 7(2), 323–355.
Koessler, F. (2004). Strategic knowledge sharing in Bayesian games. Games and Economic Behavior, 48(2), 292–320.
Lipman, B. L., & Seppi, D. J. (1995). Robust inference in communication games with partial provability. Journal of Economic Theory, 66(2), 370–405.
Milgrom, P. (1981a). Good news and bad news: Representation theorems and applications. The Bell Journal of Economics, 12(2), 380–391.
Milgrom, P. (1981b). An axiomatic characterization of common knowledge. Econometrica, 49(1), 219–222.
Milgrom, P., & Roberts, J. (1986). Relying on the information of interested parties. The RAND Journal of Economics, 17(1), 18–32.
Monderer, D., & Samet, D. (1989). Approximating common knowledge with common beliefs. Games and Economic Behavior, 1(2), 170–190.
Okuno-Fujiwara, M., Postlewaite, A., & Suzumura, K. (1990). Strategic information revelation. Review of Economic Studies, 57(1), 25–47.
Samuelson, L. (2004). Modeling knowledge in economic analysis. Journal of Economic Literature, 42(2), 367–403.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Proposition 1
Fix any agent i and suppose, contrary to hypothesis, that there exists a model \(\mathcal {F}_{i}=(S, \Pi _{i},\textbf{M}_{i})\), a state s, and an event \(E\in {\textbf{M}_{i}(s)}\) such that \(E\not \in {\mathcal {A}_{\Pi _{i}}(s)}\). Then, there exists some \(s'\in {E}\) such that \(\Pi _{i}(s')\not \subseteq {E}\). Yet consistency entails that \(E\in {\textbf{M}_{i}(s')}\), contradicting that \(\textbf{M}_{i}\) is measurable with respect to \(\Pi _{i}\). \(\square \)
Proof of Proposition 2
We first show that 1. and 2. are equivalent. Suppose that a model \(\mathcal {F}_i=(S, \Pi _i,\textbf{M}_i)\) satisfies both (IC) and (M). The former implies that \(\Pi _i(s)\in {\textbf{M}_i(s)}\) for every s. By (M), it follows that \(F\in {\textbf{M}_i(s)}\) for every s and every F such that \(\Pi _i(s)\subseteq {F}\). Thus, \(\mathcal {F}_i\) is a model of total provability. To show that 1. implies 2., notice that if \(\mathcal {F}_i\) is a model of total provability, then \(\Pi _i(s)\in {\textbf{M}_i(s)}\) for every s. Hence, \(\mathcal {F}_i\) is (IC). To show that \(\mathcal {F}_i\) satisfies (M) it is sufficient to consider known events. Since knowledge is monotonic and \(\mathcal {F}_i\) is a model of total provability, we must have \(F\in {\textbf{M}_i(s)}\) for every s and every F such that \(\Pi _i(s)\subseteq {F}\). Hence, it follows that \(\mathcal {F}_i\) satisfies (M).
To see that 1. and 3. are equivalent, notice that \(\Pi _{i}(s)\in {\mathcal {A}_{\Pi _{i}(s)}}\) for every s. If \(\mathcal {A}_{\Pi _{i}}\) is closed under supersets, it follows that \(F\in {\mathcal {A}_{\Pi _{i}}(s)}\) for every s and every F such that \(\Pi (s)\subseteq {F}\). Thus, \(\mathcal {F}_{i}\) is a model of total provability. To prove that 1. implies 3., notice that if \(\mathcal {F}_{i}\) is a model of total provability, then for every s and every E such that \(\Pi _{i}(s)\subseteq {E}\), there exists some evidence structure \(\textbf{M}_{i}\) such that \(E\in {\textbf{M}_{i}(s)}\). Thus, by Proposition 1, for every s and every E such that \(\Pi _{i}(s)\subseteq {E}\) we have \(E\in {\mathcal {A}_{\Pi _{i}}(s)}\). Since the set of events that i knows at any s is closed under supersets, \(\mathcal {A}_{\Pi _{i}}(s)\) is closed under supersets for every s. \(\square \)
Proof of Proposition 3
We show this by contradiction. Suppose that the partition is neither the finest nor the coarsest. The latter implies that there are at least two states, s and \(s'\), such that \(\Pi _i(s')\cap {\Pi _i(s)}=\emptyset \). In turn, the former implies that, without loss of generality, we can take either \(\Pi _i(s)\) or \(\Pi _i(s')\) to be non-singleton.Footnote 10 Assume that \(|\Pi _i(s)| > 1\). Then,
Since \(\Pi _i(s)\) is non-singleton by hypothesis, we reach a contradiction. \(\square \)
Proof of Proposition 4
The proof of this statement hinges on a couple of auxiliary results: \(\square \)
Claim 1
For every s such that \(\Pi _i(s)\) is not a singleton, every \(s'\), and every E,
Claim 2
For every s such that \(\Pi _i(s)\) is not a singleton, and every \(s'\)
Proof of Claim 1
Take any s such that \(\Pi _i(s)\) is not a singleton and assume, contrary to hypothesis, that there is some state \(s'\) and event E such that \(E\in {\textbf{M}_i(s')}\) but \(\Pi _i(s)\not \subseteq {E}\). The latter implies that there is some \(\bar{s}\in {\Pi _i(s)}\) such that \(\bar{s}\not \in {E}\). In fact, we must have \(\Pi _i(s)\cap {E}=\emptyset \). To see this, suppose that there is some \(\hat{s}\in {\Pi _i(s)}\) such that \(\hat{s}\in {E}\). Since \(E\in {\textbf{M}_i(s')}\), consistency entails that \(E\in {\textbf{M}_i(\hat{s})}\). Thus, \(\Pi _i(\hat{s})\subseteq {E}\). But since \(\hat{s}\in {\Pi _i(s)}\), it follows that \(\Pi _i(s)\subseteq {E}\). Contradiction.
Since \(E\in {\textbf{M}_i(s')}\), monotonicity implies that \(E\cup {\{\bar{s}\}}\in {\textbf{M}_i(s')}\) for every \(\hat{s}\in {\Pi (s)}\). By consistency, we must then have that \(E\cup {\{\bar{s}\}}\in {\textbf{M}_i(\hat{s})}\) for every \(\hat{s}\in {\Pi _i(s)}\). Thus, it follows that \(\Pi _i(s)\subseteq {E\cup {\{s\}}}\). But since \(\Pi _i(s)\cap {E}=\emptyset \), it must follow that \(\Pi _i(s)=\{s\}\). Contradiction. \(\square \)
Proof of Claim 2
To see this, take any \(E\in {\textbf{M}_i(s')}\). By Claim 1, we must have that \(\Pi _i(s)\subseteq {E}\). Hence, \(s\in {E}\). Thus, consistency implies that \(E\in {\textbf{M}_i(s)}\).
Armed with these two claims, it is easy to see that the only-if part holds since both (M) and (SM) are trivially satisfied in cheap-talk models. To see the if part, notice that, by hypothesis, there is a state s at which \(\Pi _i(s)\) is not a singleton. Then, (SM) implies that for every s such that \(\Pi _i(s)\) is not a singleton we must actually have that \(\textbf{M}_i(s')=\textbf{M}_i(s)\) for every \(s'\). Suppose that this is not the case. Then, for some states \(s'\) and s such that \(|\Pi _i(s)|> 1\), \(\textbf{M}_i(s') \subset {\textbf{M}_i(s)}\). It follows that \(\vert {\textbf{M}_i(s)}\vert {}>\vert {\textbf{M}_i(s')}\vert {}\). Then, by (SM) we have that \(\vert {\Pi _i(s')}\vert {}\ge {}\vert {\Pi _i(s)}\vert {}\). Since \(\Pi _i(s)\) is not a singleton, \(\Pi _i(s')\) is also not a singleton. But then, Claim 2 implies that \(\textbf{M}_i(s)\subseteq {\textbf{M}_i(s')}\), a contradiction. Thus, whenever \(\Pi _i\) is not the finest partition it follows that the model is a cheap-talk model. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Peralta, E., Tohmé, F. The scope of provability. Synthese 202, 19 (2023). https://doi.org/10.1007/s11229-023-04238-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04238-8