Abstract
Trust and monitoring are traditionally antithetical concepts. Describing trust as a property of a relationship of reliance, we introduce a theory of trust and monitoring, which uses mathematical models based on two classes of functions, including q-exponentials, and relates the levels of trust to the costs of monitoring. As opposed to several accounts of trust that attempt to identify the special ingredient of reliance and trust relationships, our theory characterizes trust as a quantitative property of certain relations of reliance that can be quantified and expressed as a scalar quantity. Our theory is applicable to both human–human and human–artificial agent interactions, as it is agnostic with respect to the concrete realization of trustworthiness properties, and is compatible with many views differing on which properties contribute to trust and trustworthiness. Finally, as our mathematical models make the quantitative features of trust measurable, they provide empirical studies on trust with a rigorous methodology for its measurement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Up to the present point in time, philosophers have devoted their attention to providing conceptual analyses of trust. While it may no longer be fashionable to conceive such analyses as a set of individually necessary and jointly sufficient conditions for trust to obtain, philosophical accounts are in the business of providing an explanatory definition of this object. The debate on the nature of trust centers on questions such as: “is trust the same as reliance?” (Baier, 1986; Goldberg, 2020), “is trust most fundamentally an attitude, or a belief?” (Keren, 2014; Lahno, 2020), “does trusting ascribe specific motives to the trustee?” (Becker, 1996; Hardin, 1993; Jones, 1996), and “are moral obligations, motivations, or moralized reactive attitudes essential to trust?” (Cohen, 2020; Holton, 1994; Nickel, 2007). Those who are familiar with the literature on the nature of trust will recognize such questions as pivotal points in the current debate, at least in analytic philosophy.Footnote 1
By contrast, the literature is largely silent on what it means to trust someone to a greater or lesser degree, although some seminal works have appeared, especially formal accounts, which we shall review later. Still, the topic is not considered a key philosophical issue. The current Stanford Encyclopedia Philosophy entry for trust (McLeod, 2020) mentions dozens of books, book chapters, and journal articles devoted to analyzing the concept of trust as a binary property of relationships: people either trust (or are trusted) or not, and the task of philosophy is to elucidate what this means. The entry does not include a single reference devoted to a philosophical analysis of what it means to trust someone to a certain degree. Similarly, none of the 16 chapters of the edited book on this matter (Faulkner & Simpson, 2017) discusses the idea of trust as something that obtains as a matter of degree or how to conceptualize it as such.
We maintain that the very idea of trust as a scalar quantity—something that does not just obtain or not but rather obtains as a matter of degree—deserves a careful examination. People usually do not simply indicate whether they trust others; they also talk about how much they trust others, about the processes of losing or gaining trust, and about trusting one person more than another. The gradual build-up of trust is a very important phenomenon; yet making sense of the idea of a graded notion of trust has not occupied the mind of most philosophers as much as any of the other recognized dimensions of this phenomenon.
This paper is devoted to foregrounding the graded notion of trust. We propose a philosophical account of trust as anti-monitoring to form the conceptual basis for a graded account of trust relationships. Our account is based on two key intuitions. First, trust is a property of reliance relations in which X relies on Y with a positive expectation toward the achievement of a goal of interest. Second, there is an inverse relationship between the degree to which X trusts Y and the degree to which X is disposed to monitor Y. This account of trust as anti-monitoring is original, but it shares its central intuition with the related work of Baier (2013), Taddeo (2010), Keren (2014), and others, to which we refer later.
Notice that how much one trusts somebody is not the only possible dimension of trust amenable to a scalar analysis. For example, if the trust relationship is modeled as a relation between the trustor and many individuals, degrees of trust may represent the breadth of trust, that is, how many people an individual is willing to trust. If the trust relationship is modeled as a relation between the trustor and a single individual for a range of different goals, degrees of trust may represent the scope of the trust relationship; in other words, how many goals one trusts another. Our goal here is to single out one of the clearest and most obvious scalar dimensions of trust, what we label intensity.
The structure of our paper is as follows: we will first analyze the idea of trust as anti-monitoring in the literature. Next, we will define the building blocks of an analysis of trust as anti-monitoring based on the concepts of reliance, monitoring, and trust, and establish their mutual relations. Third, we will discuss an account of trust as antithetical to monitoring (i.e., “trust as anti-monitoring”), then quantitatively formalize the idea of trust as anti-monitoring, introducing mathematical models that use functions such as q-exponentials (Tsallis, 1988, 2009). Finally, we will discuss how the formalized intuition of trust as anti-monitoring can be used to derive empirical measures of trust.
2 Quantities of trust and anti-monitoring
In this section, we present the main quantifications of trust and its conceptions as antithetical to monitoring in philosophy and the social sciences. This is a preliminary step to the philosophical analysis of the intensity of trust.
The idea that trust is antithetical to monitoring is not new in the philosophical literature: it has been endorsed, implicitly or explicitly, by a wide range of scholars from different disciplines, with disparate views about what trust is and how to measure it. The core idea of trust as anti-monitoring is that if I trust someone, I will not need to monitor that person. The action of monitoring implies the investment of resources (e.g., time and money) to ensure that the person relied upon will perform an action to achieve the goal of interest for the trustor. Therefore, we consider trust as the property of relationships where one relies on another person to achieve a given goal with little monitoring.
In the philosophical literature, monitoring is an activity that is often considered antithetical to trust. In fact, Baier (2013) writes: “As I understand trust, it itself involves economizing on monitoring, supervision, and audits, and leaving the trusted to get on with their work with minimal audits and minimal supervision. So increasing these is of course displaying decreasing trust–simply replacing it with audits, supervision, threats, sanctions and coercion.”Footnote 2
The term “economizing” does not exclude the action of monitoring in toto; instead, it reflects the idea that trust is antithetical to monitoring to some degree. Therefore, one is drawn to use vague quantitative terminology, such as “reliance with little monitoring” or “not too much monitoring,” to provide a high-level description of the relationship between trust and monitoring. Keren’s (2014) account goes further. It shows that reasons for trust, in opposition to reasons for mere reliance, are also essentially considerations that count against monitoring the trustee.Footnote 3 This is closely related to our proposal of measuring trust as a quantity that is inversely related to monitoring, which provides a basis for our graded account of trust.Footnote 4
The idea of an essential or constitutive relation between trust and monitoring attitudes is also indirectly supported by the claims of many scholars who have mentioned monitoring in an attempt to characterize trust, without placing it at the center of their account. One may find the claim that trusting occurs “before one can monitor the actions of … others” (Dasgupta, 1988, p. 51) or “when out of respect for others one refuses to monitor them” (McLeod, 2020). Mayer et al. (1995) define trust as “the willingness of a party to be vulnerable to the actions of another party based on the expectation that the other party will perform a particular action important to the trustor, irrespective of the ability to monitor or control that other party” (712). In the context of trusting decisions, monitoring is defined as the activity “aimed at ascertaining whether another action has been successfully executed” (Castelfranchi & Falcone, 2010, p. 193). According to Castelfranchi and Falcone’s definition, monitoring is subsequent to the decision to trust; it can anticipate an update of the trusting relationship, allowing for interventions or activities aimed at adjusting a process by “dealing with the possible deviations and unforeseen events” (Castelfranchi & Falcone, 2010, p. 193). In the context of trust in AI, trust has been defined as the absence of monitoring (Ferrario et al., 2020), and e-trust—namely trust between artificial agents (AA)—has been inversely related to monitoring in Taddeo’s (2010) influential model.
Some authors have proposed formalizations of trust. Among these, some include monitoring as a constitutive element of trust, some represent trust as a scalar quantity, and some do both. We summarize these contributions in Table 1 and briefly comment on the work produced by Taddeo (2010), which is the most similar approach to ours.
In Table 1, column “Risk-based?” specifies whether trustors are modeled as believing that the relation will be successful to a given degree (e.g., by considering the reputation, track records, etc. of the trustee). The column “Monitoring?” specifies whether, in the proposed formalization, trustors (plan to) control/evaluate the trustees’ actions throughout the reliance relation, that is, whether there is an investment of resources in controlling and supervising the trustee (as opposed to past evidence of success in similar endeavors). In “Graded?” we indicate whether trust or trustworthiness is a matter of degree in the proposed account, rather than a binary condition (yes/no). Finally, column “Object” specifies whether the formalization provides a measure of trust, trustworthiness, or both.
Taddeo’s (2010) model of e-trust is a forerunner of our approach, as it establishes an inverse relationship between e-trust and monitoring. The e-trust model developed by Taddeo descends from a general principle of the inverse relationship between e-trust and resources. Although Taddeo’s model is the closest to our approach, there are several relevant differences to highlight. First, Taddeo’s theory does not explain how the dimensionality of trust (being a pure number) comes about from such different measures as the measure of monitoring and the measure of belief. Second, Taddeo measures trust as the belief that a trustee will achieve a goal with a probability p that is deemed sufficient for trustworthiness. By contrast, in our account, we consider not only the probability of success but also the utility produced for the trustor without introducing any ad hoc threshold of p. Moreover, we formalize the relationship between the probability of success, the utility produced by the reliance relation, and the levels of monitoring.
Finally, we note that in economics, experimental game theory provides a quantitative account of trust, which is not coherent as a measure of anti-monitoring. Experimental game theory postulates a context requiring trust for cooperation, such as the investment game (Berg et al., 1995) and the public goods game. The intensity of trust is identified with the amount of resources a trustor is willing to put at risk in her interaction with a counterpart (Berg et al., 1995), whose behavior cannot be controlled by the trustor. This is incompatible with treating monitoring as a variable whose quantity is relevant for the measure of trust, as proposed by our formalization.
3 Reliance, monitoring, and stakes
In a few words, we propose to consider any degree of trust as a degree of reliance with a positive expectation and a given degree of monitoring. We defend a doxastic account of (measurable) trust if doxastic involves a belief state. This is because the measure of trust includes a graded belief in the probability p of the trustee’s success. Yet, trust is not reducible to any specific belief state or set of belief states because it can include a non-belief mental state, namely, an intention, desire, or other pro-attitude (our account is neutral relative to this) to avoid monitoring or supervision to some degree. However, it is not doxastic given the stronger definition of doxastic as requiring as a necessary condition a belief in the trustworthiness of the trustee.Footnote 5
We therefore propose to measure the intensity of trust as a function of both the trustor’s expectation and the intended degree of monitoring.Footnote 6 Thus, our account is based on the following primary notions: (a) reliance, (b) monitoring, and (c) a staking expectation. For the sake of brevity, we will refer to the staking expectation as “stakes” hereafter. We provide a formalization of the building blocks of our account of trust in Appendix A1.
3.1 Reliance
In the philosophical literature, reliance is commonly seen as distinct from trust (Baier, 1986; Holton, 1994), yet trust involves some (special) kind of reliance. In this work, we propose the following definition:
- Reliance::
-
Let X and Y be two agents, and g be a goal of X. The relation R(X, Y, g) is called reliance, if
- R1::
-
the relation is motivated by a shared goal g for X and Y;
- R2::
-
X believes the probability p of achieving g to depend also on Y’s properties and that p >0;
- R3::
-
it is goal-relative and bounded in time.
In what follows, we will use the notation (X, Y, g) to represent any reliance relation wherein X relies on Y to achieve the goal g.
With R1, we assume that X relies on Y to achieve the goal g. The goal g is both X’s goal and Y’s goal. We ascribe a potential gain or loss (utility) to X while abstracting from any utility produced for Y. Thus, given an ordered pair of agents with a shared goal (X, Y, g), what characterizes the first agent (X) as the trustor and the second agent (Y) as the trustee is simply the fact that in describing X and Y’s pursuit of a shared goal, we focus on X’s utility and beliefs while ignoring Y’s.
With R2, one assumes that some properties attributed to Y by X are believed by X to contribute to success in the shared endeavor. More precisely, these dispositions are believed by X to make it probable to a degree p that Y will achieve g. Examples of properties believed to influence p are competence, honesty, reliability, meticulousness, conscientiousness, and goodwill. These properties can be moral (Y’s commitment to moral norms), prudential (Y’s ability to correctly identify her own interest and value long-term reputational effects following from her performance in achieving g), epistemic (Y’s knowledge of the domain related to g), or technical (Y’s ability to know how to achieve g). The parameter p expresses X’s best guess (informed or uninformed) about the probability that g will be achieved considering such factors. Reliance is only possible when an agent X believes that Y’s properties make g’s achievement at least possible, that is, when p > 0 (if not highly probable). If X believes Y’s properties make g unachievable, X cannot rely on Y for g.
R3 defines reliance as a discrete interaction between X and Y for the specific goal g. Thus, in our parlance, reliance does not refer to a long-term relationship between two agents achieving different goals. Such complex relationships between two agents may consist of a chain of different reliance relations.Footnote 7 A discrete reliance interaction is, in our account, the entity to which a degree of trust can be attributed. This discrete interaction ends when either the goal g is accomplished or its delegation by X to Y is prematurely interrupted.
Some philosophers have discussed cases that may be inappropriately labeled as divergent reliance, in which X achieves a goal f by means of Y, and where f is not one of Y’s goals. A popular example in philosophical discussions is that of Kant’s neighbors, who relied on Kant’s regular habits to set their clocks (Baier, 1986). This is not an instance of reliance as we define it, as the goal is not convergent: Kant does not intend to contribute to clock-setting. Another interesting case is that of a sadistic manager assigning a task to an employee in full confidence that the employee cannot successfully perform the task. In this case, the goal f of X is Y’s humiliation. X’s assigning a task to Y, apparently to achieve g, is only superficially a case of reliance. In fact, if X is certain that Y is unable to achieve g, X only pretends to make herself reliant on Y to achieve g. In reality, X has already (but not openly) given up g for the sake of achieving f. The relation in this example may inappropriately be labeled reliance, but we believe that the term “reliance” in a trust context should only be used for the convergent variety. X’s so-called “divergent” reliance on Y is never what we mean by “reliance” in what follows, although we sometimes include the pleonastic adjective “convergent” to remind the reader of our conceptualization.
3.2 (Planned) monitoring
We introduce our definition of monitoring and supervision (hereafter, monitoring), inspired by the works of Castelfranchi and Falcone (2010) on the cognitive aspects of trust.
Monitoring: Let (X, Y, g) be a reliance relation. The monitoring exercised by X on Y is a set \(M_{{\left( {X, Y, g} \right)}}\) of the behaviors of X:
aimed at ascertaining whether … [Y’s] action has been successfully executed or if a given state of the world has been realized or maintained (monitoring, feedback);
[and]
aimed at dealing with the possible deviations and unforeseen events in order to positively cope with them and adjusting the process (intervention). (Castelfranchi & Falcone, 2010, 193)
Monitoring includes actions that are widely believed to be antithetical to trust. It does not only include passive observation but also active interference in the form of control. To simplify its measurement, monitoring in our account includes only those behaviors that are an investment, denoted by m, for X. For example, X may decide to spend 3 h of her weekly time supervising a Ph.D. student. These hours have a monetary value in terms of X’s annual wage.
One interesting question is whether sanctions count as monitoring activities according to our definition. Given our definition, sanctions must be included, but only when (a) they are behaviors of X, (b) they follow from ascertaining that the preconditions of the sanctions are satisfied, and (c) they are costly for X. Sanctions of public opinion and other effects of reputational losses (Pettit, 1995) count as monitoring only if X actively contributes to them to control Y in a way that produces costs for X (e.g., if X produces public feedback about Y).Footnote 8
Monitoring can affect both Y’s disposition to achieve g (particularly when monitoring involves feedback and corrections) and X’s confidence p that g will be realized. These factors can vary dynamically when Y acts to achieve g while being monitored by X. For the sake of simplicity, we abstract from updates of p resulting from X’s monitoring of Y during the reliance relation. Actual updates of p due to monitoring during the interaction are not considered in the model, but the beneficial effects of future monitoring on augmenting the value of p are considered ex ante and will be discussed in Sect. 3.4.
We consider only the investment m that is planned at the beginning of each reliance relation. Therefore, in our account, monitoring is an activity, the amount and cost of which is planned at the beginning of the reliance interaction (and not altered during it). The act of monitoring for g, as we define it, begins only after X has formed the intention to rely on a specific person. For example, merely scrutinizing the reputation of possible candidates before choosing one to rely on is not part of monitoring. Planned monitoring is a set of actions intended before the act of monitoring. This plan is associated with a cost that is estimated in a given (monetary) unit. While we speak about “monitoring” simpliciter, from now on we always mean planned monitoring investment, which is measured in a given (monetary) unit.
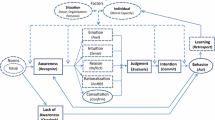
Y’s reputation acquired by virtue of accomplishing a past goal f can contribute to X’s estimate of p in relation to Y’s achievement of X and Y’s current shared goal g. Even if checking Y’s reputation has a cost for X, this is not included in X’s (planned) monitoring (costs) of Y relative to g. Similarly, when, during monitoring, X updates p and consequently takes further precautions to prevent future losses, this will not affect the variable m, which refers to X’s initially planned monitoring costs. When evaluating X’s degree of trust in Y for f, only X’s (planned) monitoring (costs) for f are allowed to determine this quantity. In Fig. 1, we provide an example of a sequence of three reliance interactions between a trustor X and a trustee Y. Each reliance relation is characterized by a given goal, a time duration, a level of trust, and a degree of monitoring. In Fig. 1, we show the case of a series of reliance relations resulting in an incremental gain of X’s trust in Y.
A sequence of three reliance relations with goals f, g, and h over the course of a longer relationship between X and Y. Each relation is characterized by a level of trust that is constant throughout the relation and inversely proportional to the amount of planned monitoring (represented by the circles at the beginning of each relation). The amount of trust in a given relation may affect the amount of monitoring exercised in the next relation (as shown by the diagonal arrows). Long-term relationships between trustors and trustees must be broken down as a sequence of discrete steps with different local and short-term goals to be analyzed with our framework
3.3 Stakes
We define the stakes of a reliance interaction between X and Y as X’s expectation of the benefits and harms resulting from Y’s reliability with respect to g. Like monitoring costs, stakes are quantified at the beginning of the reliance relation. Formally:
Stakes: Let (X, Y, g) be a reliance relation. The stakes S of (X, Y, g) are
where G is an estimate of the likely gain for X resulting from the successful pursuit of g by Y; L denotes the estimate of the likely loss deriving from Y’s failure; p is described as the chance of receiving gain by relying on Y (Coleman, 2000).Footnote 9
In the above definition, g’s (non-)achievement is the state of affairs upon which the gains G and losses L are contingent. Thus, the products \(pG\) and \(\left( {1 - p} \right)L\) denote the expected gains and losses, respectively, from achieving or not achieving the goal g. The gains and losses due to the process of pursuing g, independent of its achievement, are excluded: G and L only refer to gains and losses caused by the change in one real-world variable, g’s accomplishment.Footnote 10
In reality, X’s decision to rely on Y for g may be affected by various advantages and disadvantages of the process of relying on Y for g, which are independent of g’s accomplishment. For example, if X were coerced into relying on Y for g, X would face a disutility of some type by choosing not to depend on Y. This punishment obtains irrespective of Y’s ability to achieve g. Hence, the positive result of relying on Y (i.e., avoiding punishment) is not included in G.
We emphasize that the quantities \(\it {\text{G}}\), \(\it {\text{L}}\), and \(\it {\text{p}}\) are all X’s subjective estimates. Therefore, the stakes are also entirely subjective.Footnote 11
3.4 Monitoring, probability, and stakes
The definition of stakes in Sect. 3.3 does not include monitoring. It conveys the intuitive idea that the (subjectively) expected benefits and harms from trusting depend on both the magnitude of the possible gains and losses and the risk of not achieving the goal. Of these elements, the possibility of the gains and losses are independent of monitoring, but their probability is not. Indeed, our model must incorporate the assumption that planned monitoring influences the trustor’s confidence in the possibility of achieving the goal.
In our model, the effects of planned monitoring on the initial value of p are the reflection of the predicted effect of monitoring on the success of the interaction in the trustor’s mind before the actual interaction begins. In other words, an intention to monitor can typically affect the levels of the trustor’s confidence (probability p) that the trustee will achieve the goal g. Thus, the expected impact of future actions of monitoring on p concurs, together with its expected cost, to decide the investment in monitoring resources. Let us clarify this with an example. Suppose that the trustor plans a weekly meeting with the trustee (planned monitoring) and starts to rely on that trustee to achieve the goal g. The value of p in the trustor’s mind at the beginning of the reliance relation considers the effects of the planned (weekly) meetings on the possibility of achieving the shared goal of the reliance interaction, g. Typically, a rational trustor who invests resources in monitoring expects p to be larger than p would have been in the absence of monitoring.Footnote 12
Since planned monitoring affects the trustor’s confidence p, it is possible to express the projected contribution of monitoring costs on the probability of success as a function of monitoring. Formally, we parametrize the subjective probability level p of a reliance relation (X, Y, g) by means of a function p (bold p, while simply italicized p stands for a numerical confidence level, i.e., a probability value). We call this the “perceived reliability function.” Therefore, given a reliance relation (X, Y, g) with the level of subjective probability p > 0 and monitoring level m, we write
where p is a function that depends on the reliance relation under consideration. Thus, p is defined mathematically as a function of monitoring, given a parameter c that encodes the context in which the investment m in monitoring is performed. The gain G and the loss L is part of the context c in which the reliance relation takes place.
The function p intuitively expresses a trustor’s confidence in the possible performance of the trustee under different monitoring modalities. It expresses an important property of the trustee in relation to the trustor and the specific goal. In the remainder of the paper, we will write p(m) instead of p(m|c) to simplify the notation when c is clear from the context.
For clarity’s sake, in what follows, we will use “confidence” (and not “reliability”) to indicate the value of p at which we land after a choice of m through p. So, if X chooses to monitor Y more intensely, and obtains a higher value of p as a result, this counts as an increase in confidence, not in perceived reliability. We will use “(perceived) reliability” to indicate the function p. For example, if X increases her confidence without changing her monitoring plan, this results from a change in perceived reliability (given c).
It may seem highly unusual to feature a function as one of the basic conceptual elements of trust. Therefore, it is important to provide a philosophical interpretation of this mathematical concept. The relevant contrast, here, is between p, understood as confidence by a trustor who has already adopted a concrete monitoring plan, and the function p, which expresses the range of all possible confidence levels in the trustee as planned monitoring hypothetically changes. It seems intuitive to us that the range of all possible confidence levels considered as a whole, i.e., p(m|c), with m denoting all possible monitoring levels, provides a comprehensive outlook of Y’s reliability from X’s point of view. We distinguish between reliability and trustworthiness in Sect. 4.
Let us now discuss the parameter c. Consider X, a professor, who invests 30 h of her time into supervising her Ph.D. students, for an estimated monitoring investment of m = $30,000 for a single dissertation. However, X’s confidence of success p does not only depend on the nominal value of the investment in monitoring and reliability. In fact, the same investment in monitoring may correspond to different confidence levels that do not derive from reliability but from contextual factors; for example, the nature of the goal and the market cost of the socially necessary resources (work and equipment) for monitoring the execution of that goal, as well as cultural elements. All these elements—conceptually distinct from reliability—are grouped together as the context c.
As an example of contextual goal dependence, $30,000 worth of monitoring by a professor may correspond to a 60% chance of a successful dissertation, but only a 5% chance of the student publishing an article in a top journal before graduating. Notice that if the goal of a reliance relation changes, the possible gains G and losses L for the trustor X also normally change.
As an example of labor-cost contextual dependence, $30,000 worth of monitoring by a professor may purchase more hours of supervision in a country where professor salaries are lower, leading to a higher value of p for the same amount of investment. As an example of equipment-cost dependence, an investment of $1000 in digital surveillance technology (cameras, image recognition software, etc.) may purchase a higher degree of effective control and higher values of p after technological innovation lowers the cost of said technology. Finally, as an example of cultural dependence, an investment of $1000 in monitoring may have a higher return in a society in which education prepares workers to respond fruitfully to control and feedback and a lower return in a society in which workers resent control and supervision and try to undermine it.
We are not providing an empirical methodology for assessing c; rather, we recommend that empirical comparisons of the intensity of trust are only treated as meaningful when they apply to contexts characterized by the same c. Given these considerations, we then arrive at the final definition of the stakes of a reliance relation in our anti-monitoring account of trust:
Stakes (final): Let (X, Y, g) be a reliance relation and \(m\ge 0\) denote a level of monitoring. The stakes \(S_{{\varvec{p}}} (m)\) of (X, Y, g) are
where G is an estimate of the likely gain for X resulting from the successful pursuit of a goal g by Y; L denotes the estimate of the likely loss deriving from Y’s failure; the reliability function p describes the trustor’s confidence in receiving gain [and losses], for all levels of monitoring m. By definition, the stakes are a function of monitoring via the reliability function \({\varvec{p}}\). However, as the monitoring level m of a reliance relation (X, Y, g) is estimated before the relation starts, during the relation, the stakes are constant and equal to \(S_{{\varvec{p}}} (m)\), and the (fixed) subjective probability level satisfies \(\it \text{p} > {0}\) by property R2 of reliance relations (see Sect. 3.1). We assume that the estimated G and L are part of the context c in which the investment in monitoring m is decided.
3.5 Definition of trust
Above, we have introduced the building blocks—reliance, monitoring, and stakes—of our theory. Here, we combine these elements into a definition of trust. Our account characterizes trust as a quantitative property of certain reliance relations. Thus, trust and reliance are realized by the same real-world relations.Footnote 13 As we shall argue, all reliance relations with positive stakes have a degree of trust, which can vary in its quantity depending on the level of monitoring relative to the stakes. More precisely:
Trust: Let (X, Y, g) be a reliance relation with positive stakes,Footnote 14 i.e., \(S_{{\varvec{p}}} (m)\)>0, for a given level of monitoring \(m\ge 0\), where \(S_{\varvec{p}} (m)\) is as in Eq. (2). Given a fixed context c, wherein G and L are kept fixed, trust is a property of (X, Y, g) that satisfies the following axioms:
M1: keeping p fixed, the more X monitors Y, the less X trusts Y
M2: keeping m fixed, the greater the stakes when X relies on Y, the more X trusts Y
The M1–2 axioms are intuitively plausible assertions on the characteristics of trust and its trend when the monitoring or stakes vary. Axiom M1 is the building block of our model of trust as anti-monitoring. It is equivalent to state that had X planned a level of monitoring m’ for the same reliance relation (X, Y, g), such that \(m^{\prime} > m\) and \(S_{\varvec{p}} \left( {m^{\prime}} \right)> 0\), then the level of trust of the relation would have been lower, keeping the function p fixed.
Axiom M2 expresses the intuition that the higher the stakes \(S_{\varvec{p}} (m)\), the more one trusts, other things equal. The “other things equal” clause in axiom M2 is equivalent to keeping m fixed and letting p vary.
Let us clarify what it means for the reliability function p to vary. It is important to clearly distinguish this from the idea that one can keep p, the trustor’s confidence, fixed as m varies. We remind the reader that we are saying that p varies, not p. Remember that a change in confidence p that is due only to an increase in monitoring reduces trust.
By contrast, a change in confidence p without any change in m (context c fixed) can only be the result of a change in the trustor’s perceived reliability p of the trustee for that level of monitoring.Footnote 15 Thus, a change of confidence of this type should intuitively correspond to increased trust.Footnote 16 In line with this intuition, axiom M2 implies that had X estimated a level of subjective probability \(\user2{p^{\prime}}\left( m \right)\) such that \(S_{{\user2{p^{\prime}}}} (m) > S_{{\varvec{p}}} (m)\) for the actually planned monitoring level m, keeping G and L as elements of the context fixed, then the level of trust in Y would have been higher.
We assume that all reliance relations that exemplify trust have positive stakes. Therefore, trust always involves a (subjective) positive expectation, including when it is low. Clearly, a positive expectation is only an expected value, and it does not guarantee that the goal will be achieved.
4 The relations between trust, monitoring, and reliance
4.1 Main idea of the measurement framework
Let us explain the conceptual framework with an example. Claire, the CEO of a company, wants to know the minimum amount of monitoring she needs to trust her employees to carry out an innovation project that, if completed, would increase the profit of the company by 6% per year. The completion of the project, the length of which is estimated to be a few months, is the goal g of this case. Following our model, Claire should identify the stakes of the relation. Let us say that the 6% increase is G = $150,000 and the potential monetary loss is L = $100,000. Claire must now assess her p, namely the subjective probability that her team is reliable and will achieve g at a given level of monitoring m (see Sect. 3.2). Claire thinks that by investing m = $65,000 into monitoring the employees (the equivalent of a few working days), she will reach g with a probability p(65,000) = 0.86. Therefore, using Eq. (2), the stakes are \(S_{{\varvec{p}}} (\text{65,000})\) = $115,000. We assume that Claire assesses the probability of success before she assigns tasks to her employees and become dependent on them for its success, that is, before the innovation project starts, and we ignore any subsequent monitoring decision and its cost, as well as any subsequent update of p(m) (see Sect. 3.2).
Intuitively, we postulate that the relation between trust, monitoring, and stakes is as follows. Had the planned monitoring costs m been higher, all other things equal, Claire would have trusted the employees less than she in fact did. Had the stakes \(S_{{\varvec{p}}} \left( \text{65,000} \right)\) been higher, all other things equal, she would have trusted the employee more than she in fact did.Footnote 17
4.2 Trustworthiness in the account of trust as anti-monitoring
Trustworthiness, namely the quality of being able to be trusted, is a fundamental element of any account of trust. Accordingly, we will now present how trustworthiness is conceived in our account of trust as anti-monitoring. Roughly stated, trustworthiness is the trustee’s (higher-order) feature of having characteristics counting in favor of both relying on the trustee and economizing on monitoring the trustee. A characterization of trustworthiness in terms of reasons (not) to monitor the trustee is coherent with our approach, though it is still a simplification.
First, not all considerations that provide a trustor with a reason to reduce monitoring of the trustee contribute to trustworthiness. If X relies on Y, and X receives a threat that coerces X to avoid the monitoring of Y, this only counts as a reason for X by virtue of that further goal f (avoiding the threat), which is not the (shared) goal g of the reliance relation between X and Y. The threat provides X with a reason to avoid monitoring, but it does not follow that X believes Y to be more trustworthy as a result. More generally, when X’s monitoring choice is unrelated to Y’s properties that contribute to accomplishing g, and it is explained by X’s non-shared goal f (e.g., avoiding punishment), X’s monitoring choices and Y’s trustworthiness are unrelated.Footnote 18
Second, not all considerations that contribute to trustworthiness provide a reason to reduce monitoring. For example, Keren (2014) argues that some reasons not to monitor, including reasons provided by Y’s competence, creativity, intelligence, and conscientiousness, characterize relations of trust.Footnote 19 We point out, however, that trustworthiness is not always that which provides a reason to lower monitoring. Consider a scenario in which Y is so little trustworthy that investing resources in controlling Y’s action is extremely inefficient; for instance, if Y’s understanding of feedback is not accurate enough or Y is liable to forget or ignore corrections and advice. Supervision thus has almost no effect on Y. Still, X can rely on Y (with positive stakes) to accomplish simple tasks in the (non-optimal) way Y is used to accomplishing them. One can imagine this as a scenario in which X avoids monitoring Y not because Y is trustworthy but because Y is not. If Y were to become more trustworthy, for example, highly conscientious and highly accurate in her response to feedback, one would expect monitoring to be cost-efficient. Thus, if Y were more trustworthy, this X would have a reason to monitor Y more closely, a reason that X lacks when Y is less trustworthy. This shows that the relation between trustworthiness properties and reasons for monitoring is not simple and linear. If one wants to define trustworthiness in terms of reasons for monitoring, one should provide a more fine-grained characterization of the type of reasons in question. These reasons are not simple reasons that make it rational, in an economic sense, to avoid monitoring. Rather, they are reasons that support the avoidance of monitoring as a fitting attitude in relation to Y’s properties such as conscientiousness, silencing rather than outweighing reasons for monitoring. Providing a reductionist explanation of trustworthiness in terms of reasons to avoid monitoring is, however, not a goal we pursue in this paper.Footnote 20
Moreover, it is possible and legitimate to provide an account of trust as a graded concept in terms of monitoring, even when monitoring decisions are partly causally independent from beliefs in Y’s trustworthiness understood as reason-giving terms. We want to allow for the conceptual possibility that relations of high trust may emerge even when the trustee is not believed to be highly trustworthy. Trust may emerge, at least sometimes, because the circumstances justify a low-monitoring interaction if the stakes are positive and higher than they would be with a high-monitoring interaction or if a high-monitoring interaction is not feasible or conceivable under the given circumstances.Footnote 21
It may be objected that, while we try to disengage from modeling trustworthiness in our framework, we contradict ourselves by implicitly providing an interpretation of trustworthiness through the p function. In reply, p does not provide our interpretation of trustworthiness, nor does it provide our interpretation of trustworthiness-as-perceived-by-X. The function p includes all confidence levels, including those corresponding to very high levels of monitoring and that can never provide a reason to trust, only reasons for reliance.
In line with this distinction, notice that our measure of trust is not uniquely determined by the function expressing Y’s reliability as seen by X, but also by X’s actual choices to monitor Y in a given context.
5 The mathematical measure of trust
With the axiomatization of reliance and the description of its relationship with trust, we now describe the modeling of trust as anti-monitoring.
Let us consider axioms M1–2 satisfied by trust, according to the definition of Sect. 3.5. In Appendix A2, we prove that clauses M1–2 are satisfied by a family of functions of the level of monitoring m. We call them “level of trust” or “intensity of trust” functions. These functions provide a mathematical formulation of our theory of “trust as anti-monitoring.” They result from a single mathematical Ansatz that quantifies the relationship between the decrease in levels of trust due to the increase in monitoring using the building blocks of our theory of reliance: stakes, monitoring, and levels of trust. Mathematically, the trust functions encode the intuition that a decrease in the levels of trust due to an increase in monitoring should be proportional to the level of trust before the increase and inversely proportional to the stakes before the increase. They are examples of q-exponentials (Tsallis, 1988, 2009), that is, deformations of the classical exponential functions.
The Ansatz makes use of a free parameter, denoted q. Its formalization is discussed in Appendix A1. The values of q parameterize the functional form of the Ansatz describing the reduction in (the levels of) trust due to the increase of monitoring (see Appendix A2). The parameter q controls how much of a given level of trust is lost due to an increment of monitoring m, other things equal. Here, we discuss the general formulation of the trust functions, and we refer the reader to Appendix A2 for a more detailed discussion of the Ansatz, how to derive the trust functions, and the q parameter. Our formulation makes the assumption that the trust functions of a reliance relation are defined for all levels of monitoring such that the stakes of the relation are positive.Footnote 22
The trust functions are “normalized,” that is, they are suitable for situations in which the measurement of trust levels must lead to a finite value, which we put in the interval (0,1]. They model the intuition that full trust is trust with no monitoring, and all other forms (i.e., involving monitoring to some degree) are partial forms of trust. This is expressed most naturally by using a level of trust equal to one for full trust, and fractions of that value for all other forms of partial trust. In other words, these functions model the intuition that full trust involves no monitoring, and increasing monitoring causes a decay from a totally accomplished condition, until nothing of the initial condition remains (as monitoring approaches an infinite quantity).
Let us consider any given reliance relation (X, Y, g) with stakes \(S_{{\varvec{p}}} (m)\), for a level of monitoring \(m\ge 0\), where \(S_{{\varvec{p}}} (m)\) is given in Eq. (2). The level of trust of the relation is
where
Equation (3) states that the level of trust of the given reliance relation is modeled as a q-exponential function (Tsallis, 1988, 2009) that comprises the integral function \(I_{{\varvec{p}}} (m)\) given in Eq. (4).Footnote 23 Geometrically, the integral \(I_{{\varvec{p}}} (m)\) is the area under the function \(\frac{1}{{S_{{\varvec{p}}} \left( {\hat{m}} \right)}}\), where \(\widehat{m}\in [0,m]\), as shown in Fig. 2. The integral appears in Eq. (4) as the behavior of the stakes is described in full generality prior to choosing a reliability function p. This is the result of capturing how trust changes when the reliability function p changes, as per axiom M2. This integral is defined in terms of the only reference points of our model: the minimum level of monitoring, m = 0, and the chosen level of monitoring, m (for which there is no maximum).
The geometrical meaning of the integrals in Eq. (4). We chose the reliability functions pε given in Eq. (5). For any m, the integral \(I_{ {{\varvec{p}}_{\varepsilon} }} \left( m \right)\) is the area of the under the function \(\frac{1}{{S}_{{{\varvec{p}}}_{\varepsilon }}(m)}\) (dashed line), considering the interval [0,m]
The intuitive meaning of the integral can be explained as follows: a person’s level of trust does not reflect only the perceived reliability of Y for the planned level of monitoring m, but X’s view about Y’s reliability in all scenarios wherein X could have invested lower levels of monitoring. This follows from the mathematical resolution of the Ansatz and the reference points of our model.
As a result, by definition, the level of trust \({t}_{q}(m|G,L,{\varvec{p}})\) corresponding to the amount of monitoring m is computed by integrating over all contributions \(\frac{1}{{S}_{{\varvec{p}}}(\widehat{m})}\), where \(\widehat{m}\in [0,m]\), via the integral \({I}_{{\varvec{p}}}\)(m).
From the Ansatz (see Appendix A2), it follows that the parameter q controls the rate of the decrease in trust levels—as computed in Eq. (3)—resulting from the increase in monitoring, given that p and the context c are fixed. In fact, other things equal, the higher the value of q, the higher the level of trust, as shown in Figs. 4, 5, and 6. We note that choosing q = 2, the trust functions have the simplified expression:
\({t}_{1}(m|G,L,{{\varvec{p}}}_{\varepsilon }\)) and \({t}_{2}(m|G,L,{{\varvec{p}}}_{\varepsilon }\)), for G = 10, L = ε = 1 (in an arbitrary unit of measurement). The vertical line corresponds to the level of monitoring \(m=G-\varepsilon\). The level of trust increases when the value of q increases, other things equal
Trust functions using \({{\varvec{p}}}_{\varepsilon }\). Left panel: increasing q increases the level of trust, other things equal (G = 10, ε = 1). Right panel: increasing \(\varepsilon\) increases the level of trust, other things equal, with G = 10, \(\it {\text{q}}\) = 2 (in an arbitrary unit of measurement). For \(\varepsilon =G=10\), the trust function becomes \({t}_{2}(m|G,L,{{\varvec{p}}}_{G}\)) = \(\frac{1}{1+\frac{m}{G}}\) (dotted line). In both panels, the vertical line corresponds to the level of monitoring, \(m=G-\varepsilon =9\)
Finally, the exponential functions are retrieved in the limit case \(q\to 1\): \({t}_{1}(m|G,L,{\varvec{p}})={e}^{-{I}_{{\varvec{p}}}(m)}\). The fact that the function \(t_{q} \left( {m|G,L,p} \right)\) satisfies axiom M1 results directly from the Ansatz. Using the formula in Eq. (3), it can be proven that it satisfies axiom M2 as well.
Trust functions using \({{\varvec{p}}}_{\text{r,s}}\). Left panel: increasing q increases the level of trust, other things equal, with G = 10, L = 1, \(r=0.1\), \(s=0.1\) (in arbitrary units of measurement). Right panel: increasing the product \(\it {\text{rs}}\) increases the level of trust, other things equal (G = 10, L = 1, q = 2, in an arbitrary unit of measurement)
5.1 Explicit formulae of the trust functions
As shown in Eq. (3), each level of trust \({t}_{q}(m|G,L,{\varvec{p}})\) is defined in terms of an integral \(I_{{\varvec{p}}} \left( m \right)\), where \(m\ge 0.\) This follows from solving the Ansatz in Appendix A2.
To derive explicit formulae for the trust functions, we need to (1) choose the reliability functions p, (2) specify the context c, (3) solve the corresponding integrals \(I_{{\varvec{p}}} \left( m \right)\) analytically, and (4) insert the explicit formula of \(I_{{\varvec{p}}} \left( m \right)\) in Eq. (4). Steps 1 and 2 together identify the perceived reliability of Y from X’s point of view. Steps 3 and 4 deliver a measure of trust as a function of m, G, and L, which must be interpreted in line with the given assumptions on reliability from steps 1 and 2.
We begin by introducing the reliability functions in our account. For the sake of simplicity, we focus on two function types. Both function types encode the intuition that X’s subjective probability of achieving g should increase by investing in more monitoring (given a context c that we assume is specified by G, L, as we will see later in this section). On the one hand, the first type of function describes situations where X can obtain certainty of achieving g by exercising enough monitoring. On the other hand, the second type of function describes all situations where an arbitrarily large increase in monitoring allows X to obtain certainty of achieving g only asymptotically (see Fig. 3 for some examples).
Formally, for any reliance relation (X, Y, g), the reliability functions are either of the form \({\varvec{p}}\left( {m|G,L} \right) = \left\{\begin{array}{ll} f\left( {m|G,L} \right) & m < m^{\prime} \\ 1 & m \ge m^{\prime} \\ \end{array} \right.\), where f is continuous and strictly monotonic increasing for all \(m<{m}^{\prime}\) with \(f\left( {\left. 0 \right|G,L} \right) > \frac{L}{{G + L}}\) and \(f\left( {m^{\prime}} \right) = 1\), or continuous and strictly monotonic increasing for all \(m\ge 0\) with \(\user2{p}\left( {\left. 0 \right|G,L} \right) > \frac{L}{{G + L}}\). Doing so, we choose to specify the reliance relation’s context c in terms of the estimated G and L of the goal g, for these are the only aspects of the goal that we attempt to quantify in our framework. In other words, the model treats changes in G and L as a partial specification of the context c, which includes other features that we do not attempt to measure. This is a simplification, but it is required to arrive at a concrete mathematical measure of trust. We also note that, mathematically, c must be captured by parameters measured in terms of money, since p is a pure number and m is a quantity of money. G and L fill this requirement as well.
Before we can compute explicit formulae for the trust functions, we must choose functions p and encode perceived reliability. We do so by considering two families of reliability functions, which are examples of the two function types mentioned above. Here, we present the first family; the second is discussed in Appendix A3 for the sake of readability.Footnote 24
5.1.1 Piecewise linear reliability functions
Let us consider the reliability functions
These functions are examples of piecewise linear functions (see Fig. 3). The free parameter ε is a measure of the perceived reliability of the trustee: the higher the value of ε, the less monitoring is needed to achieve certainty that the trustee will achieve the goal g. In fact, this level of monitoring is equal to G − ε\(\text{.}\) Each reliance relation (X, Y, g) is characterized by a value of ε, which can be inferred experimentally by assessing X’s confidence in the absence of monitoring, i.e., \({\varvec{p}}_{\varepsilon }\)(0|G,L). In fact, using Eq. (6), the parameter \(\varepsilon\) satisfies the equality \(\varepsilon =(G+L){{\varvec{p}}}_{\varepsilon }\)(0|G,L) − L. Then, \(\varepsilon\) is uniquely determined by G, L, and \({{\varvec{p}}}_{\varepsilon }\)(0|G,L).
A quick check shows that \({S}_{{\varvec{p}}_{\varepsilon }}(m)>0\) for all \(m\ge 0\).Footnote 25 The functions \({\varvec{p}}_{\varepsilon }\) admit an interesting interpretation. In fact, we note that in general, \({S}_{{\varvec{p}}}(m)\) > m if and only if p(m) > \({{\varvec{p}}}_{0}(m)\), where \({{\varvec{p}}}_{0}=\underset{\varepsilon \to 0}{\mathit{lim}}{{\varvec{p}}}_{\varepsilon }\) and using the definition of stakes in Eq. (2). Therefore, the functions \({\varvec{p}}_{\varepsilon }\) represent a translation (controlled by ε) of the “limit” function \({\varvec{p}}_{0}\). This function allows for ascertaining whether, after choosing a confidence function p and a level of monitoring m, the expected gains \({S}_{{\varvec{p}}}(m)\) of the reliance relation exceed the planned cost of monitoring (or not).
Finally, using the definition of stakes in Eq. (2), it is possible to solve the integrals \({I}_{{{\varvec{p}}}_{\varepsilon }}(m)\) analytically (see Appendix A2). For example, we have
We plot both functions in Fig. 4 and refer the reader to Appendix A2 for more details on the trust levels \({t}_{q}(m|G,L,{{\varvec{p}}}_{\varepsilon }\)). Lastly, we note that the higher the value of \(\varepsilon\), the higher the level of trust \({t}_{q}(m|G,L,{{\varvec{p}}}_{\varepsilon }\)), other things equal. The limit case \(\varepsilon =G\) is such that \({{\varvec{p}}}_{G}(m)=1\) and \({S}_{{\boldsymbol{ }{\varvec{p}}}_{G}}(m)=G\) for all monitoring values m. Equation (7) reads \({t}_{2}(m|G,L,{{\varvec{p}}}_{G}\)) = \(\frac{1}{1+\frac{m}{G}}\). Note that trust can be less than 1, even if X is fully confident that the goal will be achieved with little supervision: this captures the case in which X (arguably irrationally) chooses to monitor Y.
In summary, the trust functions in Eq. (3) encode the intuition of trust as anti-monitoring via nonlinear transformations of the stakes. They satisfy axioms M1-2 and have values in (0,1], where 0 is a limit value corresponding to levels of monitoring approximating infinity, and the maximum at 1 is reached with no monitoring, i.e., m = 0.
Therefore, these trust functions are normalized, and their values can be interpreted as “percentages of trust” with respect to a maximum value, that is, that which is reached in absence of monitoring.
6 A methodology for measuring trust as anti-monitoring in empirical studies
The most common approach to the measurement of trust in social sciences, psychology, and sociology is the psychometric technique in the form of surveys, which investigate the subject’s expectations and intentions. These surveys appeal to trust indicators, which are, in turn, built on the most widespread definition of trust within a given research field, which is often not informed by the philosophical debate on trust.
The building blocks of our model of trust as anti-monitoring (Sect. 3) and trust relationships’ necessary property of low monitoring (Sect. 4) provide the theoretical toolbox that connects the definition of trust as anti-monitoring with the design of mathematical models of trust (Sect. 5). Our approach to trust provides the basis of a methodology for measuring the intensity of trust in interpersonal relationships through empirical techniques. The model of trust as anti-monitoring gives precise indications on how trust should be measured, based on measurable quantities of monitoring and the expected gains and losses deriving from achieving or not achieving the goal entrusted to a person who is relied upon.
Let us return to the example of Claire the CEO from Sect. 4. We seek to demonstrate how to empirically compute Claire’s level of trust in her team using the formalism introduced in Sect. 5. Appendix A4 includes all details on the approach we follow in this example for the interested reader. As introduced in Sect. 4, Claire thinks that the project gain is G = $150,000, and the potential monetary loss is L = $100,000. To estimate the level of Claire’s trust in her team, we can proceed as follows. First, during a meeting, Claire may answer a question to ascertain whether she believes that the project goal could be achieved with a success rate comparable to certainty by investing enough resources in monitoring her team. This would be the case, for example, for a low-risk project similar to others that have been successfully finalized in the past and with a CEO like Claire who is very confident in her team and the monitoring structure in place. In the case of a positive answer, it seems appropriate to model her subjective reliability function considering the family of piecewise linear functions \({{\varvec{p}}}_{\varepsilon }\) (see Fig. 3). Then, to estimate the parameter ε,Footnote 26 Claire may be asked about her confidence in successfully achieving her goal in the absence of monitoring, as discussed in Sect. 5. Let us suppose that her confidence in the absence of monitoring is equal to 60%. Then, we get ε = $50,000. As a result, considering a planned level of monitoring equal to m = $65,000 and using Eq. (6), we can calculate that Claire’s confidence is equal to 86% (at m = $65,000).
Finally, we must estimate the parameter q of the trust level \({t}_{q}(m|G,L,{{\varvec{p}}}_{\varepsilon }\)) function. To do so, it is sufficient to ask Claire for her estimated level of trust in her team for levels of monitoring close to m = 0.Footnote 27 In summary, if Claire plans to invest $65,000 in monitoring her team, \(\varepsilon\) =$50,000, and q = 2, then measuring trust with the function \({\text{t}}_{2}\) in Eq. (7) gives a trust level of \({t}_{2}(\text{65,000}|G,L,{{\varvec{p}}}_{\varepsilon })=0.55.\) Therefore, for a level of monitoring equal to $65,000, the level of Claire’s trust in her employees is 55% of full trust (i.e., no monitoring). Hence, despite Claire showing high confidence in achieving the project goal, her level of trust is only slightly closer to full than to no trust in virtue of the planned level of monitoring.
7 Conclusions
We have introduced the idea that trust is a property of reliance relations and is antithetical to monitoring. We have proposed a set of conditions (or axioms, in the mathematical modeling) that a measure of trust as anti-monitoring must satisfy. We have described mathematical models wherein the intensity of trust is measured as a function of expected gains, losses, and monitoring. The models satisfy the axioms encoding our essential intuitions about trust as anti-monitoring. In the Appendix, we show that these models stem from a natural Ansatz aiming at modeling the decrease in the level of trust in a reliance relation as a function of the stakes, the levels of monitoring, and trust. In the final part of the paper, we have shown how our model can be applied to a practical context by explaining how a measure of trust could be produced for a hypothetical scenario.
Data availability
Not applicable.
Code availability
Not applicable.
Notes
In this contribution, we deal with practical trust, namely trusting a trustee to reach a goal, which we will call “trust” for simplicity. Therefore, we do not tackle epistemological aspects of trust such as testimonial trust, i.e., holding a testifier’s statement p to be true.
Although Baier emphasizes the role of economizing on monitoring in trust relationships in her commentary on the work of Onora O’Neill, her approach to trust in earlier works does not treat this as an essential element of trust. Rather, she focuses on the trustor’s acceptance of some risk or vulnerability in case the trustee does not achieve the trustor’s goal (Baier, 1986). Clearly, the absence of monitoring is an aspect of vulnerability, but it is not its only cause.
This approach also helps avoid a version of the objection that risk-based definitions of trust cannot distinguish between trust and reliance; for, as Keren (2014) argues, trust involves a relation to evidence that distinguishes it from generic reliance relations. Trust involves low-monitoring relations in which some evidence relevant to trustworthiness can be (and even should be) ignored. This is because, in contrast to generic reliance relations, the trustor responds to preemptive reasons against monitoring that are typical of trust.
But not an account of trustworthiness. For reasons indicated in Sect. 4.2, the relation between trustworthiness and monitoring appears to be harder to quantify and measure than the one between trust and monitoring.
In our account, the intention to avoid monitoring the trustee need not be grounded in the belief that the trustee is trustworthy (to the corresponding degree). We argue for this position in Sect. 4.
In our view, intensity is the most salient scalar property for trust defined relative to a single agent with a single goal, but it not the only scalar properties of trust. We remain agnostic as to whether other definitions of trust justify alternative measures of its intensity. An advantage of our definition of trust is that it makes transparent why the intensity of trust should be evaluated in this way.
Although some reliance relations consist of only one interaction; for example, asking a stranger to show the way to the train station.
The simple fact that the interaction between X and Y takes place within a social context in which a reputation system exists (Pettit, 1995), where X and Y’s behaviors are both tracked and known to be tracked, and where this has an influence on X and Y’s reciprocally directed attitudes, does not count as monitoring in itself and does not detract from X’s trust in Y as such.
This can be described as X’s predictive expectation in Nickel’s (2009) definition, i.e., “a matter of regarding an event as more likely than not” (p. 347).
Notice that the concept of gain we summarize with G is not necessarily selfish. In the sense in which we use “gain,” a physician who cares intrinsically about the good of her patient will get a gain if the patient is cured, even if there is no indirect benefit in terms of keeping a good reputation, etc. Indeed, the fulfillment of X’s goal, no matter how idealistic or altruistic, will count as X’s gain as used here.
The stakes of the interaction can be described as X’s staking expectation, in the sense of Nickel (2009), i.e., X’s expectation that it is worth staking something of value (G and L) in Y’s achievement of g.
When we write that we “abstract from” updates of p, we only mean that we ignore real changes in p over time. We ignore those updates of p that occur during the interaction because of monitoring, not the overall effect of monitoring as anticipated. Clearly, a trustor’s beliefs about p, which are conditional on (the planned amount of) monitoring, can be disappointed when actual monitoring (and other events, e.g., unexpected circumstances) occur. Such disappointments may divert more (or less) resources to monitoring (e.g., the trustor may decide that weekly meetings are not enough). We abstract from this complication in our model for the sake of simplicity.
This holds only other things equal. A case in which the capacity for monitoring is very low (because of low available monitoring capacity), reliance happens (due to lack of alternatives), and there is low trust (e.g., because of a bad track record or signs of questionable intent by Y) is conceptually compatible with low trust in our account. We later clarify that this type of case is one of low trust because of X’s expectations of Y’s performance of g, which cannot be optimistic in such a case. This also contributes to determining the intensity of trust in our account.
Therefore, in the remainder of the manuscript, we assume G > 0 and \(\it {\text{L}}>\) 0.
Note that a change in the function p cannot be “pointwise” with respect to monitoring, as we will postulate the continuity and monotonicity of the perceived reliability functions in Sect. 5.1. Therefore, a change in the function p (context c fixed) impacts reliability at different (contiguous) levels of monitoring.
In fact, if \(\user2{p^{\prime}}\left( m \right) > {\varvec{p}}\left( m \right)\) for a given m and with a fixed context c, it follows that \(S_{{\user2{p^{\prime}}}} (m) > S_{{\varvec{p}}} (m)\), by Eq. (2). Section 5 provides more details about how our models incorporate X’s optimism about success conditional on merely hypothetical values of m, that is to say, values higher than the level of m of the actually implemented plan.
Considering m, G, and L all as given, the stakes could have been higher only due to a different reliability function, i.e., one mapping the planned monitoring investment onto a higher probability of success.
McMyler (2020) makes a similar distinction to that between shared-goal-related and non-shared-goal-related reasons, which is based on voluntariness. He contends that trust is non-voluntary in the same way believing is non-voluntary: just as we cannot decide what to believe at will, so the trustor cannot decide to trust somebody at will because trusting is not directly subject to the will. For McMyler, if we are induced to trust someone by what he calls “practical reasons,” which he defines as reasons of the “wrong kind” for trusting, such as threats, monetary incentives, or simply because we think that trusting will produce better consequences, we are entering a trust relationship in which we do not directly trust the trustee. McMyler’s account of the wrong kind of reasons does not match ours. We maintain that some practical reasons (e.g., some consequences of economizing on monitoring and achieving valuable goals) are reasons for trust while others (e.g., threats) are not. In our account, practical reasons reflecting Y’s probable accomplishment of g are not reasons of the wrong kind. Still, our account is compatible with McMyler’s view that practical reasons cannot influence trust if “influences on trust” are assumed to be identical to “influences on p” (the subject’s estimation of the trustee’s probability of goal achievement). Indeed, nothing in our account prevents us from committing to the view that practical reasons cannot (should not) influence the extent to which X believes Y to be likely to accomplish g. However, in our account, reasons for trust are not reducible to the evidence for p, and G and L (as well as m) also provide practical reasons for trust.
It is not our purpose here to provide an analysis of the relevant concept of a “fitting response,” and we even doubt that a non-circular account (that is, an account that characterizes the right type of reason without surreptitiously appealing to the concept of trust) may be possible. This, of course, is not an argument against Keren’s (2014) pre-emptive reasons account of trust because Keren’s goal is not to provide a reductionist account.
But notice that when the trustee is not considered trustworthy, the measure of trust will tend to be low because of the low values assigned to p by the confidence function p for the achievable levels of monitoring.
Due to our axiomatization of the reliability functions (see Sect. 5.1), the stakes of a reliance relation are positive on intervals necessarily of the form [m, + ∞), for some m ≥ 0. To simplify the notation, in what follows, we consider the case m = 0. However, our mathematical approach does not rule out the possibility of having relations where stakes are positive only on sub-intervals [m, + ∞) (m > 0) of all possible monitoring levels.
We choose to denote the variable inside the integral by \(\widehat{{m}}\), as m is an endpoint of the interval of integration. It still denotes monitoring.
In this section, we prefer to discuss the piecewise linear functions over the logistic family of reliability functions due to their simplicity. Piecewise linear reliability functions express the intuition that the subjective credence of the trustor grows linearly with an increase in the levels of planned monitoring until “saturation,” i.e., certainty, is achieved.
In particular, \({S}_{{{\varvec{p}}}_{\varepsilon }}(0)=\varepsilon >0\), therefore, the use of the parameter \(\varepsilon\) in the definition of the piecewise linear confidence functions. Note that \({S}_{{\varvec{p}}_{\varepsilon }}(m)>0\) for all \(m\ge 0\) follows from the assumption that trust values exist for reliance relations with positive stakes, as argued in Sect. 3.5.
We remind the reader that tasks perceived as being easier, i.e., requiring less monitoring for success, are characterized by higher \(\varepsilon\) (in proportion to G).
This fact descends from deriving both sides of the infinitesimal Ansatz, considering the case m = 0 and second-order differences. We refer to eq. (A2.4) and Appendix A4 for more details.
Note that \({S}_{{\varvec{p}}}(m)>0\) for all \(m\ge 0\) implies that, in particular, the stakes are positive for the level of monitoring m′, such that p(m) = \(\frac{1}{2}\). This is equivalent to stating that G > L.
More general products, such as \({{Q}_{k}({S}_{{\varvec{p}}}(m),m,t(m))= {S}_{{\varvec{p}}}(m)}^{k-1}\cdot { m}^{-k}\cdot {t}^{q}\left(m\right)\), k > 1 may also be considered. However, it can be proved that they lead to non-differentiable Ansätze. Therefore, we consider the Ansatz (A2.1), i.e., k = 0.
We choose the coefficient of the product to be equal to one for simplicity.
For example, the pair r = \(\frac{1}{2G}\text{ln}\frac{G}{L}\) and s = G satisfies the required properties.
This constraint enforces the positivity of the stakes \({S}_{{{\varvec{p}}}_{r,s}}(m)\).
More precisely, we restrict the logistic functions to \(m\ge 0\).
References
Baier, A. (1986). Trust and antitrust. Ethics, 96(2), 231–260.
Baier, A. (2013). What is trust? In D. Weinstock, N. Manson, M. Deveaux, & D. Archard (Eds.), Reading Onora O’Neill (pp. 175–184). Routledge.
Becker, L. C. (1996). Trust as noncognitive security about motives. Ethics, 107(1), 43–61.
Berg, J., Dickhaut, J., & McCabe, K. (1995). Trust, reciprocity, and social history. Games and Economic Behavior, 10(1), 122–142. https://doi.org/10.1006/game.1995.1027
Castelfranchi, C., & Falcone, R. (2010). Trust theory: A socio-cognitive and computational model. Wiley series in agent technology. Wiley.
Ceolin, D., & Primiero, G. (2019). A Granular Approach to Source Trustworthiness for Negative Trust Assessment. In W. Meng, P. Cofta, C. D. Jensen, & T. Grandison (Eds.), Trust management XIII. IFIP advances in information and communication technology (pp. 108–121). Springer.
Cohen, M. A. (2020). Trust in economy. In J. Simon (Ed.), The Routledge handbook of trust and philosophy (pp. 283–297). Routledge.
Coleman, J. S. (2000). Foundations of social theory. 3. Belknap Press of Harvard Univ Press.
Dasgupta, P. (1988). Trust as a commodity. In D. Gambetta (Ed.), Trust: Making and breaking cooperative relations (pp. 49–72). Blackwell.
Faulkner, P., & Simpson, T. (Eds.). (2017). The philosophy of trust. Oxford University Press.
Ferrario, A., Loi, M., & Viganò, E. (2020). In AI we trust incrementally: A multi-layer model of trust to analyze human–artificial intelligence interactions. Philosophy & Technology, 33(3), 523–539. https://doi.org/10.1007/s13347-019-00378-3
Goldberg, S. C. (2020). Trust and reliance. In J. Simon (Ed.), The Routledge handbook of trust and philosophy (pp. 97–108). Routledge.
Hardin, R. (1993). The street-level epistemology of trust. Politics & Society, 21(4), 505–529. https://doi.org/10.1177/0032329293021004006
Holton, R. (1994). Deciding to trust, coming to believe. Australasian Journal of Philosophy, 72(1), 63–76. https://doi.org/10.1080/00048409412345881
Jones, K. (1996). Trust as an affective attitude. Ethics, 107(1), 4–25.
Jordan, C., & Jordán, K. (1965). Calculus of finite differences. American Mathematical Society.
Keren, A. (2014). Trust and belief: A preemptive reasons account. Synthese, 191(12), 2593–2615. https://doi.org/10.1007/s11229-014-0416-3
Lahno, B. (2020). Trust and emotion. In J. Simon (Ed.), The Routledge handbook of trust and philosophy (pp. 147–159). Routledge.
Marsh, S. P. (1994). Formalising trust as a computational concept. University of Sterling.
Marsh, S., & Dibben, M. R. (2005). Trust, untrust, distrust and mistrust—An exploration of the dark(er) side. In P. Herrmann, V. Issarny, & S. Shiu (Eds.), Trust management. Lecture notes in computer science (pp. 17–33). Springer.
Mayer, R. C., Davis, J. H., & David Schoorman, F. (1995). An integrative model of organizational trust. The Academy of Management Review, 20(3), 709–734. https://doi.org/10.2307/258792
McLeod, C. (2020). Trust. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2021 Edition). Metaphysics Research Lab, Stanford University. URL = https://plato.stanford.edu/archives/fall2021/entries/trust/
McMyler, B. (2020). Trust and Authority. In J. Simon (Ed.), The Routledge Handbook of Trust and Philosophy (pp. 76–87). Routledge.
Nickel, P. J. (2007). Trust and obligation-ascription. Ethical Theory and Moral Practice, 10(3), 309–319. https://doi.org/10.1007/s10677-007-9069-3
Nickel, P. J. (2009). Trust, staking, and expectations. Journal for the Theory of Social Behaviour, 39(3), 345–362. https://doi.org/10.1111/j.1468-5914.2009.00407.x
Pettit, P. (1995). The cunning of trust. Philosophy & Public Affairs, 24(3), 202–225.
Primiero, G. (2020). A logic of negative trust. Journal of Applied Non-Classical Logics, 30(3), 193–222. https://doi.org/10.1080/11663081.2020.1789404
Primiero, G., & Taddeo, M. (2012). A modal type theory for formalizing trusted communications. Journal of Applied Logic, 10(1), 92–114.
Raz, J. (1985). Authority and justification. Philosophy & Public Affairs, 14(1), 3–29.
Taddeo, M. (2010). Modelling trust in artificial agents, a first step toward the analysis of e-trust. Minds and Machines, 20(2), 243–257. https://doi.org/10.1007/s11023-010-9201-3
Tsallis, C. (1988). Possible generalization of Boltzmann–Gibbs statistics. Journal of Statistical Physics, 52(1), 479–487. https://doi.org/10.1007/BF01016429
Tsallis, C. (2009). Introduction to nonextensive statistical mechanics: Approaching a complex world. Springer. https://doi.org/10.1007/978-0-387-85359-8
Acknowledgements
We would like to thank Synthese’s anonymous reviewers for their insightful feedback which contributed to better developing and clarifying several aspects of our theory. We would also like to thank Philip Nickel and the partecipants to the Expert Conference “Trust in Autonomous Machine”, Digital Society Initiative, University of Zurich, 26-27 Nov 2020 for comments and feedback on earlier drafts.
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement. Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Appendix A1: Formalization of our account of trust
In this appendix, we provide a formalization of our account of trust, following the formalizing approach by Marsh (1994) and Marsh and Dibben (2005). The formalization is summarized in Table
2. As a reminder, we define trust (see Sect. 3.5) as a property of a reliance relation that satisfies axioms M1 and M2.
1.2 Appendix A2: Deriving trust functions from the axioms of trust as anti-monitoring
Let (X, Y, g) denote a reliance relation with stakes \({S}_{{\varvec{p}}}(m)>0\) for \(m\ge 0\). We show that the trust functions from Sect. 5 descend from a mathematical Ansatz, which quantifies the relation between a decrease in levels of trust due to an increase in monitoring using the building blocks of our theory of reliance: stakes, monitoring, and (levels of) trust.
Let us consider non-negative differentiable functions t = t(m), where \(m\ge 0\) denotes a level of monitoring (expressed, for example, in US dollars) and \(dm>0\) represents a (small) increase in monitoring. Therefore, the quantity \(dt(m)=t(m+dm)-t(m)\) represents the change in the levels of trust corresponding to an increase of \(dm\) in monitoring for a chosen \(m\ge 0.\) In what follows, we aim to find a functional form for t(m) that is compatible with axioms M1–2 in Sect. 5.
First, due to axiom M1, we enforce \(dt\left(m\right)<0\). We want the levels of trust to decrease in the presence of an increase in monitoring. Second, we argue that the decrease \(dt(m)\) should be proportional to the increase in monitoring, i.e., \({\text{dm}}.\) We also argue that the most general Ansatz for \(dt(m)\) should make use of the building blocks of our theory of trust as anti-monitoring. Therefore, we write:
for all \(m\ge 0,\) where \(Q({S}_{{\varvec{p}}}(m),t(m))\) is a non-negative function of the stakes \({S}_{{\varvec{p}}}\left(m\right)>0\)Footnote 28 and levels of trust t(m).Footnote 29 We note that although \(dt\left( m \right)\) is a pure number, the quantity \(dm\) is expressed in the units of monitoring (e.g., US dollars), such as the stakes \(S_{\varvec{p}} \left( m \right)\); therefore, \(Q\left( {S_{\varvec{p}} (m),t(m)} \right)\) has to be in the inverse units of monitoring. There are infinite functional forms for Q, which may be considered at this stage; however, we argue that the simplest functional form for Q is the product of powersFootnote 30 in \(S_{\varvec{p}} (m)\) and t(m), i.e.,
A quick check shows that Q has the correct dimensions. Therefore, the infinitesimal version of Ansatz (A2.0) reduces to:
where we highlighted the estimates G and L of g and the reliability function p together with the parameter q in the notation of the trust level function \(t_{q} (m|G,L,\varvec{p})\). Moreover, we enforce the condition \({S}_{{\varvec{p}}}(m)>0\) for all \(m\ge 0\). Solving Eq. (A2.2) and choosing \({t}_{q}(0|G,L,{\varvec{p}})\)=1 gives:
where
Moreover, choosing \(q>1\), we ensure that the values \(t_{q} (m|G,L,\varvec{p})\) are defined for all \(m\ge 0\), and axiom M2 is satisfied. Axiom M1 follows directly from Ansatz (9), and \(t^{q} (m)\geq 0\) for all \(m\ge 0\), instead. The functions \({t}_{q}\) are examples of q-exponentials (Tsallis, 1988, 2009), i.e., deformations of the classical exponentials. Finally, the exponential functions are retrieved in the limit case i.e \(q\to 1\), \({t}_{1}(m|G,L,{\varvec{p}})={e}^{-{I}_{{\varvec{p}}}(m) }\). Lastly, we note that when deriving both sides of (9) and evaluating them at m = 0, one arrives at:
Equation (11) clarifies the role of the parameter q, showing that given G, L, p, and the stakes \(S_{p} \left( 0 \right)\), q controls the rate at which the change of trust levels increases due to an increase of monitoring at m = 0.
1.3 Appendix A3: Trust functions: explicit formulae
We can attempt to solve the integrals
analytically by specifying different families of reliability functions p where \({S}_{{\varvec{p}}}(m)>0\), for all \(m\ge 0.\) As discussed in Sect. 5.1, this is possible by choosing piecewise linear functions. This, in turn, allows for computing explicit formulae for the trust functions in Eq. (10). This is possible also with a second family of reliability functions that we introduce below.
1.3.1 Logistic reliability functions
Let us consider the following reliability functions:
where r and s are positive functions of G and LFootnote 31; r has the same unit of measurement as the inverse of monitoring; s has the same unit of measurement as monitoring; the coefficients satisfy the constraint \(rs<\text{ln}\frac{G}{{L}}\).Footnote 32\({\varvec{p}}_{\text{r,s}}\) are examples of logistic functions, a class of functions widely used in the empirical sciences, including machine learning.Footnote 33 An example is shown in Fig. 3. The coefficient r controls the rate of the functions’ increase, while the product rs specifies \({\varvec{p}}_{\text{r,s}}\)(0). In other words, rs plays an analogous role to \(\varepsilon\) in Eq. (6), encoding perceived reliability. The lower rs, the higher perceived reliability.
Finally, using the definition of stakes from Eq. (2), it is possible to solve the integrals \(I_{{\varvec{p}_{{r,s}} }} (m)\) analytically (see Appendix A2). Then, we have:
where
We plot both trust functions in Fig. 5.
In summary, considering both families of reliability functions:
Lemma 1
Let \({\varvec{p}}_{\varepsilon }\) denote piecewise linear reliability functions as in Eq. (6). Then:
Lemma 2
Let \({\varvec{p}}_{{\text{r}},{\text{s}}}\) denote logistic reliability functions as in Eq. (12). Then:
The trust functions in Eqs. (7) and (13) are then easily obtained. We show a few examples of the \({t}_{q}\) functions in Figs. 6 and 7. The proofs of the lemmata follow from the straightforward use of the definitions of the reliability functions and stakes in the integral function \({I}_{\varvec{p}}\).
1.4 Appendix A4: Computing trust levels: a step-by-step procedure for empirical studies on trust
We provide additional details on the procedure used to compute levels of trust in Sect. 6. The procedure can be used for other empirical settings as well. It consists of four steps: (1) identification of the most appropriate family of reliability functions \(p\), (2) empirical estimation of the parameter(s) of the chosen family, (3) empirical estimation of the parameter q, and (4) computation of the trust level \(t_{q} \left( {m|G,L,\mathbf{p}} \right)\), given a level of planned monitoring m. As shown in Sect. 6, in step 1, we identify the most appropriate family of reliability functions between the piecewise linear and logistic functions by investigating whether the trustor ever achieves full confidence in achieving goal g with certainty (i.e., p = 1), given a sufficient level of planned monitoring (see Fig. 3). If the answer is positive, then the family of piecewise linear functions \({{\varvec{p}}}_{\varepsilon }\) is chosen. In step 2, we note that the functional form of the functions \({{\varvec{p}}}_{\varepsilon }\) and \({{\varvec{p}}}_{r,s}\) is given. In particular, for \(m<G-\varepsilon \text{,}\) \({{\varvec{p}}}_{\varepsilon }\) is a line with constant slope. Therefore, in the case of pε, it is necessary to ask only one question to estimate the only “free” parameter (showing in its intercept), namely ε. By contrast, in the case of \({{\varvec{p}}}_{r,s}\), two questions are needed to estimate r and s. In general, all questions aim to ascertain the trustor’s subjective confidence at two arbitrary and distinct levels of monitoring. To estimate q in step 3, we consider Eq. (11), which is valid for both families \({{\varvec{p}}}_{\varepsilon }\) and \({{\varvec{p}}}_{r,s}\). As the term \(\frac{{d}^{2}{t}_{q}(0|G,L,{\varvec{p}})}{d{m}^{2}}\) is generally unknown, we must approximate it using the method of (forward) finite differences (Jordan & Jordán, 1965):
where h is an arbitrarily small increment of monitoring (for example, we may choose h = $100 in the example in Sect. 6). Eq. (14) states that \(\frac{{d}^{2}{t}_{q}(0|G,L,{\varvec{p}})}{d{m}^{2}}\) can be approximated by asking two questions aiming to ascertain the levels of trust, \({t}_{q}(2h|G,L,{\varvec{p}})\) and \({t}_{q}(h|G,L,{\varvec{p}})\), for a given (small) h. Then, using Eqs. (11) and (14), one can estimate q. In step 4, by choosing a level of monitoring m, the sought-after level of trust, \({t}_{q}(m|G,L,{\varvec{p}}\)), is computed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Loi, M., Ferrario, A. & Viganò, E. How much do you trust me? A logico-mathematical analysis of the concept of the intensity of trust. Synthese 201, 186 (2023). https://doi.org/10.1007/s11229-023-04169-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04169-4