Abstract
Why should we be means-end rational? Why care whether someone’s mental states exhibit certain formal patterns, like the ones formalized in causal decision theory? This paper establishes a dominance argument for these constraints in a finite setting. If you violate the norms of causal decision theory, then your desires will be aptness dominated. That is, there will be some alternative set of desires that you could have had, which would be more apt (closer to the actual values fixed by your sensibility/ what you intrinsically care about) no matter which world is actual. If we care about having apt desires, then, we should never let ourselves violate these norms of means-end rationality. This argument shares a form with now-standard accuracy arguments for probabilism, opening up a new terrain for that discussion. I show that the foundational assumptions about the shape of accuracy and of aptness required to run the arguments for means-end rationality and for probabilism run closely parallel. I show the argument is robust under different theories of subjective actual value, including nonclassical treatments of indeterminacy in actual value; I show the argument may (but need not!) be generalized to objective theories of value. The upshot is that aptness-domination arguments for decision theories should be added to the philosophical playbook.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Newsflash: diaphragm massages are not fun. To loosen tight muscles and break down myofascial knots, the physiotherapist really works their fingers in, causing pain. Did I want to go through this? First answer: of course not! That kind of pain makes my life worse. Second answer: of course! After all, I paid good money for it, and did so because of the benefits that it would bring for posture, for sports performance, for health.
Cases like this illustrate a divergence between two notions of desire. First, features of the world are intrinsically desirable or undesirable depending on how good they are in themselves. Massage pain is an intrinsically bad thing (at least for people with my sensibility; the masochist may take a different view). Second, features of the world are instrumentally desirable or undesirable depending on what they bring about. A massage is instrumentally desirable because the goodness of the benefits that flow from it outweigh the badness of the immediate pain. Since intrinsic and instrumental desire point in opposite directions, there’s a job to be done in sorting out their relationship.
The position of this paper is that intrinsic desires ground an evaluative standard for instrumental desire. That is: instrumental desires are correct or incorrect, given the state of the world, depending on how well they align with intrinsic desires. More carefully: instrumental desires stand to ‘actual values’ determined by what we intrinsically want to be the case just as beliefs stand to truth values. The paper’s main goal is then to show how this evaluative assumption predicts and explains patterns of structural means-end rationality that tell us which clusters of intrinsic desires, beliefs and instrumental desires make sense together.
Section 1 introduces terminology and the key evaluative concept of the comparative aptness of instrumental desire (deferring the defence of this account for later). Section 2, the heart of the paper, shows how to give an aptness-dominance argument for causal decision theory. Section 3 presents extensions of this result. Section 4 addresses the legitimacy of the account of comparative aptness that led to these results. Three appendices elaborate points made in the main text.
Unless stated otherwise, I work under the assumption there are only finitely many worlds and propositions in play.
1 Intrinsic and instrumental desire
We are going to be focusing on two notions of desire, and it will be confusing to use the same word for both notions. Established technical jargon in the area (‘utility’, ‘expected utility’) have technical meanings that I do not want to presuppose. So henceforth unless explicitly qualified, I’ll use ‘desire’ to talk about instrumental desires, and ‘sensibility’ or ‘actual value’ to talk about intrinsic desires. I start by laying out the assumptions I’m making about each of these notions.
I assume that a central functional role of Sally’s instrumental desires is to guide choice. If Sally is confronted with a choice between two options, and she has a stronger instrumental desire for the first than the second, then she is disposed to choose the first. I will assume that Sally’s instrumental desires determine a function u from propositions to real numbers. I will call this her (instrumental) desire function.
Sally, like all of us, finds some features of the world intrinsically desirable, and others intrinsically undesirable. Aggregating, each complete possible world is intrinsically desirable, for Sally, to a certain real-valued degree. I will assume, then, that Sally’s intrinsic desires determine a function M from worlds to real numbers. I will call this her sensibility function.Footnote 1
Now, the picture I’m shooting for uses sensibility to determine an evaluative standard for (instrumental) desire. But at present, M takes values only at possible worlds, not propositions more generally. I follow Bacon (2022), who introduces the notion of the actual value of an action as follows:
The actual value of an action is a measure of the good or bad outcomes that would result if you were to take that action.
I generalize this characterization of actual value from actions specifically to all propositions. Presupposing a strong counterfactual logic,Footnote 2 we may write f(p, w) for the world \(w'\) that makes true the following counterfactual at w: were it the case that p, \(w'\) would have obtained. Bacon’s proposed characterization of actual value, in present notation, is then:
\(v_p(@):=M(f(p,@))\).
Actual value is what results from projecting the goodness and badness of complete outcomes onto an assignment of goodness and badness of arbitrary propositions, via the actually true counterfactuals (all relative to the relevant subject’s sensibility).Footnote 3
Now we’re in a position to formulate an analogy between belief and truth value, and desire and actual value. Write \(t_p(w)\) for the truth value of a proposition p at world w, and c(p) for Sally’s credence in that proposition. Then the credences Sally assigns to propositions are correct (perfectly accurate) at w if and only if \(c(p)=t_p(w)\). Analogously, the degree of desire that Sally assigns to propositions will be correct (perfectly apt) at w, relative to her sensibility, if and only if \(u(p)=v_p(w)\).
It’s proven productive to quantify the comparative accuracy of credence functions at a world—intuitively, the “distance from the perfectly accurate credal state”. One influential proposal is that the comparative accuracy of a specific credence is given by the Brier score \((c(p)-t_p(w))^2\), and the accuracy of a whole credal states is determined by summing over the local accuracy of each proposition. I propose that it is likewise possible to quantify degrees of inaptness—intuitively, the “distance from the perfectly apt desire state”. Here is the account I offer, exactly analogous to that above: the degree of inaptness of u(p) at w is given by \((u(p)-v_p(w))^2\), and the inaptness of a whole desire function is determined from this by summing the results.Footnote 4
For both comparative accuracy and comparative aptness, the particular measure of distance between psychological states proposed cries out for explanation. The measure used is called Square Euclidean Distance, and is a measure of distance between vectors familiar to statisticians and formal philosophers. It achieves a minimum (i.e. perfect aptness) when desire and actual value match, and inaptness strictly increases with the gap between the two, so it meets the most basic demands we could place on such a notion. But there are many alternatives, some but not all of which would support the arguments to follow. Rationales for particular ‘scoring rules’ have been a major theme in the literature on accuracy.Footnote 5 I defer consideration of these foundational issues for the final section, after we’ve seen what we could do with comparative aptness, had we the right to it.
2 Aptness and accuracy domination
The following is a familiar result in the literature: any credence function c that fails to satisfy rational coherence constraints (formalized by probability theory) will be accuracy-dominated. That is, there will be a possible credence function \(c^*\) which is more accurate than c no matter which world is actual. This result is argued (e.g., Joyce, 1998; Pettigrew, 2016) to support the claim of probabilistic axioms to be constraints that agents should meet (probabilism). While details are controversial, the overarching line of thought is clear: if accuracy of belief is a good thing, then accuracy-dominated belief state c can always be improved (no matter which world is actual!) by a shift to the alternative \(c^*\); that is thought to be an inherent flaw in c, and the only belief states free of this flaw are the probabilistic ones.Footnote 6
I show here that any desire function u that fails to satisfy the constraints of means-end rationality (formalized by Causal Decision Theory, and relative to some probability function) will be aptness-dominated. That is, there will be a possible desire function \(u^*\) that is overall more apt than u no matter which world is actual.Footnote 7 By parity of reasoning, these results can support the claim that causal-decision-theoretic standards to be constraints that our belief-desire psychology should meet. The overarching line of thought is exactly parallel to that above: if the aptness of instrumental desire is a good thing, then an aptness-dominated desire state u can always be improved (no matter which world is actual!) by a shift to the alternative \(u^*\). That is an inherent flaw in u, and the only desire states free of this flaw are the causal-decision-theoretic ones.
Here is the basic formal result, abstractly stated.Footnote 8 Some terminology first. Let a real-valued random variable over our finite space of worlds be a function from worlds to real numbers. Take any vector of real-valued random variables, \(\langle R_1,\ldots , R_n\rangle \). At each of N worlds w, \({\bar{r}}_w:=\langle R_1(w),\ldots ,R_n(w)\rangle \) is a vector of real numbers, which we call a value distribution. We say a vector \({\bar{a}}=\langle a_1,\ldots ,a_n\rangle \) is a convex combination of these N value distributions when for each world w there is a real number \(\lambda _w\in [0,1]\) satisfying \(\sum _w \lambda _w=1\) such that \({\bar{a}}\) may be written \(\langle \sum _{w} \lambda _w.R_1(w),\ldots , \sum _{w} \lambda _w.R_n(w) \rangle \). ‘Closeness’ between vectors \({\bar{x}}\) and \({\bar{y}}\) here is measured by Sum Square Euclidean Distance, \(\sum _i (x_i-y_i)^2\). With this in place, the abstract formal result is that when \({\bar{b}}\) is a vector of real numbers that is not a convex combination of value distributions, then there is a vector \({\bar{a}}\) which is a convex combination of those value distributions, such that at every w, \({\bar{a}}\) is closer to \({\bar{r}}_w\) than \({\bar{b}}\) is.
Here is how the familiar accuracy-domination arguments fall out of this. Let the n random variables correspond to the n elements of a classical Boolean algebra of propositions with elements \(P_i\), with \(R_i\) being the function which takes as its value at w the truth value of \(p_i\) at w: 1 if true, 0 if false. Then the value distributions as defined above are possible truth value distributions over the algebra of propositions. Convex combinations of truth value distributions turn out to be probability functions over the n propositions. We can also represent any credal state over this algebra as a vector \({\bar{c}}\), where the ith entry \(c_i\) is the credence the agent invests in \(p_i\). We regard the distance of a credal state from the truth value distribution at w as a measure of the accuracy of that credal state at w. So the above result is interpreted as follows: any credal state that is not probabilistic will be accuracy-dominated by some probabilistic function (the latter will be more accurate than the former at every possible world). This is the poster-child for accuracy-first epistemology.Footnote 9
Take the original abstract formal result, and interpret it anew. We let the random variables correspond to the same n propositions again, but this time we let the value of \(R_i\) at w be the actual value of \(p_i\) at w, as determined by the agent’s sensibility. These can in principle be any real number, not just 1s and 0s, but the abstract result doesn’t care about this difference. The value distributions as defined earlier are now actual-value distributions over the selected algebra of propositions. We can represent any desire state over this algebra of propositions as a vector \({\bar{u}}\), where the ith entry \(u_i\) is the degree of desire the agent invests in \(p_i\). We regard the distance of a desire state from the actual-value distribution at w as a measure of the aptness of that desire state at w. The abstract result so-interpreted gives us a condition desires have to meet to avoid aptness-domination: the desire state must be a convex combination of actual-value distributions. That is, there must be \(\lambda _w\) as before such that for each proposition \(p_i\):
If we identify \(\lambda _w\) with the credence that the agent has in world w, and assume that the agent’s credal state is probabilistic, Bacon has shown that the following holds:Footnote 10
Putting them together, avoiding aptness-domination requires:
In the special case where \(p_i\) is the proposition that w obtains, \(\textsc {prop}_w\), this tells us that \(u(\textsc {prop}_w)=M(w)\), and so if we abuse notation in the familiar way by writing w for prop\(_w\), we get:
As Bacon notes, this is the basic equation of Stalnaker–Gibbard–Harper causal decision theory.Footnote 11 So as promised, meeting the constraints of causal-decision theory’s version of means-end rationality is required in order to avoid aptness-domination.
An extra premise was sneakily introduced in the above! We needed to assume that \(\lambda _w\) was the probabilistic credence the agent invests in world w to derive this result. What justifies this? The cautious interpretation of the above aptness-dominance argument is that it does not tell us, in the first instance, that the agent must satisfy the strictures of causal decision theory relative to her own credences, but instead, that it tells us she must satisfy them with respect to some probability function, if she is to avoid aptness-domination. If we want to say more than this, we need to add more argument. The approach I favour is to add a functionalist identification. From the accuracy-domination argument, we know that a structurally rational agent’s credences will be probabilistic. Premise: an agent is only well-described as having a given set of credences, if they play the right kind of functional role in her psychology (this is a descriptive/metaphysical claim, not a normative/rationalistic one). The \(\lambda _w\) will, descriptively, be what play the functional role within a perfectly structural rational agent’s practical reasoning of credences, and so they will be the agent’s credences. This is my official argument for causal decision theory, requiring both a dominance argument and a functionalist lemma.Footnote 12
Can we eliminate the need for the functionalist lemma, and do everything with a dominance argument? I present a direct argument of this kind in Appendix A. The idea will be to take not just a measure of accuracy of belief, or of the aptness of desire, but of the combined accuray-and-aptness of a belief-and-desire state. As I show in the appendix, this gets us a dominance argument for causal decision theory directly—at the cost of raising some delicate issues about the relation between belief and desire that the official argument sidesteps.
3 Extensions
We get a dominance argument for Stalnaker-style causal decision theory because we borrowed Bacon’s counterfactual characterization of actual value. One could plug in other axiologies of actual value replacing the counterfactual projection of actual value from worlds to propositions given above. We would get parallel results whenever a decision theory can be represented, Bacon-style, as trading in expectations of actual value. Investigating generalizations of his result, Bacon proposes that the actual value of a proposition should be independent of an agent’s credences (though not, of course, their sensibility). Assuming this, he shows that Jeffrey’s evidential decision cannot be represented as the expectation of a credence-independent notion of actual value. Bacon reports a general characterization due to Zhang: among a very broad class of decision theories, the theories’ notion of degree of desire (or ‘action-guiding quantity’) is an expectation of a credence-independence quantity iff that decision theory can be represented as a causal decision theory, in a specific generalized sense. The interested reader is encouraged to consult Bacon’s paper for details. Zhang’s result allows us to reduce the question of whether the reader’s favourite causal decision theory can be vindicated by a dominance argument using the techniques in this paper to the question of whether it has such a Stalnaker-style representation.
As a general strategy, the reader might want to plug in their favourite thoughts about what the actual value of propositions might be. This is especially attractive for readers with concerns about the particular theory of actual value on which I, following Bacon, have focused. As Bacon notes, actual value defined counterfactually will often be highly indeterminate. Neither Bacon nor I am bothered by that, but it might prompt others to look for an alternative.Footnote 13 One option, for example, is to let the actual value of a proposition p be the weighted average of the actual value of worlds w, where the respective weights are given by the conditional chance of w obtaining given p. On this basis, we can produce a dominance argument for a Skyrms-style expected-conditional-chance causal decision theory.Footnote 14 As a second example, although Bacon shows Jeffrey’s decision theory can’t be squeezed into this argument, there are evidentially-flavoured decision theories that can be developed and given a dominance-theoretic underpinning by an appropriate theory of actual value. For example, one could start from a theory of actual value of propositions based on Stalnakerian indicative conditionals, rather than counterfactuals, so that the actual value of p is the actual value of that world w which is such that if p, w. If you replace the counterfactual arrow in the above results with an indicative arrow, they go through, giving us an aptness-dominance argument for non-causal conditional decision theory.
One way in which actual values for propositions are different from truth as ordinarily conceived is that actual values are characterized relative to a subject’s sensibility and so unlike truth there is no subject-independent ‘correct value’. As far as I can see, that difference doesn’t create any relevant disanalogy, or undercut the interest of the dominance arguments I have been giving. And after all, some hold that truths about taste or time hold only relative to idiosyncratic features of subjects, but even if that is right, then we should still maintain that a person’s credence in whether something is tasty is best/correct if it matches the truth value relative to them of the proposition that it is tasty, and better/more or less correct the closer it matches this relativized truth value—and I expect the dominance arguments for probabilism would be just as attractive to the relative-truth theorist as to the absolute-truth theorist. So the relativity of actual value to sensibility doesn’t worry me at all.
On the other hand, those who think that there is a subject-independent evaluative standard for desire can run a variation of this paper’s dominance argument. Consider a hedonist, who thinks that the goodness of a world is determined by the distribution of pleasure and pain within it. The hedonist value \(M_h\) could be substituted for sensibility value M. Essentially, \(M_h\) characterizes an objectively privileged sensibility, and so gives us a new, derelativized evaluation of desire-correctness and comparative desire-aptness. But still, so long as actual value is projected onto propositions from \(M_h\) via the counterfactual characterization as before, everything formally works just as before, and one can again conclude that one must meet the constraints of causal decision theory to avoid aptness-domination.
The constraints of causal decision theory are not the only thing required to avoid aptness-domination in this revised objective sense: the agent will be aptness-dominated in the revised objective sense if her instrumental desires differ from the privileged hedonistic sensibility, even if they match her own subjective sensibility. What we have here is a dominance-argument for causal-decision-theoretic hedonism (a form of hedonistic utilitarianism). But this is no longer a dominance argument for a coherence constraint, but a dominance argument for coherently pursuing what is (presupposed to be) objectively of value. If you are interested specifically in coherence norms, then the original argument is what you need.
4 Comparative aptness defended
The results described above rest on the assumption that it makes sense to evaluate the degree of desire that an agent invests in a proposition by its ‘distance’ from the actual value of that proposition—the valu, by the agent’s lights, of the outcome that would result were the proposition to be true. Further, I made a specific assumption about what this ‘distance’ function looked like—that it was the (sum of the) square Euclidean distances between the agent’s degree of desire and its actual value.
Let me say what my ambitions for this section are. I do not aim to produce considerations that will persuade a determined sceptic that this notion is in good standing. I do not even aim to produce local considerations that will persuade a sympathetic, neutral audience that evaluations work as I say they work. I am Quinean enough to think that philosophical justification often works at the level of whole theories, which are appropriately judged by their consequences. Frankly, a large part of why I take the core evaluative notion of inaptness seriously is that it features in hypotheses which give (to my eyes) attractive and illuminating explanations of the evaluative source of structural rationality norms. But I do think that to be attractive and illuminating, the evaluative notion of aptness and the hypothesis about how it works should not be ad hoc. There needs to be a coherent and independently-motivated vision of how the aptness of degrees of desire works that the neutral audience can appreciate (whether or not they feel immediately moved to accept it). At the moment, however, the super-specific mathematical formula for the ‘badness’ of desire states I’ve appealed to cries out for some independent motivation. In this section I talk the reader through the considerations that, for me, make it an coherent attractive starting hypothesis. I will build up to the full thesis in three steps: motivating first perfect aptness, then ordinal comparisons of aptness, and then the specific quantification of degrees of aptness.
The first thesis is that an agent’s (instrumental) desires are intrinsically best when they match the actual values determined by the agent’s sensibility. I regard this as a very modest claim, and one the neutral audience should be happy to accept, just as they should accept that the best credences are those that match the truth values. I hope in particular that previous sections have already preempted the main concerns one might have. Specifically: (a) this is not the anti-Humean claim that there is a subject-independent set of values which an agent’s desires should match. We have seen how to formulate and explore such hypotheses, but the main line of argument starts from actual values determined by what the agent themselves cares about; (b) the subjectivity (sensibility-relativity) of actual value does not prevent a rational agent having a degree of desire in a proposition that diverges from its actual value, and so doesn’t undercut actual value being used as a criterion of success (as noted above, subject-relative truth would pattern similarly); (c) it is perfectly legitimate to question the particular counterfactual theory of actual value being presented above. But we’ve already seen that the results are robust in the face of variation here. Put in a different account of actual value, and you still have a dominance argument for norms of means-end rationality—it’s just that the exact formulation of the vindicated norms is adjusted.
I don’t think we should try to reduce these evaluations of desire to instrumental considerations, any more than we should try to reduce what’s good about true belief or accurate credence to instrumental considerations. Nevertheless, true beliefs are generally instrumentally useful—commonsensically, you’d think you’d be better placed to get good outcomes if you navigate by an accurate map. Fully apt desires are certainly instrumentally useful. I said when introducing the notion that part of the functional role of (instrumental) desires is that they guide choices—faced with a choice between two options, we go for the one we want more. Observation: if degrees of desire match actual values, the option with higher degree of desire is exactly the one which brings about the better outcome (by the subject’s lights). Conclusion: if your desires match actual values in a choice situation, you’ll be disposed to go for that option which in fact brings about the better outcome (by your lights). So matching actual value brings practical success.
My second thesis therefore is that an agent’s desires are better or worse the nearer or further they are from the actual values determined by the agent’s sensibility. This is the analogue of the claim that credences are better or worse, the nearer or further they are from the truth values of the proposition to which they attach. I’m imagining the audience has already granted there is a correct value for an agent’s instrumental desires—the actual values. It seems a modest step to rank instrumental desires that do not match the correct value by how closely they approximate it.
Again, I don’t think we should try to reduce this evaluation to instrumental considerations. But decent evidence that we are not mistaken to make the modest generalization of the second thesis is that the considerations above about the instrumental value of fully apt utilities generalize to the comparative case. Suppose that the difference in actual value between the two options in a situation of binary choice is x. Then whenever one’s utilities in these options are sufficiently near—whenever they are within \(\frac{x}{2}\) of the actual values—then you’ll be disposed to make the correct choice. Close enough is instrumentally good enough, for practical purposes.
My third thesis therefore is that an agent’s utilities are better or worse in a way that is measured by their Sum Squared Euclidean Distance from the actual values. By this stage of the dialectic, the audience is assumed to grant the evaluative significance of matching or approximating actual values, so they will have no problem of principle with the idea that comparative aptness could come in degrees in a way that admits of precise specification. The audience will however want to know why we should think that this is the way to measure aptness.
The typical way the analogous discussion has gone in the accuracy-first literature is to motivate—perhaps by conceptual analysis, perhaps by other means—constraints that a measure of accuracy must meet to be acceptable. One then proves that any conception of accuracy that meets those constraints generates a version of the formal result quoted earlier, and hence supports a dominance argument. A subgenre of these papers identifies (and motivates) constraints that pin down measures of accuracy uniquely, often as Sum-squared Euclidean Distance/the Brier Score.Footnote 15 This paper widens the focus from accuracy and credence to include aptness and desire, and in doing so opens up a parallel project, of formulating and motivating constraints on aptness. I think there are a set of constraints that are plausible both for accuracy and for aptness, and which pin both down as sum Square Euclidean Distance. This is bound to be controversial, and it is beyond the scope of this paper to resolve the debate on accuracy measures—but parity between the case for Square Euclidean Distance measures of accuracy and aptness is a more realistic hope, and I sketch a programme for this in Appendix B .
(It’s important to note, however, that even if the arguments for the Sum Squared Euclidean Distance measure of inaptness don’t go through we will have fallback options. Any of the measures known as Bregman divergences will allow the abstract dominance result to be proved. And conceptual arguments such as that in Appendix B might fall short of pinning the measures down uniquely, but still establish that they are of this kind. Again, this is a dialectical situation familiar from the credence/accuracy literature that will be replayed, I say, for instrumental desire and actual value.)
Once more, I don’t think we should try to reduce this evaluation to instrumental considerations. But since exactly and approximately matching actual value did bring practical success, one might hope that there would be practical significance also to the quantitative measure of how close one is to actual values. There are indeed ways of teasing out instrumental significance from quantitative measures of inaptness. I develop one way of doing this, based on an analogous argument for accuracy due to Levinstein (2017), in Appendix C.
5 Conclusion
Vindicating structural rational constraints on belief (probabilism) via a measure of closeness to truth value (accuracy) is a standard part of the contemporary philosophy playbook. This paper has shown that we can, in analogous ways, vindicate structural rational constraints of means-end rationality (causal decision theory) via a measure of closeness to actual value (aptness). Further, the foundational assumptions about the shape of accuracy and of aptness required to run the arguments are close parallels. I have shown ways in which the argument is robust under different theories of subjective actual value, including nonclassical treatments of indeterminacy in actual value; I have pointed to the way that the argument may (but need not!) be generalized to objective theories of value. Aptness-domination arguments for decision theories should be added to the philosophical playbook.
Data availability
No consent/data/materials/code/authors contribution required.
Change history
12 May 2023
A Correction to this paper has been published: https://doi.org/10.1007/s11229-023-04154-x
Notes
A familiar thesis is that an agent’s degrees of desire may be modelled by a function from propositions to real numbers, but that there may be ‘admissible’ transformations of any such function that give an equivalent, equally good model. Only properties invariant under admissible transformations are real features ascribed to the degrees of desire—other things are artefacts of this or that way of representing the degrees.
I will flag any assumptions I make about the structure the degrees of instrumental desire must have (what is or isn’t an admissible transformation) as we go along. But throughout, I will assume that her sensibility, as characterized above, will share the same structure. My picture: for each proposition there is a specific degree of desire that is ‘vindicated’ by the agent’s sensibility. Relative to any specific real-valued model of degrees of instrumental desire, this vindicated degree of desire will be represented by a real number, and the sensibility will be represented by the same real value at that proposition. The two march in lock-step: transform the real-valued representation of desires, and you must also transform the representation of the sensibility.
Following (Bacon, 2022), I’m happy to assume we’re working with the logic C2 (Stalnaker, 1968). As far as I can determine, the crucial part of C2 that is used is the principle of conditional excluded middle, which guarantees inter alia that for each possible antecedent there is a unique world that would obtain were it to be the case, and so these results may generalize to other CEM-including conditional logics.
It’ll be convenient below to have to hand a characterization of actual value in different notation, which is easier to read when reasoning about complex propositions:
 . Here, \(|q|^{@}:=t_q(@)\), i.e. the truth value of q and @. Note that
. Here, \(|q|^{@}:=t_q(@)\), i.e. the truth value of q and @. Note that 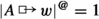 iff \(f(A,@)=w\), and 0 otherwise, and so under classical assumptions about truth value distributions, this is equivalent to Bacon’s characterization.
iff \(f(A,@)=w\), and 0 otherwise, and so under classical assumptions about truth value distributions, this is equivalent to Bacon’s characterization.As promised, I flag an assumption I’m making about the structure of degrees of desire/actual value here. In order for these differences between degrees of desire (equivalently, degrees of desire and actual value) to be meaingful, the relevant degrees must have what is known as ‘interval scale’ structure (though they could also have richer structure, as most assume credences do). Accordingly, I assume that any admissible transformations of real-valued models of degrees of desire/actual values will be positive affine (i.e. of the form \(x\mapsto ax+b\), \(a>0\). Note that many decision theories are built around interval scales, including ones that are ruled out by the dominance results of this paper (Buchak, 2013) and ones that are designed for descriptive rather than normative purposes (Elliott, 2017)
Note that under a positive affine transformation of degrees of desire, the measure of aptness will be multiplied by \(a^2\). This is not a problem, since the aptness of every proposition is scaled by the same multiple, and the comparative aptness facts we will be interested in are preserved. My picture: the ‘choice of units’ for modelling degrees of desire induces a corresponding choice of units for measuring inaptness.
See, for example, (Pettigrew, 2016) for defence of the Brier score/Square Euclidean Distance measure and a characterization of the wider class of Bregman divergences which also support this result.
In Appendix A, I show further that any credence-desire function pair (c, u) that fails to jointly satisfy the constraints of means-end rationality (formalized by Causal Decision Theory) will be accuracy-and-aptness dominated. That is, there will be a possible credence-desire pair \((c^*,u^*)\) that is overall more accurate-and-apt than (c, u) no matter which world is actual.
See Pettigrew (2016) for a book length development of this setting, formally and philosophically. See Williams (2012a, 2016) for discussion of generalizations of this to nonclassical settings, where propositions may take truth values other than 1 and 0, where the full power of the above result is required.
Recall (fn 3) \(|q|^w\) is the truth value of q at w. The two crucial things to recall here is (1) the definition of \(v_{p_i}(w)\), which we express as follows: \( {v_{p_i}(w)=\sum _{w'} M(w').|p_i\begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }w'|^{w}}\); (2) the general result that for probabilistic credences c, \(c(q)=\sum _w c(w).|q|^w\). Using the first identity at the first step and the second at the third, we calculate:
$$\begin{aligned} \sum _w c(w)v_{p_i}(w)= & {} {\sum _w c(w) .\sum _{w'} M(w').|p_i \begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }~w'|^w}\\= & {} {\sum _{w'} M(w') .\sum _w c(w).|p_i \begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }w'|^w}\\= & {} {\sum _{w'} M(w') .c(p_i\begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }w')} \end{aligned}$$Gibbard and Harper 1978. The original idea was due to Stalnaker.
Bacon, I believe, would say that the counterfactuals would take definite classical truth values at worlds, but that it is indeterminate which world is actual (Bacon, 2018). In some moods I would say the same. So, for example, there will be a world at which if I had flipped this fair coin it would have landed heads; and a world at which if I had flipped it it would have landed tails; but it is indeterminate which of these is the actual world (Barnes & Williams, 2011). Importantly, if the characterization of actual value is to be plausible, we will need to defend the thesis that when it is indeterminate which of two worlds is actual, one can adopt a partial degree of belief in each (something that doesn’t fall out of anything we have so far said Williams, 2012c, 2014a, b.).
On the other hand, if you hold that indeterminate counterfactuals take nonclassical truth values \(|A|^w\) (or nonclassically distributed truth values) at worlds, then the following generalized form of Bacon’s argument can be given. We start by asserting that the actual value of p is given by the weighted average of the actual value of worlds, where weights are the degree of truth that that world would be the result if p were the case: \( {v_p(w)=\sum _u M(u).|p\begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u|^w}\). This has Bacon’s definition as a special case, when the truth values are classical (see footnote 3 above). From this we can argue, Bacon-style:
$$\begin{aligned} \sum _w c(w)v_p(w)= & {} {\sum _w c(w) .\sum _u M(u).|p \begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u|^w}\\= & {} {\sum _u M(u) .\sum _w c(w).|p \begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u|^w}\\= & {} {\sum _u M(u) .c(p \begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u)} \end{aligned}$$This is again the Gibbard-Harper formula, though grounded in a nonclassical rather than classical setting. The final step here is given by the general thesis that rational credence in a proposition is expectation of truth value. This is something that has been defended at length in the literature on nonclassical credences (Smith, 2010; Williams, 2012a, b, 2016), on the basis of a generalization of the classical accuracy-dominance and Dutch-book arguments for classical probabilism.
See (Skyrms, 1980).
See (Pettigrew, 2016) for development and citations.
This will disrupt the standard formulations of causal decision theory, but if we replace each appeal to a credence \(c(p_i)\) with the ratio \(c(p_i)/k\), all will be well—with the standard representation arising when maximum credence is represented via the real number 1.
Thanks to Catrin Campbell-Moore for discussion of the material in this appendix.
Many thanks to Giacomo Molinari for suggesting the possible connection to Levinstein, and to Molinari and Richard Pettigrew for subsequent discussion.
I’ll note, however, that Levinstein’s setup presupposes that the agents in question conform to means-end rationality. But the current argument only needs to assume the basic functionalist thesis that utilities (instrumental desires) guide choice.
Note: unlike the Levinstein argument I am drawing from, I don’t assume that actual-you or possible-you chooses by maximizing expected utility. But I am assuming here that something like the degree of regret you’d have in ceding a choice is to be calculated by expected utility-cost. We’re showing that this quantity corresponds to measures of inaptness. This is not a circular argument. The original hypothesis is that there’s a specific quantitative notion of comparative inaptness, which by a dominance argument vindicates an expected-utility formulation of means-end rationality. You might then ask the question: does this measure, over and above its hypothesized evaluative significance, have any practical significance? And in answering this question, there’s no circularity in appealing to the right theory of means-end-rationality.
References
Bacon, A. (2018). Vagueness and thought. Oxford University Press.
Bacon, A. (2022). Actual value in decision theory. Analysis. https://doi.org/10.1093/analys/anac014
Barnes, E. J., & Williams, J. R. G. (2011). A theory of metaphysical indeterminacy. Oxford Studies in Metaphysics, 6, 103–48.
Buchak, L. (2013). Risk and rationality. Oxford University Press.
Campbell-Moore, C. (2022). Accuracy representation results and estimates.
De Finetti, B. (1974). Theory of probability (Vol. 1). Wiley.
Elliott, E. (2017). A representation theorem for frequently irrational agents. Journal of Philosophical Logic, 46(5), 467–506.
Gibbard, A., & Harper, W. L. (1978). Counterfactuals and two kinds of expected utility. In A. Hooker, J. J. Leach, & E. F. McClennen (Eds.), Foundations and applications of decision theory (pp. 125–162). D. Reidel.
Joyce, J. M. (1998). A non-pragmatic vindication of probabilism. Philosophy of Science, 65, 575–603.
Levinstein, B. A. (2017). A pragmatist’s guide to epistemic utility. Philosophy of Science, 84(4), 613–638.
Lewis, D. K. (1974). Radical interpretation. Synthese, 27, 331–44. Reprinted in Lewis, phPhilosophical Papers I (Oxford University Press, Oxford, 1983) 108–18.
Pettigrew, R. (2016). Accuracy and the laws of credence. Oxford University Press.
Predd, J., Seiringer, R., Lieb, E. H., Osherson, D., Poor, V., & Kulkarni, S. (2009). Probabilistic coherence and proper scoring rules. IEEE Transactions of Information Theory, 55(10), 4786–4792.
Ramsey, F. P. (1926 [1931]). Truth and probability. In R. B. Braithwaite (Ed.) The foundations of mathematics and other logical essays, chap. VII (pp. 156–198). Kegan, Paul, Trench, Trubner & Co.
Savage, L. J. (1954). The foundations of statistics. Wiley.
Schervish, M. J. (1989). A general method for comparing probability assessors. The Annals of Statistics, 17, 1856–1879.
Schervish, M. J., Seidenfeld, T., & Kadane, J. B. (2009). Proper scoring rules, dominated forecasts, and coherence. Decision Analysis, 6(4), 202–221.
Skyrms, B. (1980). Causal necessity: A pragmatic investigation of the necessity of laws. Yale University Press.
Smith, N. J. J. (2010). Degree of belief is expected truth value. In R. Dietz & S. Moruzzi (Eds.), Cuts and clouds. Oxford University Press.
Stalnaker, R. (1968). A theory of conditionals. In Studies in logical theory (pp. 98–112). Blackwell.
Williams, J. R. G. (2012). Generalized probabilism: Dutch books and accuracy domination. Journal of Philosophical Logic, 41(5), 811–840.
Williams, J. R. G. (2012). Gradational accuracy and non-classical semantics. Review of Symbolic Logic, 5(4), 513–537.
Williams, J. R. G. (2012). Indeterminacy and normative silence. Analysis, 72, 217–25.
Williams, J. R. G. (2014). Decision making under indeterminacy. Philosopher’s Imprint, 14(4).
Williams, J. R. G. (2014). Nonclassical minds and indeterminate survival. Philosophical Review, 123(4), 379–428.
Williams, J. R. G. (2015). Logical norms, accuracy and degree of belief. In C. Caret & O. Hjortland (Eds.), Foundations of logical consequence (pp. 329–352). Oxford University Press.
Williams, J. R. G. (2016). Nonclassical logic and probability. In A. Hajek & C. Hitchcock (Eds.), Oxford handbook of probability and philosophy (pp. 248–276). Oxford University Press.
Williams, J. R. G. (2018). Rational illogicality. Australasian Journal of Philosophy, 96(1), 127–141.
Williams, J. R. G. (2020). The metaphysics of representation. Oxford University Press.
Williams, J. R. G., & Pettigrew, R. (2022). Consequences of calibration.
Acknowledgements
Thanks for feedback to those attending the workshop on nonclassical probability and philosophy of physics at Bristol. I’d especially like to acknowledge conversations with Andrew Bacon, Thomas Brouwer, Catrin Campbell-Moore, Ed Elliott, Giacomo Molinari and Richard Pettigrew. Thanks (I think) to Alana Gill for providing the example in the first paragraph. I am very grateful for two extensive and thought-provoking reports by referees for this journal. The Group Thinking: New Foundations project leading to this application has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 818633).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No other competing interests are identified.
Ethical approval
No ethics approval was required.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Symbol was incorrectly represented in the online article.
Appendices
Appendix A: The direct dominance argument for causal decision theory
The official argument of Sect. 2 evaluated an agent’s desires for aptness, producing a dominance argument for causal-decision-theoretic constraints, relative to some probability function or other. That these probabilistic ‘decision weights’ are credences requires separate argument. This appendix considers an alternative approach that goes directly to causal-decision-theoretic constraints on degrees of desire and belief.
To run this direct argument, we need not just a measure of accuracy, or aptness, but the overall accuracy-and-aptness of a belief-desire psychology. A belief-desire psychology will be represented by a pair of a credence function and a desire function. These functions correspond to vectors of length n and so the pair is represented by a vector of length 2n, with the first n spots giving the degree of belief in n propositions, and the second n spots giving the utilities in those same propositions. The value distributions are understood accordingly, with truth values occupying the first n slots, and actual values the second n slots. Distance over belief-desire psychologies will be Square Euclidean Distance, which means that in measuring distance of a belief-desire psychology from a value distribution, we are summing together the inaccuracy of the credence function component (with respect to the truth value distribution given by the first half) and the inaptness of the desire function (with respect to the actual-value distribution given by the second half). The abstract formal result kicks in once again, and so we conclude that to be accuracy-and-aptness undominated, the credence-desire pair needs to be a convex combination of the value distributions described. From this, we get both the following, where \(t_p(w)\) is the truth value of p at w:
In the special case where \(p_i\) is the proposition that w obtains, the first line entails \(c(w)=\lambda _w\). The second line is what we earlier got from the aptness-domination argument alone. So these two together enable us to derive the basic equation of causal decision theory without caveat, as a condition that must be met in order to avoid accuracy-and-aptness domination.
This direct argument has strengths and weaknesses compared to the official version of the main text. The dialectical strength is that it avoids dependence on the functionalist lemma. Though the author is friendly to the functionalist lemma, some readers with a non-pragmatic conception of credence may not be. The weakness is detailed below.
Recall that orthodoxy has it that there are many equivalent ways to represent a person’s degrees of instrumental desire in real numbers. Maybe your preference right now for a glass of water, vs. beer, vs. wine, can be represented as 1, 5 and 10. But—orthodoxy says—the same psychological state could be represented via the numbers 10, 50 and 100. Essentially this just amounts to a change in the units by which we represent the states. As mentioned in footnotes 1 and 2, when we shift units for desire by scaling our representation in this way, we must also shift units for actual value. So if, for example, the actual values of water/beer/wine relative to your sensibility are 2/4/8 respectively on the first representation, they will be 20/40/80 on the second representation. Notice: since inaptness is the square difference between instrumental desire and actual value, the inaptness of the desire state I just attributed to you will be \((1-2)^2+(5-4)^2+(10-8)^2=6\) on the first representation, and \((10-20)^2+(50-40)^2+(100-80)^2=600\) on the second. When one scales up the units of desire/value by k, one changes the units of inaptness by \(k^2\).
The trouble is that if the inaccuracy of the agent’s credal state is unaffected by these different ways of representing her desire (as orthodoxy would assume) then we can boost or shrink the inaptness of her desire-state, while holding the inaccuracy of the credal state fixed. This would be devastating to the idea we can get a sensible combined aptness-and-accuracy score by summing the two components together. To illustrate: let us take two credence-desire pairs, \((c_1,u_1)\) and \((c_2,u_2)\). Let us suppose \(c_1\) is more accurate than \(c_2\), but \(u_2\) is more apt than \(u_1\). Now the observation is simply that by transforming the representation of utilities we can "shrink" the absolute value of the aptness scores so that \(I(u_1)-I(u_2)<I(c_2)-I(c_1)\), on which the transformed representation of \((c_1,u_1)\) has a better accuracy-and-aptness score than the transformed representation of \((c_2,u_2)\): \(I(u_1)+I(c_1)<I(c_2)+I(u_2)\). Equally, we can "grow" the absolute value of the aptness scores so that \(I(u_1)-I(u_2)>I(c_1)-I(c_2)\), on which the reverse is true. But these transformations are all supposed to be representations of the same psychological state, under different choices of units! Aptness-and-accuracy comparisons must be invariant under such changes of unit, if they are to play the role the direct dominance argument envisages for it. This is a reason for anyone who accepts the orthodox picture of degrees of belief and desire just sketched to go back to the official argument of the main text, giving up on the direct argument.
To block what would be a devastating objection, aptness and accuracy need to be comparable—so that it makes sense to add them together. This in turn entails that differences between degrees of belief and differences between degree of desire will have to be comparable for each individual, so that we can meaningfully ask whether the gap between Sally’s level of confidence that the tumbler contains beer vs. her level of confidence that it contains water is greater or less than the gap between her degree of desire that it contains beer and her degree of desire that it contain water. If credal and desire-gaps are comparable in these ways, then we can still ‘change units’ for desire by multiplying by a constant k. But we will have to ‘change units’ for credence at the same time to preserve the comparisons, so that if we started with the standard representation where maximal credence is represented by the real number 1, then on the new representation maximal credence would be represented by the real number k.Footnote 16 This is sufficient to block the argument posed in the previously paragraph, which relied on holding the representation of credence fixed while varying that of desire.
Importantly, this kind of comparability does not require that degrees of belief and desire be represented on a common scale. Just because we can compare differences, it does not follow that it makes sense to ask whether Sally’s degree of belief that the tumbler contains beer is greater than her desire that it contain beer (and indeed, boosting the representation of all degrees of desire by a constant real number can flip any such comparison while leaving the comparison of differences invariant).
In sum, the direct argument requires there be facts about cross-attitude comparisons of difference. How plausible is that? I find myself forming such judgements on the basis of introspection very easily—the difference in my degrees of belief that a coin will land heads each time if flipped 1000 times and that it will land heads each time if flipped 1001 times, is much smaller then the difference between my degree of desire for health and riches, and my degree of desire for being poked in the eye with a stick. I say: the pre-theoretic starting point is that there are facts of the matter about such comparisons. Scepticism about such comparisons is perfectly respectable, but it must be argued for. The best theory-driven reason I know to be sceptical presupposes a functionalist account of the nature of attitudes, points out the cross-attitude comparisons have no apparent role in our leading theories of how belief and desire interact in determining action, and concludes that pending elaboration of a functional role for them, scepticism is warranted. If functionalism is not in the background, I don’t know why you’d resist the comparability facts the direct argument needs.
Overall, the discussion in this appendix leaves this paper with an argument by cases. Functionalism about belief and desire is either right or wrong. If wrong, then prima facie the direct dominance argument above is cogent—or at least, there’s no obvious reason for doubting it on the basis of the cross-attitude difference comparisons it presupposes. But if functionalism is right then the functionalist lemma required to complete the argument in the main text is supported. Either way, we have a dominance argument for causal decision theory.
Appendix B: Constraints on aptness
A direct justification of sum Square Euclidean Distance as a quantitative measure of inaptness would have two steps. The first step is the identification of constraints on aptness. The second step of the project will be to show that any aptness measure meeting these constraints supports the dominance arguments.Footnote 17
If we take the literature on accuracy as our model, there are many such results one could try replicating for step one. But the one I like best is set out in (Williams & Pettigrew, ms) which is a weakening of the constraints used in Pettigrew (2016) for the same result. There it is shown that three constraints (Additivity, Continuity and Calibration Test) are sufficient for an accuracy measure to support accuracy domination. Their translation into this setting are the three constraints below:
-
1.
A measure of aptness should be additive, i.e. the inaptness of the whole desire state should be determined by summing, over all propositions, the inaptness of each individual degree of desire.
-
2.
A measure of aptness should be continuous with respect to varying degrees of desire.
-
3.
A measure of aptness should pass the following Calibration Test. Consider a bounded agent who has determined they will assign the same degree of desire to all the propositions on a given agenda. And suppose that the average actual values of propositions on that agenda is k. Then, according to the Calibration Test, the best the agent can do, given their commitment to homogeneity, is for their degrees of desire to be equal to k. The claim of the Calibration Test, then, is that most apt homogeneous desire state be the one that matches the average actual value.
This is not the place for a full defence of these claims (I promised the reader only a sketch of what an argument might look like), but I submit they are no better or worse motivated than their analogues for accuracy.
Attention turns to step two. Here there is a technical issue to be grappled with. Accuracy measures take credences and (standardly) evaluate them against distributions of truth values that are always either 0 or 1. But aptness measures take utilities and evaluate them against distributions of actual values that could, for all we have said, take any real-number as value. So we are going to need domination results for random variables in general, not just 1/0 indicator-type random variables. The standard results must be rederived in this setting. Elsewhere, I have shown that any function that meets the three conditions above meet the technical condition known in the literature as ‘strict propriety’ (this generalizes what Williams and Pettigrew show for accuracy). Campbell-Moore (2022), generalizing results by Schervish et al. (2009), shows that in the context of certain background conditions, all strictly proper accuracy/aptness measures will take a Schervish form, and that this means the accuracy/aptness measure will be generated by a Bregman divergence. Pettigrew (2016), drawing on Predd et al. (2009), shows that accuracy/aptness measures satisfying Additivity and Continuity and generated by a Bregman divergence will give rise to the relevant dominance results.
The background conditions for Campbell-Moore’s proof include Additivity and Continuity, which we have already listed as assumptions, but also that the accuracy/aptness measure is absolutely continuous, and that for every pair of possible values of a pair of random variables, there is some random variable whose possible variables include each of that pair. These are additional non-trivial conditions for which further justification would be needed. The second is true for aptness if, whenever we have possible actual values k and \(k'\), there are worlds w, u and \(w',u'\) such that the actual values of u is k, the actual value of \(u'\) is \(k'\), and there is a proposition p such that at w, \( {p\begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u}\) and at \( {w'\begin{array}{c}\Box \end{array}\ \!\!\!\!{\rightarrow }u'}\). I have shown elsewhere that the absolute continuity condition may be eliminated at the cost of strengthening the Calibration Test somewhat.
Appendix C: Measuring the cost of divergent utilities
For the purposes of this appendix alone, and purely for neat exposition, I will use the term ‘utility’ for what I have been calling to this point ‘degree of (instrumental) desire’.Footnote 18
Take two agents whose utilities are measured on the same utility scale: actual-you and possible-you. Let us suppose their utilities are matching on a rich set of propositions. We’ll suppose that there is a proposition to which actual- and possible-you assign the same utility for the continuous, complete range of utility values in play. To fix ideas, think of these as the utilities assigned to complete outcomes—the picture is then that actual-you and possible-you have the same sensibility. These propositions, on which actual-you and possible-you take the same attitude, serve as a kind of reference class to measure the instrumental (dis)value of other, diverging utilities in less specific outcomes. Actual-you and possible-you can differ on some proposition outside this class, however—and our job is to quantify the practical cost of that divergence. The argument to follow is inspired by the discussion in Levinstein (2017) of the practical significance of having accurate credences, and rests like his discussion on a remarkable representation theorem due to Schervish (1989).Footnote 19
We will measure the practical cost in a situation where you face a binary choice between P and some proposition Q drawn from the reference class. If your utility in P is higher than your utility in Q, then you will choose P, otherwise, the reverse. Now, how bad would it be for actual-you to cede this choice to the agent with divergent utilities in P, possible-you? That agent makes her choices by the same recipe, but based on the same utility for Q but a different utility for P. The argument is smoothest if we work with disutilities, i.e. utility-losses. Let x be the shared disutility of Q, \(k_a\) the disutility actual-you assigns to P, and \(k_p\) the disutility possible-you assigns to P. Without loss of generality I assume \(k_a<k_p\) (the opposite case will lead to the same conclusion by parallel reasoning). There will only be a cost to ceding the choice to possible-you, from actual-you’s perspective, if you would choose different options, which happens in the case we are considering if and only if \(k_a<x<k_p\)—in that case you would choose P, since x has a greater disutility than P by your lights, but possible-you would choose Q. The cost of ceding the choice by your lights is then \((x-k_a)\).
Now suppose that you are uncertain what Q, and therefore x, will be. In this case we are calculating the expected cost of ceding this (unknown) choice.Footnote 20 Let f be the probability density over possible values of x assigned by actual-you in this setting. Then the expected cost is given by a probability-weighted average of the above costs, for all those values of x between \(k_a\) and \(k_p\), i.e. it is given by the integral:
If, for example, this probability is flat (i.e. the density takes constant value 1 everywhere) then over all values of x, we can calculate:
And so: if we measured inaptness by Square Euclidean Distance, then the inaptness of the divergent utility in P is a measure of the expected cost of ceding one’s choices to that utility (up to a multiplicative constant).
The cleanest implementation of this setup is one where possible-you diverges from actual-you on just one proposition. In this case, the reference class from which Q is drawn can be all options other than P, and the binary choices that you might face are simply all binary choices. Flat uncertainty in this context delivers Square Euclidean Distance as a measure of the cost of this single divergence.
Another clean implementation is a highly local one. One faces an uncertain binary choice between P and some other proposition drawn from set C, and it so happens that actual- and possible-you have the same utility on all the propositions in C. The cost of diverging for this local choice situation can be calculated as above.
But it is less obvious to me whether there is an interpretation of this result which identifies practical costs to having a utility function that diverges from the actual one for multiple propositions at the same time, locally or globally. If you diverge at two propositions, and take the reference class to be all remaining propositions, one is left with the awkward question of why the calculation of the costs (or the choice setup) excludes the case where you are presented with the binary choice between those two propositions on which you diverge—which can certainly be associated with a cost if actual-you and possible-you have different preference-orderings on this pair. So the general case remains a matter for future work.
The argument shares with the Levinstein paper which inspired it a relativity to a probability distribution—in this case, the probability density over the utility of the second option in the uncertain binary choice. The flat probability density above leads to Square Euclidean Distance measure of inaptness, but other probability distributions lead to other candidate measures. Here as in that original, results due to Schervish will ensure that whatever probability density we plug in, practical costs will be expressed by some Bregman divergence between the utilities of actual-you and possible-you, and—in global form—they will always support the kind of dominance arguments in the main text. But if we wanted to use these results to argue for the practical significance of Square Euclidean Distance specifically, then one needs some additional story about why the flat density that generates it has a privileged status in calculating expected costs.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Williams, J.R.G. Aptness and means-end coherence: a dominance argument for causal decision theory. Synthese 201, 48 (2023). https://doi.org/10.1007/s11229-022-04017-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-022-04017-x





 . Here,
. Here, 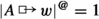 iff
iff