Modeling psychopathology: 4D multiplexes to the rescue

Abstract

Accounts of mental disorders focusing either on the brain as neurophysiological substrate or on systematic connections between symptoms are insufficient to account for the multifactorial nature of mental illnesses. Recently, multiplexes have been suggested to provide a holistic view of psychopathology that integrates data from different factors, at different scales, or across time. Intuitively, these multi-layered network structures present quite appealing models of mental disorders that can be constructed by powerful computational machinery based on increasing amounts of real-world data. In this paper, I systematically examine what challenges psychopathology models face and to what extent different species of psychopathology models can address them. My analysis highlights that while multiplexes, as they are usually conceived, appear promising, they suffer from the same problems as other approaches. To remedy this, I suggest, we must go a step further and combine different kinds of multiplexes into 4D models. Once we embrace 4D multiplexes and identify appropriate ways to constrain them, we might unlock the true potential of multiplexes for making headway in psychopathology research.

1 Introduction

Grasping psychopathology is a challenging endeavor. In order to diagnose, explain, treat and prevent mental illnesses, we need to understand their nature as well as their causes. But what does that amount to, precisely? Clinicians, scientists and philosophers have been seeking to develop models and theories of mental illnesses for centuries. While some research traditions have focused on the phenomenological aspects of mental illnesses (e.g. de Haan, 2020; Fuchs, 2013), others have been looking into neurobiological substrates (e.g. Goodkind et al., 2015; Paul, 1988; Shelton, 2007) and genetic underpinnings (e.g. Avramopoulos, 2018; Wong et al., 2008).

Nowadays, the view that mental disorders are best understood as brain disorders is quite prominent (e.g. Insel & Cuthbert, 2015; Kandel, 2018; Walter, 2013). According to this view, mental illnesses result from some sort of neurobiological dysfunction or “glitch” in neural circuits that elicits a whole range of symptoms (Insel et al., 2010; Walter, 2017, Kandel, 2018). That suggestion fits naturally within the medical tradition of seeking a common (molecular) cause for various symptoms to identify and diagnose an illness. It also squares well with popular naturalist-reductionist views of the mental. Meanwhile, a whole body of research has been attempting to transform our current symptom-based diagnostic categories for mental illnesses (as stated in the DSM-5; APA 2013) into a biology-based framework. Over the past decade, NIMH’s Research Domain Criteria (RDoC) initiative has become prominent for its attempt to try and conceptualize mental illnesses as “disorders of brain circuits” (Insel et al., 2010, p. 748).

Despite the popularity and promise of RDoC and related initiatives, however, the brain disorder view has come under pressure. For one thing, it seems to have hit a dead end: “Despite decades of work, the genetic, metabolic and cellular signatures of almost all mental syndromes remain largely a mystery.” (Adam, 2013 p. 417) For another, its exclusive focus on some kind of organic substrate seems too limited. It is widely accepted today that psychopathology is multifactorial in nature and that it is an “incorrect assumption that psychiatric illnesses can be understood from a single perspective.” (Kendler 2008, p. 695).

Thus, rather than just uncovering neural circuits, understanding mental illnesses requires looking at a variety of different factors contributing to the development and persistence of, as well as the recovery from, mental illness. That is, scientists must consider the role of, e.g., behavioral, psychological, epidemiological, neurophysiological, genetic, pharmacological and environmental influences on psychopathology rather than searching for a single common cause. This, in turn, requires a plurality of methods to measure and coordinate multifactorial data at different temporal and spatial scales (cf. Olthof et al., 2019; Sheu, 2020). While research and practice in psychiatry already exhibit a high degree of plurality (in both methods and factors considered), there is still little integration—which results in a lack of progress (cf. Sullivan, 2014). To make headway in understanding, treating, diagnosing and preventing mental illnesses, it seems, integrated multifactorial models of mental disorders are urgently needed—and those are not supplied by RDoC or other brain-centered views.

Driven by the rise of computational methods on the one hand and the availability of big amounts of real-world data in psychiatry on the other, a number of mental disorder models have recently been suggested to come to the rescue: causal graph models (e.g. Kästner, 2018; Kendler & Campbell, 2009), Bayesian hierarchical models (Linson & Friston, 2019; Sterzer et al., 2018), functional connectivity models (e.g. Woodward & Cascio, 2015; Satterthwaite et al. 2018), symptom network models (e.g. Borsboom, 2017, Bell & O’Driscoll, 2018, Bringmann & Eronen, 2018, Colombo & Weinberger, 2018, Borsboom, Cramer & Kalis, 2019) and—most recently—multiplexes (e.g. DeDomenico, 2017, Braun et al., 2018, de Boer et al., 2021).

Multiplexes essentially are networks of networks. Over the past decade or so, such multi-layered networks have become increasingly used to analyze various complex real-world systems ranging from biological over social all the way to technical ones (see Boccaletti et al., 2014 for an overview). Currently, there is an increasing interest in using multiplexes in mental disorder research (e.g. de Boer et al., 2021, van den Heuvel et al., 2019). With their network-like structure multiplexes seem intuitive and easy to grasp. At the same time, multiplexes can basically model relations between any kinds of variables and are supposed to link multiple ways of analyzing a system (e.g. Braun et al., 2018). Thus, hopes are high for multiplexes to help us gain a better grasp on the multifactorial nature of mental illnesses and to provide an integrated framework for building comprehensive models of how mental disorders develop, progress, and might be diagnosed and treated (e.g. Brooks et al., 2020, van den Heuvel et al., 2019). How precisely multiplexes are supposed to achieve this, however, remains an open question.

My project in this paper is to assess the true potential of and challenges for multiplexes as models of mental disorders. In order to do this, it will be useful to first examine systematically what challenges psychopathology models face (Sect. 2). I will continue to assess how different species of psychopathology models prominently discussed in recent literature fare with respect to these challenges (Sect. 3). My conclusion will be that none of the contenders—not even two different forms of multiplexes I shall discuss (Sect. 3.5)—meets all the relevant challenges. Still, I shall argue, multiplexes do have the potential to help us make headway in grasping psychopathology. For multiplexes to get off the ground, though, we need to create 4D multiplexes, viz. networks of networks of networks (Sect. 4.1). While 4D multiplexes simultaneously address challenges relating to the multifactorial nature of mental illnesses and their temporal dynamics, they also inherit problems from their 3D cousins. To address these, I suggest we must supplement 4D multiplexes with appropriate constraints, heuristic assumptions and mathematical tools (Sect. 4.2). I conclude that if we embrace complex 4D multiplexes and identify appropriate ways to constrain them, we might unlock the true potential of multiplexes and employ them to make headway in psychopathology research.

2 Challenges for psychopathology models

Models of mental illnesses have two key functions for grasping psychopathology: they (i) represent what we know about a given condition and (ii) provide tools for scientists and clinicians to generate hypotheses about how mental illnesses might be reliably diagnosed, how they unfold over time (in general or in specific patients), how they might be treated, and how we might prevent them. It is rather uncontroversial that models of complex phenomena do not represent the real world accurately (cf. Elgin, 2017), but instead highlight different aspects of a given phenomenon based on researchers’ tools, interests and capabilities (e.g. Haueis & Kästner, 2022; Kästner, 2018). Thus, the representational aspects of psychopathology models are not my primary concern here. Instead, I shall focus on what it takes to construct models that help us to better explain, predict and understand psychopathology and generate hypotheses about how to diagnose, treat and prevent mental illnesses. Throughout this section, I will outline a number of challenges or desiderata that I think models of mental illnesses need to meet in order to be successfully employed in psychiatry.

I already highlighted the perhaps most pressing challenge for contemporary psychopathology models, viz. (Multifactoriality) (Sect. 1). In order to understand how mental illnesses develop and unfold, a variety of different factors must be considered and incorporated in our models, including behavioral, psychological, neurophysiological, genetic, pharmacological, epidemiological and environmental ones. If we take this requirement seriously, any purely brain-centered approaches (such as RDoC or brain connectivity models) can already be ruled out as adequate attempts to build psychopathology models. Instead, the kinds of models we are seeking must be designed to incorporate multiple different factors and processes that potentially operate at different spatial and temporal scales, interact with one another, and are captured in different forms and data formats (cf. Olthof et al., 2019, 2021; Sheu, 2020).

The (Multifactoriality) challenge directly raises a number of other questions yielding further challenges. While the questions associated with each of the challenges I discuss below are conceptually distinct, they may often not be addressed independently. In some cases, a specific answer to one question may even significantly constrain how the remaining challenges might be addressed. This will become quite evident when we assess different species of mental disorder models in light of these challenges below (Sect. 3). For now, though, let us consider the different challenges in turn.

Thinking about (Multifatcoriality) immediately raises questions about variable (Selection). What factors or variables are to be considered potentially relevant and how can we distinguish them from background conditions? That is, e.g., what aspects of a patient’s development and/or surroundings should be included in a mental disorder model? Should we consider phenomenological variables as well? And how do we know what will be “good” variable sets for a mental disorder model to begin with? These questions are directly related to two further challenges: (Levels) and (Clinical Actionability).

The (Levels) challenge concerns the question of how to best analyze a complex system in the context of psychiatry. At which levels or scales should psychopathology be studied and how shall we think of the relations between them? Are we aiming to look at different ontological levels? At which scales should we look for organic or neurophysiological or environmental factors and processes to include? Answering these questions requires both conceptual and methodological considerations on how to individuate, measure, quantify and represent various factors. As a result, strategies to deal with (Levels) will often go hand in hand with specific strategies to address (Selection).

Fourth is the challenge of (Complexity). The essential question here is how complex a model should be to remain tractable without oversimplifying. While the complexity of any given model might de facto be a result of, among other things, how a given model deals with (Multifatcoriality), (Levels) and (Selection), the influence could also go the other way: a pre-determined norm of complexity may constrain possible ways to handle other challenges.

Suppose we have suitable ways of dealing with (Multifactoriality), (Selection), (Levels) and (Complexity). In this case, it would be clear what different variables should go into our multifactorial mental disorder models and how to individuate them; and the model’s complexity is set to some upper bound. But even so, further issues remain. For one thing, there is the challenge of (Integration): How can we relate the different components within a model or partial models of mental illnesses? What are the relations between different variables and data points in psychopathology models? Are there statistical, conceptual, temporal, mereological or metaphysical relations? Can there be multiple kinds of relations within a single model, e.g., causation along with implementation or realization and temporal relations? If so, how are these distinguished? As we will see in our discussion of current psychopathology models, this challenge is especially pressing for multifactorial multiplexes (Sect. 3). Besides, the attentive reader might already suspect that addressing (Integration) will often go hand in hand with addressing (Multifatcoriality) and (Levels). As a rule of thumb: the more different factors at different scales a model needs to take into account, the harder it will be to coherently integrate them (I will return to this in Sect. 4).

The challenges discussed thus far do not only apply to psychopathology models. Literally any model researchers build will have to face (Complexity), (Levels) and (Selection) and, at least where natural phenomena are concerned, only few models will get by without having to worry about some version of (Multifatcoriality) and (Integration). But it does not stop there yet; modeling mental illnesses faces some additional challenges. For instance, there is the challenge of incorporating the (Temporal Dynamics) inherent to psychopathology. As mental illnesses unfold over time, the ways in which different factors influence a patient’s condition will often vary dramatically over time, even within a single patient (e.g., Uher & Zwicker, 2017). Dynamic interactions between different factors are not only relevant in psychiatry (in fact, they are much studied in complexity science) but here they are peculiar. If we want to understand how mental illnesses develop, and what the best treatments and preventive measures are, it will be crucial to capture the temporal dynamics of psychopathology (cf. Olthof et al., 2021). In order to achieve this, we must not only determine how much time should be included in the model but also what would be an appropriate resolution (seconds, days, months, years?) for time-series data and models. We also need to think about how changes in the interactions of different factors and processes that occur over time might be captured in psychopathology models (e.g., Kendler & Gyngell, 2020).

Another issue that is particularly pressing when building psychopathology models concerns the tension between generality and specificity; I shall call it the (Generality) challenge. The main question here is to what extent mental disorder models can accommodate for, on the one hand, general features of mental illnesses that apply across patient groups and, on the other hand, patient-specific individual factors. This issue is particularly important for psychopathology models as it is well known that mental illnesses are clinically as well as biologically heterogeneous (e.g., Wolfers et al. 2018). Besides, human social and psychological processes vary significantly across individuals—both with respect to what factors are involved and how they unfold over time (e.g., Fisher et al. 2018). Thus, there has been an increasing demand to put the person back into psychiatry and consider the individual along with experiential features of mental illnesses (see Molenaar 2004, Anjum et al., 2020, Galbusera et al., 2022). At the same time, though, psychopathology models should exhibit some form of generality to allow for predictions and treatment recommendations for a broad variety of patients.

This consideration takes me to the final challenge: ideally, models of mental illnesses should provide (Clinical Actionability), viz. they should allow clinicians to extract information based on which they can deliver an accurate diagnosis or select the most promising treatments. This challenge highlights that providing a model making predictions is not enough. For a model to be successfully employed in diagnosis, treatment, and prevention of mental illnesses, it should ideally also be interpretable, viz. elicit understanding in clinicians and researchers, and it must be possible to actually implement measures (e.g., specific treatment protocols) derived from psychopathology models (cf. Tonekaboni 2019, Sheu, 2020). How this might be achieved, is a tricky question especially in modern data-driven models that are often highly complex. Thus, meeting (Clinical Actionability) will likely constrain how (Complexity), (Levels) and (Selection) might be addressed.

Addressing the above challenges (see Table 1 for an overview) is rarely an all-or-nothing matter. Rather, the various challenges can be addressed in different ways and to different degrees. And given the interdependencies between challenges, it would be unrealistic to expect that any model will succeed in giving detailed answers to all of the issues and questions raised here. Still, we can expect that each challenge will be met at least to a certain extent. I shall thus consider the following as minimal conditions: To meet (Multifatcoriality), at least some different factors and processes need to be included in a model. For (Selection), (Levels), (Integration) to be met, there must be a somewhat definite answer to the questions associated with each. For (Complexity) to be met, an upper bound should be specified (either directly or indirectly). To meet (Integration), a specification is needed of what kinds of relations the model is supposed to represent and how different kinds of data might be combined into a coherent model. To meet (Temporal Dynamics), time-series data must be incorporated. And to meet (Generality), it must be specified to whether a given model is based on between- or within-subject data and whether it is supposed to generalize to larger patient groups. Finally, for (Clinical Actionability) to be met, the model must be interpretable to clinicians and deliver insights that can be used in diagnosis or treatment. This may involve, e.g., suggesting specific clinical interventions.

Table 1 Overview of the challenges psychopathology models face

At first sight, these minimal conditions may appear rather weak. However, as we shall see in the next section, recent psychopathology models have a hard time even fulfilling these minimal conditions for all challenges.

3 Species of mental disorder models

Let us now examine to what extent the various challenges for psychopathology models are met by contemporary mental disorder models. My discussion here focuses on six different species of models that all have been proposed in light of the failure of RDoC and related initiatives (Sect. 1); my assessment is summarized in Table 2 at the end of this section.

All the model species I discuss here are driven, to some extent, by computational methods and the availability of big amounts of real-world data. As such, they might be cast under the heading of computational psychiatry, which, broadly speaking, aims to construct computational models of psychopathology that can be used to simulate, predict and explain mental illnesses (e.g., Bennett, 2019; Dayan & Huys, 2008; Durstewitz et al., 2019; Montague et al., 2012). While this sounds like a unified project, there are actually two different traditions within computational psychiatry (cf. Bennett, 2019): one that is primarily driven by theory and rooted in computational neuroscience, and one that is primarily driven by data and rooted in machine learning (ML). The main project for scientists working in the first tradition is to specify models based on existing theories and subsequently fit their parameters to real-world data (e.g. from behavioral experiments). Traditional box and arrow diagrams (e.g., Ehlers & Clark, 2000) may qualify as computational models under this reading. Such models are frequently based on strong theoretical assumptions and might not represent the real world accurately (cf. Elgin, 2017). Scientists working in the second tradition, by contrast, aim to extract patterns from big amounts of data through modern statistical inference methods like causal modeling and ML techniques, sometimes based on artificial or even deep neural networks (e.g., Durstewitz et al., 2019). This is the kind of research I shall focus on.

A data-driven approach will take as input whatever data available (behavior, clinical records, socio-economic conditions, symptoms, biomarkers, structural or functional brain data) and produce as output some model depicting systematic connections between variables. Since these models are data-driven, they might uncover relations not yet captured in scientific theories. And as such, they might be promising tools for building progressive multifactorial models of psychopathology. As we shall see below, this is the very hope attached to multiplexes (Sect. 3.5). Scientists might use data-driven models to predict the development of, recovery from, or remission of mental illnesses without recourse to theory. Common representational formats for depicting such models are differential or probabilistic equations along with (causal) diagrams or networks consisting of nodes and edges. Because network-like structures appear familiar and intuitive to grasp, these are particularly common in psychopathology models. Which takes me to the first species of models to discuss.

3.1 Symptom network models

Nomen est omen: symptom network models of mental disorders (e.g. Borsboom, 2017; Borsboom et al., 2019) emphasize the relations between different symptoms in mental illnesses. To put matters briefly, the idea behind symptom network models is that understanding mental disorders requires looking into how symptoms interact with one another over time. To give an (almost) trivial example, consider how fatigue affects mood which in turn might elicit rumination at night leading to more fatigue, etc.

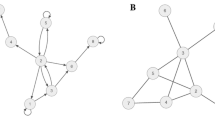
To understand the genesis, development and maintenance of mental illnesses, proponents of symptom network models claim, we must understand the causal connections between different symptoms (Borsboom, 2013, 2017, Borsboom et al., 2019). That can be achieved by estimating causal graphs, usually based on large bodies of behavioral data, that take symptoms as their nodes (cf. Borsboom, 2017; van Loo et al., 2018; Fig. 1). To estimate these graphs, causal modeling techniques (e.g., Pearl, 2000; Pearl & Mackenzie, 2018; Spirtes et al., 1993) are frequently utilized; the modern versions of which can even accommodate for feedback loops within a network of causal relations (e.gDanks & Plis, 2019; Spirtes & Zhang, 2016). In addition, vector autoregressive (VAR) modeling might be used, a method to estimate predictive (Granger-causal) relationships between variables (e.g., Bringmann, 2021). Some scientists even employ modeling techniques from complexity science (e.g., Robinaugh et al., 2020) or chaos theory and coupled differential equations to model the dynamic interactions of different factors in psychopathology over time (see Schiepek et al. 2017). Either way, the symptom-symptom interactions a model uncovers can subsequently be examined with targeted interventions on specific symptom-variables in empirical studies (e.g., Campbell, 2016; de Boer et al., 2021; Rescorla, 2018). To illustrate this, consider giving a patient suffering from insomnia a sleeping pill; this presents an intervention on the variable representing insomnia and can be used to assess, given other influences are controlled for, the effects of insomnia on other factors represented in the network.

Fig. 1

A symptom network at the core of a massively multifactorial network containing genetic (G), neurophysiological (N), and environmental (E) factors influencing the symptom network in the external field (cf. Borsboom, 2017; Borsboom et al., 2019)

Looking at our challenges, how do symptom network models fare? For starters, it should be acknowledged that studying symptom-symptom-interactions might help us make headway in understanding, e.g., the co-morbidity of mental illnesses (Borsboom & Cramer, 2013). Besides, it might be promising to gain insights into the (Temporal Dynamics) of mental illnesses. Symptom network models may deliver such insights in two ways. First, they can be static models (as shown in Fig. 1), the topological characteristics of which provide insights into the development of psychopathologies (cf. Borsboom, 2017). Resilience, for instance, is found where symptoms are less strongly connected whereas symptoms tend to reinforce one another more strongly in densely connected symptom networks. While this approach cannot reflect time series data appropriately (for instance, it cannot capture changes in connection strength over time), there is a second option available. Symptom network models can be designed dynamically (e.g., Cramer et al. 2016, Epskamp et al., 2018). In this case, the model depicts, e.g., by means of (coupled) differential or structural equations, how connection strengths and activation patterns within a network change over time. Likewise, VAR modeling can take time series data into account. Thus, in these cases, (Temporal Dynamics) is met.

Many proponents of symptom network models suggest networks should be given a causal reading (e.g., Borsboom, 2017; Kendler & Campbell, 2009). If we follow along with this, (Integration) is straightforwardly met. It should be noted, however, that the causal reading of symptom network models can at best be limited. For correlational data (on which these models are based) underdetermines what dependency relations might actually have given rise to the relations in the model (see also de Haan, 2020, p. 41) or whether there has been an undetected common cause.¹ Although there has been quite some progress in recent years to improve causal model estimation, these worries still cannot be fully eradicated.

On the bright side again, symptom network models take a clear stance as to what may be included as variables in the network model, viz. symptoms as defined by existing theoretical or diagnostic frameworks (such as the DSM). Hence, (Selection) is met and so are (Levels) and (Complexity). But there is a caveat here, too: As recent debates about DSM revisions and cognitive ontology have shown, the adequacy of DSM-based variables cannot be taken for granted (Tabb, 2016). Thus, to the extent that network models rely on established diagnostic frameworks, their potential to contribute to the long-overdue progress in explaining and treating psychiatric disorders may be undermined. On the other hand, relying on established categories may be helpful to ensure (Clinical Actionability)—at least so long as the specific symptoms can be targeted with certain treatments.

When it comes to (Generality), we see that symptom network models can in principle serve as both general and patient-specific models, depending on the data (between- vs. within-subject data) being used (see also Epskamp et al., 2018). Since this strategy is open to any of the model species discussed here, meeting the (Generality) challenge in the minimal way is somewhat unproblematic. Another way to answer the (Generality) challenge would be to suppose that the overall structure of symptom networks is general while the specific pattern of weighted connections captures differences between individuals. This matches well with the idea that the topological characteristics of a symptom network help explain resilience and susceptibility to mental illnesses, respectively. Like the first strategy, this kind of reasoning can in principle be employed for any of the model species I discuss here. No matter which of the two strategies is used to meet (Generality), it should be acknowledged that, so long as we do not take into account potential effects of factors accessible from the first-person perspective only, any form of generalization in psychiatry will be limited; for we might be missing crucial differences between patients (cf. Molenaar 2004). On the other hand, including such first-person or phenomenological data will inevitably raise additional technical and conceptual issues (cf. Hasselman and Bosmann 2020); for reasons of space, I will not go into this issue in detail but leave the question whether and how to include first-person data in multifactorial models for future research.

To sum up, it seems like symptom network models do not score too badly. If only there was not the obvious point that (Multifafcoriality) is failed; for so long as network models remain limited to symptoms, they cannot be multifactorial in nature.

3.2 Multifactorial network models

To try and remedy the symptom network models’ failure with respect to (Multifactoriality), we might adopt Borsboom et al.’ (2019) suggestion: extend symptom networks by including other factors (such as environmental, demographic, physiological or genetic ones). The result is a massively multifactorial network model (Fig. 1).

While such multifactorial network models clearly address (Multifactoriality), they do so at the expense of no longer meeting (Selection), (Levels), (Complexity). This is because multifactorial network models do not offer any constraints as to what different factors should be incorporated and no upper bound for their complexity is specified. Neither is (Integration) sufficiently answered. For once we add all kinds of environmental, neurophysiological, etc. factors to the external field, we must wonder how to link these different factors. A purely causal reading of all network connections becomes highly implausible. Instead, it seems like the network is going to contain some systematic non-causal connections between, say, certain symptoms and their neurophysiological basis, along with causal relations between variables from the same domain (e.g., symptom-symptom-relations). But how precisely different kinds of relations can be captured and distinguished within a single multifactorial model, remains completely unclear.

When it comes to (Temporal Dynamics) and (Generality), multifactorial network models perform analogously to symptom network models. For (Clinical Actionability) the situation is a little different. The challenge is still met in the minimal way so long as at least some variables can be meaningfully manipulated; but especially where genetic and environmental factors are concerned, such options will be rather limited.

Overall, then, the two species of network models face a dilemma: either they are restricted to symptoms and fail to be multifactorial; or they are extended to become multifactorial and lose traction on other important considerations. Time to consider alternatives …

3.3 Hierarchical Bayesian models

Another species of models that has recently been proposed to increase our grasp of mental illnesses are hierarchical Bayesian models, often in the context of so-called predictive processing (PP) accounts of mental disorders (e.g., Linson & Friston, 2019; Montague et al., 2012; Sterzer et al., 2018). Predictive processing assumes that “the brain is a sophisticated hypothesis-testing mechanism” (Hohwy, 2013, p. 1) and that all cognition is basically a matter of generating and testing, based on an internal hierarchical model, hypotheses about sensory input. The hierarchical model in question is a multi-layered network that has both inter- and intralevel edges. These edges have probabilistic weights and are estimated based on Bayesian inference—hence the name Bayesian models.

At any given level, predictions of sensory signals are passed down to the next lower level. If the prediction at that level does not match the actual input, the prediction error is fed back to the next higher level so that the model can be corrected (Clark, 2016; Friston, 2005; Hohwy, 2013). Alternatively, actions can be taken by the agent to change the sensory input (a process called active inference) and thereby reduce the prediction error (e.g., by looking at an object from a different angle to resolve ambiguities). Over time, the hierarchical model and sensory motor loops utilized in active inference are adjusted, corrected, and revised to minimize future prediction errors. While this is a very crude sketch of PP and there are actually various different specifications (see Spratling, 2017; Wiese & Metzinger, 2017), it suffices to illustrate the main idea of how mental illnesses can be characterized on this account: rather than being a matter of dysfunctional brain circuitry, mental illnesses are a matter of dysfunctional sensorimotor loops coupling agent and environment (cf. Linson & Friston, 2019) or ill-fitted hierarchical Bayesian models.

When visualized, Bayesian hierarchical models are often depicted as network-like structures with recurrent connections that take cognitive operations like “edge detection” as nodes.² They are frequently claimed to provide some sort of grand unifying approach (cf. Colombo & Wright, 2017) that describes information processing in complex systems and characterizes a systems’ behavior including higher-order cognitive processes such as change-blindness, object recognition, or even consciousness (Clark, 2013, 2016; Hohwy, 2013). The models are usually proclaimed to take into account—at the very least—neurobiological and environmental factors, which means (Multifactoriality) will be met, at least in the minimal way.

The architecture of hierarchical Bayesian or PP models is reminiscent of models estimated by dynamic causal modeling (DCM) techniques (see Sect. 3.4). And this is no accident since prediction error minimization—the central principle in PP—relies on the same math as DCM. However, while some neuroscientists have tried to map the mathematical concepts of PP onto neuroanatomical structures in early visual areas (see Friston, 2005; Edwards et al., 2017), the details of PP models for higher-order cognitive processes have not been spelled out. Hence, applying PP to mental illnesses is more of a theoretical outlook thus far; hierarchical Bayesian models do not meet (Clinical Actionability). Besides, it is unclear how PP accounts of mental disorders might address (Selection), (Levels), (Complexity) and (Integration). Since PP models are supposed to seamlessly integrate everything, choice of variables seems rather unconstrained and there is not really an upper bound for complexity. Besides, it remains underspecified how that integration is to be achieved. This highlights an issue already familiar from discussing massively multifactorial symptom network models (Sect. 3.2): just throwing everything together in some unifying framework does not necessarily illuminate or explain much (see also Hartmann & Colombo, 2017)—at least not without further assumptions or constraints (see Sect. 4.2).

Still, hierarchical Bayesian models may successfully address (Generality) in ways familiar from what I said about network models above (Sect. 3.1). Similarly, they may successfully address (Temporal Dynamics) if they rely on time series data and use the same math as DCM. However, it remains unclear what precisely the relation between hierarchical Bayesian models and other psychopathology models is. In principle, one might try and use DCM to identify Bayesian hierarchical models in the brain that could subsequently be used to model mental illnesses. But for such a project to be successful, a whole range of problems would first have to be overcome. To name just a few: data with much better spatial and temporal resolution would be required, it is unclear whether higher-order cognitive processes can be localized or decomposed (Rathkopf, 2018), and there is a lot of heavy-duty math to be done that does not even have definite solutions. Given these complications, perhaps it will be better to just focus on brain connectivity to come up with promising psychopathology models.

3.4 Brain connectivity models

Brain connectivity models are usually based on imaging data.³ There are three kinds of brain connectivity: structural, functional, and effective. Structural connectivity refers to anatomical links between brain regions. Based on imaging data (such as DTI revealing fiber tracts that connect different brain areas) and histology, structural connectivity models can be built that depict brain areas as nodes and the connections between them as edges. While structural connectivity is somewhat straightforward, research on mental illnesses more commonly investigates functional connectivity. Rather than anatomical connections, functional connectivity “describes the connectedness of two brain regions by means of the covariance between their time series.” (Hansen et al., 2015, p. 527). This needs a bit of explanation.

Functional connectivity models are based on methods that capture signals related to neural activity. These can be electrophysiological signals that directly measure electromagnetic signals (most notably EEG or MEG) or neuroradiological signals (MRI, PET) that measure vascular changes, i.e., blood flow phenomena indirectly related to neural activity. One standard approach in this context is to use data from resting state fMRI studies (e.g., Hansen et al., 2015; DeDomenico, 2017; Gratton et al., 2018; Woodward & Cascio, 2015; Satterthwaite 2018; van den Heuvel & Sporns, 2019). The data in question is being recorded while subjects are at rest in an fMRI machine. The variables in this case are signals from defined 3D-regions (voxels or larger regions of interest (ROIs)⁴), viz. the spatial units within which the fMRI records blood-oxygen-level dependent (BOLD) signals repeatedly over time. BOLD signals are generally used as proxies for neural activations in the brain, viz. brain activity.⁵ The data points are measured BOLD signal strengths in each voxel/ROI at different points in time for each individual subject. Based on this data, scientists can analyze which voxels/ROIs show correlated activity within and across time windows to draw inferences about functional connectivity within the brain. This can be done both for individual participants and across groups of participants. The resulting connectivity patterns can be represented as giant covariance matrices or networks where correlation strength is interpreted as connection strength within a given network of brain areas.

While the resulting networks may look somewhat like causal graphs, and functional connectivity models are frequently used to generate hypotheses about causal connections, the relation between the two is not actually straightforward. Most importantly, connectivity models visualize connections based on statistical information about correlations. While the connections may also have an anatomical basis, that is not guaranteed by their concurrent activation. Besides, we must bear in mind that voxels and ROIs are units in space rather than functional units. Thus, a single voxel/ROI may contain (parts of) different functional units. And if this is the case concurrent activation may not be indicative of some form of joint function—it might also be an artifact of how the overall brain has been carved up. While there are data analysis methods to address this issue and increasing MRI resolution also helps prevent it, a more pressing issue remains: concurrent activation does not give us a direction.

To address this issue, it might be useful to study how functional connectivity changes over time (e.g., as certain voxels or ROIs serve as nodes in different networks in different time windows, see Pedersen et al., 2018). The basic idea is that one can estimate the causal architecture of a complex dynamical system—its directed effective connectivity—based on correlational data such as resting state fMRI data by studying time series data. Different mathematical techniques have been developed to achieve this (see Sporns, 2013; Gates et al., 2010). A well-known approach is known as dynamical causal modeling (Penny et al., 2003). The resulting dynamical causal models (DCMs) are based on Bayesian model comparisons estimating the most probable set of directed connections based on time series data and using stochastic or differential equations.

How do brain connectivity models score with respect to our challenges? Somewhat like symptom network models, brain connectivity models are primarily defined in terms of the variables they take as their nodes. In all three kinds of connectivity models described above, the variables considered to build these models are usually voxels. As a result, connectivity models fail (Multifactoriality). On the upside, (Selection), (Levels) and (Complexity) have straightforward answers provided by the imaging technique being used.

Answering (Integration) is a bit more tricky. While it is true that for most brain connectivity models variables will represent BOLD signals in certain voxels, data might be acquired with different temporal and spatial resolutions. Besides, although a causal interpretation of concurrent activation is tempting, we must bear in mind that even the best connectivity analyses are usually based on purely correlational data—a problem familiar from the discussion of symptom networks. With structural and functional connectivity models that data is static; effective connectivity models based on DCM techniques, by contrast, take time series data into account. As such, at least effective connectivity models not only meet (Temporal Dynamics) but also provide genuine causal hypotheses (at least if we can gloss over the complication of a single voxel containing different functional units).

Since brain connectivity models focus on neurophysiological structures, their (Clinical Actionability) seems limited. Surgeons might be able to cut a tumor from a patient’s brain but changing connectivity patterns is not really part of their repertoire. Still, certain neurophysiological structures might be targeted with behavioral interventions—but this requires knowledge about how neural activations are linked to behavior, which brain connectivity models do not supply.

(Generality) can be addressed the same way as with network models: connectivity models can in principle accommodate for both general and individual features of mental illnesses, as they can be based on both between- and within-subject data. Empirical data even suggests both that there are relatively stable functional networks across individuals (Power et al., 2011; Raichle et al., 2001) and that functional brain networks are largely determined—rather than modulated—by individual-specific features (Gratton et al., 2018; Satterthwaite et al., 2018). Still, this finding is well compatible with the idea of relatively general static structural connectivity across subjects where capacities or deficits depend on the parameters (connection strengths) relevant for functional connectivity.

All in all, brain connectivity models resemble core symptom network models in that they can address a similar set of challenges. The precise answers are different, of course, as both species of models offer analyses of psychopathology from very different perspectives, viz. in terms of neurophysiological processes and symptom interactions, respectively. The major feat of a multifactorial account would be to incorporate insights from both these perspectives (and more) into a unified framework while also offering some means to integrate or link them. The big hope is for multiplexes to achieve precisely this.

3.5 Multiplexes: temporal and multifactorial

Multiplexes are the newest game in town when it comes to psychopathology models; they are essentially models based on networks of networks (e.g., DeDomenico, 2016, 2017, Braun et al., 2018, de Boer et al., 2021, Mucha et al., 2010, Pedersen et al., 2018). Over the past decade or so, multiplexes have become increasingly used to analyze a whole range of complex real-world systems, from biological over social all the way to technical ones (see Boccaletti et al., 2014 for an overview). This development has been driven, in part, by the increasing availability of large and high-quality data sets from the real world along with ever more powerful computing technologies. As with multifactorial network models, there is no stringent specification of what the nodes within a multiplex model are supposed to represent.

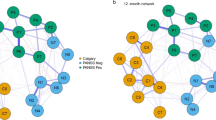
In neuroscience, multi-layer networks are frequently applied to study, e.g., functional connectivity over time (e.g., De Domenico, 2017; Pedersen et al., 2018; Vaiana & Muldoon, 2018; see also Sect. 3.3). In this case, the different layers of the network represent connectivity data from the same network recorded across different time windows. That is, the same set of nodes is being replicated at every layer within the multiplex (Fig. 2a). Although there are not actually more different variables (represented as nodes) included in this kind of multiplex than in a single-layer network, there is a huge advantage: the multiplex can take into account temporal dynamics, viz. it can model how the connectivity among a set of network nodes changes over time.

Fig. 2

Two types of multiplexes. (a) A temporal multiplex replicates the same set of nodes over time. Solid lines indicate connections between nodes within a given time window, dashed lines indicate connections between nodes across different time windows. (b) A multifactorial multiplex incorporating different factors or functions at each layer, or analyses of a system at different functional scales or spatial units. Connections occur within and across layers (see also De Domenico et al., 2016)

Note that such temporal multiplexes conceptually resemble the dynamic versions of symptom and multifactorial network models as well as DCMs of brain connectivity: they capture the dynamic interaction of factors within a given network over time. In dynamical models of complex systems, changes in connectivity are captured in terms of differential equations (e.gSugihara et al., 2012; Zou et al., 2019). In a temporal multiplex, by contrast, states of the network at different points in time are represented as connectivity patterns at individual network layers. While it is in principle possible to mathematically transform dynamic models into multi-layered networks and vice versa (at least for a specified period of time), representing dynamic processes as multiplexes is attractive: multiplexes visualize dynamic variable interactions as changes in network topology across layers—which is much more intuitive to grasp than dynamic structural equations. This might be one of the reasons why such high hopes are attached to multiplex models of mental illnesses: though in principle no less complex than dynamic models, they at least appear more interpretable.

Looking at the same network over time is not the only way to build a multiplex. Another approach is to link networks that model a system at different levels of analysis or scales (e.g., van den Braun et al., 2018; Heuvel et al., 2019); this is often captured in studying a system in different research domains. Such multiplexes may consist, for instance, in network layers containing genetic information at the microscale, cytoarchitectonic information at the mesoscale, and connectivity and behavioral information on the macroscale, respectively (Fig. 2b). In this case, the different kinds of variables or factors (and the relation between them) are being represented within each layer. As such, multiplexes can serve as integrated multifactorial models.

More than that, these multifactorial multiplexes might be extended to include not only models of a system analyzed at different scales but also factors external to the system (in additional network layers). In the context of mental disorders, we might think, for instance, of a multifactorial multiplex to include environmental or socio-economic factors along with symptoms and neurophysiological data at different scales. If this can be achieved, multiplex models of mental illnesses would be truly multifactorial, bringing together knowledge about neurophysiological mechanisms with interactions between symptoms and other relevant factors (cf. de Boer et al., 2021).

The prospect of multiplexes is exciting. However, it is worth mentioning that there is no agreed upon taxonomy of multiplexes; neither is there a clear consensus as to how multiplexes are distinct from other multi-layered networks (Kivelä et al., 2014). Some authors suppose, for instance, that multiplexes necessarily contain the same variables across layers or that all variables operate at the same temporal scales (see Hasselman, 2022). However, this does not match research practice (e.g., Boccaletti et al., 2014, van den Heuvel et al., 2019). Besides, it would limit the application of multiplexes very much; they could still be used to capture temporal dynamics as well as different coordinated behaviors of entities (such as neurons participating in oscillatory patterns at different frequency bands). But modeling the dynamic interactions of multiple different factors of different types and studied within different research domains that are relevant to psychopathology would be pretty much out of the running. Thus, I shall examine temporal and multifactorial multiplexes as described above with respect to our challenges.

Both temporal and multifactorial multiplexes are very unconstrained. They are almost universally applicable and can be constructed from all kinds of variables or networks (say, symptom networks, connectivity networks, …) linking them together into some larger construction—the multiplex. As such, they seem very tempting to build multifactorial psychopathology models. But are they really the panacea for all the challenges psychopathology models face? Unfortunately not.

The flexibility of multiplexes is as much a curse as a bliss. There are no guidelines for variable selection and there is no specification at which levels or scales a system should be analyzed that is inherent to building a multiplex. Neither is the Complexity of multiplexes constrained—they might get arbitrarily complex as there is no upper bound built into the approach itself. As a result, (Selection), (Levels) and (Complexity) all failed for both multifactorial and temporal multiplexes. Still, looking at scientific practice we find that scientists trying to build a multiplex will often deal with these challenges based on pragmatic constraints such as available data, computational power in data analyses or the researcher’s specific focus question. I will return to this point in more detail in Sect. 4.

Though multiplexes are not inherently constrained by much, we may still consider them more constrained than massively multifactorial networks (Sect. 3.2); at least if we suppose that nodes within any given layer of a multifactorial multiplex are of the same type, viz. representing the same kinds of variables or factors. In a massively multifactorial network model, by contrast, we have at best a core of symptom nodes at the center while all kinds of different factors and relations may be present anywhere in the external field. Conceptually, multifactorial multiplex may thus appear more ordered than massively multifactorial network models; but whether this makes much of a difference in practice is another matter.

More ordered or not, when it comes to (Integration) multifactorial multiplexes are on par with multifactorial networks: they fail the challenge as there is no specification of how the different variables in a multifactorial multiplex might relate to one another; there could potentially be many different relations, and if so, we have no way of distinguishing them. This is a particularly serious challenge as building networks of networks requires knowing where the different networks can be linked (see also de Haan, 2020, ch. 2.4.2). Thus, multifactorial multiplexes will not get off the ground without at least some information on how to integrate, e.g., network models at different scales.

Defenders of multiplexes may answer that this issue is precisely what powerful machine learning algorithms are supposed to shed light on: they unmask patterns of dependency across layers in a multiplex that help researchers identify interactions between variables from different domains. Based on these insights, the different networks can be linked up to form a multiplex. But even if this strategy is successful, there are two important limitations to bear in mind. The links identified through ML techniques are based on statistical relations underdetermining the metaphysical relations between entities represented by the multiplex’s variables. This issue is familiar from estimating causal relations in network and connectivity models (Sects. 3.1, 3.2 and 3.4). More than that, it is not even clear whether a statistical relation identified by an ML algorithm corresponds to any relation actually present in the system being analyzed at all.

Second, where powerful ML algorithms are utilized to construct a multiplex, modelers must initially determine what data to feed into the algorithm. That is, they must specify what data sets are to be used and how those can or should be acquired. Just because the algorithms can in principle process any kind of data, that does not mean the multiplex will magically select the factors to be included or the data to be analyzed. ML algorithms might tell you what the most relevant among your data points are, but that does not mean you have included all or only relevant factors in your data set to begin with. After all, multiplexes merely represent the (pruned) data provided by the modeler in an accessible format. In other words: in order to successfully address (Integration), multifactorial multiplexes would need to address (Selection) and (Levels)—which they do not, at least not without additional assumptions.

While (Integration) across layers remains unresolved for multifactorial multiplexes (at least without further assumptions, see Sect. 4.2), it is straightforwardly met by temporal multiplexes. In a temporal multiplex, the same variables are present in every layer and the relation between layers is time. As such, temporal multiplexes, will also easily meet (Temporal Dynamics); they can even capture dynamic interaction between variables at multiple different scales as connections can “jump” layers. For instance, short-range connections between nodes X and Y in layer N and nodes X and Y in layer N + 1, N + 2, N + 3, … in a temporal multiplex might indicate interaction at short time intervals whereas long-range connections between nodes A and B in layer N and nodes A and B in layer N + 100, N + 200, … indicate interaction at longer time intervals. Since multifactorial multiplexes have a different setup representing different factors at each layer, they do not usually represent how a system changes over time. In fact, multifactorial multiplexes that link different scales (say, genetics, cytoarchitectonics, functional connectivity, and symptoms) may present completely static models. As such, multifactorial multiplexes fail (Temporal Dynamics). On the upside, they but meet (Multifactoriality) by definition, while temporal multiplexes might not meet it all (think of, e.g., a temporal multiplex with a symptom network at each layer).

Whether (Clinical Actionability) will be met by multiplexes very much depends on the kind of multiplex under consideration. A temporal multiplex might provide quite a lot of clinically actionable insights if the variables it uses can be clinically intervened upon and the Complexity is not too high. If, by contrast, the temporal multiplex represents brain connectivity data, clinical actionability will be very limited for the psychiatrist. For a multifactorial multiplex, clinical actionability will much depend on what we know about the relations between the different network layers. Since that is something not inherent to the multiplex approach, we are probably well advised to consider (Clinical Actionability) failed for multifactorial multiplexes. Against this background, it does not come as a surprise that—to my best knowledge—there is not currently a concrete multiplex model for any specific psychiatric disorder. So far, multiplexes are primarily employed as abstract theoretical models.⁶ And even though they are intuitively appealing, the actual construction of concrete multifactorial multiplexes of any mental illness may be beyond what can be achieved given our current knowledge, available data, computational technology and clinical interventions.

Finally, multiplexes—regardless of which type—seem to fare no better or worse with respect to (Generality) than the other species of models: they can be based on within- and between-subject data and a general multiplex can be tuned to become patient-specific by fitting certain model parameters.

Table 2 Summary of which modeling approaches meet which of the challenges outlined

3.6 Taking stock

Where does all of this leave us? Table 2 summarizes my assessment of the six different model species with respect to the challenges for mental disorder models outlined in Sect. 2. As mentioned above (Sect. 3.1), all species of models are on par with respect to (Generality). Whether (Clinical Actionability) can be met will very much depend on what the variables in the model are, how complex the overall model is, and what representational format it uses. Meeting (Integration) can be achieved by knowing about the relations between different elements of a given model, which can in turn be based on how (Temporal Dynamics) or (Levels) are addressed. To meet (Temporal Dynamics) models can either work with dynamic equations or multiple layers or networks representing a system’s state at different points in time. If neither of this is done, even the most sophisticated multifactorial models taking into account all kinds of factors relevant to mental illnesses, will remain static and thus fail (Temporal Dynamics). Finally, and perhaps most saliently, Table 2 highlights that approaches meeting (Multifactoriality) usually fail with respect to (Selection), (Levels) and (Complexity) while those models that can address (Selection), (Levels) and (Complexity) fail with respect to (Multifactoriality). Even multiplexes as the newest and perhaps most sophisticated species of models proposed to grasp psychopathology, do not escape this pattern.

The lesson to learn from all this is that excitement about apparently limitless degrees of freedom in multiplex construction should not blind us to the fact that multifactorial multiplexes face the same challenges as other multifactorial models of mental illnesses: we do need to specify their ingredients and how these might work together for multifactorial models to get off the ground—even with powerful computational machinery and ever more real-world data at our hands. Thus, if our goal is to address all of the challenges outlined in Sect. 2 with a single psychopathology model, the result of my exposition is rather sobering: none of the species of models prominently discussed in the current literature on modeling mental illnesses are up to the job. What we need, I suggest, is a novel approach combining the advantages of the most promising contenders. I’ll propose such an approach in the next section.

4 Going forward: 4D multiplexes

Temporal and multifactorial multiplexes as discussed in Sect. 3.5 exhibit a 3D structure: they consist of multiple layers of two-dimensional networks; hence I collectively refer to them as 3D multiplexes. 3D multiplexes have been raising high hopes as models that can be utilized to predict and explain the genesis of mental disorders, and to help diagnose, treat and prevent them. Some of this attraction comes from the fact multiplexes can be built from large amounts of real-world data based on modern ML techniques. Another factor making multiplexes attractive is their network-like structure, which makes them appear very intuitive to work with. But just because networks look intuitive, that does not mean they have a straightforward interpretation.

In fact, as we have just seen, neither temporal nor multifactorial multiplexes make significant headway compared to other model species. Still, I do think multiplexes have the potential to help us better grasp psychopathology. But to unlock this potential, I suggest, we must build 4D multiplexes rather than 3D ones. I will introduce 4D multiplexes below, discuss their limitations, and suggest some strategies that might be employed to overcome these limitations.

4.1 The best of both worlds

Each of the two types of 3D multiplexes contributes a clear answer to one of the challenges particularly important for psychopathology models. Capturing how the dynamics within a system change as it develops, matures or ages is highly important both to understand physiological (e.g., Goldberger et al., 2002) and psychological (Bringmann et al., 2016) processes. Temporal multiplexes acknowledge this insight and successfully address (Temporal Dynamics) by capturing a system’s development over time in different layers. In multifactorial multiplexes, by contrast, the different layers represent different kinds of relevant factors (e.g., physiological, environmental, genetic, …). Thus, multifactorial multiplexes are well-suited to accommodate for the multifactorial nature of mental illnesses that is frequently emphasized (see Sect. 1); as such, they successfully meet (Multifactoriality). However, neither of the two types of 3D multiplexes (and indeed none of the other species of models discussed here) successfully meets both (Temporal Dynamics) and (Multifactoriality). To incorporate both time series and multifactorial data, I suggest, we must combine the strategies adopted by temporal and multifactorial multiplexes to build 4D multiplexes (Fig. 3). Multiplexes, that is, consisting of layers of 3D multiplexes. We can think of them as multifactorial multiplexes to which a temporal dimension has been added.

Fig. 3

A 4D multiplex incorporates time series for a multifactorial multiplex. Solid lines indicate relations between nodes within the same time window, dashed lines represent relations between nodes across different time windows

While 4D multiplexes address both (Temporal Dynamics) and (Multifactoriality), they also inherit some of the problems from each of their 3D cousins: While (Generality) can be addressed in the usual way, to what extent (Clinical Actionability) is addressed will very much depend on the specific variables in the model, what is known about their relations and to what extent they might be targeted by therapeutic or clinical interventions. Similarly, (Integration) is only addressed along the temporal dimension (as with temporal multiplexes) so long as important foundational questions are not answered. These include questions associated with (Selection), (Levels) and (Complexity). But when it comes to variable selection, or to deciding at which level or scale to best analyze a system, 4D multiplexes are just as unconstrained as 3D multifactorial ones.

My examination above (Sect. 3) has made it quite plain that any truly multifactorial psychopathology model faces issues with (Selection), (Levels) and (Complexity). 4D multiplexes are no exception to this rule; and since they have an additional dimension compared to their 3D cousins, we might fear they inevitably fail the (Complexity). I argue below that this is not the case. Still, we do need to supplement 4D multiplexes with appropriate constraints, heuristic assumptions and mathematical tools to unlock their true potential and overcome the challenges familiar from the discussion of multifactorial multiplexes (Sect. 3.5).

4.2 Addressing complexity by adding constraints

It is well known in philosophy of science that scientific inquiry needs to be meaningfully constrained by research questions, theory or heuristic assumptions (see e.g. Bechtel and Richardson 2010, Kästner, 2018; Potochnik & de Oliveria, 2020; Kästner & Haueis, 2019; Haueis & Kästner, 2022). Consider a very simple example: When asked to observe and write a report, students in a physics class will usually ask, what they are supposed to observe, under what conditions, what to focus on, what they can take for granted and what questions their report shall address (cf. Popper, 1963). If none of these factors is specified, observation is difficult or even pointless.⁷ But this is not a problem with observation per se. Rather, the problem is one of missing constraints, an outlook, or a specific research perspective.

When it comes to building 4D multiplexes we face an analogous issue: the degrees of freedom for constructing these models are almost limitless; but this is not a problem with multiplexes qua their being multiplexes. Worries about looming complexity and missing constraints are by no means new to modeling or specific to psychiatry. Yet, they do seem particularly pressing when building 4D multiplexes for several reasons. For one thing, multiplex models have not yet been spelled out for any concrete mental illness, so we do not yet have a good grasp of how they should be constrained such that they become useful to predict, explain, diagnose, treat and prevent mental illnesses. For another, constructing multiplexes may be based on huge amounts of real-world data fed into (sometimes opaque) ML algorithms constructing models no longer interpretable to humans (Sheu, 2020; Tonekaboni et al., 2019). And the fact that 4D models are quite difficult to grasp for most people living in a 3D world does not help either. However, it is essential for psychopathology models to contribute to clinicians’ understanding of a disease in order for them to be useful (e.g., Christophe et al., 2020). Happily, all of these worries can be answered.

For starters, it is worth pointing out that 4D multiplexes are just 3D multifactorial multiplexes with an additional temporal dimension. Thus, when it comes to constructing 4D multiplexes, the crucial questions we need to answer to address (Selection), (Levels) and (Complexity) are really the same as when building 3D multifactorial multiplexes: What variables are supposed to be included at different layers? How do we identify and individuate these? And what do we know about systematic variable relations within and across layers? While there will unlikely be universal answers to any of these questions, possible answers will be significantly constrained in practice by available data, methods, and tools as well as researchers’ specific focus questions, etc.

For instance, answers to the (Selection) challenge will often be constrained by experimental designs and available data. Data acquisition is inevitably constrained by researchers’ skills as well as available methods and tools (e.g. by picking questionnaire-based or imaging research), by technical features (e.g. fMRI having low temporal resolution), by computational power in complex data analysis pipelines, or by the availability of resources such as funding or research time. Besides, scientists must not only decide what factors they are interested in and how they could potentially measure them, they must also think about how to access the relevant (clinical) population. Working with clinical populations raises additional issues: scientists must accommodate for patients’ special needs without compromising their design and they must avoid comorbidities compromising the data. All of these will naturally provide constraints that contribute to addressing not only (Selection) but also, partially at least, (Levels), (Complexity) and (Clinical Actionability).

While the practical constraints just outlined are unavoidable, they are not usually universal or objective. Even with standardized brain imaging techniques, there is no objective data since data acquisition is always guided by idiosyncrasies (cf. Ward 2022). And matters get worse if we think of, e.g., data from questionnaires relying on patients’ self-assessment. Thus, again, how precisely (Selection) and its related challenges are addressed by any given model will very much depend on the specific data being used and how it has been acquired. This, in turn, may be significantly influenced by the very research questions that scientists focus on and what specific aspects of a phenomenon they are interested in. In psychiatry, as in many other life sciences, we find that specialists from different disciplines contribute research from a plurality of epistemic perspectives (Kästner, 2018) and explanatory styles (Potochnik & de Oliveria, 2020). Depending on their interest, skills and research foci, experts from different disciplines (such as neurobiology, psychology, sociology and genetics) will not only acquire different data with different methods and experimental designs; they will also contribute different heuristic or working assumptions about relations between variables (e.g. that certain neurophysiological properties elicit changes in patient behavior, that environmental factors impact gene expression, or that certain factors can be studied at the same temporal resolution). As a result, possible ways of addressing (Levels), and at least to some extent (Complexity) and (Integration), will be constrained by heuristic assumptions derived from researchers’ background knowledge and established theories.

Focusing on specific aspects or research questions, as well as employing heuristic assumptions and constraints is nothing miraculous or uncommon in scientific inquiry. Indeed, the construction of partial, competing and complementary explanatory models is part and parcel of scientific progress (Haueis & Kästner, 2022); and it is to be expected that different outlooks or perspectives on a phenomenon to be explained will illuminate different aspects of it. One way to achieve this is by division of labor between multiple models. The great promise of 4D multiplexes seems to be, though, that all the pieces of the puzzle shall eventually be integrated into a single coherent model. But how is this supposed to work?

One suggestion is that powerful ML techniques can be employed to identify patterns across different data sets that are not otherwise accessible to researchers and thus help us make significant headway in psychiatry (e.g., Tonekaboni et al., 2019; Sheu, 2020; Christophe 2020). This takes us to the last worry. Namely that while the dimensionality of 4D multiplexes may not be an issue, and practical constraints will usually ensure (Selection) and (Levels) are met, (Complexity), (Integration) and (Clinical Actionability) may not be sufficiently addressed. If, ultimately, a bunch of different data sets are fed into sophisticated ML algorithms constructing a model, that model might no longer be interpretable to clinicians; besides model complexity might well get out of hand and it is unclear how integration across different kinds of variables and data sets is supposed to work or how to ensure models will deliver clinically actionable insights. These are the perhaps deepest challenges for 4D multiplexes. Thankfully, I suggest, we can borrow strategies from other research areas—such as complexity science and explainable AI—to address them.

In a nutshell, my proposal is this: As far as (Integration) is concerned, we can not only rely on certain heuristic assumptions provided by theory and epistemic perspectives but also on mathematical tools from complex systems research. These tools are designed to incorporate data from different factors across multiple temporal and spatial scales as well as to model multi-scale interactions (e.g., Olthof et al., 2019; Zou et al. 2020; Sugihara et al., 2012). As for (Clinical Actionability), it may well be the case that the patterns ML algorithms uncover are not straightforwardly interpretable and clinically actionable. However, we can translate these patterns into actionable findings by utilizing so-called interpretation methods (familiar from the discussion about explainable AI) which can also help reduce model complexity (see Sheu, 2020). While fulfilling (Integration) and (Clinical Actionability) may be pulling towards opposite ends, it is a reasonable middle-ground that we must seek. Finally, (Complexity) will also be indirectly addressed by the answers provided to (Selection), (Levels) and (Integration) based on practical constraints.

In summary, 4D multiplexes can—once supplemented with appropriate constraints, heuristic assumptions and mathematical tools—successfully address all the important challenges for psychopathology models examined here: They are multifactorial in nature, incorporate temporal dynamics, can be based on within and between subject data to provide patient-specific or general models, respectively integrate multi-variate data across various different scales, and provide clinically actionable insights. Besides, practical constraints determine at what levels or scales a system is to be analyzed and what variables will be taken into account—which in turn provides a natural upper bound for the model’s complexity.

To assess the true potential of 4D multiplexes and the effectiveness of the various supplementary constraints, the next step for researchers will have to be to create specific 4D multiplexes for concrete mental illnesses. In addition to providing a concrete application scenario, there are a few more avenues for research in the context of 4D multiplexes worth pointing out: First, it is still unclear how to incorporate first-person or phenomenological data into psychopathology models and how the technical and conceptual issues related to it can best be addressed. Second, it is still unclear how to best specify the boundaries of system fluidly interacting with the environment; this has direct consequences for building psychopathology models. Future work will thus need to illuminate how to best accommodate for continuous agent-environment interactions and how to relate those to the interactions between other factors within the model. Third, it will be worth looking into the precise relationship between multiplexes and graph neural networks (see Zhou et al., 2020). At first sight, it seems well-worth examining whether they might be equivalent. Finally, the application of machine learning and interpretability methods to models of mental illnesses is still in its infancy; in years to come, scientists will have to develop tools and algorithms specifically tailored to clinical practice to create psychopathology models that will actually improve prediction, diagnosis, treatment and prevention of mental illnesses.

5 Conclusions

My project in this paper has been twofold. First, I offered a systematic analysis of what the desiderata, or challenges, for psychopathology models are and to what extent these are fulfilled by different species of models of mental illnesses currently discussed as alternatives to RDoC. My conclusion was rather bleak: none of the contenders—not even 3D multiplexes—are up to the job. Second, I argued that multiplexes still have potential to remedy this situation. To unlock this potential, I propose, we must build 4D multiplexes rather than 3D ones. 4D multiplexes present a novel species of psychopathology models that is simultaneously multifactorial in nature and accounts for the temporal dynamics of mental illnesses. To address the remaining challenges, 4D multiplexes must be supplemented with appropriate constraints, heuristic assumptions and mathematical tools that are well-known from scientific practice.

The prospect of 4D multiplexes is exciting and promising to make headway in psychopathology research. Still, it must be acknowledged that while meeting (Multifatcoriality), (Temporal Dynamics) and (Generality) is relatively straightforward, meeting (Selection), (Levels), (Complexity), (Integration) and (Clinical Actionability) requires a complicated dance between identifying practical constraints, linking different kinds of data, employing different mathematical and ML tools, and incorporating theoretical and heuristic assumptions. The specific choreography will vary for any given case—and much more research is needed to specify concrete 4D multiplexes for specific mental illnesses.