A coherent trio of, distance and size based, measures for nomic and actual truthlikeness

Abstract

So far, the most prominent measure for actual truthlikeness, i.e. the likeness of a theory to the actual truth, is Ilkka Niiniluoto’s minsum definition, which is purely based on distances. A competing definition is the average distance measure proposed by Pavel Tichy and Graham Oddie. We will define three related, distance and size based, measures for actual truthlikeness and compare them with the two well-known options. However, we will start, Sect. 2, from a trio of such measures for nomic truthlikeness. The nomic truth, or the true theory, here refers to what is nomically, e.g. physically, possible. In a nomic (and factual) context there are two basic kinds of theories, viz. either based on an exclusion claim or on an inclusion claim. Two-sided theories combine these claims, with the maximal claim as extreme special case. We will base truthlikeness measures for exclusion, inclusion, two-sided, and hence maximal, nomic theories on two similarity measures, one in terms of distances between conceptual possibilities and the other in terms of sizes of sets of such possibilities. In Sect. 3 we will treat actual truthlikeness as extreme special case of nomic truthlikeness, viz. assuming that there is just one nomic possibility, the actual one. Next we will compare the resulting measures mutually and with the above mentioned measures of Niiniluoto and Tichy & Oddie. Finally, in Sect. 4, we will sum up the results and explore five questions for further research.

1 Introduction

So far, the most prominent measure for actual truthlikeness, i.e. the likeness of a theory to the actual truth, is Ilkka Niiniluoto’s (1987, 2020) minsum definition, which is purely based on distances. A competing definition is the average distance measure proposed by Pavel Tichy (1978) and Graham Oddie (1981, 1986, 2013, 2016). We will define three related, distance and size based, measures for actual truthlikeness and compare them with the two well-known options. However, we will start, Sect. 2, from a trio of such measures for nomic truthlikeness. The nomic truth, or the true theory, here refers to what is nomically, e.g. physically, possible. In a nomic (and factual) context there are two basic kinds of theories, viz. either based on an exclusion claim or on an inclusion claim. Two-sided theories combine these claims, with the maximal claim as extreme special case. We will base truthlikeness measures for exclusion, inclusion, two-sided, and hence maximal, nomic theories on two similarity measures, one in terms of distances between conceptual possibilities and the other in terms of sizes of sets of such possibilities. In Sect. 3 we will treat actual truthlikeness as extreme special case of nomic truthlikeness, viz. assuming that there is just one nomic possibility, the actual one. Next we will compare the resulting measures mutually and with the above mentioned measures of Niiniluoto and Tichy & Oddie. Finally, in Sect. 4, we will sum up the results and explore five questions for further research.

2 Nomic truthlikeness

2.1 Basic notions

In this section the main distance and size based definitions of nomic truthlikeness will be given. We will present them in Niiniluoto’s cognitive problem terms, but for the rest in our favorite set-theoretical way. There are two cognitive problems to be considered, the actual and the nomic, both with corresponding partial and complete answers. The cognitive problems are:

What is the actual or factual truth?

What is the nomic truth?

Here, the nomic truth is the truth about what is e.g. physically, biologically, economically possible. It turns out to be practical to start with the nomic truth problem.

Our basic universe is a set of mutually exclusive and together exhaustive conceptual possibilities at a certain occasion in a certain fixed context. One conceptual possibility will be the (f)actual one at a certain moment and a specific subset will contain the nomic possibilities on each occasion, the other ones are nomically impossible. Apart from the assumption that all subsets to be considered are finite, it will be a very general approach.

We will use the following symbolizations throughout the paper.

• U: universe, the set of elementary conceptual possibilities in a given domain, constituting the (mutually exclusive and together exhaustive) complete answers to the (f)actual cognitive problem: what is (f)actually the case? These possibilities can be of any kind, e.g. the natural or the real numbers, the possible states or trajectories of a system, the constituents of a language, the (local) possible worlds, the elementary outcomes of an experiment, or the possible kinds of systems.

  • x, y, t, x₁, x₂, …x_k: elements of U, complete answers to the cognitive problem of the actual truth. Singleton sets {x} will also be simply indicated by x in set-theoretically isolated contexts

• d(x, y): a given, logically or mathematically well founded, underlying normalized symmetric non-trivial distance function, that is,

  • 0 ≤ d(x, y) ≤ 1, d(x, y) = 0 iff x = y, d(x, y) = d(y, x)

  • d(x, y) is a (normalized) metric if it satisfies in addition the triangle inequality: d(x, y) ≤ d(x, z) + d(z, y)

  • d is non-trivial, where d is (discrete or) trivial means that d(x, y) = 0 if x = y, otherwise d(x, y) = 1.

  • s(x, y) = _df 1 − d(x, y), the similarity of x and y¹

• X, Y, T: finite subsets of U (non-empty, except when otherwise stated), representing partial or complete answers to the cognitive problem of the nomic and the actual truth (to be characterized). (Finiteness of subsets: to be generalized).

• |X|: the size (or measure) of X;|{x}| =|x|= 1

• t ∈ U: the actual or factual truth

• tl(x, t) = s(x, t) = 1 − d(x, t): the underlying truthlikeness measure

• T ⊆ U: if |T|> 1, T represents the nomic truth, i.e. the set of nomic, e.g. physical, biological, or economic possibilities; if |T|= 1, T represents the (singleton) actual truth {t}.

The nomic cognitive problem reads: Which of the subsets of U is the set of nomic possibilities T? In Kuipers (2019, Ch. 4) I present my basic theory of qualitative (symmetric difference based) nomic truthlikeness in terms of claims of theories.² The three possible claims of ‘theory X’ are:

Exclusion claim3	T ⊆ X (⇔ cX ⊆ cT)	All excluded possibilities are nomic impossibilities (X is a law following from T)
Inclusion claim	X ⊆ T	All included possibilities are nomic possibilities (all members of X are models of T)
Combined claim	X ⊆ T ⊆ X (⇔ X = T)	the maximal claim,4,5

These theories will may be called exclusion (E-), inclusion (I-), and maximal theories, respectively.

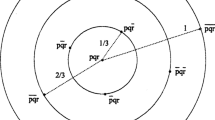
Figure 1 depicts the first two claims. The third claim represents of course a complete answer to the nomic cognitive problem. The first two claims represent partial answers. The exclusion claim ‘T ⊆ X’ can be reconstructed as the disjunction of complete answers for all subsets Y of X (Y ⊆ X) with the claim ‘Y = T’. The inclusion claim ‘X ⊆ T’ can be reconstructed as the disjunction of complete answers for all supersets Y of X (X ⊆ Y) with the claim ‘Y = T’.

Fig. 1

The exclusion and inclusion claim

A theory X is called E-true (or, an E-theory is true) when its exclusion claim is true (T − X = ∅), it is E-false (or, an E-theory is false) otherwise (T − X ≠ ∅). A theory X is called strongly E-false (or, an E-theory is strongly false) when X and T do not even overlap (T − X = T or equivalently, X − T = X). Note that the exclusion claim has due to the equivalence T ⊆ X ⇔ cX ⊆ cT a Popperian flavor, the complement of X, cX, is its empirical content, i.e. what X excludes, by this claim, to be or to happen.

Similarly, with similar (but not mentioned) alternative formulations, a theory X is called I-true when its inclusion claim is true (X − T = ∅), it is I-false otherwise (X − T ≠ ∅). It is called strongly I-false when X and T do not even overlap (X − T = X). Of course, X is strongly I-false iff X is strongly E-false.

In many contexts it will be possible to give a syntactical formulation of the three kinds of claims, as well as examples of true and false claims. Let L₅ indicate an interpreted propositional language of five atomic propositions p₁, p₂, p₃, p₄, and q, representing a connected electric circuit with 4 switches that are on (p_i) or off (¬p_i), and one bulb that may give light (q) or not (¬q). Let T be the, as yet unknown, L₅-proposition representing precisely all physically possible states of affairs of the circuit, that is, the nomic truth (one of which will be the (f)actual truth at a certain occasion). Let S be some L₅-proposition. Then T → S is an exclusion claim, viz. claiming that ‘¬S-states’ are excluded from T, and S → T is an inclusion claim, claiming that all S-states are included in T, in the sense that they are compatible with T. Finally, combined maximal claims are of the form T ↔ S. Let, for a specific circuit (represented in Kuipers, 2019, p. 24, but easy to reconstruct) T amount to: T = _df q ↔ (((p₁∧p₂)∨p₃)∧p₄). Since T → (q → p₄) is valid, T → (q → p₄) is a true exclusion claim, whereas T → (p₄ → q) is a false one. Similarly, ((q∧p₁∧p₂∧p₄) ∨ (q∧p₃∧p₄)) → T is a true inclusion claim and ((q∧p₁∨p₂∧p₄) ∨ (q∧p₃∧p₄)) → T is a false one. Finally, replacing ín all examples ‘ → ’ by ‘ ↔ ’ leads to false maximal claims; T ↔ T is the only true maximal claim. By the way, it would be possible to continue the bold / non-bold distinction (T / T), but as a rule it will be clear which ‘T’ is intended, the unknown or the specified one.

The above example deals with the conceptually and nomically possible states of a system. An example dealing with conceptually and nomically possible (kinds) of systems is the following. Let U represent the conceptually possible (stable) molecules, each consisting of a selection of (stable) chemical elements. Let T represent the subset of chemically possible (stable) molecules. As we know, specifying T will be a matter of fitting chemical valences and the like. Of course, the actual truth can be represented as some member of T.

It turns out to be useful (Kuipers, 2019) to introduce separate symbols for E- and I-theories: P represents a postulate (or a conjunction of postulates) that is supposed to include all nomic possibilities (T ⊆ P) and M represents a set of (tentative) models that are supposed to be nomic possibilities (M ⊆ T). Combining them, we get two-sided theories < M, P > with the (combined) claim ‘M ⊆ T ⊆ P’. An < M. P > theory is (EI-) true if both claims are true, false otherwise. Note that a quasi two-sided theory of the form < ∅, P > is just an exclusion theory, and of the form < M, U > it is just an inclusion theory.

In Kuipers (2019) it is still assumed, as a matter of course, that M should be a subset of P. However, on second thoughts this is not self-evident. In an early stage of research one may have rather separate ideas about both M and P such that M is not (yet) a subset of P. But, if so, it is clear, in view of the inconsistency of the combined claim ‘M ⊆ T ⊆ P’, that at least one of them should be revised. Ultimately, one will aim at a pair satisfying the subset relation. As a kind of intermediate, one may assume that at least |M| ≤|P|, the size condition, should hold.

Finally, an < M, P > -theory is maximal if M = P = _df X, and hence with the claim ‘X ⊆ T ⊆ X’, that is, X = T. It is (EI-) true if X = T, false otherwise.

2.2 Truthlikeness of nomic exclusion theories

In this subsection we focus on an exclusion theory P, hence with the exclusion claim ‘T ⊆ P’. Recall that P can be seen as the conjunction of tentative postulates satisfied by T. We define the (normalized distance based) exclusion similarity of P as the average maximal similarity of T relative to P, where s_max(z, P) = 1 − d_min(z, P) = 1 − min{d(z, x)| x ∈ P}⁶:

$${\text{ES}}_{{\text{T}}} \left( {\text{P}} \right) \, =_{{{\text{df}}}} \sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ P}}} \right)/\left| {\text{T}} \right| \, = { 1} - \sum_{{{\text{z}} \in {\text{T}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{z}},{\text{ P}}} \right)/\left| {\text{T}} \right|$$

Note that if P is E-true, i.e. T ⊆ P, ES_T(P) = 1.

ES_T(P) is a prima facie plausible definition of exclusion truthlikeness of P. However, several different P-theories can have the same average maximal similarity. What also matters is the size of P, |P|, in comparison with that of T, |T|. In (Manuscript, 2023) we argue for a general definition of the similarity of two quantities, leading in the present context to the following definition of the relative size or the similarity in size of X and Y⁷:

$$\tt {\text{s}}^{*} \left( {{\text{X}},{\text{ Y}}} \right)\; = \;{\text{s}}^{*} \left( {\left| {\text{X}} \right|, \, |{\text{Y}}|} \right)\; ={{\text{df}}} \;\frac{{_{} {\text{min}}(\left| {\text{X}} \right|, \, \left| {\text{Y}} \right|)}}{{{\text{max}}\left( {\left| {\text{X}} \right|, \, |{\text{Y}}|} \right)}}$$

For now it is important to know that d^*(X, Y) = _df 1 – s^*(X, Y) is a genuine normalized metric:

$$0 \le {\text{d}}^{*} \left( {{\text{X}},{\text{ Y}}} \right) \le {1},{\text{ d}}^{*} \left( {{\text{X}},{\text{ Y}}} \right)\; = \;0\;{\text{iff}}\;{\text{X}}\; = \;{\text{Y}},\;{\text{d}}^{*} \left( {{\text{X}},\;{\text{Y}}} \right)\; = \;{\text{d}}^{*} \left( {{\text{Y}},\;{\text{X}}} \right),\;{\text{d}}^{*} \left( {{\text{X}},\;{\text{Y}}} \right) \le {\text{d}}^{*} \left( {{\text{X}},\;{\text{Z}}} \right)\; + \;{\text{d}}^{*} \left( {{\text{Z}},{\text{ X}}} \right)$$

Moreover, s^*(X, Y) has two especially desirable general properties:

Scale invariance:

For any positive real number a, if |X’|= a|X| and |Y’|= a|Y|, then s^*(X’, Y’) = s^*(X, Y).

Translation convergence:

For variable set X and constant set C, s*(|X|, |X| +|C|) monotone increases to 1 if |X| goes to ∞.⁸

Translation convergence seems plausible enough.⁹ However, if one has doubts about the desirability of scale invariance, e.g., in terms of (size) numbers, s^*(1, 2) = s^*(100, 200), one should realize that if one is inclined to make a difference in this case, one is almost forced to make also differences from the beginning, i.e. between s(1, 2), s(2, 4), s(3, 6),….

We list some special values of s^*(X, Y), where U corresponds to a tautology and ∅ to a contradiction:

$$\begin{array}{ll} {{\text{Y }} = {\text{ U}}: } & {{\text{s}}^{*} \left( {{\text{X}},{\text{ U}}} \right) \, = \left| {\text{X}} \right|} \\ {{\text{Y }} = \emptyset }: & {{\text{s}}^{*} ({\text{X}},\emptyset ) \, = \, 0} \\ {{\text{Y }} = \left\{ {\text{y}} \right\}:} & {{\text{s}}^{*} (\left( {\left| {\text{X}} \right|, \, |\{ {\text{y}}\} |} \right) \, = { 1}/\left| {\text{X}} \right|} \\ \end{array}$$

Now we define the exclusion truthlikeness of P as the product¹⁰ of the size based similarity of P and T and the ‘normalized distance based average maximal similarity’, henceforth simply, distance based similarity of T relative to P¹¹:

$$\begin{gathered} {\text{ETL}}\left( {{\text{P}};{\text{ T}}} \right) \; = \;{\text{s}}^{*} \left( {{\text{P}},{\text{ T}}} \right) \times {\text{ES}}_{{\text{T}}} \left( {\text{P}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\frac{{{\text{min}}\left( {\left| {\text{P}} \right|, \, \left| {\text{T}} \right|} \right)}}{{\max \left( {\left| {\text{P}} \right|, \, \left| {\text{T}} \right|} \right)}} \times \left( {\sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ P}}} \right)} \right)/\left| {\text{T}} \right|) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac{{{\text{min}}\left( {\left| {\text{P}} \right|, \, \left| {\text{T}} \right|} \right)}}{{\max \left( {\left| {\text{P}} \right|, \, \left| {\text{T}} \right|} \right)}} \times \left( {{1} - \sum_{{{\text{z}} \in {\text{T}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{z}},{\text{ P}}} \right)/\left| {\text{T}} \right|} \right) \hfill \\ \end{gathered}$$

If P is E-true, i.e. T ⊆ P, ES_T(P) = 1, and hence ETL(P; T) =|T|/|P|. In a note¹² we specify some special values that may be interesting.

It is easy to check that ETL(P; T) has the following general properties:

${\mathcal{TL}}$.1	Normalized (i.e. unit interval) range	0 ≤ ETL(P; T) ≤ 1
${\mathcal{TL}}$2	Unique target	ETL(P; T) = 1 iff P = T
${\mathcal{TL}}$.3	(Conceptual) continuity	ETL(x. t) = s(x, t) = df tl(x, t)

A frequently subscribed or critically discussed condition of adequacy (Popper, 1963; Niiniluoto 1987, 2020; Oddie 2013, 2016; & Cevolani & Festa, 2020)¹³ is that among true statements, in the sense of E-true statements, truthlikeness covaries with logical strength, here called E-conditional covariance. In our terms, the principle amounts for P-theories to the claim that if T ⊂ P’ ⊂ P the truthlikeness should increase when going from P to P’.

${\mathcal{TL}}$E.4

E-conditional covariance

If T ⊂ P’ ⊂ P, ETL(P’; T) > ETL(P; T)14

Whereas the first three properties can be seen as general conditions of adequacy, whatever the truth claim is, conditional covariance can only be seen as such if the truthlikeness of exclusion (E-)claims is concerned (i.e. ${\mathcal{TL}}$_E.4).

Finally, it is important to note again that ETL(P; L) need not be symmetric: ETL(P; T) = ETL(T; P) does not hold in general.

2.3 Truthlikeness of nomic inclusion theories

Now we turn our attention to the inclusion claim ‘M ⊆ T’, or equivalently, cT ⊆ cM, of inclusion theory M. Recall that M can be seen as a set of tentative models of T. We define the distance based inclusion similarity of M as the average maximal similarity of M relative to T:

$${\text{IS}}_{{\text{M}}} \left( {\text{T}} \right) \, =_{{{\text{df}}}} \sum_{{{\text{z}} \in {\text{M}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ T}}} \right)/\left| {\text{M}} \right| \, = { 1} - \sum_{{{\text{z}} \in {\text{M}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{z}},{\text{ T}}} \right)/\left| {\text{M}} \right|$$

Note that if M is I-true, i.e. M ⊆ T, IS_T(M) = 1.

Again, several different I-theories can have the same average maximal similarity of M relative to T. Hence, what also matters is the size of M, |M|, in comparison with that of T, |T|. It is plausible to use also here the same definition of the size similarity between M and T:

$${\text{s}}^{*} \left( {{\text{M}},{\text{ T}}} \right)\; = {{\text{df}}}\;\frac{{_{} {\text{min}}\left( {\left| {\text{M}} \right|, \, |{\text{T}}|} \right) }}{{{\text{max}}\left( {\left| {\text{M}} \right|, \, |{\text{T}}|} \right)}}$$

Recall that s^*(,) is based on the metric d^*(,) = (1 − s^*(,)) and has two especially desirable general properties: scale invariance and translation convergence.

Now we define the inclusion truthlikeness of inclusion theory M of course as the product of the size based similarity of M and T and the distance based similarity of M relative to T:

$$\begin{gathered} {\text{ITL}}\left( {{\text{M}};{\text{ T}}} \right) \; = \;{\text{s}}^{*} \left( {{\text{M}},{\text{ T}}} \right) \times {\text{IS}}_{{\text{M}}} \left( {\text{T}} \right)) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\;\;\,= \; \frac{\text{min} ( {| {\text{M}} |, \, |{\text{T}}|)}}{\text{max} ( {| {\text{M}} |, \, |{\text{T}}|)}} \times (\Sigma_{{{\text{z}} \in {\text{M}}}} \, {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{T}}} \right))/\left| {\text{M}} \right|) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\;= \;\frac{\text{min} ( {| {\text{M}} |, \, |{\text{T}}|)}}{\text{max} ( {| {\text{M}}|, \, |{\text{T}}|)}} \times ( {{1} - \Sigma_{{{\text{z}} \in {\text{M}}}} \;{\text{d}}_{{{\text{min}}}} \left( {{\text{z}},{\text{ T}}} \right)/\left| {\text{M}} \right|} ) \hfill \\ \end{gathered}$$

If M is I-true, i.e. M ⊆ T, IS_M(T) = 1, and hence ITL(M; T) =|M|/|T|. Some more sp cial values are listed in the note.¹⁵

Again it is easy to check that ITL(M; T) has the following general properties.

${\mathcal{TL}}$.1	Normalized range	0 ≤ ITL(M; T) ≤ 1
${\mathcal{TL}}$.2	Unique target	ITL(M; T) = 1 iff M = T
${\mathcal{TL}}$.3	Continuity	ITL(x. t) = s(x, t) = tl(x, t)

Moreover, among true inclusion (I-true) claims, truthlikeness covaries again with the logical strength between the claims. In our terms, the principle amounts here to the claim that if M ⊂ M’ ⊂ T the inclusion truthlikeness should increase when going from M to M’:

${\mathcal{TL_{I}}}$.4

I-conditional covariance

If M ⊂ M’ ⊂ T, then ITL (M’; T) > ITL(M; T)

Hence, it is a kind of mirror version of (E-)conditional covariance of ETL. The proof is similar.

Finally, it is important to note again that, like, ETL(P; L), ITL(M; T) need not be symmetric: ITL(M; T) = ITL(T; M) does not hold in general. However, it is easy to check that ITL(X; T) = ETL(T; X),¹⁶ where the latter formula expresses the exclusion truthlikeness of T relative to X, i.e. when X would be the truth and T would be an E-theory, a property that might be called crosswise equality of ITL and ETL.

2.4 Truthlikeness of two-sided and maximal theories

2.4.1 Two-sided theories

The following general schematic definition for the combined truthlikeness of two-sided theories < M, P > , with the combined claim ‘M ⊆ X ⊆ P’, is now plausible, viz. the weighted sum of ETL(P; T) and ITL(M; T), where the weights are determined by a parameter α, 0 ≤ α ≤ 1:

$$\begin{gathered} {\text{CTL}}^{\alpha } \left( { < {\text{M}},{\text{ P}} > ;{\text{ T}}} \right) \; = \;\alpha {\text{ETL}}\left( {{\text{P}};{\text{ T}}} \right) \, + \, ({1} - \alpha ){\text{ ITL}}\left( {{\text{M}};{\text{T}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\alpha {\text{s}}^{*} \left( {{\text{P}},{\text{ T}}} \right){\text{ ES}}_{{\text{T}}} \left( {\text{P}} \right) \, + \, ({1} - \alpha ){\text{ s}}^{*} \left( {{\text{M}},{\text{ T}}} \right){\text{ IS}}_{{\text{M}}} \left( {\text{T}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \; \alpha \frac{{{\text{min}}\left( {\left| {\text{P}} \right|, \, |{\text{T}}|} \right)}}{{\max \left( {\left| {\text{P}} \right|, \, |{\text{T}}|} \right) }}\left(\sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},\;{\text{P}}} \right)/\left| {\text{T}} \right|\right)\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+ \;({1} - \alpha )\frac{{{\text{min}}\left( {\left| {\text{M}} \right|, \, |{\text{T}}|} \right)}}{{{\text{max}}\left( {\left| {\text{M}} \right|, \, |{\text{T}}|} \right)}}\left( {\sum_{{{\text{x}} \in {\text{M}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{ T}}} \right)/\left| {\text{M}} \right|} \right) \hfill \\ \end{gathered}$$

Note that CTL^α(< M, P > ; T) reduces to ETL(P; T) and ITL(M; T) when α is assigned the value 1 or 0, respectively.

So far, I do not see convincing reasons to assign to α another value than ½. One could be inclined to argue for objective reasons to let α and (1 − α) account for different values of the relevant size similarities, but this is already done by the relevant factors in ETL(P; T) and ITL(M; T). However, to keep room for convincing reasons, I will continue with the weights α and (1 − α), with 1/2 as preferred value.

Assuming the general definition, if theory < M, P > is (EI-) true, i.e. M ⊆ T ⊆ P, and hence s^*(M, T) =|M|/|T| and s^*(P, T) =|T|/|P|, we get:

$${\text{CTL}}^{\alpha } \left( { < {\text{M}},{\text{ P}} > ;{\text{ T}}} \right) \; = \;\alpha \left| {\text{T}} \right|/\left| {\text{P}} \right|\; + \;({1}\; - \;\alpha ) \, \left| {\text{M}} \right|/\left| {\text{T}} \right|$$

This formula shows clearly that CTL^α(< M, P > ; T) takes care of the fact that a genuine two-sided theory (M ≠ P), even if true, cannot reach the maximal value of 1. If, for example, M ⊆ T ⊆ P and α = ½, |T|= 2|M|= ½ |P|, we get CTL(< M, P > ; T) = 1/2, in our view an intuitively plausible value for this special case.

Another interesting special case is the following. If < M, P > is such that |M| =|P| =|T|, hence if the sizes are already correct, hence s^*(P, T) = s^*(M, T) = 1, we get:

$${\text{CTL}}^{\alpha } \left( { < {\text{M}},{\text{ P}} > ;{\text{ T}}} \right) \; = \;\alpha \left( {\sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ P}}} \right)/\left| {\text{T}} \right|} \right) + ({1} - \alpha )(\sum_{{{\text{x}} \in {\text{M}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{ T}}} \right)/\left| {\text{M}} \right|)$$

If we take α = 1/2, this amounts to just taking the average of the exclusion and inclusion (distance based) similarity.

CTL^α has the following general properties:

${\mathcal{TL}}$.1	Normalized range	0 ≤ CTLα(< M, P > ; T) ≤ 1
${\mathcal{TL}}$.2	Unique target	CTLα(< M, P > ; T) = 1 iff M = T = P
${\mathcal{TL}}$.3	Continuity	CTLα(< x, x} > , t) = s(x, t)) = tl(x, t)
${\mathcal{TL}}$EI.4	EI-conditional covariance:	if M ⊂ M’ ⊂ T ⊂ P’ ⊂ P, then CTLα(< M’, P’ > ; T) > CTLα (< M, P > ; T)

2.4.2 Maximal theories

For maximal theories X, i. e., a theory < M, P > with M = P = X, hence with the claim ‘X = T’, we define TL^α(X; T) = _df CTL^α(< X; X > ; T), and get:

$$\begin{gathered} {\text{TL}}^{\alpha } \left( {{\text{X}};{\text{ T}}} \right) = \alpha {\text{ETL}}\left( {{\text{X}};{\text{ T}}} \right) \, + \, ({1} - \alpha ){\text{ ITL}}\left( {{\text{X}};{\text{ T}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right) \, (\alpha {\text{ES}}_{{\text{T}}} \left( {\text{X}} \right) \, + \, ({1} - \alpha ){\text{ IS}}_{{\text{X}}} \left( {\text{T}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right)\left[ {\left( {\alpha \sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ X}}} \right)/\left| {\text{T}} \right|} \right)\;{ + }\;({1} - \alpha )\left( {\sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{ T}}} \right)/\left| {\text{X}} \right|} \right)} \right] \, \hfill \\ \end{gathered}$$

Hence, TL^α(X; T) is the product of the size similarity of X and T and the weighted average of the exclusion and inclusion (distance based) similarity.¹⁷ If maximal theory X is (EI-) true, i.e. X = T, we get of course TL^α(X; T) = 1.

For maximal theories there seems a plausible objective value of α other than 1/2: α⁺ =|T|/(|T| +|X|). Then we get¹⁸:

$$\begin{gathered} {\text{TL}}^{ + } \left( {{\text{X}};{\text{ T}}} \right)\; = \;{\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right)\left[ {\frac{{\left| {\text{T}} \right|}}{{\left| {\text{T}} \right|\; + \;\left| {\text{X}} \right|}}\; \Sigma_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ X}}} \right)/\left| {\text{T}} \right|\, + \; \frac{\left| {\text{X}} \right|}{\left|{\text{T}}\right|+\left|{\text{X}}\right|} \;\left( { \Sigma_{{{\text{x}} \in {\text{X}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{T}}} \right)/\left| {\text{X}} \right|} \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right)\left[ {\frac{{\sum_{{{\text{z}} \in {\text{T}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ X}}} \right) + \sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{T}}} \right)}}{{\left| {\text{T}} \right|\; + \;\left| {\text{X}} \right|}}} \right] \hfill \\ \end{gathered}$$

Hence, TL⁺(X; T) is now the product of the size based similarity of X and T and the average of the sum of the distance based similarities in both directions.¹⁹

Returning to TL^α(X; T), or ‘α-truthlikeness’, it has the following properties:

${\mathcal{TL}}$.1	Normalized range	0 ≤ TLα(X; T) ≤ 1
${\mathcal{TL}}$.2	Unique target	TLα(X; T) = 1 iff X = T
${\mathcal{TL}}$.3	Continuity	TLα(x, t) = s(x, t) = tl(x, t)
${\mathcal{TL}}$EI.4	EI-conditional covariance	not applicable20

In this section we have introduced a coherent trio of distance and size based measures of nomic truthlikeness, guided by the three different claims that a theory may make: nomic truthlikeness of exclusion, inclusion, and maximal theories, ETL(P; T), ITL(M; T), and TL^α(X; T). For the last one we introduced first two-sided theories < M, P > , combining the first two claims, and their truthlikeness CTL^α(< M, P > ; T), introducing a parameter α. The truthlikeness of maximal theories (M = P = X), TL^α(X; T), was obtained from CTL^α(< M, P > , T) by replacing M and P by X. All four measures are finite subsets of U²¹ and satisfy the plausible conditions of a normalized range (${\mathcal{TL}}$.1), a unique target (${\mathcal{TL}}$.2), conceptual continuity with the underlying (distance based) truthlikeness measure (${\mathcal{TL}}$.3), and the relevant kind of conditional covariance (${\mathcal{TL}}$.4), as far as applicable.²² ETL(P; T) and ITL(M; T) are the product of the relevant size based similarity and the relevant distance based similarity. CTL^α(< M, P > , T) and TL^α(X; T) are the weighted sums of the relevant terms, where α = (1 − α) = ½ is, for the time being, our favorite value. In general, the more similar the size of a theory is to the size of that of the nomic truth, the more the distance based similarities are valued.

To be sure, the direct practical value of these measures is limited as long as one does not know the nomic truth, respectively. But this paper is about the logical problem of truthlikeness, leaving the epistemological problem for a later occasion.²³ However, if one would know the nomic (or actual truth, see below), the measures clearly indicate which revisions of theories bring us closer to the truth and each measure suggests, besides adjusting size, its own focus for attempts to truth approximation: ETL on increasing the exclusion similarity, ITL suggests to focus on increasing the inclusion similarity, and CTL^α (hence TL^α) on both.

Hence we have good reasons to assume that, even without knowing the truth, all three measures provide meaningful guidelines for nomic and actual truth approximation, but also that ETL and ITL have their own risks of detours, whereas CTL^α (hence TL^α) is more cautious in both respects. However, the latter needs a parameter, be it with a plausible role.

3 Actual truthlikeness and the comparison with the minsum and the average definition

3.1 Actual truthlikeness as extreme special case of nomic truthlikeness and as average maximal similarity (Tichy & Oddie)

Most discussions about truthlikeness measures deal mainly, or even only, with actual truthlikeness. At first sight it may seem that the only complete answers to the cognitive problem of the actual truth are factual claims of the form ‘x = t’, with distance measure d(x, t) and truthlikeness measure tl(x, t) = 1 − d(x, t). Moreover, factual claims of the form ‘{t} ⊆ X’, i.e. ‘t ∈ X’, seem typically partial answers, and it is plausible to apply ETL.²⁴ However, formally nothing prevents us to take a more general outlook, and to apply the other ‘nomic’ definitions, ITL and TL^α, in case of a factual claim of the form ‘X ⊆ {t}’²⁵ (formally also being a partial answer), or ‘X = {t}’, respectively. That is, doing so, even though knowing that the corresponding theories are false as soon as X has more than one element, whether or not including t. One could even argue that, if t is the only nomic possibility, this approach is the appropriate one. However, if t is just one of more nomic possibilities, one could perhaps argue for a different approach.

We assume non-empty subsets P, M, X, except when otherwise stated and replace everywhere T by {t} or, more practically, by t. Note that s^*(X, t) = 1/|X|.

We turn first to actual truthlikeness of the exclusion type, i.e. ETL(P; t). Of course, we have now that P is X-true if t ∈ P holds, and E-false otherwise. Note that in the case of the actual truth, there is no distinction between being merely E-false and being strongly E-false, for being merely E-false implies the non-overlap of {t} and X. We get²⁶:

$$\begin{gathered} {\text{ETL}}\left( {{\text{P}};{\text{ t}}} \right)\; = \;{\text{s}}^{*} \left( {{\text{P}},{\text{ t}}} \right) \times {\text{ES}}_{{\text{t}}} \left( {\text{P}} \right)) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{P}}|} \right) \times \sum_{{{\text{z}} \in \left\{ {\text{t}} \right\}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ P}}} \right)/\left| {\left\{ {\text{t}} \right\}} \right| \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{P}}|} \right) \times {\text{s}}_{{{\text{max}}}} \left( {{\text{t}},{\text{ P}}} \right)\; = \;\left( {{1}/|{\text{P}}|} \right)\; \times \;({1} - {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ P}}} \right)) \hfill \\ \end{gathered}$$

If P is E-true, i.e. t ∈ P, ETL(P; t) = 1/|P|.

Turning to actual truthlikeness of the inclusion type, i.e. ITL(M, t), recall that M is assumed to be non-empty. Hence, M being I-true is a very special case: M = {t}. But the formal definition of ITL(M; t) makes perfect sense:

$$\begin{gathered} {\text{ITL}}\left( {{\text{M}};\;{\text{t}}} \right)\; = \;{\text{s}}^{*} \left( {{\text{M}},\;{\text{t}}} \right) \times {\text{IS}}_{{\text{M}}} \left( {\text{t}} \right)) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{M}}|} \right) \times \sum_{{{\text{x}} \in {\text{M}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{M}} \right|\; = \;\left( {{1}/|{\text{M}}|} \right) \times \sum_{{{\text{x}} \in {\text{M}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{M}} \right| \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{M}}|} \right) \times ({1} - \sum_{{{\text{x}} \in {\text{M}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{M}} \right|)\; = \;\left( {{1}/|{\text{M}}|} \right) \times \left({1} - \sum_{{{\text{x}} \in {\text{M}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{M}} \right|\right) \hfill \\ \end{gathered}$$

If M is I-true, hence M = {t}, ITL(t; t) = 1/|{t}|= 1.

Note that e.g. ∑_{x ∈ M} d_min(x, t) could now be replaced by ∑_{x ∈ M} d(x, t) and hence that the second factor in the ‘d-version’ of ITL(M; t) amounts to “1 minus the average distance from M to t”, which is the so-called average distance definition of truthlikeness of Pavel Tichy (1978) and Graham Oddie (1981, 1986, 2013, 2016), recently defended by Cevolani and Festa (2020). From our perspective the size factor (1/|M|) is a crucial refinement of that definition.

For actual truthlikeness from the two-sided perspective we get:

$${\text{CTL}}^{\alpha } \left( { < {\text{M}},{\text{ P}} > ;{\text{ t}}} \right)\; = \;\alpha {\text{ETL}}\left( {{\text{P}};{\text{ t}}} \right)\; + \;({1} - \alpha ){\text{ ITL}}\left( {{\text{M}};{\text{ t}}} \right)$$

Again, if (< M, P > is (E- and I-)true, viz. just in one case, M = P = {t}, the CTL^α-value is 1.

CTL^α(< M, P > ; t) may not be that interesting, except for maximal theories: if M = X = P, we get:

$$\begin{gathered} {\text{TL}}^{\alpha } \left( {{\text{X}};{\text{ t}}} \right) \; = \;\alpha {\text{ETL}}\left( {{\text{X}};{\text{ t}}} \right)\; + \;({1} - \alpha ){\text{ ITL}}\left( {{\text{X}};{\text{ t}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{X}}|} \right) \, \left[{\text{as}}_{{{\text{max}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;({1} - \alpha )\sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|)\right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{X}}|} \right) \, \left[\alpha ({1} - {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right))\; + \;({1} - \alpha )\;({1}\; - \;\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|)\right] \hfill \\ \end{gathered}$$

If X is E-true, i.e. t ∈ X, s_max(t, X) = 1, and hence

$${\text{TL}}^{\alpha } \left( {{\text{X}};{\text{ t}}} \right) \; = \;\left( {{1}/|{\text{X}}|} \right)\;[\alpha \; + \, ({1} - \alpha )\sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|)]$$

If X is I-true, hence X = {t}, for X is assumed to be non-empty, we get, TL^α(X; t) = 1. Similarly, if X is E-true and I-true (EI-true), i.e. X ⊆ {t} ⊆ X, hence X = {t}, we get, TL^α(X; t) = 1.

If X = {x} we get TL^α(x; t) = αs(t, x)) + (1 − α) s(x, t)) = s(x, t) = 1 − d(x, t), i.e. conceptual continuity of ‘actual truthlikeness’.

For the special value α⁺ =|T|/(|T| +|X|), TL^α(X; T) was indicated by TL⁺(X; T), and we get:

$${\text{TL}}^{ + } \left( {{\text{X}};{\text{ t}}} \right)\; = \;\left( {{1}/|{\text{X}}|} \right)\frac{{[{\text{s}}_{{{\text{max}}}} \left( {{\text{t}},{\text{ X}}} \right) \, + \sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)] }}{{{1}\; + \;\left| {\text{X}} \right|}}$$

When X is E-true, t ∈ X, this becomes:

$${\text{TL}}^{ + } \left( {{\text{X}};{\text{ t}}} \right)\; = \;\left( {{1}/|{\text{X}}|} \right)\frac{{\left[ {1 + \sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)} \right] }}{{{1}\; + \;\left| {\text{X}} \right|}}$$

TL⁺(X; t) remains of course 1 when X is I-true or, in the present context equivalently, when X is EI-true, X = {t}.

Regarding the principles of a normalized range (${\mathcal{TL}}$.1), a unique target (${\mathcal{TL}}$.2), conceptual continuity (${\mathcal{TL}}$.3) to the underlying (distance based) truthlikeness measure, and the relevant kind of conditional covariance (${\mathcal{TL}}$.4), it is easy to check that the first three remain to hold straightforwardly in the case of actual truthlikeness. However, it is worthwhile to look in detail to (${\mathcal{TL}}$.4), for the situation is here more complicated.

E-conditional covariance (${\mathcal{TL}}$_E.4) now amounts to: if t ∈ P’ ⊂ P, ETL(P’; t) > ETL(P; t). This is precisely the version of the covariation principle as it is discussed in the literature. I-conditional covariance (${\mathcal{TL}}$_I.4) now amounts to: if M ⊂ M’ ⊂ {t}, then ITL (M’; t) > ITL(M; t). Hence, even if M might be empty, the antecedence cannot be satisfied in the case of inclusion theories. Finally, EI-conditional covariance (${\mathcal{TL}}$_EI.4) was already not applicable to nomic maximal theories (TL^α(X; T)), hence certainly not in the context of actual truthlikeness.

Regarding inclusion and maximal theories it is perhaps more important to remark that among E-true of such theories, covariation between (actual) truthlikeness and logical strength (in the sense in which the exclusion claim of a proper subset of a set is stronger than that of that set) is certainly not valid. We illustrate this for inclusion theories, for which: ITL(M; t) = (1/|M|) × (1 − ∑_{x ∈ M} d(x, t)/|M|). Here it is evident that if t ∈ M’ ⊂ M, i.e. both are E-true, the average similarity (1 − ∑_{x ∈ M’} d(x, t)/|M’|) may decrease so much that it is not compensated by the increase of the size factor (1/|M’|.

In sum, formally derived from the nomic definitions, we have now three different ways of measuring actual truthlikeness, based on size based similarity and distance based similarity, viz., replacing P and M by X, ETL(X; t), ITL(X; t), TL^α(X; t). Here ITL(M; t) is a size sensitive refined version of the ‘average minimal distance’, or better, ‘average maximal similarity’ definition of Tichy and Oddie, and TL^α(X; t) will turn out to be formally a bit similar to Niiniluoto’s minsum measure: both are based on weighted sums of terms related to ETL(X; t) and ITL(X; t).

It will be useful to formulate the definition of Tichy and Oddie explicitly:

$$\begin{gathered} {\text{TO}}\left( {{\text{X}};{\text{ t}}} \right) = {\text{ IS}}_{{\text{X}}} \left( {\text{t}} \right)) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}_{{{\text{max}}}} \left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right| \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sum_{{{\text{x}} \in {\text{X}}}} {\text{s}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right| = { 1} - \sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|\; = \;{1} - \sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right| \hfill \\ \end{gathered}$$

If X is I-true, hence X = {t}, TO(t; t) = 1.

It is easy to check that TO(X; t) satisfies the principles of a normalized range (${\mathcal{TL}}$.1), a unique target (${\mathcal{TL}}$.2),²⁷ and conceptual continuity (${\mathcal{TL}}$.3) to the underlying truthlikeness measure. The inclusion kind of conditional covariance (${\mathcal{TL}}$_I.4), if X ⊂ X’ ⊂ {t}, then TO (X’; {t}) > TO(X; {t}), is not applicable, like in the case of ITL(X; t). The exclusion kind is just not generally valid.

3.2 Actual truthlikeness according to the minsum definition of Niiniluoto

Niiniluoto’s minsum (ms-) definition of actual truthlikeness is evidently guided by an exclusion claim of the form ‘t ∈ X’, because a theory is supposed to be true, when this claim is true. But size considerations play, indirectly, also a role. Note that, if X’ ⊂ X, the (E-) theory X’ is stronger than (E-) theory X. For the comparison of our trio of definitions with Niiniluoto’s ms-definition of actual truthlikeness we first specify the relevant components (see Niiniluoto, 1987, (44) p. 216, (40) p. 214, (85) p. 228)²⁸:

$$\begin{array}{*{20}c} {{\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)} & { = \;{\text{min}}\left\{ {{\text{d}}\left( {{\text{x}},{\text{ t}}} \right)|\;{\text{x}}\;{\text{in}}\;{\text{X}}} \right\}} & \quad \quad \quad{{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;} \\ \end{array} \frac{{\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)}}{{\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)}}$$

Assuming positive parameters γ and γ’ such that γ + γ’ ≤ 1,²⁹ the crucial definition is:

$$\begin{gathered} {\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;\gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;\gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}};{\text{t}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \; \gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;\gamma^{\prime}\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right) \hfill \\ \end{gathered}$$

Some critical remarks are already in order. Note first that, despite the suggestive notation, d_sum is of a different order than d_min. The latter is a normalized distance and the former a ratio of (summations of) such distances. Hence, ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) adds two terms of a different order, which seems conceptually problematic.

Note also that there is no straightforward continuity connection to the underlying distance function:

$${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{x}},{\text{ t}}} \right)\; = \;\gamma {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)\; + \;\gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{x}},{\text{ t}}} \right)\; = \;\gamma {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)\; + \;\gamma^{\prime}{\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\sum_{{{\text{y}} \in {\text{U}}}} {\text{d}}\left( {{\text{y}},{\text{ t}}} \right)$$

is not in general equal to d(x, t), i.e. ${\mathcal{TL}}$.3 is not generally valid. As Niiniluoto (1987, p. 299) shows, this expression equals d(x, t) in case of a balanced distance function (∑_x∈U d(x, y)/m(U) = ½) and the (very) special relation between the parameters: γ + 2γ’/m(U) = 1. Although a balanced distance function is plausible, the special relation does not seem to have a conceptual backing other than getting the desired consequence. However, as a reviewer noted, ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (x, t) is proportional to d(x, t) and hence order equivalent with d(x, t) in the sense that ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (x, t) < ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (y, t) iff d(x, t) < d(y, t). Be this as it may, in my view is conceptual continuity still to be preferred.

The resulting definition of actual truthlikeness is of course:

$$\begin{gathered} {\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right) \; = \;({1} - {\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right))\; = \;{1} - [\gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right) \, + \gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}};{\text{ t}}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{1} - [\gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;\gamma^{\prime}\frac{{\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)]}}{{\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)]}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{1} - \left[ {\gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;\gamma^{\prime}\frac{{\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|}}{{\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{U}} \right|}} \times \frac{{\left| {\text{X}} \right|}}{{\left| {\text{U}} \right|}}} \right] \hfill \\ \end{gathered}$$

Note the similarity in form with our TL^α(X; t), for this can be written as:

$$\begin{gathered} {\text{TL}}^{\alpha } \left( {{\text{X}};{\text{ t}}} \right) \; = \;\left( {{1}/|{\text{X}}|} \right) \, \left[\alpha ({1} - {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right))\; + \;({1} - \alpha ) \, ({1} - \sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|)\right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;\left( {{1}/|{\text{X}}|} \right) \, ({1}\; - \;\left[\alpha {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)\; + \;({1} - \alpha )\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right)/\left| {\text{X}} \right|\right]) \hfill \\ \end{gathered}$$

Both are based on weighted sums of terms related to ETL and ITL. But, of course, they are substantially different and have a substantially different conceptual background. Despite some similarity with TL^α(X; t) in form, for conceptual reasons, ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) can best be compared with ETL(X; t) = (1 − d_min(t, X))/|X|, for Niiniluoto is focusing, in our terms, on the exclusion claim ‘t ∈ X’, i.e. ‘t ∉ U − X’.

It is easy to check that ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) satisfies the principles of a normalized range (${\mathcal{TL}}$.1) and a unique target (${\mathcal{TL}}$.2). Naturally, again there is no simple continuity connection (${\mathcal{TL}}$.3) to the underlying truthlikeness measure: ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (x, t) ≠ 1 − d(x, t), but it is order equivalent (M6, below), though it is now not proportional to 1 − d(x, t) = s(x, t).³⁰

It is important to note that although, apart from the parameters, only underlying distances occur in ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t), it is indirectly, via d_sum, also substantially based on content or strength, hence size, considerations.

If X is true, i.e. E-true in our terms, i.e. t ∈ X, hence d_min(t, X) = 0, we get:

$$\begin{gathered} {\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;\gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right) \, /\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right) \hfill \\ {\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;{1} - \;{\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;{1} - \gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}};{\text{ t}}} \right)\; = \;{1}\; - \;\gamma^{\prime}\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right) \, /\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}\left( {{\text{x}},{\text{ t}}} \right) \hfill \\ \end{gathered}$$

Now it is easy to see that Niiniluoto’s definition satisfies the E-conditional covariation principle for E-true claims, TL_E.4 above (and M4 below), i.e. ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) increases when X shrinks but remains including t, i.e., E-true. This is simply because d_sum(X; t) gets smaller whenever X shrinks in view of its size-independent normalization denominator. The construction seems an ingenious but also somewhat ad hoc way to get the principle satisfied. Moreover, as said before, the construction is conceptually problematic for, in contrast to d_min, d_sum is not a normalized distance, but as a ratio of such distances.

3.3 Comparisons

For the comparison of Niiniluoto’s definition and our triple of definitions we take Niiniluoto’s total set of conditions of adequacy for actual truthlikeness (Niiniluoto, 1987, p. 232/3) as point of departure, of course in his favorite logico-linguistic terms, for which reason we also quote the introductory sentences of his survey as well:

“Our previous discussion in Chapters 5 and 6 has suggested a number of adequacy conditions which an explicate of the concept of truthlikeness should satisfy. We shall state these conditions for a measure Tr(g, h*): D(B) x B → IR for a statement g ∈ D(B) relative to the target h* ∈ B. Further, a non-trivial distance function Δ: B x B → ℜ between the elements of B is assumed to be given.

(M1):

(Range) 0 ≤ Tr(g, h_*) ≤ 1.

(M2):

(Target) Tr(g, h_*) = 1 iff g = h_*

(M3):

(Non-triviality) All true statements do not have the same degree of truthlikeness; all false statements do not have the same degree of truthlikeness.

(M4):

(Truth and logical strength) Among true statements, truthlikeness covaries with logically strength.

• (a) If g and g’ are true statements and g |– g’, then Tr(g’, h_*) ≤ Tr(g, h_*).

• (b) If g and g’ are true statements and g |– g’ and g’ |-/- g, then Tr(g’, h_*) < Tr(g, h_*).

(M5):

(Falsity and logical strength) Among false statements, truthlikeness does not covary with logical strength: there are false statements g and g’ such that g |-- g’ but Tr(g, h_*) < Tr(g’, h_*).

(M6):

(Similarity) Tr(h_i, h_*) >  =  < Tr(h_j, h_*) iff [Δ(h_*, h_i) =] Δ_*i >  =  < Δ_*j for all h_i and h_j ∈ B.

(M7):

(Truth content) If g is a false statement, then Tr(h_* ∨ g, h_*) > Tr(g, h_*).

(M8):

(Closeness to the truth) Assume j ∉ I_g [the index set of g]. Then Tr(g ∨ h_j, h_*) > Tr(g, h_*) iff Δ_*j < Δ_min(h_*, g).

(M9):

(Distance from the truth) Let Δ_*1 < Δ_*i. Then Tr(h₁ ∨ h_i, h_*) decreases when Δ_*i increases.

(M10):

(Falsity may be better than truth) Some false statements may be more truthlike than some true statements.

(M11):

(Thin better than fat) If Δ_*i = Δ_*j > 0, i ≠ j, then Tr(h_i ∨ h_j, h_*) < Tr(h_i, h_*).

(M12):

(Ovate better than obovate) If Δ_*1 < Δ_*i <Δ_*2, then Tr(h₁ ∨ h_i ∨ h₂, h_*) increases when Δ_*i decreases.

(M13):

(Δ-complement³¹) Tr(g, h_*) is minimal if g consists of the Δ-complements of h_*.”

On p. 234, Niiniluoto lists the scoring of his definition on these conditions and a couple of other definitions, with the result that his definition scores the best. Among the other candidates is the average measure of Tichy and Oddie, indicated by Niiniluoto as M_av,³² here as TO, amounting to TO(X; t) = (1 − ∑_{x ∈ X} d(x, t)/|X|). We will translate Niiniluoto’s conditions in our set-theoretic terms and present the scores of his measure ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) = (1 − ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t)) and those of ETL(X; t), ITL(X; t), and TL^α(X; t).³³ In the ITL column we also list, between brackets, the scores of TO(X; t). Finally, recall that we assume that X is non-empty and that d is non-trivial in all cases. Note that the conditions M1 and M2 directly correspond to our ${\mathcal{TL}}$.1 and ${\mathcal{TL}}$.2, respectively, as applied to the case T = {t}. Connections between M-conditions and ${\mathcal{TL}}$.3 and ${\mathcal{TL}}$.4 will be indicated at the spot.

In the first table we list the relevant definitions and in the second table their scores on Niiniluoto’s conditions of adequacy, M1 – M13. In Table 1 we prefer to list the ‘distance versions’ of the five definitions. We also list the (most plausible) underlying claim and the result when X is E-true, i.e., t ∈ X.

Table 1 Truthlikeness measures to be compared

We like to start with a global comparison of these five measures, viz. in terms of their plausible sufficient conditions for increasing actual truthlikeness. The crucial terms are |X|, d_min(t, X), and d_av (X; t) (= _df ∑_{x ∈ X} d(x, t)/|X|). To increase TO(X; t) it is (necessary and) sufficient that d_av(X; t) decreases. To increase ETL(X; t) it is enough that |X| and d_min(t,X) do not increase, and at least one of them decreases. To increase ITL(X; t) it is enough that |X| and d_av(t,X) do not increase, and at least one of them decreases. Finally, both TL^α(X; t) and ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) increase when all three terms |X|, d_min(t,X), and d_av(X; t) do not increase and at least one of them decreases.

The technical way in which they guarantee these sufficient conditions, is rather different. In view of its nomic background, TL^α(X; t) is a rather plausible construction, with a clear role of the parameter, whereas ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) is a rather complicated construction, with parameters without a clear conceptual background³⁴ and based on (1 −) the sum of two terms of a different order.³⁵ For this reason, we prima facie prefer TL^α(X; t) relative to ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t). However, ETL(X; t) and ITL(X; t) are also plausible, and are parameter free. Finally, TO(X, t) can get a similar plausible background by the nomic generalization of it, TO(X; T) = _df 1 − ∑_{z ∈ X} d_min(z, T)/|X|, but compared to ITL(X; t), it fails to take the size factor into account.

In view of the fact that all measures, except TO(X; t), satisfy the target condition ${\mathcal{TL}}$.2, viz. Tr(X; t) = 1 iff X = {t}, see below, one might say that all (these four) roads lead to the truth, as all roads lead to Rome (which was in fact the case in the Roman Empire!). Compared to both ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) and TL^α(X; t), the other measures may be seen as less cautious, they run the risk of detours as measured by the two more demanding measures.³⁶

So far for the global comparison. In Table 2 we evaluate the five measures in terms of Niiniluoto’s 13 conditions of adequacy. Besides the conditions of Niiniluoto, we have inserted rows for ${\mathcal{TL}}$.3, below M6, and some substitution versions of Niiniluoto’s conditions, viz. M7 and M8.

Table 2 Scores of the discussed truthlikeness measures on Niiniluoto’s conditions of adequacy

Overviewing the scores of the five measures with respect to the conditions M1-M13, we may draw some general comparative conclusions.

Comparing TO and ITL, the main differences concern M8 and above all M11. Regarding M8, TO scores half positive and ITL just negative. However, the at least as plausible substitution version of M8, M8^#, is straightforwardly satisfied by both. The score difference with respect to M11 illustrates that sets of different sizes may well have the same average distance to t. For precisely this reason, ITL takes also size differences into account. For both it may remain strange that they have the underlying claim ‘X ⊆ {t}’ (and hence ‘X = {t}’, because X is non-empty). However, this type of claim is in the context of nomic truthlikeness conceptually very plausible: ‘X ⊆ T’.

So, let us focus on the comparison of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ and our trio. In view of the apparently underlying claim of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$, viz. ‘t ∈ X’, Niiniluoto’s definition should primarily be compared with ETL, but in view of the size related term d_sum also with TL^α. In all cases the validity of a principle may need some restriction on a parameter or on some other value. However, as far as the scores of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ and ETL differ, viz. regarding M9 and M12, these principles seem irrelevant for the supposedly underlying (exclusion or maximal) claim. Although I do not see a good reason to claim that ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ in fact presupposes the maximal claim ‘X = {t}’, in view of the technical definition there is good reason to also compare ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ with TL^α. Apart from M4, they largely share the other principles, now including M9 and M12. In two cases, M7 and M8, TL^α satisfies plausible substitution versions. In case of M13, TL^α satisfies it under a plausible condition, which need not be assumed if there is at least one x such that d(x, t) is maximal (1).

Comparing ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ with ITL, the scores regarding M4, M6, M7, and M8 need some clarification. Recall that there is a straightforward nomic mirror version of M4 (${\mathcal{TL}}$_E.4) satisfied by ITL. That the relevant condition happens to be inapplicable in the factual case, is of course not a genuine negative point of ITL. Regarding M6, although both score positive, it is in my view to be preferred that the stronger version, M6^# (conceptual continuity), is satisfied. Regarding M7, which is a mixture of a distance and a size condition and which is only conditionally satisfied by ITL, the at least as plausible substitution version M7^# is straightforwardly satisfied by all four measures. Regarding M8, again a mixture of a distance and a size condition, the substitution version M8^# assumes a plausible purely distance condition and is again satisfied by all four measures. Finally, in general, whereas ITL satisfies all (if relevant, substitution versions of) conditions without restriction, ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ has parameter restrictions with respect to three conditions, viz. M5, M8,³⁷ and M13.

In sum, in the comparison of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ with our triple of definitions, the technical difference may not clearly be in favor of one of the two. However, our main claim is that our three definitions are conceptually more balanced and simpler constructions than Niiniluoto’s definition. The distance measure underlying the latter, i.e. ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t), though technically serving its purposes, is a conceptually strange sum of two terms of a different order. Finally, in contrast to the triple of definitions (and TO), ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ does not straightforwardly satisfy the continuity principle (see M6 and M6^# = ${\mathcal{TL}}$.3 in Table 2), which is conceptually unsatisfactory.

4 Conclusion and questions for further research

4.1 Conclusion

In this paper we have introduced a coherent trio of distance and size based normalized measures of nomic truthlikeness, guided by the three different claims that a theory may make: truthlikeness of exclusion, inclusion, and combined (maximal two-sided) theories, ETL, ITL, and TL^α, respectively. The measures can formally also be used as measures for actual truthlikeness by assuming the extreme special case in which the set op nomic possibilities is the singleton of the actual possibility. The direct practical value of these measures is limited as long as one does not know the nomic and the actual truth, respectively. However, if one would know them they clearly indicate which revisions of theories bring us closer to the truth and each measure suggests its own focus for attempts to truth approximation. Hence we may at least conclude, as we did at the end of Sects. 2.4 and 3.1, that we have good reasons to assume that, even without knowing the truth, all three measures provide meaningful guidelines for nomic and actual truth approximation, but also that ETL and ITL have their own risk of detours, whereas TL^α (and more generally, CTL^α) is more cautious in both respects. However, the latter need a parameter, be it with a plausible role. Hence, we have no clear preference.

Comparing the main quantitative definitions of actual truthlikeness in the literature, Niiniluoto’s minsum definition and Tichy and Oddie’s average definition, with our trio, we may conclude, in view of the scores with respect to Niiniluoto’s 13 conditions, the reasons behind the deviations and the alternative ways to deal with them, that the technical difference may not clearly be in favor of one the two. However, in view of simplicity, it is already defensible to prefer ETL and TL^α above Niiniluoto’s minsum definition ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ of the truthlikeness of claims of the form ‘t ∈ X’ and ‘X = {t}’, respectively. Moreover, ITL provides a size sensitive refined version of the ‘average minimal distance’ definition TO of Tichy and Oddie, and can compete very well with ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$.

There are important extra reasons to favor, depending on the claim, the relevant member of our trio, that is, ETL, ITL, or TL^α. They have some very attractive exclusive properties: 1) they cover actual as well as nomic truthlikeness, the latter even for two-sided theories, 2) they not only satisfy (like ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ and TO) the unit range and the target condition, but also the conceptual continuity principle, that is, in contrast to M^γγ_ms, but like TO, they reduce straightforwardly to the underlying distance based truthlikeness measure for singleton theories, and finally 3) ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ is a rather complicated construction, with puzzling parameters and based on (1 −) the sum of two terms of a different order, whereas ETL, ITL, and TL^α are conceptually transparent and simple constructions. Only TL^α needs a parameter, however with a plausible role.

4.2 Questions for further research

• (1) In a note about the definition of ‘exclusion similarity’ we suggested already that another route was possible for defining ‘exclusion truthlikeness’ due to the equivalence of the claims ‘T ⊆ X’ and ‘cX ⊆ cT’. This leads to the following two possibilities, the one in the text, ETL(X; T), and the complement variant, ETL^c(X; T):

  $${\text{ETL}}\left( {{\text{X}};{\text{ T}}} \right) \; = \;\frac{{{\text{min}}\left( {\left| {\text{X}} \right|, \, |{\text{T}}|} \right)}}{{{\text{max}}\left( {\left| {\text{X}} \right|, \, |{\text{T}}|} \right)}} \times ({1} - \sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ T}}} \right))/\left| {\text{X}} \right|)$$
  $${\text{ETL}}^{{\text{c}}} \left( {{\text{X}};{\text{ T}}} \right) \; = \;\frac{{{\text{min}}\left( {\left| {{\text{cX}}} \right|,\;|{\text{cT}}|} \right)}}{{{\text{max}}\left( {\left| {{\text{cX}}} \right|,\;|{\text{cT}}|} \right)}} \times \left( {{1} - \sum_{{{\text{x}} \in {\text{cX}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ cT}}} \right)/\left| {{\text{cX}}} \right|} \right)$$

As is easy to see, ETL^c(X; T) presupposes a finite universe for the size factor is undefined in case of an infinite universe and the denominator in the summation, |cX| =|U − X| =|U| −|X|, needs to be finite.

Against the first, ‘direct version’, ETL(X; T), one may object that it is conceptually problematic in comparison with ITL, for there seems no good reason to treat the complement version of the exclusion claim, i.e. ‘cX ⊆ cT’, formally different from the inclusion claim ‘X ⊆ T’. Treating this complement version, ‘cX ⊆ cT’, formally like the inclusion claim leads to the second, complement variant of exclusion truthlikeness, ETL^c(X; T). It is easy to check that both versions satisfy the unit range condition (${\mathcal{TL}}$.1), 0 ≤ ETL(^c)(X; T) ≤ 1, the unique target condition (${\mathcal{TL}}$.2), E(^c) TL(X; T) = 1 iff X = T, and the exclusion version of conditional covariance (${\mathcal{TL}}$_E.4), if T ⊂ X’ ⊂ X, then ETL(^c)(X’; T) > ETL(^c)(X; T). However, whereas the direct version satisfies conceptual continuity (${\mathcal{TL}}$.3), ETL(x. t) = s(x, t) = tl(x, t), ETL^c does not, as is easy to check, for we get, using |c{x}| =|c{t}| =|U|− 1,

$$\begin{gathered} {\text{ETL}}^{{\text{c}}} \left( {{\text{x}};{\text{ T}}} \right) \; = \;\frac{{{\text{min}}\left( {\left| {{\text{c\{x\}}}} \right|,\;|{\text{c\{t\}}}|} \right)}}{{{\text{max}}\left( {\left| {{\text{c\{x\}}}} \right|,\;|{\text{c\{t\}}}|} \right)}} \times \left( {{1} - \sum_{{{\text{y}} \in {\text{cX}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{y}},{\text{ c\{t\}}}} \right)/\left| {{\text{c\{x\}}}} \right|} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \;{1} - \sum_{{{\text{y}} \in {\text{c}}\left\{ {\text{x}} \right\}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{y}},{\text{ c}}\{ {\text{t}}\} } \right)/\left( {\left| {\text{U}} \right| - {1}} \right) \hfill \\ \end{gathered}$$

In fact, ETL^c(x; t) is not even order equivalent with tl (x, t) = 1 − d(x, t).

In sum, despite the formal objection, the need of assuming a finite universe and the lack of conceptual continuity seem enough reason to favor ETL above ETL^c. However this may be, by combining ETL^c with ITL and using a parameter like α one can get also a truthlikeness measure for two-sided and hence maximal theories, i.e. theories with the claim ‘X = T’. Further comparative evaluation of the two alternatives is needed.

• (2) This paper is restricted to the logical problem of actual and nomic truthlikeness. For the epistemic or epistemological problem, that is, not knowing the truth aiming at actual and nomic truth approximation in the face of evidence, we may focus on a definition of quantitative success guided by our measures and for the rest remain in line with my previous publications (Kuipers, 2000, 2019). For nomic truth approximation, the latter goes in terms of a set of experimentally realized possibilities, R, and, on their basis, induced laws, where S indicates the strongest law. Note that cS is the set of induced impossibilities. Assuming we made no mistakes, a strong assumption indeed, we get R ⊆ T ⊆ S,³⁸ whatever T is. This leads to the, for the realist-instrumentalist debate, challenging question to what extent a ‘success theorem’ holds, that is, to what extent does ‘quantitatively more truthlike’ predict ‘quantitatively more successful’.

It seems plausible to define, in line with ETL and ITL, the (empirical) exclusion success as s^*(S, X) × (∑_{x ∈ X} s_max(x, S))/|X| and the inclusion success as s^*(R, X) × (∑_{y ∈ R} s_max(y, X))/|R|, and for the combined success the α-weighted sum. Note that all three success notions are, though suggested by, not laden with the corresponding truthlikeness definitions, hence perhaps acceptable for instrumentalists. The following is easy to prove: if R has no counterexamples to X (R ⊆ X), the inclusion success reduces to s^*(R, X), and if X explains, or at least entails, S, (X ⊆ S), the exclusion success reduces to s^*(S, X). However, to what extent the three corresponding success theorems can be proved is not easy to determine.

To be sure, for the epistemological problem, we may also focus, in line with Niiniluoto (1987), on probabilistically estimating the truthlikeness of theories on the basis of the available evidence. Inevitably, such evaluations of theories by empirical results are explicitly laden with the presupposed definition of truthlikeness.

• (3) A number of topics in (Kuipers, 2019), in particular with respect to nomic truthlikeness, ask for extension and comparison (Chapters refer to that book).

• (a) Ch. 1 and 4 explore and defend the (qualitative) symmetric difference definition of more truthlikeness: Y is more truthlike than X iff YΔT is a proper subset of XΔT. The Δ-definition was first proposed for actual truthlikeness by David Miller (1978) and independently for theoretical or nomic truthlikeness by myself (Kuipers, 1982), and further developed in (Kuipers, 2000, 2019). It will be interesting to compare this definition with our trio, in particular assuming that the distance function is trivial: d(x, y) = 0 if x = y, otherwise d(x, y) = 1.³⁹ Moreover, it is interesting to investigate to what extent the ‘trivial’ trio measures are susceptible to the so-called⁴⁰ child’s play objection of Pavel Tichy (1978) and Graham Oddie (1981, 1986, 2016) against the Δ-definition. Finally, it would be interesting to evaluate the (trivial and non-trivial) trio in the light of Zwart’s (2001) distinction, emphasized by Niiniluoto (2003), between content (e.g. Miller, 1978, Kuipers, 2000, 2019) and likeness (e.g. Niiniluoto, 1987; Oddie, 1986) approaches to truthlikeness.

• (b) Ch. 6 deals with a ‘refined’ qualitative (two-sided) approach, in which the ternary notion of structurelikeness (possibility y is more similar to z than x) plays a crucial role. In the present setup it is plausible to interpret this relation in terms of (non-trivial) distances (d(y, z) < d(x, z)), and the question is how refined truthlikeness relates to our trio.

• (c) Ch. 5 deals with a quantitative version of the qualitative approach in terms of symmetric differences in Ch, 4. The interesting question is whether this version also coheres with TL^α, viz. as an extreme case for trivial d?

• (d) Finally, Ch. 7 deals with a (observational—theoretical) stratified version of the symmetric difference approach. Assuming a (reduction or) projection function π from the theoretical level to the observational level, and an order preserving relation between the underlying distance measures, the plausible relational questions are: to what extent does e.g. ETL(Y; T) > ETL(X; T) entail ETL(πY; πT) > ETL(πX; πT)?

• (4) Niiniluoto’s minsum definition asks for a generalization that is also applicable for the nomic truth T. Such a generalization is not only interesting in itself, but also for the comparison with other proposals that work for t and T, such as our trio. Besides some related ways in Ch. 11, Niiniluoto (1987) has defined (Ch. 10, (121), p. 248) a distance measure between statements, of which he points out that it gives his minsum measure as a (very) special case, when one of the statements is the true constituent.

Our tentative proposal for a straightforward generalization of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; t) to nomic truthlikeness in Niiniluoto’s style of defining actual truthlikeness of (exclusion) theories is, assuming positive parameters γ and γ’ such that γ + γ’ ≤ 1:

$$\begin{array}{*{20}c} {{\text{d}}_{{{\text{min}}}} \left( {{\text{T}},{\text{ X}}} \right) \, = } \,\, {{\sum}_{{{\text{y}} \in {\text{T}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{y}},{\text{ X}}} \right)/{\text{m}}\left( {\text{T}} \right)} \quad \quad \quad \quad { {\text{d}}_{{{\text{sum}}}} ({\text{X}},{\text{T}}) = \frac{{\sum_{{{\text{x}} \in {\text{X}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ T}}} \right)}}{{\sum_{{{\text{x}} \in {\text{U}}}} {\text{d}}_{{{\text{min}}}} \left( {{\text{x}},{\text{ T}}} \right)}}} \\ {{\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}},{\text{ T}}} \right)} \,\, { = \gamma {\text{d}}_{{{\text{min}}}} \left( {{\text{T}},{\text{ X}}} \right) \, + \gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}},{\text{ T}}} \right)} \,\, {} \\ {{\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}};{\text{ T}}} \right)} \,\, { = { 1} - {\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}} \left( {{\text{X}},{\text{ T}}} \right) = {1} - [{\text{gd}}_{{{\text{min}}}} \left( {{\text{T}},{\text{ X}}} \right) \, + \gamma^{\prime}{\text{d}}_{{{\text{sum}}}} \left( {{\text{X}},{\text{ T}}} \right)]} & {} \\ \end{array}$$

Note that ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X, t) is straightforwardly the special case of ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; T) when T = {t}. Note also that d_min(T, X) = 0, and hence ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; T) = 1 − γ’d_sum(X, T), if X is E-true, that is, if T ⊆ X.

${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; T) = _df 1 − ${\text{d}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X, T) satisfies at least the following principles:

M1::

(Generalized Range) 0 ≤ Tr(X; T) ≤ 1.

M2::

(Generalized Target) Tr(X; T) = 1 iff X = T.

M3::

(Generalized Non-triviality).

For (E-)true ((E-)false) statements / claims, i.e., T ⊆ X (T − Y ≠ ∅),

Tr(X; T) (Tr(Y; T)) has not always the same value for varying X (Y)

M4::

(Generalized Truth and logical strength).

• (a) If T ⊆ Y ⊆ X then Tr(X; T) ≤ Tr(Y; T)

• (b) If T ⊂ Y ⊂ X then Tr(X; T) < Tr(Y; T)

It would be interesting to also generalize M5 – M13 as plausible as possible and to compare ${\text{M}}_{{{\text{ms}}}}^{{\gamma \gamma^{\prime}}}$ (X; T), with our trio, in particular ETL(X; T) and TL(X; T), and with Niiniluoto’s distance measure between statements referred to at the beginning, and finally with Leg(D(X), C(T)) below.

There is still another way to deal with nomic truthlikeness in the style of Niiniluoto’s treatment of actual truthlikeness, viz. a kind of transformation in terms of ‘propositional nomic constituents’. As a reviewer remarked, a maximal theory “X = T” can be seen as a kind of constituent. Let C(X) = _df “X = T”, where bold T indicates that T has not yet been characterized in the ‘language of U’. That is, C(X) can be seen as the propositional nomic constituent: ∀_{x ∈ X} x ∈ T & ∀_{x ∉ X} x ∉ T.⁴¹ Of course, just one of them is true, to be indicated by C(T) = “T = T”, where the non-bold T is a characterization of T in the language of U. Now we can define nomic truthlikeness of a nomic exclusion theory X, (claiming ‘T ⊆ X’), i.e., a disjunction or set of nomic constituents, D(X) = {C(Y) / Y ⊆ X}, relative to the true nomic constituent, in Niiniluoto’s style. It corresponds to his discussion of legisimilitude (Niiniluoto, 1987, pp. 376–380), in particular by the definition of ‘leg₃’ ((7), p. 377). However, he deals with monadic nomic constituents, i,e, conjunctions of the form &_i( ±)⋄(∃_x)Q_i(x), which we do not consider. In terms of our propositional nomic constituents, we first need a plausible (normalized symmetric) distance function between constituents, δ(C(X), C(Y)). This function may or may not be (relative) size dependent but will almost certainly be based on some underlying (normalized symmetric) distance function d(x, y).⁴² The crucial definition then is, again assuming positive parameters γ and γ’ such that γ + γ’ ≤ 1:

$${\text{Leg}}\left( {\left( {{\text{D}}\left( {\text{X}} \right),{\text{ C}}\left( {\text{T}} \right)} \right)} \right)\; = \;{1} - {\text{d}}^{{\gamma \gamma^{\prime}}}_{{{\text{ms}}}} \left( {{\text{D}}\left( {\text{X}} \right),{\text{ C}}\left( {\text{T}} \right)} \right) = { 1} - [\gamma \delta_{{{\text{min}}}} \left( {{\text{C}}\left( {\text{T}} \right),{\text{ D}}\left( {\text{X}} \right)} \right) \, + \gamma^{\prime}\delta_{{{\text{sum}}}} \left( {{\text{D}}\left( {\text{X}} \right),{\text{ C}}\left( {\text{T}} \right)} \right)]$$

where

$$\delta_{{{\text{min}}}} \left( {{\text{C}}\left( {\text{T}} \right),{\text{ D}}\left( {\text{X}} \right)} \right)\; = \;{\text{min}}\{ \delta \left( {{\text{C}}\left( {\text{Y}} \right),{\text{ C}}\left( {\text{T}} \right)} \right)|{\text{Y}} \subseteq {\text{X}}\} \break \delta_{{{\text{sum}}}} \left( {{\text{D}}\left( {\text{X}} \right),{\text{ C}}\left( {\text{T}} \right)} \right) \, = \frac{{\sum_{{{\text{Y}} \subseteq {\text{X}}}} \delta \left( {{\text{C}}\left( {\text{Y}} \right),{\text{ C}}\left( {\text{T}} \right)} \right)}}{{\sum_{{{\text{Y}} \subseteq {\text{U}}}} \delta \left( {{\text{C}}\left( {\text{Y}} \right),{\text{ C}}\left( {\text{T}} \right)} \right)}}$$

So far for the generalization, respectively transformation, of Niiniluoto’s minsum definition of actual truthlikeness (in)to nomic truthlikeness.

• (5) So far we assumed that all considered subsets of the universe are finite. Plausible challenges are extending the measures to denumerable infinite and continuous subsets. The latter problem brings us, among other, to the topic of the truthlikeness of an interval hypothesis relative to the actual truth (Festa, 1986). Surprisingly enough, our measures are easy to extend to the nomic truthlikeness of such an hypothesis. Let U be the set of real numbers, or the non-negative ones, with a suitable normalized distance function d(x, y) and s(x, y) = 1 − d(x, y). Let X and T be closed intervals. Then e.g. our combined measure TL^α can directly be applied, replacing sums by integrals.

  $$\begin{aligned} {\text{TL}}^{\alpha } \left( {{\text{X}};{\text{ T}}} \right)& = \;{\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right) \, [\alpha {\text{ES}}_{{\text{T}}} \left( {\text{X}} \right) \, + \, ({1} - \alpha ){\text{IS}}_{{\text{X}}} \left( {\text{T}} \right)] \hfill \\ &\quad =_{{{\text{df}}}} {\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right)\left[ {\alpha \int\limits_{{\text{T}}} {{\text{s}}_{{{\text{max}}}} \left( {{\text{z}},{\text{ X}}} \right)dz/ \, \left| {\text{T}} \right|} \; + \;({1} - \alpha )\int\limits_{{\text{X}}} {{\text{s}}_{{{\text{max}}}} } \left( {{\text{z}},{\text{ T}}} \right)dz/|{\text{X}})} \right] \hfill \\ & \quad ={\text{s}}^{*} \left( {{\text{X}},{\text{ T}}} \right) \, [\alpha ({1} - \int\limits_{{\text{T}}} {{\text{d}}_{{{\text{min}}}} \left( {{\text{z}},{\text{ X}}} \right)dz/ \, \left| {\text{T}} \right|)} \\ &\quad + \;({1} - \alpha )\;({1} - \int\limits_{{\text{X}}} {{\text{d}}_{{{\text{min}}}} } \left( {{\text{z}},{\text{ T}}} \right)dz/\left| {\text{X}} \right|)] \hfill \\ \end{aligned}$$

Here we assume:

$$\begin{gathered} \left| {\text{X}} \right|\; = \,{\text{b}}\, - \,{\text{a}}\;{\text{for}}\;{\text{X}}\, = \,[{\text{a}},\;{\text{b}}] \hfill \\ {\text{s}}^{*} \left( {{\text{X}},\;{\text{T}}} \right)\, = \,{\text{min}}\left( {\left| {\text{X}} \right|,\;|{\text{T}}|} \right)/{\text{max}}(\left| {\text{X}} \right|,\;\left| {\text{T}} \right|) \hfill \\ {\text{d}}_{{{\text{min}}}} \left( {{\text{z}},\;\left[ {{\text{a}},\;{\text{b}}} \right]} \right)\, = \,{\text{d}}\left( {{\text{z}},\;{\text{a}}} \right)\;{\text{if}}\;{\text{ z}}\, < \,{\text{a}},\;0\;{\text{if}}\;{\text{ a}}\, \le \,{\text{z}}\, \le \,{\text{b}},\;{\text{d}}\left( {{\text{z}},\;{\text{b}}} \right)\;{\text{if}}\;{\text{ b}}\, < \,{\text{z}}. \hfill \\ \end{gathered}$$

For the underlying distance function d(x, y) we can use the normalized geometric distance if the reals are the universe: d(x, y) =|x − y| / (|x − y| + 1). If we are dealing with genuine quantities, i.e. a ratio scale on the non-negative reals, we would use of course d^*(x, y) = 1 − s^*(x, y) = 1 − min(x, y)/max(x, y) =|x − y| / max(x, y) (Sect. 2.2, and Manuscript, 2023).

Note, finally, that TL^1/2(X; T) with α =1/2 and TL⁺(X; T) with α =|T|/(|T| +|X|) make perfect sense.

Unfortunately, it is now impossible to treat actual truthlikeness just as the extreme special case in which T = [t, t] = {t}. For, since |{t}|= 0, s^*(X, {t}) = 0, which makes TL^α(X; T) uniformly equal to 0. Perhaps one may defend to set s^*(X, {t}) = 1/(1 +|X|) or to restrict actual truthlikeness to the second factor. In the second case, it is perfectly possible that d(x, y) is such that ∫_Td_min(z, X)dz / |T| goes to d_min(t, X) if T = [t, t + x] and x goes to 0. If so, we get:

• (1)
  $$\alpha ({1} - {\text{d}}_{{{\text{min}}}} \left( {{\text{t}},{\text{ X}}} \right)) \, + \, ({1} - \alpha ) \, \left( {{1} - \int\limits_{{\text{X}}} {{\text{d}}\left( {{\text{z}},{\text{ t}}} \right)dz/ \, \left| {\text{X}} \right|} } \right)$$

Note that the second factor of the second term, i.e., (1 − ∫_X d(z, t)dz / |X)), is a straightforward generalization of the average measure of Tichy and Oddie. Note also that (1) reduces to this term when α = α⁺ =|[t, t]|/(|[t, t]| +|X|) = 0 for |[t, t]|= 0. We leave the detailed comparison of (1) with the definition of Festa (1986) as an interesting question for further research.

In conclusion, the proposed trio of truthlikeness measures, raises a number of challenging questions for further research.