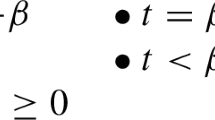On the pure logic of justified belief

Abstract

Justified belief is a core concept in epistemology and there has been an increasing interest in its logic over the last years. While many logical investigations consider justified belief as an operator, in this paper, we propose a logic for justified belief in which the relevant notion is treated as a predicate instead. Although this gives rise to the possibility of liar-like paradoxes, a predicate treatment allows for a rich and highly expressive framework, which lives up to the universal ambitions of investigating epistemological concepts. We start with a base theory for justified belief, and then systematically present putative additional axioms for justified belief. We provide an overview of (in)consistency results when the additional principles are added to the base theory, and discuss their philosophical plausibility.

1 Introduction

Justified belief is a fundamental epistemological concept. Even though there is deep disagreement among epistemologists about the content of the concept of justified belief, most philosophers believe that there is a core concept of justified belief that this disagreement is about. In this paper, we are concerned with the logical principles that govern this core concept.

Over the past two decades, the logic of justification has been more intensively investigated than before. It has been investigated in different frameworks and in different ways. Often a multi-modal framework is adopted, in which the notion of justified belief is related to certain other modal notions (such as being in a position to know, truth, or necessity). At times, the logic of justified belief is investigated in a purely propositional setting, at times it is investigated in a partially quantified setting (where one can quantify, for instance over objects or over reasons).¹

Our aim in this article is to carry out a logical investigation of the concept of justified belief in a quantificational setting that is highly expressive in the specific sense that the objects of justified belief can explicitly be quantified over. Moreover, our investigation is pure in the sense that in our framework, we do not relate justified belief to other specific notions (such as truth or knowledge) or to other specific entities (such as reasons or agents). Indeed, we believe that it is beneficial to gain some clarity about the pure logical laws of justified belief before investigating the logical interaction between justified belief and other modal concepts.

The line of research to which we aim to contribute started around 1980 with (Thomason, 1980; Burge, 1978), building on earlier work such as (Hintikka, 1962; Kaplan & Montague, 1960; Myhill, 1960). It continued at a modest pace over the decades following that, up to the present day, see e.g. (Thomason, 1980; Koons, 1992; Cross, 2001; Cieśliński, 2017; Van Fraassen, 2022).

After a discussion of the background of the problem of the logic of justified belief (Sects. 2 and 3), we formulate a minimal base theory of principles and inference rules for justified belief, and develop a philosophical argument for the thesis that this base theory is incontrovertible (Sect. 4.1). Then we consider a list of additional principles concerning justified belief that have been advocated and criticised in the literature (4.2). We prove that almost every one of them cannot consistently be added to our base theory (4.3). Most of these inconsistency results are not our own: our aim in this section is mainly to collect, extend, and systematically connect results that are scattered in different places in the literature. We then proceed to discuss a few additional principles that can consistently be added to the base theory (Sect. 4.4). In the closing sections, we discuss philosophical arguments for and against the additional principles (Sects. 5 and 6), and sum up our findings (Sect. 7).

2 The framework

Justified belief is a relation between cognitive agents and entities of some kind. In this article, we keep the cognitive agent fixed, and we will call her Catrin. Moreover, we formally treat justified belief not as an operator but as a predicate (J). We do this because we want to work in an expressively strong framework. For instance, we want to be able to capture inferences such as:

$$\begin{aligned} \frac{\text {Catrin believes that fire is hot.}}{\text {There is something that Catrin believes.}} \end{aligned}$$

In the epistemological literature, the objects of propositional attitudes such as belief are often taken to be propositions. From a formal perspective, this complicates matters, because there is currently no satisfactory theory of propositions. But the structural properties of propositions closely resemble those of sentences, and there are excellent theories of the grammatical structure of sentences. So we will take the objects of the attitude of justified belief to be sentences.

It is well-known that, modulo coding, the grammatical structure of sentences is well described by elementary theories of arithmetic, such as Peano Arithmetic ($\mathrm {PA}$). So we take Peano Arithmetic as a background theory of the formal theories of justified belief that will be considered. We will take mathematical induction to govern all properties of numbers. So our theories will be expressed in the language of arithmetic ${\mathcal {L}}_{\mathrm {PA}}$ plus the new justified belief predicate J, and we call this extended language ${\mathcal {L}}_J$. And we take the background theory to be $\mathrm {PA}^J$, which is Peano Arithmetic formulated in the extended language, with J allowed to occur in instances of the induction scheme. In the interest of readability, we will be somewhat sloppy in our notation, especially when it comes to the details of Gödel coding.

Although in our framework we are investigating justified belief only, it is rewarding to consider analogies between justified belief (by a fixed agent) on the one hand, and the concept of truth on the other hand. In formal truth theory, truth is treated as a predicate (T). If we work in the language ${\mathcal {L}}_{\mathrm {PA}}$ +T, which we may call ${\mathcal {L}}_{T}$, then we can generate the liar paradox from the unrestricted Tarski-biconditionals. This has profound implications for axiomatic theories of the fundamental laws governing truth see (Halbach, 1996). In epistemic contexts, similiar situations have occured, so that we find liar like paradoxes for epistemic notions, too.² Those epistemic analogues of the liar paradox will play a major role in the investigations that are carried out in this paper.

In epistemology, justified belief is often implicitly or explicitly treated as an operator instead of as a predicate. In the resulting expressively impoverished setting, liar-like, self-referential arguments cannot be carried out anymore. Despite this advantage, we consider this practice, for certain purposes, unsatisfactory, for it greatly diminishes our ability to identify fundamental laws governing justified belief. Epistemology, like other fundamental philosophical disciplines such as metaphysics, has universal ambitions: it aims to uncover basic principles that hold for all instances of justified belief (empirical beliefs, moral beliefs, mathematical beliefs, philosophical beliefs, etcetera). In particular, these basic principles should also cover beliefs about oneself and one’s own beliefs.³ In other words, it would be a dereliction of duty of the epistemologist to disregard self-referential beliefs from the outset. So, in order to guarantee sufficient expressiveness, we will take justified belief to be a predicate.

We take being justified in one’s belief to be a matter of having good reasons for one’s belief, where the reasons themselves have propositional structure. In this sense, we are working with an ontologically internalist conception of justification. We do not thereby exclude that there may be other, external ways of being epistemically warranted in one’s belief.⁴ For instance, suppose Catrin looks out of her window and on the basis of her perception forms the belief that there is an apple tree outside. Then we would normally say that this belief is epistemically warranted. Yet, the perception on which it is based may not have propositional structure, and therefore not even being a candidate for being a reason for her belief. If that is so, then there are also warrants that do not take the form of reasons, and therefore—in the sense in which we use the term—are not justifications. Hence, we accept that there might be different types of epistemic warrants, but reserve the term justification for reason-based warrants. In this sense, for the purposes of this article, we want to stay neutral in the debate between internalism and externalism in epistemology. As we are talking about justified belief, we will be concerned with doxastic rather than so-called propositional justification (Rosenkranz, 2018, p. 310).

3 From Montague and Kaplan to Thomason

The aforementioned parallels between results in truth theory and similar results concerning epistemic notions led to a brace of interesting results in formal epistemology. Montague and Kaplan (and, independently, Myhill), proved a strengthening of Tarski’s result about the undefinability of truth:

Theorem 1

(Kaplan and Montague (1960), Myhill (1960)) Let S be the closure of $\mathrm {PA}^T$ + $\{ T\ulcorner \phi \urcorner \rightarrow \phi \mid \phi \in {\mathcal {L}}_T \}$ under the Necessitation rule

$$\begin{aligned} \frac{\vdash \phi }{\vdash T\ulcorner \phi \urcorner } \end{aligned}$$

then S is inconsistent.

Proof

As for all the inconsistency results in this article, this is proved by a simple diagonal argument. The argument is based on a sentence $\alpha$ which is such that

$$\begin{aligned} \textit{1)}~~ \mathrm {PA}^T \vdash \alpha \leftrightarrow \lnot T\ulcorner \alpha \urcorner , \end{aligned}$$

which can be obtained by the Diagonal Lemma, see (Horsten, 2011, Theorem 12, p. 37). In order to derive the inconsistency assume

The Tarski-biconditionals (i.e., sentences of the form $T\ulcorner \phi \urcorner \leftrightarrow \phi$) are not valid when the predicate T is interpreted not as truth, but as ‘it is known that’. But on the interpretation of T as ‘it is known that’, both the unrestricted schematic principle $T\ulcorner \phi \urcorner \rightarrow \phi$ (T-Out) and the unrestricted schematic rule

$$\begin{aligned} \frac{\vdash \phi }{\vdash T\ulcorner \phi \urcorner } \end{aligned}$$

(Nec) seem plausible. So the argument for Theorem 1 yields an epistemic paradox. This is why, when the sentence $\alpha$ in Theorem 1 is given an epistemic interpretation, it is called the knower sentence in the literature, see e.g. (Kaplan & Montague, 1960; Anderson, 1983).

It is sometimes objected that this is only a paradox for a highly idealised notion of knowledge (“knowledge by God”, perhaps). Whereas God’s knowledge is (presumably) closed under Nec, we, as finite beings, can only ever apply Nec finitely many times. However, this argument is unconvincing. Only a few instances of Nec (only one, in fact) are required to obtain a contradiction. So Catrin can be assumed to have gone through this finite argument in S. This is exactly what we assume in the present article. So we have a paradox not for an idealised version of knowledge, but for ordinary knowledge by ordinary finite agents. We claim this not only for this specific theory S, but also for other inconsistent theories that we will consider later.

When we regard the Kaplan-Montague theorem as a theorem about truth, then there are two prima facie reasonable ways of reacting to it:

• 1. reject T-Out, but preserve Nec;

• 2. reject Nec, but preserve T-Out.

(Of course one can also reject both, and it is also possible to doubt the applicability of some of the laws of classical logic in this context.)

These two reactions have resulted in the two corresponding main families of axiomatic theories of truth:⁵)

• 1. $\textit{FS}$-like theories of truth;

• 2. $\textit{KF}$-like theories of truth.

The same two prima facie reasonable reactions suggest themselves when we interpret the predicate T in theory S instead as knowledge. However, when we interpret T in the Kaplan-Montague theorem as justified belief, only the first reaction seems to have initial plausibility. Nec (for J) seems eminently plausible. Indeed, proving a sentence $\phi$ from basic logical principles concerning justified belief seems a paradigmatic way of justifying $\phi$. (Indeed, the connection between justifying and proving is worth bearing in mind.) On the other hand, the justified belief-analogue of T-Out, let us call it J-Out, is totally implausible, as epistemology has taught us.

So the Kaplan-Montague theorem presents a paradox for knowledge, but not for justified belief. This raises the question whether the principles of S can somehow be weakened in such a way that a paradox for justified belief is obtained.

This question was first addressed by Thomason (1980). Consider the theory THO consisting of $\mathrm {PA}^J$ plus the following principles governing J:

• 1. $J\ulcorner \phi \urcorner \rightarrow J(\ulcorner J\ulcorner \phi \urcorner \urcorner )$;

• 2. $J(\ulcorner J\ulcorner \phi \urcorner \rightarrow \phi \urcorner )$;

• 3. $J\ulcorner \phi \urcorner$ if $\phi$ is a logical axiom;

• 4. $J(\ulcorner \phi \rightarrow \psi \urcorner ) \rightarrow (J\ulcorner \phi \urcorner \rightarrow J\ulcorner \psi \urcorner )$;

• 5. $\lnot J \ulcorner \bot \urcorner$, where $\bot$ is your favourite contradiction.

Observe that J-Out does not belong to the axioms of THO, but a slight weakening of this axiom (Axiom 2) does. Observe also that the Rule 3 is a (weak) form of Nec. Then we have (Thomason (1980)):⁶

Theorem 2

THO is inconsistent.

Thomason describes his theorem as a paradox for idealised belief (Thomason, 1980, p. 392). But belief is a logically very unconstrained notion: a madman may believe or not believe just about anything. It is more accurate to describe it as a paradox about rationally justifiable belief (Koons, 1992, p. 14), or even ordinary justified belief. As with the Kaplan-Montague paradox for knowledge, Thomason’s argument indeed yields a paradox about ordinary justified belief, since, in the light of what we said on p. 4, we may (and will) assume that Catrin has gone through the handful of logical steps that it takes to reach the contradiction, without assuming logical omniscience.⁷

4 Inconsistency, consistency, strength

Friedman and Sheard (1987) step back and adopt a more general perspective to truth and paradox. They start with a base theory containing $\mathrm {PA}^T$ and a few basic principles of truth that at least for the purposes of their discussion can be taken to be non-negotiable. Then they draw up a list L of principles that can make some prima facie claim to being basic truth laws. Subsequently they show that certain subsets of L are inconsistent over the base theory, and that certain other subsets of L are consistent. Moreover, they give a proof-theoretic analysis of some of these consistent truth systems.

In this section, we want to at least make a start at providing a similar overview for justified belief and thereby helping to explicate the concept of justified belief and the interaction of certain prima facie plausible principles of justified belief.

4.1 Base theory

We take it that $\mathrm {PA}^J$ must be included in the base theory, which we will call B. The reason is that the principles of classical logic hold not only for arithmetical formulas, but also for formulas including the justification predicate J. Moreover, the induction axiom is open-ended, so it also holds for formulas that include J. Let us now turn to the non-arithmetical axioms of B.

First, epistemic closure (CL) is the principle

$$\begin{aligned} (J\ulcorner \phi \urcorner \wedge J(\ulcorner \phi \rightarrow \psi \urcorner ))\rightarrow J\ulcorner \psi \urcorner . \end{aligned}$$

This principle is also included in B. It expresses that logical reasoning preserves justification.

Second, epistemic coherence (CO) is the principle $\lnot J\ulcorner \bot \urcorner$, where $\bot$ is your favourite explicit contradiction of the form $p\wedge \lnot p$. If Catrin’s reasoning process has reached such a conclusion, then something has gone wrong: she is not justified in believing this conclusion. We include CO in B. Together with CL, this principle also prevents Catrin from being justified in principles from which a contradiction follows by logical reasoning.

Third, we have argued above (p. 4), that the Necessitation rule (Nec) should be accepted. It expresses the thought that proof (from the laws and rules of justification plus the principles of arithmetic) yields justification. We also include it in B.

In sum, we take our Base Theory B to be

$$\begin{aligned} \mathrm {\mathrm {PA}^J + \mathrm {CL} + \mathrm {CO}+ \mathrm {Nec}}. \end{aligned}$$

An agent who satisfies all theorems of B must have justified belief in infinitely many statements, and is for this reason super-human. But for every finite subset of the theorems of B, there is a finite rational agent whose justified beliefs are exactly the statements belonging to this finite set. So the base system B is best seen as describing not one infinite ideal rational agent, but an infinite family of finite non-idealised rational agents: an infinite family of finite “Catrins”. One can go even further, and hold that only those small finite sets of theorems of B that have short proofs in B are intended to describe flesh and blood rational human agents.

In view of this and of what we said on p. 4, we stress that Nec and epistemic closure do not commit us to Catrin being an “unrealistically idealised” epistemic agent: the proofs in B and its putative extensions that will be considered are all short, and contain very few instances of CL and Nec. In fact all proofs require at most five applications of either Nec or CL.⁸ This is a completely realistic job for a non-ideal agent.

Still, whether our choice of B as non-negotiable base theory is a judicious one, is a non-trivial question.⁹

Epistemic closure is a controversial principle. As Smith¹⁰ in a recent article rightly points out (Smith, 2018, Section 1), some swear by it,¹¹ others reject it. Doubts about CL relate to lottery paradox-like situations. Suppose I give a party for 10 people, and for each of them I justifiedly believe, with a degree of certainty of 0.9, that (s)he will come to the party. Moreover, suppose that I know that these 10 people will arrive at their ultimate decision whether to attend completely independently. Then, by CL, I can come justifiedly to believe that they will all attend. But at the same time, my credence that they all attend will be $< 0.4$. Our response to this objection is that in the scenario, I was not justified in believing, for each of these 10 people, that (s)he will attend. This is because the notion of belief in the concept of justified belief that we are investigating, is one of unreserved, unqualified belief. Given this concept of justified belief, I was, for each possible attendant, only justified to have a graded belief that (s)he will attend.

Another critical view on epistemic closure can be found in the discussion of Heylen (2016) and Rosenkranz (2016). Heylen discusses the notion of being in a position to know and introduces a counterexample to the agglomeration principle ($K\phi \wedge K\psi \rightarrow K(\phi \wedge \psi )$) for this notion.¹² Since agglomeration follows from closure (assuming the subject is in a position to know some easy tautology), closure has to be rejected. Rosenkranz (2016) picks up on this argument and continues to show that closure has to be rejected for justification, too. This, though, heavily relies on Rosenkranz’s principle $K\phi \rightarrow J\phi$, see also (Rosenkranz, 2018) and (Rosenkranz, 2021). This argument is not applicable for our predicate, though. Since we are considering J to be justified belief, or what Rosenkranz (2018) calls doxastic justification¹³ rather than propositional justification, it is not that case that having a justified belief in $\phi$ can be derived from being in a position to know $\phi$, which makes the argument against the closure for J not applicable to our theory.

Epistemic coherence is, in comparison with epistemic closure, less controversial. Pace dialethism, very few philosophers believe that one can ever be justified in believing a blatant contradiction.¹⁴ Still, in Sect. 7 we briefly discuss the ramifications of excluding epistemic coherence from the base theory for the inconsistency results that will be presented in Sect. 4.3.

Lastly, there is Nec. As said on p. 4 and p. 5, we subscribe to this inference rule.¹⁵ We take the basic logical principles of justified belief to express elementary conceptual truths about justified belief. So reflection on the content of these principles yields justified belief in them. However, in the light of what was said earlier (p. 4), we should not expect Nec to be automatically extended when Catrin’s theory¹⁶ is extended.

We want to note at this point that our base theory also proves the principle of agglomeration (Agg), $(J\ulcorner \phi \urcorner \wedge J\ulcorner \psi \urcorner )\rightarrow J(\ulcorner \phi \wedge \psi \urcorner )$, which we will use in the upcoming section:¹⁷

4.2 Candidate principles for justified belief

We will investigate the following additional principles for justified belief:

TH was adopted in (Thomason, 1980, p. 391). For versions of the principle GH, see (Boolos, 1995, p. 294) and (Wang, 1974, p. 324–325). PI, CPI, CNI and NI are discussed widely in contemporary epistemology; early discussions investigations of these principles can be found in (Hintikka, 1962) and (Lenzen, 1980, p. 38–39). MO is discussed in (Van Fraassen, 2022, p. 17) and (Cross, 2001). CI and WRef are discussed in (Cieśliński, 2017) and (Cieśliński, unpublished). In their discussion of these principles, most of these scholars interpret J not as justified belief but as some related notion; a philosophical discussion of many of these principles in terms of justification can be found in (Rosenkranz, 2018).

The introspection principles listed above have the form of a material implication. Certain rule forms of such principles might be considered. For instance, one might wonder about the following rule-form of converse postive introspection:

$$\begin{aligned} \frac{ \vdash J(\ulcorner J\ulcorner \phi \urcorner \urcorner )}{\vdash J\ulcorner \phi \urcorner } , \end{aligned}$$

or even, more generally, about the converse of Nec, namely the Co-Necessitation rule CoNec:

$$\begin{aligned} \frac{\vdash J\ulcorner \phi \urcorner }{\vdash \phi } . \end{aligned}$$

Although the rules versions can be derived from the material implication versions, this is not the case the other way around. Investigating only the rule versions would, thus, lead to weaker theories. These matters are left for another occasion. We merely pause to note that the philosophical justification of CoNec is no trivial matter, given that justified belief is not a factive notion.

4.3 Some impossibility theorems

It turns out that many of the additional principles in Sect. 4.2 are inconsistent with the base theory B. Indeed, simple diagonal arguments show:

Theorem 3

• (A) When the base theory B is extended by any of the following as extra axioms, an inconsistent theory results:

  • (a) PI + TH;

  • (b) TH;

  • (c) GH;

  • (d) PI;

  • (e) NI.

• (B) When the theory theory $B-CO$ (i.e., the system B without epistemic coherence) is extended by any of the following as extra axioms, an inconsistent theory results:

  • (f) CNI;

  • (g) MO.

Proof

a) has already been proven by Thomason (1980).

b)

c)

d)

e)

f)

g)

Observe that every single one of these inconsistency results follow by straightforward application of the axioms and rules of B to the “knower” sentence. Several of these results can already be found in the literature. Case a) is Thomason’s theorem. Case b) is a slight improvement on Thomason’s theorem, so is case d), as both b) and d) only use one of the two additional principles that were used in Thomason’s theorem a). Moreover, Koons observes that Gödel’s incompleteness theorem can be translated into epistemic logic and is then basically represented by case d) (Koons, 1992, p. 54–55). Burge, on the other hand, used both the positive and negative introspection to prove an inconsistency (Burge, 1978, p. 29;) this is also discussed in (Koons, 1992, p. 53). Cases d) and e) are likewise slight strengthenings of this result. Some of the remaining inconsistency results are undoubtedly folklore; we just have not found references to them in the literature.¹⁸

Theorem 3 reveals that all candidate additional principles are straightforwardly inconsistent over B, except CPI, CI and WRef. Moreover, most of the inconsistency results rely on Nec. So Nec imposes strong restrictions on the logic of justification.

4.4 Quantification

The base system B does not say anything about the logical interaction between the universal quantifier and the modal predicate J. The collective scholarly experience in axiomatic truth theory suggests that such a system is likely to be conservative over the background theory. Indeed, for B this is the case:

Theorem 4

B is arithmetically conservative over $\mathrm {PA}$.

Proof

This follows from Theorem 3 of (Cieśliński et al., 2022). The translation $\tau$ which distributes over logical connectives, is homophonic for purely mathematical statements, and which is such that $\tau (J \phi )$ is set equal to $\mathrm {Pr} (\tau ( \phi ) ) = 1$ translates theorems of B into theorems of the system RKf, which is (by Theorem 3 of (Cieśliński et al., 2022)) proof-theoretically conservative over its background theory.¹⁹$\square$

Cieśliński has developed a formal theory of ‘believability’ (Cieśliński, 2017), which is a notion which is closely related to that of justified belief. A few years after the publication of his book Cieśliński proposed an improved axiomatic theory of believability (Cieśliński, unpublished): we base our discussion on the later version of his theory.

Cieśliński’s original theory contains a rule form of CI; in Cieśliński’s later theory, CI is one of the axioms. This axiom contains information about the interaction between universal quantification and J, and is a strengthening of converse positive introspection (CPI). Indeed, CI expresses a sort of effective, finitised $\omega$-rule for J in the following sense. Hilbert’s $\omega$-rule says that from an infinite list of premises $\phi ({0})$, $\phi ({1})$ we can conclude $\forall n \phi (n)$. Since this rule has infinitely many premises, it cannot humanly be applied and is, thus, not effective. However, the antecedent of CI requires that we have one uniform justification of the fact that $\forall n J \Phi (n)$. This finitises the rule and makes it suitable as a principle of reasoning.

Observe that we did not prove inconsistency results for CI. Cieśliński proved that it is consistent not only to add CI, but in addition also WRef to the base system:

Theorem 5

$B + \mathrm {WRef} + \mathrm {CI}$ is arithmetically sound.

Proof

This follows from Cieśliński (unpublished), Theorem 5 $\square$

This immediately entails the following corollary:

Theorem 6

$B + \mathrm {WRef} + \mathrm {CPI}$ is arithmetically sound.

Proof

This follows immediately from Theorem 5, since CPI follows from CI. $\square$

Since CI has the flavour of a constructive $\omega$-rule, we might expect that it adds some proof theoretic strength. In Cieśliński’s work, a slight weakening of the system $B+CI$ plays a central role, namely $B+\mathrm {WRef}+ \mathrm {CI} - \mathrm {CO}$, which he calls $Bel^*(\mathrm {PA})$.²⁰ He shows that this system is significantly non-conservative over $\mathrm {PA}$.

We recall the definition of Uniform Reflection extensions of a ground theory S:

Definition 1

• $URF^0(S) \equiv S$;

• $URF^{n+1}(S) \equiv URF^n + \{ \forall x: Bew_{URF^n}(\phi (x)) \rightarrow \phi (x) \mid \phi (x) \in {\mathcal {L}}_J \}.$

Furthermore, we define the internal logic of a logical system of justified belief S (denoted as Int(S)) as those sentences $\phi$ such that $J\phi \in S$. Since J is not factive, Int(S), rather than S, should be taken as showing the strength of S. There will be theorems that are provable using CI and that are of the form $J\ulcorner \phi \urcorner$ with $\phi$ being an arithmetical statement that is unprovable in the background theory $\mathrm {PA}$. Because we do not have the principle J-Out, this will not result in outright arithmetical non-conservativness of the theory of S.

More precisely, Cieśliński shows:

Theorem 7

For every natural number n:

$$\begin{aligned} URF^n(B)\subseteq Int(Bel^*(\mathrm {PA})) . \end{aligned}$$

Proof

See (Cieslinski, unpublished, Theorem 8). Cieśliński proves that for every natural number n and for all $\phi (x)\in L_{PAB}$: $B \forall (x Pr_{URF^n(S)} (\phi (x))\rightarrow x) \in Bel^*(PA)$. By the definition of the concept of internal logic above, this means that for all n and for all $\phi (x)\in L_{PAB}$: $\forall (x Pr_{URF^n(S)} (\phi (x))\rightarrow x) \in Int(Bel^*(PA))$. $\square$

The positive news here is of course that we have finally found some additional principles that are consistent (and indeed arithmetically sound) over our base theory. The fact that CI is mainly responsible for considerable extra arithmetical strength may be taken as a reason not to take it as belonging to the basic laws of justified belief. Something similar might be said about WRef, which explicitly has the form of a proof theoretic reflection principle.

5 Discussion of the additional principles

The additional principles that were presented in Sect. 4.3 have been discussed in the epistemological literature, and different arguments for and against them have been formulated. However, often the arguments are embedded in a discussion where J is taken to be not justified belief, but another epistemic notion, such as some other kind of belief, knowledge, subjective provability, etcetera. So we cannot simply transfer all epistemological arguments from the literature to the notion of justified belief that we are discussing in this article.

5.1 Thomason and Gödel–Hilbert

Koons (1992, p. 49) argues for Thomason’s original principle TH but interprets J as subjective provability. He argues that every instance of the formula $J\ulcorner \phi \urcorner \rightarrow \phi$ is self-evident, and hence also subjectively provable. This argument might (or might not) be plausible when taking J to represent subjective provability. But it does not carry over to justified belief. After all, provability (in its informal sense) is a factive notion, whereas justified belief is not. Nonetheless, one might think that despite the fact that Catrin rationally believes or even knows that some of her justified beliefs are false, it is rational for her to believe for each individual $\phi$ that $J\ulcorner \phi \urcorner \rightarrow \phi$, on the basis that rational belief is a good (but not infallible) guide to truth, i.e., one might believe that TH is still true.

The principle GH is a generalisation of a thesis of Kant, who asserted that (Kant, 1993, A 476/B 504):

[...] there are sciences [and pure mathematics is one of them (Kant, 1993, A 480/B 508)] the very nature of which requires that every question arising within their domain should be completely answerable in terms of what is known, inasmuch as the answer must issue from the same sources from which the question proceeds.

In other words, by asking unanswerable questions while asserting that only reason can answer them, reason would be irrational. Hence, when asking the question whether $\phi$, reason should be able to answer that question, i.e., decide whether $J\ulcorner \phi \urcorner$ or $J\ulcorner \lnot \phi \urcorner$. With this we get the principle $J(\ulcorner J\ulcorner \phi \urcorner \vee J\ulcorner \lnot \phi \urcorner \urcorner )$. This principle is a consequence of the GH principle.

His own incompleteness theorems notwithstanding, some such belief seems also to have been held by Gödel. In any case, GH is an expression of a form of rational optimism (Wang, 1974, p. 325), to which also Hilbert gave voice in his famous slogan that “in mathematics, there can be no ignoramibus.”

On the other (pessimistic) side, we may have good reasons to know, for certain specific propositions, that they are absolutely undecidable. Some believe that even in arithmetic some such statements can be found: Feferman and Solovay speculate that the question “Is it true that if w is the sequence of the first $2^{2^{^{100}}}$ terms in the binary expression of $7 \pi -3$, then the last term of w is 0?” may be a case in point (Feferman & Solovay, 1990, p. 292).

5.2 Moore and introspection

For Moore’s principle the situation is more positive. Already Hintikka (1962, p. 125) defends MO for the notion of belief. Explicit arguments for MO for the notion of justified belief can be found in (Smithies, 2012). Smithies argues that instances of Moore’s paradox can be found not only for belief, but also for knowledge and justification. In the same way that it is somehow wrong for someone to assert “p, but I do not believe that p”, it seems irrational for someone to assert “p, but I do not have a justification for believing p” or “I have a justification for believing p but it is not the case that p”, (see Smithies, 2012, pp. 283–284).

Moreover, Smithies argues that there is a tension between accepting MO on the one hand, and rejecting positive or negative reflection principles on the other hand. In this argument, he uses what he calls an exhaustiveness assumption: for each sentence $\phi$, I am either justified in believing $\phi$, justified in disbelieving $\phi$ (i.e., justified in believing $\lnot \phi$), or justified in believing that I withhold judgement (W) about $\phi$. He shows that if any of the four introspection principles fail, and the exhaustiveness assumption holds, then MO must fail, too. For example in the case of PI: If one takes PI to be false, then there is a sentence $\phi$, such that $J\ulcorner \phi \urcorner$ and $\lnot J(\ulcorner J\ulcorner \phi \urcorner \urcorner )$. From $\lnot J(\ulcorner J\ulcorner \phi \urcorner \urcorner )$ Smithies concludes (using exhaustiveness) that I am either justified in disbelieving that I am justified in $\phi$ or I am justified in believing that I withhold whether I am justified in $\phi$, so we have either $J\ulcorner \phi \urcorner \wedge J(\ulcorner \lnot J\ulcorner \phi \urcorner \urcorner )$ or $J\ulcorner \phi \urcorner \wedge J(\ulcorner W(\ulcorner J\ulcorner \phi \urcorner \urcorner )\urcorner )$. In either case, using the agglomeration principle, we obtain a contradiction with MO. Since, for Smithies, MO is non-negotiable, he also accepts all four introspection principles for justified belief (Smithies, 2012, p. 286). A similar reductio can be distilled for NI, CNI and CPI (see Smithies, 2012, pp. 285–287).²¹

More considerations about relevant principles for the notion of justification can be found in (Rosenkranz, 2018).²² In his paper, Rosenkranz considers an all-things considered notion of justification which aims at being neutral on the debate about externalism versus internalism and a knowledge-first approach. The presented minimal logic of this neutral account of justification includes necessitation but neither epistemic closure, nor epistemic coherence. Rosenkranz’s notion of justification is different from ours, as he considers only propositional justification which does not entail having a belief, in contrast to our notion of justified belief, which can be described as doxastic justification.²³ Although epistemic closure fails for J in his theory, still he introduces a rule for deducing $\vdash K\phi \rightarrow K\psi$ from $\vdash \phi \rightarrow \psi$, which in combination with Nec (which Rosenkranz accepts in (Rosenkranz, 2018)) comes quite close to closure. However, in (Rosenkranz, 2021), Rosenkranz presents a more articulated story, describing a logic for justification that does not use Nec, stating that this rule is “way too strong” and “highly suspect” (Rosenkranz, 2021, pp. 86 and 186). In his theory from 2018, though, Rosenkranz proves (by the use of others principles connecting justification to the other introduced modality of “being in a position to know”) Moore’s principle, and asserts that this principle is “eminently plausible” (Rosenkranz, 2018, p. 324).

Moreover, Rosenkranz considers an extension for his logical background theory. He calls this extension a logic of luminous justification; he takes it to be somewhat more internalism-directed but still compatible with many externalistic views. In this extension, Rosenkranz (2018, pp. 325–327) proves the third principle of our base theory, namely epistemic coherence.²⁴ Moreover, within this logic the principles of (converse) positive introspection and (converse) negative introspection are all four provable for justification.

Although the extended logic, from which these four principles are obtained, might slightly favor internalism, Rosenkranz still argues for their plausibility and stresses that they are obtained from externalist-friendly principles; see (Rosenkranz, 2018, p. 327). Moreover, Rosenkranz’ theory strongly suggests the plausibility of Moore’s principle, since this principle was already obtained in his minimal logic.²⁵

These considerations are in harmony with conclusions that are reached in (Van Fraassen, 2019). Van Fraassen investigates a notion of belief that is stipulatively taken to be self-transparent. Then he argues, much like Smithies, that Moore’s principle should hold, and constructs a class of models in which these constraints are all satisfied. Thus van Fraassen includes PI and CPI into his logic of a self-transparent believer, (Van Fraassen, 2019, 2022), as his modelled believer cannot be wrong about his own beliefs and is aware of them. Moreover, Van Fraassen (2022, p. 17) derives Moore’s principle for his logic, using PI and CPI.

All this does not mean that introspection principles are uncontroversial in epistemology. Firstly, it is not clear that all four introspection principles that we have considered stand or fall together.²⁶ Secondly, and perhaps more importantly, over the past decades all introspection principles have come to be regarded with suspicion. This is, to a significant extent, a consequence of Williamson’s attack against luminosity theses in epistemology (Williamson, 2000, chapter 4). On this view, mental states are in general not fully transparent to those who have them. So all introspection principles for the notion of justified belief are questionable. For instance, Williamson argues against a form of positive introspection for even in mathematical cases, stating that one could very well have a proof of a theorem without being in a position to know that one has a proof (Williamson, 2000, p. 111).²⁷

6 The restrictiveness of the minimal theory of justified belief

One of the principal aims of epistemology is to uncover absolutely general laws governing doxastic concepts such a justified belief. We have argued that the axioms and rules of the minimal basic system B may qualify as such. What about the additional principles that were introduced in Sect. 4.2?

Theorem 3 shows that many of them cannot be consistently added to B. This means that they fail to qualify as theorems governing justified belief. This implies that we can bypass the philosophical arguments in the literature that support them: these arguments miss their mark. Nonetheless, these arguments need not be without merit. It is possible that some authors who defend these principles, implicitly assume a typing restriction on the version of the principle that they have in mind, whereby self-referential counterexamples such as the knower sentence are ruled out. Of course, where this is so, it would be helpful if any restriction on the principles defended were explicitly stated.

What about the quantificational principle CI and its consequence CPI? We have seen that they can be consistently added to B (Theorem 5). Nevertheless, we think that CPI, and therefore also CI, is questionable. There seem to be cases where Catrin is justified in believing that she justifiably believes a proposition $\phi$, without being actually justified in believing $\phi$. Suppose that Catrin finds an apparent proof, which is complicated and long, for a mathematical statement $\phi$. She takes her argument to be a valid mathematical proof, and checks it several times. She lets some of her colleagues check her proof, too: no one finds a mistake. Yet there is a subtle mistake in Catrin’s mathematical argument. In this situation, it seems that Catrin is not justified in $\phi$, since her argument contains a mistake. Nonetheless she is justified in believing that she is justified in believing $\phi$. She fulfilled her epistemic obligations in that regard: she did all she could do to secure her belief that she has justified the conclusion of her mathematical argument.

In sum, already the minimal system B is highly restrictive. Moreover, among the class of statements that can be consistently added, it is not easy to find ones that are plausible. Of course we have mainly looked at propositional modal principles, CI being the only exception. There may well be quantificational principles extending B that are promising, but this exceeds the scope of the present investigation.

It may be of interest to note that certain results are deducible even without the principle of epistemic coherence CO. Let the theory B without CO be called B-CO. In Sect. 4.3 we saw that adding CNI (f) or adding MO (g) to the base theory leads to inconsistency even without CO. Moreover, the remaining principles lead to more fine-grained results when CO is left out of the base theory. We found that B-CO + CNI $\vdash \bot$, B-CO + MO $\vdash \bot$, and we easily see that B-CO + TH $\vdash J\ulcorner \bot \urcorner$, B-CO + NI $\vdash J\ulcorner \bot \urcorner$, B-CO + GH $\vdash J\ulcorner \bot \urcorner \vee J(\ulcorner J\ulcorner \bot \urcorner \urcorner )$. We leave the verification of these results to the reader,²⁸ but we find this differential role of the principle of coherence in the impossibility results interesting per se and worth pursuing in future work. Although not all principles lead against the context of the base theory without CO to straightforward contradictions, or even to ‘a’ Catrin being justified in a contradiction, we still find the consequences of all of these principles problematic. If ‘a’ Catrin notices that, in the context of B, taking GH as an additional axiom would allow her to prove $J\ulcorner \bot \urcorner$, then she rightly concludes that GH should not be taken as an axiom.

7 In closing

In this paper we have investigated the concept of pure justified belief. We tried to lay down basic laws of the logic of justified belief. This resulted in the base theory B. We discussed several additional principles for this logic and provided an overview of inconsistency and consistency results concerning justified belief, in the spirit of what Friedman and Sheard (1987) did for truth. Moreover, we showed that most of the additional principles that have been considered in the literature cannot consistently be added to B, and that the only propositional modal logical principle that can be added (CPI), is questionable. These results mirror results from Cieśliński, Horsten and Leitgeb about rational subjective probability that is though more fine grained still to some extent comparable to justified belief (Cieśliński et al., 2022). The results in that article therefore invite similar conclusions about the notion of rational subjective probability.

It is tempting to conclude from this that all the additional principles that were discussed in Sect. 4.2 should be either restricted somehow, or rejected outright. Indeed, our findings are largely in harmony with (but independent from) Williamson’s anti-luminosity arguments.

One can try to resist this conclusion in several ways:

• 1. Exclude self-referential sentences from the scope of the principles;

• 2. Argue against the base theory.

But neither of these reactions is appropriate.

Self-referential statements such as the knower sentence can be excluded in two ways. One can treat justified belief as an operator instead of as a predicate, or one can impose a type restriction (of the form “where J does not occur in $\phi$”) on the principles of the logic of justified belief. Both of these strategies result in a limitation of the generality of the principles of the logic of justified belief, and thus conflicts with the universal ambitions of epistemology. Concerning the base system, we have seen how one may be worried that B is beset by a variant of the problem of logical omniscience due to Nec and CL. We have argued that these worries are unfounded. It is true that no non-idealised agent can serve as a model of all theorems of B. But for every finite fragment of B, there is a non-idealised rational agent that models it. In particular, for each of the inconsistency arguments in this article, there are flesh and blood agents who have gone through them step by step. Also Williamson (2000, pp. 116–118) argues that the closure principle is intuitive and should not be rejected, especially, when one formulates it only over the pertinent propositions: “If we reject it, in what circumstances can we gain knowledge by deduction?”

A third way to avoid the conclusion that all the principles that were considered in Sect. 4.2 are unacceptable, consists in restricting the background logic. For instance, we know from the literature on truth theories that no go-theorems tend to melt away when the background logic is weakened from classical logic to partial logic (Halbach & Horsten, 2006). An attempt to partial logic to epistemological notions can, for example, be found in (Schuster, 2022) or (Horsten, 1998).

Another non-classical approach can be found in (Zardini, 2020). Whether some such move might be an acceptable route for epistemologists, is a moot question. One possible ground for scepticism on this score is that in virtually all the literature in contemporary epistemology, full classical logic is assumed.