Abstract
Connectives such as Tonk have posed a significant challenge to the inferentialist. It has been recently argued (Button 2016; Button and Walsh 2018) that the classical semanticist faces an analogous problem due to the definability of “nasty connectives” under non-standard interpretations of the classical propositional vocabulary. In this paper, we defend the classical semanticist from this alleged problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inferentialism about logical vocabulary is the view that the meaning of a logical connective is conferred on it by its rules of use (or some privileged subset thereof). One well-known problem for the view concerns connectives like tonk, which are defined in terms of a set of rules from which unwanted consequences can be derived.Footnote 1 In the case of tonk, for instance, it allows the derivation of any conclusion from any non-empty set of premises, and should therefore be rejected by the inferentialist as a meaningful connective, despite being well-defined in terms of a pair of intelim rules. The inferentialist is therefore left with the difficult task of separating in some principled manner those sets of rules that define genuinely meaningful bits of language from those that do not.Footnote 2
The problem of tonk is particular to inferentialism. It is not a problem that arises for one who believes that (model-theoretic) truth conditions confer meanings on connectives. Call such a person a semanticist. However, Tim Button (2016) has recently argued that the semanticist faces an analogous tonk-like challenge, which runs as follows. The language of classical propositional logic has an intended two-valued interpretation expressed by the familiar truth tables. It also has unintended interpretations, such as that given by any matrix defined in terms of a boolean algebra with more than two elements, where the designated set of values forms a filter (the familiar filter consisting of just the top element, truth). Such interpretations are unintended because there are more than the standard two truth values, truth and falsity, and the truth functions take more than these two values as input and may return non-standard truth values as output. An example of such a matrix is given by the four-valued lattice four whose Hasse diagram is depicted thus:

The top element 1 is the only designated—i.e. truth-like—value, negation is boolean complementation, and conjunction is meet. Relative to this interpretation one can define a connective, called Knot by Button, given by the following truth table:
A |
|
|---|---|
1 | 1 |
a | b |
b | a |
0 | 0 |
1.1 Digression
It is worth pointing out that Knot, taken as a truth function, occurs elsewhere in the literature. For instance, it is equivalent to the mixed double negation \({\sim }\lnot \), where \({\sim }\) is a de Morgan negation and \(\lnot \) is classical negation:
A | \({\sim }A\) | \(\lnot A\) |
|---|---|---|
1 | 0 | 0 |
a | a | b |
b | b | a |
0 | 1 | 1 |
De Morgan negation is familiar from non-classical logics, such as Belnap and Dunn’s four-valued logic FDE (also known as FDE), and is itself definable from Knot and classical negation by  . (Note, however, that the set of designated values of FDE is \(\{1,b\}\) rather than \(\{1\}.\)) The language with Knot is thus truth-functionally equivalent to the language of BD+ of De and Omori (2015), which is the classical negation expansion of FDE. Knot is more commonly known as “conflation” at least since Fitting (1994) and is the natural counterpart of negation in the information ordering variant of four. End of digression.
. (Note, however, that the set of designated values of FDE is \(\{1,b\}\) rather than \(\{1\}.\)) The language with Knot is thus truth-functionally equivalent to the language of BD+ of De and Omori (2015), which is the classical negation expansion of FDE. Knot is more commonly known as “conflation” at least since Fitting (1994) and is the natural counterpart of negation in the information ordering variant of four. End of digression.
With the introduction of Knot into the language, we lose some desirable properties of logical consequence, such as substitutivity (of equivalents), conditional-introduction, disjunction-elimination, and negation-introduction.Footnote 3 If these are regarded by the semanticist to be properties essential to logical consequence, then despite the fact that Knot is definable in a semantics that characterizes classical logic, the semanticist will have to somehow rule out Knot in much the same way the inferentialist has to rule out tonk. And there lies the alleged analogy between Knot and tonk.
Our aim in this paper is to discuss some potential semanticist responses to the problem. The first kind involves meaning-theoretic constraints that pin down the intended two-valued interpretation and thereby rule out Knot. The second kind involves accepting in some sense Knot as a coherent connective and attempting to fit it into a classical semantic framework. To this end we consider Knot as a functional modality and provide a two-valued world semantics for the operator. This renders Knot more analogous to something like an ‘actually’ operator than to a logical connective such as conjunction. We conclude with some final remarks.Footnote 4
2 Constraints on meaning as responses to the problem
We should make clear that the following argument poses no problem for the semanticist (or the usual inferentialist, for that matter).
[The problem of many-valued truth-tables] arises as follows. As we saw [...] there are systems of truth-tables with more than two truth-values, which nonetheless characterize classical sentential logic. Call these many-valued truth-tables for classical sentential logic. Consequently, the classical inference rules for the connectives \(\lnot \), \(\wedge \), \(\vee \) and \(\rightarrow \) fail to pin down the two-valued truth-tables uniquely (up to isomorphism). From this, one might conclude that the connectives’ inference rules fail to determine their meanings. I say ‘might’, because it is not entirely obvious that the availability of many-valued truth-tables amounts to a problematic indeterminacy of meaning. But if it does, then inferentialism fails. (Button, 2016, p. 11)
If this line of reasoning poses a problem, it is one for a special—and likely rare—version of inferentialism or semanticism, viz. one according to which the syntactic rules governing the usual connectives need to uniquely secure the intended interpretation of the connectives. But this is a view that inferentialists and semanticists alike can and largely do reject. So the argument against the semanticist must be one concerning the relation between truth conditions and semantics, not one concerning the relation between rules (syntax) and semantics.
The argument above can be seen as a specific case of a more general categoricity problem, akin to the problem of pinning down the standard model of arithmetic in a first-order language. Button and Walsh say, for example:
Moderate semanticists may yet insist that they can provide the logical expressions with exactly as precise a meaning as they should have. In particular, they may insist that they can lay down the meaning of the logical vocabulary up to isomorphism [...] We first mentioned this option in §2.5, we outlined a problem facing this moderate objects-modelist in Chapter 7: no theory with a finitary proof system can pin down the natural numbers up to isomorphism [...]] The moderate semanticist faces a similar problem: by Theorem 13.6, our inference rules cannot pin down the semantic structure up to isomorphism. (Button & Walsh, 2018, p. 305)
One may ask why this is an objection to semanticism rather than inferentialism, since the semanticist does not claim that the inference rules for the connectives uniquely secure (up to isomorphism) the intended two-valued interpretation of the connectives.Footnote 5 The answer is that being unable to secure the intended interpretation is a problem for a certain kind of semanticist, viz. what Button and Walsh call the moderate semanticist. The moderate semanticist maintains moderate objects-platonism, which is roughly the view that:
- Moderate objects-platonism::
-
Mathematical entities are genuine objects we can talk about or refer to, not by way of a faculty of mathematical intuition, but by way of description.
Since mathematical entities are abstract, Button and Walsh argue that moderation entails referential indeterminacy concerning mathematical entities. The argument goes roughly as follows. The only way we can refer to mathematical entities (says the moderate objects-platonist), such as the natural numbers, is via a theory about them such as first-order Peano arithmetic (PA for short). But given well-known properties of first-order logic, PA has models of arbitrarily large infinite cardinality. It is therefore impossible, via a first-order theory such as PA, to pick out the intended model (up to isomorphism). And even though there is a categorical theory of the naturals, viz. second-order Peano arithmetic interpreted by the full semantics for its second-order language, that theory also has models of arbitrarily large infinite cardinality, e.g. Henkin models. Since nothing about a formal language fixes its interpretation for the moderate objects-platonist, they are thereby lead to referential indeterminacy.
The moderate semanticist has a similar problem. Truth-values and models are abstract entities, so the only way we can refer to them (according to the moderate semanticist) is by way of theory. And even though the theory of two-element boolean algebras is categorical with respect to its usual semantics, it has models of various sizes.Footnote 6 There is, therefore, no way for the moderate semanticist to secure the intended two-valued interpretation of the language, and therefore no way to rule out the definability of nasty connectives.
We are mostly in agreement with Button and Walsh concerning the problem of referential indeterminacy faced by the moderate semanticist.Footnote 7 However, that problem rests crucially on an acceptance of moderation which is not part and parcel of semanticism. Moreover, the semanticist that rejects moderation still needs to address the problem of many-valued truth-tables, i.e. they still need to rule out unintended models as playing a meaning-constitutive role. This is why we are focusing on the problem as we formulate it below, namely, as a problem for the semanticist who accepts no more than the (possibly restricted) claim that truth conditions are meaning-conferring. Let us therefore set up the problem as we understand it.
Button tells us that “Knot clearly implements a well-defined semantic function [so] semanticists need, at least, to tell us which kinds of semantic constraints succeed in ‘suitably’ assigning meanings” (Button, 2016, p. 11). One might wonder why any such story needs to be told. After all, the intended two-valued interpretation of the (propositional) logical vocabulary can be expressed in natural language, and we have no reason to think we are unable to refer to the intended interpretation in natural language. All other interpretations of the logical language may be claimed to be mere algebraic constructs that may (or may not) have practical utility but which otherwise play no meaning-theoretic role. Such non-standard interpretations are what Copeland (Copeland, 1983) calls pure rather than applied semantics. The classicist can then agree with Button that “we should refuse to add Knot to our language” (Button, 2016, p. 10, our emphasis), but not because there is a potentially meaningful but problematic connective that needs to be ruled out by general meaning-theoretic constraints, but because Knot is simply undefinable relative to our language whose meanings are specified informally in natural language and hence not subject to categoricity worries. Call this the natural language response to the problem.
Is this response plausible? There is good reason to think not. For, if the inferentialist is burdened with the task of delineating the rules that confer meaning on the connectives from those that do not, why isn’t the semanticist burdened with the analogous task of delineating the truth conditions that confer meaning from those that do not? After all, the inferentialist and semanticist maintain analogous principles concerning meaning—one holds that inference rules are meaning-conferring and the other that truth conditions are. If the semanticist is free to stipulate a highly constrained set of truth conditions that confer meaning on the connectives (i.e. those that yield the intended semantics), the inferentialist should be entitled to the same concerning inference rules. The problem is that the each needs to rule out undesirable connectives on general, well-motivated, meaning-theoretic grounds. The inferentialist holds that:
- IMP::
-
(introduction or elimination) rules are meaning-conferring.
Since, taken unrestrictedly, IMP leads to trouble, the inferentialist must provide general, meaning-theoretic constraints that rule out connectives such as tonk. The same should be true of the semanticist who endorses an analogous meaning-theoretic principle:
- SMP::
-
truth conditions are meaning-conferring.
Like IMP, unrestricted SMP arguably leads to trouble. Thus, the semanticist must also come up with general, meaning-theoretic constraints that rule out undesirable connectives such Knot. For the remainder of the paper it is this problem that we shall refer to as the problem of many-valued truth-tables, as Button calls it:
- The problem of many-valued truth-tables::
-
In order to rule out nasty logical connectives such as Knot, the semanticist must provide general, well-motivated, meaning-theoretic constraints that entail the indefinability of such logical connectives.
One way of meeting this problem is by providing constraints that pin down the intended two-valued semantics since, relative to that semantics, no nasty connective is definable.
We should briefly say something about what truth conditions are. Just as the inferentialist is entitled to assume a background proof-theoretic framework, such as natural deduction, the semanticist is entitled to assume a background semantic framework, such as one in which an interpretation consists of assigning sentences one of possibly more than two truth-values relative to a set of recursive truth conditions. The truth conditions for a connective \({\otimes }\) amounts to providing a means for determining the value of any formula containing \(\otimes \) as main connective.
What constraint can the semanticist endorse that would rule out the definability of nasty connectives? The following is discussed in Button (2016), Button and Walsh (2018).
- CON-SUB::
-
A semantics is meaning-conferring only if every expansion of the language validates the Substitution of Equivalents (SUB):
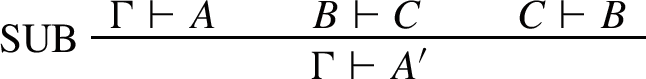
in which \(A'\) and A differ only in that one contains an occurrence of B where the other contains an occurrence of C.Footnote 8
For instance, it is easy to see that the intended two-valued semantics satisfies CON-SUB because the base language is, relative to the semantics, truth-functionally complete—i.e. no expansion of the language involves a connective that is not already definable from the base. We will come back to functional completeness later.
The reason CON-SUB solves the problem of many-valued truth-tables is due to the following equivalence:
-
A semantics satisfies CON-SUB iff it is the intended two-valued semantics.
Concerning the constraint, Button says:
[CON-SUB] seems in the spirit of inferentialism: it mentions only inferential concerns, and inferentialists can insist upon Substitutivity as a constraint on inference (perhaps as a structural rule) [...] a single inferentialist idea explains both why we should refuse to add Knot to our language and dissolves the problem of many-valued truth-tables. Semanticists, however, still owe us a discussion of Knot. (Button, 2016, p. 12)
Note that SUB can be formulated in terms of semantic entailment rather than deducibility, so it is not clear why CON-SUB would be available only to the inferentialist. Moreover, the inferentialist does not typically take CON-SUB as a primitive meaning-theoretic constraint that somehow guides their choice of meaning-conferring (e.g. introduction-elimination) rules. Rather, SUB is a consequence of setting up one’s meaning-conferring rules in the right way. (A typical meaning-theoretic constraint for the inferentialist would be something such as harmony.) Regardless of whether CON-SUB is available only to the inferentialist, let us look to what we think are in any case more plausible meaning-theoretic constraints for the semanticist.
No classical semanticist would deny the following concerning the relation between truth and falsity:
- CON-SUB:
-
A semantics is meaning-conferring only if, relative to any interpretation, (i) each sentence is assigned either truth or falsity (no-gaps) and (ii) no sentence is assigned both (no-gluts).
The first part of CON-BIV is sometimes called bivalence and the second contravalence. What does this constraint amount to? It can be seen as a generalized version of the constraint that negation be a contradictory-forming operator, i.e. an operator that is both contrary- and subcontrary-forming. Two propositions are contraries if they cannot be true together, and they are subcontraries if they cannot be false together. (In a more generalized setting, it is natural to identify truth with designationhood and falsity with non-designationhood.) Since the classicist takes negation to be a contradictory-forming operator, they endorse the following:
- Neg-contrariety::
-
For every sentence, it and its negation cannot both be true;
- Neg-subcontrariety::
-
For every sentence, it and its negation cannot both be false.
Given the usual truth conditions for conjunction and negation, we arrive at the following general constraint concerning truth conditions:
- CON-TC::
-
A semantics is meaning-conferring only if the connectives are given their usual truth conditions; e.g. a disjunction is true iff each disjunct is true, a negation is true iff its negand is false, etc.Footnote 9
Bivalence, i.e. CON-BIV, and the usual truth conditions, i.e. CON-TC, would seem to imply that there are two truth-values that are exclusive and exhaustive, i.e. that there are precisely two-values. However, assuming the two conditions does not beg the question since they alone cannot secure the intended two-valued semantics. For if we equate generally truth with designationhood and falsity with undesignationhood, then there are many-valued semantics satisfying CON-BIV and CON-TC together. For instance, take the four-valued diamond with the top and one of the intermediate values as designated (as with FDE); relative to such a semantics both CON-BIV and CON-TC are satisfied and yet Knot is definable. Thus, the semanticist should be entitled to assume CON-BIV and CON-TC as a general constraints on the sorts of truth conditions that count as meaning-conferring.
This allows us to restrict the sort of semantics deemed legitimate from the semanticist’s perspective. Following Button, call a semantic pair \(\langle {\mathcal {A}},D\rangle \) (for a given language) a pair consisting of an algebra for the language (hence each connective is an operation in \({\mathcal {A}}\)), plus a set of designated values from \({\mathcal {A}}\). Call a semantic pair proto-classical just in case classical consequence is coextensive with the consequence relation valid over the semantic pair in the language with logical vocabulary from \(\{\lnot ,\wedge ,\vee ,\rightarrow \}\). Then according to Theorem 3 of Button (2016), any proto-classical semantic pair satisfying no-gaps, i.e. for each a of \({\mathcal {A}}\), either \(a\in D\) and \(\lnot a\in D\), implies CON-TC and CON-BIV. However, although omitted from Button (2016), the converse is also true, i.e. CON-TC and CON-BIV imply that any semantics we discuss must be proto-classical and satisfy no-gaps.
Using the four-valued truth-tables as an example (with only the top value as designated), notice that disjunction (i.e. the algebraic operation join) takes the two intermediate values—neither of which are truth—to truth. Thus, on the four-valued semantics, a disjunction can be true when neither disjunct is, and so disjunction fails have its usual truth conditions in the four-valued setting. So CON-TC rules out certain seemingly legitimate semantic pairs from consideration, such as the four-valued boolean algebra with only the top value designated. However, and to reemphasize, assuming CON-TC does not beg the question by implying by itself the intended two-valued semantics. For consider the four-valued boolean algebra with both the top and one intermediate value as designated. This is the same as the semantics for FDE with the important difference that de Morgan negation is replaced by classical negation (i.e. boolean complementation). The resulting semantics—relative to which nasty connectives are definable—gives rise to classical logic while ensuring that all the connectives, including disjunction, are given their rightful truth conditions. The semanticist will therefore need more than CON-TC to secure the intended two-valued semantics.Footnote 10
This leads us to what will become the final piece of the semanticist’s solution to the problem of many-valued truth-tables. Consider the following constraint:
- CON-SUB:
-
A semantics is meaning-conferring only if its base vocabulary (consisting e.g. of negation, conjunction, and disjunction) is functionally complete.
It is easy to see that the four-valued semantics is not functionally complete since none of the intermediate values are definable from the classical connectives. Moreover, we know that the intended two-valued semantics satisfies CON-FUNC since its classical vocabulary is functionally complete. However, CON-FUNC is not sufficient by itself to secure the intended two-valued semantics since CON-TC or proto-classicality are needed.Footnote 11 Now, CON-FUNC is equivalent to CON-SUB under the assumption that the semantics is a boolean algebra with only the top element designated, but we do not see any general constraint that would yield such a restriction on the range of legitimate semantics.Footnote 12 However, it is only once we combine CON-FUNC, CON-TC, and CON-BIV that we are able to pin down the intended two-valued semantics.Footnote 13
The only question that remains is whether CON-FUNC is a plausible constraint on meaning for the classicist. We think it is since functional completeness is a propositional version of expressive adequacy, viz. the ability to express any logical notion, i.e. propositional function, implicitly definable in one’s semantic framework. Now one might wonder why the classical vocabulary needs to be functionally complete. Aren’t there other propositional operators that are not definable from the classical ones, such as possibility or belief? To be sure, there are, but CON-FUNC ought not be a requirement not that every semantic notion be expressible in terms of the classical ones, but that every logical notion be so-expressible, and notions like possibility (in the non-logical sense) and belief are non-logical. Clearly no semanticist would maintain that every notion is definable from purely logical ones since not every notion is logical. Moreover, the typical semanticist holds that the usual connectives such as \(\wedge \) and \(\lnot \) are the only logical connectives, and the sense in which they are the only logical connectives is that all other logical connectives (i.e. truth-functions) are definable from them. This is just to say that the usual connectives form a functionally complete set. Thus, we maintain, CONF-FUNC expresses a natural meaning-theoretic constraint for the semanticist.Footnote 14
To sum up the discussion so far, we presented the problem of many-valued truth-tables. We then discussed a “natural language” response according to which the semanticist can pick out the intended semantics using natural language, thereby ruling out the definability of nasty connectives. We then explained why such a solution is not available to the semanticist since it does not follow from general, meaning-theoretic constraints and it therefore does not take seriously the parallel between the problem of tonk for the inferentialist and the semanticist’s problem concerning nasty connectives. We then went on to discuss a solution in terms of general, meaning-theoretic constraints including CON-BIV, CON-TC, and CON-FUNC, and concluded that each is a legitimate meaning-theoretic constraint for the semanticist. While none of them individually secures the intended two-valued semantics, putting them all together, the semanticist is able to provide an answer to the problem of many-valued truth-tables.
3 A modal semantics for Knot
Even if the semanticist rejects Knot as a piece of logical vocabulary, there is still room to accept it as a piece of non-logical, modal vocabulary. For Knot can be given a modal semantics.Footnote 15 Doing so may even be instructive, since it indicates a potential reason for the nastiness of the connective that concerns a distinction between two types of consequence within a modal framework, viz. local versus global consequence. We begin with formalities.
Definition 1
A  -model for the language is a triple \(\langle W, \bullet , V \rangle \), where W is a non-empty set (of states); \(\bullet : W\longrightarrow W\) with \(\bullet \bullet w=w\) for all \(w\in W\); and \(V: W\times \mathsf {Prop} \longrightarrow \{ 0, 1 \}\) is an assignment of truth values to state-variable pairs. Valuations V are then extended to interpretations I to state-formula pairs by the following conditions:
-model for the language is a triple \(\langle W, \bullet , V \rangle \), where W is a non-empty set (of states); \(\bullet : W\longrightarrow W\) with \(\bullet \bullet w=w\) for all \(w\in W\); and \(V: W\times \mathsf {Prop} \longrightarrow \{ 0, 1 \}\) is an assignment of truth values to state-variable pairs. Valuations V are then extended to interpretations I to state-formula pairs by the following conditions:
-
\(I(w,p)=V(w,p)\);
-
\(I(w, \lnot A)=1\) iff \(I(w, A)=0\);
-
\(I(w, A\wedge B)=1\) iff \(I(w, A)=1\) and \(I(w, B)=1\);
-
\(I(w, A\vee B)=1\) iff \(I(w, A)=1\) or \(I(w, B)=1\);
-
\(I(w, A{\rightarrow } B)=1\) iff \(I(w, A)=0\) or \(I(w, B)=1\);
-
 iff \({I(\bullet w, A)=1}\).Footnote 16
iff \({I(\bullet w, A)=1}\).Footnote 16
Semantic consequence is then defined globally:  iff for all
iff for all  -models \(\langle W, \bullet , V \rangle \), if for all \(w\in W\), \(I(w, B)=1\) for all \(B\in \Gamma \), then for all \(w\in W\), \(I(w,A)=1\).
-models \(\langle W, \bullet , V \rangle \), if for all \(w\in W\), \(I(w, B)=1\) for all \(B\in \Gamma \), then for all \(w\in W\), \(I(w,A)=1\).
We now show that  and the consequence relation \(\models \) defined over the four-valued semantics for Knot (given in Button (2016)) are equivalent.
and the consequence relation \(\models \) defined over the four-valued semantics for Knot (given in Button (2016)) are equivalent.
Lemma 2
If  then \(\Gamma \models A\).
then \(\Gamma \models A\).
Proof
Immediate since the four-valued semantics is just a special case in which the number of states is two for the  -models. \(\square \)
-models. \(\square \)
Lemma 3
If \(\Gamma \models A\) then  .
.
Proof
We prove the contrapositive. Suppose that  . Then, there is a
. Then, there is a  -model \({\mathcal {M}}:=\langle W, \bullet , V \rangle \) such that \(I(w, B)=1\) for all \(w\in W\) and \(I(w, A)\ne 1\) for some \(w\in W\). Call such a witness state u, and consider the submodel \(M^u\) of \({\mathcal {M}}\) such that \(W^u:=\{ u, \bullet u \}\), and \(\bullet ^u\) and \(V^u\) are the restrictions of \(\bullet \) and V to \(W^u\). Since for all \(w\in M^u\) and for all \(B\in \Gamma \), \(w\models B\) and yet \(u\not \models A\), \(\Gamma \not \models _{M^u}A\). Given that \(M^u\) corresponds to a 4-interpretation \(I^4\) such that \(\Delta \models _{M^u} C\) iff \(\Delta \models _{I^4}C\) by setting \(I^4(p)=1\) iff \(I^u(w,p)=I^u(\bullet w,p)=1\), we have that \(\Gamma \not \models _{I^4}A\). Whence \(\Gamma \not \models A\). \(\square \)
-model \({\mathcal {M}}:=\langle W, \bullet , V \rangle \) such that \(I(w, B)=1\) for all \(w\in W\) and \(I(w, A)\ne 1\) for some \(w\in W\). Call such a witness state u, and consider the submodel \(M^u\) of \({\mathcal {M}}\) such that \(W^u:=\{ u, \bullet u \}\), and \(\bullet ^u\) and \(V^u\) are the restrictions of \(\bullet \) and V to \(W^u\). Since for all \(w\in M^u\) and for all \(B\in \Gamma \), \(w\models B\) and yet \(u\not \models A\), \(\Gamma \not \models _{M^u}A\). Given that \(M^u\) corresponds to a 4-interpretation \(I^4\) such that \(\Delta \models _{M^u} C\) iff \(\Delta \models _{I^4}C\) by setting \(I^4(p)=1\) iff \(I^u(w,p)=I^u(\bullet w,p)=1\), we have that \(\Gamma \not \models _{I^4}A\). Whence \(\Gamma \not \models A\). \(\square \)
Note that the above lemmas rest on the well-known observation that two worlds will suffice for the purpose of characterizing FDE in terms of the Routley star semantics (cf. Example 8.13.12 of Humberstone (2011)).
Thus, we have now established the following.
Proposition 4
\(\Gamma \models A\) iff  .
.
Based on the above alternative semantics, we may conclude that the connective Knot is a symmetric, functional modality, in the sense that the accessibility relation governing Knot is symmetric and functional.Footnote 17 Admittedly, we currently know of no useful application of this modality. However, a symmetric, functional negative modality was employed in a recent paper by Odintsov and Wansing (2020) in which they provide an alternative semantics for the logic HYPE of Leitgeb (2019). Note here that Odintsov and Wansing deployed the local consequence relation instead of the global one we used above. If we also consider the local consequence relation based on  -models, then we obtain the expansion of FDE obtained by adding the conflation operator which is also equivalent to BD+. In terms of the four-valued semantics, this means designating both 1 and a instead of only 1, which gives us back all of the lost properties.Footnote 18
-models, then we obtain the expansion of FDE obtained by adding the conflation operator which is also equivalent to BD+. In terms of the four-valued semantics, this means designating both 1 and a instead of only 1, which gives us back all of the lost properties.Footnote 18
4 Is there a legitimate problem?
The problem of many-valued truth-tables presupposes that the familiar rules, such as conditional-introduction and substitutivity, are valid no matter what. We have two concerns with this. The first is that, it is clear that the inferentialist regards rules such as conditional-introduction to be valid in this way since such rules are meaning-conferring, and it makes little sense (for the inferentialist) to say that a rule that can’t be endorsed by their own lights confers meaning on a connective. However, it is no commitment of the semanticist that rules such as conditional-introduction are valid no matter what, since these rule do not play the sort of meaning-theoretic role they play for the inferentialist. This brings us to the second concern. There are good reasons to think that rules such as conditional-introduction simply are not valid no matter what, unless you look at only a very restricted fragment of our entire language. Consider our modal vocabulary which includes, not just two familiar notions of possibility and necessity, but also notions like actuality that are not definable from just these two. Let us denote ‘Actually A’ by ‘@A’. Then a popular and simple interpretation of @ (relative to a Kripke model) is that @A is true at a world just in case A is true at some distinguished element, the actual world.Footnote 19 Truth in a model is defined as truth at the actual world, and validity is defined in terms of the preservation of truth over the class of models.Footnote 20
Relative to this semantics, if A is true at the actual world of a model, then so is @A and conversely—that is, A and @A are logically equivalent. Yet it is also well-known that A and @A are not intersubstitutable salva veritatae. For instance, if A is true in a model (i.e. true at the actual world), then @A is true at every world in the model, and so its necessitation is true in the model. But clearly the necessitation of A need not be true in the model. The failure of substitutivity here has never been considered a problem, let alone a problem that is analogous to the problem of tonk. There are two reasons for this. First, assuming our semantics is adequate (even if only in a range of limited cases), it tells us why substitutivity is invalid. It does not make sense to stubbornly defend substitutivity and to reject any semantics for ‘actually’ that invalidates the rule, and the same goes for Knot on its modal interpretation. To do so would be to hold an unjustified dogma in the validity of the rule no matter what the language. Second, since ‘actually’, like Knot, conservatively extends the language, our beloved classical rules remain valid when reasoning in the usual extensional language. They fail only where they should.Footnote 21
The moral is that there is nothing problematic about breaking rules by expanding the language. On the contrary, Button says:
I think that we should refuse to add Knot to our language, since doing so would force us to adopt an undesirable logic. To be clear, Knot is less horrible than Tonk. Adding Tonk to a language leads to logical triviality, and
is certainly not trivial. However, the lesson of §2 is that, if we add Knot to our language, then we must abandon [certain rules, such as SUB]. Classical logic validates all [of these rules]. By contrast, logics lacking [these rules] are extremely weak; too weak, I think, for us to want to use them. (Button, 2016, p. 10)
However, consider expansions of classical logic, such as modal logic. These logics are classical, and yet we have seen that within these frameworks, e.g. within a possible worlds semantics, it is easy to define connectives that violate principles that classically hold in the base language. First, we would not say that such modal expansions of the language are non-classical. Second, we would not say these logics are too weak to be useful. In the purely classical language, they’re just as strong as classical logic, and when they are weaker they are justifiably so. One ought not reason unrestrictedly with substitutivity when using the operator ‘actually’ (as it was defined above), for instance, since the rule is invalid. Given the richness of natural language, we would be surprised if more than a very small handful of the rules valid in classical propositional logic were universally valid in ordinary language, and yet weakness of logic over our entire language has not been a hindrance to our reasoning in ordinary language.
An acceptance of Knot is, therefore, far less problematic than an acceptance of tonk would be for an inferentialist, since the former merely weakens the logic whereas the latter trivializes it.Footnote 22 The semanticist could therefore bite the bullet and accept Knot, agreeing that rules like conditional-introduction are in general invalid.Footnote 23 Moreover, the semanticist remains entitled to use all classically valid rules when reasoning within the classical fragment of the language. So perhaps there is room for a response that simply embraces a completely general version of SMP and the definability of nasty connectives that comes with it.
Notes
For a biased overview of some prominent such attempts, see Prior (2010).
The reason substitutivity fails, for instance, is that logical equivalence no longer guarantees sameness of truth-value.
That certain proof systems for classical (propositional) logic are not capable of uniquely pinning down the two-valued semantics is an observation originally made by Carnap in the fourties and it is a topic revived by Timothy Smiley (1996) under the label the categoricity problem.
See Button and Walsh (2018, Sect. 13) for details.
However, we do have our reservations about an argument that depends on directly referring to abstract entities, such as boolean-valued models, in order to radically undermine direct reference to abstract entities. But aside from that worry, we wonder whether the moderate semanticist could, for purely semantic purposes, identify truth values with concretia since they need only two of them.
To be clear, an expansion of a language \({\mathcal {L}}\) relative to a semantics \({\mathcal {S}}\) is obtained by adding to \({\mathcal {L}}\) a truth-function definable over the set of truth-values of \({\mathcal {S}}\).
When truth is understood as designationhood and falsity as undesignationhood, the usual truth conditions are called the truth principles in (Button & Walsh, 2018).
CON-TC’s failure to secure the intended semantics is discussed in Button and Walsh (2018, Sect. 13.4).
See footnote 13 for details.
The equivalence is easily seen since, given a many-valued semantics, none of the constants corresponding to the intermediate values (i.e. between the top and bottom of the algebra) will be definable from the classical vocabulary.
A proof of this result relies on Theorem 6 of Button (2016). For suppose a semantic pair satisfies CON-FUNC and CON-TC. By CON-TC the semantics is protoclassical. Since functional completeness implies that every signature expansion of the underlying algebra validates SUB, we have (b) of Theorem 6. Together with protoclasicality, we get (a) of Theorem 6, i.e. that the semantics is (up to isomorphism) the intended two-valued one.
As a referee points out, it is not clear whether such a response would extend to the problem of many-valued truth-tables generalized to first- and higher-order languages. However, note that if a solution to the propositional version of the problem exists, then the first-order semantics must be two-valued. This rules out potentially problematic connectives such as \(\heartsuit \) discussed in Button and Walsh (2018, pp. 311–312).
A modal semantics is mentioned in Button (2016, p. 10), but the one provided here is more general since it does not involve a single, two-world frame.
The reader may notice that the semantics for Knot is similar to the semantics of negation in relevance logic on the so-called Australian plan, i.e. in terms of the Routley star (see Routley and Routley (1972)).
Since our main focus is on the semanticist reply to Knot, proof systems do not have much of a role to play. However, the curious reader may find a few remarks about proof theory interesting. Recalling that the expansion of classical propositional logic by Knot is (algebraically) equivalent to FDE plus boolean negation or conflation, we may borrow some proof-theoretic considerations on a variant of FDE obtained by taking only the top element as designated. This variant is referred to as ETL in Pietz and Rivieccio (2013). Then, a tableau system can be given along the lines of Marcos (2011), an axiomatic proof system along the lines of Pietz and Rivieccio (2013), and a signed sequent calculus along the lines of Wintein and Muskens (2016).
We are not endorsing this as the correct or best formal rendering of the ordinary language ‘actually’. We are using it merely for illustrative purposes.
In other words, \(\Gamma \models A\) iff for every model M, if each member of \(\Gamma \) is true at the actual world of M, then A is true at the actual world of M.
Since we are assuming that a semantics consists of an algebra and a set of designated values drawn from the algebra, and that an expansion of the language involves the addition of a connective interpreted by a operator definable over the algebra, any expansion of the language is conservative.
As a referee points out, the claim that weakening one’s preferred logic is preferable to strengthening it may require additional argument. However, since we are talking about strengthening it to the point of triviality, we think it safe to assume this much for present purposes.
This is unproblematic for the semanticist since they do not claim that such rules are meaning-conferring. However, since the inferentialist takes it be part of the meaning of the conditional that conditional introduction is valid, the introduction of a connective that invalidates conditional introduction—if legitimate by the inferentialist’s light—would bring into question the very meaning of the conditional.
References
Button, T. (2016). Knot and tonk: Nasty connectives on many-valued truth-tables for classical sentential logic. Analysis, 76(1), 7–19.
Button, T., & Walsh, S. (2018). Philosophy and model theory. Oxford University Press.
Copeland, B. J. (1983). Pure semantics and applied semantics. Topoi, 2(2), 197–204.
De, M., & Omori, H. (2015). Classical negation and expansions of Belnap-Dunn logic. Studia Logica, 103, 825–851.
Fitting, M. (1994). Kleene’s three valued logics and their children. Fundamenta Informaticae, 20(1, 2, 3), 113–131.
Humberstone, L. (2011). The connectives. MIT Press.
Leitgeb, H. (2019). HYPE: A system of hyperintensional logic (with an application to semantic paradoxes). Journal of Philosophical Logic, 48(2), 305–405.
Marcos, J. (2011). The value of the two values. In J. Béziau & M. Coniglio (Eds.), Logic without Frontiers: Festschrift for Walter Alexandre Carnielli on the occasion of his 60th birthday (pp. 277–294). College Publication.
Odintsov, S. P., & Wansing, H. (2020). Routley star and hyperintensionality. Journal of Philosophical Logic, 50, 33–56.
Pietz, A., & Rivieccio, U. (2013). Nothing but the truth. Journal of Philosophical Logic, 42, 125–135.
Prior, A. N. (1960). The runabout inference-ticket. Analysis, 21(2), 38–39.
Ramírez-Cámara, E., & Estrada-González, L. (2021). Knot is not that nasty (but it is hardier than tonk). Synthese, 198, 5533–5554.
Read, S. (2010). General-elimination harmony and the meaning of the logical constants. Journal of Philosophical Logic, 39, 557–576.
Routley, R., & Routley, V. (1972). The semantics of first-degree entailment. Noûs, 6(4), 335–390.
Segerberg, K. (1986). Modal logics with functional alternative relations. Notre Dame Journal of Formal Logic, 27(4), 504–522.
Smiley, T. (1996). Rejection. Analysis, 56(1), 1–9.
Standefer, S. (2018). Proof theory for functional modal logic. Studia Logica, 106(1), 49–84.
Teijeiro, P. (2020). Not a Knot. Thought: A Journal of Philosophy, 9(1), 14–24.
Wintein, S., & Muskens, R. (2016). A gentzen calculus for nothing but the truth. Journal of Philosophical Logic, 45(4), 451–465.
Acknowledgements
We would like to thank the audience at The Society for Exact Philosophy 2018, and the referees for their helpful comments. The research of Hitoshi Omori was supported by a Sofja Kovalevskaja Award of the Alexander von Humboldt-Foundation, funded by the German Ministry for Education and Research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De, M., Omori, H. Knot much like tonk. Synthese 200, 149 (2022). https://doi.org/10.1007/s11229-022-03655-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-022-03655-5






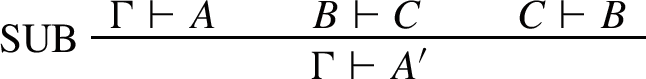
 iff
iff  is certainly not trivial. However, the lesson of §2 is that, if we add Knot to our language, then we must abandon [certain rules, such as SUB]. Classical logic validates all [of these rules]. By contrast, logics lacking [these rules] are extremely weak; too weak, I think, for us to want to use them. (Button,
is certainly not trivial. However, the lesson of §2 is that, if we add Knot to our language, then we must abandon [certain rules, such as SUB]. Classical logic validates all [of these rules]. By contrast, logics lacking [these rules] are extremely weak; too weak, I think, for us to want to use them. (Button, 