Abstract
This paper offers the Boolean many-valued solution to the Sorites Paradox. According to the precisification-based Boolean many-valued theory, from which this solution arises, sentences have not only two truth values, truth (or 1) and falsity (or 0), but many Boolean values between 0 and 1. The Boolean value of a sentence is identified with the set of precisifications in which the sentence is true. Unlike degrees fuzzy logic assigns to sentences, Boolean many values are not linearly but only partially ordered; so there are values that are incomparable. Despite this fact, the sentences in a sorites series can be taken as having values in a linear order, and losing (or gaining) value as we move from sentence to sentence in the series. So there is no sharp borderline between 0 and 1. Assigning Boolean many values instead of the two truth values to sentences for their vagueness values is analogous to assigning propositions instead of the truth values to sentences for their semantic values, as propositions are, from our viewpoint, also Boolean many values.





Similar content being viewed by others
Notes
These are the schemas of the standard Łukasiewicz infinite-valued logic \(L_{1}\), on which the most standard fuzzy logic (Klir and Yuan 1995) is based. So far as the negation, conjunction, and disjunction are concerned, Machina’s (1976) schemas are the same. On Goguen’s (1969) schemas, \({\left[ \left[ \phi \wedge \psi \right] \right] }^V={\left[ \left[ \phi \right] \right] }^V \cdot {\left[ \left[ \psi \right] \right] }^V\). In what follows I will focus on and criticize the version of fuzzy logic that employs these schemas, but similar criticisms can be given against other versions with only slight modifications.
The degenerate Boolean lattice has only one element.
This four-valued semantics is different from Dunn’s (1977) four-valued semantics for first-degree entailment. The tables for the conjunction and disjunction are exactly the same, but in Dunn’s semantics, the table for the negation will be
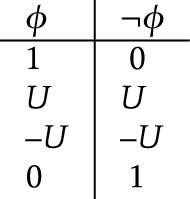
in the present notation.
In a more general, multiple-conclusion, setting, ‘Set \(\Delta \) of sentences is a logical (or semantic) consequence of set \(\Gamma \) of premises on Boolean algebra B’, \(\Gamma \ \models _B \ \Delta \), can be defined as follows:
\({\Gamma } \ {\models }_B \ {\Delta } \ {\Longleftrightarrow }_{df} \ \prod _{\phi \in {\Gamma }}{{\left[ \left[ \phi \right] \right] }^V_B \sqsubseteq \coprod _{\psi \in {\Delta }}{{\left[ \left[ \psi \right] \right] }^V_B \ (\Longleftrightarrow \ -\prod _{\phi \in {\Gamma }}{{\left[ \left[ \phi \right] \right] }^V_B \sqcup \coprod _{\psi \in {\Delta }}{{\left[ \left[ \psi \right] \right] }^V_B=1}})}}\) for every valuation V on B.
Note that in a multiple-conclusion logic, the premises are read conjunctively and the conclusions are read disjunctively. Gentzen’s (1935) classical sequent calculus and its popular variant, the truth tree system (Smullyan 1968; Jeffrey 1991), are typical deductive systems of multiple-conclusion logic.
That is, if P and Q are in the set, so are -P, \(P\cap Q\), and \(P\cup Q\).
Generally it is not exactly a ‘tree’ in the strict, mathematical sense, for, as you see in Fig. 4, there may be more than one way to reach a node like e. However, I will continue using the word ‘tree’ in a loose sense.
Some conditions, such as that the actual world includes all true precise sentences, are not amenable to formalization.
More strictly, the \(\Vdash \) relation is relative to the precisification space P (or the valuation scheme V), so ‘\({\Vdash }_{P}\)’ (or ‘\({\Vdash }_{V}\)’) is the correct notation; however, the subscript ‘P’ (or ‘V’) will be dropped for the sake of simplicity in what follows.
One important feature of precisification spaces I omitted is Separativity:
\(\forall p.\ \forall q\ngeq p. \ \exists r\ge q.\ \lnot \exists s \ \left( s\ge p\ \ \mathrm {and} \ \ s\ge r\right) \); that is, for any p and q, if \(q\ngeq p\), then there is some \(r\ge q\) that does not converge with p (Separativity).
A separative space makes up a tree-like structure; if a space is not separative, all separating branches are destined to converge at a later point. Obviously we don’t expect that to happen. I’ve omitted this condition from the main text because it is not directly relevant to our discussion. However, we need to use the condition in the proof of 13 in the Appendix.
The (classical) conditional \(\phi \rightarrow \psi \) can be defined as \(\lnot (\phi \wedge \lnot \psi )\); then
\(p \ \Vdash \ \phi \rightarrow \psi \ \Longleftrightarrow \ \forall q\ge p \ (q\ \ \mathop {\nVdash } \ \ \phi \ \ \mathrm {or} \ \ \exists r \ge q. \ r\ \Vdash \ \psi )\).
It should be noted, however, that the intuitionistic conditional can also be introduced into the language as follows:
\(p \ \Vdash \ \phi \rightarrow \psi \ \Longleftrightarrow \ \forall q\ge p \ (q\ \ \mathop {\nVdash } \ \ \phi \ \ \mathrm {or} \ \ q\ \Vdash \ \psi )\).
In this case, \(\lnot \phi \) can be defined as \(\phi \rightarrow \bot \).
The standard notations for \(\blacksquare A\) and \(\blacklozenge A\) are \(A^{\circ }\) and \(A^{-}\), respectively.
Rumfitt (2015) derives the same equations as those in 13 from his own distinctive semantics for vagueness called polar semantics. He also concludes that classical logic need not be bivalent. However, Rumfitt arrives at this conclusion after much philosophical investigation, whereas I point it out as a trivial fact, and his overall picture is very different from mine. Brown and Garson (2017) also offer a semantics of vagueness that results in similar equations.
This is called global validity. Another definition of logical consequence that has been suggested in the literature (Dummett 1975; Varzi 2007) is that of local validity:
\({\Gamma }\ {\models }_{SVL} \ \psi \ {\Longleftrightarrow }_{df}\) in every precisification space \(P=\left\langle D,\ \le ,\ @\right\rangle \) and for every precisification \(p\in D\), if, for every \(\phi \in {\Gamma },\ p \ {\Vdash }_P \ \phi \), then \(p \ {\Vdash }_P \ \psi .\)
Both definitions are based on the truth-preservation notion of logical consequence. The difference is that in the former, supertruth (i.e., truth in every precisification) is preserved, while in the latter, truth is preserved in each precisification; hence the global vs local distinction. In the main text of this paper, we will focus on global validity, as it is the more popular notion among the supervaluationists.
I presented a system of this kind in Akiba (2014b).
In fact, the relevant logic can be stronger than S4 and at least as strong as S4.1 (= S4 + M: \(\square \lozenge \phi \rightarrow \lozenge \square \phi \)). Generally, M holds in S4 frames if they contain final worlds, i.e., \(\forall p.\ \exists q\ge p.\ \forall r\ge q.\ q=r\). If we may assume that there are only finitely many atomic sentences in the relevant language, 10(D) will guarantee the existence of final worlds. This point does not affect the main contention in the text and, thus, will be set aside.
As is often pointed out, S4’s way of making gradation in truth by repeatedly appending ‘determinately’ to sentences is somewhat limited. Since Axiom 4, \(\square \phi \rightarrow \square \square \phi \), holds in S4, you cannot say ‘\(\phi \) is determinately true but that’s not determinately so’. Still, since Axiom 5, \(\lnot \square \phi \rightarrow \square \lnot \square \phi \), does not hold in S4, S4 allows you to say ‘\(\phi \) is not determinately true, but that’s not determinately so’.
In his probabilistic-psychological treatment of vagueness, Field (2000) starts off assigning probability values to a modal language with the S 4 ‘determinately’ operator and then switches to the corresponding nonmodal language which ‘hides’ the operator. Although his overall approach is very different, the idea that our nonmodal language has an S 4 modal counterpart is the same.
In the present framework, we still can introduce a ‘determinately’ operator, D, metalogically as follows:
\({\left[ \left[ D\phi \right] \right] }^V=1 \ \Longleftrightarrow \ {\left[ \left[ \phi \right] \right] }^V=1;\)
\({\left[ \left[ D\phi \right] \right] }^V=0 \ \Longleftrightarrow \ {\left[ \left[ \phi \right] \right] }^V\ne 1.\)
We define I, the ‘indeterminate whether’ operator, in the usual manner:
\(I\phi =_{df}\lnot D\phi \ \wedge \ \lnot D\lnot \phi .\)
Then
\({\left[ \left[ I\phi \right] \right] }^V=1\ \Longleftrightarrow \ {\left[ \left[ \phi \right] \right] }^V\ne 1\ \ \mathrm {and}\ \ {\left[ \left[ \phi \right] \right] }^V\ne 0;\)
\({\left[ \left[ I\phi \right] \right] }^V=0 \ \Longleftrightarrow \ {\left[ \left[ \phi \right] \right] }^V=1\ \ \mathrm {or} \ \ {\left[ \left[ \phi \right] \right] }^V=0.\)
Obviously, this ‘determinately’ operator is not very interesting. It doesn’t have to be, for, unlike in the ‘determinately’ operator approach, in the current approach the necessary gradation in truth values are given by Boolean many values and not by the ‘determinately’ operator.
Smullyan and Fitting (2010) use S4 modal logic in their explication of Cohen’s independence results.
Specifically, the forcing conditions for the disjunction and the conditional in intuitionistic logic are:
\(p\ \Vdash \ \phi \vee \psi \ \Longleftrightarrow \ p\ \Vdash \ \phi \ \ \mathrm {or} \ \ p\ \Vdash \ \psi ;\)
\(p \ \Vdash \ \phi \rightarrow \psi \ \Longleftrightarrow \ \forall q\ge p \ (q \ \ \nVdash \ \ \phi \ \ \mathrm {or} \ \ q\ \Vdash \ \psi ).\)
\(\lnot \phi \) can be defined as \(\phi \rightarrow \bot \); so the primitive operators will be \(\wedge \), \(\vee \), \(\rightarrow \), and \(\bot \). Compare these with 11(c) and note 12.
In a complete Boolean algebra, even an infinite set of sentences has a supremum and an infimum. A Boolean algebra that can be used as a model of quantificational logic must be complete.
References
Akiba, K. (2004). Vagueness in the world. Noûs, 38, 407–429.
Akiba, K. (2014a). Boolean-valued sets as vague sets. In K. Akiba & A. Abasnezhad (Eds.), Vague objects and vague identity (pp. 175–195). Dordrecht: Springer.
Akiba, K. (2014b). A defense of indeterminate distinctness. Synthese, 191, 3557–3573.
Akiba, K. (2017). A unification of two approaches to vagueness: The Boolean many-valued approach and the modal-precisificational approach. Journal of Philosophical Logic, 46, 419–441.
Barnes, E., & Williams, J. R. G. (2011). A theory of metaphysical indeterminacy. In K. Bennett & D. W. Zimmerman (Eds.), Oxford studies in metaphysics (Vol. 6, pp. 103–148). Oxford: Oxford University Press.
Bell, J. L. (2005). Set theory: Boolean-valued models and independence proofs (3rd ed.). Oxford: Clarendon Press.
Brown, J. D. K., & Garson, J. W. (2017). A new semantics for vagueness. Erkenntnis, 82, 65–85.
Cohen, P. J. (1966). Set theory and the continuum hypothesis. New York: Benjamin.
Crossley, J. N., & Humberstone, I. L. (1977). The logic of ‘actually’. Reports on Mathematical Logic, 8, 11–29.
Dummett, M. (1975). Wang’s paradox. Synthese, 30, 301–324.
Dunn, J. M. (1977). A useful four-valued logic. In J. M. Dunn & G. Epstein (Eds.), Modern uses of multiple-valued logic (pp. 5–37). Dordrecht: Springer.
Evans, G. (1978). Can there be vague objects? Analysis, 38, 208.
Field, H. (2000). Indeterminacy, degree of belief, and excluded middle. Noûs, 34, 1–30.
Fine, K. (1975). Vagueness, truth and logic. Synthese, 30, 265–300.
Gentzen, G. (1969). Investigation into logical deduction. In M. E. Szabo (Ed.), The collected papers of Gerhard Gentzen (pp. 68–131). Amsterdam: North-Holland. (Originally, 1935).
Givant, S., & Halmos, P. (2009). Introduction to Boolean algebras. New York: Springer.
Goguen, J. A. (1969). The logic of inexact concepts. Synthese, 19, 325–373.
Jeffrey, R. (1991). Formal logic: Its scope and limits (3rd ed.). New York: McGraw-Hill.
Jónsson, B., & Tarski, A. (1950). Boolean algebras with operators, part 1. American Journal of Mathematics, 73, 891–939.
Keefe, R. (2000). Theories of vagueness. Cambridge: Cambridge University Press.
Klir, G. J., & Yuan, B. (1995). Fuzzy sets and fuzzy logic: Theory and applications. Upper Saddle River, NJ: Prentice-Hall.
Kripke, S. (1965). Semantical analysis of intuitionistic logic, I. In J. N. Crossley & M. A. E. Dummett (Eds.), Formal systems and recursive functions (pp. 92–130). Amsterdam: North-Holland.
Lemmon, E. J. (1966). Algebraic semantics for modal logics I and II. Journal of Symbolic Logic, 31, 46–65, 191–218.
Lewis, D. (1993). Many, but almost one. In K. Campbell, J. Bacon, & L. Reinhardt (Eds.), Ontology, causality, and mind: Essays in honor of D.M. Armstrong (pp. 23–38). Cambridge: Cambridge University Press.
Machina, K. F. (1976). Truth, belief and vagueness. Journal of Philosophical Logic, 5, 47–78.
McKinsey, J., & Tarski, A. (1944). The algebra of topology. Annals of Mathematics, 45, 141–191.
Monk, J. D. (2018). The mathematics of Boolean algebra. In E. N. Zalta (Ed.), Stanford encyclopedia of philosophy (Fall 2018 edition). https://plato.stanford.edu/archives/fall2018/entries/boolalg-math/
Rumfitt, I. (2015). The boundary stones of thought. Oxford: Clarendon Press.
Smith, N. J. J. (2008). Vagueness and the degrees of truth. Oxford: Oxford University Press.
Smullyan, R. M. (1968). First-order logic. New York: Springer.
Smullyan, R. M., & Fitting, M. (2010). Set theory and the continuum problem (Revised ed.). Mineola, NY: Dover.
Sorensen, R. (2002). Vagueness and contradiction. Oxford: Clarendon Press.
Stone, M. (1936). The theory of representations for Boolean algebras. Transactions of the American Mathematical Society, 41, 321–364.
Unger, P. (1979). There are no ordinary things. Synthese, 41, 117–154.
Varzi, A. C. (2007). Supervaluationism and its logics. Mind, 116, 633–675.
Weatherson, B. (2005). True, truer, truest. Philosophical Studies, 123, 43–70.
Wheeler, S. (1979). On that which is not. Synthese, 41, 155–173.
Williamson, T. (1994). Vagueness. London: Routledge.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338–353.
Acknowledgements
The basic idea of this paper was presented in the symposium on indeterminacy at the American Philosophical Association Central Division Meeting in Chicago on February 27, 2020. I would like thank the audience and co-participants, especially, Patrick Greenough, David Taylor, and Alessandro Torza, for their input. I also thank the anonymous referees for Synthese for valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
This Appendix will sketch the proof of 13. Since (a) through (e) in 13 have two sets of equations, those on the right and those on the left, we need to show that both hold. The right equations tell us what group of sets constitutes the relevant Boolean algebra, and the left equations tell us about the fact that the negation, conjunction, disjunction, etc., still correspond to the complement, infimum, supremum, etc., of the algebra.
For the right equations, we can take advantage of the following well-known theorem that bridges topology and Boolean algebras (Givant and Halmos (2009)[Chapter 10]). A set A is called a regular open set if \(A=\blacksquare \blacklozenge A.\) Then the theorem states:
The class RO(S) of regular open subsets of a topological space \(S=\left\langle D,\ \subseteq \right\rangle \) is a completeFootnote 21 Boolean algebra, the regular open algebra of S, \(\left\langle RO\left( S\right) , -,\sqcap ,\sqcup ,0,1\right\rangle \), in which, for any sets \(F,\ G\in RO\left( S\right) \), the following holds:
- (a)
\(-F=\blacksquare (D-F);\)
- (b)
\(F\sqcap G=F\cap G;\)
- (c)
\(F\sqcup G=\blacksquare \blacklozenge (F\cup G);\)
- (d)
\(0=\emptyset \);
- (e)
\(1=D.\)
So what we need to show is that \({\left[ \left[ \phi \right] \right] }^V\) and \({\left[ \left[ \psi \right] \right] }^V\) in 13 are in RO(P), where P is the precisification space discussed in the main text. However, obviously \({\left[ \left[ \phi \right] \right] }^V\) and \({\left[ \left[ \psi \right] \right] }^V\) are some of the cones designated as [p]. Thus, it suffices to show that generally, [p]s are in RO(P), i.e., \([p]=\blacksquare \blacklozenge [p]\).
Proof of \([p]\subseteq \blacksquare \blacklozenge [p]\). For any q,
\(\begin{array}{ll} &{} q\in \left[ p\right] \\ &{} \Longleftrightarrow \forall r\ge q.\ r\in \left[ p\right] \\ &{}\Longrightarrow \forall r\ge q. \ \left[ r\right] \cap \left[ p\right] \ne \emptyset \\ &{}\Longleftrightarrow \forall r\ge q. \ r\in \blacklozenge \left[ p\right] \\ &{} \Longleftrightarrow [q]\subseteq \blacklozenge [p]\\ &{} \Longleftrightarrow q\in \blacksquare \blacklozenge \left[ p\right] . \end{array}\)
Proof of \(\blacksquare \blacklozenge [p] \supseteq [p]\). For any q,
\(\begin{array}{ll} &{} q\in \blacksquare \blacklozenge \left[ p\right] \\ &{}\Longleftrightarrow \left[ q\right] \subseteq \blacklozenge \left[ p\right] \\ &{}\Longleftrightarrow \forall r\ge q. \ r\in \blacklozenge \left[ p\right] \\ &{}\Longleftrightarrow \forall r\ge q. \ \left[ r\right] \cap \left[ p\right] \ne \emptyset \\ &{}\Longleftrightarrow \forall r\ge q. \ \exists s\ge r. \ s\ge p\\ &{}\Longrightarrow q\ge p \ \ \mathrm {(by \ Separativity \ mentioned \ in \ note \ 11)} \\ &{}\Longleftrightarrow q\in \left[ p\right] . \end{array}\)
Proofs of the left equations of 13 are straightforward. I will just give a proof for the negation; the rest is analogous.
\(\begin{array}{ll} &{} p\in {\left[ \left[ \lnot \phi \right] \right] }^V\\ &{}\Longleftrightarrow p \Vdash \lnot \phi \\ &{}\Longleftrightarrow \forall q\ge p. \ q \ \ \mathop {\Vdash }/ \ \ \phi \\ &{}\Longleftrightarrow \forall q\ge p. \ q\notin {\left[ \left[ \phi \right] \right] }^V\\ &{}\Longleftrightarrow \left[ p\right] \cap {\left[ \left[ \phi \right] \right] }^V=\emptyset \\ &{}\Longleftrightarrow \left[ p\right] \subseteq D-{\left[ \left[ \phi \right] \right] }^V\\ &{}\Longleftrightarrow p\in \blacksquare (D-{\left[ \left[ \phi \right] \right] }^V)\\ &{}\Longleftrightarrow p\in \mathrm {-}{\left[ \left[ \phi \right] \right] }^V. \end{array}\)
Thus, we have a proof of 13.
Rights and permissions
About this article
Cite this article
Akiba, K. The Boolean Many-Valued Solution to the Sorites Paradox. Synthese 200, 80 (2022). https://doi.org/10.1007/s11229-022-03561-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-022-03561-w