The epistemic benefits of generalisation in modelling II: expressive power and abstraction

Abstract

This paper contributes to the philosophical accounts of generalisation in formal modelling by introducing a conceptual framework that allows for recognising generalisations that are epistemically beneficial in the sense of contributing to the truth of a model result or component. The framework is useful for modellers themselves because it is shown how to recognise different kinds of generalisation on the basis of changes in model descriptions. Since epistemically beneficial generalisations usually de-idealise the model, the paper proposes a reformulation of the well-known distinction between abstraction and idealisation. A reformulated notion of abstraction is needed because the extant accounts yield wrong judgments when model-modifications introduce implicit assumptions.

1 Introduction

There are many kinds of generalisation, and they have different benefits in formal modelling. This paper provides an account that is able to identify epistemically beneficial generalisations on the basis of different modifications in model descriptions. A model-modification is epistemically beneficial if it justifiably increases the modellers’ confidence in the truth of a model component or result. Generalising a model has important epistemic benefits when the model result remains the same, that is, when the result is generalised (Lehtinen, 2021).

Representations that omit from representing some aspects of the systems they purport to describe are commonly called abstractions. The generality of a model refers to the number of phenomena it can explain or predict, or to the number of systems to which it applies (Levins, 1966, 1993; Lewis & Belanger, 2015; Matthewson & Weisberg, 2009; Weisberg, 2004, 2013).

Proper subset relations are necessary for recognising generalisations that increase the number of systems to which a model applies (Lehtinen, 2021). I will show that such proper subset relations are established by decreasing the number of assumptions of a model. Abstracting a model means describing the systems of interest in less detail, and this is achieved by making fewer assumptions than before. Abstracting a model generalises it because the more abstract model description applies to a larger number of systems. When a model is abstracted, its ability to apply to a larger number of systems is bought at the price of no longer being able to account for some properties.

There are, however, also generalisations that remove assumptions and that apply to a larger number of systems even though they are able to describe a larger number of properties than before. I will say that such generalisations increase the expressive power of a model. Increasing the expressive power is epistemically beneficial because it may show that one can prove a model result with fewer false assumptions. This justifiably increases modellers’ confidence in the results and the rest of the model components. This epistemic benefit is similar to that provided by demonstrating the robustness of the result (cf. Räz, 2017). Increasing the expressive power of a model explains how model results are generalised. The two concepts are closely related but not identical because expressive power may also increase in such a way that the model result changes.

I will also show that increasing the expressive power of a model is often epistemically beneficial in the weaker sense of de-idealising the model. These model-modifications thus accomplish the miraculous feat of simultaneously generalising and de-idealising a model (cf. Rol, 2008) by reducing the number of assumptions, while at the same time describing a larger number of properties explicitly.

Generalisations are not equivalent to abstractions (as in Strevens, 2008) because one can generalise a model both by abstracting and by de-idealising it. This is why a large part of the paper is devoted to formulating a clear distinction between abstractions and de-idealisations via increases in expressive power. The distinction is needed for determining which generalisations are epistemically beneficial.

Abstractions and increases in expressive power often remove different kinds of assumption: generalisations that increase expressive power remove implicit false assumptions (i.e., implicit idealisations), whereas abstractions remove explicit (true or false) or implicit (true or false) assumptions. An abstraction removes an assumption altogether, and the abstracted model no longer has the expressive power to describe the properties pertaining to the removed assumptions, whereas a model with more expressive power has the resources to describe all the properties described by the model that it generalises. Furthermore, it expresses the implicit assumption explicitly, but it does so without committing the model to asserting the assumption. The actual but implicit assumption becomes expressible but potential.

I will propose a notion of abstraction that enables distinguishing between idealisations and abstractions in a satisfactory way. I will take as my starting point the well-known approach of making this distinction in terms of omission (e.g., Godfrey-Smith, 2009; Jones, 2005; Levy & Bechtel, 2013) or the level of detail (Levy, 2018) versus distorting some properties of the system. According to this account, abstractions are representations that omit from mentioning some properties of the target system, and idealisations are representations that describe some property in the target, but do so with a model-description that distorts the property.

Some recent work (Levy, 2018; Portides, 2018) suggests that it is difficult to draw such a distinction because some representations are simultaneously abstract and idealised. I agree, and I only study ‘dynamic’ epistemic benefits: this is a study of how and when model-modifications bring about epistemic benefits. I will thus show how to partition generalising model-modifications into abstractions and de-idealisations. A representation resulting from a model-modification may well continue to contain idealisations, but the change itself can be clearly identified as an abstraction. Similarly, a de-idealisation may result in a representation that continues to contain idealisations, but the change itself can be a matter of de-idealisation.

I will show that all the previous attempts to draw the distinction, even if it is drawn in terms of model-modifications (Levy, 2018), still fail because they consider certain kinds of model-modification simultaneously as abstractions and idealisations with respect to the same property. They fail because they do not pay attention to the fact that false assumptions may be implicit. That is, they ignore the existence of implicit idealisations. Simpler, less detailed model descriptions that omit more properties often do not express their implicit false assumptions. This explains why increases in expressive power are attained by introducing more detailed model descriptions that omit less than the original ones. The proposed notion of abstraction is thus a model-modification that removes some assumptions from the model, but does not to remove any implicit idealisations. In contrast, an increase in the expressive power of a model usually removes an implicit idealisation.

Note that introducing an implicit idealisation into an existing model description counts as an idealisation, even though the false assumption is not visible, but it also counts as an omission. This is why abstraction cannot be equated with omission. The proposed notion of abstraction thus also requires that the model-modification does not introduce any new assumptions. This is why the notion of an assumption has to be clearly defined. They are propositions to which the model descriptions commit the model, irrespective of whether they are explicit or implicit.

Given that the purpose of discussing the distinction in this paper is to help understand the epistemic properties of different kinds of generalisation, the notions of idealisation and abstraction adopted here cannot possibly do justice to the rich variety of meanings that these terms have had in philosophy of science. For example, my notion of abstraction has nothing to do with processes of thought and the associated epistemic benefit of distinguishing between the important and the negligible factors in the study of some system (see Nowak, 1980 for a classic formulation, and Martínez & Huang, 2011 for an account of the variety of such thought processes). Similarly, the notion of idealisation does not aim to elucidate the variety of ways in which the target may be distorted by the model descriptions (viz., approximations, limit concepts etc.). I also do not discuss the various reasons why one may wish to idealise (unlike in e.g., Mäki, 2020) or abstract a model, and the associated epistemic benefits, or the different ways in which one may de-idealise (Knuuttila & Morgan, 2019). The only kind of de-idealisation I discuss is one that removes an implicit idealisation from the model. Such a straightforward notion is particularly suitable for an account that endeavours to establish the truth-related epistemic benefits of generalisation. However, although the distinction between abstraction and de-idealisation is introduced in order to better understand generalisation, scholars working on idealisation and abstraction may find it independently interesting.

I will thus argue that generalisations have truth-related epistemic benefits when they involve increases in expressive power in such a way that the generalised model entails fewer false, implicit assumptions about the (target) system, but continues to entail the model result. Generalisations may have other benefits relating to, for example, explanatory power. In this paper, however, such other benefits and the possible trade-offs between them and the ones identified in this paper are ignored. Studying them is left for future work.

Although this paper is written in a self-contained manner, it relies on a distinction between three different notions of generalisation presented in the first part of this double article (Lehtinen, 2021): (a) applying a model to new systems or to new phenomena, (b) abstracting the model and (c) generalizing a result. It is advisable to read the first part before this one, especially if the reader is interested in generality, applicability and the various kinds of systems and targets that they may concern. The present paper goes considerably deeper in distinguishing between (b) and a different way of looking at (c) (namely, expressive power), but it is almost entirely silent on (a).

I will use modifications to the Dixit-Stiglitz (1977) (DS) model of monopolistic competition from economics as an illustration. It is briefly described in Sect. 2. Section 3 shows how the number of actual assumptions in two models under comparison provides a way to identify proper subset relations. Section 4 develops precise definitions for expressive power and increasing expressive power. Section 5 proposes a notion of abstraction that allows for distinguishing between de-idealisations and abstractions in model-modifications. Section 6 discusses the scope of the account and presents the main conclusions.

2 The Dixit-Stiglitz model of monopolistic competition

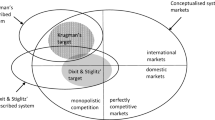
Economists study various markets and their characteristic forms of competition. Under perfect competition all commodities are assumed to be identical and firms cannot wield monopoly power because competition drives prices towards marginal costs. Monopolistic competition (henceforth MC) is a market form in which consumers’ preferences for a variety of similar but not identical goods leads firms to engage in product differentiation.

The Dixit-Stiglitz (DS) model simultaneously describes the demand for goods x_i ($i = 1, \ldots ,n$) in the MC markets and for a composite good x₀ that covers all other markets. In this sense, it applies to the general equilibrium, that is, the set of all markets, which is a proper superset of the set of MC markets. The most commonly used functional form for ‘Dixit-Stiglitz preferences’ looks like this:

$$U = x_{0}^{1 - \mu } V^{\mu } , \, V = \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho }$$

(DSP)

Here, $\mu$ is the share of nominal income spent on goods in the monopolistically competitive markets, and $\rho$ measures the substitutability among product varieties and thereby stands for the strength of the preference for variety and, as we shall see, firms’ monopoly power. The basic idea of the Dixit-Stiglitz model is that the Constant Elasticity of Substitution (CES)¹ utility function $V = \left( {\sum \nolimits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho }$ describes preferences for variety, and gives the incentive for firms to provide a range of differentiated products that are close but not perfect substitutes to each other. Each firm produces exactly one product x_i, and it has a monopoly in the market of that product. However, the monopoly power is not as strong as in proper monopolies because, if they charge too high a price, consumers may choose a closely related product instead: if shampoo for dyed hair is too expensive, you can settle for ordinary shampoo or sports shampoo. The consumers’ preference for variety (the cause) thus gives firms some monopoly power (the effect).

For our purposes, it is important to understand two aspects of the DS model.² First, different formulations of the theory of monopolistic competition apply to different sets of markets, and these markets enter into proper subset relations. Secondly, the modifications to the DS model concern the utility function (DSP) that describes preferences for variety. In (DSP), the cause and the effect are indistinguishable because they are merged into a single parameter $\rho$.

3 Generalisation, implicit assumptions and the number of assumptions

If a model applies to some set of systems in virtue of describing properties that such systems share, it applies to those systems generically (Lehtinen, 2021). When a model is abstracted, it is also generalised because some properties that the original model depicted are no longer attributed to the set of systems. For example, if a model that concerns international MC trade is abstracted by stripping away all assumptions that describe properties specific to international trade, it becomes more general because it then applies generically to all MC markets, no matter whether they are international or domestic. The set of international MC markets is a proper subset of MC markets. It is these proper subset relations that provide a way to compare the models with respect to generality.

However, one may also generalise a model by increasing its expressive power. Increasing a model’s expressive power also means demonstrating a proper subset relation, but it is done in such a way that all the properties described by the less general model are also described by the more general one. Yet, the more general model makes fewer assumptions about its target system. Think about a property X that many systems share, but which may take various different quantitative values in different systems. Due to problems of tractability in modelling, such properties are sometimes represented with particular values. In mathematical models this is often achieved with idealising limit concepts (like X = 0, X = 1, X = Y or X =  ∞). Increasing a model’s expressive power then means that one can derive results for all the possible quantitative values. It is usually not a matter of actually deriving such results for each of the different values. Instead, one shows that the original model results do not depend on the particular values because they can be derived with a more general model in which X can take any value. Alternatively, if the model results depend on the value of X, then the more general model is able to show how it depends on the different values.

Abstracting a model and increasing its expressive power both require that the set of systems to which the less general model applies is a proper subset of the set of systems to which the more general one applies.³ Since increasing the expressive power of a model retains the ability to describe all the properties of the original model, it does not change the model’s target. In contrast, abstracting a model changes the target in such a way that the new target includes fewer properties: it involves making a conscious decision to account for a larger number of systems by describing the systems to which it applies in less detail.

Given that both abstracting a model and increasing its expressive power remove assumptions from the model, we need a way to distinguish between them. The difference is that abstracting a model removes explicit or implicit assumptions whereas increasing a model’s expressive power removes implicit assumptions. In order to understand this claim that may sound stipulative at this stage, we must have a closer look at what implicit assumptions are.

More importantly, implicit means not explicitly expressed, but there are at least three different kinds of implicit assumption, and only one of them is relevant for increasing expressive power. Let us call these simply type 1, type 2, and type 3 implicit assumptions. The differences between these types of implicit assumption derive from the different conceptual and inferential resources needed to express the implicit assumption explicitly.

When an epistemically beneficial generalisation removes a type 1 implicit assumption, the original model does not have the expressive power to represent it, but yet the model is committed to it in that it is implicitly asserted. In contrast, a model already has the expressive power to describe type 2 implicit assumptions. One does not need to add anything to the conceptual and derivational resources of the model in order to be able to express the assumption, even though it is only implicitly assumed in some model description. This is why the removal of such assumptions represents a decrease rather than an increase in expressive power. Finally, type 3 implicit assumptions can be removed from a model and their removal is epistemically beneficial, but the removal cannot be done by modifying the functional form that embeds the implicit assumption as in epistemically beneficial generalisations. Instead, it is possible to find out that a functional form implies an implicit assumption of type 3 only by combining it with other parts of the model, and comparing the entailed assumptions with those entailed by combining an alternative functional form that does not entail this implicit assumption with those other parts of the model. Types 1 and 3 could also be called implicit idealisations because the model descriptions jointly commit the model to an idealisation.⁴

The reason why one must distinguish between different implicit assumptions is thus that while removing implicit assumptions of type 1 counts as making an epistemically beneficial generalisation, removing a type 2 implicit assumption would⁵ count as abstraction, and removing a type 3 implicit assumption may occur when a model result is shown to be robust.⁶ It is possible that the set of implicit assumptions for a given functional form is not entirely known either because deriving some consequences of functional forms may be complicated (type 3), or because a sufficiently powerful representation has not been found yet (type 1). However, economists typically know that their models are constrained by implicit assumptions.

Given the existence of several kinds of implicit assumption, it is necessary to look in some detail at particular model descriptions. I will discuss type 1 and type 2 implicit assumptions in this and the next section that defines increasing expressive power.

The model descriptions in mathematical models consist of various functional forms along with their interpretations. Modelling assumptions express a proposition: they depict something as being so-and-so. They need not be true, even approximately, to count as assumptions, nor do they need to be intended to be true. However, given that assumptions express propositions, they have truth values (as in Odenbaugh, 2019, p. 7). Model results, given that they are propositions derived from a model, also have truth values (Bailer-Jones, 2003).

I will refer to various collections of model descriptions (functional forms) as ‘models’. I agree with Odenbaugh (2018; see also Levy, 2015) who argues that models are simply the representational vehicles and the content they represent. Thus, when I use the term ‘model description’, I do not mean descriptions of models but rather descriptive elements in models. What is important for the purposes of this paper is that a given model description does not usually constitute the whole model because several model components are needed for deriving conclusions. This paper compares different combinations of equations that share some assumptions and do not share some others. Calling such collections ‘models’ is the shortest way of referring to them without causing confusion and without raising the question of what exactly counts as THE Dixit-Stiglitz model.

In what follows, I will formulate the definitions for increasing expressive power and abstraction in terms of ‘functional forms’ because most of my examples concern mathematical models. However one could substitute ‘model descriptions’ for ‘functional forms’ and thereby indicate that the account is applicable to any models whose model descriptions can be taken to have truth values.

Assumptions can be explicitly expressed as in, ‘Assume that…’, or embedded in functional forms, which are not to be identified with assumptions because a given functional form usually expresses several assumptions, and different functional forms entail different sets of assumptions. Hence, the number of assumptions depends on the functional forms employed in a model. To see how, let us consider the following functional forms for utility:

$$u\left( {x_{0} , \, V \, } \right) \, = U{\left( {x_{0} ,V \left( {x_{1} , \ldots ,x_{n} } \right)} \right), V = \mathop \sum \limits_{i = 1}^{n} v\left( x_{i} \right) }, v^{\prime} > 0,v^{\prime\prime} < 0$$

(1)

$$u\left( {x_{0} , \, V \, } \right) \, = \, U\left( {x_{0} , V \left( {x_{1} , \ldots ,x_{n} } \right)} \right),\,V = n^{\eta - \lambda } \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\lambda } } \right)^{{\frac{1}{\lambda }}} , 0 < \lambda < \infty$$

(2)

$$u\left( {x_{0} , \, V \, } \right) \, = \, U\left( {x_{0} , V \left( {x_{1} , \ldots ,x_{n} } \right)} \right),\,V = \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho } , 0 < \rho < \infty$$

(3)

$$U = \left( {\mathop \sum \limits_{i = 0}^{n} x_{i}^{\rho } } \right)^{1/\rho }$$

(K)

In Eq. (2), $\eta$ parameterisizes the market power of producers of differentiated goods, and $\lambda$ captures the preference-for-variety effect. All these functional forms have been used in formulations and modifications of the Dixit-Stiglitz (1977) model: (1) in Krugman (1979), (2) in Brakman and Heijdra (2004), (K) in Krugman (1980), and (3) in the original DS model. Let us now see what assumptions (abbreviated as ‘A_i’) they entail, and how the functional forms differ in this respect. The assumption that consumers’ utility in goods depends positively on their amount (= A₀) is explicitly expressed in (1): $v^{\prime} > 0$, and implicitly expressed in (2), (3) and (K). One can see this by noting that (since λ, ρ > 0) $\partial V/\partial x_{i} > 0$ in (2) and (3).

Consider now the assumptions entailed by (2) and (3). They both assume that consumers have a preference for variety ($\lambda , \, \rho \, < \, \infty$) (= A₁), their utility functions exhibit constant elasticity of substitution (= A₂), the sub-utility functions are homothetic⁷ (= A₃) and symmetric (= A₄), but (3) also assumes that market power ($\eta$) and preference for variety (λ) can be merged (= A₅) into one parameter $\rho .$ For the time being, it is sufficient to understand that firms’ market power and consumers’ preference for diversity are different properties in real monopolistically competitive markets.

Economists explicitly call (2) a generalisation of (3) (e.g., Brakman & Heijdra, 2004, p. 22; Neary, 2004, p. 175). One way of making sense of this is to note that the assumptions implied by functional forms (2) and (3) can be expressed as a nested hierarchy:

$$\left( {A_{0} ,A_{1} ,A_{2} ,A_{3} ,A_{4} } \right)$$

(2)

$$\left( {A_{0} ,A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5} } \right).$$

(3)

Equation (2) is more general than (3) in that it does not entail assumption A₅, but otherwise entails the same assumptions as (3). This proper subset relation implies that there are more systems that fit the description. (2) is more general than (3) in the sense that every proposition entailed by (2) is also entailed by (3) (cf. Hamminga, 1983, pp. 67–8; Strevens, 2004, 2008, p. 97; Rol, 2008).

(3) can be expressed as a special case of (2) by setting $\eta = \lambda$ but (3) does not explicitly represent this assumption (A₅). It is an implicit assumption that can be explicitly represented only with a functional form that has more expressive power (viz. 2). Similarly, (K): $U = \left( {\mathop \sum \nolimits_{i = 0}^{n} x_{i}^{\rho } } \right)^{1/\rho }$ is a special case of (DSP): $U = x_{0}^{1 - \mu } V^{\mu }$, $V = \left( {\mathop \sum \nolimits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho }$ when $\mu = 1$, but again (K) itself does not explicitly represent this implicit assumption. The fact that one can express implicit idealisations with more powerful forms justifies the claim that implicit idealisations have truth values (i.e., they are false) even though they are not explicitly asserted by the model descriptions.

Let us refer to assumptions that are expressible but not asserted by a given functional form as potential. If assumptions are explicitly or implicitly asserted, they are actual. It is now easy to see that assumption A₅ ($\eta = \lambda$) is implicit but actual in (3), and explicitly expressible but potential in (2), and that assumption $\mu = 1$ is implicit but actual in (K), and explicitly expressible but potential in (DSP). These characterisations will become important when I argue below that increasing expressive power removes implicit actual assumptions from models. Abstractions, in contrast, remove explicit or implicit assumptions. The difference to increasing expressive power is that abstractions remove assumptions in such a way that the model loses its ability to express the property that the assumption concerns altogether. This is why abstractions, unlike increases in expressive power, may also remove potential assumptions. These claims will be better understood once we have a more precise definition of expressive power.

4 Increasing expressive power

In this section I will provide a precise definition for increasing the expressive power of a model. Given that functional forms come with different degrees of expressive power, one has to start with a definition for them, and then consider the complications that arise from the fact that models often consist of several interacting functional forms, and increasing the expressive power of a model must exclude trade-offs that arise when several model components are modified at the same time.

Intuitively, (2) has more expressive power than (3) because (3) is a special case of (2) when $\eta = \lambda$(cf. Evans et al., 2013), and because it is able to describe all the desired properties of (3), and then some additional ones. A functional form is thus explicitly representable with another if the former model description can be deductively derived from the latter as a special case. Before defining an increase in expressive power, let us define expressive power.

(EPF) A functional form has the expressive power to represent a property p if its model descriptions include, implicitly or explicitly, a description of p.

An equivalent definition can be given to models.

(EPM) A model has the expressive power to represent a property p if its model descriptions include, implicitly or explicitly, a description of p.

The reason why a functional form may have the expressive power to represent some implicit assumptions can be understood by considering (2) and (3) above. They have the expressive power to represent the type 2 implicit assumption that the utility depends positively on goods because the partial derivative $\partial V/\partial x_{i}$ is positive in (2) and (3).

One cannot increase the expressive power of a functional form with respect to an implicit assumption if the form already has the expressive power to express that assumption. Although this may seem obvious, this explains why removing an implicit assumption like A₀ from the model would entail a loss in expressive power. In contrast, functional form (3) is not able to represent the properties $\eta$ (market power) and $\lambda$ (elasticity of substitution) separately. According to (EPF), then, (3) does not have the expressive power to represent the type 1 implicit assumption A₅: $\eta = \lambda$. The difference between the two implicit assumptions $A_{0} :\partial V/\partial x_{i} > 0$ and A₅: $\eta = \lambda$ is that A₀ can be derived from the functional form (3) without adding any properties into it, whereas $\eta = \lambda$ cannot thus be derived from (3). The crucial point is that its own derivational resources are sufficient to express $\partial V/\partial x_{i} > 0$ but not $\eta = \lambda$. Functional forms may thus have the expressive power to represent some implicit assumptions (type 2), but not those that require a more powerful functional form to be expressible (type 1).

A model-modification with a functional form F_j can be taken to entail a loss in expressive power if there is at least one property that F_i but not F_j has the expressive power to express. An increase in expressive power (IEP) of a functional form is defined as follows⁸:

(IEP) A functional form F_i has more expressive power than F_j if

• (i) F_j is explicitly representable as a special case of F_i, and if

• (ii) F_i has the expressive power to express all the properties that F_j expresses.

The notion of an increase in expressive power is related to expressive power as follows. Increasing expressive power means that the more powerful functional form F_i represents some properties of a system that the less powerful form F_j is not able to represent. At the same time, it characterises a whole range of such properties (in (2) all the different possible values of $\eta$ and $\lambda$) in such a way that the model is not committed to assuming any particular value within the range. In contrast, the less powerful form F_j commits the model to assuming a specific proposition $\left(\eta = \lambda\right)$, viz. the proposition that the more powerful form F_i identifies as the implicit assumption in the less powerful form F_j.

Let us now consider an example of an epistemically beneficial generalisation which is related to Abraham Wald’s proof of the existence of a general equilibrium (see Wald, 1951; Weintraub, 1985). Let x_i denote the demand for good i, and p_i its price. f is a monotonic function with f’ < 0. Wald’s initial assumption in 1935 was:

$$x_{i} = f\left( {p_{i} } \right).$$

(W35)

The next year, he generalised this into

$$x_{i} = f\left( {p_{1} , \, p_{2} , \ldots p_{i} , \ldots , \, p_{n} } \right).$$

(W36)

Consider now the assumption $x_{i} = f\left( {p_{i} } \right)$ that Wald generalised. This assumption is formulated by representing a whole range of possible assumptions by means of a specific instance; $x_{i} = f\left( {p_{i} } \right)$ is a specific instance of possible demand relationships between a commodity and various prices. Wald’s 1935 model is not able to express the implicit assumption that the prices of goods other than i do not have an effect on the demand for good i: $\partial f\left( {x_{i} } \right)/\partial p_{j} = 0$. This assumption can only be expressed by adding properties p_j into W35.This representation in terms of a specific instance is the reason why the implicit idealisation can be removed by a generalisation that increases expressive power. For readers familiar with Mäki’s (1992, 1994) notion of horizontal isolation, it may be illuminating to see that Wald’s generalisation provides an epistemically beneficial horizontal de-isolation.⁹

One could also define the expressive power of a functional form by appealing to the set of systems about which it is true:

A functional form F_i has more expressive power than F_j if

• (i) F_j is explicitly representable as a special case of F_i, and

• (ii) F_i is able to express all the properties that F_j expresses.

• (iii) The set of systems about which F_j is approximately true is a proper subset of the set of systems about which F_i is approximately true,

Consider now Wald’s generalisation to see how the more specific form is representable as a special case of the more general. (W35) can be derived as a special case of (W36), as follows. Let p_-i denote the set of prices of all goods except i. A modified version of (W35) can now be expressed by separating its explicit (A_E) and the implicit (A_I) assumptions:

$$\begin{aligned} & \left( {A_{E} } \right) \, x_{i} = f\left( {{p}_{i} } \right), \hfill \\ & \left( {A_{I} } \right) \, \partial f\left( {x_{i} } \right)/\partial p_{j} = 0, \, for \, all \, j \in {\mathbf p}_{{- i}} \hfill \\ \end{aligned}$$

(W35′)

(W35′) can be obtained from (W36) by inserting the implicit assumption A_I into it: if $\partial f\left( {x_{i} } \right)/\partial p_{j} = 0$, for all $j \in {\mathbf{p}}_{ - i}$, then $x_{i} = f\left( {p_{1} , \, p_{2} , \ldots p_{i} , \ldots , \, p_{n} } \right) = \, f\left( {p_{i} } \right)$. (W35) has exactly the same actual assumptions (A_I and A_E) as (W35′), but its set of explicit assumptions (A_E) is smaller than that of (W35′) (A_I and A_E). (W36) removes the idealisation expressed by A_I. Similarly, Krugman’s (1980) functional form (K) can be obtained by inserting its implicit assumption $\mu = 1$ into (DSP), and (3) can be obtained by inserting (A₅):$\left( {\eta = \lambda } \right)$ into (2).

Being able to represent functional form F_j as a special case of F_i entails that it is possible to demonstrate that the set of systems to which F_j applies is a proper subset of the set to which F_i applies. Hence, one can also define an increase in expressive power of a functional form by positing that the derivational resources of F_i are sufficient to demonstrate such a proper subset relation.

Thus far we have been discussing the expressive power of functional forms. Given that models may consist of several different combinations of functional forms, the conditions for an increase in expressive power of a model need to exclude trade-offs among the functional forms. To see this, suppose that F_i has more expressive power than F_j, and that F_k has more expressive power than F_m. If one now modifies model M₁ = (F_j, F_k, F_n) into M₂ = (F_i, F_m, F_n), model M₁ does not have more expressive power than M₂, nor vice versa. M₁ has more expressive power than M₂ only if no functional form in M₂ has more expressive power than the corresponding form in M₁, and if at least one functional form in M₁ has more expressive power. In practice, an increase in the expressive power of a functional form translates into an increase in the expressive power of a model only if the two models are otherwise identical. The definition for an Increase in Expressive Power of a Model (IEPM) is thus considerably more stringent.

(IEPM) Model M₁ has more expressive power than M₂ if

• (i) There is (at least) one functional form in M₁, F_i, and one in M₂, F_j, such that F_j is explicitly representable as a special case of F_i, and

• (ii) F_i is able to express all the properties that F_j expresses, and

• (iii) There is no functional form in M₂ that has more expressive power than the corresponding form in M₁ and

• (iv) There are no other functional forms or separate individual assumptions in M₂ that express properties not expressed in M₁.

The third condition (iii) rules out cases in which the increase in the expressive power of one functional form is traded off by a loss in the expressive power of another. The fourth condition (iv) rules out cases in which model M₂ specifies details about some system that M₁ does not represent at all. Condition (ii) is not sufficient for this because it only concerns one pair of functional forms but models may have functional forms that do not have a counterpart in the other model under comparison.

If model M₁ has more expressive power than M₂ according to (IEPM), it is also necessarily more general. However, the converse need not be true. A model may be more general than another but not be able represent all the properties that the more specific model describes. This is what it means to be more abstract. Furthermore, a model does not necessarily have more expressive power than another even if it can describe a property that the other model is not able to describe.

Let us consider an example to clarify these points. The Dixit-Stiglitz model is more general than Krugman’s model in the sense that the set of systems to which the latter applies generically (international MC markets) is a proper subset of that of the former (all MC markets). Yet, the Dixit-Stiglitz model does not have the expressive power to describe any characteristics specific to international trade. Hence, even though the Dixit-Stiglitz model is more general in terms of the set of systems to which it applies, it does not have more expressive power than Krugman’s model because condition (iv) is violated. If Krugman would have presented his model before Dixit and Stiglitz, the Dixit-Stiglitz model would have generalised Krugman’s model, but it would have done so by abstracting it.

Despite describing some properties that the Dixit-Stiglitz model does not describe, Krugman’s model does not provide an increase in expressive power compared to the Dixit-Stiglitz. Krugman’s model obtains the expressive power to describe properties specific to international trade by adding system-specific assumptions about international trade into the Dixit-Stiglitz model. Instead of increasing the expressive power of existing functional forms in the Dixit-Stiglitz model, it introduces new assumptions that have no counterpart in the latter. Although Krugman’s model can be said to have generalised the DS model, it did so by increasing rather than decreasing the number of assumptions in the model. The increased expressive power with respect to properties concerning international trade is thus achieved in a way that makes the model more specific rather than more general. Condition (i) is designed to rule such cases out by requiring that the increase in expressive power with respect to a property must be attained by showing how to derive a functional form as a special case of another.

Krugman provides a generalisation of the Dixit-Stiglitz model (of type (a)), but one that is different from abstracting a model and from increasing its expressive power. It shows that the derivational resources of the latter can be applied in a new specific context, in this case international markets, and it explains new phenomena (international trade in similar commodities).¹⁰ Generalisations that explain new phenomena, such as Krugman’s model, cannot increase the expressive power of a more abstract model, even though the former has the expressive power to express some properties that the latter is not able to express. Generalisations that explain new phenomena thus have more expressive power with respect to properties concerning those new phenomena, but since such attaining such expressive power about new phenomena always requires completely new assumptions rather than increases in the expressive power of existing functional forms, they cannot satisfy the considerably stronger conditions for increasing the expressive power of a model.

As it happens, Krugman’s model also has less expressive power with respect to the assumption that $\mu = 1$ because the functional form in Krugman’s model (K): $U = \left( {\mathop \sum \nolimits_{i = 0}^{n} x_{i}^{\rho } } \right)^{1/\rho }$ is a special case of (DSP): $U = x_{0}^{1 - \mu } V^{\mu }$, $V = \left( {\mathop \sum \nolimits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho }$ when $\mu = 1$. This means that with respect to conditions (i), (ii) and (iii), the Dixit-Stiglitz model has more expressive power than Krugman’s model. An increase in the expressive power of a model thus requires not merely being able to express some additional properties, it also requires no loss in expressive power with respect to all the properties that were expressed by the less powerful model.

The definition for increasing the expressive power of a model is deliberately so stringent as to be applicable only when two models are otherwise identical but contain functional forms that can be compared with respect to expressive power. It must be stringent in order to recognise cases in which an increase in expressive power of a functional form can be interpreted as an increase in the generality of the model. If model 1 has more expressive power than model 2 with respect to one functional form or property, and less expressive power with respect to another, models 1 and 2 cannot be compared with respect to generality and expressive power. IEPM is designed to rule out such cases.

To summarise the two sections thus far, the number of actual assumptions is used as the criterion for identifying differences in generality in terms of model descriptions. The notion of increasing expressive power characterises the representational properties of generalisations that typically allow for epistemic benefits via generalising results. Generalisations that increase expressive power de-idealise by removing implicit false assumptions from models. It is necessary to distinguish cases in which expressive power increases from other cases in which the number of assumptions also decreases as a result of a generalisation. Such generalisations typically decrease the expressive power, and they fall under a suitably defined notion of abstraction.

5 A notion of abstraction

I will now propose a notion of abstraction which is helpful in analysing generalisations. I will start by explaining how expressive power should be distinguished from abstraction, that is, the desiderata for the distinction. Consider functional forms (SE), (2), and (3).

$$u\left( {x_{0} , \, V} \right) \, = \, U \, \left( {x_{0} , \, V\left( {x_{1} , \, ..., \, x_{n} } \right)} \right),$$

(SE)

$$u\left( {x_{0} , \, V \, } \right) \, = \, U \, \left( {x_{0} , \, V\left( {x_{1} , \, ..., \, x_{n} } \right)} \right),\,V = n^{\eta - \lambda } \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\lambda } } \right)^{{\frac{1}{\lambda }}}$$

(2)

$$u\left( {x_{0} , \, V \, } \right) \, = \, U \, \left( {x_{0} , \, V\left( {x_{1} , \, ..., \, x_{n} } \right)} \right),\,V = \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho }$$

(3)

(SE) is an abstract functional form for utility that Stiglitz and Dixit (1993) introduced to describe the bare bones of their model. A model is said to be generically applicable to a set of systems if it has the expressive power to represent the properties specified in the target, and the target subsumes those systems in virtue of the fact that the systems possess those properties. In other words, a model can only apply to a set of systems if it has the expressive power to explicitly represent those of their features that are considered important. (SE) is more general than (2) and (3) in virtue of making fewer assumptions, but it is not able to express preferences for variety because it does not specify the property of an elasticity of substitution. It does not have the expressive power to describe monopolistically competitive markets because it is too abstract. Hence, it does not apply to those markets according to the generic notion.

I have previously argued that (2) has more expressive power than (3), and that it is also more general in virtue of making fewer assumptions. The difference between generalising (3) with (2), and generalising (3) or (2) with (SE) is that the latter generalisation entails a loss in expressive power, but the former an increase in it. Hence, distinguishing between expressive power and abstraction in the right way requires that generalising (3) with (2) should not be counted as an abstraction, but rather as a de-idealisation because it increases expressive power, while generalising (3) or (2) with (SE) should be counted as an abstraction because it entails a loss in expressive power. It is thus necessary to come up with a definition that pinpoints which feature of the model descriptions makes (2) less idealised than (3), but (3) less abstract than (SE).

The notion of abstraction I will formulate is similar in spirit to various extant accounts based on omissions and lack of detail, but I will first explain why all the previous proposals fail in properly distinguishing between idealisation and abstraction. The general theme is that since they do not pay attention to implicit assumptions, they end up providing the wrong kind of classification.

Various authors have argued that abstraction does not introduce any new falsities into a model, whereas idealisation does (e.g., Godfrey-Smith, 2009; Jones, 2005; Levy & Bechtel, 2013; Rol, 2008). Abstraction is defined as the omission of some properties of a (target) system in a representation. According to such a definition, (3) is more abstract than (2) in virtue of the fact that it omits representing the preference for diversity separately from market power. The problem with this definition is that (3) is also more idealised than (2) in the sense of being false about the property that it asserts implicitly (A₅:$\eta = \lambda )$, whereas (2) does not make this false assumption. (2) is capable of representing this property but makes the assumption only potentially. If it is made actual, it is by using a limit (i.e., $\eta = \lambda$) to express the falsehood. According to this definition, then, (3) is more abstract and more idealised than (2) about the very same assumption A₅! If (3) were taken to abstract (2), it would do so by introducing a new false assumption, albeit one that is implicitly expressed. Abstraction cannot thus be defined as mere omission because one is then not able to properly distinguish between cases in which an omission involves an implicit false assumption, and cases in which it involves an explicit (true or false) assumption.

Levy (2018) claims that defining abstraction as decreasing the level of detail of a representation clarifies cases in which a representation could simultaneously be taken to be an idealisation and an abstraction. As he states, ‘a representation A is more abstract than representation B just in case B provides more detail than A about the same set of objects’. Levy’s proposal is not helpful, however, because describing fewer details in this case yields exactly the same wrong judgment that (3) is more abstract than (2): (3) is less detailed than (2) because it uses one parameter $(\rho$) to express two essentially different properties merged into one, whereas (2) uses two ($\eta$ and $\lambda$) parameters to express these properties.

Strevens (2008, see also Rol, 2008) can be taken to define abstraction on the basis of proper subset relations because he identifies the abstractness of a model with the ‘number of possible physical systems that fit the model’ (Strevens, 2004, 2008, p. 474). M is more abstract than M’ “just in case (a) all causal influences described by M are also described by M’ and (b) M’ says at least as much as M, or, a little more formally, every proposition in M is entailed by the propositions in M’” (2008, p. 97). Consider the following example of demand relationships from Mäki (1992) that illustrates genuine abstraction.

$$ q = f\left( p \right)$$

(D1)

$$ q = a + bp$$

(D2)

$$q = 8.5 - 0.85p$$

(D3)

(D1) expresses the assumption that the quantity q demanded depends on the price p: A_Q1. ‘Fleshing out’ (D1) yields more specific forms. (D2) can be expressed as a special case of (D1) by inserting its explicit assumptions (D2) A_Q2: $f\left( p \right) = a + bp$ into it, and (D3) can be expressed as a special case of (D2) by inserting its explicit assumptions A_Q3: a = 8.5, and b = -0.85. The assumptions implied by functional forms (D1) to (D3) can again be expressed as a nested hierarchy:

$$ \left( {A_{{{\text{Q}}1}} } \right) $$

(D1)

$$ \left( {A_{{{\text{Q}}1}} , \, A_{{{\text{Q}}2}} } \right)$$

(D2)

$$\left( {A_{{{\text{Q}}1}} , \, A_{{{\text{Q}}2}} , \, A_{{{\text{Q}}3}} } \right)$$

(D3)

In this case, making fewer actual assumptions as one goes up the list also means a loss in expressive power because the more abstract form does not have the ability to express the more specific properties at all. This is why the more abstract forms can be deductively derived from the more specific by removing assumptions, thus guaranteeing that there is a proper subset relation between the systems to which they apply. Strevens’ definition of abstraction yields correct judgments in this example.

However, recall now the nested hierarchy of assumptions entailed by (2) and (3):

$$ \left( {A_{0} ,A_{1} ,A_{2} ,A_{3} ,A_{4} } \right)$$

(2)

$$\left( {A_{0} ,A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5} } \right).$$

(3)

Consider two ways of expressing the deductive relations between (2) and (3).

$$\begin{aligned}\left( {A_{0} \& A_{1} \& A_{2} \& A_{3} \& A_{4} \& A_{5} } \right)\vdash\left( {A_{0} \& A_{1} \& A_{2} \& A_{3} \& A_{4} } \right)\end{aligned}$$

but

$$\left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\rho } } \right)^{1/\rho } \nvdash\,n^{\eta - \lambda } \left( {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\lambda } } \right)^{{\frac{1}{\lambda }}} .$$

If one considers the propositions (i.e., assumptions) entailed by the functional forms, (3) entails all the propositions in (2) but if one considers what can be deductively derived in terms of the model descriptions, (3) does not entail (2). Instead, (2) entails (3) when $\eta = \lambda$. I venture to guess that Strevens would use the first relation for defining abstraction because it concerns the number of systems that fit the description. Furthermore, the first inference is deductive (see also Rol, 2008) which is an important part of Strevens’ eliminative procedure. (2) would then be more abstract than (3). This conclusion, however, is not consistent with the commonly accepted idea that more abstract means less detailed (and Strevens, 2008, p. 80 also accepts this idea). Furthermore, (2) ‘says more’ than (3) in the sense that it is able to express $\eta \ne \lambda$.

I take Strevens to be defining abstraction in the same way as I have defined assumption-reducing generalisation because abstractions and increases in expressive power both enter into proper subset relations that can be analysed with deductive derivability relations among sets of assumptions. This explains why he does not distinguish between abstractions and generalisations (2008, pp. 134–5, 474). Increasing the expressive power of a functional form involves demonstrating a proper superset relation that is better interpreted as an instance of removing idealisations. This is why abstractions should not introduce any new implicit assumptions, whereas idealisations may be allowed to do so.

In sum, all the previous attempts to define abstraction suffer from an inability to take into account implicit assumptions. The definition must recognise the difference between removing explicit and implicit assumptions. The only omissions that count as abstraction are those that do not introduce any new assumptions. My definition of abstraction is this:

(ABS) A functional form F₁ is more abstract than F₂ just in case it

• (i) Removes at least one explicit (or type 2 implicit) assumption from F₂ but

• (ii) Either does not remove any type 1 implicit assumptions from F₂, or loses the expressive power to describe the removed implicit assumption and

• (iii) Does not introduce any new assumptions to F₂.

This definition is designed to guarantee that an abstraction does not introduce any new false assumptions (iii), and that it always implies a loss of expressive power (i) in that it is no longer able to express at least one property that was explicitly expressed in the less abstract functional form. The second requirement (ii) is imposed so as not to be compelled to claim that (2) is more abstract than (3). The third requirement (iii) ensures that replacing (2) with (3) does not count as an abstraction because (3) introduces a new type 1 implicit assumption A₅ ($\eta = \lambda ),$ which was expressible but merely potential in (2).

Although (ABS) does not explicitly state that abstractions always involve omitting something from a representation and describing something in less detail, the three conditions together guarantee that they do, and it is additionally required that they do not introduce any new type 1 implicit assumptions. (ABS) accommodates the idea that the more abstract functional forms can be deductively derived from the more specific, but it rules out cases in which a generalisation is brought about by an increase in expressive power. According to (ABS), more abstract entails more general, but the converse does not hold because abstracting a model is not the only way of generalising it.

(ABS) does not provide conditions for when a representation is abstract, but rather for comparing when a representation is more abstract than another. As in Levy (2018) and Portides (2018), the interest here is in changes and differences in functional forms rather than the semantic properties of a single functional form.

Replacing (3) with (2) counts as de-idealising the model by means of a generalisation that increases the expressive power of the representation. In contrast, (SE) is more abstract than (3) and (2) because it has entirely lost the expressive power to represent the properties that assumptions A₁ A₂, A₃, and A₅ concern, and these assumptions are not implicit in it, either. If one starts with an abstract form such as (SE), adding properties is the only way to attain the ability to express the assumptions that (2) and (3) express. Note that the only assumptions economists really want to express are A₀ and A₁, but they can only represent them with models that also include A₂ to A_4, and usually A₅.

(ABS) is formulated for individual model descriptions such as functional forms rather than models. Here is what it takes for a model to be more abstract than another:

(ABSM) Model M₁ is more abstract than M₂ just in case it

• (i) Removes at least one explicit (or type 2 implicit) assumption from M₂ but

• (ii) Either does not remove any type 1 implicit assumptions from M₂, or loses the expressive power to describe the removed implicit assumption and

• (iii) Does not introduce any new assumptions to M₂.

Just like in the case of expressive power, the conditions for being able to compare two models with respect to abstractness are demanding. For example, suppose that functional form F_i is more abstract than F_j, and that F_k is more abstract than F_m. If one now modifies model M₁ = (F_j, F_k, F_n) into M₂ = (F_i, F_m, F_n), model M₁ is not more abstract than M₂, nor vice versa.

Let us now take stock on the differences between increasing expressive power and abstraction. Recall that increasing expressive power removes implicit false assumptions whereas abstraction may also remove explicit assumptions. We now see that increasing expressive power requires removing not just any kind of implicit assumption, but rather those are not expressible with the derivational resources of the non-generalised functional form (type 1). Abstraction has been defined in such a way that it inevitably entails a loss in expressive power with respect to those properties that are no longer represented in the more abstract functional form. The requirement of being able to show explicitly that the functional form with less expressive power is derivable as a special case of the more powerful form is only possible if the removed implicit assumption is an idealisation and thus false. This is why, even though the definition of increasing the expressive power does not mention it, it is intimately related to de-idealisation.

Now that I have distinguished between abstraction and increases in expressive power, I have an important clarification to make. Generalising a model by abstracting its functional forms could bring the same epistemic benefit as increasing the expressive power, at least in principle. Let us look again at D₁-D₃. Suppose that the true demand relation is $D^{\prime}_{2} : \, q = a + bp^{2}$ so that $D_{2} :q = a + bp$ is false. In that case, abstracting D’₂ (or D₃) into D₁ could bring an epistemic benefit because a false assumption would be removed from the model. This assumption-reducing generalisation would simultaneously count as an abstraction according to (ABS) and as a de-idealisation in the sense in which it has beeen defined in this paper; as a removal of an idealisation.¹¹ Even though de-idealisation and abstraction cannot be distinguished from each other in this example, there is no reason to provide a definition of abstraction that would explicitly rule such cases out because the change entails a loss in expressive power. This kind of trading off of decreased expressive power for making fewer idealisations brings about an epistemic benefit only if the model result remains the same. If it does not, then the modellers are merely relaxing the standards concerning how much has to be said about a system and there is no epistemic benefit.

I noted above that model modifications that satify ABS could, at least in principle, provide epistemic benefits. This might seem unsatisfyingly vague and would seem to call for concrete illustrations. However, it is difficult to come up with concrete examples because when an idealisation (like $q = a + bp$ above) is removed with an abstraction, and the model result remains the same, modellers do not bother to mention any epistemic benefits because they were probably sure that this particular idealisation could not affect the model result in the first place. The true demand relation $q = a + bp^{2}$ would be demonstrably irrelevant for the model result in this fictional case. It is hard to imagine a case in which modellers would be genuinely worried that an idealisation affects a result, but yet could easily remove it with an abstraction while still being able to derive the model result. Generalising a model by increasing its expressive power usually requires solving a difficult tractability problem, but it is hard to see why the idealisation would be introduced in the first place if one could remove it by simply abstracting it away.

Furthermore, many real-world cases of abstraction yield not only changes to a functional form, but also further changes elsewhere in the model. Such changes mean that it is no longer likely that the new model is more general with respect to all those other changes, making generality comparisons impossible. As soon as two models contain at least two different assumptions, one can no longer make generality comparisons based on the number of assumptions because the sets of assumptions do not enter into proper subset relations. The number-of-assumptions criterion can only be employed when the two models are otherwise identical.

6 Reflections on the scope of the account and conclusions

There is nothing in my account of generalisation that would limit its usefulness to economics. For example, generalising the ideal gas law (PV = RT) by means of the van der Waals equation (P + (a/V²))(V-b) = RT increases the expressive power by de-idealisation. It does so by removing the type 1 implicit assumptions that the intermolecular forces are zero and that the size of the molecules is zero. The ideal gas law can be obtained as a special case of the van der Waals equation by setting the intermolecular forces (a = 0) and the size of the molecules (b = 0) to zero. With ABS and IEPM, one is not compelled to make the implausible claim that moving to the other direction, from the van der Waals equation to the ideal gas law, means abstracting it. Instead, the change counts as a straightforward idealisation. Furthermore, ABS does not apply to the question of whether the model description (PV = RT) is an abstraction tout court, and in this case, its limited applicability can be seen as its strength. The main difference to the examples I have discussed earlier is that the ideal gas law and the van der Waals equation give several model results, depending on the values of the variables. The latter is more general than the former in that it provides correct results in a wider set of circumstances (i.e., also in low pressures and in high temperatures).

The notion of increasing a model’s expressive power is limited to formal modelling, and this means that it does not apply to all types of method and thereby to all disciplines. However, in addition to mathematical modelling, it may be applied to computer simulations. Consider, for example Lehtinen’s (2007) Monte Carlo simulation of strategic voting (i.e., giving one’s vote to a candidate that one does not consider best). The model result is that strategic voting is beneficial in the sense that it increases the frequency with which the best candidate is selected (compared to sincere voting). Lehtinen (2015) generalises this result by showing that it holds for any number of candidates instead of just three (as in Lehtinen, 2007).

The model is based on formulating expected utilities for voters. The main difference to the examples considered earlier is that Lehtinen (2015) does not modify the analytical functional forms expressing these expected utilities. Instead, I introduced an indexing method for the candidates and the other relevant components of the model (utilities, beliefs, etc.) that can be used to calculate the expected utilities for any number of candidates.¹² The analytical expressions of expected utilities encode the assumptions of the model, and they were only formulated for three candidates in 2007. It would have been trivially easy, albeit cumbersome, to write them down on paper, for any number of candidates. In contrast, it is technically very challenging to write a programming code that computes them for any number of candidates.

The 2015 version increases the expressive power of the model because one can express every individual component of the three-alternative version with the 2015 model. It is the computer implementation of the indexing method that has more expressive power than the earlier programming code. It takes the number of candidates as a variable, and expresses the analytical equations and the corresponding results for any value of the variable.

Unlike in the previous examples, my 2015 model does not remove an implicit false assumption because the 2007 model was written for three candidates (n = 3), and thus this assumption (viz., that n = 3) was explicit and true for elections that actually have three candidates. However, I do not think that increasing expressive power without removing an implicit idealisation is intrinsically related to the fact that my model is a computer simulation. What is similar to the earlier cases is that the generalisation provides a model which is able to express all values of a parameter (n) simultaneously.

One might claim that the 2015 model introduces new assumptions because there is a huge number of new variables (in the programming sense) and algorithms in the programming code. However, the indexing methods do not introduce any new assumptions in the sense in which they have been defined in this paper, and neither do the algorithms that put the method into action in the computer. They merely give instructions to the computer for calculating the expected utilities for any number of candidates. However, there is an interesting difference between this example and the ones on analytical models. Namely, in the generalised 2015 model, the equations for the expected utilities are not explicitly expressed in the model descriptions (i.e., the programming code). Unlike in the three-candidate programming code for the model of 2007, there are no equations that look like the analytical expressions for these equations in the 2015 model, even though the calculations conducted by the computer are exactly the same (when n = 3). Furthermore, it would not make any sense to write them into the programming code because the text strings expressing the expected utilities of, say, 10 candidates would be several kilometers long, and for 10 candidates one needs 2¹⁰ = 1024 of them. This is one reason why I claimed that there are at least three kinds of implicit assumption rather than that there are just three.

While there do not seem to be important disciplinary limitations of applicability, there are some conceptual ones. In particular, the notion of abstraction ABS is rather specific. Recall that ABS refers to a change in model descriptions but a single model description is not suitable for being analysed by ABS. I presume that one of the main motivations for distinguishing between idealisations and abstractions (in the tradition of Jones, 2005, Rol, 2008, Godfrey-Smith, 2009, and Levy & Bechtel, 2013 and their predecessors) has been that abstractions are epistemically more acceptable than idealisations because they do not distort any properties in the target system. An argument like this has to concern abstractions as representations rather than as changes in representations.

However, just like Levy (2018) and Portides (2018), I believe that model descriptions that simultaneously abstract and idealise are ubiquitous. Each and every one of the functional forms discussed in this paper are like this. De-idealising (3) with (2) does not remove all idealisations from (2), and neither does abstracting (2) with (SE) because all these functional forms are interpreted as utility functions of a ‘representative consumer’. This means that each individual person’s utility function is assumed to be identical. This is obviously an idealisation. In the context of industrial organisation and international trade, it may be a rather harmless idealisation. However, various versions of (3) are extensively used in macroeconomics (where variants of it are usually referred to as the ‘Dixit-Stiglitz aggregators’), and in that context, this assumption is no longer harmless because it implies that economic development and macroeconomic fluctuations do not depend on the distribution of income. This is why macroeconomists have generalised (3) in a different way by removing the assumption of homothetic utility (Kimball, 1995), and by using several utility aggregators at the same time (starting with Iacoviello, 2005). I interpret Morrison (2005) as making similar claims about the van der Waals equation.

With these comments in mind, it seems natural to say that a single representation may abstract from some feature of a target system, as long as one does not make the implausible claim that the representation is an abstraction that does not contain any idealisations. It goes without saying that I have not tried to argue for or against accounts of abstraction that consider it primarily as a process of thought or a research strategy (as in Morrison, 2015). Furthermore, if abstraction is considered in such ways, it may have some epistemic benefits about which I have been entirely silent (see e.g., Batterman & Rice, 2014; Rice, 2018).

My main motivation for distinguishing between idealisation and abstraction is conceptual clarity. The distinction helps demonstrate how epistemically beneficial generalisations can be distinguished from other generalisations that decrease the number of assumptions, namely, abstractions satisfying the conditions for ABS. The resulting notion of abstraction is impoverished in that it only indicates the direction of changes in the ‘ladder of abstraction’ (Cartwright & Hardie, 2012, pp. 79–80) or between ‘levels’ of abstraction, but it is silent on non-truth-related epistemic benefits there may be in moving up or down in this ‘vertical’ dimension.

IEPM is also rather restrictive in that it is designed to be used for identifying epistemically beneficial generalisations of models. The recent philosophical literature on generalisation has been employed in the study of trade-offs in modelling. But being able to use IEPM entails that there is no trade-off between increasing expressive power and realisticness of assumptions. However, increasing expressive power (IEP) provides a new conceptual tool for analysing attenuating trade-offs in modelling (Matthewson & Weisberg, 2009). An attenuation is a non-strict trade-off in which increasing one attractive model attribute makes it pragmatically more difficult to increase or even retain other attractive attributes, but there is no logical incompatibility. Modellers often face an attenuating tradeoff between increasing the expressive power of one part of a model while decreasing it in another. However, analysing such attenuations in more detail must be left for future work.

The three kinds of generalisation have been defined in such a way that there is a strict trade-off between each kind. We have seen that it is impossible to abstract a model at the same time as its expressive power is increased. It is also impossible to apply a model to new phenomena without losing expressive power and without making the model less abstract. These trade-off relations hold between models but not between model-components. This opens up new ways of looking at trade-offs: one may increase the expressive power of one part of a model while abstracting it in another and so on.

The take-home message of this paper is that epistemically beneficial generalisations increase the expressive power of a model. They usually do so by making implicit false assumptions expressible, while at the same time removing them from the set of assumptions to which the model is committed. Increasing the expressive power of a model thus usually de-idealises it by removing implicit false assumptions from it.