Ontology, neural networks, and the social sciences

Abstract

The ontology of social objects and facts remains a field of continued controversy. This situation complicates the life of social scientists who seek to make predictive models of social phenomena. For the purposes of modelling a social phenomenon, we would like to avoid having to make any controversial ontological commitments. The overwhelming majority of models in the social sciences, including statistical models, are built upon ontological assumptions that can be questioned. Recently, however, artificial neural networks (ANNs) have made their way into the social sciences, raising the question whether they can avoid controversial ontological assumptions. ANNs are largely distinguished from other statistical and machine learning techniques by being a representation-learning technique. That is, researchers can let the neural networks select which features of the data to use for internal representation instead of imposing their preconceptions. On this basis, I argue that neural networks can avoid ontological assumptions to a greater degree than common statistical models in the social sciences. I then go on, however, to establish that ANNs are not ontologically innocent either. The use of ANNs in the social sciences introduces ontological assumptions typically in at least two ways, via the input and via the architecture.

1 Introduction

The field of social ontology remains riddled with controversies. It is a matter of persistent disagreement which social objects exist and which ontological dependence relations¹ hold between them. To get a taste of these ontological controversies, consider the following questions:

• Are social facts (partially) grounded in facts about non-human objects? (Epstein 2015)

• What is the nature of social groups? (Uzquiano 2004; Sheehy 2006; Ritchie 2013, 2015, 2020; Epstein 2015; Thomasson 2019; Hawley 2017; Strohmaier 2018; Uzquiano 2018; Epstein 2019)

• Do group agents exist? (List and Pettit 2011; Huebner 2014; Tollefsen 2015; Epstein 2019; Strohmaier 2020)

These are fundamental and substantial questions that also affect more narrow issues. Consider the nature of families as a type of social group. There is no straightforward agreement on who composes or should compose a family (cf. Satz 2017; Kane 2019). Can there be families with more than two parents per child? Is recognition according to social norms or laws required to make a group of people a family? The fundamental disagreements about the nature of groups also render these more specific ontological issues controversial.

Given the controversial nature of social ontology, there is a demand for ontologically neutral approaches to predictive models. Models that allow social scientists to make predictions without committing to any controversial ontological assumptions, would be of great value, especially if their results could then be compared to models with different ontological commitments. The more ontological assumptions a model can avoid, the better it meets this demand.

Common statistical and machine learning methods, however, require social scientists to specify features, which often come loaded with ontological assumptions.² For example, to model the impact of family structure on a child’s educational achievement, the structure needs to be encoded using selected features such as how many parents are present. This feature selection is bound to run into ontological controversies.

Increasingly, however, artificial neural networks (ANNs) have made their way into the social sciences, raising the question of whether they fare any better. In contrast to other statistical and machine learning methods, an ANN does not require feature selection. Instead of imposing our controversial metaphysics on the social, we seem to leave ontology almost completely to the empirical data. Or, as two computational social scientists used to working with the explicit ontologies of agent-based models have put it:

Neural networks have the absolute minimum in the way of ontological structure it is possible to have. Their ‘content’ comes from the data they are trained to fit. (Polhill and Salt 2017, p. 144)

I will explore whether neural networks live up to these high hopes of ontological neutrality. While I will conclude that ANNs allow social scientists to avoid some ontological assumptions, they only do so partially. To establish this thesis, I will first introduce the functioning of ANNs and their use in the social sciences. After this set-up, I will compare neural models to other statistical and machine learning models and argue that neural networks achieve greater ontological neutrality. I will then, however, consider two ways in which neural networks are not ontologically innocent. The input and the architecture of neural networks provide openings for ontological assumptions. Before concluding, I will sketch how mistaken ontological assumptions can lead to multiple problems.

2 Neural networks

In the past decade, artificial neural networks have made impressive progress. While some of the most prominent examples of this progress—such as winning in go against a professional human player (Silver et al. 2016)—have mainly been of show-value, neural networks have also become a valuable tool for scientific investigations (e.g. Schmidt et al. 2019; Guest et al. 2018; Lakhani and Sundaram 2017). The social sciences have been no exception.

To see how neural networks figure in the work of social scientists, we need to understand how they work. Accordingly, I will begin by sketching the history and functioning of the most common types of neural networks. Then, I will discuss the current use of ANNs in the social sciences. On this basis we will be able to assess the role of ontological assumptions for neural networks.

2.1 History and functioning

ANNs are an old technology with deep roots in the history of artificial intelligence research. Drawing upon the description of neuronal activity by McCulloch and Pitts (1943), Rosenblatt (1958) popularised the perceptron as an early form of neural artificial intelligence. A single perceptron can be understood as a neural unit which takes multiple inputs, multiplies them with weights, adds a bias, and feeds the result through a threshold function, the output of which is the prediction (see Fig. 1). Thus, the computation by a single unit with three input values can be represented as

$$\begin{aligned} Y=f(w_1 x_1+w_2x_2+w_3x_3+b) \end{aligned}$$

(1)

where $x_1, x_2, x_3$ are the input values, $w_1, w_2, w_3$ their respective weights, b a bias term, and f a threshold function such as the step function. In the neural unit of a contemporary ANN, the threshold function is replaced by a non-linear activation function such as the sigmoid function.³

Fig. 1

Structure of a perceptron, similar to a unit in a neural network. The main difference is that the threshold function is typically replaced by a different activation function

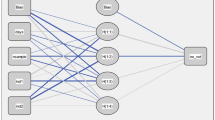
After influential and critical work by Minsky and Papert (1972), interest in neural networks declined for a period only to rise and fall again in the 80s and 90s with the connectionism movement in cognitive science (cf. Buckner and Garson 2019). By then, multiple layers of units were connected to each other (see Fig. 2). These nodes receive either the original input or the output of the previous layers, perform a linear operation on them, and apply a non-linear activation function to them.

Fig. 2

Structure of a fully connected feed-forward network with five input values. Each node represents a neural unit, including the activation function. Current networks are rarely fully connected and contain additional computational mechanisms

During the era of connectionism, ANNs were shown to be universal function-approximators. Theoretical results have established that ANNs can in principle approximate continuous functions with very few restrictions (see Cybenko 1989; Hornik et al. 1989) and that they can simulate all Turing machines (Siegelmann and Sontag 1992). One should keep in mind, however, that these results do not show that it is feasible to train a neural network to approximate any function or Turing machine (cf. Goodfellow et al. 2016, pp. 192–193). That is a much harder task.

One of the most important innovations in training ANNs is the backpropagation-algorithm (Rumelhart et al. 1986), which allows researchers to train multi-layer neural networks. Training a neural network is the single greatest hurdle on the way to deployment and remains so despite the development of ready-made toolkits. The training process can be varied in many ways and I will describe the mere outlines. In the most common procedure, labelled training data is fed into the neural network and then used to calculate a loss function, that is a measure of error. By way of backpropagation, this error is used to adapt the parameters of the neural layers, most importantly their weights.

Advances in engineering of the training procedure and the development of new architectures enabled the recent wave of ANNs under the name “deep learning”, which refers to the multiplicity of layers. How the layers of an ANN are connected and how other computations, such as so-called attention-mechanisms (Bahdanau et al. 2014) and softmax-functions, are applied, determine its architecture.⁴ Different architectures have proved valuable for different purposes. For example, the convolutional neural network architecture might be more appropriate for image recognition than for document classification.

2.2 The use of neural networks in the social sciences

The use of neural networks in the social sciences goes back decades (Bainbridge 1995; Garson 1998; Herbrich et al. 1999), but only with the latest wave have computational power, software, and data collection reached a point at which training neural networks on massive social datasets has become a feasible and tempting endeavour. They have become a valuable method in the toolbox for data mining in the social sciences (e.g. Attewell and Monaghan 2015).

ANNs have shown promise for predicting the default risk of countries (Cooper 1999) and have been used to study international conflict (Beck et al. 2000; de Marchi et al. 2004), poverty (Jean et al. 2016), and public corruption (López-Iturriaga and Sanz 2018). In the Fragile Families Challenge, researchers competed to predict variables such as GPA, grit, and material hardship using data collected as part of the Fragile Families & Child Wellbeing Study ( Waldfogel et al. 2010).⁵ Neural network models were one type of model used in this challenge (Davidson 2019), although the performance of machine learning models was overall disappointing (cf. Salganik et al. 2020).

The aim in these applications is to predict a variable of direct interest to social scientists, usually on the assumption that the available data are especially suited for this methodology. In addition, there have been many adjacent uses of ANNs with bearing on the social sciences, such as enriching datasets with demographic information based on facial recognition (Mancosu and Bobba 2019), classifying messages on Twitter (Gambäck and Sikdar 2017; Liao et al. 2019), and recognising collective actions in image sequences (Bagautdinov et al. 2017). Such applications of neural networks can form part of a larger investigation employing more traditional types of models.

Although the use of neural networks in the social sciences is growing, it has been mostly confined to subfields of economics (Li and Ma 2010; Falat and Pancikova 2015) and minor exceptions in other fields. A major reason for this reluctance of social scientists towards using neural networks is the difficulty of interpreting them. While this issue is not the main focus of my investigation, it has such influence that a few comments are required to understand the current use of ANNs in the social sciences.

Social scientists largely consider ANNs to have a black-box character (but see Lipton (2018) on this issue).⁶ A standard ANN might classify examples by providing a probability distribution over possible classes, but it will not provide explicit reasons for doing so. The weights and biases of the neural network have no direct interpretation.

For many social scientists, it would be at best disappointing to be able to predict the outcome of a social situation but unable to provide any reasons for the prediction. Practitioners in the computational social sciences have responded by stressing the value of prediction and connecting it to more classical goals of the social sciences, such as identifying causal connections (Hofman et al. 2017; Watts et al. 2018).⁷

Independently of the value of prediction, however, there has been much work into making ANNs interpretable, often motivated by ethical concerns such as the need to detect unwanted social biases.⁸ For example, some technologies can indicate which part of the original data was especially important in reaching the classification (Ribeiro et al. 2016). These techniques can also be applied to making neural networks interpretable for the purposes of the social sciences, rendering them more similar to common statistical methods (see the discussion in Davidson 2019).

While trained neural networks are initially black boxes to social scientists, additional tools and effort can shed light on their internal workings. Given that they perform well, which is not yet sufficiently shown (see the disappointing results in the Fragile Families Challenge), this effort might be justified. If one model predicts social developments better than any other, then the best way to advance the social sciences might lie in investigating how the model achieves such a performance, rather than ignoring them and working on more limited approaches. A sufficiently powerful predictor of X is part of the research domain for those studying the regularities of X.

A potential reason for social scientists to take neural networks seriously despite the challenges of interpretability is to avoid ontological assumptions. In the next section, I will suggest that ANNs in fact have such an advantage compared to other models.

3 Comparing neural networks to other statistical and machine learning methods

Neural networks are both statistical and machine learning models. A comparison with other methods in these fields, however, reveals differences suggesting greater ontological neutrality on the side of neural networks. I will discuss both comparisons in order.

3.1 Comparison to other statistical models

Neural networks, at least in their most common forms, are statistical models (cf. Lee 2004, p. 21). That being said, ANNs differ greatly from the standard statistical methods employed in the social sciences in the assumptions they have to make.

For a simple example of standard models, consider a linear regression investigating whether the variable of favourability in Gallup polls is predictive of success in the US Presidential election (e.g. Lewis-Beck and Rice 1982). The form of such a linear regression resembles that a single neural unit, except for the lack of an activation function. For the case where we only estimate the presidential vote share based on the Gallup favourability rating on the day of the election, the equation can be written as:

$$\begin{aligned} Y=w X+b \end{aligned}$$

(2)

where X is the Gallup rating and w and b are the parameters to be estimated.

Linear regression and similar standard approaches require explicit choices by the modellers about the relationships between the features of the input. In a linear regression, the relevant variables between which a correlation is suspected need to be specified. Lewis-Beck and Rice (1982) went at their research with a specific hypothesis in mind and selected the features—in this case only the Gallup rating—to which they fitted the regression line. From all the available data, they select one feature and encode it. As a consequence of the explicit selection of predictive features in the data, constructing such models tends to be guided by controversial ontological assumptions.⁹

Common statistical models can be taken to mediate between the underlying substantive model, which is supposed to represent the actual explanatory factors, and the observed data, which are partially the result of chance patterns. As a results, statistical models can be substantively adequate or inadequate (this understanding is based on Spanos (2006) and Spanos and Mayo (2015)).¹⁰

In the case of the regression predicting voting behaviour, the underlying substantive model assumes that a favourable impression of the candidates could be an explanatory factor for the presidential vote. In virtue of the connection the substantive model, the weight w estimated by the model is interpretable as the impact of the feature Gallup favourability rating. The size and direction of this weight is the subject matter of the investigation using linear regression.

In the sketched instance, these assumptions pose little problem, because it is widely accepted that the outcome of the vote is largely the result of the decisions by the individual voters who are supposedly polled. In other instances, however, the underlying assumptions are bound to be more controversial.

For example, a linear regression might be used to evaluate the correlation between the family structure and the educational outcomes of a child. In this case, a need to provide a coding for the different types of family structures arises. Such a coding is likely to be ontologically controversial and requires assumptions about what constitutes a family. Is only the nuclear family included in the structure? What about families in which the primary parents practice polyamory or have separated and entered new relationships?

The creation of such feature codings for a statistical model is dependent on ontological assumptions about families. The prevalent forms of statistical modelling in the social sciences carry an ontological burden, because they rely on decisions about coding the data.¹¹

When using an ANN, however, researchers typically do not build upon an underlying substantive model, i.e. they do not parametrically nest such a substantive model by deliberate design. The researchers do not estimate the weight and bias for specific features, but instead the network serves predictive purposes and estimates non-interpretable weights and biases. Consequently, no feature selection is required. While not picking out features for estimation reduces the interpretability of ANNs, it also means that the issue of ontological bias in coding does not arise.

To see the difference between statistical methods such as linear regression and ANNs even more clearly, consider how each of these approaches can make use of open-ended survey questions. Open-ended questions are supposed to allow survey respondents to draw from a broader range of possible responses. To make statistical use of these open-ended questions, however, they are often coded again, which creates challenges (e.g. Behr 2015) and partially undermines the purpose of employing open-ended questions in the first place. By contrast, the open-ended responses can be directly used by ANNs without an intermediate coding step. The open response can be used as a text input into an ANN without the need for a unified coding. Similar to open questions, other collected texts and images, even video evidence can be used more directly without a coding step, as currently common in the social science.

But if the researchers do not specify the features on which to train ANNs, the question arises of how they represent data at all. I address this question in the next subsection by comparing ANNs to other machine learning models.

3.2 Comparison to other machine learning models

ANNs are distinguished from many other machine learning methods, such as Support Vector Machines and Decision Trees, by being a representation-learning technique.¹² For most machine learning techniques researchers need to painstakingly identify relevant features of the data to represent it, just as in the case of a linear regression.

To give an example from natural language processing, consider the task of classifying social media messages according to whether they express a positive or negative sentiment.¹³ For such classification with a classical machine learning method, one has to define various features. As a simple approach one might simply select the presence of word tokens as features, a so-called bag-of-words representation. In this case, the message is encoded as a vector with as many dimensions as word types in the vocabulary and each dimension includes the count of word tokens belonging to the respective type (see Fig. 3).

Fig. 3

Despite expressing a reversed preference ranking, the bag-of-words representations are identical. Vocabulary: [I, prefer, Shakespeare, to, Goethe]

But to achieve better results the engineer has to select more sophisticated features. For example, one might want to take into account whether the word “not” appears before other words such as “great”. To achieve this one can use positional encodings as another feature. The selected features together determine a complete vector of a fixed dimensionality which is then put into a Support Vector Machine to classify examples, but only on the basis of pre-created representations.

Even though the goal of machine learning techniques is typically not to estimate weights and biases, they require feature selection like linear regression. Accordingly, the process of hand-crafting such representations is prone to be led by ontological assumptions. In the case of natural language processing, the assumption might be that the meaning of a sentence depends on the syntactic arrangement of words. Such ontological assumptions are bound to be much more controversial in the social sciences.

Assume again that the aim is to predict the impact of a child’s family structure on its educational outcomes. Creating a coding for the structure is dependent on social ontological assumptions. The choice between features such as “divorced parents” and “hours spent with grandparents” offers an opening for ontological assumptions to influence the models. For example, the features used to represent family structures could exclusively be drawn from properties of the nuclear family. Such a selection would taint the encoding of data with a controversial ontological assumption.

By contrast, ANNs are an instance of representation-learning and therefore do not rely on so-called feature engineering. They create their own internal representations guided by the data and the loss function. In the case of natural language processing tasks, neural networks often only receive the string of tokens (or even characters) as input without the need to select any further features. On the basis of a selected vocabulary, these tokens are then mapped to a vector in an initial layer of the neural network, the so-called embedding layer. This approach results in word embeddings, dense vectors created in many natural language tasks. Such embedding vectors serve as representations of word meanings for a pre-selected vocabulary.¹⁴

In the case of the social sciences, ANNs can use trace data, that is raw data that is found rather than created for research purposes (see Howison et al. (2011) for a discussion of digital trace data). Such trace data can include behavioural traces left on social networks or image data. On the basis of such data, neural networks can create representations and predict social phenomena. Hence, there is no need to design an encoding of the family structure to predict the educational outcomes of children, instead an ANN can create such a representation internally for the purpose of the prediction task.¹⁵ All that is required is that the relevant data are either directly available as real-valued vectors or that they can be fitted into a vocabulary so that embedding representations can be trained for them. For text and image data there are standard ways of doing so, which can be readily used in the social sciences.

Having seen that neural networks stand out from other modelling approaches in virtue of being a representation-learning technique, the next section will discuss where ontological assumptions nonetheless affect ANNs.

4 The ontological assumptions of neural networks

Modelling remains a contentious practice in the social sciences. All approaches to modelling social phenomena face criticisms, but the approaches differ in regard to the assumptions they make. As discussed, neural networks are an instance of representation-learning and thereby distinguished from common statistical and other machine learning approaches. In principle, ANNs are trained on extensive data, learn how to represent it internally, and employ these representations for approximating a function. This picture suggests that no or very few ontological assumptions are built into neural networks. To quote again the computational social scientists Polhill and Salt:

Essentially, apart from the labels assigned to the input and output units of a neural network, neural networks don’t have an ontology at all. (Polhill and Salt 2017, p. 142)

While it is correct that neural networks don’t have much of an explicit ontology compared to agent-based models—the main point of comparison for Polhill and Salt—the impression given by this quote is misleading at best. The choice of labels is not the only point where ontology can make a difference. Typically, neural network approaches in the social sciences include ontological assumptions in at least two ways, via the input and via the architecture.¹⁶

4.1 Input

Compared to most machine learning and statistical methods, the data fed into neural networks are raw, but the data still need to be selected and put into a format that can be processed by neural networks. This selection and processing offers an opening for ontological assumptions. It would be incoherent to bemoan the way a statistical model codes family relations so as to include only the nuclear family and then feed an ANN exclusively data about the nuclear family.

Of course, avoiding the manual selection of relevant features was supposed to be the advantage of representation-learning techniques such as neural networks. The problem is that an ANN can learn its representations only from the data it is given. One cannot feed the social directly into the neural network; one has to select an input. A linear regression requires the specification of features, but both a linear regression and an ANN require data.

The situation is even worse when ANNs are trained for a prediction task with closed-question survey data.¹⁷ For example, Davidson (2019) participated in the Fragile Families Challenge and therefore the predictions of his neural model are based on the pre-selected survey data supplied by the organisers. Such surveys select features for their closed-questions and, thus, reintroduce all the problems of non-representation-learning-based methods. The data encodes interviews with mother, father, child, and “primary caregiver”.¹⁸ This selection already suggests that the features in the survey were guided by ontological assumptions about families and the ANN can only draw on them.

The partial neutrality and power of ANNs are much better served by raw behavioural data, for example, unfiltered text messages sent by members of the family. An ANN might then pick up on parenting style and effort or on any other set of features that are included in the messages. Of course, the selection of such trace data can also be influenced by ontological assumptions.

Assume that an ANN is supposed to predict a child’s educational outcomes based on family interactions. For this purpose, the ANN can be trained on raw text messages between family members. While the use of such behavioural traces mitigates the issue of selection compared to survey data, such traces still need to be collected by someone, often research assistants who bring their own assumptions. For example, an assistant might make sure to collect the trace data for parents and grandparents, but not friends of the parents, because they assume that the family of the child is constituted by parents and grandparent. In this case, the ANN would approximate a function based on ontologically problematic data.

As can be seen, ontological commitments can be reduced but hardly avoided in the selection of input. If available, the use of raw trace data reduces the ontological burden of ANNs relative to common statistical methods in the social sciences. But their availability in sufficient quantity is a major challenge and even with trace data the selection can introduce ontological assumptions. In sum, being a representation-learning technique does not remove all openings to ontological assumptions through the input.

4.2 Architecture

While neural networks are sometimes sold as a one-size-fits-all solution, they often need to be adapted to the problem at hands. Not only the input needs to be selected, but the architecture of the neural network. I will argue that architectural choices can come with a considerable ontological burden, contrary to the following passage on ANNs by Polhill and Salt:¹⁹

“[A]ssumptions about functional form are embedded in the structure of the network itself—how the nodes are arranged into layer and/or connected to each other. This structure, however, only reflects the flexibility will have to achieve certain combinations of outputs on all the inputs it might be given (its ‘wiggliness’). This is a rather weak ontological commitment to make to a set of data.” (Polhill and Salt 2017, p. 153)

Polhilll and Salt suggest that architecture primarily affects how easy it is to make a neural network approximate a function without creating large ontological commitments. Their suggestion is correct for some architectural choices, which are relatively innocent by any measure. For example, Davidson (2019) explored different activation functions for the Fragile Families Challenge and found tangible effects on the performance of the models, but it is hard to see how this architectural choice could bear on any ontological controversies. That being said, other choices bring greater commitment.

Some architectures assume dependence patterns. For example, convolutional neural networks (CNNs), which have been widely used for image recognition, including the social scientific work of Jean et al. (2016), are suitable for recognising local patterns (LeCun et al. 1990; see also Buckner 2019 for a philosophical discussion). The LSTM-architecture (Hochreiter and Schmidhuber 1997), by contrast, has enjoyed prominence in natural language processing, because it is better suited for long term dependencies in a string of input, such as text. The original LSTM-architecture comes with the assumption that the dependence is one-directional from left to right (see Fig. 4), although a bidirectional version exists as well.

Fig. 4

Unfolded Recurrent Neural Network (RNN) encoder, of which the LSTM encoder is a special form. In the case of the LSTM, the L units are constructed to ensure that the network can maintain a memory of the previous input

As can be seen, the architecture encodes important assumptions about how the input data are related. While the dependence is not necessarily ontological, ontological assumptions are likely to make a difference. In the case of encoding the meaning of words, the dependence assumed by an LSTM-encoder might very well be ontological. Assuming a form of contextualism, the meanings of the encoded word tokens are partially constituted by the meaning of the surrounding tokens. Using a one-directional LSTM for this purpose assumes that the meaning of word tokens only depends on previous tokens, not the subsequent ones. This directionality assumption is not just a minor factor of wiggliness, as suggested by Polhill and Salt, but a strict commitment to a direction of dependence.

In the case of the social sciences, one might also choose an architecture because it fits one’s assumption about the dependence between input data. In some cases, this might be defensible, for example when one chooses a one-directional LSTM for modelling time-series data from financial markets. Presumably, the earlier data do not depend on the later one. Nonetheless, the choice of the architecture is one place where ontological assumptions can creep in.

Assume that the decision of an organisation is to be encoded using a neural network. For this purpose, indicators of the current decision state of various individuals, groups, and departments might be passed into a one-directional LSTM.²⁰ The ordering of the input might then make the assumption that the decision state of the marketing department depends on that of the departmental managers which in its turn is dependent on that of the leading manager, but not vice versa. This assumed hierarchy of dependence, which could be ontological or causal, would be enforced by the architecture of the LSTM.

In virtue of the architecture, the encoding is unable to capture that the decision state of the leading manager might constitutively depend on that of the department. For example, if the decision of the leading manager is the result of deferring to the attitude of the group of managers, this would not be appropriately reflected. Hence, the assumptions underlying the LSTM create an ontological commitment, undermining the neutrality of ANNs.

Mitigating such ontological troubles is a trend towards broad-purpose architectures in neural networks. The transformer-architecture (Vaswani et al. 2017), which has overtaken the natural language processing world, largely displacing LSTMs, is one example of such a more generic architecture. Via a so-called attention-mechanism they can account for dependence relations and learn their relative strength from the data. The researcher can withhold judgement and let the data do more of the work.²¹

As can be seen, architectural choices influence the ontological commitment of neural models. In addition, they affect the interpretability of ANNs. For example, the attention scores can be extracted and used to interpret the functioning of the neural network (e.g. Mullenbach et al. 2018). A classical example for this can be found in neural machine translation. If the translation of an English sentence into a French one is undertaken using a transformer-architecture one can identify and visualise to which word tokens in the English sentence the mechanism attended when creating a French token (Bahdanau et al. 2014). Translating “This concerns all of us.” to “Cela nous concerne tous.”, the model puts more attention to “all” when outputting the token “tous”.

By studying attention scores, neural networks can help to uncover dependence relations, although one ought not overinterpret them. Standard ANNs with attention have no sense of the difference between ontological dependence and mere correlation. They will track whatever helps them to locally reduce the loss-function.²² Nonetheless, the case of attention-mechanisms shows that the choice of architecture also influences the interpretability of ANNs, in addition to creating or avoiding ontological commitments.

5 The impact of mistaken assumptions

I have established that while ANNs are ontologically less committed than other statistical and machine learning models, they are not entirely neutral either. But do the ontological assumptions underlying a neural network matter?

Of course, if ontological assumptions affect the performance of the network negatively, for example because a researcher chooses a CNN rather than an LSTM-architecture despite a long-distance linear dependence, then this is an issue worth addressing. The model might make worse predictions or classifications in virtue of mistaken assumptions.²³ However, that incorrect ontological assumptions lead to a performance penalty is far from given. It might very well be that the best-performing model a social scientist trains neglects some ontological dependence relations. Hence, the question arises whether mistaken assumptions can pose a problem when the performance on the existing benchmarks is not negatively affected.

For other types of statistical models, this is certainly the case. In the case of linear regression, social scientists are interested in the estimation of the parameters for a specific feature, be it favourability rating in Gallup polls or family structure. If the feature coding for family structure is based on mistaken ontological assumptions, then this will lead to a misinterpretation of these parameters.

But the typical use of an ANN in the social sciences has no such ambitions. The use does not aim at interpreting the weights and biases of the neural networks directly. Nonetheless, a mistaken ontology can have at least two problematic consequences in the absence of a performance penalty.

First, the ANN might in fact address another predictive task than the one intended. This case is illustrated by the previous examples of trace data being selected to detect whether the features of a child’s family allow to predict its future educational outcomes. If in the collection of the trace data, support networks are assumed to be exclusively constituted by nuclear families, then the ANN might effectively address another research goal than intended. It would only show whether the educational outcomes could be predicted on the basis of data about the parents, rather than the extended family. The selected input data might hide ontological assumptions undermining the research goal.

Second, even if an ANN addresses the correct task, incorrect ontological assumptions can limit the interpretation of the network. To see this issue, reconsider the case of a social scientist encoding the decision process in an organisation using a one-directional LSTM-architecture. The use of the LSTM assumes that that the decision state of the marketing department depends on that of the group of managers in the department which in its turn is dependent on that of the leading manager. With this architectural choice, the researcher never gave the ANN a chance to also learn dependence in the other direction. Hence, the architecture and its ontological commitments limit the possible interpretations of the model. Without comparing it to another architectural choice, we cannot conclude that the LSTM correctly captured the dependence relations.

In sum, the ontological assumptions of ANNs matter in at least three ways, for the performance, for meeting the task specification, and for interpretation. Neural networks are not ontologically neutral and it makes a difference for the purposes of the social sciences.

6 Conclusion

I compared ANNs to other statistical and machine learning models with a special focus on whether they can avoid problematic ontological assumptions in the social sciences. The result is that they can avoid more assumptions than other models, but are not free of them. Choices regarding the input and the architecture of neural networks will reflect ontological assumptions. There are, however, comparatively easy ways to mitigate these problems.

Common statistical models cannot deal with relatively raw data and require ontologically-laden feature selection, since they are not a form of representation-learning. For the time being, ANNs stand out in virtue their ontological flexibility.

Although it was not the focus of the present investigation, the issue of interpretability is on the mind of everyone interested in the use of neural networks for the social sciences. The recent and quickly expanding literature on interpreting ANNs ameliorates this situation considerably, but neural networks are not well-suited for interpreting parameters for selected features of data. For this purpose, other statistical approaches are preferable.

While the limitations of ANNs should make social scientists hesitate to throw out their established tools in favour of the shiny new technology, which in fact has a decades long history, neural networks make a tempting offer. They are universal function-approximators with considerably fewer ontological assumptions than other approaches. While awareness of where the controversies of social ontology afflict neural networks is required, ANNs are the modelling tool best placed to avoid them.