The variety of evidence thesis and its independence of degrees of independence

Abstract

The intuitive Variety of Evidence Thesis states that, ceteris paribus, more varied evidence for a hypothesis confirms it more strongly than less varied evidence. Recent Bayesian analyses have raised serious doubts in its validity. Claveau suggests the existence of a novel type of counter-example to this thesis: a gradual increase in source independence can lead to a decrease in hypothesis confirmation. I show that Claveau’s measure of gradual source independence suffers from two unsuspected types of inconsistencies. I hence put forward a more natural measure of gradual source independence which is not plagued by inconsistencies. Claveau’s counter-examples to the variety of evidence thesis disappear with the measure I suggest. I hence argue that my measure is preferable and that this thesis does at least not seem to be troubled by Claveau’s arguments.

1 Introduction

It is widely agreed among scientists and philosophers of science that evidential variety among consistent and confirmatory items of evidence is beneficial for hypothesis confirmation (Borm et al. 2009; Hüffmeier et al. 2016; Meehl 1990). In particular, the independence of the source providing the evidence has been stressed (Thurmond 2001; Downward and Mearman 2007; Istituto Nazionale di Fisica Nucleare 2011). Philosophers have cast this agreement in the intuitive Variety of Evidence Thesis (VET). The VET states that, ceteris paribus, more varied evidence for a hypothesis confirms it more strongly than less varied evidence, see (Carnap 1962; Keynes 1921; Horwich 1982; Franklin and Howson 1984; Hempel 1966; Earman 1992) for classical treatments.

The VET has received much recent attention highlighting its surprising failures, (Bovens and Hartmann 2002, 2003; Claveau 2013; Claveau and Grenier 2019; Osimani and Landes 2020; Fitelson 1996; Landes 2020a; Casini and Landes 2021) discover cases within Bayesian models of scientific inference in which a less diverse body of evidence bestows more confirmation upon a hypothesis of interest than a more diverse body of evidence. Related to these formal investigations is the general debate on the confirmatory value of varied evidence, in which the confirmatory value of evidential variety is widely accepted (Kuorikoski and Marchionni 2016; Heesen et al. 2019; Schupbach 2015; Woodward 2006).¹

One important open problem in these discussions is the question of how to interpret the intuition that a body of evidence is more, or less, varied. A number of interpretations have been put forward, explications of evidential variety were offered in terms of likelihoods of evidence propositions Horwich (1982), rate of increase of conditional probabilities of evidence propositions Earman (1992), “consequence variety” (Landes 2020b; Claveau and Grenier 2019), variety of (medical) study design Worrall (2007), variety of the structure (or lack thereof) of data in Big Data (Lukoianova and Rubin 2014; Sagiroglu and Sinanc 2011).

This paper, however, is situated within a greater research project inaugurated in Bovens and Hartmann (2002). There it is suggested that evidential variety may be interpreted in terms of the number of independent evidence providing sources²: ceteris paribus, evidential variety increases with the number of independent evidence providing sources. For example, measuring the speed of light with two different clocks produces more varied evidence than performing these two measurements and obtaining the same times with a single clock, ceteris paribus. The ceteris paribus condition in the VET ensures that the clocks employed are equally good at keeping time. This greater research project is built on the assumption that, ceteris paribus, evidential variety increases with an increasing source variety.

Bovens and Hartmann take the VET to entail that, ceteris paribus, two evidence propositions confirming a hypothesis provided by two independent sources are more confirmatory than the same two evidence propositions provided by a single source. They go on to develop a Bayesian network model for scientific inference for testing hypotheses with multiple sources. Surprisingly, the VET fails in a substantial part of their model.³ So, obtaining the same two confirmatory measurements from one single instrument is more confirmatory than obtaining these two measurements from two independent instruments—in some cases (cf. Sect. 2.1). Osimani and Landes (2020) replicate this initially surprising result in a modified model which, they claim, is closer to realistic scientific inference (cf. Sect. 2.3).

Claveau (2013) refined this binary notion of source independence suggesting that it is instead a continuous notion, it comes in degrees varying from fully independent sources to fully dependent sources, the latter being, in essence, a single source. Instruments may be (in-)dependent to a degree, if they share some common experimental device and/or they both require auxiliary and/or background theories to interpret measurements; witnesses may be (in-)dependent to a degree, if they witnessed an event standing next to each other and/or they are family members; the output of algorithms may be (in-)dependent to a degree, if they run on the same experimental computer hardware or employ similar random number generators.

Plausibly, the VET entails that, ceteris paribus, confirmation increases with an increasing degree of source independence. While in Claveau’s model two fully independent sources always confirm more strongly than a single source, there are surprisingly cases in which a gradual increase in source independence entails a decrease in confirmation (Claveau 2013, Section 5). Claveau’s work thus suggests that the introduction of intermediate degrees of source independence leads to novel VET failures.

In this paper, I investigate this intriguing suggestion. If it were found to be true, then the beleaguered VET would face yet another difficulty. After briefly introducing the pertinent parts of the formal models (Sect. 2), I apply Claveau’s measure of gradual source independence to the models developed in Bovens and Hartmann (2002); Osimani and Landes (2020) which produces novel VET failures in both models (Sect. 3.2). More bad news for the VET—one might think.

However, Claveau’s measure of gradual source independence is plagued by two inconsistencies (Sect. 4). I hence suggest an arguably more natural and definitely simpler measure of gradual dependence which is not plagued by inconsistencies (Sects. 5.1 and 5.2). My measure of gradual source independence does not produce novel VET failures in the models in Bovens and Hartmann (2002), Claveau (2013), Osimani and Landes (2020) (Sect. 5.3).

I hence (Sect. 6) that the measure I put forward is to be applied in explications of the VET. This means that the purported bad news for the VET do not pose a further challenge to this intuitive thesis. Out of this discussion the VET does not emerge vindicated but at least it does not seem to be troubled by Claveau’s notion of gradual source independence.

2 Binary source variety

2.1 Bovens and Hartmann

Our story begins with Bovens and Hartmann interpreting evidential variety in terms of the number of independent sources of evidence. They develop a Bayesian network model (see Darwiche 2009; Neapolitan 2003 for technical background on Bayesian networks) of scientific inference which crucially incorporates the number of sources of evidence and their assessed reliabilities.

On an abstract level, VET failure is explained by the fact that successful replications—here construed as consistent confirmatory evidence propositions originating from the same source—contribute to confirmation, since successful replications increase the assessed reliability of the source. Naturally, a more reliable source providing consistent confirmatory evidence leads to stronger hypothesis confirmation. In some cases, the confirmation increase from repeatedly testing the same source outweighs the confirmation increase from evidence provided by multiple sources (Bovens and Hartmann 2003, p. 98).

I now briefly sketch parts of the Bovens and Hartmann model that are relevant for my discussion. For full details and justifications, the reader is referred to Bovens and Hartmann (2002, 2003). As mentioned, they use a Bayesian network model which represents two distinct epistemic states in an inquiry concerning a scientific hypothesis.

The (scientific) hypothesis is modelled by a binary propositional variable HYP which takes values hyp and $\overline{hyp}$ with intended interpretations: the hypothesis is true, respectively false. Evidence is modelled in terms of binary report variables $E_i$ taking values $e_i$ and $\overline{e_i}$ meaning: the hypothesis is true is reported, respectively the hypothesis is false is reported. Finally, the evidence is not taken at face value and thus modulated by the reliability of the source. The reliability of a source is modelled by a binary reliability variable $REL_i$ taking values $rel_i$ and $\overline{rel_i}$ standing for reliable, respectively unreliable.⁴ In the first epistemic state, all evidence originates from a single source, in the second situation every report originates from a different source.

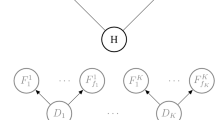
The Bayesian probabilities of the inquiring agent are constrained by the network topology of the directed acyclic graph in the Bayesian network.⁵ The hypothesis variable and the reliability variables are root nodes (they do not have any parents). Every report depends only on the reliability of the source and the truth of the hypothesis, i.e., there are no edges connecting the $e_i$ with each other.⁶ Typical network topologies are depicted in the two leftmost graphs in Fig. 1.

Fig. 1

Topologies of Bayesian networks for fully dependent, fully independent and to a degree independent sources, respectively, for the two items of evidence case. The REL-nodes represent the reliability of the evidence providing sources. The dotted arrow indicates a gradual independence between two sources introduced in Claveau (2013), cf. Sect. 3

The agent’s probability function P satisfies the ceteris paribus clause which says that all sources are indistinguishable in terms of their reliabilities and that all reports are indistinguishable in terms of their conditional probabilities. Formally speaking, we may drop all indices.

The prior probabilities of the root nodes, $P(hyp)=h$ and $P(rel)=\rho$, are only constrained to be somewhere in the open unit interval, (0, 1). A reliable source is perfect in that reports from that source perfectly determine the truth of the hypothesis, $P(e|hyp\,rel)=1$ and $P(e|\overline{hyp}\,rel)=0$. An unreliable source is taken to be a randomiser, which is not sensitive to truth of the hypothesis. It thus reports that the hypothesis with a constant probability, denoted by $a\in (0,1)$, $P(e|hyp\,\overline{rel})=P(e|\overline{hyp},\overline{rel})=a$, see Table 1.

Table 1 Conditional probabilities in Bovens and Hartmann model of an evidential variable, E. A reliable source provides perfect information, an unreliable source is a randomiser providing irrelevant evidence for hypothesis confirmation, the “Bayes factor”, $\frac{P(e|hyp\,{rel})}{P(e|hyp\,\overline{rel})}=\frac{a}{a}$ is equal to 1

Bovens and Hartmann discover cases in which it is the less diverse body of evidence (depicted on the left in Fig. 1, one source) that confirms the hypothesis more strongly than the diverse body of evidence (depicted in the middle in Fig. 1, two independent sources), ceteris paribus. These cases constitute instances of VET failure.

2.2 Claveau

Claveau (2013) adopts the Bovens and Hartmann model with two modifications. First,⁷ he takes issue with Bovens and Hartmann’s notion of an unreliable source which is a randomiser. A randomiser flips a (possibly biased) coin and then reports depending only on the outcome of the coin flip and independently of the state of nature. Claveau thinks that modelling unreliable scientific instruments as systematically biased is more appropriate, a systematically biased instrument will always report the same state of nature only depending on the bias of the instrument—whatever the state of nature.

Unlike Bovens and Hartmann, Claveau thus considers a ternary (3-ary) notion of reliability with modes: (i) fully reliable (perfectly tracking the truth of the hypothesis), (ii) systematically positively biased (always reporting that the hypothesis holds, independently of the actual truth of the hypothesis) and (iii) systematically negatively biased (always reporting that the hypothesis is false, independently of the actual truth of the hypothesis). This gives rise to a model which employs a now ternary propositional reliability variable (REL) which may take three different values (in the above order: (i) rel (ii) $b^h$ and (iii)$b^{\lnot h}$) with prior probabilities (i) $P(rel)=\rho$, (ii) $P(b^h)=\bar{\rho }\alpha$ (where $\alpha$ is the probability that a source is systematically positively biased conditional on not being reliable) and (iii) $P(b^{\lnot h})=\bar{\rho }\bar{\alpha }$, see Table 2. One may thus think of an unreliable source in Claveau’s sense as a broken instrument, since it always provides the same report independently of the true state of nature.

Table 2 Conditional probabilities in Claveau’s model of an evidential variable, E. The systematically biased sources are unreliable

Claveau (2013) Sect. 4 reports that there are no VET failures in this model: For all prior probability assignments, two consistent confirmatory evidence propositions from two independent sources are more confirmatory than the same two consistent confirmatory evidence propositions from a single source, ceteris paribus.

2.3 Landes and Osimani

Recall that for Bovens and Hartmann a reliable source always reports the true state of the world (Claveau agrees with this but not with their understanding of an unreliable source) while an unreliable source’s reports do not depend on the state of nature.⁸ Osimani and Landes (2020) think that it is more appropriate for modern-day science that even reliable sources of evidence for scientific inference get things wrong, from time to time. For more debate on the notion of reliability (see Landes and Osimani 2020; Bonzio et al. 2020). Hence, even reliable sources make Type I (falsely reporting that the hypothesis holds) and Type II (falsely reporting that the hypothesis fails) errors. In their model, both errors are made with (not necessarily equal) non-negative probability. Unreliable sources are construed as biased which report, by convention, that the hypothesis of interest holds more often than a reliable source—whatever the state of nature. That is, a biased source has a greater probability of reporting that the hypothesis holds than a reliable source.

One motivation to consider such a source is sponsorship bias which tilts reports to align with sponsors’ interests. Osimani and Landes, as well as Bovens and Hartmann, thus consider a binary notion of reliability, either a source is reliable or it is not. See Table 3 for an overview.

Table 3 Different notions of reliability. An unreliable source in Claveau’s sense can be broken in two ways, either it always reports that the hypothesis holds or it always reports that the hypothesis fails

Osimani and Landes thus use a binary propositional variable to model the reliability of a source (like Bovens and Hartmann but unlike Claveau). Their model differs from that of Bovens and Hartmann (2002) only by the restrictions on the conditional probabilities of the evidential variables, $P(e|HYP\,REL)$, see Table 4.⁹

Table 4 Conditional probabilities in Osimani and Landes model of an evidential variable, E. $\epsilon _- ,\epsilon _+$ are the Type I/II error probabilities conditional on the source being reliable, $\gamma ,1-\alpha$ are these conditional probabilities for unreliable sources. Osimani and Landes restrict their considerations to $\alpha >1-\epsilon _+$ and $\gamma >\epsilon _-$, which is motivated by their construal of bias

As did Bovens and Hartmann, Osimani and Landes report VET failures. There are cases in which the less diverse body of evidence (depicted on the left in Fig. 1, one source) that confirms the hypothesis more strongly than the diverse body of evidence (depicted in the middle in Fig. 1, two independent sources), ceteris paribus. But since these two models use different conditional probabilities, it is not straight-forward to compare the areas of VET failure. What is important for current purposes is that these two models, but not Claveau’s model, exhibit VET failures.

3 Exponential degree of source independence

3.1 Ternary reliability

Claveau’s main conceptual contribution is to refine the notion of source variety in that the variety of sources now comes in degrees; the degree of variety is captured by the degree to which sources are independent. Fully dependent sources are, in essence, just one source, since all fully dependent sources will always provide the same evidence proposition.¹⁰ Fully independent sources on the other hand provide evidence fully independently from each other; there is hence maximal source variety. Two sources are dependent to a degree, if there is a probabilistic association between the prior probabilities of the reliability variables (Claveau 2013, p. 107), see the plot on the right in Fig. 1 for the topology of the underlying Bayesian network.

The joint prior probabilities of two fully dependent [left below] and fully independent [middle below] sources, P(REL, REL), are given in (Claveau 2013, Table 3):

$$\begin{aligned} \begin{matrix} \rho &{} 0 &{} 0 \\ 0 &{} \bar{\rho }\alpha &{} 0 \\ 0 &{} 0&{} \bar{\rho }\bar{\alpha }\end{matrix} \begin{matrix} \rho ^2 &{} \rho \bar{\rho }\alpha &{} \rho \bar{\rho }\bar{\alpha }\\ \rho \bar{\rho }\alpha &{}(\bar{\rho }\alpha )^2 &{}\bar{\rho }^2\alpha \bar{\alpha }\\ \rho \bar{\rho }\bar{\alpha }&{} \bar{\rho }^2\alpha \bar{\alpha }&{} (\bar{\rho }\bar{\alpha })^2 \end{matrix} \begin{matrix} \omega _{rr} &{} \omega _{rh} &{} \omega _{r\bar{h}} \\ \omega _{hr} &{} \omega _{hh} &{} \omega _{h\bar{h}} \\ \omega _{\bar{h}r} &{}\omega _{\bar{h} h}&{} \omega _{\bar{h}\bar{h}} \end{matrix}. \end{aligned}$$

The nine values on the right formalise the general case of a prior probability assignment, P(REL, REL). For example, the probability that the first source is positively biased and the second source is negatively biased, $P(b_1^h,b_2^{\lnot h})$, is equal to zero for two fully dependent sources, it is equal to $\bar{\rho }^2\alpha \bar{\alpha }$ for two fully independent sources and equal to $\omega _{h\bar{h}}$ in the general case. In general, the probability of entry i, j in every 3x3-matrix equals the prior probability of $REL_1$ being equal to the i-th and $REL_2$ being equal to the j-th value of the reliability variable.

Claveau then puts forward a formal model of gradual source independence by defining a one-parameter curve from full dependence to full independence, parametrised by a real-valued distance parameter, $\delta \in [0,1]$, the curve from (Claveau 2013, §C1) is re-produced in Table 5. For $\delta =0$ there is full dependence and for $\delta =1$ full independence obtains. That is, he puts forward a way to specify intermediate degrees of source independence along this curve by imposing four requirements:¹¹

• R1 exponential law: $\omega _{rr}=\rho ^{1+\delta },\omega _{hh}=(\bar{\rho }\alpha )^{1+\delta },\omega _{\lnot h\lnot h}=(\bar{\rho }\bar{\alpha })^{1+\delta }$,

• R2 probabilities sum to one: $\sum _{\omega }\omega =1$,

• R3 the $\omega$ are symmetric: $\omega _{rh}=\omega _{hr},\omega _{r\bar{h}}=\omega _{\bar{h}r},\omega _{h\bar{h}}=\omega _{\bar{h} h}$, and

• R4 the marginal probabilities of $REL_1$ and $REL_2$ are not a function of the distance parameter: for $i=\{1,2\}$

  $$\begin{aligned} P(rel_i)&=\omega _{rr} + \omega _{rh} + \omega _{r\bar{h}}=\rho \nonumber \\ P(b^h_i)&=\omega _{rh} + \omega _{hh} + \omega _{h\bar{h}}=\bar{\rho }\alpha \\ P(b^{\bar{h}}_i)&=\omega _{r\bar{h}}+\omega _{h\bar{h}}+ \omega _{\bar{h}\bar{h}}=\bar{\rho }\bar{\alpha }.\nonumber \end{aligned}$$

  (1)

Indeed, these requirements are prima facie not implausible and uniquely determine his model of degree of source independence in terms of a one parameter curve depending on the distance parameter $\delta$.¹²

Claveau goes on to formalise the VET as the requirement that the posterior probability of the hypothesis increases with increasing source independence:

Ceteris paribus, $\frac{\partial P(hyp|e_1e_2)}{\partial \delta }>0$, for all admissible values of $\rho ,\alpha$ and $\delta$. (Claveau 2013, p. 109)

The unexpected result is there is VET failure in Claveau (2013)’s model for gradual source independence, see (Claveau 2013, p. 109), while there was no VET failure in the binary source variety approach (Sect. 2.2). That is, there are no VET failures in Claveau’s base model (binary source variety) but there are such failures in the general model (gradual source variety). The introduction of grades of source independence generates novel VET failures.

I now investigate effects of applying a gradual notion of source independence on the VET in models with a binary reliability variable. Does the introduction of source independence generate novel VET failures? I will then apply these investigations to the models developed in Bovens and Hartmann (2002) and Osimani and Landes (2020).

3.2 Binary reliability

Since the reliability variable is binary, the axioms for ternary variables cannot simply be copied and pasted. In close analogy to Claveau (2013), I suggest that the exponential degree requirements for binary reliability variables could be

• P1 exponential law: $\omega _{rr}=\rho ^{1+\delta }$ and $\omega _{\bar{r}\bar{r}}=\bar{\rho }^{1+\delta }$,

• P2 probabilities sum to one: $\sum _{\omega }\omega =\omega _{r r}+\omega _{r\bar{r}}+\omega _{\bar{r}r}+\omega _{\bar{r}\bar{r}}=1$, and

• P3 symmetry: $\omega _{r\bar{r}}=\omega _{\bar{r} r}$.

P1–P3 axiomatically characterise an exponential degree of source independence for binary reliability variables in terms of a one-parameter curve parametrised by $\delta$, see Table 6. I impose P1–P3¹³ and ask what happens to the fate of the VET. The VET is here taken to entail the incremental change of posterior probability of the hypothesis, ${\partial P(hyp|e_1e_2)}/{\partial \delta }$, is an increasing function in $\delta$.

The general expression for the derivative of the posterior probability with respect to the exponential degree of independence, $\delta$, is not immediately comprehensible (even in its most simple form):

Proposition 1

(VET Failure for an exponential Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ ) \epsilon _- \rho ^{1+\delta }\ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad -\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}) (\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr ). \end{aligned}$$

All proofs can be found in the appendix, where I restate the claims to be proved for ease of reference. I here used the conventions of Table 4 to more compactly denote conditional probabilities.

While the general formula is rather involved, we can make one simple observation:

Proposition 2

In case one is indifferent about the source being reliable, $\rho =\bar{\rho }=0.5$, the sign of derivative does not depend on $\delta$.

That is, for $\rho =0.5$ and for fixed conditional probabilities of the evidence variables given their parent variables in the topology of the Bayesian network, the parameters $\alpha ,\gamma ,\epsilon _- ,\epsilon _+$, and fixed prior probability of the hypothesis, P(hyp), the VET either holds along the entire exponential curve or it fails along the entire exponential curve.

I now turn to the models of Bovens and Hartmann and Osimani and Landes as special cases of Proposition 1. Although things simplify significantly, no clear pattern will emerge.

3.2.1 Bovens and Hartmann

For the Bovens and Hartmann model, $\alpha =\gamma =a$ and $\epsilon _+ =\epsilon _- =0$, the expression from Proposition 1 simplifies significantly:

Proposition 3

(VET Failure for Bovens and Hartmann for an exponential Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr ) ={{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\bar{a}[\ln (\rho )-\ln (\bar{\rho })]-a\ln (\bar{\rho })\Bigr ) . \end{aligned}$$

As in Claveau (2013), the expression determining the sign of the derivative cannot be solved analytically. I content myself with pointing out rules of thumb which indicate the sign of the derivative. If $\rho >\bar{\rho }$, then $\ln (\rho )-\ln (\bar{\rho })>0$ and the VET holds. If $\rho$ is small, $\rho \ll 0.5$, then $\ln (\rho )-\ln (\bar{\rho })\ll 0$ and the VET fails for all a that are not too close to one. If a is close enough to one, the VET holds. The greater $\delta$ the more important is the term $-\ln (\bar{\rho })a>0$, the area of VET failure hence decreases with increasing $\delta$. The situation in the $\rho -a$-plane for different $\delta$ is illustrated in Fig. 2 which somewhat resembles (Bovens and Hartmann 2003, Figure 4.5) in that both figures display VET failure near the origin. Since gradual source independence is not part of the Bovens and Hartmann model (the fate of the VET in their model only depends on $\rho$ and a but not on $\delta$), (Bovens and Hartmann 2003, Figure 4.5) only displays a single drawing of VET failures in the $\rho -\alpha$-plane.

Fig. 2

Bovens and Hartmann model: For $\delta =0.1,0.5,0.9$ from left to right: plot of the sign of $\rho ^{1+\delta }\bar{a}(\ln (\rho )-\ln (\bar{\rho }))-\ln (\bar{\rho })a$ in the $\rho -a$-plane. Yellow indicates VET failure, blue indicates that the VET holds

3.2.2 Landes and Osimani

The rather complex expression in Proposition 1 does not simplify in the Osimani and Landes model. Since investigating the expression in full detail is not very illuminating, I report two special situations. First, I consider what happens for the previously reported VET failures and then show that there are novel VET failures for the exponential degree of source independence.

Firstly, for the only reported constraint along which posterior probabilities are equal (borderline of VET failure), $\epsilon _- \alpha =\gamma (1-\epsilon _+ )$, it follows that

$$\begin{aligned} \frac{\partial }{\partial \delta }P(hyp|e_1e_2)=0 . \end{aligned}$$

So, all posterior probabilities of the hypothesis are equal along the exponential curve, if the conditional probabilities of the evidential variables satisfy $\epsilon _- \alpha =\gamma (1-\epsilon _+ )$.

Secondly, there are, however, novel VET failures for the exponential degree of source independence:

Proposition 4

(VET Failure for Landes and Osimani for an exponential Degree of Independence)

For $\alpha > rapprox 1-\epsilon _+ >0$ and $\gamma > rapprox \epsilon _- >0$, the VET holds for small $\rho$ and fails for large $\rho$. The smaller $\delta$, the smaller the area in which the VET holds.

See Fig. 3 for a plot of the sign of $\ln (\frac{\bar{\rho }}{\rho })-[\frac{\rho }{\bar{\rho }}]^{1+\delta }$ which approximately demarcates the boundary of VET failure for $\alpha > rapprox 1-\epsilon _+ >0$ and $\gamma > rapprox \epsilon _- >0$ (see proof of Proposition 4). The conditions $\alpha > rapprox 1-\epsilon _+ >0$ and $\gamma > rapprox \epsilon _- >0$ represent an unreliable instrument which is barely distinguishable from a reliable one.

Fig. 3

Osimani and Landes model: Plot of $\ln (\frac{\bar{\rho }}{\rho })-[\frac{\rho }{\bar{\rho }}]^{1+\delta }$ in the $\rho -\delta$-plane which approximates VET failure (Proposition 4). Yellow indicates VET failure, blue indicates that the VET holds. Consistent with Proposition 2, there is no change of colour near $\rho =0.5$

3.3 Summing up

Bovens and Hartmann reported the borderline of VET failures to be parametrised by $1=2\bar{a}\bar{\rho }$, which is no longer such a boundary under the exponential degree of source independence (Proposition 3). Osimani and Landes’s borderline of VET failure $\alpha \epsilon _- =\gamma (1-\epsilon _+ )$ continues to be a borderline of VET failure (Proposition 1). However, the introduction of gradual source variety produced novel VET failures in both these models. Some of these novel VET failures obtain for parameter values ($\rho ,a,\epsilon _+ ,\epsilon _- ,\alpha ,\gamma$) close to those previously reported. Overall, no clear pattern emerges for which the VET holds/fails.

4 Inconsistencies

In the above section, I applied Claveau’s measure of gradual source independence to the models developed in Bovens and Hartmann (2002) and Osimani and Landes (2020) which produces novel cases in both models in which more source independence entails less confirmation. More bad news for the VET—one might think. However, I now argue that these “VET failures” do not spell further trouble for the VET.

4.1 Ternary reliability

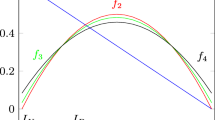
Claveau’s degree of source independence has a serious formal flaw which has not yet been pointed out. Some of the one parameter curves connecting full dependence with full independence for ternary reliability variables as used in Claveau (2013) leave the realm of probabilities, some $\omega$ are negative. Here are some examples:

$$\begin{aligned} \omega _{rh}&=\omega _{hr}=P(rel_1,b_2^h)=\rho +\bar{\rho }\alpha -\frac{1+\rho ^{1+\delta }+(\bar{\rho }\alpha )^{1+\delta } -(\bar{\rho }\bar{\alpha })^{1+\delta }}{2}\approx -0.03\% \nonumber \\&\text { for }\rho =2.5\%,\alpha = 90\%,\delta =20\%\nonumber \\ \omega _{r\bar{h}}&=\omega _{\bar{h}r}=P(rel_1,b_2^{\lnot h})=\rho +\bar{\rho }\bar{\alpha }-\frac{1+\rho ^{1+\delta }-(\bar{\rho }\alpha )^{1+\delta } +(\bar{\rho }\bar{\alpha })^{1+\delta }}{2}\approx -0.32\% \nonumber \\&\text { for }\rho =95\%, \alpha =95\%,\delta =50\%\nonumber \\ \omega _{h\bar{h}}&=\omega _{\bar{h}h}=P(b_1^h,b_2^{\lnot h})=-\rho +\frac{1+\rho ^{1+\delta }-(\bar{\rho }\alpha )^{1+\delta } -(\bar{\rho }\bar{\alpha })^{1+\delta }}{2}\approx -0.15\% \nonumber \\&\text { for }\rho =12.5\%,\alpha =97.5\%,\delta =10\% . \end{aligned}$$

(2)

Apparently, for all three different off-diagonal $\omega$ there exists a curve and an intermediate degree of independence, $\delta \in (0,1)$, at which the $\omega$ (a Bayesian probability) becomes negative. The three sample curves in (2) leaving the realm of probabilities are not the only such curves, see Figs. 4 and 5 for graphical illustrations.

Fig. 4

Plot of $\min \{\inf _{\delta \in [0,1]}\omega _{rh}(\rho ,\alpha ,\delta ),\inf _{\delta \in [0,1]}\omega _{r\bar{h}}(\rho ,\alpha ,\delta ),\inf _{\delta \in [0,1]}\omega _{h\bar{h}}(\rho ,\alpha ,\delta )\}$ in the $\alpha -\rho$-plane on the grid $[0,01,0.99]^2$ with step size 0.01. A negative “heat” at a point $(\alpha ,\rho )$ indicates that the exponential curve connecting dependent sources to independent sources leaves the realm of probabilities. At full dependence, these three $\omega$ are all equal to zero; hence every infimum is at most zero and all values are at most zero in this plot

So, until Bayesians are ready to endorse and make sense of negative “probabilities”, Claveau’s axioms R1–R4 are inconsistent with the Bayesian paradigm. This means that exponential degrees of dependence as proposed in Claveau (2013) for ternary reliability fail to properly explicate a notion of gradual source independence in Bayesian epistemology.

Since the introduction of gradual source independence only produced VET failures in Claveau’s model for exponential degrees and these degrees of source independence fail to properly explicate source independence in Bayesian terms, there are no known instances in which the introduction of degrees of source independence produces troubling VET failures for ternary reliability.

A contrarian might object that some of Claveau (2013)’s curves producing VET failure do not leave the realm of positive probabilities as depicted in the bottom right plot in Fig. 5 and hence the VET is troubled by gradual source independence. However, until these curves are found to be part of a canonical family of curves consistent with the Bayesian paradigm which cover all plausible parameter configurations for full source dependence and full source independence, I blame these alleged “VET failures” on the peculiarity of the curves which stray away too far from a straight line.

Fig. 5

Top: Plot of $P(rel_1,b_2^h)=\omega _{rh}$ depending on $\delta$. Left: $\rho =0.025,\alpha =0.9$ where $\omega _{rh}$ dips into the negative until becoming positive at around $\delta \approx 23.75\%$. Right: $\rho =0.05,\alpha =0.8$ where $\omega _{rh}$ is positive throughout for all $\delta \in [0,1]$. Bottom: Plot of the three different off-diagonal values of $P(REL_1,REL_2)$. Left: $\rho =0.025,\alpha =0.9$, yellow indicates that the VET holds and $\omega _{rh}$ is positive, green indicates that the VET fails and $\omega _{rh}$ is positive while red indicates that the VET fails and $\omega _{rh}$ is negative. Right: $\rho =0.05,\alpha =0.8$, yellow indicates that the VET holds, green that it fails. The straight blue lines represent the linear degree of source independence (cf. Sect. 5)

This inconsistency also reappears in Claveau and Grenier (2019) which extends Claveau (2013) by adding a further notion of gradual evidential variety.

4.2 Binary reliability

The exponential degree of source independence for binary reliability does not produce intermediate degrees of source independence which contradict the Bayesian paradigm. They seem like a sensible explication of gradual source independence. Nevertheless, these degrees of source independence ought not to be used in an explication of the VET, as I shall now argue.

The attentive reader will have noted that I only suggested three axioms to characterise binary gradual source independence (Sect. 3.2), when there were four axioms put forward in Claveau (2013) for ternary variables (Sect. 3.1). Claveau’s fourth axiom says that while increasing (or decreasing) source independence the prior probability of the reliability variable $REL_1$ does not change. In close analogy to the ternary case, for a binary reliability variable this axiom is:

• P4 The marginal probabilities of $REL_1$ is not a function of the distance parameter $\delta$, for all $\delta \in [0,1]$

  $$\begin{aligned} P(rel_1)&=\omega _{rr} +\omega _{r\bar{r}}=\rho \\ P(\overline{rel}_1)&=\omega _{\bar{r}r}+\omega _{\bar{r}\bar{r}}=\bar{\rho }. \end{aligned}$$

P4 and the symmetry axiom P2 jointly entail that the marginal probabilities of $REL_2$ is also not a function of the distance parameter $\delta$. All seems good—for the moment.

It may come as a surprise that this close analogy leads to disaster for binary reliabilities:¹⁴

Proposition 5

P1, P3 and P4 are jointly inconsistent.

Unlike the inconsistency for ternary reliability variables, this inconsistency arises entirely from within the axioms P1, P3 and P4,¹⁵ there is no clash here with Bayesian (or other) postulates.

Now recall that the exponential degree of source independence for binary reliability variables satisfies P1 and P3, and since these three axioms are inconsistent, it follows that these degrees do not satisfy P4. This means that increasing source independence leads to a change of the prior belief in a source being reliable. Formally, this follows from observing that the prior probability of a source being reliable

$$\begin{aligned} P(rel)=\rho ^{1+\delta }+\frac{1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta }}{2} =\frac{1+\rho ^{1+\delta }-\bar{\rho }^{1+\delta }}{2} \end{aligned}$$

(3)

does depend on the distance parameter $\delta$. A priori, this dependence is unproblematic.

What does this mean for the thesis of interest? The thesis clearly states that confirmation increases with increasing evidential variety, ceteris paribus. We here explicate evidential variety in terms of gradual source independence. Increasing gradual source independence should increase confirmation, ceteris paribus. I have shown in Sect. 3.2, that an increase in gradual source independence decreases confirmation in the models of Bovens and Hartmann (2002); Osimani and Landes (2020). These troubling results however were not obtained ceteris paribus. Ceteris paribus means that all other things must remain equal. While increasing evidential variety (increasing gradual exponential source independence for binary variables) the prior probability of the reliability was not held constant, (3) changes with varying $\delta$ . Hence, the VET is not troubled by the results in Sect. 3.2 for a exponential degree of source independence and binary reliability.

As I argued in Sect. 4.1, the VET is also not troubled by Claveau’s results (Sect. 3.1) for an exponential degree of source independence and ternary reliability. If my arguments are found to be compelling, and I think they should be, then the exponential degree of gradual source independence does not produce any troubling VET failures.

At long last, some good news for the besieged VET.

5 Linear degree of source independence

Claveau’s work suggests that the introduction of intermediate degrees of independence leads to novel VET failures. As I just argued, the suggested exponential degree of gradual source independence is not a viable option for analysing the VET. To follow-up on Claveau’s conceptual contribution I develop a measure of gradual source independence for explicating the VET which permits an axiomatisation to binary and ternary reliability variables.

Claveau’s notion of distance is exponential and thus rather complicated. It seems more natural to consider a simpler notion of distance which linearly increases in the distance parameter.¹⁶ It is hence natural to wonder what happens if a linear requirement instead of the exponential requirement R1 is imposed.

5.1 Ternary reliability

Applying a linear approach to gradual source independence, it is natural to take the VET to entail that, ceteris paribus, the posterior probability of the hypothesis increases with increasing source independence with respect to the degree parameter $\lambda$. Formally,

Ceteris paribus, $\frac{\partial P(hyp|e_1e_2)}{\partial \lambda }>0$, for all $\rho ,\alpha ,\lambda ,P(hyp)\in (0,1)$.

Following Claveau, I begin by first considering a ternary reliability notion. In close analogy to R1, I now consider a linear distance measure:

$$\begin{aligned} (R1')\text { linearity: for all }\lambda \in [0,1]&\\&\omega _{rr}=\rho +\lambda (\rho ^2-\rho ),\\&\omega _{hh}=\bar{\rho }\alpha +\lambda ((\bar{\rho }\alpha )^2-{(\bar{\rho }\alpha )})\text { and }\\&\omega _{\lnot h\lnot h}=\bar{\rho }\bar{\alpha }+\lambda ((\bar{\rho }\bar{\alpha })^2-{(\bar{\rho }\bar{\alpha })}) . \end{aligned}$$

Enforcing Requirements R1’, R3 and R4 I obtain a unique curve which connects dependence ($\lambda =0$) and independence ($\lambda =1$) of sources. Note that the linear and the exponential notion of gradual source independence lead to different degrees of source independence, the linear curve given in Table 7 is different than the exponential curve given in Table 5.

Proposition 6

R1’, R3 and R4 are mutually consistent. Furthermore, they jointly entail R2 and

$$\begin{aligned} \omega _{rh}=\omega _{hr}=\lambda \alpha \rho \bar{\rho }\quad \quad \quad \omega _{r\bar{h}}=\omega _{\bar{h}r}=\lambda \bar{\alpha }\rho \bar{\rho }\quad \quad \quad \omega _{\bar{r}\bar{h}}=\omega _{\bar{h}\bar{r}}=\lambda \alpha \bar{\alpha }\bar{\rho }^2 . \end{aligned}$$

Note that for the linear degree of source independence all values are in the unit interval, as they should be, because they are all convex combinations of probabilities. They are hence not plagued by inconsistency as the exponential degree (Sect. 4.1).

In stark contrast to Claveau’s degree of source independence, there is no failure of the VET under the linear degree of source independence in Claveau’s model:

Proposition 7

(No VET failures in Claveau’s model for Linear Degree) Ceteris paribus, for all $\rho ,\alpha ,\lambda ,P(hyp)\in (0,1)$ it holds that

$$\begin{aligned} \frac{\partial P(hyp|e_1e_2)}{\partial \lambda }>0. \end{aligned}$$

Claveau’s main result is thus sensitive to the way the degree of source independence is formalised. The introduction of a linear degree of source independence does not introduce any (novel) VET failures. Even stronger, there are no VET failures whatsoever in Claveau’s model, since there are no VET failures in the base model (Sect. 2.2).

5.2 Binary reliability

Recall that Bovens and Hartmann as well as Osimani and Landes employ binary but different reliability concepts, either a source is reliable or not and there is only one kind of unreliability. This leads them to employ a binary reliability variable whereas Claveau employs a ternary reliability variable. Hence, a slightly different formalisation capturing that sources are independent to a degree is required.

Technically, I am looking for a way to connect the probability assignment, $P(REL_1,REL_2)$, from two fully dependent sources (left below) to two fully independent sources (middle below) via some intermediate linear degree of source independence (right below)

$$\begin{aligned} \begin{matrix} \rho &{} 0 \\ 0 &{} \bar{\rho }\end{matrix} \begin{matrix} \rho ^2 &{} \rho \bar{\rho }\\ \rho \bar{\rho }&{}\bar{\rho }^2 \end{matrix} \begin{matrix} \omega _{rr} &{} \omega _{r\bar{r}} \\ \omega _{\bar{r}r} &{} \omega _{\bar{r}\bar{r}} \end{matrix} \end{aligned}$$

via a one parameter curve. In full analogy to R1’, R2–R4, I consider four requirements:

• L1 linearity: $\omega _{rr}=\rho +\lambda (\rho ^2-\rho )$ and $\omega _{\bar{r}\bar{r}}=\bar{\rho }+\lambda (\bar{\rho }^2-\bar{\rho })$

• L2 probabilities sum to one: $\sum _{\omega }\omega =\omega _{r r}+\omega _{r\bar{r}}+\omega _{\bar{r}r}+\omega _{\bar{r}\bar{r}}=1$,

• L3 the $\omega$ are symmetric: $\omega _{r\bar{r}}=\omega _{\bar{r} r}$, and

• L4 the marginal probabilities of $REL_1$ and $REL_2$ are not a function of the distance parameter $\lambda$: for all $i=\{1,2\}$ and all $\lambda \in [0,1]$

  $$\begin{aligned} P(rel_i)&=\omega _{rr} +\omega _{r\bar{r}}=\rho \\ P(\overline{rel}_i)&=\omega _{r\bar{r}}+\omega _{\bar{r}\bar{r}}=\bar{\rho }. \end{aligned}$$

Proposition 8

L1–L4 are mutually consistent and have a unique solution:

$$\begin{aligned}\omega _{r\bar{r}}=\omega _{\bar{r} r}=\lambda \rho \bar{\rho }. \end{aligned}$$

The proof is obtained by inspecting Table 8.¹⁷

As it was the case for a ternary reliability variable, I here take the VET to entail that the posterior probability of the hypothesis given two confirmatory evidence propositions, $P(hyp|e_1e_2)$, increases with increasing source independence, ceteris paribus. For a linear degree of source independence this means that $\partial P(hyp|e_1e_2)/\partial \lambda$ is an increasing function in $\lambda$ for all prior probability functions consistent with the topology of the Bayesian network.

Proposition 9

(VET Failure for Linear Degree of Independence)

Ceteris paribus, for all $\rho ,\alpha ,\gamma ,\epsilon _- ,\epsilon _+ ,P(hyp)\in (0,1)$ it holds that

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr ) ={{\,\mathrm{sign}\,}}\Bigl (\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr )\cdot \\&(\rho \cdot [\epsilon _- [(1-\epsilon _+ )-\alpha ]+(1-\epsilon _+ )[\epsilon _- -\gamma ]] +\bar{\rho }\cdot [\gamma ((1-\epsilon _+ )-\alpha )+\alpha (\epsilon _- -\gamma )])\Bigr ) . \end{aligned}$$

That is, whether the VET holds or fails along the linear curve connecting full dependence and full independence of sources is fully determined by comparing posterior probabilities of the endpoints connecting full dependence to full independence, since the sign of the derivative in Proposition 9does not depend on $\lambda$. If the VET fails for a particular set of parameters, $\epsilon _- ,\epsilon _+ ,\alpha ,\gamma$, between endpoints, then increasing independence decreases confirmation along the entire curve. Vice versa, if the VET holds for a particular set of parameters between endpoints, then increasing independence increases confirmation along the entire curve. The introduction of intermediate linear degrees of independence does not lead to novel VET failures for a binary reliability variable.

I now briefly investigate the models of Bovens and Hartmann (2002); Osimani and Landes (2020) as special cases of Proposition 9.

5.2.1 Bovens and Hartmann

The Bovens and Hartmann model is specified by two constraints: i) reliable sources are perfect, i.e., they do not commit any errors, $\epsilon _+ =\epsilon _- =0$ and ii) an unreliable source is randomiser, i.e., the Bayes factor of an unreliable source is equal to one, $\alpha =\gamma =:a$.

Proposition 10

(VET Failure for Bovens and Hartmann for Linear Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr )={{\,\mathrm{sign}\,}}\Bigl (1-2\bar{a}\bar{\rho }\Bigr ) . \end{aligned}$$

This is precisely the formula obtained in (Bovens and Hartmann 2003, p. 97, 4.11) for VET failure between fully dependent and fully independent sources.

5.2.2 Landes and Osimani

The Osimani and Landes model is specified by the constraint that unreliable sources are more likely to report that the hypothesis holds whatever the state of nature: $\alpha >1-\epsilon _+$ and $\gamma >\epsilon _-$. Since all differences between conditional probabilities in the second large bracket in Proposition 9 are negative, it is now easily observed that:

Proposition 11

(VET Failure for Landes and Osimani for Linear Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr ) =-{{\,\mathrm{sign}\,}}\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr ) . \end{aligned}$$

This is precisely the formula obtained in Osimani and Landes (2020) for VET failure between fully dependent and fully independent sources.

5.3 Summing up

I just showed in Proposition 9 that under a linear degree of source independence, VET failures obtain, if and only if they obtain between fully independent and fully dependent sources for a binary reliability variable. The same holds true for the ternary reliability variable in Claveau’s model (Proposition 7). That is, the introduction of a linear degree of source independence does not cause novel VET failures. Compare this with Claveau’s exponential degree of source independence which does introduce novel VET failures in all three models.

6 Conclusions

While the VET was once held to be an “undeniable element of scientific methodology” (Horwich 1982, p. 77) and a “truism of scientific methodology” (Earman 1992, p. 77), recent Bayesian explications of the VET have shattered the belief in its validity. Bovens and Hartmann (2002); Osimani and Landes (2020) established that in certain situations evidence for a hypothesis is more confirmatory, if it originates from a single rather than two sources. Claveau’s work suggests that the introduction of degrees of source independence produces novel VET failures.

Contra Claveau (2013) I conclude that the VET is not (yet!) troubled by gradual source independence, because the exponential degree of source independence (Sect. 3) is not applicable in an analysis of the VET (Sect. 4) and the preferable linear degree of source independence does not produce any novel VET failures (Sect. 5). Why do I write “yet”? Because I only investigated one particular degree of source independence, while I do think that the linear degree is indeed the most natural degree, I have not investigated other degrees of gradual source independence. Another reason for saying “yet” is the limitation to two items of evidence in this paper. While I do believe that considering multiple items of evidence will not change matters significantly, I do not have a proper proof for this belief. Furthermore, the case of reliabilities of greater arities is open, since the axioms considered here are too weak to determine a family of one parameter curves (Proposition 12).

Finally, note that Claveau’s measure of gradual source independence does not assign all joint probabilities, $P(REL_1,REL_2)$, which are intuitively somewhere between full dependence and full independence, a degree of independence. This evident from Fig. 5 in which the exponential and the linear curve only cover little of the space “in between” full dependence and full independence. To the best of my knowledge, this constitutes a, previously unmentioned, limitation of Claveau’s approach. This limitation applies to the linear degree of source independence introduced here, too. Statisticians have long studied degrees of (in-)dependence under the term correlation and produced a number of non-equivalent measures of correlation. Bringing in insights and concepts from statistics (correlation [coefficients], anticorrelation, Bayes factors (Morey et al. 2016) and others) into philosophy as urged in (Mayo 2018, p. 74) may well shed further light on our concept(s?) of source independence and further illuminate the VET.

Out of this discussion the VET does not emerge vindicated, this is impossible given the apparent VET failures reported in Bovens and Hartmann (2002), Osimani and Landes (2020), Landes (2020b) and Fitelson (1996), but the VET is at least not (yet) troubled by gradual source independence.

A Formal analysis

1.1 A.1 Probabilities and ceteris paribus conditions

All variables are binary propositional variables, with the exception of the reliability variable in Claveau’s approach which is ternary. Variable names are capitalised, a variable name in lower letters indicates that the variables assigned the value true. The prior probabilities of the root nodes, $HYP,REL_i$, are: $P(hyp)=h, P(rel_i)=\rho$, in Claveau’s approach also: $P(b^h_i)=\bar{\rho }\alpha$ and $P(b_i^{\lnot h})=\bar{\rho }\bar{\alpha }$; where the ceteris paribus condition entails that the prior probabilities of the reliability of the sources are equal. The conditional probabilities of the evidential variables, $E_i$, are for all fixed possible values of the parent variables $P(e_1|{HYP}\,REL_1)=P(e_2|{HYP}\,REL_2).$ To simplify notation, the index $_i$ is dropped in the following.

Different authors make different model assumptions for the conditional probabilities of the evidential variables, in chronological order (Bovens and Hartmann 2002; Claveau 2013; Osimani and Landes 2020):

$$\begin{aligned}&P(e|hyp\,rel)=1\quad \quad P(e|\overline{hyp}\,rel)=0\quad \quad P(e|{hyp}\,\overline{rel})=P(e|\overline{hyp}\,\overline{rel})=a\\&P(e|hyp\,rel)=1\quad \quad P(e|\overline{hyp}\,rel)=0\quad \quad P(e|b^{h})=1\quad \quad P(e|b^{\lnot h})=0\\&P(e|hyp\,rel)=\overline{\epsilon _+ }<P(e|{hyp}\,\overline{rel})=\alpha \quad P(e|\overline{hyp}\,rel)=\epsilon _- < P(e|\overline{hyp}\,\overline{rel})=\gamma . \end{aligned}$$

All conditional probabilities not explicitly set to zero, are always assumed to be non-extreme lying the open interval (0, 1). The fully general case for binary reliability is obtained by dropping the assumptions $1-\epsilon _+ <\alpha$ and $\epsilon _- <\gamma$ for the Osimani and Landes model.

1.2 A.2 Degrees of independence

The degrees of independence for prior probabilities of P(REL, REL) are given by the following tables:

Table 5 Degree of source independence suggested by Claveau for ternary reliability variables; axiomatised by R1–R4

Table 6 Exponential degree of source independence for binary reliability variables; axiomatised by P1–P3

Table 7 Alternative linear degree of source independence for ternary reliability variables; axiomatised by R1’, R3 and R4. See Proposition 6 for a proof

Table 8 Linear degree of source independence for binary reliability variables; axiomatised by L1–L3

1.3 A.3 Proofs

Proposition 1

(VET Failure for an exponential Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )\\&=-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ )\epsilon _- \rho ^{1+\delta } \ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\quad - \bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}) (\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr )\\ =&-{{\,\mathrm{sign}\,}}\Bigl ([\rho ^{1+\delta }\ln (\rho )[(1-\epsilon _+ )\epsilon _- -\bar{\rho }^{1+\delta } (\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\\&\quad \quad -\bar{\rho }^{1+\delta }\ln (\bar{\rho })[\alpha \gamma -\rho ^{1+\delta } (\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]]\cdot [\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\Bigr ) . \end{aligned}$$

Proof

This proof is a tedious exercise in keeping concentrated. To double-check my calculations (here and in the proofs below) I subtracted the first line from the last line within a symbolic programming environment, luckily my computer told me that the difference was always zero.

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }\Bigl (\frac{\sum _{REL_1REL_2}P(e_1|rel_1\overline{hyp})P(e_2|rel_2\overline{hyp})P(REL_1REL_2)}{\sum _{REL_1REL_2}P(e_1|rel_1{hyp})P(e_2|rel_2{hyp})P(REL_1REL_2)}\Bigr )\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }\Bigl (\frac{\epsilon _- ^2\rho ^{1+\delta }+2\epsilon _- \gamma (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })/2+\gamma ^2\bar{\rho }^{1+\delta }}{(1-\epsilon _+ )^2\rho ^{1+\delta }+2(1-\epsilon _+ )\alpha (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })/2+\alpha ^2\bar{\rho }^{1+\delta }}\Bigr )\Bigr )\\&\qquad \curvearrowright _{\text {calculating derivative}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\ln (\rho )\epsilon _- ^2\rho ^{1+\delta }+\epsilon _- \gamma (-\ln (\rho )\rho ^{1+\delta }-\ln (\bar{\rho })\bar{\rho }^{1+\delta })+\ln (\bar{\rho })\gamma ^2\bar{\rho }^{1+\delta }]\\&\qquad \cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }+2(1-\epsilon _+ )\alpha (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })/2+\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad -[\epsilon _- ^2\rho ^{1+\delta }+\epsilon _- \gamma (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })+\gamma ^2\bar{\rho }^{1+\delta }]\\&\qquad \cdot [\ln (\rho )(1-\epsilon _+ )^2\rho ^{1+\delta }+(1-\epsilon _+ )\alpha (-\ln (\rho )\rho ^{1+\delta }-\ln (\bar{\rho })\bar{\rho }^{1+\delta })+\ln (\bar{\rho })\alpha ^2\bar{\rho }^{1+\delta }]\Bigr )\\&\qquad \curvearrowright _{\text {expanding brackets}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\ln (\rho )\epsilon _- ^2\rho ^{1+\delta }]\cdot [(1-\epsilon _+ )\alpha (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })+\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad +[\epsilon _- \gamma (-\ln (\rho )\rho ^{1+\delta }-\ln (\bar{\rho })\bar{\rho }^{1+\delta })]\cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }+\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad +[\ln (\bar{\rho })\gamma ^2\bar{\rho }^{1+\delta }]\cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }+(1-\epsilon _+ )\alpha (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })]\\&\qquad -[\epsilon _- ^2\rho ^{1+\delta }]\cdot [(1-\epsilon _+ )\alpha (-\ln (\rho )\rho ^{1+\delta }-\ln (\bar{\rho })\bar{\rho }^{1+\delta })+\ln (\bar{\rho })\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad -[\epsilon _- \gamma (1-\rho ^{1+\delta }-\bar{\rho }^{1+\delta })]\cdot [\ln (\rho )(1-\epsilon _+ )^2\rho ^{1+\delta }+\ln (\bar{\rho })\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad -[\gamma ^2\bar{\rho }^{1+\delta }]\cdot [\ln (\rho )(1-\epsilon _+ )^2\rho ^{1+\delta }+(1-\epsilon _+ )\alpha (-\ln (\rho )\rho ^{1+\delta }-\ln (\bar{\rho })\bar{\rho }^{1+\delta })]\Bigr )\\&\quad \quad \quad \curvearrowright _{\text {move terms in line 4 to 1, 5 to 2 and 6 to 3}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- ^2\rho ^{1+\delta }]\cdot [(1-\epsilon _+ )\alpha (\ln (\rho )-\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}))+\alpha ^2\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})]\\&\qquad +[\gamma ^2\bar{\rho }^{1+\delta }]\cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }\ln (\frac{\bar{\rho }}{\rho })+(1-\epsilon _+ )\alpha (\ln (\bar{\rho })-\rho ^{1+\delta }\ln (\frac{\bar{\rho }}{\rho }))]\\&\qquad -[\epsilon _- \gamma (\ln (\rho )-\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}))]\cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }]\\&\qquad -[\epsilon _- \gamma (\ln (\bar{\rho })-\rho ^{1+\delta }\ln (\frac{\bar{\rho }}{\rho }))]\cdot [\alpha ^2\bar{\rho }^{1+\delta }]\Bigr )\curvearrowright _{\text {collecting terms with }\epsilon _- ^2\alpha ^2 \text {and} (1-\epsilon _+ )^2\gamma ^2}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- ^2\rho ^{1+\delta }]\cdot [(1-\epsilon _+ )\alpha (\ln (\rho )-\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}))]\\&\qquad +[\gamma ^2\bar{\rho }^{1+\delta }]\cdot [(1-\epsilon _+ )\alpha (\ln (\bar{\rho })-\rho ^{1+\delta }\ln (\frac{\bar{\rho }}{\rho }))]\\&\qquad -[\epsilon _- \gamma \ln (\rho )]\cdot [(1-\epsilon _+ )^2\rho ^{1+\delta }]-[\epsilon _- \gamma \ln (\bar{\rho })]\cdot [\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad +\rho ^{1+\delta }\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})[\epsilon _- ^2\alpha ^2-\gamma ^2(1-\epsilon _+ )^2+\epsilon _- \gamma (1-\epsilon _+ )^2-\epsilon _- \gamma \alpha ^2]\Bigr )\\&\qquad \curvearrowright _{\text {combining lines 1 and 2, 3 and 4,}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\alpha [\epsilon _- ^2\rho ^{1+\delta }[\ln (\rho )-\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})]+\gamma ^2\bar{\rho }^{1+\delta }[\ln (\bar{\rho })-\rho ^{1+\delta }\ln (\frac{\bar{\rho }}{\rho })]]\\&\qquad -[\epsilon _- \gamma ][\ln (\rho )(1-\epsilon _+ )^2\rho ^{1+\delta }+\ln (\bar{\rho })\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad +\rho ^{1+\delta }\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})[\epsilon _- \alpha ^2(\epsilon _- -\gamma )+\gamma (1-\epsilon _+ )^2(\epsilon _- -\gamma )]\Bigr )\\&\qquad \curvearrowright _{\text {shuffling terms in every line}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\alpha [[\epsilon _- ^2\rho ^{1+\delta }\ln (\rho )+\gamma ^2\bar{\rho }^{1+\delta }\ln (\bar{\rho })]+\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})[-\epsilon _- ^2+\gamma ^2]]\\&\qquad -[\epsilon _- \gamma ][\ln (\rho )(1-\epsilon _+ )^2\rho ^{1+\delta }+\ln (\bar{\rho })\alpha ^2\bar{\rho }^{1+\delta }]\\&\qquad +\rho ^{1+\delta }\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})[\epsilon _- \alpha ^2+\gamma (1-\epsilon _+ )^2](\epsilon _- -\gamma )\Bigr )\\&\qquad \curvearrowright _{\text {collect terms in lines 1 and 2 w.r.t.} \ln (\rho ),\ln (\bar{\rho })}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )[\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\\&\qquad +\alpha \gamma \ln (\bar{\rho })\bar{\rho }^{1+\delta }[\gamma (1-\epsilon _+ )-\alpha \epsilon _- ]\\&\qquad +(1-\epsilon _+ )\alpha \bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )(\epsilon _- +\gamma )\\&\qquad +\rho ^{1+\delta }\bar{\rho }^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})[\epsilon _- \alpha ^2+\gamma (1-\epsilon _+ )^2](\epsilon _- -\gamma )\Bigr )\\&\qquad \curvearrowright _{\text {collect terms in lines 3 and 4}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )[\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\\&\qquad +\alpha \gamma \ln (\bar{\rho })\bar{\rho }^{1+\delta }[\gamma (1-\epsilon _+ )-\alpha \epsilon _- ]\\&\qquad +\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )[(\epsilon _- +\gamma )(1-\epsilon _+ )\alpha -[\epsilon _- \alpha ^2+\gamma (1-\epsilon _+ )^2]]\Bigr )\\&\qquad \curvearrowright _{\text {shuffle terms in line 3}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )[\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\\&\qquad +\alpha \gamma \ln (\bar{\rho })\bar{\rho }^{1+\delta }[\gamma (1-\epsilon _+ )-\alpha \epsilon _- ]\\&\qquad +\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )[\gamma (1-\epsilon _+ )[\alpha -(1-\epsilon _+ )]-\alpha \epsilon _- [\alpha -(1-\epsilon _+ )]]\Bigr )\curvearrowright _{\text {simplify line 3}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )[\epsilon _- \alpha -\gamma (1-\epsilon _+ )]+\alpha \gamma \ln (\bar{\rho })\bar{\rho }^{1+\delta }\\&\qquad \cdot [\gamma (1-\epsilon _+ )-\alpha \epsilon _- ]+\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))[\gamma (1-\epsilon _+ )-\alpha \epsilon _- ]\Bigr )\curvearrowright _{\text {factor out}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\qquad -\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr ) . \end{aligned}$$

$\square$

Proposition 2

In case one is indifferent about the source being reliable, $\rho =\bar{\rho }=0.5$, the sign of derivative does not depend on $\delta$.

Proof

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )&=-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ )\epsilon _- \rho ^{1+\delta } \ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\quad -\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }}) (\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr )\\&=-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ )\epsilon _- -\alpha \gamma ]\Bigr ) . \end{aligned}$$

$\square$

Proposition 3

(VET Failure for Bovens and Hartmann for an exponential Degree of Independence)

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr ) ={{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\bar{a}[\ln (\rho )-\ln (\bar{\rho })]-a\ln (\bar{\rho })\Bigr ) . \end{aligned}$$

Proof

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )&=-{{\,\mathrm{sign}\,}}\Bigl ([\rho ^{1+\delta }\ln (\rho )[(1-\epsilon _+ )\epsilon _- -\bar{\rho }^{1+\delta }(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\\&\quad -\bar{\rho }^{1+\delta }\ln (\bar{\rho })[\alpha \gamma -\rho ^{1+\delta }(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]]\cdot [\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\Bigr )\\&={{\,\mathrm{sign}\,}}\Bigl ([\rho ^{1+\delta }\ln (\rho )[-\bar{\rho }^{1+\delta }a(a-1)]-\bar{\rho }^{1+\delta }\ln (\bar{\rho })[a^2-\rho ^{1+\delta }a(a-1)]]\cdot a\Bigr )\\&={{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\ln (\rho )\bar{\rho }^{1+\delta }\bar{a}-\bar{\rho }^{1+\delta }\ln (\bar{\rho })[a+\rho ^{1+\delta }\bar{a}]\Bigr )\\&={{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\ln (\rho )\bar{a}-\ln (\bar{\rho })[a+\rho ^{1+\delta }\bar{a}]\Bigr )\\&={{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\bar{a}(\ln (\rho )-\ln (\bar{\rho }))-\ln (\bar{\rho })a\Bigr ) . \end{aligned}$$

$\square$

Proposition 4

(VET Failure for Landes and Osimani for an exponential Degree of Independence) For $\alpha > rapprox 1-\epsilon _+ >0$ and $\gamma > rapprox \epsilon _- >0$, the VET holds for small $\rho$ and fails for large $\rho$. The smaller $\delta$, the smaller the area in which the VET holds.

Proof

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \delta }P(hyp|e_1e_2)\Bigr )&=-{{\,\mathrm{sign}\,}}\Bigl ([\epsilon _- \alpha -\gamma (1-\epsilon _+ )]\cdot [(1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\quad -\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr )\\&=-{{\,\mathrm{sign}\,}}\Bigl ((1-\epsilon _+ )\epsilon _- \rho ^{1+\delta }\ln (\rho )-\alpha \gamma \bar{\rho }^{1+\delta }\ln (\bar{\rho })\\&\quad -\bar{\rho }^{1+\delta }\rho ^{1+\delta }\ln (\frac{\rho }{\bar{\rho }})(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))\Bigr )\\&=-{{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\ln (\rho )[(1-\epsilon _+ )\epsilon _- -\bar{\rho }^{1+\delta }(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\\&\quad -\bar{\rho }^{1+\delta }\ln (\bar{\rho })[\alpha \gamma -(\gamma -\epsilon _- )(\alpha -(1-\epsilon _+ ))]\Bigr )\\&\approx -{{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\ln (\rho )[(1-\epsilon _+ )\epsilon _- ]-\bar{\rho }^{1+\delta }\ln (\bar{\rho })[\alpha \gamma ]\Bigr )\\&\approx -{{\,\mathrm{sign}\,}}\Bigl (\rho ^{1+\delta }\ln (\rho )-\bar{\rho }^{1+\delta }\ln (\bar{\rho })\Bigr )\\&=-{{\,\mathrm{sign}\,}}\Bigl ([\frac{\rho }{\bar{\rho }}]^{1+\delta }-\ln (\frac{\bar{\rho }}{\rho })\Bigr )\\&={{\,\mathrm{sign}\,}}\Bigl (\ln (\frac{\bar{\rho }}{\rho })-[\frac{\rho }{\bar{\rho }}]^{1+\delta }\Bigr ) . \end{aligned}$$

$\square$

Proposition 5

P1, P3 and P4 are jointly inconsistent.

Proof

P1, P3 and P4 jointly entail the following constraints for all $\rho ,\delta \in [0,1]$

$$ \begin{aligned} \rho -\rho ^{1+\delta }{\mathop {=}\limits ^{P1 \& P4}}\omega _{r\bar{r}}{\mathop {=}\limits ^{P3}}\omega _{\bar{r}r}{\mathop {=}\limits ^{P1 \& P4}}\bar{\rho }-\bar{\rho }^{1+\delta } . \end{aligned}$$

This however forces that $\rho -\rho ^{1+\delta }=(1-\rho )-(1-\rho )^{1+\delta }$ must hold. The left hand side monotonically increases in $\rho$ while the right hand side monotonically decreases in $\rho$. Hence, the equation cannot be satisfied for all $\rho ,\delta \in [0,1]$. $\square$

Proposition 6

R1’, R3 and R4 are mutually consistent. Furthermore, they jointly entail R2 and

$$\begin{aligned} \omega _{rh}=\omega _{hr}=\lambda \alpha \rho \bar{\rho }\quad \quad \quad \omega _{r\bar{h}}=\omega _{\bar{h}r}=\lambda \bar{\alpha }\rho \bar{\rho }\quad \quad \quad \omega _{\bar{r}\bar{h}}=\omega _{\bar{h}\bar{r}}=\lambda \bar{\rho }^2\alpha \bar{\alpha }. \end{aligned}$$

Proof

We need to solve three linear Eq. 1 for the variables $\omega _{rh},\omega _{r\bar{h}},\omega _{\bar{h}\bar{h}}$. It is easy to check that the claimed expressions satisfy R1’, R3 and R4. The equation also admit only the claimed expressions, as I shall now show.

$$\begin{aligned} \rho +\lambda (\rho ^2-\rho )+\omega _{rh}+\omega _{r\bar{h}}&=\rho \\ \omega _{rh}+\bar{\rho }\alpha +\lambda ((\bar{\rho }\alpha )^2-{(\bar{\rho }\alpha )})+\omega _{\bar{r}\bar{h}}&=\bar{\rho }\alpha \\ \omega _{r\bar{h}}+\omega _{\bar{r}\bar{h}}+\bar{\rho }\bar{\alpha }+\lambda ((\bar{\rho }\bar{\alpha })^2-{(\bar{\rho }\bar{\alpha })})&=\bar{\rho }\bar{\alpha }. \end{aligned}$$

Inserting the first equality into the second gives

$$\begin{aligned} -\omega _{r\bar{h}}-\lambda (\rho ^2-\rho )+\lambda ((\bar{\rho }\alpha )^2-{(\bar{\rho }\alpha )})+\omega _{\bar{r}\bar{h}}=0 . \end{aligned}$$

Adding the third equality to this gives the following set of logically equivalent equations

$$\begin{aligned} -\lambda (\rho ^2-\rho )+\lambda ((\bar{\rho }\alpha )^2-{(\bar{\rho }\alpha )})+2\omega _{\bar{r}\bar{h}}+\lambda ((\bar{\rho }\bar{\alpha })^2-{(\bar{\rho }\bar{\alpha })}&=0&\curvearrowright _{\lambda \bar{\rho }\alpha +\lambda \bar{\rho }\bar{\alpha }=\lambda \bar{\rho }}\\ \lambda \cdot (\rho (\rho -1)-(\bar{\rho }\alpha )^2-(\bar{\rho }\bar{\alpha })^2+\bar{\rho })&=2\omega _{\bar{r}\bar{h}}&\\ \lambda \cdot (-\rho \bar{\rho }-\bar{\rho }^2[\alpha ^2-\bar{\alpha }^2]+\bar{\rho })&=2\omega _{\bar{r}\bar{h}}&\curvearrowright _{-\rho \bar{\rho }+\bar{\rho }=\bar{\rho }^2}\\ \lambda \bar{\rho }^2\cdot (1-[\alpha ^2-(1-\alpha )^2])&=2\omega _{\bar{r}\bar{h}}&\\ \lambda \bar{\rho }^2\cdot (-2\alpha ^2+2\alpha )&=2\omega _{\bar{r}\bar{h}}&\\ \lambda \bar{\rho }^2\alpha \cdot (-\alpha +1)&=\omega _{\bar{r}\bar{h}}&\\ \lambda \bar{\rho }^2\alpha \bar{\alpha }&=\omega _{\bar{r}\bar{h}} . \end{aligned}$$

Inserting this into the third equality gives

$$\begin{aligned} \omega _{r\bar{h}}+\lambda \bar{\rho }^2\alpha \bar{\alpha }+\lambda ((\bar{\rho }\bar{\alpha })^2-{(\bar{\rho }\bar{\alpha })})&=0&\\ -\lambda \bar{\rho }\bar{\alpha }\cdot [\bar{\rho }\alpha +\bar{\rho }\bar{\alpha }-1]&=\omega _{r\bar{h}}&\curvearrowright _{\bar{\rho }\alpha +\bar{\rho }\bar{\alpha }-1=-\rho }\\ \lambda \rho \bar{\rho }\bar{\alpha }&=\omega _{r\bar{h}} .&\end{aligned}$$

Inserting this into the first equation we find $\omega _{rh}=\lambda \alpha \rho \bar{\rho }$.

R2 follows from the simple observation that all values sum to one, as they ought to. $\square$

Proposition 7

(No VET failures in Claveau’s model for Linear Degree) Ceteris paribus, for all $\rho ,\alpha ,\lambda ,P(hyp)\in (0,1)$ it holds that

$$\begin{aligned} \frac{\partial P(hyp|e_1e_2)}{\partial \lambda }>0. \end{aligned}$$

Proof

Following (Claveau 2013, p. 116):

$$\begin{aligned} \frac{\partial P(hyp|e_1e_2)}{\partial \lambda }>0\text {, if and only if }\frac{\partial \frac{\omega _{hh}}{\omega _{rr}+2\omega _{rh}+\omega _{hh}}}{\partial \lambda }<0 . \end{aligned}$$

After taking the derivative, the denominator on the right hand side is always positive. I hence ignore it for the remainder of this proof. Denoting by $'$ the partial derivative with respect to $\lambda$, one finds

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial \frac{\omega _{hh}}{\omega _{rr}+2\omega _{rh}+\omega _{hh}}}{\partial \lambda }\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (\omega _{hh}'[\omega _{rr}+2\omega _{rh}+\omega _{hh}]-\omega _{hh}[\omega _{rr}+2\omega _{rh}+\omega _{hh}]'\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (\omega _{hh}'[\omega _{rr}+2\omega _{rh}]-\omega _{hh}[\omega _{rr}+2\omega _{rh}]'\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl ([(\bar{\rho }\alpha )^2-\bar{\rho }\alpha ]\cdot [\rho +\lambda (\rho ^2-\rho )+2\lambda \alpha \rho \bar{\rho }]\\&\quad \quad -[\bar{\rho }\alpha +\lambda ((\bar{\rho }\alpha )^2-\bar{\rho }\alpha )]\cdot [\rho ^2-\rho +2\alpha \bar{\rho }\rho ]\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl ([(\bar{\rho }\alpha )^2-\bar{\rho }\alpha ]\cdot [\rho +\lambda (\rho ^2-\rho )]\\&\quad \quad -[\bar{\rho }\alpha +\lambda ((\bar{\rho }\alpha )^2-\bar{\rho }\alpha )]\cdot [\rho ^2-\rho ]-2\alpha ^2\bar{\rho }^2\rho \Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl ([(\bar{\rho }\alpha )^2-\bar{\rho }\alpha ]\rho -[\bar{\rho }\alpha ]\cdot [\rho ^2-\rho ]-2\alpha ^2\bar{\rho }^2\rho \Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (-[\bar{\rho }\alpha ]\rho ^2-\alpha ^2\bar{\rho }^2\rho \Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (-\rho \bar{\rho }\alpha (\rho +\alpha \bar{\rho })\Bigr ) . \end{aligned}$$

This sign is negative. $\square$

Proposition 9

(VET Failure for Linear Degree of Independence)

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr ) ={{\,\mathrm{sign}\,}}\Bigl (\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr )\cdot \\&\quad (\rho \cdot [\epsilon _- [(1-\epsilon _+ )-\alpha ]+(1-\epsilon _+ )[\epsilon _- -\gamma ]]+\bar{\rho }\cdot [\gamma ((1-\epsilon _+ )-\alpha )+\alpha (\epsilon _- -\gamma )])\Bigr ). \end{aligned}$$

Proof

$$\begin{aligned} P(hyp|e_1e_2)=&\frac{P(hype_1e_2)}{P(e_1e_2)}\\ =&\frac{\sum _{REL_1REL_2}P(hype_1e_2REL_1REL_2)}{\sum _{HYP}\sum _{REL_1,REL_2}P(HYPe_1e_2REL_1REL_2)}\\ =&\frac{1}{1+\frac{\sum _{REL_1,REL_2}P(\overline{hyp}e_1e_2REL_1REL_2)}{\sum _{REL_1REL_2}P(hype_1e_2REL_1REL_2)}}\\ =&\frac{1}{1+\frac{h}{\bar{h}}\frac{\sum _{REL_1REL_2}P(e_1|rel_1\overline{hyp})P(e_2|rel_2\overline{hyp})P(REL_1REL_2)}{\sum _{REL_1REL_2}P(e_1|rel_1{hyp})P(e_2|rel_2{hyp})P(REL_1REL_2)}}. \end{aligned}$$

Using that $\rho +\lambda (\rho ^2-\rho )=\rho ^2+\bar{\lambda }\rho \bar{\rho }$ and that $\bar{\rho }+\lambda (\bar{\rho }^2-\bar{\rho })=\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho }$, I embark on a long calculation.

$$\begin{aligned}&{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }\Bigl (\frac{\sum _{REL_1REL_2}P(e_1|rel_1\overline{hyp})P(e_2|rel_2\overline{hyp})P(REL_1REL_2)}{\sum _{REL_1REL_2}P(e_1|rel_1{hyp})P(e_2|rel_2{hyp})P(REL_1REL_2)}\Bigr )\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }\Bigl (\frac{\epsilon _- ^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2\epsilon _- \gamma \lambda \rho \bar{\rho }+\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })}{(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })}\Bigr )\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2\rho \bar{\rho }+2\epsilon _- \gamma \rho \bar{\rho }-\gamma ^2\rho \bar{\rho }]\\&\quad \quad \quad \cdot [(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\qquad -[\epsilon _- ^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2\epsilon _- \gamma \lambda \rho \bar{\rho }+\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\quad \quad \quad \cdot [-(1-\epsilon _+ )^2\rho \bar{\rho }+2(1-\epsilon _+ )\alpha \rho \bar{\rho }-\alpha ^2\rho \bar{\rho }]\Bigr ) \curvearrowright _{\rho \bar{\rho }>0}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2+2\epsilon _- \gamma -\gamma ^2]\\&\quad \quad \quad \cdot [(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\qquad -[\epsilon _- ^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2\epsilon _- \gamma \lambda \rho \bar{\rho }+\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\quad \quad \quad \cdot [-(1-\epsilon _+ )^2+2(1-\epsilon _+ )\alpha -\alpha ^2]\Bigr )\curvearrowright _{\text {cancelling of terms}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2]\cdot [2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\qquad +[2\epsilon _- \gamma ]\cdot [(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\qquad +[-\gamma ^2]\cdot [(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }]\\&\qquad -[2\epsilon _- \gamma \lambda \rho \bar{\rho }+\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\cdot [-(1-\epsilon _+ )^2]\\&\qquad -[\epsilon _- ^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\cdot [2(1-\epsilon _+ )\alpha ]\\&\qquad -[\epsilon _- ^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+2\epsilon _- \gamma \lambda \rho \bar{\rho }]\cdot [-\alpha ^2]\Bigr )\\&\qquad \curvearrowright _{\text {move terms in line 5 to 1, cancelling terms in line 1-6 and 3-4 }}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2]\cdot [2(1-\epsilon _+ )\alpha (\lambda \rho \bar{\rho }+\bar{\lambda }\rho \bar{\rho }+\rho ^2)+\alpha ^2(\bar{\rho }^2-\rho ^2)]\\&\qquad +[2\epsilon _- \gamma ]\cdot [(1-\epsilon _+ )^2(\rho ^2+\bar{\lambda }\rho \bar{\rho })+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\\&\qquad +[-\gamma ^2]\cdot [(1-\epsilon _+ )^2(\rho ^2-\bar{\rho }^2)+2(1-\epsilon _+ )\alpha \lambda \rho \bar{\rho }]\\&\qquad -[2\epsilon _- \gamma \lambda \rho \bar{\rho }]\cdot [-(1-\epsilon _+ )^2]\\&\qquad -[\gamma ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho })]\cdot [2(1-\epsilon _+ )\alpha ]\\&\qquad -[2\epsilon _- \gamma \lambda \rho \bar{\rho }]\cdot [-\alpha ^2]\Bigr )\curvearrowright _{\text {move terms in line 4 to 2 and 6 to 2, cancelling terms in line 3-5}}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2]\cdot [2(1-\epsilon _+ )\alpha (\lambda \rho \bar{\rho }+\bar{\lambda }\rho \bar{\rho }+\rho ^2)+\alpha ^2(\bar{\rho }^2-\rho ^2)]\\&\qquad +[2\epsilon _- \gamma ]\cdot [(1-\epsilon _+ )^2(\rho ^2+(\lambda +\bar{\lambda })\rho \bar{\rho })+\alpha ^2(\bar{\rho }^2+\bar{\lambda }\rho \bar{\rho }+\lambda \rho \bar{\rho })]\\&\qquad +[-\gamma ^2]\cdot [(1-\epsilon _+ )^2(\rho ^2-\bar{\rho }^2)]\\&\qquad -[\gamma ^2(\bar{\rho }^2+(\lambda +\bar{\lambda })\rho \bar{\rho })]\cdot [2(1-\epsilon _+ )\alpha ]\Bigr )\curvearrowright _{\text {simplify, using }x+\bar{x}=1}\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl ([-\epsilon _- ^2]\cdot [2(1-\epsilon _+ )\alpha \rho +\alpha ^2(1-2\rho )]+[2\epsilon _- \gamma ]\cdot [(1-\epsilon _+ )^2\rho +\alpha ^2\bar{\rho }]\\&\qquad +[-\gamma ^2]\cdot [(1-\epsilon _+ )^2(2\rho -1)]-[\gamma ^2\bar{\rho }]\cdot [2(1-\epsilon _+ )\alpha ]\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (2\rho (1-\epsilon _+ )\epsilon _- (\gamma (1-\epsilon _+ )-\alpha \epsilon _- )-2\bar{\rho }\alpha \gamma (\gamma (1-\epsilon _+ )-\alpha \epsilon _- )\\&\qquad +(2\rho -1)(\alpha ^2\epsilon _- ^2-\gamma ^2(1-\epsilon _+ )^2)\Bigr )\\&\quad =-{{\,\mathrm{sign}\,}}\Bigl (2\rho (1-\epsilon _+ )\epsilon _- (\gamma (1-\epsilon _+ )-\alpha \epsilon _- )-2\bar{\rho }\alpha \gamma (\gamma (1-\epsilon _+ )-\alpha \epsilon _- )\\&\qquad +(2\rho -1)(\alpha \epsilon _- -\gamma (1-\epsilon _+ ))(\alpha \epsilon _- +\gamma (1-\epsilon _+ ))\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl ([\alpha \epsilon _- -\gamma (1-\epsilon _+ )]\cdot [2\rho (1-\epsilon _+ )\epsilon _- -2\bar{\rho }\alpha \gamma -(2\rho -1)(\alpha \epsilon _- +\gamma (1-\epsilon _+ )]\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl ([\alpha \epsilon _- -\gamma (1-\epsilon _+ )]\cdot [2\rho (1-\epsilon _+ )\epsilon _- -2\bar{\rho }\alpha \gamma -(\rho -\bar{\rho })(\alpha \epsilon _- +\gamma (1-\epsilon _+ )]\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr )\cdot \Bigl (\rho \cdot [2(1-\epsilon _+ )\epsilon _- -\alpha \epsilon _- -\gamma (1-\epsilon _+ )]\\&\quad -\bar{\rho }\cdot [2\alpha \gamma -\alpha \epsilon _- -\gamma (1-\epsilon _+ )]\Bigr )\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr )\cdot \Bigl (\rho \cdot [\epsilon _- [(1-\epsilon _+ )-\alpha ]+(1-\epsilon _+ )[\epsilon _- -\gamma ]]\\&\quad -\bar{\rho }\cdot [\alpha (\gamma -\epsilon _- )+\gamma (\alpha -(1-\epsilon _+ ))]\Bigr )\Bigr )\\&\quad ={{\,\mathrm{sign}\,}}\Bigl (\Bigl (\alpha \epsilon _- -\gamma (1-\epsilon _+ )\Bigr )\cdot \\&\quad (\rho \cdot [\epsilon _- [(1-\epsilon _+ )-\alpha ]+(1-\epsilon _+ )[\epsilon _- -\gamma ]]+\bar{\rho }\cdot [\gamma ((1-\epsilon _+ )-\alpha )+\alpha (\epsilon _- -\gamma )])\Bigr ) . \end{aligned}$$

$\square$

Proposition 10

(VET Failure for Bovens and Hartmann for Linear Degree of Independence)

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr )={{\,\mathrm{sign}\,}}\Bigl (1-2\bar{a}\bar{\rho }\Bigr ) . \end{aligned}$$

Proof

Since $\epsilon _+ =\epsilon _- =0$ and $\alpha =\gamma =a$, I obtain

$$\begin{aligned} {{\,\mathrm{sign}\,}}\Bigl (\frac{\partial }{\partial \lambda }P(hyp|e_1e_2)\Bigr ) =&{{\,\mathrm{sign}\,}}\Bigl ((-a)\cdot [-\rho a-\bar{\rho }(a^2+a(a-1))]\Bigr )\\ =&-{{\,\mathrm{sign}\,}}\Bigl (-\rho -\bar{\rho }(a+(a-1))]\Bigr )\\ =&-{{\,\mathrm{sign}\,}}\Bigl (-(1-\bar{\rho }) -\bar{\rho }(1-\bar{a}-\bar{a})]\Bigr )\\ =&{{\,\mathrm{sign}\,}}\Bigl (1-2\bar{a}\bar{\rho }\Bigr ) . \end{aligned}$$

$\square$

Proposition 12

For reliability variables of arity 4 and greater, neither the linear nor the exponential axioms are strong enough to uniquely determine a one-parameter curve along which independence increases.

Proof

Denote the arity of the reliability variable by $ar\ge 4$ and $\varrho _i$ for the prior probability of REL being equal to the i-th value. There are $(ar-1)ar/2$-many unknown $\omega _{jk}$ and ar-many equalities of the form $\sum _{k}\omega _{jk}=\rho _j$. Since $(ar-1)ar/2>ar+1>ar$, there are strictly more unknowns, than there are constraints. $\square$

Note that this proposition does not make a claim about the satisfiability of axioms.