Abstract
David Lewis’s counterpart theory (CT) is often seen as involving a radical departure from the standard, Kripke-style semantics for modal logic (ML), suggesting that we are dealing with deeply divergent accounts of our modal talk. However, CT captures but one version of the relevant semantic intuition, and does so on the basis of metaphysical assumptions (all worlds are equally real, individuals are world-bound) that are ostensibly discretionary. Just as ML can be translated into a language that quantifies explicitly over worlds, CT may be formulated as a semantic theory in which world quantification is purely metalinguistic. And just as Kripke-style semantics is formally compatible with the doctrine of world-boundedness, a counterpart-based semantics may in principle allow for cases of trans-world identity. In fact, one may welcome a framework that is general enough to include both Lewis’s counterpart-based account and Kripke’s identity-based account as distinguished special cases. There are several ways of doing so. The purpose of this paper is to outline a fully general option and to illustrate its philosophical significance, showing how the large variety of intermediate relations that lie between Lewisian counterparthood and Kripkean identity yield a corresponding variety of modal theories that would otherwise remain uncharted.
Similar content being viewed by others
1 Introduction
David Lewis’s Counterpart Theory (CT) is naturally seen as a bold alternative to the standard analysis of our modal discourse—a “rival way”, in Lewis’s own words (1968, p. 114).Footnote 1 According to CT, when we engage in de re modal discourse about a particular individual, say Hubert Humphrey, we do not speculate about how Humphrey himself is at other possible worlds. Rather, we speculate about Humphrey’s other-wordly counterparts. A statement such as ‘Humphrey might have won the presidential election’ would be true, not because there is a possible world at which Humphrey wins the election, but because there is a counterpart of Humphrey’s, in some possible world, who wins.
There are indeed two respects in which this account departs crucially from the standard one. The first is that the counterpart relation falls short of identity. Someone other than Humphrey enters into the story of how it is that Humphrey might have won the election. Saul Kripke famously complained that this is bizarre: “Probably, Humphrey could not care less whether someone else, no matter how much resembling him, would have been victorious in another possible world” (1972, p.344, n.13).Footnote 2 So be it, says Lewis; the fact remains that the someone else is one of Humphrey’s counterparts. “Thanks to the victorious counterpart, Humphrey himself has the requisite modal property: we can truly say that he might have won” (1986, p.196). The second point of departure is that CT takes all talk of possible worlds strictly and literally. On the standard, Kripke-style account, possible worlds only enter the picture (if at all) in the semantic metalanguage; the object language is intensional and modalities are expressed by means of sentential operators. CT is formulated instead in the extensional language of classical elementary logic and, hence, includes explicit commitment to modal realism: “The domain of quantification is to contain every possible world and everything in every world” (1968, p.114).Footnote 3 This is CT’s official cost. But for Lewis it is also its main selling point. CT does not require that we go beyond “our all-purpose extensional logic” (p.113). So long as our domain of quantification is “suited to the subject matter” (ibid.), we can hold to elementary logic to conduct formalized discourse about modality just as we do when our topic is mereology, sets, numbers, strings of symbols, or whatnot.
Both points of departure play a chief role in Lewis’s original formulation of CT. However, by now there is general agreement that CT captures but one version of the fundamental intuition on which it rests, and that the metaphysical assumptions it embodies are formally inessential. One can preserve the spirit of CT while forgoing the letter.
For one thing, nothing really prevents a counterpart-based account of modal discourse from allowing for genuine cases of trans-world identity. Lewis was adamant that “things in different worlds are never identical” (1968, p.114), and later argued extensively against the idea that worlds may “overlap” (1986, §4.2). However, his reasons were entirely philosophical, and he himself acknowledged from the start that, formally, “it would not matter if some things were identical with their counterparts after all”; the world-boundedness postulate of CT “serves only to rule out avoidable problems of individuation” (1968, n.2). Thus, from a formal perspective,Footnote 4 the first point of departure is inessential to the idea that our modal discourse should be explained in terms of counterparts. One may see CT and the standard account as two species of the same genus, corresponding to the limit cases where no things are identical with their other-wordly counterparts or all things are, respectively.
On the other hand, explicit world quantification in the object language is itself neither exclusive nor necessary to the counterpart approach. It isn’t exclusive for the obvious reason that we can accept modal realism and translate intensional modal logic into extensional elementary logic without bringing in counterparts; plain identity would work just as fine. (The temporal analogue is familiar enough. One can subscribe to the reality of time and still be free to choose between a counterpart-based account of persistence—the so-called stage view—or an identity-based account—endurantism.Footnote 5) But, more importantly, there is a sense in which explicit world quantification is not necessary to the counterpart approach, either. It isn’t necessary insofar as the main idea of CT can be recovered and formulated in pure semantic terms, consigning all world quantification to the metalanguage exactly as in the standard account. In this regard, Lewis himself was less open, and he would never speak of CT as a semantic theory.Footnote 6 Yet the idea of extracting a possible-world semantics from CT is at least as old as Hazen (1979) and the phrase “counterpart-theoretic semantics” has since become popular. And once we have a counterpart-theoretic semantics, where possible worlds may be treated standardly as mere indices or points of evaluation, the second point of departure appears to vanish, too.Footnote 7 One may still object that metalinguistic quantification is quantification nonetheless, so that semantic ascent would deliver no real gain in terms of ontological costs. As Barwise and Perry put it, “A semantical theory is committed to the reality of the entities it uses in its explanations. [...] Saying possible worlds are ‘just indices’ is not a responsible theory” (1985, p.116).Footnote 8 Yet this worry applies to any sort of “possible-world semantics”. The present point is simply that a counterpart-based account would be no special in this regard. Indeed, one should welcome a semantic framework where, again, the standard identity-based account and its counterpart-based alternative may be seen as two species of the same genus, two distinguished special cases of an otherwise uniform semantic framework.
My purpose, in the following, is to explore the full potential of the above remarks, particularly with reference to the second point: modal realism, in the sense of explicit commitment to first-order quantification over worlds, is neither exclusive nor necessary to a counterpart-based account of modality. I shall deal with the two sides of this point in Sects. 2–5. The remainder of the paper will then be devoted to comparisons and developments, with special attention to a number of modal principles whose controversial status in CT has attracted special attention in the critical literature. In the end, my hope is to evidence that a counterpart-based approach to the analysis of modality is, not only less distant from the standard account than CT might suggest, but also more comprehensive and extremely powerful for the study of a large variety of modal logics that would otherwise remain uncharted. As a militant philosopher, Lewis would not care much. [(“It is the substantive theory, not the metalogic, for which we need possible worlds”; (1986, p.20)]. For the rest of us, it may nonetheless serve as a further illustration, if such were needed, of the huge potential of Lewis’s legacy, regardless of how one feels about the full metaphysical package with which it was delivered.
2 Modal realism with identity
Let us begin with the claim that modal realism, in the relevant sense, is not exclusive to counterpart theory; it is perfectly compatible with the standard, identity-based account. I said that this part of the story is obvious, but spelling out the details is worth the while and will pave the way to the second, less obvious part.
There are many ways of substantiating the claim. The one I hinted at is by means of an algorithm for embedding intensional Modal Logic (ML) into extensional Elementary Logic (EL) of the sort familiar from so-called correspondence theory (van Benthem 2001): just translate the modal operators as explicit quantifiers over worlds and increase the arity of each non-logical predicate to make room for an additional world-relative parameter.
Here is a more precise description of the algorithm for our present purposes.Footnote 9 Let \(L_{M}\) be the language of quantified ML (with equality and, say, \(\lnot \), \(\rightarrow \), \(\forall ,\) and \(\Box \) as logical primitives) and let \(L_{E}\) be the EL language obtained from \(L_{M}\) by deleting the modal connective (\(\Box \)) and adding instead a distinguished individual constant, \(\alpha \) (read: ‘the actual world’), a unary predicate, W (read: ‘is a possible world’), and two binary predicates, E (read: ‘exists at’) and R (read: ‘has access to’).Footnote 10 The intended reading of these non-logical primitives is governed by the following conditions:
- (1):
-
- (a):
-
\(W\alpha \)
- (b):
-
\(Exy \rightarrow Wy\)
- (c):
-
\(Rxy \rightarrow (Wx \wedge Wy)\)
Moreover, with the exception of the equality predicate \(\approx \), let every n-place predicate P of \(L_{M}\) count as an \(n + 1\)-place predicate in \(L_{E}\), subject to the following conditions:
- (2):
-
- (a):
-
\(Pt_1 \dots t_nt \rightarrow Wt \)
- (b):
-
\(Pt_1 \dots t_nt \rightarrow \exists x_1 \dots \exists x_n(Et_1x_1{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Et_nx_n)\)
Finally, for every \(L_{M}\)-formula \(\phi \) and every \(L_{E}\)-term t, define a corresponding \(L_{E}\)-formula \(\phi ^t\) (read: ‘\(\phi \) holds at t’) by recursion:
- (3):
-
- (a):
-
\(Pt_1 \dots t_n^{ ~ ~t} = Pt_1 \dots t_nt\)
- (b):
-
\(t_1 \approx t_2^{ ~ ~t} = t_1 \approx t_2\)
- (c):
-
\((\lnot \psi )^t = \lnot \psi ^t\)
- (d):
-
\((\psi \rightarrow \xi )^t = \psi ^t \rightarrow \xi ^t\)
- (e):
-
\((\forall x\psi )^t = \forall x(Ext \rightarrow \psi ^t)\)
- (f):
-
\((\Box \psi )^t = \forall x(Rtx \rightarrow \psi ^x)\)
(where in the last clause we may take x to be alphabetically the first individual variable not occurring in \(\psi \)). Then the desired embedding is obtained by translating every \(L_{M}\)-formula \(\phi \) in accordance with the following schema:
- (4):
-
\(\tau (\phi ) = \phi ^{\alpha }\)
For example, if Ph is the atomic \(L_{M}\)-formula for the sentence ‘Humphrey wins the presidential election’, then its \(L_{E}\)-translation will be \(Ph\alpha \), i.e., intuitively, ‘Humphrey wins presidential the election at the actual world’; the modal formula \(\Box Ph\) (‘Humphrey necessarily wins the election’) will be translated as \(\forall x(R\alpha x \rightarrow Phx)\) (‘Humphrey wins the election at every accessible world’); and so on.
It’s clear that this translation requires a modal realist stance: on the intended interpretation, all \(L_{M}\)-formulas result in \(L_{E}\)-formulas that involve explicit reference to or quantification over worlds. The adequacy of the translation lies precisely in the fact that, given (1) and (2), \(\tau (\phi )\) always reflects the truth conditions of \(\phi \) in the standard (Kripke-style) possible-world semantics. This is why the embedding forms the basis of correspondence theory: adding specific axioms on the accessibility relation R will yield EL theories matching specific ML systems.Footnote 11 At the same time, it’s clear that the embedding is not counterpart-theoretic, for the standard (Tarski-style) truth conditions of \(\tau (\phi )\) will always rest on interpreting the singular terms occurring in \(\phi \) once and for all. It’s just that all predications are relativized to worlds. The referent of ‘Humphrey’ will be a certain individual that may be victorious at a world x while not being victorious at another world y, and modal claims about Humphrey become quantified claims about such relational facts concerning him, that one self-same individual.
Other options are available, too. Given (1) and (2), the algorithm defined by (3) and (4) reflects the so-called “standard translation” (van Benthem 1983), but there is room for variations. For instance, one may hold that in order for an atomic formula to hold at a given world, the individuals mentioned in the formula must exist at that world (the so-called “falsity principle”; Fine 1981, §3). To capture this view, one may strengthen condition (2)(b) accordingly:
- (2):
-
- (b\('\)):
-
\(Pt_1 \dots t_nt \rightarrow (Et_1t{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Et_nt)\)
Alternatively, one may capture the view directly by strengthening the first translation clause in (3):
- (3):
-
- (a\('\)):
-
\(Pt_1 \dots t_n^{ ~ ~t} = Pt_1 \dots t_{n}t{\tiny ~}\wedge {\tiny ~}Et_{1}t{\tiny ~}\wedge {\tiny ~}\dots {\tiny ~}\wedge {\tiny ~}Et_{n}t\)
and perhaps the second clause, too:
- (3):
-
- (b\('\)):
-
\(t_1 \approx t_2^{ ~ ~t} = t_1 \approx t_2{\tiny ~}\wedge {\tiny ~}Et_{1}t{\tiny ~}\wedge {\tiny ~}Et_{2}t\)
Moreover, one might hold that, say, in order for it to be the case that Humphrey is necessarily a winner it is not required that Humphrey be victorious at every accessible world, as per (3)(f), but only that he be victorious at every accessible world at which he exists (so-called “weak necessity”; Kripke 1971, p. 137). To express this view generally, the last clause in (3) may be reformulated as follows, where \(t_1\), ..., \(t_n\) are all the terms occurring free in \(\psi \) other than t:
- (3):
-
- (f \('\)):
-
\((\Box \psi )^t = \forall x((Rtx \wedge Et_{1}x{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Et_{n}x) \rightarrow \psi ^x)\)
Such plurality of options is telling. It reminds us that modal talk is no straightforward business; we need to make choices. However, from the present perspective that is beyond the point. What matters is the nature of the options, which is the same in each case: one can easily endorse modal realism and embed ML into EL without going counterpart-theoretic.
3 Counterpart semantics
Less obvious is the converse claim: one can favor a counterpart-based account of modality without endorsing modal realism. One option, in this regard, would be to try and construe counterparts as abstract entities of some sort—e.g., as maximally consistent sets of complex predicates of an ersatz world-making language.Footnote 12 Unfortunately this option faces several difficulties, which have led some critics to conclude that counterparts sine modal realism is not a viable option.Footnote 13 As I said, however, here I am interested in a different approach. I am interested in the possibility of eluding explicit commitment to modal realism by consigning all world quantification to the semantic metalanguage. More precisely, I am interested in the idea that a counterpart-based account of our modal talk can be fully articulated, not as a first-order theory in the extensional language of EL, as in Lewis’s CT, but as a formal semantics for the intensional language of ML. We saw that it is controversial whether metalinguistic quantification over possible worlds may truly be claimed to carry no realist commitment, but never mind; the worry applies already to the standard, Kripke-style semantics for ML. The point is rather that a counterpart-based alternative would be no worse off. To the extent that the former does, or does not, “seriously commit one to Ludovician polycosmology” (in the words of Burgess 2011, p.127), so would the latter.
As I mentioned, the idea of trading CT for a semantic theory is by itself rather old. It may be found already in Hazen (1979) and has been explored extensively by several authors, from Forbes (1985, §3.4) to Stalnaker (1987, 1995) to Hazen (2012) himself and others. There are even textbook treatments where counterpart theory is introduced from the start as an alternative semantics for ML, beginning with Hughes and Cresswell (1996, pp. 353ff). Thus, in a way we could stop here. However, such treatments tend to be rather idiosyncratic, often involving significant departures from the standard Kripke-style machinery and, hence, reinforcing the thought that we are still dealing with two radically competing accounts. For example, Hughes and Cresswell’s treatment requires that counterparthood be either handled in terms of intensional objects or else built ad hoc into the truth conditions for modal formulas. That is fine, but somewhat disturbing. We want to say that the choice between trans-world identity and counterparthood is strictly metaphysical. It does result in different semantic accounts of our modal talk; but this difference would be better appreciated if assessed within a common framework—a semantic framework that is structurally neutral with regard to the relevant metaphysics and general enough to include both Kripke’s identity-theoretic account and Lewis’s counterpart-theoretic alternative as distinguished, philosophically motivated special cases. More to the point, only a general semantic framework of this sort can vindicate the claim that the two accounts are ultimately on equal footing with regard to the issue of modal realism.
A good example of what I have in mind is the semantic framework recently proposed by Bacon (2014), whose “counterpart structures” are essentially Kripke structures with variable domains enriched with a reflexive but otherwise unrestricted counterpart relation defined across worlds. As Bacon notes, such structures are “compatible with the same metaphysical hypotheses the Kripke structures can be used to model” (p. 100), including, if one wishes, genuine trans-world identity. Earlier examples may also be found in (1998, pp. 60ff) and in the detailed treatments put forward by Corsi (2001, (2002), Kracht and Kutz (2002a, (2005b, (2007), and Schwarz (2012, (2013).Footnote 14 While these theories vary in generality and matters of detail, they all share to some degree the important feature stressed by Bacon with regard to metaphysical neutrality, encompassing both Lewisean and Kripkean accounts of modality as different species of the same genus. In the remainder of the paper I want to take a closer look at precisely this sort of approach, outlining a framework that is as general as possible and briefly exploring its potential vis-á-vis the desiderata mentioned above.
4 Neutral embeddings
To this end, it will prove useful to go back for a moment to our first point, to the effect that a standard, identity-based account is no less compatible with modal realism than its competitor.
As things stand, there is of course a significant structural divergence between the extensional embedding of ML supported by Lewis’s CT and the standard embeddings delivered by the algorithms of Sect. 2. The two are on a par with regard to modal realism, but differ precisely insofar as one is counterpart-based whereas the other is identity-based. Thus, the extensional language of Lewis’s embedding is not \(L_E\). It is a language, call it \(L_C\), that differs from \(L_E\) in two crucial ways: it contains an additional binary primitive, C (for ‘is a counterpart of’), and its non-logical predicates are exactly those of \(L_M\), with no increase of arity (a point particularly stressed in Lewis , 1993).Footnote 15 Correspondingly, Lewis’s translation algorithm differs from (3) in two respects, viz. in the initial clause for atomic formulas, which is simply
- (3):
-
- (\(a_C\)):
-
\(Pt_1 \dots t_n^{ ~ ~t} = Pt_1 \dots t_n\)
and in the clause for modal formulas, which involves the C predicate:
- (3):
-
- (\(f_C\)):
-
\((\Box \psi )^t = \forall x \forall x_1\dots \forall x_n((Rtx \wedge Ex_{1}x \wedge Cx_1t_1{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Ex_{n}x\)\(\wedge {\tiny ~}Cx_nt_n) \rightarrow \psi ^x [x_1/t_1 \dots x_n/t_n])\)
(where \(t_{1}, \dots , t_{n}\) are all the terms occurring free in \(\psi \) other than t while \(x, x_{1} \dots , x_{n}\) are the first \(n+1\) variables foreign to \(\psi \), and where \(\psi ^x [x_1/t_1 \dots x_n/t_n]\) is obtained from \(\psi ^x\) by replacing each \(t_i\) by \(x_i\)).
Now, this structural divergence reflects the contrast between the two approaches. In particular, it’s clear that Lewis’s translation algorithm is committed to a weak understanding of necessity, since the only worlds that play a role in (3)(\(f_C\)) are those at which there exist suitable counterparts. However, there is also a sense in which both sorts of embedding may be seen as special instances of a single, more general schema. This is rather obvious if we stick to weak necessity. In that case, note that the identity theorist can easily trade (3)(\(f'\)) for (3)(\(f_C\)) so long as C is interpreted and axiomatized as the identity relation. For then (3)(\(f_C\)) is just a logically redundant reformulation of (3)(\(f'\)), so the change would be ultimately immaterial. On the other hand, counterpart theorists can easily trade (3)(\(a_C\)) for (3)(a). Given that CT assumes all individuals to be world-bound, the additional world parameter in (3)(a) would be superfluous and so, again, the concession would be formally immaterial. Thus, if instead of \(L_E\) or \(L_C\) we employed a mixed language that agrees with \(L_E\) on increasing the arity of the non-logical predicates but also agrees with \(L_C\) in containing C as an additional primitive, the hybrid embedding obtained by adopting clause (3)(a) for the atomic formulas and clause (3)(\(f_C\)) for the modal formulas could in principle be agreeable to both parties alike, identity theorists and counterpart theorists. Their rivalry would show up elsewhere—not in the translation algorithm as such, but in the axioms that fix the underlying metaphysical presuppositions.
The general case, where the restriction to weak necessity can be dropped, is only slightly more elaborate. Consider a modification of our translation algorithms obtained by extending \(L_{E}\), not with C, but with a new four-place predicate, D, with Dxyzw to be read as ‘x at y defers to z at w’, or also ‘z at w does duty for x at y’. The relevant meaning postulate is:
- (5):
-
\(Dxyzw \rightarrow (Wy \wedge Ww)\)
With reference to the basic scheme in (3), the new recursive definition of \(\phi ^t\) will be the same except for the last clause, which becomes:
- (3):
-
- \((f_D)\):
-
\((\Box \psi )^t = \forall x \forall x_1\dots \forall x_n((Rtx \wedge Dt_{1}tx_{1}x{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Dt_{n}tx_{n}x)\)\(\rightarrow \psi ^x [x_1/t_1 \dots x_n/t_n])\)
(where all terms and variables are as in (3)(\(f_C\))). Similarly, the variant clause for weak necessity, (3)(\(f'\)), will become:
- (3):
-
- (\(f'_D\)):
-
\((\Box \psi )^ = \forall x \forall x_1\dots \forall x_n((Rtx \wedge Dt_{1}tx_{1}x{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Dt_{n}tx_{n}x\)\(\wedge {\tiny ~}Ex_{1}x{\tiny ~}\wedge {\tiny ~}\dots \wedge {\tiny ~}Ex_{n}x) \rightarrow \psi ^x [x_1/t_1 \dots x_n/t_n])\)
In both cases, we may think of D as expressing the fundamental relation that holds between individuals that match up across worlds, so that the third relatum does duty (at the relevant world) for the first relatum (at the relevant world) as we engage in modal talk about the latter. Accordingly, the new translations tell us that to speculate about the modal profile of, say, Humphrey at the actual world (actual Humphrey) is to look at the properties of those individuals that do duty for him at other worlds. For example, (3)(\(f_D\)) tells us that ‘Humphrey necessarily wins the presidential election’ (\(\Box Ph\)) translates to ‘Whatever does duty for actual Humphrey, at any accessible world, wins the presidential election at that world’ (i.e., \(\forall x \forall y((R\alpha x \wedge Dh\alpha yx) \rightarrow Pyx)\)), and similarly for the weak variant corresponding to (3)(\(f'_D\)).
It’s clear that these embeddings, like the hybrid embedding described earlier, subsume both the identity-theoretic and the counterpart-theoretic embeddings as special cases—this time with no restriction. For the identity theorist, nothing can defer to anything else, so again D must reduce to strict identity:
- (6):
-
- (a):
-
\(Dxyzw \leftrightarrow x \approx z\)
This requirement immediately entails the equivalence between (3)(\(f_D\)) and (3)(f), and between their respective weak variants, making the new translation algorithms a convoluted but logically equivalent substitute for each of the original algorithms of Sect. 2. For their part, the friends of CT will reject (6)(a) and rather insist on the following conditions, the last of which corresponds to the world-boundedness postulate:Footnote 16
- (6):
-
- (b):
-
\(Dxyzy \rightarrow x \approx z\)
- (c):
-
\(Exy \rightarrow Dxyxy\)
- (d):
-
\((Exy \wedge Exz) \rightarrow y \approx z\)
In addition, most counterpart theoristsFootnote 17 would follow Lewis in requiring that nothing can do duty or receive duty in absentia:Footnote 18
- (6):
-
- (e):
-
\(Dxyzw \rightarrow Exy\)
- (f):
-
\(Dxyzw \rightarrow Ezw\)
This would immediately entail the equivalence between (3)(\(f_D\)) and the variant in (3)(\(f'_D\)). More importantly, it would justify replacing D by a binary counterpart relation such as C,Footnote 19 so that both clauses would reduce to (3)(\(f_C\)). Thus, again, the new translation algorithm would in the end amount to a convoluted but equivalent variant of the CT algorithm. In short, both the identity and the counterpart theorist may speak the D language. As with the hybrid option based on mixing \(L_E\) and \(L_C\), but without its restrictions, both parties can use the same translation algorithm for embedding ML into EL.Footnote 20 Their disagreements lie elsewhere, viz. in their specific views concerning the interpretation and axiomatic treatment of the relevant syntactic primitives.
It is a short step, now, to see that these remarks generalize to a variety of intermediate views, including the unorthodox takes on world-boundedness mentioned in Sect. 1. Typically an identity theorist committed to (6)(a) rejects (6)(d), but strictly speaking the two postulates are mutually compatible. Similarly, it is typical but not compulsory for a counterpart theorist to accept (6)(d). If, pace Lewis, actual Humphrey exists at other possible worlds, then one may suppose that at those worlds Humphrey and only Humphrey will do duty for his actual self. More generally, a counterpart theorist is free to accept the following strengthening of (6)(c):
- (6):
-
- (\(c'\)):
-
\((Exy \wedge Exw) \rightarrow (Dxyzw \leftrightarrow x \approx z)\)
It’s just that if actual Humphrey does not exist at world y, someone else may be doing duty for him at y, whereas the typical identity theorist rules that out by endorsing (6)(a) holus bolus (i.e., effectively, by dropping the antecedent of (6)(\(c'\))). Views such as these are not popular and may be hard to defend philosophically.Footnote 21 Yet again they are all covered by the same translation algorithms.
With all this, it’s fair to conclude that from a modal realist perspective there is indeed a clear sense in which CT and the standard account of modality may be seen as distinguished special cases of a single, unified formal framework. Not only can the identity theorist endorse the realist stance (the mundane point of Sect. 2); they can do so while sharing with counterpart theorists a single common apparatus for embedding intensional ML to extensional EL. The apparatus is available across the board and for everyone alike, including hybrid views that combine identity- and counterpart-theoretic inclinations.
With this picture in place, we are now in a better position to address the dual claim regarding the possibility of escaping explicit commitment to modal realism by semantic ascent. Not only are there ways of converting CT into a suitable possible-world semantics, as we know from the early work of Hazen, Forbes, Stalnaker, et al. There is also a way of doing so within a framework that applies equally well to the standard, Kripke-style semantics. We just have to extract the framework from the general embedding algorithm just outlined.
5 Neutral semantics
With this end in mind, let us first fix on some ordinary way of setting up a semantics for ML. We want to allow that different worlds may involve different individuals, so I am alluding to a semantics à la Kripke (1963). We may summarize its main steps as follows.
First, a model for the language \(L_{M}\) may be defined as an ordered quintuple \(M = \langle W, I, \prec , U, V\rangle \), where W is a non-empty set (of ‘worlds’), I is another non-empty set (of ‘individuals’), \(\prec \) is a binary relation on W (of ‘accessibility’), U is a function assigning a non-empty set \(U(w) \subseteq I\) to each \(w \in W\) (the ‘universe’ of w), and V is an interpretation function for the terms and predicates of \(L_{M}\):
- (7):
-
- (a):
-
for each term t (constant or variable), \(V(t)\in I\);
- (b):
-
for each n-ary predicate P and each \(w \in W, V(P,w) \subseteq I^n\).
Next, given any terms \(t_1\), ..., \(t_n\), let a \(t_1\dots t_n\)-variant of a model \(M \!= \!\langle W, I, \prec , U, V\rangle \) be any model \(M' = \langle W, I, \prec , U, V'\rangle \) such that \(V'\) agrees with V on every argument except possibly for some \(t_i\)s (\(1 \le i \le n\)). Then a formula \(\phi \) is said to be satisfied at a world w in a model M, written \(M, w \models \phi \), according to the following recursive conditions:
- (8):
-
- (a):
-
\(M, w \models Pt_1 \dots t_n \ \mathrm{iff}\ \langle V(t_1), \dots , V(t_n)\rangle \in V(P,w);\)
- (b):
-
\(M, w \models t_1 \approx t_2 \ \mathrm{iff}\ V(t_1) = V(t_2);\)
- (c):
-
\(M, w \models \lnot \psi \ \mathrm{iff}\ M, w \not \models \psi ;\)
- (d):
-
\(M, w \models \psi \rightarrow \xi \ \mathrm{iff}\ M, w \not \models \psi \ \mathrm{or}\ M, w \models \xi ;\)
- (e):
-
\(M, w \models \forall x\psi \ \mathrm{iff}\ M', w \models \psi \) for every x-variant \(M'\) of M such that \(V'(x) \in U(w);\)
- (f):
-
\(M, w \models \Box \psi \ \mathrm{iff}\ M, w' \models \psi \) for every \(w' \in W\) such that \(w \prec w'.\)
The rest of the picture can be completed in the usual way: a formula \(\phi \) is said to be true at a world w in a model M iff \(\phi \) is satisfied at w in every \(x_1\dots x_n\)-variant \(M'\) of M, where \(x_1\), ..., \(x_n\) are the variables occurring free in \(\phi \); it is said to be valid in M iff it is true at every world in W; it is said to be valid in a class of models iff it is valid in each model of that class; and so on.
Again, there is some leeway concerning matters of detail. As with the variant translation algorithms of Sect. 2, one may think that an atomic formula can be satisfied at a given world only by individuals existing at that world, or that modal claims should be assessed only by reference to those worlds at which the relevant individuals exist. The first thought may be accommodated by revising condition (7)(b) in the obvious way:
- (7):
-
- (\(b'\)):
-
for each n-ary predicate P and \(w \in W, V(P,w) \subseteq U(w)^n.\)
Alternatively, one may go for a direct strengthening of the basic recursive condition in (8):
- (8):
-
- (\(a'\)):
-
\(M, w ~\models Pt_1 \dots t_n\) iff \(\langle V(t_1), \dots , V(t_n)\rangle \in V(P,w) \) and \(\{V(t_1), \dots , V(t_n)\} \subseteq U(w),\)
and perhaps also a strengthening of the next condition:
- (8):
-
- (\(b'\)):
-
\(M, w \models t_1 \approx t_2~\mathrm{iff}~ V(t_1)= V(t_2)\) and \(\{V(t_1),V(t_2)\} \subseteq U(w).\)
These stronger conditions are the semantic analogues of the translation rules in (3)(\(a'\)) and (3)(\(b'\)). As for the second thought, one would have to replace condition (8)(f) by the semantic analogue of (3)(\(f'\)):
- (8):
-
- (\(f'\)):
-
\(M, w ~\models \Box \psi ~\mathrm{iff}~M, w' \models \psi \) for every \(w' \in W\) such that \(w \prec w'\) and \(\{V(t_1), \dots , V(t_n)\} \subseteq U(w'),\)
where \(t_1\), ..., \(t_n\) are the free terms in \(\psi \). These choices are not immaterial and will result in different logical theories, but never mind. Once again, this is simply a sign of the many delicate choices we have to make when providing a detailed account of our modal talk.
Now, as noted, this sort of semantics comes with the proviso that the elements of W are called ‘worlds’ only by courtesy, as a halfhearted convenient heuristic, though it may be debatable whether this suffices to claim genuine ontological neutrality. On the other hand, it’s pretty clear that the semantics is not neutral with regard to how the different worlds represent the modal profile of an individual. The identity-theoretic perspective is built directly into the satisfaction condition for modal claims, (8)(f) (or (8)(\(f'\))), which requires a formula to be evaluated at different worlds under one and the same interpretation of its singular terms. This lack of neutrality, however, is perfectly analogous to the lack of neutrality of the translation algorithms of Sect. 2. In both cases, it stems from the fact that the account itself fulfills two tasks at once: (i) providing a semantics, or a translation algorithm, respectively, and (ii) specifying what does duty for what when we engage in modal talk. We have seen that these two tasks can be separated out in such a way as to render the translation algorithm of the modal realist neutral with respect to (ii). We can now follow the same strategy so as to render the semantics equally neutral in that respect. All we have to do is to provide a more general characterization of (i) in which the fundamental does duty for relation that links an individual to its other-wordly correlates is left unspecified: it can be strict identity, as implicitly assumed above, or it can be a weaker relation of some sort. This is precisely the idea behind the general semantic theories mentioned at the end of Sect. 3. In particular, reversing our general translation algorithm will deliver a semantic framework that is very much akin to that of Corsi (2001, (2002), though even slightly more general.Footnote 22 Here are the details.
First, let us enrich our models by adding the trans-world relation explicitly. A model for \(L_{M}\) will now be a sextuple \(M = \langle W, I, \prec , \asymp ,\) \(U, V\rangle \), where W, I, \(\prec \), U, and V are as before and, in addition, \(\asymp \) is a binary relation on \(I \times W\). Intuitively, \(\asymp \) is the semantic analogue of D: when \(\langle i_1, w_1\rangle \asymp \langle i_2, w_2 \rangle \) we may speak of the individual \(i_2\) as doing duty at \(w_2\) for the individual \(i_1\) at \(w_1\), and we may write \(i_1|w_1 \asymp i_2|w_2\).
On this basis, the recursive definition of satisfaction will be just as in (8), except that the condition for modal formulas with free terms will now make appeal to \(\asymp \), paralleling the revised translation algorithm of Sect. 4:
- (8) :
-
- (\(f_{\scriptscriptstyle \asymp }\)):
-
\(M, w ~\models \Box \psi \) iff \(M', w' \models \psi \) for every \(t_1\dots t_n\)-variant \(M'\) of M and every \(w' \in W\) such that \(w \prec w'\) and \(V(t_1)|w\asymp V'(t_1)|w',\)\(\dots , V(t_n)|w\asymp V'(t_n)|w'.\)
(Here, again, \(t_1\), ..., \(t_n\) are the terms occurring free in \(\psi \). If there aren’t any, (8)(f) will do.) Alternatively, with reference to the weaker condition in (8)(\(f'\)), the revised definition is obtained by further stipulating that the relevant \(t_1\)...\(t_n\)-variants be selected among those models that reinterpret each \(t_i\) as an individual existing in the relevant world \(w'\):
- (8) :
-
- (\(f_{{\scriptscriptstyle \asymp }}'\)):
-
\(M, w ~\models \Box \psi \) iff \(M', w' \models \psi \) for every \(t_1\dots t_n\)-variant \(M'\) of M and every \(w' \in W\) such that \(w \prec w'\) and \(V(t_1)|w \asymp V'(t_1)|w',\)\(\dots , V(t_n)|w \asymp V'(t_n)|w'\) and \(\{V'(t_1), \dots , V'(t_n)\} \subseteq U(w').\)
Thus, intuitively, condition (8)(\(f_{\scriptscriptstyle \asymp }\)) says that a sentence such as ‘Humphrey necessarily wins the presidential election’ (\(\Box Ph\)) is satisfied at a world w just in case, for every accessible world \(w'\), ‘Humphrey wins the presidential election’ is satisfied for every way of reinterpreting ‘Humphrey’ as a name for an individual who at \(w'\) does duty for Humphrey at w—an individual which, if clause (8)( ) is employed instead, must belong to the universe of \(w'\) (weak necessity).Footnote 23
) is employed instead, must belong to the universe of \(w'\) (weak necessity).Footnote 23
Now, the relation \(\asymp \) is in principle unconstrained.Footnote 24 But just as the standard account allows us to distinguish different sorts of models by reference to specific conditions on the accessibility relation \(\prec \) (for instance, that it be reflexive) and on the universe-selecting function U (for instance, that it be increasing with respect to \(\prec \)), we may now distinguish different sorts of models also by reference to specific conditions on the duty-doing relation \(\asymp \). In particular, we can say that \(M = \langle W, I, \prec , \asymp , U, V\rangle \) is an identity model when \(\asymp \) relates identical individuals across all worlds in W:
- (9):
-
- (a):
-
\(i|w \asymp i'|w'\) iff \(i = i'.\)
This is the semantic analogue of (6)(a). By contrast, we can say that M is a counterpart model iff \(\asymp \) satisfies the analogues of (6)(b)–(d):
- (9):
-
- (b):
-
if \(i|w \asymp i'|w\), then \(i = i';\)
- (c):
-
if \(i \in U(w)\), then \(i|w \asymp i|w;\)
- (d):
-
if \(i \in U(w)\) and \(i \in U(w')\), then \(w=w'.\)
And we can say that M is austere iff it satisfies the analogues of (6)(d) and (6)(f) (no duty-doing in absentia):
- (9):
-
- (e):
-
if \(i|w \asymp i'|w'\), then \(i \in U(w);\)
- (f):
-
if \(i|w \asymp i'|w'\), then \(i' \in U(w').\)
Thus, if M is an identity model, Humphrey and only Humphrey will do duty for himself at any world, so (8)( ) is just a cumbersome way of rephrasing the original clause in (8)(f) (just as (3)(\(f_D\)) was a cumbersome but equivalent reformulation of (3)(f)). Similarly for the corresponding weak variants. If M is a counterpart model, however, then Humphrey’s duty-doers at other worlds must be distinct individuals, so (8)(
) is just a cumbersome way of rephrasing the original clause in (8)(f) (just as (3)(\(f_D\)) was a cumbersome but equivalent reformulation of (3)(f)). Similarly for the corresponding weak variants. If M is a counterpart model, however, then Humphrey’s duty-doers at other worlds must be distinct individuals, so (8)( ) cannot be further reduced. At best we can say that if M is also austere, then (8)(
) cannot be further reduced. At best we can say that if M is also austere, then (8)( ) coincides with (8)(
) coincides with (8)( ) and \(\asymp \) could be reconstrued as a simple binary relation on I, as in familiar presentations of counterpart semantics (e.g. Hughes and Cresswell 1996, pp. 354ff). As they stand, the satisfaction conditions for modal formulas apply equally to all sorts of models and are therefore adequate to the general picture we are after. The two main accounts—identity-theoretic and counterpart-theoretic—do not differ regarding what a model is. They differ regarding which models embody the right sort of trans-world matching of individuals, just as each account will in turn provide for a variety of theories that differ with regard to which of their models involve the right sort of accessibility relation between worlds.
) and \(\asymp \) could be reconstrued as a simple binary relation on I, as in familiar presentations of counterpart semantics (e.g. Hughes and Cresswell 1996, pp. 354ff). As they stand, the satisfaction conditions for modal formulas apply equally to all sorts of models and are therefore adequate to the general picture we are after. The two main accounts—identity-theoretic and counterpart-theoretic—do not differ regarding what a model is. They differ regarding which models embody the right sort of trans-world matching of individuals, just as each account will in turn provide for a variety of theories that differ with regard to which of their models involve the right sort of accessibility relation between worlds.
6 Model theory
Summing up, the point of this general picture is not only to uncover the relative independence of a counterpart semantics for intensional ML from the strict commitment to modal realism that comes with Lewis’s extensional formulation of counterpart theory (CT), but also to emphasize the conceptual similarity of such a semantics with the standard semantics that we got from Kripke. In this sense, the picture completes our defense of the claims with which we started. But the picture is also general enough to entail a number of derivative advantages, some of which are especially important from a metalogical perspective.
The main advantage is that it now becomes possible to explore intensional ML without deciding in advance what sort of principles should govern \(\asymp \), just as we need not decide in advance what principles should govern \(\prec \). Some modal theses will be valid no matter what we think; others will depend on specific choices. And the choices are not limited to the identity- or counterpart-theoretic conditions in (9)(a) and (9)(b)–(d), or (9)(b)–(f). As with the neutral translation algorithms of Sect. 4, any consistent set of conditions is in principle available (with the additional advantage that, of course, we are not limited to conditions that are first-order characterizable).Footnote 25
For a concrete illustration, let us initially focus on the basic semantics defined by (8)(\(f_{\scriptscriptstyle \asymp }\)) (along with (8)(a)–(e)) and consider such familiar modal principles as
- T:
-
\(\Box \phi \rightarrow \phi \)
- B:
-
\(\phi \rightarrow \Box \Diamond \phi \)
- 4:
-
\(\Box \phi \rightarrow \Box \Box \phi \)
- 5:
-
\(\Diamond \phi \rightarrow \Box \Diamond \phi \)
In the standard semantics for ML, such principles correspond with specific requirements on the accessibility relation \(\prec \), namely that it be reflexive, symmetric, transitive, and euclidean, respectively:
- (9):
-
- (g):
-
\(w \prec w;\)
- (h):
-
if \(w \prec w'\), then \(w' \prec w;\)
- (i):
-
if \(w \prec w'\) and \(w' \prec w''\), then \(w \prec w'';\)
- (j):
-
if \(w \prec w'\) and \(w \prec w''\), then \(w' \prec w''.\)
In the broader semantic framework under consideration, however, these conditions on \(\prec \) are naturally matched by similar requirements concerning the duty-doing relation \(\asymp \):
- (9):
-
- (\(g'\)):
-
\(i|w \asymp i|w;\)
- (\(h'\)):
-
if \(i|w \asymp i'|w'\), then \(i'|w' \asymp i|w;\)
- (\(i'\)):
-
if \(i|w \asymp i'|w'\) and \(i'|w' \asymp i''|w''\), then \(i|w \asymp i''|w'';\)
- (\(j'\)):
-
if \(i|w \asymp i'|w'\) and \(i|w \asymp i''|w''\), then \(i'|w' \asymp i''|w''.\)
If we just focus on identity models, the latter conditions are automatically satisfied by virtue of identity being reflexive, symmetric, etc., so we are back to the standard picture. Strictly speaking, however, this means that the status of the modal schemas does not depend exclusively on the relevant properties of \(\prec \); it also depends on the general properties of identity. If we focus on counterpart models, the picture is reversed. Typically, counterpart theorists ignore \(\prec \) altogether, which amounts to treating world accessibility as a universal relation.Footnote 26 Thus, (9)(g)–(j) are automatically satisfied and all the work is done by the relevant conditions on \(\asymp \). Strictly speaking, however, this means that the status of the modal schemas depends also on the universal relation being reflexive, symmetric, etc.
This is not to say that in the general case it’s just a matter of conjoining a condition on \(\prec \) with the parallel condition on \(\asymp \). With some schemas that will do. For instance, the conjunction of the two reflexivity conditions (9)(g) and (9)(\(g'\)) is indeed necessary and sufficient for the validity of T.Footnote 27 Other cases, however, are less straightforward. In particular, with regard to B, 4, and 5 it is good exercise to compare the corresponding pairs of conditions, viz. (9)(h) plus (9)(\(h'\)) (symmetry), (9)(i) plus (9)(\(i'\)) (transitivity), and (9)(j) plus (9)(\(j'\)) (euclideanness), with the following unitary conditions, respectively:Footnote 28
- (9):
-
- (\(h^*\)):
-
if \(w \prec w'\) and \(i|w \asymp i'|w'\), then \(w' \prec w\) and \(i'|w' \asymp i|w;\)
- (\(i^*\)):
-
if \(w \prec w', i|w \asymp i'|w', w' \prec w''\), and \(i'|w' \asymp i''|w''\), then \(w \prec w''\) and \(i|w \asymp i''|w'';\)
- (\(j^*\)):
-
if \(w \prec w', i|w \asymp i'|w', w \prec w''\), and \(i|w \asymp i''|w''\), then \(w' \prec w''\) and \(i'|w' \asymp i''|w''.\)
Note that these three conditions reduce to (9)(\(h'\))–(9)(\(j'\)) if \(\prec \) and \(\asymp \) are connected by a general bridging principle to the effect that duty-doing is only attainable at those worlds that are accessible from the given one:
- (9):
-
- (k):
-
if \(i|w \asymp i'|w'\), then \(w \prec w'.\)
Moreover, even when determining the relevant necessary and sufficient conditions is a straightforward affair, as with T, there are subtle ramifications to consider. For example, in the presence of the austerity requirements (9)(e)–(f), the \(\asymp \)-reflexivity condition (9)(\(g'\)) can only hold in models where every individual in I exists at every world in W. This is a strong constraint. Particularly, no austere counterpart model will meet this condition so long as W contains more than one world. For a counterpart theorist, that is hardly tolerable. One solution would be to restrict (9)(e)–(f) ad hoc so as to allow for self-duty-doing as a special case that may obtain even in absentia:
- (9):
-
- (\(e'\)):
-
if \(i|w \asymp i'|w'\) and \(i\ne i'\), then \(i \in U(w);\)
- (\(f'\)):
-
if \(i|w \asymp i'|w'\) and \(i\ne i'\), then \(i' \in U(w').\)
Alternatively, an austere counterpart theorist may wish to restrict (9)(\(g'\)) itself to those cases where \(i \in U(w)\). This is actually tantamount to assuming the local reflexivity condition in (9)(c), which is already constitutive of all counterpart models. The restriction would have no impact on those instances of T that contain no free terms.Footnote 29 More generally, (9)(c) would suffice to validate the universal closure of any other instance.Footnote 30 It would not, however, validate the T-schema in full. A simple instance of the form
- (10):
-
\(\Box Pt \rightarrow Pt\)
would fail at any world w of any austere model M where V(t) is not an element of \(U(w) \cup V(P,w)\).Footnote 31
This may seem like a limitation of counterpart theories, and in a way it is. But note that the identity theorist would be exactly in the same position if we shifted to the alternative semantics based on (8)( ) (which in their case coincides with (8)(\(f'\))). Every identity model satisfies the \(\asymp \)-reflexivity condition (9)(\(g'\)), hence, a fortiori, (9)(c); yet this would again not be enough to validate the T-schema in full if \(\phi \) is allowed to contain free terms. Specifically, an instance such as (10) might still fail at any world w of an identity model M where V(t) is not an element of \(U(w) \cup V(P,w)\), e.g. if there were no accessible world \(w'\) such that \(V(t) \in U(w')\), or if every such world satisfied Pt. (Consider: from the fact that Pegasus is a winged horse at every accessible world where it exists it doesn’t follow that it is a winged horse at the actual world, where Pegasus does not exist and ‘is a winged horse’ has empty extension.) Now, for an austere counterpart theorist the shift from (8)(\(f_{\scriptscriptstyle \asymp }\)) to (8)(
) (which in their case coincides with (8)(\(f'\))). Every identity model satisfies the \(\asymp \)-reflexivity condition (9)(\(g'\)), hence, a fortiori, (9)(c); yet this would again not be enough to validate the T-schema in full if \(\phi \) is allowed to contain free terms. Specifically, an instance such as (10) might still fail at any world w of an identity model M where V(t) is not an element of \(U(w) \cup V(P,w)\), e.g. if there were no accessible world \(w'\) such that \(V(t) \in U(w')\), or if every such world satisfied Pt. (Consider: from the fact that Pegasus is a winged horse at every accessible world where it exists it doesn’t follow that it is a winged horse at the actual world, where Pegasus does not exist and ‘is a winged horse’ has empty extension.) Now, for an austere counterpart theorist the shift from (8)(\(f_{\scriptscriptstyle \asymp }\)) to (8)( ) is immaterial, since (9)(f) obliterates all relevant differences, so the previous remarks continue to apply.Footnote 32 But this amounts to saying that, on this semantics, both positions are perfectly on a par with regard to T. It’s just that the identity theorist need not make the shift, whereas austere counterpart theorists are inherently committed to it.
) is immaterial, since (9)(f) obliterates all relevant differences, so the previous remarks continue to apply.Footnote 32 But this amounts to saying that, on this semantics, both positions are perfectly on a par with regard to T. It’s just that the identity theorist need not make the shift, whereas austere counterpart theorists are inherently committed to it.
7 Modal principles
Indeed this is where things begin to get interesting. Critics of CT have often complained that Lewis’s method of counterparts yields unpalatable results when it comes to the status of familiar modal principles. Lewis has shown that, on his embedding of LM into CT, principles such as B, 4, and 5 depend for their validity on specific conditions on the counterpart relation, and we have just seen that this point can be given a nice, more direct and fully general model-theoretic characterization. But Lewis’s embedding has the additional effect that a number of modal theses turn out to be provable in CT regardless of any special condition on the counterpart relation, including theses that are highly controversial. In the present setting, this means that such theses turn out to be automatically valid in the class of all austere counterpart models. It is tempting, therefore, to reiterate the complaint and resolve for this reason to hold on to a standard semantics based on identity models. Yet this would be a hurried move. The unwanted results need not depend on the fact that the models in question are counterpart models; they may depend on the fact that the models are austere models, forcing the shift to (8)( ), and, hence, to a weak understanding of all necessities.
), and, hence, to a weak understanding of all necessities.
A notable case in point is the controversial modal thesis known as the Necessity of Existence:
- NE:
-
\(\forall x ~\Box ~\exists y ~x \approx y\)
If necessity is weak necessity, then NE is trivially valid, since everything will always have an existing duty-doer (a duty-doer witnessing the existential quantifier) at every world at which it has an existing duty-doer (a duty-doer in the universe of that world). Lewis himself discusses this worry at length (1986, pp.10ff), since the translation of NE is an immediate theorem of CT. However, it’s clear that NE would be valid on any way of understanding necessity as weak necessity,Footnote 33 hence, from the present perspective, any semantics based on (8)( ), including semantics restricted to identity models. If counterpart theorists have a problem, it doesn’t lie in the fact that they reject (9)(a), trading trans-world identity for weaker forms of duty-doing. It lies in the fact that they tend to focus on austere models, thus trading (8)(\(f_{\scriptscriptstyle \asymp }\)) for (8)(
), including semantics restricted to identity models. If counterpart theorists have a problem, it doesn’t lie in the fact that they reject (9)(a), trading trans-world identity for weaker forms of duty-doing. It lies in the fact that they tend to focus on austere models, thus trading (8)(\(f_{\scriptscriptstyle \asymp }\)) for (8)( ). There may be good reasons for doing so, and Lewis himself was adamant about austerity: “What can it mean to say that the counterpart is ‘at w’ if not that, at w, the counterpart exists?” (1986, p.10). But the friend of trans-world identity may feel exactly the same way: What could it mean to say that the original individual is ‘at w’ if not that it exists also at w?Footnote 34 The problem does not issue from the rejection of (9)(a), the hallmark of identity models; it comes with the unconditional endorsement of the austerity condition (9)(f).
). There may be good reasons for doing so, and Lewis himself was adamant about austerity: “What can it mean to say that the counterpart is ‘at w’ if not that, at w, the counterpart exists?” (1986, p.10). But the friend of trans-world identity may feel exactly the same way: What could it mean to say that the original individual is ‘at w’ if not that it exists also at w?Footnote 34 The problem does not issue from the rejection of (9)(a), the hallmark of identity models; it comes with the unconditional endorsement of the austerity condition (9)(f).
Similar considerations apply to other contentious modal principles whose translation is a theorem of Lewis’s CT, such as the Converse Barcan Formula:
- CBF:
-
\(\Box \forall x\phi \rightarrow \forall x\Box \phi \)
In the standard semantics defined by (8)(a)–(f), CBF is not valid unless we ask all models to satisfy a condition of “existential inclusion”:
- (7):
-
- (c):
-
if \(i \in U(w)\) and \(w \prec w'\), then \(i \in U(w').\)
This is hardly an innocent requirement if U is to pick out the set of individuals that exist at the relevant worlds, since it would seem that what exists at a given world w need not exist at every other world accessible from w. In particular, it is plausible to suppose that actually existing individuals might not have existed. Now, all this remains true in the general framework based on (8)(\(f_{\scriptscriptstyle \asymp }\)), where the existential inclusion requirement can be recast in terms of a more general condition of “existential faithfulness” (adapting from Kracht and Kutz 2002a; Corsi 2003):
- (9):
-
- (l):
-
if \(i \in U(w), w \prec w'\), and \(i|w \asymp i'|w'\), then \(i' \in U(w').\)
If we do not like this condition, we are free not to endorse it and CBF won’t be valid. However, this is a genuine option only if we are not committed to austerity, particularly to condition (9)(f), as the latter obviously implies (9)(l). Since Lewis’s counterpart relation is austere, it is not surprising that his translation of CBF is a theorem of CT. More generally, it is not surprising that CBF is valid in the class of all austere counterpart models. But, again, this is not to be blamed on the fact that such models trade identity for weaker forms of duty-doing. As with NE, the validity of CBF does not stem from the rejection of (9)(a); it comes with the (optional) endorsement of (9)(f).Footnote 35
Things are a bit more complex when it comes to other modal principles that fueled the critical discussion around CT. Consider, for instance, the standard distribution schema:
- K:
-
\(\Box (\phi \rightarrow \psi ) \rightarrow (\Box \phi \rightarrow \Box \psi )\)
Unlike all schemas discussed so far, K (so named after Kripke) is unconditionally valid in the standard semantics defined by (8)(a)–(f); it is satisfied at any world in any model no matter what properties govern the relevant accessibility relation \(\prec \). It is not, however, a valid schema according to CT and, correspondingly, in the semantics based on austere counterpart models.Footnote 36 A simple counterexample (originated with Hazen , 1979) is a model with a world w comprising two individuals, \(i_1\) and \(i_2\), one of which, \(i_1\), has a counterpart at some accessible world \(w'\) at which the other has no counterpart at all (i.e., more precisely, there is some \(i'_1\) such that \(i_1|w \asymp i'_1|w'\) but no \(i'_2\) such that \(i_2|w \asymp i'_2|w'\)). Then it may turn out that, say, both \(\Box (Pab \rightarrow Qa)\) and \(\Box Pab\) are satisfied at w while \(\Box Qa\) is not,Footnote 37 falsifying the following K-instance:
- (11):
-
\(\Box (Pab \rightarrow Qa) \rightarrow (\Box Pab \rightarrow \Box Qa)\)
Here the worry is exactly dual to the one illustrated by the status of NE and CBF: it’s not that an undesired principle turns out to be automatically valid; we have an utterly uncontroversial schema that counterpart theorists seem forced to abandon. What is the explanation?
To some extent, the explanation is the same as before. If we are committed to austerity (as Lewis is), then all necessities are weak necessities, and (11) fails to be valid on the weak semantics based on (8)( ) regardless of whether we go counterpart-theoretic or identity-theoretic. It fails already on the weak Kripke semantics based on (8)(\(f'\))Footnote 38 (as does (10) in reflexive contexts).
) regardless of whether we go counterpart-theoretic or identity-theoretic. It fails already on the weak Kripke semantics based on (8)(\(f'\))Footnote 38 (as does (10) in reflexive contexts).
On the other hand, it’s clear that in this case we cannot leave it at that. For if we relinquish austerity (and orthodox counterpart theory with it) and focus on the strong notion of necessity delivered by (8)(\(f_{\scriptscriptstyle \asymp }\)), then (11) may still fail in the class of counterpart models whereas the identity models defined by (9)(a) will validate (11) along with every other instance of K. The reason is that identity models obliterate all the difference between (8)(\(f_{\scriptscriptstyle \asymp }\)) and the standard, Kripkean clause in (8)(f) and therefore preserve all standard validities. Not so if we admit other models.
Does it follow that in this case the problem is indeed peculiar, not to Lewis’s austere counterpart theory, but to counterpart-theoretic accounts more generally? It doesn’t. It’s easy to see that K may also fail in models where nothing ever does duty for anything else, i.e., models satisfying as much as the left-to-right direction of the identity-theoretic condition (9)(a):
- (9):
-
- (\(a'\)):
-
\(\mathrm{if}\, i|w \asymp i'|w', \,\mathrm{then}\, i =i'.\)
The model described earlier is a case in point: just read ‘has a counterpart at’ as ‘does duty for itself at’ (so that \(i_1=i'_1\)) and nothing will prevent the model from fulfilling (9)(\(a'\)) while falsifying (11). This shows that the problem has nothing to do with the world-boundedness condition (9)(d), which is the distinctive feature of counterpart models.
Indeed, here is a condition that would secure full validity to the K-schema no matter what:
- (9):
-
- (m):
-
\(\mathrm{if}\ w \prec w', \ \mathrm{then}, \ i|w \asymp i'|w' \ {\text {for some}}\ i'.\)
This condition is trivially implied by (9)(a), which is why identity-theorists have the K-schema.Footnote 39 But the same condition is compatible with (9)(\(a'\)) as well as (9)(b)–(d) and may thus be adopted by conditional identity theorists and counterpart theorists alike. Alternatively, someone committed to the austerity tenets (9)(e)–(f) may adopt the following weaker condition:
- (9):
-
- (\(m'\)):
-
\(\mathrm{if}\ w \prec w' \ \mathrm{and}\ i \in U(w)\), then \(i|w \asymp i'|w' \ {\text {for some}}\ i' \in U(w')\)
(otherwise (9)(m) plus (9)(e) would imply that any world w accessing at least one world has an all-comprehensive universe, i.e., \(U(w)=I\)). We know Lewis would not accept (9)(m) as he would not accept (9)(\(m'\)), since he explicitly denies that every individual must have a counterpart at every (accessible) world (1968, p.116). Indeed it might be objected that both conditions are overkill, and it is an interesting question which weaker sufficient conditions are also necessary, given other conditions one may endorse, to validate every instance of K.Footnote 40 But never mind. The point is simply that this question does not only arise in the context of counterpart models. It arises in any context where the identity-theoretic condition (9)(a) fails to hold in its full strength, including models where all duty-doing is still based on strict trans-world identity.
Similar remarks apply to other standard schemas whose extensional translation is not a theorem of Lewis’s CT, and which fail to hold unrestrictedly in the class of austere counterpart models. For example:
- \(\textsf {S}_{1}\):
-
\(\Box (\phi \wedge \psi ) \rightarrow \Box \phi \)
- \(\textsf {S}_{2}\):
-
\(\Box \phi [t/x] \rightarrow \Box \exists x \phi \)
- \(\textsf {S}_{3}\):
-
\(\Box (\forall x \phi \wedge \phi [t/x]) \rightarrow \Box \forall x \phi \)
The failure of such principles may be deemed problematic on various grounds.Footnote 41 Yet it is not intrinsic to the spirit of a counterpart-theoretic analysis of modality. It is rather a feature of certain ways of implementing the analysis. Those principles fail in counterpart theories that (i) are committed to austerity, and (ii) refrain from making certain common assumptions concerning trans-world duty-doing—assumptions that come for free if we focus on identity models but that on their own are available more generally, as with the conditions expressed by (9)(m) and (9)(\(m'\)). Austere trans-world-identity accounts in which (9)(a) is weakened to (9)(\(a'\)) face exactly the same worries. Indeed, it is a virtue of the counterpart-theoretic approach, and more generally of semantic theories based on the broader concept of duty-doing, that such assumptions can be recognized for what they are. Each assumption may be accepted or it may be rejected, and each decision can and ought to be judged on its own merits.
8 Modal logic for everyone
At this point it should be clear how the picture can be completed. In his 1968 article, Lewis showed that there is a certain correspondence between the principles of propositional and quantified ML and various specific conditions that may be assumed to govern the counterpart relation of CT (not conditions that Lewis himself adopted, but conditions that one is free to endorse if one so wishes). In the present setting, where the spirit of CT is built directly into the semantics of intensional ML, that amounts to saying that the status of such principles depends on specific conditions on the relation \(\asymp \). Really we know that this is a simplification, due to the fact that CT was originally formulated without any reference to an accessibility relation (which amounts to treating \(\prec \) implicitly as unrestricted). With \(\prec \) back in the picture, as we saw, the right thing to say is that generally speaking the status of a modal principle depends on specific conditions on both \(\asymp \) and \(\prec \). Similarly for the standard Kripkean semantics for ML, which is typically formulated without any reference to the relation of duty-doing (i.e., effectively, by treating \(\asymp \) implicitly as identity). This is why the two approaches can be seen as two species of the same genus, in fact as two special cases that result from ignoring one relation altogether in favor of the other. No doubt the approaches are in competition with each other, and the competition manifests itself most clearly when it comes to principles concerning the modal behavior of equality:
- NI:
-
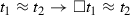
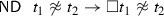
Principles such as these are valid in the class of identity models but not in the class of counterpart models, owing to the respective obtaining and non-obtaining of the corresponding conditions on \(\asymp \):
- (9):
-
- (n):
-
if \(i|w \asymp i'_1|w'\) and \(i|w \asymp i'_2|w'\), then \(i'_1 = i'_2;\)
- (o):
-
if \(i_1|w \asymp i'|w'\) and \(i_2|w \asymp i'|w'\), then \(i_1 = i_2.\)
Yet this competition is no different from the competition that may arise with regard to any other modal principles, including propositional or quantificational schemas such as those discussed by Lewis. Indeed nothing would prevent a non-identity theorist from endorsing (9)(n) and (9)(o) and reclaiming validity for both NI and ND.Footnote 42 Lewis would find that unacceptable, but so be it. As we have learned to say, “Strange! But not impossible” (1976, p.149).
What about other options? In the explicit modal realist setting of Sect. 4 we saw that while an identity theorist committed to (6)(a) is almost certain to reject (6)(d) (the thesis that nothing exists at more than one world), strictly speaking the two postulates are compatible with one another. From the present perspective, this means that one is free to endorse (9)(a), which defines identity models, along with the world-boundedness condition (9)(d), which is characteristic of counterpart models. Strange, but not impossible. So long as we do not require that the extension of a predicate at a given world may only include individuals from the universe of that world (as in (7)(\(b'\))), such a choice would not prevent us from engaging in modal talk. And such talk would be governed by its own set of logical principles. For instance, regardless of one’s preference concerning (8)(\(f_{\scriptscriptstyle \asymp }\)) and (8)( ), the following schema would be valid whenever t is free in \(\phi \)Footnote 43:
), the following schema would be valid whenever t is free in \(\phi \)Footnote 43:
- WB:
-
\((\exists xx \approx t \wedge \phi ) \rightarrow \Box (\exists xx\approx t \rightarrow \phi )\)
Similarly, we said it is typical but not compulsory for a friend of counterparts to endorse world-boundedness. One may want to deny that trans-world identity is strictly necessary for the job of duty-doing while acknowledging that it is nonetheless possible and, in case, sufficient for the job. Someone with such views would discard both (9)(a) and (9)(d) and would presumably go for a simple strengthening of (9)(c):
- (9):
-
- (\(c'\)):
-
\(\mathrm{if}\ i \in U(w) \ \mathrm{and}\ i \in U(w'), \ \mathrm{then}\ i|w \asymp i'|w' \ \mathrm{iff}\ i = i'.\)
This may not result in a logic of its own. Nonetheless it might reflect a conception of counterparthood that, if properly motivated, would add plausibility to certain modal principles rather than others, including perhaps the equality principles NI and ND.
Lots of other options are possible, too. Most of them, insofar as they admit a first-order characterization, could of course be put directly in terms of axiom systems formulated in EL, and in Sect. 4 we saw what it would take. Doing so would vindicate Lewis’s contention that we can conduct formalized discourse about modality “by means of our all-purpose extensional logic”. It would also vouch for Lewis’s realism about possible worlds. Yet both benefits are part of a compact philosophical agenda that tends to obfuscate the independent appeal of going counterpart-theoretic. Disentangling the ontological assumptions of such treatments from their metaphysical assumptions concerning accessibility and duty doing shows that all the work is done by the latter assumptions. This is the force of model theory, and the few examples offered above should suffice to illustrate its extent.Footnote 44
When Kripke in 1963 introduced accessibility relations into his modal structures, a whole unprecedented spectrum of formal options was instantly added to our way of thinking about modality and modal logic itself became the rich and powerful area or research that we know. Five years later Lewis offered counterpart theory as an alternative, and for some time that is how we have looked at it. But it isn’t just an alternative. As soon as we abstract from Lewis’s specific account of how counterparthood works, the framework we obtain is just as rich and powerful as Kripke’s and may prove adequate for the study of a large variety of modal logics. Subsuming both frameworks within a general semantic theory delivers a picture that is even richer and more powerful. We get all of Kripke’s logics along with all of sorts of Lewisian logics, plus a new range of hybrid theories that would otherwise remain uncharted. For a down-to-earth philosopher this need not be a plus; one theory is good enough, better if simple and homogeneous. For a logician it can be heaven. But both will agree on one thing: in logic as in philosophy, the worst mistake is to stick to heaven or earth, ignoring all undreamt-of options that lie in between.Footnote 45
Notes
I shall use ‘CT’ for the basic theory presented in Lewis (1968), disregarding later revisions [(obtained e.g. by providing for a multiplicity of counterpart relations, as in Lewis (1971))] or extensions (e.g. to the analysis of counterfactuals, as in Lewis (1973)). The phrase ‘counterpart theory’ (lowercase) and cognates will refer more generally to any view in keeping with the spirit of CT, though not necessarily with the details.
Virtually the same objection was raised by Plantinga (1974, p. 116).
This is how I will understand modal realism for the purpose of this paper. Lewis’s official view—sometimes called ‘concretism’ (van Inwagen 1986; Plantinga 1987)—includes the further claim that non-actual worlds are spatiotemporally concrete objects “of a kind with this world of ours” (Lewis 1986, p. 2). This claim is central to Lewis’s overall picture, but plays no role in the formulation of CT.
The closest he comes is in the context of the general discussion of possible-world semantics for modal logic at the beginning of Lewis (1986), but even there the purpose is to stress the difference between his genuine “metaphysical” account and the purely “metalogical” character of such semantics (p.17).
I am treating \(\alpha \) as an individual constant to keep things simple. The alternative (paralleling Lewis) would be to add instead a second unary predicate, to be read ‘is actual’, and introduce \(\alpha \) as a definite description (‘the world at which there exist all and only actual things’). Note that, given (1)(b), the predicate W could in turn be introduced by definition on the assumption that every world has something existing at it.
With some limitations. For instance, the requirement that R be reflexive corresponds with the modal schema \(\Box \phi \rightarrow \phi \), but that R be irreflexive does not correspond with any schema. Conversely, there are modal schemas that do not correspond with any first-order conditions on R, a notable example being the McKinsey Axiom \(\Box \Diamond \phi \rightarrow \Diamond \Box \phi \). On these issues, see e.g. Hughes and Cresswell (1996), chs.10 and 12.
A further notable difference is that \(L_C\) does not include R. However, this is not an essential feature of CT and Lewis himself eventually allows for relative modalities (1968, §5). Moreover, Lewis’s reading for E (in his notation: I) is ‘is in’, which his concretism equates to ‘is part of’ (1983, §1), but, again, this is formally inessential.
Cf. Lewis (1968), postulate P2. The other two conditions would correspond to postulates P5 (Nothing is a counterpart of anything else in its world) and P6 (Anything in a world is a counterpart of itself). P5 was later rejected by Lewis (1986, p.232, n.22) as inappropriate under some resolutions of the vagueness of the counterpart relation; here we shall ignore such complications.
A notable exception is Forbes (1987).
Given P2, (6)(e) and (6)(f) correspond to CT’s postulates P4 (Whatever has a counterpart is in a world) and P3 (Whatever is a counterpart is in a world).
This is because, given Dxyzw, (6)(d)–(f) jointly entail that x and z uniquely identify the relevant ‘world’ variables y and w, so the latter can be dropped and the formula can be abbreviated as ‘Cyx’.
Other options may be considered, e.g. adapting the translation scheme mentioned by Lewis (1968, p. 119) or the alternative schemes of Forbes (1982, (1983), Ramachandran (1989), or Steinberg (2018). None of these schemes involves the accessibility relation predicate R, though see again above, note 15.
For example, Corsi’s semantics includes certain assumptions on the relationship between accessibility and counterparthood (corresponding to \(\asymp \) below) that here will be dropped altogether. Corsi’s approach is further investigated in Belardinelli (2006, (2007), to which the present developments are also greatly indebted.
Here I am following Lewis in treating names as taking wide scope over modal operators. In Corsi’s semantics, naming is relativized to worlds, hence (7)(a) would include the proviso that \(V(t,w)\in U(w)\) when t is a constant. See Corsi (2002, p. 10).
This is another point of difference with Corsi’s semantics, since her models restrict duty doing to the accessible worlds (2002, p.10). In our formalism, this would amount to assuming from the start the bridging principle (9)(k) introduced below.
Thus, the limitations mentioned in note 11 do not a rise here, as they would not arise if ML were translated into languages more expressive than \(L_E\); see e.g. Montanari et al. (2002), Ohlbach (1991), and Ohlbach and Schmidt (1997). On the other hand, there remains the fact that not all conditions need correspond to a principle of ML. Indeed, Lewis (1968, §2) placed considerable emphasis on the fact that the language of CT allows the formulation of a number of theses—beginning with the postulates of CT itself—that cannot even be expressed in ML, and the point generalizes to the D-based language of Sect. 4. On these issues, see Torza (2013, esp. §4).
This assumption is reflected in the absence of R from the extensional language of Lewis’s original formulation of CT; see again above, note 15.
Sufficiency: Let \(\phi \) be an arbitrary formula with free terms \(t_1,\dots ,t_n\) and suppose for arbitrary M, w that \(M, w \models \Box \phi \). By (8)(\(f_{\scriptscriptstyle \asymp }\)), this means that \(M', w' \models \phi \) for every \(t_1\)...\(t_n\)-variant \(M'\) of M and every \(w' \in W\) such that \(w \prec w'\) and \(V(t_i)|w \asymp V'(t_i)|w'\) for each \(t_i\). Given (9)(g), it follows that \(M', w \models \phi \) for every such variant with \(V(t_i)|w \asymp V'(t_i)|w\) for each \(t_i\). Given (9)(\(g'\)), M itself is one such, and so \(M, w \models \phi \). Hence, \(M, w \models \Box ~\phi \rightarrow \phi \) by (8)(d). Necessity: Suppose T is valid, let M be any model, and pick arbitrary \(w \in W\) and \(i \in I\). Define \(M^*\) to be just like M except that, for some term t and some unary predicate P, \(V^*(t) = i\) and \(V^*(P, w') = A(w')\) for all \(w' \in W\), where \(A(w') =\{i' \in I\): \(i|w \asymp i'|w'\}\) if \(w \prec w'\) and \(A(w') = \varnothing \) otherwise. Pick \(w'\) such that \(w \prec w'\) and let \(M'\) be any t-variant of \(M^*\) such that \(V^*(t)|w \asymp V'(t)|w'\), i.e. \(i|w \asymp V'(t)|w'\). Then \(V'(t) \in V^*(P, w')\), i.e. \(V'(t) \in V'(P, w')\), and so \(M', w' \models Pt\) by (8)(a). By generalization and (8)(\(f_{\scriptscriptstyle \asymp }\)), this means that \(M^*, w \models \Box Pt\). Since T is valid, we also have that \(M^*, w \models \Box Pt \rightarrow Pt\), hence \(M^*, w \models Pt\) by (8)(d), and hence \(V^*(t) \in V^*(P, w)\) by (8)(a). But \(V^*(t) = i\) and \(V^*(P, w) = A(w)\). Therefore \(i \in A(w)\), i.e., \(i|w \asymp i|w\) (satisfying (9)(\(g'\))), and hence \(A(w) \ne \varnothing \), i.e., \(w \prec w\) (satisfying (9)(g)).
Cf. the remarks at the end of Lewis (1968), where Lewis finally considers the possibility of accommodating relative modalities into the extensional framework of CT. It is worth stressing, as he does, that the comparison may yield different answers depending on whether the formulas in B, 4, and 5 are allowed to contain free terms.
If \(\phi \) contains no free terms, then \(\Box \phi \) is satisfied at a world w according to (8)(\(f_{\scriptscriptstyle \asymp }\)) iff it is satisfied at w according to (8)(f), and so the validity of \(\Box \phi \rightarrow \phi \) depends exclusively on the \(\prec \)-reflexivity condition (9)(g).
Proof: Assume \(\prec \) is reflexive. If \(\phi \) contains no free terms, then again (8)(\(f_{\scriptscriptstyle \asymp }\)) will agree with (8)(f) and \(\Box \phi \rightarrow \phi \) will be valid for standard reasons. Otherwise, suppose \(\phi \) has free terms \(t_1, \dots , t_n\) and consider the universal closure \(\forall x_1 \dots \forall x_n (\Box \psi \rightarrow \psi )\), where \(\psi \) is \(\phi [x_1/t_1 \dots x_n/t_n]\). Pick arbitrary M and w, let \(M^*\) be any \(x_1\dots x_n\)-variant of M such that \(V^*(x_i) \in U(w)\) for each \(x_i\), and suppose \(M^*, w \models \Box \psi \). By (8)(\(f_{\scriptscriptstyle \asymp }\)), we have \(M', w' \models \psi \) for every \(x_1\dots x_n\)-variant \(M'\) of \(M^*\) and every \(w' \in W\) such that \(w \prec w'\) and \(V^*(x_i)|w \asymp V'(x_i)|w'\) for each \(x_i\). Since \(w \prec w\), it follows that \(M', w \models \psi \) for every such variant with \(V^*(x_i)|w \asymp V'(x_i)|w\) for each \(x_i\). And since \(V^*(x_i) \in U(w)\) for each \(x_i\), (9)(c) implies that \(M^*\) itself is such a variant, hence \(M^*, w \models \psi \). Therefore \(M^*, w \models \Box \psi \rightarrow \psi \) by (8)(d). Because \(M^*\) was an arbitrary variant with \(V^*(x_i) \in U(w)\) for each \(x_i\), it follows by generalization and (8)(e) that \(M, w \models \forall x_1 \dots \forall x_n (\Box \psi \rightarrow \psi )\).
If \(V(t) \not \in U(w)\), then by (9)(e) there can be no \(w' \in W\) and no t-variant \(M'\) of M such that \(V(t)|w \asymp V'(t)|w'\), and so \(M, w \models \Box ~Pt\) (vacuously). On the other hand, if \(V(t) \not \in V(P,w)\), then \(M, w \not \models Pt\) by (8)(a). Hence \(M, w \not \models \Box Pt \rightarrow Pt\) by (8)(d).
It’s easy to check that the proof in note 30 goes through just as well if (8)(
 ) is used instead of (8)(\(f_{\scriptscriptstyle \asymp }\)). Similarly for the argument in note 29, since (8)(
) is used instead of (8)(\(f_{\scriptscriptstyle \asymp }\)). Similarly for the argument in note 29, since (8)( ) agrees with (8)(f) on formulas containing no free terms.
) agrees with (8)(f) on formulas containing no free terms.Witness Kripke: “Am I myself necessarily self-identical? Someone might argue that in some situations [...] I would not even have existed and therefore the statement ‘Saul Kripke is Saul Kripke’ would have been false” (1971, p. 137). This is actually one motivation that may lead one to replace (8)(a)–(b) with the stronger conditions in (8)(\(a'\))–(\(b'\)).
Forbes ’s (1982) variant of CT departs from Lewis’s precisely on this score: it rejects austerity and the translation algorithm validates neither CBF nor NE.
For example, suppose \(W=\{w,w'\}\), \(U(w)=\{i_1,i_2\}\), \(U(w')=\{i'_1\}\), \(V(a)=i_1\), \(V(b)=i_2\), \(V(Q,w)=\{i_1\}\), \(V(Q,w')=\varnothing \), and \(V(P,w)=\{\langle i_1,i_2\rangle \}\).
This is often neglected in the literature, though see e.g. Davies (1978) for an early discussion.
Proof: Suppose \(M, w \not \models \Box \phi \rightarrow \Box \psi \) and assume without loss of generality that \(\phi \) and \(\psi \) involve some free terms, say \(t_1^{\scriptscriptstyle \phi }, \dots , t_j^{\scriptscriptstyle \phi }\) and \(t_1^{\scriptscriptstyle \psi }, \dots , t_k^{\scriptscriptstyle \psi }\). By (8)(d) we have that (i) \(M, w \models \Box \phi \) and (ii) \(M, w \not \models \Box \psi \). By (8)(\(f_{\scriptscriptstyle \asymp }\)), (ii) implies the existence of a \(t_1^{\scriptscriptstyle \psi }, \dots , t_k^{\scriptscriptstyle \psi }\)-variant \(M^{\scriptscriptstyle \psi }\) of M and some \(w' \in W\) such that (iii) \(M^{\scriptscriptstyle \psi } , w' \not \models \psi \), where \(w \prec w'\) and \(V(t_h^{\scriptscriptstyle \psi })|w \asymp V^{\scriptscriptstyle \psi }(t_h^{\scriptscriptstyle \psi })|w'\) for each \(t_h^{\scriptscriptstyle \psi }\). Given (9)(m), M must also have a \(t_1^{\scriptscriptstyle \phi }, \dots , t_j^{\scriptscriptstyle \phi }\)-variant \(M^{\scriptscriptstyle \phi }\) such that \(V(t_i^{\scriptscriptstyle \phi })|w \asymp V^{\scriptscriptstyle \phi }(t_i^{\scriptscriptstyle \phi })|w'\) for each \(t_i^{\scriptscriptstyle \phi }\), and (i) implies that (iv) \(M^{\scriptscriptstyle \phi } , w' \models \phi \). In particular, we can choose \(M^{\scriptscriptstyle \phi }\) so that \(V^{\scriptscriptstyle \phi }(t_i^{\scriptscriptstyle \phi })=V^{\scriptscriptstyle \psi }(t_h^{\scriptscriptstyle \psi }\)) whenever \(t_i^{\scriptscriptstyle \phi }=t_h^{\scriptscriptstyle \psi }\). Now let \(t_1, \dots , t_n\) be the free terms in \(\phi \rightarrow \psi \) and define a \(t_1, \dots , t_n\)-variant \(M'\) of M by setting \(V'(t_i)=V^{\scriptscriptstyle \psi }(t_i)\) if \(t_i=t_h^{\scriptscriptstyle \psi }\) for some \(t_h^{\scriptscriptstyle \psi }\), and \(V'(t_i)=V^{\scriptscriptstyle \phi }(t_i)\) otherwise. Given (iii) and (iv), it’s easy to verify that \(M', w' \not \models \psi \) and \(M', w' \models \phi \). Thus \(M', w' \not \models \phi \rightarrow \psi \) by (8)(d) and hence \(M, w \not \models \Box (\phi \rightarrow \psi )\) by (8)(\(f_{\scriptscriptstyle \asymp }\)).
For more on this sort of logic, see Varzi (2006).
References
Bacon, A. (2014). Representing counterparts. The Australasian Journal of Logic, 11, 90–113.
Barwise, J., & Perry, J. (1985). Shifting situations and shaken attitudes. An interview. Linguistics and Philosophy, 8, 105–161.
Belardinelli, F. (2006). Quantified modal logic and the ontology of physical objects. Pisa, Scuola Normale Superiore, Ph.D. thesis.
Belardinelli, F. (2007). Counterpart semantics for quantified modal logic. In R. Honzík & O. Tomala (Eds.), The logica yearbook 2006 (pp. 11–22). Prague: Filosofia.
Braüner, T., & Ghilardi, S. (2007). First-order modal logic. In P. Blackburn, J. van Benthem, & F. Wolter (Eds.), Handbook of modal logic (pp. 549–620). Amsterdam: Elsevier.
Burgess, J. P. (2011). Kripke models. In A. Berger (Ed.), Saul Kripke (pp. 119–140). Cambridge: Cambridge University Press.
Chihara, C. S. (1998). The worlds of possibility. Modal realism and the semantics of modal logic. Oxford: Oxford University Press.
Corsi, G. (2002). Counterpart semantics. A foundational study on quantified modal logics. Amsterdam, Institute for Logic, Language and Computation, research report PP-2002-20.
Corsi, G. (2001). Counterparts and possible worlds. A study on quantified modal logic. Bologna: CLUEB.
Corsi, G. (2003). BF, CBF and Lewis semantics. Logique et Analyse, 46, 103–122.
Cresswell, M. J. (2004). Adequacy conditions for counterpart theory. Australasian Journal of Philosophy, 82, 28–41.
Davies, M. K. (1978). Weak necessity and truth theories. Journal of Philosophical Logic, 7, 415–439.
Fara, D. G. (2008). Relative-sameness counterpart theory. The Review of Symbolic Logic, 1, 167–189.
Fine, K. (1981). Model theory for modal logic—Part III: Existence and predication. Journal of Philosophical Logic, 10, 293–307.
Fine, K. (1994). Essence and modality. Philosophical Perspectives, 8, 1–16.
Fitting, M. (2004). First-order intensional logic. Annals of Pure and Applied Logic, 127, 171–193.
Forbes, G. (1982). Canonical counterpart theory. Analysis, 42, 33–37.
Forbes, G. (1983). More on counterpart theory. Analysis, 43, 149–152.
Forbes, G. (1985). The metaphysics of modality. Oxford: Clarendon.
Forbes, G. (1987). Free and classical counterparts: Response to Lewis. Analysis, 47, 147–152.
Hazen, A. P. (1979). Counterpart-theoretic semantics for modal logic. The Journal of Philosophy, 76, 319–338.
Hazen, A. P. (2012). Reflections on counterpart theory. Oxford Studies in Metaphysics, 7, 41–63.
Heller, M. (1998). Property counterparts in ersatz worlds. The Journal of Philosophy, 95, 293–316.
Hughes, G. E., & Cresswell, M. J. (1996). A new introduction to modal logic. London: Routledge.
Hunter, G., & Seager, W. E. (1981). The discreet charm of counterpart theory. Analysis, 41, 73–76.
Kracht, M., & Kutz, O. (2002). The semantics of modal predicate logic I: Counterpart frames. In F. Wolter, H. Wansing, M. de Rijke, & M. Zakharayaschev (Eds.), Advances in modal logic, Volume 3 (pp. 295–316). Stanford, CA: CSLI Publications.
Kracht, M., & Kutz, O. (2005). The semantics of modal predicate logic II: Modal individuals revisited. In R. Kahle (Ed.), Intensionality (pp. 60–97). Wellesley, MA: Association for Symbolic Logic.
Kracht, M., & Kutz, O. (2007). Logically possible worlds and counterpart semantics for modal logic. In D. Jacquette (Ed.), Handbook of the philosophy of science. Volume 5: Philosophy of logic (pp. 943–996). Amsterdam: Elsevier.
Kripke, S. A. (1959). A completeness theorem in modal logic. The Journal of Symbolic Logic, 24, 1–14.
Kripke, S. A. (1963). Semantical considerations on modal logic. Acta Philosophica Fennica, 16, 83–94.
Kripke, S. A. (1971). Identity and necessity. In M. K. Munitz (Ed.), Identity and individuation (pp. 135–164). New York: New York University Press.
Kripke, S. A. (1972). Naming and necessity. In D. Davidson, & G. Harman (Eds.), Semantics of natural language (pp. 253–355, 763–769). Dordrecht: Reidel.
Lewis, D. K. (1968). Counterpart theory and quantified modal logic. The Journal of Philosophy, 65, 113–126.
Lewis, D. K. (1971). Counterparts of persons and their bodies. The Journal of Philosophy, 68, 203–211.
Lewis, D. K. (1973). Counterfactuals. Oxford: Basil Blackwell.
Lewis, D. K. (1976). The paradoxes of time travel. American Philosophical Quarterly, 13, 145–152.
Lewis, D. K. (1983). Postscripts to ‘Counterpart theory and modal logic’. In Philosophical papers, Volume 1 (pp. 39–46). Oxford: Oxford University Press.
Lewis, D. K. (1986). On the plurality of worlds. Oxford: Blackwell.
Lewis, D. K. (1993). Counterpart theory, quantified modal logic, and extra argument places. Analysis, 53, 69–71.
McDaniel, K. (2004). Modal realism with overlap. Australasian Journal of Philosophy, 82, 137–152.
McDaniel, K. (2006). Modal realisms. Philosophical Perspectives, 20, 303–331.
McLeod, S. (2008). How to reconcile essence with contingent existence. Ratio, 21, 314–328.
Menzel, C. (1990). Actualism, ontological commitment, and possible world semantics. Synthese, 85, 355–389.
Merricks, T. (2003). The end of counterpart theory. The Journal of Philosophy, 100, 521–549.
Montanari, A., Policriti, A., & Slanina, M. (2002). Alternative translation techniques for propositional and first-order modal logics. Journal of Automated Reasoning, 28, 397–415.
Ohlbach, H. J. (1991). Semantics-based translation methods for modal logics. Journal of Logic and Computation, 1, 691–746.
Ohlbach, H. J., & Schmidt, R. A. (1997). Functional translation and second-order frame properties of modal logics. Journal of Logic and Computation, 7, 581–603.
Plantinga, A. C. (1974). The nature of necessity. Oxford: Clarendon.
Plantinga, A. C. (1987). Two concepts of modality: Modal realism and modal reductionism. Philosophical Perspectives, 1, 189–231.
Ramachandran, M. (1989). An alternative translation scheme for counterpart theory. Analysis, 49, 131–141.
Ramachandran, M. (2003). Contingent identity and Kripkean counterpart theory. In T. Childers & O. Majer (Eds.), The logica yearbook 2002 (pp. 207–219). Prague: Filozofia.
Ramachandran, M. (2008). Kripkean counterpart theory. Polish Journal of Philosophy, 2, 89–106.
Schwarz, W. (2012). How things are elsewhere: Adventures in counterpart semantics. In G. Russell & G. Restall (Eds.), New waves in philosophical logic (pp. 8–29). New York: Palgrave Macmillan.
Schwarz, W. (2013). Generalising Kripke semantics for quantified modal logics. Manuscript http://www.umsu.de/papers/generalising.pdf.
Stalnaker, R. (1987). Counterparts and identity. Midwest Studies in Philosophy, 11, 121–140.
Stalnaker, R. (1995). The interaction of modality with quantification and identity. In W. Sinnott-Armstrong, D. Raffman, & N. Asher (Eds.), Modality, morality, and belief: Essays in honor of Ruth Barcan Marcus (pp. 12–28). Cambridge: Cambridge University Press.
Steinberg, A. (2018). Adequate counterpart translations. Mind, 127, 547–563.
Torza, A. (2011). Models for counterparts. Axiomathes, 21, 553–579.
Torza, A. (2012). ‘Identity’ without identity. Mind, 121, 67–95.
Torza, A. (2013). How to Lewis a Kripke–Hintikka. Synthese, 190, 743–779.
van Benthem, J. (1983). Modal logic and classical logic. Naples: Bibliopolis.
van Benthem, J. (2001). Correspondence theory. In D. M. Gabbay & F. Guenthner (Eds.), Handbook of Philosophical Logic, Second Edition. Volume 3 (pp. 325–408). Dordrecht: Kluwer.
van Inwagen, P. (1986). Two concepts of possible worlds. Midwest Studies in Philosophy, 11, 185–213.
Varzi, A. C. (2001). Parts, counterparts, and modal occurrents. Travaux de Logique, 14, 151–171.
Varzi, A. C. (2006). Strict identity with no overlap. Studia Logica, 82, 371–378.
Wiggins, D. (1976). The de re “must”: A note on the logical form of essentialist claims. In G. Evans & J. McDowell (Eds.), Truth and meaning: Essays in semantics (pp. 131–160). Oxford: Oxford University Press.
Woodward, R. (2017). Ersatz counterparts. Oxford Studies in Metaphysics, 10, 235–257.
Woollaston, L. (1994). Counterpart theory as a semantics for modal logic. Logique et Analyse, 37, 255–263.
Funding
Open access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Varzi, A.C. Counterpart theories for everyone. Synthese 197, 4691–4715 (2020). https://doi.org/10.1007/s11229-020-02720-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-020-02720-1



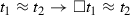
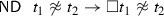
 ) is used instead of (8)(
) is used instead of (8)( ) agrees with (8)(f) on formulas containing no free terms.
) agrees with (8)(f) on formulas containing no free terms.