Two morals about a modal paradox

Abstract

Chisholm’s paradox serves as an important constraint on our modal theorising. For example, one lesson of the paradox is that widely accepted essentialist theses appear incompatible with metaphysical necessity obeying a logic that includes S4. However, this article cautions against treating Chisholm’s paradox in isolation, as a single line of reasoning. To this end, the article outlines two crucial morals about Chisholm’s paradox which situate the paradox within a broad family of paradoxes. Each moral places significant constraints on the paradox’s solution space. In light of this perspective, the paper applies the two morals to a recently proposed solution to Chisholm’s Paradox by Benj Hellie, Murray and Wilson (in: Bennett and Zimmerman (eds) Oxford studies in metaphysics, Oxford University Press, Oxford, 2012).

Chisholm’s Paradox serves as an important constraint on our modal theorising.¹ In response to the paradox, Nathan Salmon (1986, 1989) has proposed that S4 is not a lower bound on the logic of metaphysical necessity. Others, such as Chisholm (1967) himself, have adopted an extremely stringent form of essentialism. More recently, Benj Hellie, Adam Murray, and Jessica Wilson (2012; forthcoming) have developed an interesting view of relativised metaphysical necessity according to which metaphysical necessity exhibits a distinctive type of relativity.

The purpose of this article is to emphasise, bolster, and apply two important morals about Chisholm’s Paradox. Each moral places significant constraints on the paradox’s solution space. The moral of equivalence is that in certain systems of modal logic Chisholm’s Paradox is a mere logical variant of a paradox involving no iterated necessity claims. This moral was first noticed by Graeme Forbes (1984, pp. 172–173); however, the current article clarifies it significantly and bolsters the moral in crucial respects. In light of that discussion, the article argues that the moral of equivalence creates significant awkwardness for Hellie, Murray, and Wilson’s treatment of Chisholm’s paradox in terms of relativised metaphysical necessity. Supplementing this, the moral of revenge is that some proposed solutions to Chisholm’s Paradox are susceptible to revenge versions of the paradox. Following Andrew Bacon’s (2018, chap. 15) recent discussion of an essentialist paradox, the article develops a revenge paradox for Hellie, Murray, and Wilson’s proposed solution in terms of relativised metaphysical necessity. Although each moral will be applied to this proposed solution, it will be clear that they embody more general lessons.

The structure of the article is as follows. Section 1 introduces Chisholm’s Paradox in its canonical form, as developed by Hugh Chandler (1976) and Nathan Salmon (1986; 1989), and charts the surrounding logical geography. In doing so, the article draws and bolsters the moral of equivalence. With an eye to applying each moral, Sect. 2 outlines Hellie, Murray, and Wilson’s proposed solution in detail. Subsequently, the article outlines how the moral of equivalence creates significant awkwardness for their solution. Section 3 then turns to developing the moral of revenge. Since revenge paradoxes must be developed in the context of a proposed solution, the article constructs a revenge paradox in the context of Hellie, Murray, and Wilson’s proposal. Finally, Sect. 4 concludes.

A family of paradoxes?

Essence is not an utterly liberal notion: typically it is assumed that an object’s modal profile does not permit total variation in how that object may be.² For example, one notable essentialist constraint is the idea that no material object could have originated from material totally different to that from which it actually does. As Kripke (1980, p. 113; final emphasis mine) wrote in his now influential discussion:

How could a person originating from different parents, from a totally different sperm and egg, be this very woman? One can imagine, given the woman [Queen Elizabeth II], that various things in her life could have changed: that she should have become a pauper; that her royal blood should have been unknown, and so on. [...] This seems to be possible. And so it’s possible that even though she were born of these parents she never became queen. Even though she were born of these parents, like Mark Twain’s character [in The Prince and The Pauper] she was switched off with another girl. But what is harder to imagine is her being born of different parents. It seems to me that anything coming from a different origin would not be this object.

Let us call this idea Kripke’s Thesis:

Kripke’s Thesis Material objects cannot originate from matter totally different to that from which they do.

There appears to be reasonable textual evidence for attributing Kripke the view that no material object can originate from matter totally different to that from which it does; see in particular Kripke (1980, p. 114, n. 56). For this reason, Kripke’s Thesis should be understood in terms of a universal restricted quantifier over material objects (as should Tolerance below).

Although Kripke’s Thesis serves as one constraint on material objects’ modal profiles, ordinary objects are not utterly intolerant to modal variation. Indeed, as Nathan Salmon (1986, 1989) famously noted, essence is reasonably tolerant. For example, although Queen Elizabeth II could not have had a totally different origin, surely she could have originated from a sperm with a difference of only one mitochondrion to the one from which she actually originated. As Salmon (1989, p. 5; his emphasis) describes a similar, now also famous case:

[A] particular material artifact—say, a particular wooden table which we may call ‘Woody’—could have originated from matter slightly different from its actual original matter $m^*$ (while retaining its numerical identity, or its haecceity) but not from entirely different matter.

To be explicit again, let us call this thesis Tolerance:

Tolerance Material objects can originate from matter slightly different to that from which they do.

Note that Tolerance is not itself to be read as implicitly necessitated, although its explicit necessitation will be considered at various points in what follows.

Hugh Chandler (1976) and Nathan Salmon (1986, 1989) both credit Roderick Chisholm (1967) with the observation that under natural assumptions Kripke’s Thesis and Tolerance together lead to paradox.³ Following Salmon’s (1986, 1989) presentation, the argument leads with the idea that Tolerance is no contingent accident, and that it is a matter of necessity that material objects can originate from matter slightly different to that from which they do. An informal version of the argument, which eventually will be regimented much more carefully, is then often presented as follows.

Let ‘Woody’ refer to some actual wooden table which originates from six, equally sized and shaped pieces of matter, $mm_{6}$. (Here, ‘$mm_{6}$’ is a plural name.) For simplicity, assume that it necessary, and necessarily necessary ... that Woody originates from six parts. Now consider $mm_{5}$, the actual pieces of matter just like $mm_{6}$ except whereas $mm_{6}$ include $m_1$, $mm_{5}$ include $n_1$—an object distinct from but qualitatively similar to $m_1$. By Tolerance, Woody could have originated from $mm_{5}$. However, by the necessitation of Tolerance, Woody then could have originated from $mm_{4}$, the pieces of matter just like $mm_{5}$ except whereas $mm_{5}$ include $m_2$, $mm_{4}$ include $n_2$—an object distinct from but qualitatively similar to $m_2$. Yet iterating this reasoning leads to the claim that had Woody originated from $mm_{1}$, then it could have originated from matter completely different from that which it actually does, in apparent violation of Kripke’s Thesis.

An immediate observation is that the behaviour of iterated modalities in the argument requires articulating with greater care. In order to do so, it will help to introduce some formal resources in the form of a simple modal propositional logic.

The official regimentation will proceed in a simple modal propositional language $\mathcal {L}$, which consists of countably many proposition letters ($p_{0}, p_{1},\ldots$), $\lnot$ (negation) and $\rightarrow$ (the material conditional) as the only truth-functional connectives, and $\Box$ (metaphysical necessity), with $\Diamond$ and the other connectives introduced metalinguistically as usual. Informally, think of ‘$p_{6}$’ as the sentence ‘Woody originates from six parts, $m_{1}$,..., $m_{6}$’, ‘$p_{5}$’ as the sentence ‘Woody originates from six parts, $m_{1}$,..., $m_{5}$, $n_{6}$’, ‘$p_{4}$’ as the sentence ‘Woody originates from six parts, $m_{1}$,..., $m_{4}$, $n_{5}$, $n_{6}$’, and so on. Under this informal understanding, the sentence $\lnot \Diamond p_0$ formalises a relevant instance of Kripke’s Thesis for Woody and the sentence $p_{6} \rightarrow \Diamond p_{5}$ formalises the instance of Tolerance concerning Woody. Similarly, sentences of the form $\Box (p_{i} \rightarrow \Diamond p_{i-1})$ (for $1 \le i \le 6$) may be understood as formalising instances of the necessitated version of Tolerance concerning Woody. Working in $\mathcal {L}$, one version of Salmon’s argument then runs as follows:

Premise (1) is the assumption that Woody originates from the six $mm_{6}$. Again, premise (2) is the relevant instance of Tolerance concerning Woody, and premises (3)–(7) may be understood as formalising instances of the necessitated version of Tolerance concerning Woody. Yet (8) contradicts the claim that it is not possible for Woody to originate from material totally different to that from which it actually does ($\lnot \Diamond p_{0}$), the formalisation of the relevant instance of Kripke’s Thesis. Following the extant practice, let us call this argument Chisholm’s Paradox.

Chisholm’s Paradox is valid in any normal system of modal logic that contains K4 in the sense that it has all instances of the following schemas as theorems:

K  $\Box (\phi \rightarrow \psi ) \rightarrow \Box \phi \rightarrow \Box \psi$

4  $\Diamond \Diamond \phi \rightarrow \Diamond \phi$

The K and 4 schemas are used to prove that $\Diamond p_{i-1}$ is implied by $\Box (p_{i} \rightarrow \Diamond p_{i-1})$ and $\Diamond p_{i}$, for in K one can derive all instances of the following schema:

K$^\Diamond$  $\Box (\phi \rightarrow \psi ) \rightarrow \Diamond \phi \rightarrow \Diamond \psi$

Yet with K$^\Diamond$ one can show that $\Box (p_{i} \rightarrow \Diamond p_{i-1})$ implies $\Diamond p_{i} \rightarrow \Diamond \Diamond p_{i-1}$. So given that $\Diamond p_{i}$, it follows that $\Diamond \Diamond p_{i-1}$. Thus from 4, one may conclude $\Diamond p_{i-1}$.

Another essentialist paradox, however, can be extracted from the above Woody case which does not require any instance of the 4 schema.⁴ This paradox takes the form of a straightforward modal sorites. It begins with the idea of Tolerance, that Woody could have originated from matter $mm_5$ slightly different to that from which it actually does ($mm_6$). But, the soritical thought goes, if $mm_i$ is slightly different from $mm_6$, so is $mm_{i-1}$. Thus, the argument runs, if Woody could have originated from $mm_5$ it could have originated from $mm_4$. However, by iterating this thought, Woody could have originated from $mm_0$. Formally:

Call this paradox the Modal Sorites. The striking feature of this argument is that it does not involve any modal rules of inference or applications of modal axiom schemata. As in the case of an ordinary non-modal sorites, the conclusion (8$'$) is derived from the premise via repeated application of modus ponens. Indeed, (2$'$) is the merely unnecessitated instance of Tolerance concerning Woody. Moreover, the other premises are instances of the soritical principle that if it is metaphysically possible for a material object to originate from certain matter, then it is metaphysically possible for that material object to originate from slightly different matter.

Although the Modal Sorites and Chisholm’s Paradox are based on the same principles and case, superficially they might appear quite dissimilar. After all, the Modal Sorites is based on very typical soritical reasoning, whereas the necessitated version of Tolerance behind Chisholm’s Paradox may not appear at all soritical in nature. Naturally, this has lead to a discussion in the literature of whether they are one and the ‘same’ paradox. For example, Forbes (1984, pp. 172–173) stresses the similarity of Chisholm’s Paradox with the Modal Sorites, and recommends a treatment of the former which follows that of the latter. Salmon (1986, p. 89; his emphasis), however, explicitly argues that Chisholm’s Paradox “comes out differently in a very important respect from a standard sorites argument”, and emphasises that Chisholm’s Paradox is a “paradox of modality”, presumably in contrast to the Modal Sorites, a paradox of vagueness. In later work, Salmon (1993) repeats this point in response to Williamson (1990, p. 127), who observes the similarity of the Modal Sorites to Chisholm’s Paradox and suggests that it would be insufficiently general to weaken the logic of metaphysical necessity in order to handle the latter exclusively.

Clearly, this is a contested issue. Moreover, the debate will not be advanced by trading instinct-based judgements about what is at the ‘heart’ of each paradox, or what they are genuinely ‘about’. What is required is an agreed upon working sufficient condition for treating the paradoxes uniformly. And, indeed, one naturally suggests itself: logical equivalence. As will be shown, each premise (m) (for $1 \le m \le 8$) of Chisholm’s Paradox is logically equivalent to premise $(m')$ of the Modal Sorites in logics which contain K45, the least normal modal system with all instances of K, 4, and the following schema as axioms:

5 $\Diamond \phi \rightarrow \Box \Diamond \phi$

In this sense, Chisholm’s Paradox and the Modal Sorites may be said to be logically equivalent in logics which contain K45.

Moral of Equivalence  Chisholm’s Paradox and the Modal Sorites are logically equivalent in logics which contain K45.

To show that Chisholm’s Paradox and the Modal Sorites are logically equivalent in the above sense, the only non-trivial equivalences that require establishing are between (3)–(7) and (3$'$)–(7$'$) all of which have the following respective forms (for $1 \le n < 6$):⁵

(m) $\Box (p_{n} \rightarrow \Diamond p_{n-1})$

$(m'$) $\Diamond p_{n} \rightarrow \Diamond p_{n-1}$

Yet Proof 1 in the appendix establishes that (m) implies $(m'$) in K4, the least normal modal system which extends system K with all instances of 4. Moreover, Proof 2 in the appendix establishes that $(m'$) implies (m) in K5, the least normal modal system which extends system K with all instances of 5. Thus, given a logic for metaphysical necessity which includes K45, one must treat the paradoxes uniformly.

It is worth stressing the importance of this observation to certain discussions of Chisholm’s Paradox. In particular, some authors have argued that ‘soriticality’ is inessential to Chisholm’s Paradox since there are versions of the paradox which do not involve minuscule variations in the possible origins of a given object, but instead larger scale variations in its origins. For example, Sarah-Jane Leslie (2011, pp. 282–283) presents the case of an axe made from three macroscopic parts, a handle, a blade, and a shaft. Leslie then considers a version of Chisholm’s Paradox, the major premise of which is that necessarily if the axe originates from a certain handle, blade, and shaft, then it is possible that the axe originates from exactly two but not all three of the handle, blade, and shaft.⁶ However, the moral of equivalence demonstrates that this ‘large scale’ version of Chisholm’s Paradox will be equivalent in logics containing K45 to arguments involving no nested modal claims, and whose validity is guaranteed merely by modus ponens. Thus, even though the non-nested equivalent may not have the form of a standard sorites series (since it does not appeal to minuscule variations in the axe’s origins), this does not negate the fact that in K45 one cannot blame iterated modalities for generating the ‘large-scale’ version of Chisholm’s Paradox. Moreover, if one were attracted to a vagueness-based solution to these modal paradoxes, it would not be unreasonable to believe that it is indeterminate whether the major premise of the ‘large-scale’ version of Chisholm’s Paradox is true, just as it would not be unreasonable to believe that it is indeterminate whether certain ‘large-scale’ removals of hair result in a person becoming bald.

Interestingly, one can also show that (m) and $(m'$) are not equivalent when the logic of necessity does not include K45.⁷ This highlights that those who take the logic of metaphysical necessity not to include K45 lose some warrant for treating the paradoxes uniformly, since the two paradoxes are no longer logically equivalent in the sense above. Put contrapositively, if one wishes to equate the paradoxes on the basis of their logical equivalence then one’s modal logic must include all instances of 4 and 5. To demonstrate the technical claim, it suffices to establish the following fact.

(EQ-45)  Let KEQ be the normal modal system which extends K with the following axiom: EQ  $(\Diamond p \rightarrow \Diamond q) \leftrightarrow \Box (p \rightarrow \Diamond q)$. KEQ includes all instances of 4 and 5.

Proof 3 in the appendix establishes (EQ-45). Thus, in modal systems weaker than K45, (m) and $(m'$) simply cease to be logically equivalent. Of course, this would not force one into treating the paradoxes non-uniformly in such settings, since logical equivalence was not necessary for a uniform treatment of the paradoxes. However, it does suggest that motivation for a uniform treatment of the paradoxes in settings weaker than K45 is somewhat lacking.

The non-equivalence of (m) and $(m'$) in systems weaker than K45 can be brought out vividly by certain non-K45 models. Since it will be helpful to have a model theory in which to situate the discussion in the following sections, we shall define a class of Kripke models for $\mathcal {L}$. To this end, let a frame $\mathfrak {F}$ be a pair $\langle \mathcal {W}, \mathcal {R}\rangle$, where $\mathcal {W}$ is a non-empty set (‘the worlds’), and $\mathcal {R}$ is a binary relation on $\mathcal {W}$ (‘accessibility’). A model $\mathfrak {M}$ of $\mathcal {L}$ based on $\mathfrak {F}=\langle \mathcal {W}, \mathcal {R}\rangle$ is a triple $\langle W, \mathcal {R}, \mathcal {V}\rangle$ where $\mathcal {V}$ is a total function from pairs of the form $\langle \phi , w\rangle$, for some proposition letter $\phi$ and $w \in W$, to either 0 (falsity) or 1 (truth). We define ‘($\mathfrak {M}, w) \models \phi$’ for $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$, $w\in \mathcal {W}$, and $\phi$ a formula of the language, recursively as follows (where ‘A’ is an atomic formula, and $\phi$ and $\psi$ formulae of $\mathcal {L})$:

• $(\mathfrak {M}, w) \models A$ iff $\mathcal {V}(A, w) = 1$;

• $(\mathfrak {M}, w) \models \lnot \phi$ iff $(\mathfrak {M}, w) \not \models \phi$;

• $(\mathfrak {M}, w) \models \phi \rightarrow \psi$ iff either $(\mathfrak {M}, w) \not \models \phi$ or $(\mathfrak {M}, w) \models \psi$;

• $(\mathfrak {M}, w) \models \Box \phi$ iff $(\mathfrak {M}, u) \models \phi$, for all $u \in W$ such that $w\mathcal {R}u$.

For an $\mathcal {L}$ model $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$, a formula $\phi$ of $\mathcal {L}$ is true at $w \in \mathcal {W}$ iff $(\mathfrak {M}, w) \models$ $\phi$. A formula $\phi$ of $\mathcal {L}$ is true in an $\mathcal {L}$ model $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$ iff it is true at all $w \in \mathcal {W}$. A formula $\phi$ of $\mathcal {L}$ is valid iff it is true in every $\mathcal {L}$ model. A set $\Gamma$ of $\mathcal {L}$ formulas entails an $\mathcal {L}$ formula $\phi$ iff for every $\mathcal {L}$ model $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$ and every $w \in \mathcal {W}$, if $(\mathfrak {M}, w) \models$ $\gamma$ for every $\gamma \in \Gamma$, then $(\mathfrak {M}, w) \models$ $\phi$. We shall say that an argument with premises $\Gamma$ and conclusion $\phi$ is valid when $\Gamma$ entails $\phi$.

With this formal apparatus, one can see that the following S4 model $\mathfrak {M}_4$ = $\langle \mathcal {W}_4, \mathcal {R}_4, \mathcal {V}_4\rangle$ shows that $(m'$) does not even imply (m) in S4:

• $\mathcal {W}_4 = \mathbb {N}$

• $\mathcal {R}_4$ = $\{\langle w,u\rangle : w=6\,\,\text {or}\,\,w=u\}$

• $\mathcal {V}_4(p_{n},w) = 1$ iff $w=n\le 6$

This model can be represented in diagram form. In these diagrams, ‘worlds’ are represented as labelled circles with the name of the ‘world’ occurring outside the circle. Inside the circle are the proposition letters which are ‘true’ at that ‘world’ in the given model. Moreover, ‘accessibility’ amongst ‘worlds’ is represented by arrows, although some instances of ‘accessibility’ will be left implicit for presentational reasons. For example, if ‘accessibility’ is reflexive, arrows from circles to themselves are omitted; when ‘accessibility’ is universal, arrows are omitted altogether.

As can be checked, $\mathfrak {M}_4, 6 \models \Diamond p_{n} \rightarrow \Diamond p_{n-1}$ for positive n. However, $\mathfrak {M}_4, 6 \not \models \Box (p_{n} \rightarrow \Diamond p_{n-1})$, for positive $n< 6$. At this point, it is pertinent to emphasise that Salmon (1986, p. 87) claims that the paradoxes are equivalent in S4.⁸ However, although (m) implies $(m'$) in systems which include K4, the above is an S4 model in which the converse fails. This is significant because, contra Salmon’s suggestion, it demonstrates that there is no analogue of the moral of equivalence merely with respect to S4.

Similarly, we can specify a T model $\mathfrak {M}_{\text {T}}$ = $\langle \mathcal {W}_{\text {T}}, \mathcal {R}_{\text {T}}, \mathcal {V}_{\text {T}}\rangle$ to establish that (m) does not imply $(m'$) in T (in this model, the function |.| takes an integer to its absolute value):

• $\mathcal {W}_{\text {T}} = \mathbb {N}$

• $\mathcal {R}_{\text {T}}$ = $\{\langle w,u\rangle : |w - u| = 1\}$

• $\mathcal {V}_{\text {T}}(p_{n},w) = 1$ iff $w=n\le 6$

Again in diagram form:

In this model, it can be checked that $\mathfrak {M}_{\text {T}}, 5 \models \Box (p_{4} \rightarrow \Diamond p_{3})$ despite $\mathfrak {M}_{\text {T}}, 5 \not \models \Diamond p_{4} \rightarrow \Diamond p_{3}$. Moreover, it is worth emphasising that $\mathfrak {M}_{\text {T}}$ is a B model too, since $\mathcal {R}_{\text {T}}$ is symmetric and reflexive over $\mathcal {W}_{\text {T}}$, which highlights the importance of the 4 schema to securing the implication of $(m'$) by (m).

These technical facts vindicate the above claim that weakening the logic of metaphysical necessity in the appropriate way renders $(m'$) and (m) non-equivalent. More specifically, even in S4 $(m'$) and (m) are not equivalent.

Relativised metaphysical necessity

In a series of recent articles, Benj Hellie, Adam Murray, and Jessica Wilson (2012; forthcoming) have developed a view of metaphysical necessity according to which it exhibits a type of relativity.⁹ According to their view, what is metaphysically necessary is relative to which world is considered as ‘indicatively actual’. This view of relativised metaphysical modality, hereafter RMM, promises interesting solutions to a variety of modal puzzles and paradoxes such as Chisholm’s Paradox, Fine’s (2005) arguments against Modal Monism, and arguments for the necessity of existence. One of the most attractive features of these solutions is their advertised capacity to maintain an S5 logic for metaphysical necessity. Moreover, as Murray and Wilson (2012, pp. 190–198) note, an advantage of RMM is that it is ‘formally analogous’ (2012, pp. 190–198) to the epistemic interpretation of the two-dimensional semantic framework, which provides a natural class of models that are ‘heuristically useful’ (2012, pp. 190–191; forthcoming, p. 2) for studying RMM. Nevertheless, despite the promise of RMM, the purpose of this section is to argue that the moral of equivalence creates significant awkwardness for RMM’s solution to Chisholm’s Paradox. To this end, this section will present the details of RMM in the context of a two-dimensional modal logic. The strategy will first be to outline the epistemic interpretation of the two-dimensional semantic framework and then clarify the formal analogy between it and RMM.

According to Chalmers’ version of two-dimensionalism, with every expression of a language—not just each predicate letter—is associated a two-dimensional intension. One can think of a two-dimensional intension as complex semantic value from which two subsidiary intensions can be recovered, a primary intension and a secondary intension. In the simple case of monadic predicates, primary intensions are functions from metaphysically possible worlds considered as actual to sets of individuals, and secondary intensions are functions from metaphysically possible worlds considered as counterfactual to sets of individuals.¹⁰ Consider some world $w_{1}$ where the clear, transparent, drinkable liquid which runs from taps, makes up roughly 55% of the human body, etc., has the chemical composition XYZ. The primary intension of ‘water’ takes $w_{1}$ to XYZ. But the secondary intension we actually assign ‘water’ takes $w_{1}$ to H$_{2}$O. Roughly speaking, the thought is that when we consider a world as actual, we consider what the expression ‘water’ would pick out at that world had its usage been the same as it actually is. When we consider a world as counterfactual, we consider what water (i.e. H$_{2}$O) would have been like at that world.

Clearly, two-dimensionalism and the twin-earth thought experiments used to motivate semantic externalism are closely connected. The lesson of semantic externalism is that there are aspects of an expression’s meaning which in some sense depend on how the non-linguistic world turns out. If the clear, transparent, drinkable liquid which runs from taps, makes up roughly 55% of the human body, etc., has the chemical composition XYZ, then ‘water’ refers to XYZ; if the clear, transparent, drinkable liquid which runs from taps, makes up roughly 55% of the human body, etc., has the chemical composition H$_{2}$O, as it actually does, then ‘water’ refers to H$_{2}$O. Two-dimensionalism incorporates the fact that the semantic values of expressions like ‘water’ exhibit non-trivial dependence on the non-linguistic world into its semantic theory by assigning them a primary intension whose extension varies with which world is considered as actual.

An upshot to the two-dimensional picture is that truth-value assignments to sentences governed by metaphysical modal operators will be sensitive to which world is considered as actual. For instance, considering the actual world as actual it is metaphysically necessary that water is H$_{2}$O. But considering $w_{1}$ as actual, it is metaphysically impossible that water is H$_{2}$O, for under that supposition necessarily it is XYZ. It can help to see a tabular representation of the two-dimensional intension the epistemic two-dimensionalist assigns to a given expression. Take the sentence ‘water is H$_{2}$O’. In the following table, the labels of rows correspond to which world is considered as actual, and the labels of the columns correspond to which world is considered as counterfactual:

‘Water is H$_{2}$O’	H$_{2}$O world	XYZ world
H$_{2}$O world	T	T
XYZ world	F	F

The diagonal of Ts and Fs reaching from the top left T to the bottom right F corresponds to the sentence’s primary intension—hence its aptronym ‘the diagonal intension’. The rows correspond to the secondary intension that the sentence is assigned when the H$_{2}$O-world and XYZ-world are respectively considered as actual, which clearly represent two different functions. Thus an expression’s secondary intension along with its extension varies with which world is considered as actual, hence why metaphysical necessities are sensitive to which world we consider as actual.

Murray and Wilson (2012) offer a ‘metaphysical’ interpretation of the Chalmersian framework, whilst retaining the “formal analogy” (p. 198) to it. To be specific, Murray & Wilson depart from epistemic two-dimensionalism in their interpretation of secondary intensions. The traditional line is to treat all secondary intensions, except the one assigned when the actual world is considered as actual, as mere epistemic necessities for all we know a priori. However, Murray and Wilson (2012, p. 211) regard them as genuine ‘relativised’ metaphysical necessities. Hellie, Murray and Wilson (forthcoming, p. 15; their emphasis) later describe this view as follows.

Our intended picture is moderate modal naturalism: facts about natural law (and, in turn, about metaphysical possibility) have a hybrid explanation: some such facts are underdetermined either by any abstract metaphysical principles alone, or by any actual contingent ‘categorical’ facts alone, but instead only become determined through the concretization of certain true such principles in actual categorical facts.

Nevertheless, whatever departure Murray and Wilson make from epistemic two-dimensionalism, they still endorse (2012, p. 203) the claim that not all truths vary with which worlds are considered as actual, since there must be some ‘basic’ ways of individuating or specifying worlds which are invariant as such. Indeed, like Chalmers, they (2012, p. 202) hold that “the basic individuation of worlds [...] might proceed by way of, e.g., ‘semantically stable’ (Bealer 2000) or ‘canonical’ (Chalmers 2006) descriptions.” Effectively, this guarantees that Murray and Wilson’s ‘metaphysical’ interpretation of the Chalmersian framework does not depart foundationally from Chalmers’ preferred epistemic construal. At points in the following discussion, this will become pertinent.¹¹$^,$¹²

A central moral that Murray and Wilson want to draw from Chisholm’s Paradox is that truth-value assignments to essentialist claims about Woody’s material makeup are highly sensitive to which world is considered as actual. As one way of predicting this sensitivity, they (2012, p. 206) entertain a view on which proper names like ‘Woody’ function similarly to natural kind terms. On this implementation of RMM, just as the denotation of ‘water’ varies with which world is considered as actual, so does the denotation of ‘Woody’. As a consequence, the various denotations of ‘Woody’ differ in their modal profiles, specifically regarding the matter from which they can originate. Advocates of RMM suggest that acknowledging this sensitivity dissolves Chisholm’s Paradox.

To provide more detail, regarding Chisholm’s Paradox Murray and Wilson would claim that when we consider world 6 as actual it is necessary that amongst all six of Woody’s original parts are, say, at least three of those which it has at 6. However, when we consider world 4 as actual it is not necessary that amongst all six of Woody’s original parts are at least three of those which it has at 6, for when world 4 is considered as actual ‘Woody’ changes its denotation. Thus, when world 4 is considered as actual, it is necessary that amongst all six of Woody’s parts are at least three of those it has at 4 (and so one of those which it has at 6).

To clarify this proposal, it helps to provide a simple model of Chisholm’s Paradox within the RMM framework.¹³ To do so, the previously used propositional language $\mathcal {L}$ is extended to $\mathcal {L}^\downarrow$ with the modal operator $\downarrow$, which will be used in the object-language to express which world is considered as actual. An RMM-frame $\mathfrak {F}=\langle \mathcal {W}, \mathcal {R}\rangle$ is an $\mathcal {L}$ frame in which $\mathcal {R}$ is an equivalence relation. An RMM-model $\mathfrak {M}$ of $\mathcal {L}^\downarrow$ based on an RMM-frame $\mathfrak {F}=\langle W, \mathcal {R}\rangle$ is a triple $\langle W, \mathcal {R}, \mathcal {V}\rangle$ in which $\mathcal {V}$ is now a total function from triples of the form $\langle \phi , w, u\rangle$, for some proposition letter $\phi$ and $w,u \in W$, to either 0 (falsity) or 1 (truth). The idea will be that truth at $\langle w, u\rangle$ corresponds to truth at world u when w is considered as indicatively actual. We thus define ‘($\mathfrak {M}, w, u) \models \phi$’ for $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$, $w, u \in \mathcal {W}$, and $\phi$ a formula of the language, recursively as follows (where ‘A’ is an atomic formula, and $\phi$ and $\psi$ formulae of $\mathcal {L}_{p})$:

• $(\mathfrak {M}, w, u) \models A$ iff $\mathcal {V}(A, w, u) = 1$;

• $(\mathfrak {M}, w, u) \models \lnot \phi$ iff $(\mathfrak {M}, w, u) \not \models \phi$;

• $(\mathfrak {M}, w, u) \models \phi \rightarrow \psi$ iff either $(\mathfrak {M}, w, u) \not \models \phi$ or $(\mathfrak {M}, w, u) \models \psi$;

• $(\mathfrak {M}, w, u) \models \Box \phi$ iff $(\mathfrak {M}, w, u') \models \phi$, for all $u' \in W$ such that $u\mathcal {R}u'$;

• $(\mathfrak {M}, w, u) \models \, {\downarrow }\phi$ iff $(\mathfrak {M}, u, u) \models \phi$.

For an RMM-model $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$, a formula $\phi$ of $\mathcal {L}$ is true at $\langle w, u\rangle$ for $w,u \in \mathcal {W}$ iff $(\mathfrak {M}, w, u) \models$ $\phi$. A formula $\phi$ of $\mathcal {L}$ is true in an RMM-model $\mathfrak {M}$ = $\langle \mathcal {W}, \mathcal {R}, \mathcal {V}\rangle$ iff it is true at $\langle w, u\rangle$ for all $w,u \in \mathcal {W}$.¹⁴ A formula $\phi$ of $\mathcal {L}$ is RMM-valid iff it is true in every $\mathcal {L}$ model.

At this point, it is worth highlighting that officially Murray and Wilson (2012, pp. 190–191, n. 1) note that their proposal “does not involve any additional [modal] operators” such as $\downarrow$, which is typically present in two-dimensional logics.¹⁵ However, Murray and Wilson (2012, p. 197) offer a specification of Salmon’s argument in terms of subscripted possibility operators in order to clarify their diagnosis of it. The $\downarrow$ operator is used here as a mere alternative to such subscripted operators.

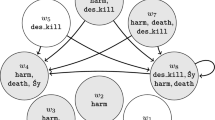
Consider a particular RMM-model $\mathfrak {M}_2$ = $\langle W_2, \mathcal {R}_2, \mathcal {V}_2\rangle$ of $\mathcal {L}^\downarrow$, defined as follows.

$\mathcal {W}_2 =\{n \in \mathbb {N} : n \le 6\}$

$\mathcal {R}_2$ = $\mathcal {W}_2\times \mathcal {W}_2$

$\mathcal {V}_2(p_{n},w,m) = {\left\{ \begin{array}{ll} 1,&{} \text {if}\,\,m=n\,\,\wedge \,\, |w-n|\le 3 \\ 0, &{}\text {otherwise} \end{array}\right. }$

This model can also be represented in diagram form. As before, ‘worlds’ are represented as labelled circles with the name of the ‘world’ occurring outside the circle, and proposition letters which are ‘true’ at that ‘world’ in the given model occurring inside the circle. Each row corresponds intuitively to ‘metaphysical modal space’ when a certain ‘world’ (the marked node) is considered as ‘indicatively actual’. Since accessibility is universal, the diagram uses no arrows.

Put informally, in this RMM-model when world 6 is considered as indicatively actual, Woody must originate from at least half of the matter it does at 6. Yet considering world 4 as indicatively actual, Woody can originate from just less than half of the matter it does at 6. One can see this formally by noticing the following facts about the model:

• $\mathcal {V}_2(p_{n}, n, n) = 1$, for all $n \in \mathcal {W}$

• $\mathcal {V}_2(p_{2}, 6, n) = 0$, for all $n \in \mathcal {W}$

• $\mathcal {V}_2(p_{2}, 4, 2) = 1$

As a result $(\mathfrak {M}_2, 6, 6) \not \models \Diamond p_{2}$, yet $(\mathfrak {M}_2, 4, 6) \models \Diamond p_{2}$. However, despite this, $\mathfrak {M}_2$ does not serve as a countermodel to any instance of axiom schema 4. For all instances of $\Diamond \Diamond \phi \rightarrow \Diamond \phi$ are true in $\mathfrak {M}_2$ given the definition of $\mathcal {R}_2$. Indeed, all the axioms of S5 are true in $\mathfrak {M}_2$, since S5 is sound over the class of RMM-frames. Indeed, Murray and Wilson (2012, p. 204; p. 208) view the retention of S5 as a central advantage of the RMM solution, particularly over Nathan Salmon’s (1986, 1989) anti-S4 proposal.

Of course, it follows that advocates of RMM view Chisholm’s Paradox, i.e. the above formal line of reasoning in $\mathcal {L}$, as an RMM-valid argument. Thus, advocates of RMM will reject one of its premises. Yet they will not reject premise (1), since it is a fact about Woody’s actual origins. Moreover, they will not reject premise (2) since in their terms it merely amounts to the claim that (considering the actual world as indicatively actual) Woody could have originated from slightly different matter, which their approach is designed to recognise. Thus they must reject at least one of premises (3)–(7). To be more precise, say that advocates of RMM accept (reject) a claim exactly when that claim is true (false) when the actual world is considered as indicatively actual. Since in the above model world 6 models the actual world, advocates of RMM will reject premise (5), the formula $\Box (p_3 \rightarrow \Diamond p_2)$. Read informally, (5) is the claim that it is metaphysically necessary that if Woody originates from six parts, $m_1, m_2, m_3, n_4, n_5, n_6$ then it is metaphysically possible that Woody originates from six parts, $m_1, m_2, n_3, n_4, n_5, n_6$ (recall that $p_6$ is understood informally as the claim that Woody originates from six parts, $m_1,\ldots , m_6$). However, advocates of RMM would be keen to stress that (5) is true when world 4 is considered as indicatively actual. Hence Murray and Wilson (2012, p. 198–199; my emphasis) diagnose the fallacy of Chisholm’s Paradox to be that accepting its premises involves “iterated or in situ shifts in which world is held fixed as indicatively actual” that “illegitimately shift indicatively actual horses in modal mid-stream”.

Murray and Wilson (2012, p. 197) specify a version of Salmon’s argument in terms of subscripted possibility operators in order to clarify how iterated shifts in which world is held fixed as indicatively actual figure in the reasoning. As mentioned before, the $\downarrow$ operator is used here as a mere alternative to such subscripted operators. In terms of this alternative, Murray and Wilson would accept all of the following claims:

(RMM1) $\lnot \Diamond p_2$

(RMM2) $\Box (p_3 \rightarrow \, {\downarrow }\Diamond p_2)$

(RMM3) $\Diamond {\downarrow }\Diamond p_2$

Indeed, in the above model one can easily verify that (RMM1)–(RMM3) are all true at $\langle 6, u\rangle$ for any $u \in \mathcal {W}$. Thus although the advocate of RMM will reject $\Box (p_3 \rightarrow \, \Diamond p_2)$, they will accept (RMM2) which involves the iterated shift in which world is considered as indicatively actual

Nevertheless, despite this novel diagnosis of Chisholm’s Paradox, the moral of equivalence creates significant awkwardness for the proposed RMM solution. As emphasised in Sect. 1, the moral of equivalence is that Chisholm’s Paradox and the Modal Sorites are logically equivalent in logics which contain K45. Since S5 is one such logic, this generates the consequence that the advocate of RMM must recognise that (3)–(7) are equivalent with (3$'$)–(7$'$) respectively. But in the context of RMM, this consequence is bizarre. The crucial point is that the Modal Sorites involved no nested modal claims, so it is extremely difficult to see why it would result from ‘iterated shifts’ in which world is considered as indicatively actual. Indeed, as stressed previously, the distinctive feature of the Modal Sorites is that it can be run solely from the perspective of the actual world since its premises are all claimed to be actually true. However, since the advocate of RMM will reject one of (3)–(7) from Chisholm’s Paradox, given S5 they must also reject one of (3$'$)–(7$'$) from the Modal Sorites. But there is no scope to ameliorate the denial of one of (3$'$)–(7$'$) by merely prefixing its consequent with an occurrence of ${\downarrow }$, as the advocate of RMM attempted to with (RMM2) in response to their denial of (5). To appreciate this, notice that both of the following two formulas would be rejected by advocates of RMM in the above model:

(5$'$) $\Diamond p_3 \rightarrow \, \Diamond p_2$

(5$'{\downarrow }$) $\Diamond p_3 \rightarrow \, {\downarrow }\Diamond p_2$

Thus one cannot ameliorate the denial of (5$'$) by blaming its allure on an iterated shift in perspective.

The concern can be stated more generally by appeal to the so-called reduction theorem of S5. Say that a formula of $\mathcal {L}^\downarrow$ is nested iff it belongs to $\mathcal {L}$ and contains an occurrence of $\Box$ which occurs within the scope of some other occurrence of $\Box$. Similarly, say that a formula of $\mathcal {L}^\downarrow$ is non-nested iff it belongs to $\mathcal {L}$ and contains no occurrence of $\Box$ within the scope of some other occurrence of $\Box$. According to these definitions, $\Box \Box p$ and $\Box (p \rightarrow \lnot \Box \lnot q)$ are nested formulas, $\Box p$ and $(\lnot \Box \lnot p \rightarrow \Box p)$ are non-nested formulas, and any formula which contains any occurrences of $\downarrow$ is neither nested nor non-nested. The S5 reduction theorem may then be stated as follows.¹⁶

S5 Reduction Theorem Any nested $\mathcal {L}^\downarrow$ formula is S5 equivalent to a non-nested $\mathcal {L}^\downarrow$ formula.

According to the S5 Reduction Theorem, nested modal claims are always S5 equivalent to non-nested claims. Thus, S5 is simply not hospitable to blaming modal paradox on ‘iterated shifts’ of perspective induced by nested modal claims. In doing so, the advocate of RMM rejects a nested claim. However, given the S5 Reduction Theorem, that nested claim is S5 equivalent to a non-nested claim, which the advocate of RMM must therefore reject. But they cannot explain their rejection of the non-nested claim by appeal to ‘iterated shifts’ of perspective induced by nested modal claims.

Supplementing this, it does not seem persuasive to ameliorate the denial of (5$'$) by merely citing its S5 equivalence to (5), even if we grant that (5)’s denial can be ameliorated by blaming its allure on an iterated shift in perspective. First, there is the point that one should not expect hyperintensional features like allurement to be closed under logical implication (or known logical implication). For example, one might be allured to the axioms of ZFC on the grounds of set-theoretic platonism, yet not be so allured to the Banach-Tarski theorem despite knowing the axioms to imply it. Moreover, in addition, the manoeuvre does not appear to constitute a satisfactory amelioration of one’s rejection of (5$'$) anyway. To offer an analogy in point, consider two different formulations of an ordinary non-modal sorites paradox. As its major premises, the first employs a collection of ‘no sharp boundary’ theses of the form $\lnot (p_n \wedge \lnot p_{n+1})$. In contrast, as its major premises the second employs collection of ‘inductive’ conditionals of the form $p_n \rightarrow p_{n+1}$. Now, consider an advocate of a solution to the sorites paradox who refuses to accept one of the ‘no sharp boundary’ theses but explains its allure in terms of a very specific cognitive mechanism pertaining to embeddings of negations in the context of vagueness. Regardless of the explanation’s idioscyncracy, surely even this character should recognise that either they ought to reject classical logic or find some other way to ameliorate their rejection of the inductive conditional which is classically equivalent to the negated conjunction in question.

In summary, the retention of S5 creates significant awkwardness for RMM’s diagnosis of why Chisholm’s Paradox is fallacious. Like Nathan Salmon’s anti-S4 solution, the RMM diagnosis places great emphasis on the occurrence of nested necessity operators. Yet blaming modal paradox on ‘iterated shifts’ of perspective induced by nested necessity operators is difficult to reconcile with the characteristic feature of S5 that possibility is simply a non-contingent matter. This casts doubt on whether RMM offers a satisfactory solution to Chisholm’s Paradox.

The moral of revenge

Adequate solutions to paradoxes must have the capacity to handle ‘revenge’ variants of the paradox. Infamously, crude non-bivalent solutions to the Liar Paradox suffer from revenge paradoxes in the form of ‘strengthened liar’ sentences.¹⁷ Similarly, proposed solutions to Chisholm’s Paradox must have the capacity to handle revenge variants of it, if they are susceptible them.

The exact formulation of revenge Chisholm paradoxes will of course depend on the proposed solution to the initial paradox. However, in recent work Andrew Bacon (2018, pp. 280–281) has formalised a quantified version of the Modal Sorites in which all the non-modal terms involved in the argument are precise. Since there is a close similarity—indeed an S5 equivalence—between Chisholm’s Paradox and the Modal Sorites, Bacon’s non-modally precise Modal Sorites can be adapted to construct revenge Chisholm’s Paradoxes. In particular, it can be adapted to generate a revenge paradox for the RMM treatment of Chisholm’s Paradox.

To appreciate this point, recall the connection between semantic externalism and two-dimensionalism. As was previously emphasised, expressions susceptible to twin-earth style thought experiments—twin-earthable expressions—are assigned primary intensions which assign different secondary intensions to the expression at different worlds considered as actual. But not all expressions are twin-earthable. As Chalmers (2012, p. 374) himself recognises, many expressions are non-twin-earthable, or semantically neutral, in that their primary intension assigns the expression the same secondary intension across all worlds considered as actual.¹⁸ Such expressions include items of purely logical vocabulary like quantifiers and the truth-functional connectives, the predicates which feature in developed mathematical theories, foundational physics, and phenomenal terms like ‘consciousness’. Indeed, as Chalmers (2012, pp. 233–243) emphasises, that there are such semantically neutral expressions is crucial to one’s being in principle capable of articulating a semantically neutral description of the world—something which is integral to the two-dimensionalist program. Moreover, as highlighted previously, Murray and Wilson appeal to this feature of the two-dimensionalist program in their development of RMM. Consequently, if there are variants of Chisholm’s Paradox formulated solely in terms of semantically neutral expressions, the RMM proposal lacks the resources to handle them, for the modal status of semantically neutral sentences is not sensitive to which world is considered as indicatively actual. But by adapting Bacon’s non-modally precise Modal Sorites, there are variants of exactly this kind. The strategy will be to purge all non-semantically neutral expressions such as proper names from the paradox and replace them with semantically neutral expressions such as logical vocabulary. Likewise, we shall ensure that there are only semantically neutral predicates in the statement of the paradox. Given that it is key to the two-dimensionalist (and RMM) program that worlds can be described in semantically neutral terms, there is always guaranteed to be such a paradox which makes use of only semantically neutral predicates.

To present such a variant, a quantified modal language is required. Thus let $\mathcal {L}^+$ contain countably many individual variables ($x, y,\ldots$), countably many plural variables ($xx, yy,\ldots$), the two-place logical predicates $=$ (identity) and $\prec$ (is one of), the non-logical predicates $\Sigma$ (originates from) and < (is an original proper part of), $\lnot$ (negation) and $\rightarrow$ (the material conditional) as the only truth-functional connectives, $\forall$ (universal quantification), and $\Box$ (necessity), all of which are semantically neutral. The predicates $\Sigma$ and $\prec$ take individual variables in their first argument and plural variables in their second argument; the predicates and $=$ and < take individual variables in both arguments. Although not formally required by the argument, informally one might want to think of the formula $\Sigma (x, xx)$ as being true (under a given assignment) only when (what is assigned to) the xx do not merely comprise only (what is assigned to) x. One could formalise this claim with the formula $\Sigma (x, xx) \rightarrow \exists y (y \prec xx \wedge y \not =x)$, but, to reiterate, that assumption is not strictly required.

We also define numerical quantifiers $\exists _{n}$ read as ‘there are at least n’ (for $n>0$) in the usual way:

where $\phi [x_i/x]$ is the result of substituting all free occurrences of x in $\phi$ for $x_i$, and $x_1$–$x_n$ are the first n variables not to occur free in $\phi$ given some fixed ordering.

As metalinguistic abbreviations, we introduce an identity-like predicate $\equiv$ which takes plural variables in both its arguments and an existence predicate E which applies to plural variables as follows:

$xx \equiv yy =_{df} \forall x(x \prec xx \leftrightarrow x \prec yy)$

$Exx =_{df} \exists yy(yy \equiv xx)$

As is standard, the background modal plural logic requires that plural variables behave rigidly with respect to $\prec$, in the sense that if this thing is (not) one of those things, then necessarily that thing is (not) one of those things, provided those things exist.¹⁹

(Rgd$^+$)  $x \prec xx \rightarrow \Box (Exx \rightarrow x \prec xx)$

(Rig2$^-$)  $\lnot x \prec xx \rightarrow \Box (Exx \rightarrow \lnot x \prec xx)$

As Linnebo (2016, p. 645) highlights, in the presence of standard background assumptions (Rgd$^+$) and (Rgd$^-$) imply the necessity of the co-extensionality of plurals:

(NC)  $\forall xx \forall yy(xx \equiv yy \rightarrow \Box \, xx \equiv yy)$

Less formally, (NC) states that when these things are exactly those things, they are necessarily as such. In this setting, it is also natural to assume that necessarily an individual’s original proper parts are exactly those things which it originates from:

(${\Sigma }{<}$)  $\Box \forall xx\forall x(\Sigma (x, xx) \rightarrow \forall y(y < x \leftrightarrow y \prec xx))$

However, this assumption is neither required by nor used in the following argument.

A semantically neutral variant of the paradox may now be stated in $\mathcal {L}^+$. For simplicity, let us reconsider a simplified version of the Woody case in which, as before, actually Woody originates from six parts, however there is only one complex object (Woody) and nothing else besides its six original proper parts.²⁰ This added simplicity will merely reduce the complexity in what follows, and is not key to the broader point about being able to construct revenge Chisholm Paradoxes. In this semantically neutral version of the paradox, informally the first premise states that actually there is only one complex object and nothing else besides its original proper parts. Formally, this can be stated as the premise that there are some things from which some other thing originates, and this is the only case of some thing originating from some things:

(R1) $\exists xx\exists x(\Sigma (x,xx) \wedge \forall yy \forall y(\Sigma (y, yy) \rightarrow y =x \wedge yy \equiv xx))$

Premise (R1) will be abbreviated by the formula $\exists ! xx\exists ! x\Sigma (x,xx)$, and I shall use a similar convention in the case of other formulas.

An instance of Tolerance then states that if some thing originates from some things, it is possible that that thing exists but one of those things is not one of its original proper parts.

(R2) $\exists ! xx\exists ! x(\Sigma (x,xx) \rightarrow \Diamond (\exists z(z=x) \wedge \exists _{1}y(y \prec xx \wedge \lnot y<x)))$

The remaining premises can be viewed as instances of necessitated Tolerance. For instance, the third premise formalises the claim that if some thing originates from some things, then necessarily if that thing exists but one of those things is not one of its original proper parts, then it is possible that the thing exists but two of those things are not amongst its original proper parts.

(R3)

$\exists ! xx\exists ! x(\Sigma (x,xx) \rightarrow \Box [(\exists z(z=x) \wedge \exists _{1}y(y \prec xx \wedge \lnot y<x)) \rightarrow \Diamond (\exists z(z=x) \wedge \exists _{2}y(y \prec xx \wedge \lnot y<x))])$

Again as before, there are a number of similar premises terminating in the premise that if some thing originates from some things, then necessarily if that thing exists and five of those things are not amongst its original proper parts, then it is possible that the thing exists and six of those things are not amongst its original proper parts.

In standard plurally quantified modal systems which contain S4, one can then derive the claim that the only thing which originates from some things is such that it could exist whilst originating from totally different matter.

(R8) $\exists ! xx\exists ! x(\Sigma (x,xx) \rightarrow \Diamond (\exists z(z=x) \wedge \exists _{6}y(y \prec xx \wedge \lnot y<x)))$

More precisely, in the appendix it is shown that premises (R1)–(R7) entail (R8) over a standard class of models for a typical quantified modal plural logic. But from Kripke’s Thesis and the assumption that there is only one complex object and nothing else besides its six original proper parts, the following claim may be inferred:

(R9) $\exists ! xx\exists ! x(\Sigma (x,xx) \rightarrow \lnot \Diamond (\exists z(z=x) \wedge \exists _{6}y(y \prec xx \wedge \lnot y<x)))$

Yet plainly (R9) contradicts (R8).

This is merely a quantified variant of Chisholm’s Paradox. The two-dimensional approach, however, does not have the capacity to handle this particular argument, for it is formulated entirely in terms of semantically neutral vocabulary. Specifically, logical expressions like quantifiers do not exhibit the same variability in extension across worlds considered as actual as proper names like ‘Woody’ do. Since all variations of a paradox ought to be afforded the same treatment, the RMM solution lacks the required scope.

One can anticipate the complaint that $\Sigma$ (originates from) and < (is an original proper part of) are not semantically neutral, perhaps due to it being contested that they are susceptible to twin-earth style thought experiments. However, regardless of whether they are, remember that it is key to the two-dimensionalist (and RMM) program that entire worlds can be described in semantically neutral terms. This includes their facts about mereology and origins. Accordingly, there must be some semantically neutral conditions in terms of which $\Sigma$- and <-facts can be redescribed. A variant of the above argument could then be run in which those neutral conditions are uniformly substituted for $\Sigma$ and < in the appropriate manner. Indeed, given RMM’s reliance on basic semantically neutral descriptions of worlds, there will always be revenge versions of Chisholm Paradox that they are unable to handle. More generally, the following moral may be drawn.

Moral of Revenge  Some proposed solutions to Chisholm’s Paradox are susceptible to revenge versions of the paradox.

Concluding remarks

As stated in the beginning, Chisholm’s Paradox provides important constraints on our modal theorising. However, as the morals of equivalence and revenge demonstrate, one should be cautious about treating Chisholm’s Paradox in isolation, as a single line of reasoning. There are subtle variations on the canonical form of the paradox whose treatment must be incorporated into a holistic solution. Just as Chisholm’s Paradox provides important constraints on our modal theorising, these two morals provide crucial constraints on the space of solutions to the paradox.

Appendix

Definition 1

The language $\mathcal {L}$ is defined using: countably many proposition letters ($p, p_1, ...$); material implication ($\rightarrow$) and negation ($\lnot$) as the only truth-functional connectives, and the unary modal operator $\Box$ (metaphysical necessity).

The well-formed formulas of $\mathcal {L}$ are given by the following rule (where $\alpha$ is a propositional variable):

$\phi := \alpha \,\,|\,\, \lnot \psi \,\,|\,\, (\psi \rightarrow \chi ) \,\,|\,\, \Box \psi$

We write $\top$ as an abbreviation for the string $(p \rightarrow p)$ and $\Diamond$ as an abbreviation for the string $\lnot \Box \lnot$. We introduce $\wedge , \vee ,$ and $\leftrightarrow$ by the usual abbreviations.

Definition 2

K is the axiomatic system for $\mathcal {L}$ with the following axioms and following rules of proof. (Where $\Gamma$ is a set of $\mathcal {L}$ formulas and $\phi$ is an $\mathcal {L}$ formula, $\Gamma \vdash _\mathbf{K} \phi$ abbreviates the claim that there is a finite sequence of formulas each of which is either one of the axioms, a member of $\Gamma$, or follows from earlier items in the sequence by applying one of the rules of proof. $\vdash _\mathbf{K} \phi$ abbreviates $\emptyset \vdash _\mathbf{K} \phi$.)

• PL All tautologies of propositional logic.

• K $\Box (p \rightarrow q) \rightarrow (\Box p \rightarrow \Box q)$

• MP If $\Gamma \vdash _\mathbf{K} \phi$ and $\Gamma \vdash _\mathbf{K} \phi \rightarrow \psi$, then $\Gamma \vdash _\mathbf{K} \psi$

• US If $\vdash _\mathbf{K} \phi$ then $\vdash _\mathbf{K} \psi$, where $\psi$ results from uniformly substituting proposition letters in $\phi$ by arbitrary formulas

• Nec If $\vdash _\mathbf{K} \phi$ then $\vdash _\mathbf{K} \Box \phi$

The formula $\Box (p \rightarrow q) \rightarrow (\Diamond p \rightarrow \Diamond q)$ is labelled K$^\Diamond$; note that $\vdash _\mathbf{K}$ K$^\Diamond$.

Definition 3

Consider the following formulas of $\mathcal {L}$.

• 4 $\Diamond \Diamond p \rightarrow \Diamond p$

• 5 $\Diamond p \rightarrow \Box \Diamond p$

• EQ $(\Diamond p \rightarrow \Diamond q) \leftrightarrow \Box (p \rightarrow \Diamond q)$

When S is an axiomatic system and $\phi$ is an $\mathcal {L}$ formula, S$\phi$ is the axiomatic system which extends S by the addition of $\phi$ as an axiom. In what follows, we consider the following axiomatic systems: K4, K5, K45, and KEQ. When S is an axiomatic system, $\vdash _\mathbf{S }$ should be understood in the same manner as $\vdash _\mathbf{K }$ with the obvious changes.

Theorem 1

$(m) \vdash _\mathbf{K4 } (m')$

Theorem 2

$(m') \vdash _\mathbf{K5 } (m)$

In this proof, note that Nec is not applied to the non-theorem premise $(m'$) or anything which is shown to follow from $(m'$).

Theorem 3

$\vdash _\mathbf{KEQ } \mathbf{5}$

Theorem 4

$\vdash _\mathbf{KEQ } \mathbf{4}$

Definition 4

The language $\mathcal {L}^+$ is defined using: countably many individual variables ($x, y,\ldots$); countably many plural variables ($xx, yy,\ldots$); material implication ($\rightarrow$) and negation ($\lnot$) as the only truth-functional connectives; the unary modal operator $\Box$ (metaphysical necessity); the two-place non-logical predicates < (is an original proper part of) and $\Sigma$ (originates from); the logical predicates $=$ (identity) and $\prec$ (is one of), and, finally, $\forall$ (universal quantification) left ambiguous between both plural and individual quantification.

The well-formed formulas of $\mathcal {L}^+$ are given by the following rule (where v and $v'$ are individual variables and vv is a plural variable):

• $\phi := v = v \,\,|\,\, \Sigma (v, vv) \,\,|\,\, v \prec vv \,\,|\,\, v < v' \,\,|\,\, \forall v\phi \,\,|\,\, \forall vv\phi \,\,|\,\, \lnot \psi \,\,|\,\, (\psi \rightarrow \chi ) \,\,|\,\, \Box \psi$

We use the same abbreviations as before and write $\exists$ for the string $\lnot \forall \lnot$.

Definition 5

A model of $\mathcal {L}^+$ is a triple $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$. In these models, $\mathcal {W}$ is a non-empty set, $\mathfrak {D}$ is a non-empty set, $\mathcal {D}$ is a total function from elements $w \in \mathcal {W}$ to subsets $\mathcal {D}(w)$ of $\mathfrak {D}$. Moreover, $\mathcal {V}$ is a total function from pairs $\langle \Phi , w\rangle$ of non-logical predicates $\Phi$ and elements $w \in \mathcal {W}$ such that:

$\mathcal {V}\langle \Sigma , w\rangle \subseteq \mathcal {D}(w)\times \mathcal {P}(\mathcal {D}(w))$

$\mathcal {V}\langle <, w\rangle \subseteq \mathcal {D}(w)\times \mathcal {D}(w)$

A variable assignment g over an $\mathcal {L}^+$ model $\mathfrak {M}$ is total function from individual variables to elements of $\mathfrak {D}$ and plural variables to subsets of $\mathfrak {D}$. We write g(d/v) for the variable assignment just like g except that it assigns d to the individual variable v; similarly, we write g(S/vv) for the variable assignment just like g except that it assigns S to the plural variable vv.

Definition 6

‘$(\mathfrak {M}, w) \models _g \phi$’ (‘true at w on g’) is defined recursively in the following manner, where $\phi$ is a well-formed formula of $\mathcal {L}^+$, $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$, and $w \in \mathcal {W}$. In this definition, v and $v'$ are individual variables, vv is a plural variable, and $\phi$ and $\psi$ are both well-formed formulas of $\mathcal {L}^+$.

• $(\mathfrak {M}, w) \models _g \Sigma (v, vv)$ iff $\langle g(v), g(vv) \rangle \in \mathcal {V}\langle \Sigma , w\rangle$

• $(\mathfrak {M}, w) \models _g v < v'$ iff $\langle g(v), g(v') \rangle \in \mathcal {V}\langle <, w\rangle$

• $(\mathfrak {M}, w) \models _g v=v'$ iff $g(v)=g(v') \in \mathcal {D}(w)$

• $(\mathfrak {M}, w) \models _g v \prec vv$ iff $g(v) \in g(vv) \subseteq \mathcal {D}(w)$

• $(\mathfrak {M}, w) \models _g \lnot \phi$ iff $(\mathfrak {M}, w) \not \models _g \phi$

• $(\mathfrak {M},w) \models _g \phi \rightarrow \psi$ iff $(\mathfrak {M}, w) \not \models _g \phi$ or $(\mathfrak {M}, w) \models _g \psi$

• $(\mathfrak {M}, w) \models _g \Box \phi$ iff $(\mathfrak {M}, u) \models _g \phi$, for all $u \in W$

• $(\mathfrak {M}, w) \models _g \forall v\phi$ iff $(\mathfrak {M}, w) \models _{g(d/v)} \phi$, for all $d \in \mathcal {D}(w)$

• $(\mathfrak {M}, w) \models _g \forall vv\phi$ iff $(\mathfrak {M}, w) \models _{g(S/vv)} \phi$, for all $S \subseteq \mathcal {D}(w)$

For an $\mathcal {L}^+$ model $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$, a formula $\phi$ of $\mathcal {L}^+$ is true at $w \in \mathcal {W}$ iff $(\mathfrak {M}, w) \models _g$ $\phi$ for all variable assignments g. A formula $\phi$ of $\mathcal {L}^+$ is $\mathcal {L}^+$ valid in a model $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$ iff $\phi$ is true at all $w \in \mathcal {W}$; $\phi$ is valid iff it is valid in all models. A set $\Gamma$ of $\mathcal {L}^+$ formulas $\mathcal {L}^+$ entails an $\mathcal {L}^+$ formula $\phi$ iff for any $\mathcal {L}^+$ model $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$, any $w \in \mathcal {W}$, and any variable assignment g, if every $\gamma \in \Gamma$ is true at w on g then so is $\phi$.

Remark

The semantics validates a standard ‘contingentist’ S5 plurally quantified modal logic including (Rgd$^+$), (Rgd$^-$), and (NC).

Theorem 5

(R1)–(R7) $\mathcal {L}^+$ entail (R8).

Proof

Consider an arbitrary $\mathcal {L}^+$ model $\mathfrak {M}=\langle \mathcal {W}, \mathfrak {D}, \mathcal {D}, \mathcal {V}\rangle$, arbitrary $w \in \mathcal {W}$, and an arbitrary variable assignment g. If (R1) is true at w on g then there is some variable assignment $g'$ different from g at most in what it assigns to x and xx such that $\{\langle g'(x), g'(xx) \rangle \} = \mathcal {V}\langle \Sigma , w\rangle$. Since (R2) is true at w on g, there is some $u \in \mathcal {W}$ such that $g'(x) \in \mathcal {D}(u)$ and there is at least one $d \in g'(xx)$ such that $\langle d, g'(x)\rangle \not \in \mathcal {V}\langle <, u\rangle$. By similar reasoning and the fact that (R3)-(R7) are all true at w on g, there is some $u' \in \mathcal {W}$ such that $g'(x) \in \mathcal {D}(u')$ and there are least six $d \in g'(xx)$ such that $\langle d, g'(x)\rangle \not \in \mathcal {V}\langle <, u'\rangle$. Thus, $(\mathfrak {M}, u') \models _{g'} \exists z(z=x) \wedge \exists _{6}y(y \prec xx \wedge \lnot y<x)$. Hence, $(\mathfrak {M}, w) \models _{g'} \Sigma (x,xx) \rightarrow \Diamond (\exists z(z=x) \wedge \exists _{6}y(y \prec xx \wedge \lnot y<x))$. Given how $g'$ was introduced, $(\mathfrak {M}, w) \models _g \exists ! xx\exists ! x(\Sigma (x,xx) \rightarrow \Diamond (\exists z(z=x) \wedge \exists _{6}y(y \prec xx \wedge \lnot y<x)))$. In other words, (R8) is true at w on g, which completes the proof. $\square$