Abstract
Distance, it is often argued, is the only coherent and empirically adequate world-making relation that can glue together the elements of the world. This paper offers entanglement as an alternative world-making relation. Entanglement is interesting since it is consistent even with quantum gravity theories that do not feature space at the fundamental level. The paper thereby defends the metaphysical salience of such non-spatial theories. An account of distance (space) is the predominant problem of empirical adequacy facing entanglement as a world-making relation. A resolution of this obstacle utilizes insights from the Ryu–Takayanagi formula (a holographic relation between entanglement and spacetime) and Susskind and Maldacena’s related ER = EPR conjecture (a relation between bell pairs and wormholes). Together these indicate how distance can be recovered from entanglement and thus carves the way for entanglement fundamentalism.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A number of our most prominent contending theories of quantum gravity—among them causal set theory and loop quantum gravity—do not feature space at the fundamental level of their ontology (Huggett and Wüthrich 2013).Footnote 1 In these ‘non-spatial’ theories of quantum gravity, space is instead conjectured to be emergent from or reducible to underlying non-spatial degrees of freedom, for instance non-metrical lattices or spin networks. But is a world metaphysically possible, if it does not feature distances as part of its fundamental furniture?
Recently, some have suggested that this question should be answered in the negative questioning the coherence (e.g. Hagar and Hemmo 2013; Lam and Esfeld 2013) and the very metaphysical salience (e.g. Maudlin 2007a; Esfeld 2019) of ontologies without distance.Footnote 2 Most outspoken is perhaps Michael Esfeld (2020; see also Esfeld and Deckert 2017), who argues that we need a relation—a world-making relation—that can connect or glue together the elements of our ontology so they form one world, and distance, according to Esfeld, is the only likely candidate for such a world-making relation.Footnote 3 While Esfeld’s want of a world-making relation is part of the larger metaphysical program of minimalist ontology (which will not be assumed here), the need for a world-making relation can be seen as originating in the apparent fact that we—and the elements we surround ourselves with—belong to the same world: “given a plurality of objects, there has to be a certain type of relations in virtue of which these objects make up a world” (Esfeld and Deckert 2017, p. 3). Distance offers itself as an immediate candidate for such a relation; we are ‘world-mates’ in virtue of being at a distance from each other. Even if distance is absent at the fundamental level as described by non-spatial theories of quantum gravity, the question, however, remains what makes it true that we are world-mates: “in this case, we need another world-making relation than the spatial or spatiotemporal one” (Esfeld 2019, p. 4). In the absence of such an alternative to distance, Esfeld questions the apparent metaphysical import of these non-spatial theories: “as things stand, it is reasonable to recommend caution about proposing far reaching ontological consequences such as the disappearance of spacetime or fundamental spatiotemporal relations” (Esfeld 2019, p. 13).
In this paper, the case will instead be made for an affirmative answer to the question whether fundamentally non-spatial worlds are metaphysically possible and at that, an affirmative answer that should be satisfactory even by the standards of minimalist ontology. Entanglement, it will be proposed, can serve as the fundamental relation that constitutes a world and from which distance (and possibly all other relations) is derived.Footnote 4 Where an ontology with distance as the fundamental relation is at tension with the non-spatial theories of quantum gravity,Footnote 5 entanglement is arguably compatible with these theories: Entanglement is low maintenance in the sense that it can occur in any system with quantum degrees of freedom. It should therefore feature in any theory of quantum gravity. In this regard, entanglement is a promising world-making relation; it is a candidate for a fundamental relation that can build even the fundamentally non-spatial worlds of quantum gravity.
However, answering the question ‘what makes it true that we are worldmates?’ with entanglement involves a metaphysical commitment that goes beyond the usual recognition in quantum mechanics of non-local phenomena and non-separable quantum states. It involves, in the terminology of Glick and Darby (2019), an entanglement realism: that there is real entanglement in the world. Entanglement realism is in itself not new and is also defended, in one form or another, by for instance Teller (1986), Morganti (2009), and Calosi (2014). No one, however, has hitherto argued for entanglement fundamentalism: The view that entanglement is the only fundamentally real relation, though Lam (2013, pp. 67–68) alludes to the possibility. However, already in endorsing entanglement realism, the account of entanglement as the world-making relation is vulnerable to some recent objections to entanglement realism. Since entanglement seems to disappear upon mixing, Seevinck (2006) argues that entanglement cannot be ontologically robust. Healey (2012) argues in a similar fashion, based on delayed-choice entanglement-swapping experiments, that entanglement cannot be real. Finally, Schaffer (2010) has argued that entanglement cannot be a single relation since both two, three and N particles can be entangled. Neither will be dealt with here, and the reader is referred to Timpson and Brown (2010) for a reply to Seevinck, Egg (2013) and Glick (2019) for a reply to Healey, and in reply to Schaffer, it will be observed that entanglement can always be regarded as a relation between a subsystem and the rest of the system (see Sect. 3 for further details and Morganti (2009) for further discussion).
In any case, these challenges to entanglement realism are dwarfed by the ensuing challenges to the more radical entanglement fundamentalism and its claim that entanglement is the world-making relation: how to account for the varied phenomena of both intricate experiments and our everyday world; most prominently in this regard those of distances and generally spatial extension. Though more can and must in general be said about the empirical adequacy of entanglement as the world-making relation, only an account of distance from entanglement will be taken up here. But notice that with such an account, entanglement should be just as empirically adequate, and thus hopefully as successful a world-making relation, as distance. Getting distance from entanglement, however, is no simple matter, and the argument to this effect utilizes recent research on a holographic relation between entanglement and spacetime proposed by Ryu and Takayanagi (2006) and advanced by van Raamsdonk and collaborators (2010a, 2014). The argument will also draw on the related ER = EPR conjecture due to Maldacena and Susskind (2013) that proposes a relation between entanglement and Einstein–Rosen bridges (wormholes). Together, it is argued, these schemes indicate that space, spatial connectivity, and distance can be related to entanglement such that distances might be recovered from entanglement. Here, ‘indicate’ and ‘might’ must be emphasized. The account does not demonstrate that entanglement is the world-making relation, or that we can actually recover all of space from entanglement; for such conclusiveness, the quantum gravity research has to advance significantly. Instead, the modest claim of this paper is that quantum gravity research—in its current preliminary stage—features surprising relations between space and entanglement that render entanglement the most promising candidate for a world-making relation in worlds (possible, and perhaps even most likely, including the actual world) where distance is absent at the fundamental level.
The account of entanglement as the world-making relation is modelled on the minimalist ontology of distanced matter points proposed by Esfeld (2020) and developed in further detail by Esfeld and Deckert (2017). Here distance serves as the world-making relation that grounds spatial extension, individuates simple objects—the matter points—and accounts for change in the world. The first issue, extension, is the central concern of the present paper, while the latter two roles of a world-making relation in minimalist ontology will be the topic of a companion piece to this one. In modelling itself on this ontology of distanced matter points, the account of entanglement as the world making relation has the ambition to be a real alternative to distance in the minimalist ontology. Both the entanglement and distance relation can ground spatial extension, or so it will be argued in Sect. 5, and neither fares better than the other in dealing with the counterexample discussed in Sect. 6 of two entangled particles moving away from each other. Entanglement, however, has the advantage of being consistent even with non-spatial theories of quantum gravity; in contrast with the ontology of distanced matter points.
A contentious element of the ontology of distanced matter points is the matter points themselves. If these are meant to be permanent, discernible, local beables,Footnote 6 they are suspicious from the perspective of most non-Bohmian interpretations of quantum mechanics and due to the observer dependence of particle number in quantum field theory (Unruh 1976). It is therefore important to stress that the proposal to conceive of entanglement as the world-making relation involves no commitment to such permanent, local matter points. As explicated further below, the entanglement relation is a relation between a subsystem and the rest of the system and all it requires is therefore a notion of subsystem. Since space and distance are absent in the fundamental ontology with entanglement as the world-making relation, these subsystems cannot be local beables. However, if their spatial connotations are left behind, matter points do seem compatible with such subsystems and thus with entanglement as the world-making relation. In conceiving entanglement as the world-making relation, proponents of minimalist ontology can therefore preserve most of its metaphysical framework simply with distance replaced by entanglement, while those suspicious of matter points can construe the account more abstractly in terms of subsystems. With the present ambition to offer an alternative world-making relation, the exact ontological character of the relata will only be touched upon in Sect. 7 and a deeper investigation of this ontology will, for the most part, be postponed to future work. For now, the proposed ontology will simply be denoted ‘entangled subsystems’ with the suggestion that the subsystems are not imbued with too much ontological significance beyond their formal characteristics.
The paper proceeds as follows: The first section below introduces world-making. This is followed in Sect. 3 by the development of a definition of entanglement that is independent of references to distances. Section 4 remarks on some quantum field theoretic aspects of entanglement, before it is indicated how entanglement might account for distance, space and extension (Sect. 5). Section 6 refutes the most obvious counterexample to an account of distance in terms of entanglement: That particles can move away from one another without changing their entanglement. It is argued how this counterexample relies on too simple a conception of the proposed relation between distance and entanglement. In this light, Sect. 7 gives a more thorough presentation of the metaphysical conjecture that entanglement is the world-making relation before the conclusion (Sect. 8) summarizes the findings and returns where it started: Quantum gravity.
Along the way, several relevant themes will be left unexplored. In combination with the somewhat controversial nature of the physics relied upon, the present account of the ontology of entangled subsystems is perhaps best regarded as programmatic. Still, the hope is to at least suggest the initial viability of this type of entanglement fundamentalism and thus to invite consideration and further study of ontologies with a central role for entanglement.
2 World-making (in minimalist ontology)
The quest for a world-making relation has its origin in Lewis’ metaphysics where it finds a role both in the Humean supervenience thesis (Lewis 1994) and in his modal realism. By the latter, all the possible worlds exist, and Lewis therefore needs some explanation why something belongs to one rather than another of these worlds. He needs, in other words, an answer to how two entities can be recognized as worldmates: “things are worldmates iff they are spatiotemporally related. A world is unified, then, by the spatiotemporal interrelation of its parts” (Lewis 1986, p. 71). For Lewis, both the notion of world and the worldmate relation are grounded in spatiotemporal relations. As Wüthrich (2019) observes, this generates a tension between Lewisian metaphysics and non-spatial theories of quantum gravity. However, as Darby (2009) observes, Lewis regarded his thesis as fallible. Another “analogically spatiotemporal” relation could be the “worldmate relation” (Lewis 1986, p. 77) and still provide for a consistent metaphysics. By analogically spatiotemporal Lewis (1986, pp. 75–76) means relations that are natural, pervasive, discriminating, and external.Footnote 7 Entanglement is immediately promising as an analogically spatiotemporal relation: entanglement is an external relation that—by the argument of Sect. 4—is pervasive. As will be argued in the companion piece, entanglement is also discriminating which leaves only its naturalness for debate. Entanglement might, in other words, relieve the tension between Lewisian metaphysics and non-spatial theories of quantum gravity. The aim here, however, is not Lewis exegesis, and the exact extent to which entanglement qualifies as an analogically spatiotemporal relation that fulfils the needs of Lewis’ worldmate relation is the topic for another occasion.
While inspired by Lewis, Esfeld and Deckert (2017, p. 56) explicitly state that they are neutral about the metaphysics of modality. The Lewisian inspiration for their minimalist ontology is instead the Humean supervenience thesis; adopting, however, the more radical super-Humean version of it which Esfeld explicates as follows:
While the standard Humean, following Lewis’s thesis of Humean supervenience [...], holds that there are spatial or spatiotemporal relations connecting points and natural intrinsic properties instantiated at these points, the Super-Humean maintains that there are only sparse points that then are matter points with distance relations individuating these points (Esfeld 2020, pp. 1896–1897).
With the matter points having no intrinsic properties and in being individuatedFootnote 8 by the distance relations, “there is nothing more to these objects than standing in these relations” (Esfeld and Deckert 2017, p. 3). Super-Humenism provides for a minimalist ontology in that distance is the only moving part: Distance grounds the plurality of matter points. Distance connects these otherwise detached matter points into a configuration. Any change of this configuration consists of variations of the relative distances between the matter points. Distance relations are the relations in virtue of which the matter points make up a world. Distance, Esfeld and Deckert (2017) argue, is the world-making relation that together with the matter points it itself individuates comprise the best candidate for a coherent and empirically adequate minimalist ontology of the natural world.Footnote 9
While there is this rather straightforward sense in which distance makes the world of Esfeld and Deckert’s minimalist ontology, one may rightfully wonder if this notion of world-making connects at all with that associated with Lewis’ modal realism. Esfeld and Deckert, like Lewis, argue that distance is world-making because it is the relation in virtue of which the elements of the ontology make up a world. However, this question, how are two entities recognized as worldmates, seems to carry a different significance once detached from modal realism. The question no longer concerns why they belong to the same world rather than different worlds among all the existing ones. And relatedly, if only the actual world exists, then two entities could be argued to be worldmates simply in virtue of existing; the appeal to distance thus seems superfluous.Footnote 10 In my view, however, there are at least affinities between Lewis’ worldmate relation and world-making as it features in minimalist ontology. For Esfeld and Deckert, it appears, not all existing entities have to be distanced: “We conceive the distance relations as establishing the order of what coexists” (Esfeld and Deckert 2017, 7, emphasis added). As the world-making relation, distance defines a configuration and thus establishes what exists together at an instant in time. Though Esfeld and Deckert never consider the possibility, an imagined set of matter points—each associated with a list of their distances to other matter points—might prove to comprise of two spatially disconnected configurations. The matter points would form two configurations rather than one in virtue of the distance relations that obtain between the matter points. Both configurations would exist; one could possibly conceive of them as two decoupled sections of a multiverse. However, only the matter points within each configuration would coexist, whereas the two decoupled configurations would not coexist. In this sense, spatial distance establishes what coexists. In Lewis’ metaphysics, spatiotemporal relations has an analogous role: If Lewis were given a set of entities, the spatiotemporal relations between them would tell him how many possible worlds they were gathered from. Due to the differences in the ontologies, the possible types of entities in Lewis’ set of entities are very different from those of Esfeld and Deckert’s set which only admits matter points and possibly only those of the actual world. This, however, is a question about the type of entities of the ontology—the relata—and not about the role of the relations it features. In particular, a single notion of world-making relation seems to be able to capture both cases well, despite their differences:
Definition: The world-making relation is the relation that accounts for the connectedness in the ontology including why some elements may be completely detached from one another.Footnote 11
It is arguably a stretch to say that this definition captures all the subtleties of Lewis’ worldmate relation, but it at least covers the idea that it is the spatiotemporal interrelations that unify a world and, by the same argument, why different worlds are not unified but instead decoupled from each other. As regards Esfeld and Deckert, the definition is still consistent with their agnosticism whether there actually are any decoupled sectors; either in the form of other possible worlds or disconnected parts of a single multiverse. With or without such decoupled sectors, the world-making relation accounts for the connectedness of the ontology as exemplified by distance when it—in the minimalist ontology—establishes the coexistence of matter points.
As such, the need for a world-making relation neither depends on modal realism nor on minimalist ontology. Rather, it originates in the aspiration to account for the apparent fact that we and our surroundings at every instance in time do form a connected whole. More abstractly, the world-making relation is meant to account for the fact that certain collections of (token) objects of the actual ontology are connected to one another or, if there are structures all the way down, it explains what connects these structures both internally and externally. The world-making relation must, in other words, explain why this whole of elements—they being objects or structures—of the ontology make up one rather than two or more configurations. This is not to say that we cannot conceive of a world without a world-making relation; a world of Leibnizian monads might be an example. However, it would be surprising if the absence of distance in quantum gravity required for the return of monads. The motivation of the present project is therefore to explore first the ontologically more parsimonious possibility that the non-spatial theories of quantum gravity just feature another world-making relation than distance, namely entanglement. In the absence of spatial distance, entanglement is proposed to be the glue that connects the elements of the ontology. As such, I argue that this investigation of entanglement as the world-making relation is relevant regardless of one’s view on modal realism or minimalist ontology.
In being a possible replacement for distance as the world-making relation, entanglement is still of particular interest to Lewisian metaphysics, as indicated above, and to minimalist ontology. While the program of minimalist ontology has its outset in a search for the relation that binds matter points together, a world-making relation, the program is minimalist by the hypothesis that the world-making relation also individuates the matter points and accounts for all change. While Esfeld and Deckert recognize that their minimalist ontology is fallible, i.e. that one could replace distance as the world-making relation, Esfeld elsewhere observes that “no one has hitherto worked out a proposal for another type of relations than distances that could (a) do the trick of individuating simple objects and (b) be empirically adequate” (Esfeld 2020, p. 1892). What I contend is that entanglement can meet this challenge.Footnote 12
To be an empirically adequate world-making relation in minimalist ontology, Esfeld proposes the necessary (but not sufficient) conditions that the world-making relation “introduces an evolution of the configuration” (Esfeld 2020, p. 1892) and that it can “qualify as providing for extension” (Esfeld 2020, p. 1892). Intuitively, we might motivate these empirical adequacy conditions as originating in a requirement that the world-making relation must at least be able to support the reality of motion (in space). This fact, as explicated by the condition of evolution and extension, is to be accounted for in the minimalist ontology by the world-making relation as it obtains between the objects it itself individuates; the evolution of the configuration, for instance, can ensue as changes in the magnitude of these relations (assuming that the world-making relation is quantifiable). The minimalist ontology, in other words, require more than connectedness from the world-making relation. Nevertheless, I claim that entanglement can do just as well as distance in meeting these requirements. This claim will not be defended here in its entirety. A companion piece to this one will argue that entanglement can achieve individuation and thereby determine a configuration and its evolution. The task taken up presently is primarily to show how entanglement can “qualify as providing for extension.” Though the account as such is part of a larger minimalist program, it is on its own an attempt to show that entanglement is an alternative to distance as the type relation in virtue of which the elements of the world are unified.
The conjecture, however, is not simply that entanglement can replace distance in worlds where distance is absent. This would be insufficient to defend the metaphysical salience of non-spatial theories of quantum gravity; another aim of this paper. These theories are not meant to be descriptions of esoteric worlds without space. Rather, they try to account for the physics of the actual world where distance, space, and extension are manifest but—according to these theories—emergent. The conjecture, therefore, is that the elements of the actual world make up a (connected) world in virtue of being entangled and not in virtue of being distanced. Assuming space is absent at the fundamental level of the ontology—thus disqualifying it as the world-making relation—this conjecture can be defended based solely the pervasiveness of entanglement as discussed in Sect. 4. However, without a relation between distance and entanglement, the emergence of space would be a miracle in this ontology: We would be no closer at an answer to what grounds distance relations. With distance no longer acting as the world-making relation, such an account might be less urgent from the perspective of metaphysical coherence, but it certainly remains as part of the empirical adequacy of the ontology (as suggested by Esfeld). It is therefore this stronger program that will be pursued here: How an ontology of entangled subsystems can (1) make a world where (2) spatial distances are manifest, but non-fundamental. To achieve (1), entanglement must be pervasive enough to be a candidate for the relation in virtue of which the elements of the actual world are unified. To achieve (2), the entanglement structure must be shown to be rich enough to account for distance relations and in doing so presumably “qualify as providing for extension.” The qualification ‘presumably’ is added since Esfeld is never quite clear what exactly this empirical adequacy conditions amounts to, however, distance, we are told, satisfies it. If entanglement can account for distance and distance satisfies the extension condition, then so does entanglement.Footnote 13 Thus, if entanglement satisfies (1) and (2), it proposes itself as a world-making relation for a minimalist ontology though it remains to be shown that entanglement can account for individuation and change.Footnote 14
How to recover space in each of the non-spatial theories of quantum gravity is an active field of research which has not yet produced any conclusive results. The present account of distance from entanglement does not resolve this problem. Accordingly, it is not demonstrating how distance can be recovered from entanglement. Rather, the ambition is to indicate that physics usually described in terms of distance (and more generally space) also admits a description in terms of entanglement. Such re-descriptions are symmetric whereby distance and entanglement are on equal footing in these instances. This, however, does not obstruct the asymmetry entailed in entanglement accounting for distance. Rather, these instances will be employed to argue that distance is a particular type of entanglement structure and that changes of distance are particular changes of these structures. This paves the way for the proposal that distance supervenes on entanglement; that there can be no change of distance without change of entanglement. Indeed, the evidence suggests that most entanglement structures and changes of entanglement do not admit a description in terms of distances or space. This is the sense in which entanglement accounts for distance and why entanglement is to be regarded as more fundamental.Footnote 15 Explicating fundamentality like this, the present proposal conforms to the recent conceptualization of how space is non-fundamental in non-spatial theories of quantum gravity: “the relationship between spatiotemporal and quantum gravitational structures is best understood in terms of some relevant functional (rather than constitutive) roles these latter instantiate in appropriate circumstances” (Lam and Wüthrich 2018, p. 12). For the generic spin-network states of loop quantum gravity, for instance, special circumstances have to obtain in order for the state to admit a description as extended space. Space occurs when the underlying degrees of freedom play a particular role; space is a function in this sense. As Lam and Wüthrich (2018) put it: “Spacetime is as spacetime does. No more, no less” (12). In this light, one might regard the present proposal as partaking in this program attempting to indicate that the distance role can be played by entanglement.
3 An independent definition of entanglement
The minimalist ontology of distanced matter points employs a similar functionalist strategy in its analysis of properties such as mass, charge, and entanglement:
“they are defined in terms of the effects that they bring about under certain conditions – in other words, by the functional or causal role that they exercise for the evolution of the objects to which they are attributed” (Esfeld 2020, p. 1902).
This sits well with the standard explication of entanglement as a correlation between outcomes of measurements on two particles. Suppose that we repeatedly measure the spin of two fermions and that we for both particles measure spin up half of the time and spin down half of the time. In addition we find, as we compare the series of measurements of the two particles, that when one particle is spin up the other particle is found to have spin down. It is this and similar correlations peculiar to quantum mechanics that we identify as entanglement.Footnote 16
An immediate worry is that this characterization of entanglement in terms of certain statistics relies too closely on a measurement context in space. Thus, if entanglement cannot be explicated in any other way, then it might depend on space in its very definition. Entanglement, however, may be defined independently of these appeals to the statistics in outcomes of measurements.Footnote 17 Suppose we know the state,  , of some quantum system as defined by the Hilbert space \({\mathcal {H}}\). Decomposing \({\mathcal {H}}\) into two subsystems, we have
, of some quantum system as defined by the Hilbert space \({\mathcal {H}}\). Decomposing \({\mathcal {H}}\) into two subsystems, we have
where \({\mathcal {H}}_A\) and \({\mathcal {H}}_B\) are the Hilbert spaces of the two subsystems (denoted A and B respectively).Footnote 18 In the example above, the natural choice would be to treat each particle as a subsystem associated with their respective Hilbert spaces. One can then define the reduced density matrix, \(\rho \), for one of the subsystems as:

where  span \({\mathcal {H}}_B\). Having thus obtained an expression for the reduced density matrix for subsystem A, we say that this subsystem is entangled with the rest of the system if and only if the reduced density matrix, \(\rho _A\), has more than one non-zero eigenvalue. Entanglement is in other words the failure of the full system to be represented by a product of pure states of the two subsystems.
span \({\mathcal {H}}_B\). Having thus obtained an expression for the reduced density matrix for subsystem A, we say that this subsystem is entangled with the rest of the system if and only if the reduced density matrix, \(\rho _A\), has more than one non-zero eigenvalue. Entanglement is in other words the failure of the full system to be represented by a product of pure states of the two subsystems.
This demonstrates that entanglement can be defined independently of the notion of distance. However, as shown by Earman (2015), this definition of entanglement is not without its subtleties. To rule out all states, where the failure to factorize as product states can be a consequence of classical mechanisms (including hidden variables), it will be assumed here that the whole system (the universe) is in a pure state and that any single subsystem is entangled with the full system in such a way the Bell inequalities are violated. The notion of entanglement adopted here is therefore equivalent to what Earman (2015, p. 313) calls (E3) or Bell entanglement.Footnote 19
Having sorted out these subtleties in the definition of entanglement, the next question is how to quantify it. Given the reduced density matrix for a subsystem, \(\rho _A\), the entanglement between the subsystem and the rest of the system may be quantified in terms of the von Neumann entropy, \(S_A\):

However, even with the quantification of entanglement in terms of the von Neumann entropy, it remains a relation between a subsystem and the rest of the system. Thus, it is not (manifestly) a relation between two subsystems in contrast with the ontology of distanced matter points, where every matter point is related to any other by a distance relation. A relation constructed from entanglement entropy that is more analogous to the distance relation is mutual information:
where S(M) is the entanglement entropy between a subsystem, M, and the rest of the system.
Mutual information shares a number of the structuring properties of the distance relation. Since von Neumann entropy satisfies subadditivity, \(S_{AB} \le S_A + S_B\), it follows that \(I(A,B) \ge 0\), i.e. mutual information quantifies the entanglement between subsystems by a non-negative scalar. Mutual information is symmetric since \(A \cup B = B \cup A\) and it is connex since I(A, B) is well defined for all subsystems. However, mutual information is not irreflexive: \(I(A,A) = S(A) + S(A) - S(A \cup A) = S(A) \ne 0\) and it does not satisfy the triangle inequality. Mutual information is not distance. When it is here proposed that entanglement can be the world-making relation, it does not entail that distances can simply be exchanged for mutual information. This is obvious from the difference in their structuring properties, but the point generalizes: No entanglement-based relation is trivially interchangeable with distance.
What has been achieved so far is a definition of entanglement independent of distance in the well known framework of quantum mechanics. However, since the account of extension from entanglement will take place in relativistic quantum field theory, it is relevant to stress some differences between these two theories when it comes to entanglement before we proceed to the account itself.
4 Entanglement in quantum field theory
As the name suggests, relativistic quantum field theory (RQFT) is a theory of relativistic quantum fields or more precisely quantized operator valued fields; a quantum mechanics for systems with infinitely many degrees of freedom (see Ruetsche (2012a, b) for a philosophical introduction). In the RQFT formalism, particles are treated as excitations of these quantum fields.Footnote 20 This entails that we cannot conceive of entanglement as the correlation between the properties of permanent particles such as their spin. In RQFT, entanglement instead obtains as correlations between the fields of a subsystem and the rest of the system. Thus, it is the quantum fields that are entangled. For a RQFT defined on a background spacetime, such a subsystem could comprise of the fields living on some subregion of that background spacetime. Entanglement would in this case take the form of correlations between the excitations (real or virtual) of the fields inside and outside of this region. This can still be captured by the formalism above:Footnote 21A is the spacetime region and \(H_A\) is the Hilbert space of the quantum fields living on A. If we define B to be the compliment of A (i.e. the rest of the background spacetime) such that \(H_B\) is the Hilbert space for the rest of the system, then we can find the reduced density matrix, \(\rho _A\), by Eq. (2). We can then use Eq. (3) to evaluate the entanglement entropy and thus how much the subsystem is entangled with the rest of the system. All we have to remember is that it is now the quantum fields that are entangled.
In the algebraic approach to RQFT, a number of interesting results can be shown regarding entanglement that have direct bearing on its potential role as the world-making relation.Footnote 22 This is not the place to review the algebraic approach to RQFT or the details of the arguments establishing these results. Rather, these results will be taken as given, and further details can be acquired from the references. The first result is that spacelike separated quantum field subsystems are highly entangled even in the vacuum state of a RQFT due to vacuum fluctuations (Redhead 1995).Footnote 23 This result is generalized by Clifton and Halvorson (2001): spacelike separated quantum field subsystems are entangled in generic RQFT states (even considering non-interacting, free fields). As Swanson (2019) observes: “Such states encompass many (if not all) physically reasonable global states” (10). In other words, only in very special (and most likely non-physical) RQFT states are there spacelike separated quantum field subsystems that are not entangled. In addition, this generic entanglement can be proved to violate Bell-inequalities and thus satisfies Earman’s (E3) (Summers and Werner 1987; Halvorson and Clifton 2000). Based on these results, Lam (2013) concludes “that entanglement (non-locality) is a universal feature of physical quantum field systems in the sense that all quantum field systems (including free, non-interacting ones) satisfying certain physically reasonable conditions tend to be ultimately entangled (in particular with their environment understood as their causal complement)” (66, emphasis in original). However, entanglement is not only universal and generic in RQFT, it is also very difficult to remove. Again by means of the algebraic approach, Clifton and Halvorson (2001) show that for generic RQFT states “[t]here are many regions of spacetime within which no local operations can be performed that will disentangle that region’s state from that of its spacelike complement” (28). Valente (2010) qualifies that it is necessary (but not sufficient) for disentanglement by a local operation that the two regions are strictly spacelike separated, i.e. that they remain spacelike separated even if one is displaced by a small amount. This entails that it is always impossible to completely disentangle a RQFT subsystem (on a spacelike region) from the rest of the system, since they are not strictly spacetime separated. Such systems are intrinsically entangled.
Being quantum field theories themselves, it is likely that these results carry to the theories of quantum gravity of interest here, and we shall simply proceed on this assumption. The results testify to the pervasiveness of entanglement between spacelike separated degrees of freedom. In all (physically reasonable) states, spacelike separated subsystems are entangled. Since all elements in the ontology of distanced matter point are spacelike separated (presumably by definition), entanglement thus relates all the elements related by distance.
In light of these results coming out of algebraic RQFT, Lam (2013) proposes an ontology that takes entanglement seriously:
the ontology of (the algebraic approach to) RQFT is an ontology of ‘entanglement structures’, understood in the sense of networks of entanglement relations among quantum field systems whose existence—what it means for a quantum field system to be the one it is—depends on the entanglement relations they enter into and on the structures they are part of (Lam 2013, pp. 67–68).
This type of ontology will serve as a template for the ontology of entangled subsystems in the account of distance from entanglement. However, with this aim in mind, one may wonder what happened, in the explication of this ontology, to space and the apparently central role for it in the exposition above. Likewise, the ambition for entanglement is moreover to be the relation in virtue of which elements make up world even when no spatial description is available whereby being spacelike separated is ill-defined.
While entanglement certainly can relate degrees of freedom even in the absence of a spatial description, both worries are warranted. The typical set-up of RQFT, both in the algebraic and field formulation, assumes a fixed background spacetime. The more general worry would therefore be that this hinders the utility of RQFT for the present purposes since it has an inbuilt ontological commitment to space(time). Indeed, in the algebraic approach, the algebras are associated with regions of spacetime. Against this, Dieks (2001) argues that the background spacetime can be regarded as auxiliary, and that we can simply take the total algebra and the structure of subalgebras as primitive (in the Hilbert space formalism, we could similarly take the full Hilbert space and the Hilbert space of all possible subsystems as primitive).Footnote 24 These algebras contain the entanglement structure such that this construction admits questions about the entanglement between subsystems to be formulated independently of any background spacetime. Still, the pervasiveness of entanglement beyond spacelike separation remains unknown, though perhaps only due to the lack of systematic scrutiny of the spacetime-free context.Footnote 25 Taking the algebras as ontologically primitive also (re)introduces the problem—as Dieks (2001, p. 237) recognizes—of getting space out this abstract structure; be it algebras or Hilbert spaces. How this problem might be resolved within algebraic RQFT will not be discussed here.Footnote 26 Notice instead that the ontology promoted here is not eliminative of space. Space exists, it is just derivative from entanglement. Thus, it is meaningful to ask if two subsystems are spacelike separated under the assumption that the entanglement structure of the full system admits a spatial description. This will exactly be the case where the results from algebraic RQFT are put to use below. However, the account of space is instead developed based on results coming out of quantum gravity research, as detailed in the next section.
5 Extension from entanglement
For the minimalist ontology of distanced matter points, extension is a feature not a difficulty. For the prospective minimalist ontology of entangled subsystems, extension seems like an insurmountable obstacle. Two recent research programs will here be appealed to in the development of an account of how distances might be recovered from entanglement: the conjectured relation between entanglement and areas of spacetime due to Ryu and Takayanagi (2006), and the ER = EPR conjecture due to Maldacena and Susskind (2013) that relates Einstein Rosen bridges (wormholes) to entanglement.
The Ryu–Takayanagi formula is originally conceived in the context of the AdS/CFT correspondence; a conjectured string duality.Footnote 27 Here it is sufficient to know that the AdS/CFT correspondence implies the physical equivalence between certain (semi-)classical asymptotically anti de-Sitter (AdS) spacetimes (with a particular field content) and certain states of a conformal field theory (CFT) defined on a fixed spacetime background identical to the asymptotic boundary of the dual spacetime.Footnote 28 Hence, the CFT state is defined in one dimension less than the dual spacetime.
To introduce the Ryu–Takayanagi formula, consider a quantum state  on the CFT side with an AdS dual that features a classical spacetime \(M_{\Psi }\). Define
on the CFT side with an AdS dual that features a classical spacetime \(M_{\Psi }\). Define  as a state in the Hilbert space for a CFT defined on a spacetime identical to the asymptotic boundary of \(M_{\Psi }\) which we denote \(\partial M_\Psi \). We will also refer to \(\partial M_\Psi \) as ‘the boundary’. The non-boundary spacetime, \(M_{\Psi } \backslash \partial M_\Psi \), is referred to as the bulk. To construct the Hilbert space, one must define a spatial slice of \(\partial M_\Psi \) which will be denoted \(\Sigma _{\partial M_\Psi }\). We then have
as a state in the Hilbert space for a CFT defined on a spacetime identical to the asymptotic boundary of \(M_{\Psi }\) which we denote \(\partial M_\Psi \). We will also refer to \(\partial M_\Psi \) as ‘the boundary’. The non-boundary spacetime, \(M_{\Psi } \backslash \partial M_\Psi \), is referred to as the bulk. To construct the Hilbert space, one must define a spatial slice of \(\partial M_\Psi \) which will be denoted \(\Sigma _{\partial M_\Psi }\). We then have  .
.
Now, divide \(\Sigma _{\partial M_\Psi }\) into two spatially separated regions B and \(\overline{B}\), such that \(B \cup \overline{B} = \Sigma _{\partial M_\Psi }\) (see Fig. 1). Since a CFT is a local quantum field theory, there are specific degrees of freedom associated with specific spatial regions. We can therefore regard the full quantum system as composed of two subsystems, \(Q_B\) and \(Q_{\overline{B}}\), associated with the two spatially separated regions B and \(\overline{B}\). As a consequence, the Hilbert space of the full system, \({\mathcal {H}}_{\Sigma _{\partial M_{\Psi }}}\), can be decomposed as a tensor product of the Hilbert spaces of \(Q_B\) and \(Q_{\overline{B}}\). With this construction, we can, following the procedure of Sect. 3,Footnote 29 associate an entanglement entropy to these subsystems which quantifies the entanglement between the two subsystems in the state  .
.
The discovery by Ryu and Takayanagi (2006) is that the entanglement between \(Q_B\) and \(Q_{\overline{B}}\) as quantified by the entanglement entropy, \(S_B\), is proportional (to leading order) to the smallest area surface on the AdS side, \({\tilde{B}}\), that divides region B from \(\overline{B}\), i.e. B from the rest of \(\Sigma _{\partial M_\Psi }\) (see Fig. 1).Footnote 30 The formula reads:
where G is Newton’s constant. While this Ryu–Takayangi formula is originally conceived in the context of the AdS/CFT correspondence and therefore string theory, there are indications that it generalizes and has thus recently been proposed to obtain in other prominent prospective theories of quantum gravity: causal set theory (Sorkin and Yazdi 2018),Footnote 31 loop quantum gravity (Smolin 2016; Han and Hung 2017), and in the broader context of generic group field theories via a relation to tensor networks with indications of even further generalization (Chirco et al. 2018). Thus, any conclusions drawn from the Ryu–Takayanagi formula alone appear to be more generic features of quantum gravity.
As observed by Van Raamsdonk (2010a), it follows from the Ryu–Takayanagi formula alone that changes in the entanglement between \(Q_B\) and \(Q_{\overline{B}}\) entail changes in the area of the smallest surface that divides the two corresponding regions in the spacetime dual. When all entanglement is removed between \(Q_B\) and \(Q_{\overline{B}}\), the entanglement entropy, \(S_B\), goes to zero and so does the area of \(\tilde{B}\) according to the Ryu–Takayanagi formula. More explicitly stated, in this limit the bulk metric changes such that the minimal area dividing the two asymptotic regions B and \(\overline{B}\) in the spacetime goes to zero; the spacetime connecting these two regions have vanished with the entanglement. For the spatial surface \(\Sigma _{\partial M_{\Psi }}\), Fig. 2 depicts the limit where all entanglement is removed between \(Q_B\) and \(Q_{\overline{B}}\). The Ryu–Takayanagi formula suggests that entanglement between \(Q_B\) and \(Q_{\overline{B}}\) is closely related to spacetime connectivity between B and \(\overline{B}\) in the spacetime dual. More generally, it signifies that the physics described in terms of spacetime on the AdS side is described in terms of entanglement on the CFT side.
Depiction of the behavior of the spatial slice \(\Sigma _{\partial M_{\Psi }}\) when all entanglement is removed between \(Q_B\) and \(Q_{\overline{B}}\). Note that the quantum state is defined on a fixed spacetime identical to the asymptotic boundary of the spacetime dual. Thus, the change in \(\tilde{B}\) is solely due to changes in the bulk metric despite the appearance to the contrary
Considering the mutual information in these scenarios provides a more direct relation between entanglement on the CFT side and distance on the AdS side (Van Raamsdonk 2010a). Define an arbitrary point in region B denoted by \(x_B\) and one in region \(\overline{B}\) denoted by \(x_{\overline{B}}\) as in Fig. 2. For any operators \({\mathcal {O}}_B(x_B)\) and \({\mathcal {O}}_{\overline{B}}(x_{\overline{B}})\) that only act on \(Q_B\) and \(Q_{\overline{B}}\) respectively, the following inequality holds (Wolf et al. 2008):

where \(I(x_B,x_{\overline{B}})\) is the mutual information between \(x_B\) and \(x_{\overline{B}}\) (see Eq. 4) and

is recognized as a connected two-point correlator. On the AdS side, certain two-point field correlators can serve as a direct measure of the distance between the points.Footnote 32 Assuming, as above, that the AdS side is approximated by a classical spacetime, two-point field correlators between boundary pointsFootnote 33 correspond to connected two-point correlators on the CFT side (Banks et al. 1998). Using this, one can relate the connected two-point correlator in Eq. (6) between \(x_B\) and \(x_{\overline{B}}\) to the bulk distance, L, between \(x_B\) and \(x_{\overline{B}}\) (Balasubramanian and Ross 2000):

where m is a constant. Removing all entanglement between \(Q_B\) and \(Q_{\overline{B}}\), it follows by inserting Eq. (7) into Eq. (6) that the proper distance between \(x_B\) and \(x_{\overline{B}}\) must go to infinity. More precisely, \(I(x_B,x_{\overline{B}}) \rightarrow 0\) for \(S(B) \rightarrow 0\). Thus, we get the following:

and \(0 \ge e^{-2 m L}\) iff \(L \rightarrow \infty \). Thus, when all entanglement is removed between the two subsystems, the distance between any point in B and one in \(\overline{B}\) goes to infinity. This indicates that the mutual information between subsystems (of sufficient size) can account for the spatial proximity of these subsystems (see Cao et al. (2017) for further details).
Based on the Ryu–Takayanagi formula alone, it has also been shown how a restriction on entanglement entropy on the CFT side (analogous to the first law of thermodynamics) is equivalent to imposing semi-classical, linearized Einstein equations on the AdS side (Faulkner et al. 2014; Lashkari et al. 2014; Swingle and Van Raamsdonk 2014). Again, this signifies how entanglement can describe the same physics as spacetime (see Jaksland (2019, section 5.3) for further details).Footnote 34
A related field of research providing further indications of the relation between entanglement and distance is Maldacena and Susskind’s \(\hbox {ER}=\hbox {EPR}\) conjecture:
We argue that the Einstein Rosen bridge between two black holes is created by EPR-like correlations between the microstates of the two black holes [...]. We call this the ER = EPR relation. In other words, the ER bridge is a special kind of EPR correlation in which the EPR correlated quantum systems have a weakly coupled Einstein gravity description (Maldacena and Susskind 2013, p. 782).
The conjecture, in other words, is that the same physical system can be represented as two spatially disconnected, but entangled black holes or as two black holes spatially connected by a Einstein–Rosen (ER) bridge. However, the relation, they speculate, should generalize to all entangled particles, though the ER bridge will not in general take the form of a classical spacetime. Still, the conjecture remains that entanglement and ER bridges encode the same information about the relation between two particles or collections of particles such as black holes.
In the spirit of the \(\hbox {ER}=\hbox {EPR}\) conjecture, Susskind has advanced the more universal claim \(\hbox {QM}=\hbox {GR}\), i.e. “the conjecture that where there is quantum mechanics there is also gravity” (Susskind 2017, p. 10). As part of this, Susskind has explored what might be the quantum mechanical explanation for the gravitational attraction on a body from a black hole and finds “that the gravitational attraction is nothing but the statistical tendency for complexity to grow in chaotic quantum systems” (Susskind 2018, p. 1). The account is interesting, since it offers an alternative view of the radial direction in black hole solutions as quantum complexity due to entanglement.Footnote 35 In the quantum mechanical representation of the physical system, rather than changing its distance to the black hole, the ‘falling’ body instead increases its quantum complexity; despite the initial appearance to the contrary, no movement takes place.
For a test-particle in the vicinity of an AdS black hole, the momentum, P, of the particle in the radial direction grows exponentially in terms of the Rindler time, \(\tau \): \(P = P_0 e^{a \tau }\) where \(P_0\) is the initial radial momentum and a is a parameter such that \(a=1\) represents particles going into the black hole and \(a \le 1\) represents time-like trajectories for particles that never cross the black hole horizon. Trajectories with \(a \ge 1\) are non-physical since they represent particles travelling faster than the speed of light.
In chaotic CFTs, the size—as related to complexity—of operators grows exponentially in terms of the boundary time, t, which is proportional to the bulk Rindler time such that \(t = \frac{\beta }{2 \pi } \tau \). The growth is controlled by Lyapunov exponent, \(\lambda \), and one therefore gets:
Thus, the size of the boundary operators grows at the same rate as the momentum of the falling particle. This, of course, is no proof of a relation and might be accidental, but the relation can be made a little stronger observing that \(\lambda \le \frac{2 \pi }{\beta }\) as shown by Maldacena et al. (2016). The significance of this is manifest if one introduces a rescaling of \(\lambda \) such that \(\tilde{\lambda } = \lambda \frac{\beta }{2 \pi }\). We then have:
This rescales the bound, \(\lambda \le \frac{2 \pi }{\beta } \Rightarrow \tilde{\lambda } \le 1\), and manifests a rather remarkable result: Not only does the size of a CFT operator grow at the same rate as the momentum of an infalling test particle in the gravity representation of the scenario, also the bounds of the respective growth parameters, \(\tilde{\lambda }\) and a, agree. The trajectories that are non-physical due to the Einstein bound on velocities, \(a \le 1\), exactly correspond to the non-physical growth rates as restricted by the bound on the Lyapunov exponent, \(\lambda \frac{\beta }{2 \pi } \le 1\). While this is at best circumstantial evidence, it suggests how the bulk radial coordinate in black hole solutions can be associated with complexity in quantum theories. The complexity can in turn be related to entanglement: “the state complexity of  is the minimum number of gates required to convert it to an unentangled state” (Brown and Susskind 2018, p. 38). This case study of a body falling towards a black hole therefore indicates that distance may be described in terms of entanglement; something that is in accordance with the picture already obtained from the Ryu–Takayanagi formula and the conjecture: \(\hbox {ER}=\hbox {EPR}\).
is the minimum number of gates required to convert it to an unentangled state” (Brown and Susskind 2018, p. 38). This case study of a body falling towards a black hole therefore indicates that distance may be described in terms of entanglement; something that is in accordance with the picture already obtained from the Ryu–Takayanagi formula and the conjecture: \(\hbox {ER}=\hbox {EPR}\).
6 Two distanced, entangled particles
Despite these expositions, it seems just manifestly wrong that distance supervenes on entanglement. This is signified by the simple example of two entangled particles. We can imagine changing the distance between such particles without changing the entanglement between them which immediately appears to be a counterexample to the proposed relation between distance and entanglement. However, it would be too quick to dismiss entanglement as the world-making relation and generally entanglement fundamentalism on these grounds.
First, observe how this is no more of a counterexample to the conjecture that entanglement is the world-making relation than it is to the claim that distance is the world-making relation. According to Esfeld’s ontology of distanced matter points, entanglement is a “functional or causal role” (Esfeld 2020, p. 1902). However, it is difficult to see how any functional or causal role recognizable as entanglement can be exercised in a world of only two particles moving away from one another. Esfeld simply dismisses such symmetric configurationsFootnote 36 as irrelevant, since “the actual configuration of matter of the universe is not symmetrical” (Esfeld 2020, p. 1894). In any real example, these two particles would sit in an environment of many particles. The ontology of entangled subsystem can simply help itself to the same assumption.
Initially, this assumption looks absurd and thus appears to refute both minimalist ontologies. Particles with constant entanglement and changing distance are not only possible, they are actual; this is for instance used in experiments (e.g. Aspect et al. 1982) that demonstrate the violation of Bell’s inequality by measuring entangled particles emitted from the same source at spacelike separated points. But even though the particles in the experiments are regarded as an isolated system, they do find themselves in an environment. This is particularly vivid if we remember that particles in relativistic quantum mechanics are to be treated as excitations of fields. Thus, even the idealized form of the example is more appropriately cast as two entangled excitations of a quantum field that moves away from each other. But following the results of Sect. 4, generic RQFT states are highly entangled, and the example will therefore include much more entanglement than that between the two excitations; an effect that is only amplified when the environment also features excitations, which it does in real situations.
Still, if we have two isolated particles such that their entanglement with the environment vanishes, i.e. such that they are only entangled with each another, then they would arguably be unaffected by the environment. This actually discloses a deeper issue for entanglement as the world-making relation: if entanglement is the only relation of the ontology, then a completely disentangled subsystem is not, and can never be, related to the rest of the system. Obviously, this questions in what sense such systems are even subsystem, but if such disentangled configurations exist, entanglement cannot be what makes it true that the disentangled subsystems are part of the same connected configuration which they obviously are. For entanglement to be a world-making relation all elements must be connected which precludes scenarios where subsystems are completely disentangled from the rest. Thus, for entanglement to even candidate as the world-making relation, no subsystem—such as that comprised of the two entangled particles—can be completely disentangled from the rest of the system. But actual experiments are carried out with isolated entangled particles which therefore seem to refute entanglement as the world-making relation altogether. As a counter to this version of the example, remember the intrinsic entanglement between a subsystem and its complement proven in algebraic RQFT. This implies that it is impossible to isolate the two particles (excitations) from their environment, since the environment, in this case, is the complement of the subsystem comprised of the two particles. But if actual experiments do involve such isolated particles, then this might be all the worse for algebraic RQFT. The isolation in such experiments, however, is good enough for all practical purposes, but not perfect. No perfectly closed systems can exist in quantum mechanics! Regardless of the care with which these two particle states are prepared, they are inevitably entangled with their environment.Footnote 37 For the experiments in question, these entanglements are negligible, but in principle “radical non-separability of quantum states” (Howard 1989, p. 248) holds—due to the pervasiveness of the gravitational and electromagnetic interactions—for all quantum systems except perhaps the universe as a whole. Moreover, since the environment cannot be entirely decoupled, the entanglement between the particles will inevitably decay over time and be replaced by entanglement with the environment (see Mintert et al. (2005) for a review of entanglement dynamics).Footnote 38
Thus, for this example to accord with our current best physics—in the form of quantum field theory—the configuration must consist of two particles (field excitations) that are almost maximally entangled, but with a deficit due to an ineliminable non-zero entanglement with the environment where many additional entangled degrees of freedom reside. Furthermore, the entanglement between the particles will dissipate over time and therefore dissipate as they move away from each other.Footnote 39 With these qualification, such experiments are not counterexamples to the claim that distance derives from entanglement: These experiments are rich in entanglement structure that even changes over time. The example of two entangled particles moving away from each other at most shows that the relation between distance and entanglement is complicated. However, this was already stated above: It is not such that any distance relation can simply be replaced by the entanglement between the distanced subsystems. This may appear to be an ad hoc solution; certainly, if the distance between two objects is derivative from entanglement, it must recovered from the entanglement between these two particles. However, even in the ontology of distanced matter points the relation between distance and entanglement is not that simple. In this ontology the same problem arises: Distance can change while the entanglement remains constant.Footnote 40 The solution in terms of distanced matter points is that the changes of relative position from which the entanglement derives are among particles in the environment (or measuring device) and not the two entangled particles (Esfeld 2014). Adopting some terminology from Maudlin (2007b), entanglement is not a metaphysically pure relation in the ontology of distanced matter points: it does not satisfy the necessary condition that a relation is metaphysically pure if “it is at least possible that the relation be instantiated in a world in which only the relata of the relation exist” (Maudlin 2007b, p. 86). Maudlin gives the example of being siblings as a relation that is not metaphysically pure: siblinghood requires the existence of other things, namely parents, and it furthermore depends on the existence of parenthood. In this respect, entanglement in the ontology of distanced matter points resembles siblinghood: it requires additional elements than those entangled standing in additional relations. We might even push this analogy further, proposing that siblinghood derives from parenthood in the sense that it applies when a particular structure obtains between the objects standing in the parenthood relation. Likewise, entanglement obtains for a particular structure of distance relations (and changes thereof). In the ontology of entangled subsystems, it is distance that is not metaphysically pure.Footnote 41 For two relata to be distanced in this ontology, more elements than those relata are required. The response to the counterexample is, in other words, that the changing distance between two entangled particles is accounted for by changes in the entanglement structure of the whole system including both the two particles and their environment thus mirroring the way entanglement is accounted for in the ontology of distanced matter points.
This may come across as a rather vague solution to the problem of two entangled particles moving away from each other. One might be suspicious of an ontology that has nothing else to say about such a simple example. Below, we shall see that there is indeed a little more to be said, though it remains at best schematic. First, however, the intuition must be resisted that this is a simple example just because it is simple to formulate. Generally, “simplicity in ontology and simplicity in representation tend to pull in opposite directions” (Esfeld 2020, pp. 1895–1896). Simplicity is deceiving; what is easily described in terms of the usual full arsenal of representational devices might be a very complicated situation once one restricts these to the bare minimum of a minimalist ontology. Indeed, this complication obtains in the example of two entangled particles with changing distance and generally in any example that features distances; distances are very complex constructions in the ontology of entangled subsystems. One might object that this just looks like a convenient fall back position, however, it is not grabbed out of thin air. In the context of AdS/CFT correspondence, most CFT states will not be holographic, i.e. not have a dual with (semi-)classical spacetime (Rangamani and Takayanagi 2017, Chapter 13). For any CFT state we can (in principle) evaluate an entanglement entropy for every possible subsystem of every possible Cauchy surface. By the Ryu–Takayanagi formula, these can be related to areas of co-dimension two surfaces in the bulk. One can then search for spacetimes that reproduce all these areas which will generally be a highly overdetermined problem. Often, therefore, no (semi-)classical spacetime will satisfy this, and quantum states that admit an alternative representation as (semi-)classical spacetimes must therefore be expected to be rare. Those circumstances where there is a spacetime dual, van Raamsdonk finds, are those that “have low-energy states which are highly entangled” (2010b, p. 19). In addition, they must have a large number of strongly coupled degrees of freedom and have large central charge (Rangamani and Takayanagi 2017, p. 188). However, the details are not important. Rather, the point is simply that any world that features (semi-)classical spacetime will, in the ontology of entangled subsystems, be represented by a very rich entanglement structure between a large number of underlying degrees of freedom and in this regard not be simple. In addition, even only slightly geometrically different (semi-)classical spacetimes will correspond to quantum states with very different entanglement structure due the significant overdetermination of the spacetime by the entanglement entropies (observe in addition that this overdetermination suggests how entanglement structure contains more than enough information to encode spacetime). In summary, the apparently simple example of two distanced, entangled particles is a highly complex situation in the ontology of entangled subsystems because the manifestation of distance in the example requires very specific conditions to be satisfied by a large number of highly entangled degrees of freedom. Even assuming that these two particles are the only excitations of a RQFT in Minkowski spacetime, in order for there to be Minkowski spacetime in the first place requires a very specific and very rich underlying entanglement structure and in addition, already the vacuum state of a RQFT on Minkowski spacetime is a highly entangled state. In general, (semi-)classical spacetimes are by no means simple in an ontology of entangled subsystems since the physics requires very many degrees of freedom for such spacetimes to even exist. This also provides a physical motivation for the claim that distance is not metaphysically pure in the ontology of entangled subsystems. Distance not only presumes two additional elements—like siblinghood requires the existence of parents—but many more degrees of freedom than those whose distance is inquired about. Together, these features complicate the possibility of giving more than the schematic account below of how the distance between two elements is recovered from entanglement.
The central claim in this schematic account is the point already made above: The distance between two particles will generally depend on the entanglement between many particles; possibly not including the distanced particles themselves (at least to leading order). This may be exemplified by two large, entangled black holes, \(BH_A\) and \(BH_B\), under the assumption of the ER = EPR conjecture of Maldacena and Susskind (2013). According to this conjecture, the two entangled black holes will under certain conditions have an alternative representation as two black holes connected by an ER bridge such that the precise nature of the ER bridge will depend on the details of the entanglement between \(BH_A\) and \(BH_B\) (see Fig. 3). In the example, we assume that the black holes are large—they contain many degrees of freedom—and are highly entangled.Footnote 42 Denote this configuration (I). Suppose we have pair of particles, a and b, that are almost maximally entangled with mutual information I(a, b) and place the particles such that a is in \(BH_A\) and b is placed in \(BH_B\) (see left hand side of Fig. 4). Since \(BH_A\) and \(BH_B\) already contain a large number of highly entangled degrees of freedom, the additional entanglement due to the pair of entangled particles will not change (at least to leading order) the ER bridge connecting \(BH_A\) and \(BH_B\). The distance between a and b depends on the ER bridge, so since the ER-bridge is independent (to leading order) of the entanglement between a and b, then the distance between a and b is independent of their mutual entanglement.
Keeping the mutual information (and therefore the mutual entanglement) between a and b fixed at value I(a, b), we can still change the ER bridge by changing the entanglement between all the other degrees of freedom. In particular, we want the configuration to be such that the ER bridge grows in length;Footnote 43 call this configuration (II). Since the distance between a and b depends on the ER bridge, the distance between a and b will be larger in configuration (II) than in configuration (I). This, even though we, by construction, have held I(a, b) fixed. Thus, in this scenario at least, the distance between two particles can be independent (to leading order) of their mutual entanglement, and it can be explained how their distance can increase without their mutual entanglement changing (see right hand side of Fig. 4). The distance between a and b supervenes on entanglement as required by the conjecture that entanglement is the world-making relation, but it just happens to be independent (to leading order) of the specific entanglement between a and b. There is plenty of other entanglement with which to recover this distance.
There is no reason to think that these observations do not generalize to other spacetimes. In an ontology of entangled subsystems, those worlds that feature (semi-)classical spacetimes and therefore distances were above claimed to have a large number of entangled degrees of freedom; something that accords well with the abundance of entanglement even in the RQFT vacuum state. Thus, even in the example of two entangled, distanced particles, there will—just as in the black hole case—be plenty of entanglement and degrees of freedom to account for the distance between these particles such that the distance can change while the entanglement between those specific particles remains fixed. Thus, the counterexample is refuted.
7 Entanglement as the world-making relation
Together, the examples from Sect. 5 offer a picture where what is usually described as distance, space and extension can instead be described in a theory as entanglement structure. Section 6 further disclosed that those entanglement structures that admit a description as a space with distances were highly specific structures with a large number of entangled degrees of freedom. Thus, distance can be described in terms of entanglement, whereas most entanglement structures cannot be described in terms of distance. This suggests a picture where distance supervenes on entanglement, and this is the sense in which entanglement accounts for distance. Section 6 also indicates how this conjecture can deal with—or at least is not refuted by—the most immediate counterexample. On Esfeld’s minimalist ontology of distanced matter points, entanglement is a particular sort of change of relative distance. With entanglement as the world-making relation, distance is a particular sort of entanglement structure and changes of distance are particular changes of this structure in accordance with the basic tenet of supervenience.
Importantly, the conjecture that entanglement is the world-making relation does not imply that distance, as the relation occurs in our theories, can just be replaced for instance by mutual information; distance is not metaphysically pure in the ontology of entangled subsystems. This is immediately evident by the difference in their structuring properties (see Sect. 3). But also in general, the relation between distance and entanglement is much more complicated. This is signified by the example of the two entangled particles (Sect. 6). The distance between such particles can be increased without changing the entanglement between them.
These remarks are indicative of a general point, mutual information is not the world-making relation, entanglement is. The developed ontology proposes that we should be realist with respect to subsystems (as individuated by entanglement) and the entanglement pertaining between these; thus largely mirroring the ontological picture proposed by Lam (2013, pp. 67–68). However, if mutual information is insufficient to capture this realism with respect to entanglement, then what does this realism translate to in the quantum formalism? What elements of the quantum formalism are ontologically significant if one adopts the ontology of entangled subsystems?
As it turns out, the procedures to recover space and generally distances in Sect. 5 imposes the strongest requirements on the ontology. Here one of the central and quantitatively most precise elements of the account of distance was the Ryu–Takayanagi formula that relates the entanglement entropy of arbitrary subsystems to areas: That we can evaluate numerous such entropies is for instance central to the observation that the entanglement structure highly overdetermines any possible corresponding spacetime. In the informal ontological picture, these entanglement entropies are supposed to be derived from the fundamental entanglement relations among subsystems. In the formalism, the entanglement entropy for a subsystem is evaluated from the density matrix of that subsystem. This suggests that the density matrices of subsystems are the ontologically significant elements of the quantum formalism in the ontology of entangled subsystems.
Promoting the density matrix thus, the ontology of entangled subsystems bears some resemblance to the spacetime state realism defended by Wallace and Timpson (2010). Here, the fundamental ontology consists of the density matrices of all possible subsystems including the density matrix of the full universe such that the ontology features non-separability at the fundamental level. However, as the name indicates, spacetime state realism associates the density matrices with spacetime regions. Without space at the fundamental level of the ontology of entangled subsystems, the subsystems and their associated density matrices cannot be those of spacetime regions, but must be individuated in another way. The two ontologies thus come apart.
However, the analogue to spacetime state realism can serve to ease the worry that the ontology of entangled subsystems requires an esoteric ontological commitment to matrices. As Wallace and Timpson (2010) observes, “the density operator assigned to each [subsystem] represents the intrinsic properties that each subsystem instantiates” (709). In the particular context of entangled subsystems, the density matrix is simply a codification of the entanglement between a subsystem and the rest of the system and any ontological commitment to this abstract mathematical entity should be seen in this light.Footnote 44
The ontology of entangled subsystems might come across as rather elaborate with its apparent need to take the density matrix (i.e. the entanglement structure) of all subsystems as primitively given; just as it is the case in spacetime state realism (Wallace and Timpson 2010, p. 709). To see just how elaborate this ontology is, notice that information is lost when taking the partial trace. The density matrix of a system can therefore not in general be recovered from the density matrices associated with a set of subsystems even if these together comprise the whole system.Footnote 45 Thus, when the workings of the Ryu–Takayanagi formula require the density matrix for arbitrary subsystems, this promotes the significance of the density matrices of all possible subsystem including composite subsystems.
However, the density matrix for an arbitrary subsystem can (given a Hilbert space with a basis for the subsystemFootnote 46) be derived from the density matrix of the full system; as observed by Ismael and Schaffer (2016) in the context of spacetime state realism: “[o]nce we have a universe replete with parts, the only fundamental density operator needed is the universal one” (footnote 23).Footnote 47 Given such parts, Ismael and Schaffer (2016) promotes what they call spacetime state realism streamlined (SSRS) where the “fundamental ontology is that of the whole spacetime bearing a density operator” (21). In other words, SSRS proposes that the density matrix of the universe as a whole and the structure of subsystems is fundamental and that the density matrices of the subsystems are derivative. Similarly, in the ontology of entangled subsystems, it might be ontologically more parsimonious to be realist with respect to the state of the full system (as encoded by its density matrix). However, since this presumes “a universe replete with parts” it is unclear whether this difference actually comes to anything.
8 Conclusion and quantum gravity
This paper has defended entanglement as the world-making relation. Defining entanglement in terms of the density matrix of a system and quantifying it by von Neumann entropy, it was argued how distances—and with it possibly all other relations—can be recovered from entanglement by means of resources coming out of quantum gravity. Entanglement therefore promises itself as an alternative to distance as the world-making relation. This, however, is more than an esoteric exploration of metaphysical possibility. With serious contending theories of quantum gravity being fundamentally non-spatial, this calls for the development of non-spatial ontologies. Without such ontologies, one might worry about the metaphysical salience of these non-spatial theories of quantum gravity. With a number of details still to be worked out, the ontology of entangled subsystems will not silence these worries, but at least the account offers a way forward: to replace distance with entanglement as the fundamental world-making relation and thus to promote entanglement fundamentalism. The hope here is to have shown that it is not unlikely that we can construct an ontology that is compatible with non-spatial theories of quantum gravity. While we have to wait for these theories to obtain to get the details of this ontology, a sketch—entangled subsystems—has been defended here. Theories that are fundamentally non-spatial do not pose an insurmountable obstacle to the possibility of a coherent and empirically adequate (minimalist) ontology of the world.
The account of how distance relations might be recovered from entanglement relations was largely dependent on the Ryu–Takayanagi formula that relates entanglement entropy to areas. Due to the origin of this formula in string theory, one might worry that the ontology of entangled subsystems would be inappropriate for other approaches to quantum gravity; for instance those that proceed by canonical quantization such as loop quantum gravity. Both a direct and an indirect argument tells against this view. The indirect argument was already mentioned above: the Ryu–Takayanagi formula promises to generalize to most of the contending theories of quantum gravity. A more direct response comes from a comparison between the ontology of entangled subsystems and the emanating ontology of loop quantum gravity.
Central to the current best account of loop quantum gravity are spin networks. These are structures represented by graphs with a spin (SU(2)) representation for the nodes of the graph and one for the links. In loop quantum gravity, these spin networks are conjectured to give rise to spacetime: “the spin network states are not quantum states of a physical system in space; rather they are the quantum states of physical space” (Wüthrich 2017, p. 313). This is so since the nodes of the spin network can—via a construction called twister geometry (Rovelli and Speziale 2010)—be given a geometric interpretation as quantum polyhedra (Bianchi et al. 2011).Footnote 48 Due to the nature of the spin network, the polyhedra are uncorrelated with one another. To relate the polyhedra—these nodes of spacetime—and ultimately to recover the semi-classical regime of loop quantum gravity, it has been argued that the polyhedra must be entangled; this has been exemplified for nearest-neighbour polyhedra with indications towards a generalization by Baytaş et al. (2018). Identifying the polyhedra with proper subsystems, the similarity between this picture of loop quantum gravity and the ontology of entangled subsystems is striking. While it may be circumstantial, it indicates that the ontology of entangled subsystems is at least prima facie compatible also with the emanating ontology of loop quantum gravity.
Indeed, it might seem that string theory is the theory of quantum gravity most at tension with entangled subsystems if the subsystems are identified with matter points. The fundamental object of string theory is the extended string and not a point as explicit in ‘matter point’. Again, the commitment here is merely to those formal aspects of the subsystems introduced above. In promoting entanglement as the world-making relation, nothing has been assumed that obstructs entangled strings; the important element is that they cannot be in space. The ambition is only to indicate that it is possible to have an ontology that does not feature distances on the fundamental level since we seem to be able to recover the distance relations from entanglement.
On this therefore we end: Entanglement promises to be a coherent and empirically adequate world-making relation that can serve as the fundamental relation in an ontology of the world; even taking into account non-spatial theories of quantum gravity. As will be argued elsewhere, entanglement can support change, individuate the simple objects of the ontology, but most importantly, entanglement can—as argued here—account for distance (and possibly all other relations) and be the relation in virtue of which the elements of the ontology—the subsystems—make up a world. Adopting entanglement as the world making relation comes at the price of giving up separability. But those who are ready to take this step should perhaps look to entanglement for the fundamental relation with which to constitute this world (and perhaps all the other possible ones).
Notes
In addition to these explicit metaphysical worries about non-spatial theories of quantum gravity, one might expect that the caution towards such theories is shared by those who prefer the Bohmian interpretation of quantum mechanics out of a concern for the absence of local beables in other interpretations; especially those expressing a sympathy for Humean supervenience (e.g. Loewer 1996; Maudlin 2007b; Miller 2014). Also, the primitive ontology program (most often pursued in the context of quantum mechanics) explicitly requires that “any satisfactory fundamental physical theory [...] contains a metaphysical hypothesis about what constitutes physical objects [...] which lives in three-dimensional space or space-time and constitutes the building blocks of everything else” (Allori 2015, p. 107). According to (this strand of) primitive ontology, space is a precondition for any satisfactory metaphysics of a physical theory. Finally, proponents of spacetime state realism (e.g. Wallace and Timpson 2010) might share this preference for spatial ontologies.
See Wallace (2018, section 8) for a recent criticism of such metaphysical biases in the context of quantum physics.
In arguing that elements make up a world in virtue of being entangled, it follows that the branching, but entangled worlds of the Everett interpretation of quantum mechanics comprise only one world. It is left for the reader to decide whether this counts for or against entanglement as the world-making relation. See Skyrms (1976) and Percival (2013) for further discussion of the relation between possible worlds and the branching worlds of the Everett interpretation. Thank you to an anonymous reviewer of Synthese for bringing this consequence to my attention.
It should be mentioned that there are attempts to develop Bohmian mechanics on shape space that might extend to quantum gravity (Dürr et al. 2018). Thus, there is still the hope to save distance as the world-making relation even in quantum gravity.
In the sense of Bell (2001).
For further details and discussion, see Darby (2009, pp. 196–201).
This in such a way that the objects are absolutely discernible rather than merely weakly discernible. See Saunders (2006) for more on this difference.
In a few more words, a minimalist ontology is one that posits as few (types of) elements as possible and requires the minimal number of different relations between these elements. In addition, the posited elements and relations themselves have to be simple. In summary, a minimalist ontology must satisfy a general parsimony criterion. Whether the ontology of entangled subsystems satisfies this criterion will also be discussed in the companion piece.
Thank you to an anonymous reviewer of Synthese for pressing me on this issue.
One might object that this relation is not world-making, but making connectedness in the world. Calling this relation ‘world-making,’ however, can be motivated if we, like Lewis, do not take ‘world’ as a primitive but rather introduce ‘world’ as “a maximal mereological sum of worldmates” (Darby 2009, p. 196) where worldmates in turn are exactly those entities connected by the world-making relation. This usage of ‘world-making’ also follows the recent use in the literature on the metaphysics of quantum gravity (see in particular Esfeld 2019).
Interestingly, Esfeld has also entertained this possibility, or so it seems from his remark elsewhere that “what there is at the basic level of the world are relations of quantum entanglement” (Esfeld 2004, p. 616).
Notice how this might also contribute to an account of individuation and change from entanglement. If entanglement can account for distance and distance can achieve individuation and change, then entanglement should be able to do the same.
The minimalist ontology also requires that the world-making relation is the only relation. While entanglement might indeed candidate as the single relation from which all other relations derive, this view cannot be justified by the present argument which is strictly limited to distance. Relative charge, for instance, might for all said here have independent existence from entanglement. With that said, I do find such entanglement fundamentalism compelling and worthy of further exploration.
See Oriti (2009) for further discussion of this relation between scope and fundamentality in the context of quantum gravity.
The more precise statement of this: If
 is not a product state of \({\mathcal {H}}_A\) and \({\mathcal {H}}_B\), it follows that a pure state,
is not a product state of \({\mathcal {H}}_A\) and \({\mathcal {H}}_B\), it follows that a pure state, 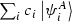 , cannot give the same outcomes as
, cannot give the same outcomes as 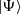 for measurements on subsystem A. However, the outcome of such measurements can be reproduced by a mixture: some ensemble of orthogonal states in \({\mathcal {H}}_A\), where each of these states,
for measurements on subsystem A. However, the outcome of such measurements can be reproduced by a mixture: some ensemble of orthogonal states in \({\mathcal {H}}_A\), where each of these states,  , are associated with a (classical) probability, \(p_i\), of finding the system in that state when making the measurement on A.
, are associated with a (classical) probability, \(p_i\), of finding the system in that state when making the measurement on A.Still, we need measurement to know about entanglement, and a related worry is therefore that of the empirical coherence of non-spatial theories: “if the local beables and the locations are removed from the physical ontology, it is hard to see how evidential contact with the world is to be made [...]” (Maudlin 2007a, p. 3160). See Huggett and Wüthrich (2013) for a response to this problem.
Some complications are involved in making such a decomposition in quantum field theory in a gauge invariant way; something that naively leads to an unphysical gauge fixing dependence of the entanglement entropy (Casini et al. 2014). These complications will not be considered here, but see Delcamp et al. (2016) and references therein for various (proposed) resolutions of this problem.
As shown by Ladyman et al. (2013), this notion of entanglement ensures that we only include genuine entanglement even in the case of indistinguishable fermions.
It is disputed whether the ontology of RQFT is one of particles or fields. See Baker (2016) for a recent survey.
Truth be told, there are indications that the Hilbert space formalism faces some difficulties in RQFT. In a nutshell, the problem is that the high amount of entanglement in RQFT states entails that not even a mixed state in \(\mathcal {H}_A\) uniquely determines the subsystem (see also footnote 18). Swanson (2019) discusses this problem in the context of spacetime state realism that in Sect. 7 below is argued to resemble the ontology of entangled subsystem (aside from the spacetime part). Swanson’s proposed solution in terms algebraic RQFT might therefore also be applicable to entangled subsystems. We shall here stick with the Hilbert space formalism—despite its issues—since this is the formalism used in the quantum gravity literature referenced throughout Sect. 5. How this affects the analysis of Sect. 5 will be left for future work.
See Swanson (2017) for an introduction, comparison, and discussion of the different approaches to RQFT.
This may come as no surprise. Already in quantum mechanics, the vacuum state of for instance the coupled harmonic oscillator is also highly entangled (Srednicki 1993).
More recently, a programmatic spacetime-free approach to algebraic quantum theory has been proposed by Raasakka (2017).
Even having such results might not settle whether entanglement is the relation in virtue of which non-spatial elements make up a world for the simple reason that the exact nature of these elements remains unexplored with the present focus on the world-making relation. This would, in other words, be another interesting venue for further exploration.
For details on how this issue in approached in algebraic RQFT, see the survey by Dieks (2001, section 12–13) and references therein.
In its strongest form, the AdS/CFT correspondence is a duality between type IIB string theory and \(\mathcal {N}=4\) super Yang-Mills theory. For a more rigorous introduction to AdS/CFT and to some of the philosophical issues that the correspondence raises, see Teh (2013), Rickles (2013), Butterfield et al. (2016), and de Haro (2017).
More precisely, this is a particular limit of the AdS/CFT correspondence where the string length on the AdS side is assumed to be much smaller than the characteristic length scale of the spacetime background and the string coupling is much smaller than one (see Callan et al. 1985; Huggett and Vistarini 2015). On the CFT side, this corresponds to the limit where the rank of the gauge group goes to infinity and the t’Hooft coupling is large but finite (for further details, see Ammon and Erdmenger (2015, chapter 5)).
To repeat, this involves finding the reduced density matrix and then evaluate the von Neumann entropy.
More precisely, \({\tilde{B}}\) is the co-dimension two surface of minimal area whose boundary (“endpoints”) is such that it separates B from \(\overline{B}\) and which is homologous to B.
Observe that this evidence is very conjectural and not quantum!
More precisely the length of the shortest bulk geodesic connecting the two points.
To avoid divergences, these have to be properly regulated, see Ammon and Erdmenger (2015, section 5.4) for further details.
This also suggests a route for entangled subsystems to overcome the worry of Wallace and Timpson (2010), who claim that “[i]t is opaque to us how semiclassical quantum gravity can be understood except via a quantum ontology which treats spacetime as fundamental” (709). Their reasons will not be spelled out here, since the resolution offered is simply to discard semiclassical gravity altogether (as a dynamical spacetime) once it is realized that the gravitational dynamics can instead be encoded as dynamical constraints on entanglement.
Interestingly, this picture shares some similarities with Verlinde’s (2011) entropic gravity.
Though motivated by the problem how to individuate matter points with distance in symmetric configurations.
In unitary quantum mechanics (such as the Everett interpretation), the two entangled particles will moreover be entangled with the system that prepared them in this state. For instance in the cascade transition, used by Aspect et al. (1982), the two entangled photons are the decay product of a highly-excited calcium atom; a process that, in the terminology of the Everett interpretation, involves a splitting of the universal wave function into entangled branches (decayed and not decayed).
This effect is only further amplified by entanglement sudden dead phenomena (Yu and Eberly 2009).
Furthermore, Venugopalan et al. (1995) indicates a direct relation between the entanglement decay and the spatial separation of an EPR pair.
Interestingly, Lam and Esfeld (2013) insists that “this fact does not justify the conclusion [...] that the relations of quantum entanglement are somehow ontologically more fundamental than the metrical relations that make up spacetime” (291). Arguably, the same should hold the other way around.
Interestingly, Maudlin finds that the distance relation is not even metaphysically pure in distance-based ontology. This further questions the viability of the scenario of two distanced, entangled particles in a void.
Regardless of the initial entanglement between \(BH_A\) and \(BH_B\), after a scrambling time (of order \(M \log (M)\), where M is the mass) \(BH_A\) and \(BH_B\) becomes scrambled and therefore becomes highly entangled (Maldacena and Susskind 2013, p. 794).
See Maldacena and Susskind (2013, pp. 789–790) for further details how this might be achieved.
A simple example is that the singlet state,
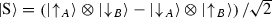 , and the triplet state,
, and the triplet state,  , give the same reduced density matrix for the one-particle subsystem,
, give the same reduced density matrix for the one-particle subsystem, 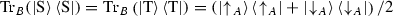 .
.In more plain language, this involves knowing all the possible states that the subsystem might be in if it were isolated.
Obviously, it must be an implicit assumption here that each part (subsystem) is associated with a Hilbert space such that the partial trace is well defined.
A polyhedron is a geometrical object that is uniquely described by the areas and normals to its faces. The details of this representation of the nodes shall not concern us here. The interested reader is referred to Bianchi et al. (2011).
References
Allori, V. (2015). Primitive ontology in a nutshell. International Journal of Quantum Foundations, 1(2), 107–122.
Ammon, M., & Erdmenger, J. (2015). Gauge/gravity duality: Foundations and applications. Cambridge: Cambridge University Press.
Aspect, A., Grangier, P., & Roger, G. (1982). Experimental realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A new violation of Bell’s inequalities. Physical Review Letters, 49(2), 91–94.
Baker, D. J. (2016). The philosophy of quantum field theory. Oxford Handbooks Online. Retrieved 14 May 2020. https://doi.org/10.1093/oxfordhb/9780199935314.013.33.
Balasubramanian, V., & Ross, S. F. (2000). Holographic particle detection. Physical Review D, 61(4), 044007.
Banks, T., Douglas, M. R., Horowitz, G. T., & Martinec, E. (1998). AdS dynamics from conformal field theory. URL https://arxiv.org/abs/hep-th/9808016.
Baytaş, B., Bianchi, E., & Yokomizo, N. (2018). Gluing polyhedra with entanglement in loop quantum gravity. Physical Review D, 98(2), 026001.
Bell, J. S. (2001). The theory of local beables. In M. Bell, K. Gottfried, & M. Veltman (Eds.), John S. Bell on the foundations of quantum mechanics (pp. 50–60). Singapore: WORLD SCIENTIFIC.
Bianchi, E., Doná, P., & Speziale, S. (2011). Polyhedra in loop quantum gravity. Physical Review D, 83(4), 044035.
Brown, A. R., & Susskind, L. (2018). Second law of quantum complexity. Physical Review D, 97(8), 086015.
Butterfield, J., de Haro, S., & Mayerson, D. R. (2016). Conceptual aspects of gauge/gravity duality. Foundations of Physics, 46(11), 1381–1425.
Callan, C. G., Friedan, D., Martinec, E. J., & Perry, M. J. (1985). Strings in background fields. Nuclear Physics B, 262(4), 593–609. https://doi.org/10.1016/0550-3213(85)90506-1. ISSN 0550-3213.
Calosi, C. (2014). Quantum mechanics and priority monism. Synthese, 191(5), 915–928.
Cao, C. J., Carroll, S. M., & Michalakis, S. (2017). Space from Hilbert space: Recovering geometry from bulk entanglement. Physical Review D, 95(2), 024031. https://doi.org/10.1103/PhysRevD.95.024031.
Casini, H., Huerta, M., & Rosabal, J. A. (2014). Remarks on entanglement entropy for gauge fields. Physical Review D, 89(8), 085012.
Chirco, G., Oriti, D., & Zhang, M. (2018). Group field theory and tensor networks: Towards a Ryu–Takayanagi formula in full quantum gravity. Classical and Quantum Gravity, 35(11), 115011.
Clifton, R., & Halvorson, H. (2001). Entanglement and open systems in algebraic quantum field theory. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 32(1), 1–31. https://doi.org/10.1016/S1355-2198(00)00033-2. ISSN 1355-2198.
Darby, G. (2009). Lewis’s worldmate relation and the apparent failure of Humean supervenience. Dialectica, 63(2), 195–204.
David Mermin, N. (1998a). The Ithaca interpretation of quantum mechanics. Pramana, 51(5), 549–565. https://doi.org/10.1007/BF02827447. ISSN 0973-7111.
David Mermin, N. (1998b). What is quantum mechanics trying to tell us? American Journal of Physics, 66(9), 753–767. https://doi.org/10.1119/1.18955. ISSN 0002-9505.
de Haro, S. (2017). Dualities and emergent gravity: Gauge/gravity duality. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 59, 109–125.
Delcamp, C., Dittrich, B., & Riello, A. (2016). On entanglement entropy in non-Abelian lattice gauge theory and 3D quantum gravity. Journal of High Energy Physics, 2016(11), 102.
Dieks, D. (2001). Space and time in particle and field physics. Spacetime, Fields and Understanding: Persepectives on Quantum Field, 32(2), 217–241. https://doi.org/10.1016/S1355-2198(01)00004-1. ISSN 1355-2198.
Dürr, D., Goldstein, S., & Zanghi, N. (2018). Quantum motion on shape space and the gauge dependent emergence of dynamics and probability in absolute space and time. arXiv:1808.06844.
Earman, J. (2015). Some puzzles and unresolved issues about quantum entanglement. Erkenntnis, 80(2), 303–337.
Egg, M. (2013). Delayed-choice experiments and the metaphysics of entanglement. Foundations of Physics, 43(9), 1124–1135. https://doi.org/10.1007/s10701-013-9734-4. ISSN 1572-9516.
Esfeld, M. (2004). Quantum entanglement and a metaphysics of relations. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 35(4), 601–617.
Esfeld, M. (2014). Quantum Humeanism, or: Physicalism without properties. The Philosophical Quarterly, 64(256), 453–470.
Esfeld, M. (2019). Against the disappearance of spacetime in quantum gravity. Synthese,. https://doi.org/10.1007/s11229-019-02168-y. ISSN 1573-0964.
Esfeld, M. (2020). A proposal for a minimalist ontology. Synthese, 197(5), 1889–1905. https://doi.org/10.1007/s11229-017-1426-8.
Esfeld, M., & Deckert, D.-A. (2017). A minimalist ontology of the natural world. New York: Routledge.
Faulkner, T., Guica, M., Hartman, T., Myers, R. C., & Van Raamsdonk, M. (2014). Gravitation from entanglement in holographic CFTs. Journal of High Energy Physics, 2014(3), 51.
Glick, D. (2019). Timelike entanglement for delayed-choice entanglement swapping. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics.,. https://doi.org/10.1016/j.shpsb.2019.06.001. ISSN 1355-2198.
Glick, D., & Darby, G. (2019). In defense of the metaphysics of entanglement. In D. Glick, G. Darby, & A. Marmodoro (Eds.), The foundation of reality: Fundamentality, space, and time. Oxford: Oxford University Press.
Hagar, A., & Hemmo, M. (2013). The primacy of geometry. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 357–364. https://doi.org/10.1016/j.shpsb.2013.01.003. ISSN 1355-2198.
Halvorson, H., & Clifton, R. (2000). Generic Bell correlation between arbitrary local algebras in quantum field theory. Journal of Mathematical Physics, 41(4), 1711–1717. https://doi.org/10.1063/1.533253. ISSN 0022-2488.
Han, M., & Hung, L.-Y. (2017). Loop quantum gravity, exact holographic mapping, and holographic entanglement entropy. Physical Review D, 95(2), 024011.
Healey, R. (2012). Quantum theory: A pragmatist approach. The British Journal for the Philosophy of Science, 63(4), 729–771. https://doi.org/10.1093/bjps/axr054. ISSN 0007-0882.
Howard, D. (1989). Holism, separability, and the metaphysical implications of the Bell experiments. In J. T. Cushing & E. McMullin (Eds.), Philosophical consequences of quantum theory (pp. 224–253). Notre Dame: University of Notre Dame Press.
Huggett, N. (2017). Target space is not equal to space. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 59, 81–88.
Huggett, N., & Vistarini, T. (2015). Deriving general relativity from string theory. Philosophy of Science, 82(5), 1163–1174.
Huggett, N., & Wüthrich, C. (2013). Emergent spacetime and empirical (in)coherence. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 276–285.
Ismael, J., & Schaffer, J. (2016). Quantum holism: Nonseparability as common ground. Synthese,. https://doi.org/10.1007/s11229-016-1201-2.
Jaksland, R. (2019). The multiple realizability of general relativity in quantum gravity. Synthese,. https://doi.org/10.1007/s11229-019-02382-8. ISSN 1573-0964.
Ladyman, J., Linnebo, Ø., & Bigaj, T. (2013). Entanglement and non-factorizability. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 215–221.
Lam, V. (2013). The entanglement structure of quantum field systems. International Studies in the Philosophy of Science, 27(1), 59–72. https://doi.org/10.1080/02698595.2013.783976. ISSN 0269-8595.
Lam, V., & Esfeld, M. (2013). A dilemma for the emergence of spacetime in canonical quantum gravity. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 286–293.
Lam, V., & Wüthrich, C. (2018). Spacetime is as spacetime does. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics.,. https://doi.org/10.1016/j.shpsb.2018.04.003. ISSN 1355-2198.
Lashkari, N., McDermott, M. B., & Van Raamsdonk, M. (2014). Gravitational dynamics from entanglement “thermodynamics”. Journal of High Energy Physics, 2014(4), 195.
Lewis, D. (1986). On the plurality of worlds (Vol. 97). Hoboken: Blackwell Publishers.
Lewis, D. (1994). Humean supervenience debugged. Mind, 103(412), 473–490.
Loewer, B. (1996). Humean supervenience. Philosophical Topics, 24(1), 101–127.
Maldacena, J., Shenker, S. H., & Stanford, D. (2016). A bound on chaos. Journal of High Energy Physics, 2016(8), 106.
Maldacena, J., & Susskind, L. (2013). Cool horizons for entangled black holes. Fortschritte der Physik, 61(9), 781–811.
Maudlin, T. (2007a). Completeness, supervenience and ontology. Journal of Physics A: Mathematical and Theoretical, 40(12), 3151.
Maudlin, T. (2007b). The metaphysics within physics. Oxford: Oxford University Press.
Miller, E. (2014). Quantum entanglement, Bohmian mechanics, and Humean supervenience. Australasian Journal of Philosophy, 92(3), 567–583.
Mintert, F., Carvalho, A. R. R., Kuś, M., & Buchleitner, A. (2005). Measures and dynamics of entangled states. Physics Reports, 415(4), 207–259. https://doi.org/10.1016/j.physrep.2005.04.006. ISSN 0370-1573.
Morganti, M. (2009). Ontological priority, fundamentality and monism. Dialectica, 63(3), 271–288.
Oriti, D. (Ed.). (2009). Approaches to quantum gravity: Toward a new understanding of space, time and matter. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511575549. ISBN: 978-0-521-86045-1.
Percival, P. (2013). Branching of possible worlds. Synthese, 190(18), 4261–4291. ISSN 00397857, 15730964.
Raasakka, M. (2017). Spacetime-free approach to quantum theory and effective spacetime structure. SIGMA, 13, 006.
Rangamani, M., & Takayanagi, T. (2017). Holographic entanglement entropy. Cham: Springer.
Redhead, M. (1995). More ado about nothing. Foundations of Physics, 25(1), 123–137. https://doi.org/10.1007/BF02054660. ISSN 1572-9516.
Rickles, D. (2013). AdS/CFT duality and the emergence of spacetime. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 312–320.
Rovelli, C., & Speziale, S. (2010). Geometry of loop quantum gravity on a graph. Physical Review D, 82(4), 044018.
Ruetsche, L. (2012a). Philosophical aspects of quantum field theory: I. Philosophy Compass, 7(8), 559–570.
Ruetsche, L. (2012b). Philosophical aspects of quantum field theory: II. Philosophy Compass, 7(8), 571–584.
Ryu, S., & Takayanagi, T. (2006). Holographic derivation of entanglement entropy from the anti-de Sitter space/conformal field theory correspondence. Physical Review Letters, 96(18), 181602.
Saunders, S. (2006). Are quantum particles objects? Analysis, 66(289), 52–63.
Schaffer, J. (2010). Monism: The priority of the whole. The Philosophical Review, 119(1), 31–76.
Seevinck, M. (2006). The quantum world is not built up from correlations. Foundations of Physics, 36(10), 1573–1586. https://doi.org/10.1007/s10701-006-9073-9. ISSN 1572-9516.
Skyrms, B. (1976). Possible worlds, physics and metaphysics. Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition, 30(5), 323–332. ISSN 00318116, 15730883.
Smolin, L. (2016). Holographic relations in loop quantum gravity. arxiv:1608.02932.
Sorkin, R. D., & Yazdi, Y. K. (2018). Entanglement entropy in causal set theory. Classical and Quantum Gravity, 35(7), 074004.
Srednicki, M. (1993). Entropy and area. Physical Review Letters, 71(5), 666–669.
Summers, S. J., & Werner, R. (1987). Maximal violation of Bell’s inequalities is generic in quantum field theory. Communications in Mathematical Physics, 110(2), 247–259. https://doi.org/10.1007/BF01207366. ISSN 1432-0916.
Susskind, L. (2017). Dear Qubitzers, GR=QM. arxiv:1708.03040.
Susskind, L. (2018). Why do things fall?arXiv:1802.01198.
Swanson, N. (2017). A philosopher’s guide to the foundations of quantum field theory. Philosophy Compass, 12(5), e12414. https://doi.org/10.1111/phc3.12414. ISSN 1747-9991.
Swanson, N. (2019). How to be a relativistic spacetime state realist. British Journal for the Philosophy of Science,. https://doi.org/10.1093/bjps/axy041.
Swingle, B, & Van Raamsdonk, M. (2014). Universality of gravity from entanglement. arXiv:1405.2933v1.
Teh, N. J. (2013). Holography and emergence. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 300–311.
Teller, P. (1986). Relational holism and quantum mechanics. The British Journal for the Philosophy of Science, 37(1), 71–81.
Timpson, C. G., & Brown, H. R. (2010). Building with quantum correlations. Quantum Information Processing, 9(2), 307–320. https://doi.org/10.1007/s11128-010-0173-2. ISSN 1573-1332.
Unruh, W. G. (1976). Notes on black-hole evaporation. Physical Review D, 14(4), 870–892.
Valente, G. (2010). Can entanglement be destroyed by any local operation in relativistic quantum field theory? Philosophy of Science, 77(5), 1029–1041. https://doi.org/10.1086/656547. ISSN 00318248, 1539767X.
Van Raamsdonk, M. (2010b). Comments on quantum gravity and entanglement. arxiv:0907.2939v2.
Van Raamsdonk, M. (2010a). Building up spacetime with quantum entanglement. General Relativity and Gravitation, 42(10), 2323–2329.
Venugopalan, A., Kumar, D., & Ghosh, R. (1995). Environment-induced decoherence II. Effect of decoherence on Bell’s inequality for an EPR pair. Physica A: Statistical Mechanics and its Applications, 220(3), 576–584. https://doi.org/10.1016/0378-4371(95)00183-8. ISSN 0378-4371.
Verlinde, E. (2011). On the origin of gravity and the laws of Newton. Journal of High Energy Physics, 2011(4), 29.
Wallace, D. (2018). Lessons from realistic physics for the metaphysics of quantum theory. Synthese,. https://doi.org/10.1007/s11229-018-1706-y. ISSN 1573-0964.
Wallace, D., & Timpson, C. G. (2010). Quantum mechanics on spacetime I: Spacetime state realism. The British Journal for the Philosophy of Science, 61(4), 697–727.
Wolf, M. M., Verstraete, F., Hastings, M. B., & Ignacio Cirac, J. (2008). Area laws in quantum systems: Mutual information and correlations. Physical Review Letters, 100(7), 070502.
Wüthrich, C. (2012). The structure of causal sets. Journal for General Philosophy of Science, 43(2), 223–241.
Wüthrich, C. (2017). Raiders of the lost spacetime. In D. Lehmkuhl, G. Schiemann, & E. Scholz (Eds.), Towards a theory of spacetime theories (pp. 297–335). New York: Springer.
Wüthrich, C. (2019). When the actual world is not even possible. In D. Glick, G. Darby, & A. Marmodoro (Eds.), The foundation of reality: Fundamentality, space, and time. Oxford: Oxford University Press.
Yu, T., & Eberly, J. H. (2009). Sudden death of entanglement. Science, 323(5914), 598. https://doi.org/10.1126/science.1167343.
Acknowledgements
Open Access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital). I would like to express my gratitude to Michael Esfeld, Simon Saunders, James Ladyman, Hans Halvorson, Andreas Bartels, Frida Trotter, Lucy James, Niels Linnemann, Andrea Oldofredi, Vera Matarese, Jan Faye, and three anonymous reviewers of Synthese for their valuable feedback on and helpful discussion of earlier drafts of this paper. I also send my thanks for constructive comments to the audiences in Geneva, Lausanne, Stockholm, Uppsala, Bristol, and Bonn where earlier versions of this paper were presented.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jaksland, R. Entanglement as the world-making relation: distance from entanglement. Synthese 198, 9661–9693 (2021). https://doi.org/10.1007/s11229-020-02671-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-020-02671-7


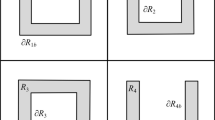





 is not a product state of
is not a product state of 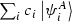 , cannot give the same outcomes as
, cannot give the same outcomes as 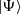 for measurements on subsystem A. However, the outcome of such measurements can be reproduced by a mixture: some ensemble of orthogonal states in
for measurements on subsystem A. However, the outcome of such measurements can be reproduced by a mixture: some ensemble of orthogonal states in  , are associated with a (classical) probability,
, are associated with a (classical) probability, 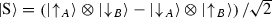 , and the triplet state,
, and the triplet state,  , give the same reduced density matrix for the one-particle subsystem,
, give the same reduced density matrix for the one-particle subsystem, 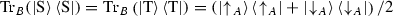 .
.