Abstract
We use a deontic logic of collective agency to study reducibility questions about collective agency and collective obligations. The logic that is at the basis of our study is a multi-modal logic in the tradition of stit (‘sees to it that’) logics of agency. Our full formal language has constants for collective and individual deontic admissibility, modalities for collective and individual agency, and modalities for collective and individual obligations. We classify its twenty-seven sublanguages in terms of their expressive power. This classification enables us to investigate reducibility relations between collective deontic admissibility, collective agency, and collective obligations, on the one hand, and individual deontic admissibility, individual agency, and individual obligations, on the other.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the philosophy of the social sciences, individualism is the methodological precept that any social phenomenon is ultimately to be explained in terms of the actions and interactions of individuals. One of the central questions in the debate on individualism is whether statements about collectives can be reduced to statements about individuals. Does it hold that for every statement about collectives there is a logically equivalent statement about individuals? In this paper, we use techniques from modal logic to find answers to specific reducibility questions, including: Does it hold that for every statement about collective agency there is a logically equivalent statement about individual agency? Does it hold that for every statement about collective obligations there is a logically equivalent statement about collective agency and individual obligations?
By way of a formal study of expressivity relations, we aim to assess which sorts of reductionism about collective agency and collective obligations are tenable. Accordingly, we rephrase the reducibility questions as questions of expressivity: Can statements from a specific language that includes specific statements about collectives be expressed with statements from another language? We follow standard practice in modal logic and develop new notions of bisimulation to determine the answers to these questions of expressivity. Doing so enables us to answer our reducibility questions with logical precision.
To answer our expressivity questions, we use a deontic logic of collective agency. This multi-modal logic is a simplified and generalized version of Horty’s (1996, 2001) deontic logic of agency.Footnote 1 Alongside the usual sentential connectives and the universal modality, our full formal language has constants for collective and individual deontic admissibility, modalities for collective and individual agency, and modalities for collective and individual obligations.Footnote 2 Truth-conditions for the formulas of the full formal language are specified in terms of deontic game models (Tamminga and Hindriks 2020 § 3.2).
There are twenty-seven sublanguages of the full language, depending on (a) whether constants for collective and/or individual deontic admissibility are excluded, (b) whether modalities for collective and/or individual agency are excluded, and (c) whether modalities for collective and/or individual obligations are excluded. Because each of these three items gives rise to three possibilities, there are exactly twenty-seven sublanguages. The main technical contribution of this paper consists in charting this new territory and ordering these twenty-seven sublanguages in terms of their expressive power.
Our paper is organized as follows. In Sect. 2, we first define the full language and give truth-conditions for its formulas in terms of deontic game models. The twenty-seven sublanguages are then defined. Next, we define the concept of expressivity and give three criteria on expressivity that help to classify the twenty-seven sublanguages in terms of their expressive power (Sect. 3). We chart the sublanguages that are equally expressive in Sect. 4 and then give the full picture of the expressivity relations in Sect. 5. Subsequently, we introduce a class of bisimulation relations between pointed deontic game models and prove a Hennessy–Milner theorem for each of the twenty-seven sublanguages (Sect. 6). In the following three sections, we prove that the full picture of expressivity relations is accurate. We briefly discuss two assumptions on our models and languages in Sect. 10. A short summary and some philosophical considerations conclude the paper.
2 Languages and semantics
Let \(\mathfrak {P}\) be a fixed countable set of atomic propositions and let \(\mathcal {N}\) be a fixed finite set of individual agents that contains at least three elements. (We return to this assumption in Sect. 10.) We use p and q as variables for atomic propositions, i, j, and k as variables for individual agents, and \(\mathcal {F}\) and \(\mathcal {G}\) as variables for non-empty sets of individual agents. We use \(-\mathcal {G}\) to refer to the complement \(\mathcal {N}{-}\mathcal {G}\). The full language \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\) of our deontic logic of collective agency contains (i) deontic admissibility constants of the form “Group \(\mathcal {G}\) of agents performs a deontically admissible group action” (formalized as \(\star ^{}_\mathcal {G}\)) and “Agent i performs a deontically admissible individual action” (formalized as \(\star _i\)). Moreover, it contains (ii) necessity statements of the form “It is settled true that \(\phi \)” (formalized as \(\Box \phi \)), (iii) agentive statements of the form “Group \(\mathcal {G}\) of agents sees to it that \(\phi \)” (formalized as \([\mathcal {G}]\phi \)) and “Agent i sees to it that \(\phi \)” (formalized as \([i]\phi \)), and (iv) deontic statements of the form “Group \(\mathcal {G}\) of agents ought to see to it that \(\phi \)” (formalized as \((\mathcal {G})\phi \)) and “Agent i ought to see to it that \(\phi \)” (formalized as \((i)\phi \)). Its Backus-Naur form is the following:
where p ranges over \(\mathfrak {P}\) and \(\mathcal {G}\) ranges over non-empty subsets of \(\mathcal {N}\).
The operators \(\rightarrow \), \(\leftrightarrow \), \(\Diamond \), and \(\langle \mathcal {G}\rangle \) abbreviate the usual constructions. We leave out brackets and braces if the omission does not give rise to ambiguities. Accordingly, the formulas \(\star _i\), \([i]\phi \), and \((i)\phi \) are shorthand for the formulas \(\star _{\{i\}}\), \([\{i\}]\phi \), and \((\{i\})\phi \), respectively.
2.1 Deontic game models
Truth-conditions for the formulas of \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\) are specified in terms of deontic game models. A deontic game model is a one-shot game in which each individual agent i is assigned a non-empty and finite set \(A^{}_i\) of available individual actions. The set \(A^{}_\mathcal {G}\) of group actions that are available to a non-empty set \(\mathcal {G}\) of individual agents is given by \(A^{}_\mathcal {G}=\times ^{}_{i\in \mathcal {G}}A^{}_i\). The set A of action profiles equals the set \(A^{}_\mathcal {N}\) of group actions that are available to the grand coalition \(\mathcal {N}\) of all individual agents and is given by \(A=A^{}_\mathcal {N}=\times ^{}_{i\in \mathcal {N}}A^{}_i\). The set of action profiles plays the role of the set of worlds in possible-worlds models for standard deontic logic. A deontic ideality function d assigns to each action profile a in A a value d(a) that is either 0 or 1. A valuation function assigns to each atomic proposition p in \(\mathfrak {P}\) a set v(p) of action profiles where p is true.Footnote 3 Formally,
Definition 1
(Deontic Game Model) A deontic game model M is a quadruple \(\langle \mathcal {N},(A_i),d,v\rangle \) such that for each agent i in \(\mathcal {N}\) it holds that \(A^{}_i\) is a non-empty and finite set of actions available to agent i, \(d:A\rightarrow \{0,1\}\) is a deontic ideality function such that there is at least one a in A with \(d(a)=1\), and \(v:\mathfrak {P}\rightarrow \wp (A)\) is a valuation function.
To specify truth-conditions for deontic admissibility constants and for deontic statements, we order the group actions that are available to any (possibly singleton) set \(\mathcal {G}\) of individual agents by way of a dominance relation:
Definition 2
(Weak Dominance) Let \(M=\langle \mathcal {N}, (A^{}_i), d,v\rangle \) be a deontic game model. Let \(\mathcal {G}\subseteq \mathcal {N}\) be a non-empty set of individual agents. Let \(a^{}_\mathcal {G},b^{}_\mathcal {G}\in A^{}_\mathcal {G}\). Then
Strong dominance is defined in terms of weak dominance: \(a^{}_\mathcal {G}\succ ^{}_M b^{}_\mathcal {G}\) if and only if \(a^{}_\mathcal {G}\succeq ^{}_M b^{}_\mathcal {G}\) and \(b^{}_\mathcal {G}\not \succeq ^{}_M a^{}_\mathcal {G}\).
A group action that is available to any (possibly singleton) set \(\mathcal {G}\) of individual agents is deontically admissible if and only if it is not strongly dominated by any of \(\mathcal {G}\)’s available group actions. Accordingly,
Definition 3
(Deontic Admissibility) Let \(M=\langle \mathcal {N}, (A^{}_i), d,v\rangle \) be a deontic game model. Let \(\mathcal {G}\subseteq \mathcal {N}\) be a non-empty set of individual agents. Then the set of \(\mathcal {G}\)’s deontically admissible actions in M, denoted by \({ Adm}_M(\mathcal {G})\), is given by
We can now specify the truth-conditions for the formulas of the full language \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\). (Note that by setting \(\mathcal {G}=\{i\}\) we obtain the truth-conditions for the individualistic formulas \(\star _i\), \([i]\phi \), and \((i)\phi \).)
Definition 4
(Truth-Conditions) Let \(M=\langle \mathcal {N}, (A^{}_i), d, v\rangle \) be a deontic game model. Let \(\mathcal {G}\subseteq \mathcal {N}\) be a non-empty set of individual agents. Let \(a\in A\) be an action profile. Let \(p\in \mathfrak {P}\) be an atomic formula and let \(\phi ,\psi \in \mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}\) be arbitrary formulas. Then
Given a deontic game model M, we write \(M\models \phi \) if for all action profiles a in A it holds that \((M,a)\models \phi \). A formula \(\phi \) is valid (notation: \(\models \phi \)) if for all deontic game models M it holds that \(M\models \phi \).
2.2 Twenty-seven sublanguages
The full language \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\) of the deontic logic of collective agency contains constants for collective and individual deontic admissibility, modalities for collective and individual agency, and modalities for collective and individual obligations. Our basic language is the standard modal language \(\mathfrak {L}\) built from the set \(\mathfrak {P}\) of atomic propositions, using negation (\(\lnot \)), conjunction (\(\wedge \)), and the universal modality (\(\Box \)). (We return to the assumption of including the universal modality in Sect. 10.) The sublanguages of our full language are obtained from the basic language \(\mathfrak {L}\) by adding (a) either collective deontic admissibility constants, individual deontic admissibility constants, or no deontic admissibility constants; (b) collective agency modalities, individual agency modalities, or no agency modalities; and/or (c) collective obligation modalities, individual obligation modalities, or no obligation modalities. This gives us twenty-seven languages, ranging from \(\mathfrak {L}\) to \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\). Their names are systematized as follows: we use \(\mathfrak {L}_{x,y,z}\) with \(x\in \{\star _\mathcal {G},\star _i,\epsilon \}\), \(y\in \{[\mathcal {G}],[i],\epsilon \}\), and \(z\in \{(\mathcal {G}),(i),\epsilon \}\), where \(\epsilon \) represents the omission of the relevant constant or modality. Their Backus-Naur forms are read off from their names. For instance, if \(x=\star _i\), \(y=[\mathcal {G}]\), and \(z=\epsilon \), we obtain the language \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\). Its Backus-Naur form is
where p ranges over \(\mathfrak {P}\), i ranges over \(\mathcal {N}\), and \(\mathcal {G}\) ranges over non-empty subsets of \(\mathcal {N}\).
We use \(\mathbf {L}\) to refer to the set that consists of exactly all of our twenty-seven sublanguages. Truth-conditions for the formulas of any \(\mathfrak {L}^*\in \mathbf {L}\) are specified by Definition 4. We now order the twenty-seven languages in \(\mathbf {L}\) in terms of their expressive power.Footnote 4
3 Expressivity
Let us first recall the concept of expressive power, as standardly used in modal logic. We say that a formula \(\psi \) from language \(\mathfrak {L}^{**}\) can be expressed in language \(\mathfrak {L}^*\) if and only if there is a \(\phi \) in \(\mathfrak {L}^*\) such that \(\phi \) and \(\psi \) are logically equivalent. If every formula from the language \(\mathfrak {L}^{**}\) can be expressed in the language \(\mathfrak {L}^*\), we say that \(\mathfrak {L}^*\) is at least as expressive as \(\mathfrak {L}^{**}\). Formally,
Definition 5
Let \(\mathfrak {L}^*,\mathfrak {L}^{**}\in \mathbf {L}\). Then \(\mathfrak {L}^*\) is at least as expressive as \(\mathfrak {L}^{**}\) (notation: \(\mathfrak {L}^*\succeq \mathfrak {L}^{**}\)) if and only if for every \(\psi \) in \(\mathfrak {L}^{**}\) there is a \(\phi \) in \(\mathfrak {L}^*\) such that \(\models \psi \leftrightarrow \phi \).
As usual, \(\mathfrak {L}^*\equiv \mathfrak {L}^{**}\) abbreviates the conjunction of \(\mathfrak {L}^*\succeq \mathfrak {L}^{**}\) and \(\mathfrak {L}^{**}\succeq \mathfrak {L}^*\). Moreover, \(\mathfrak {L}^*\succ \mathfrak {L}^{**}\) abbreviates the conjunction of \(\mathfrak {L}^*\succeq \mathfrak {L}^{**}\) and \(\mathfrak {L}^{**}\not \succeq \mathfrak {L}^*\). Note that \(\mathfrak {L}^{**}\not \succeq \mathfrak {L}^*\) if and only if there is a \(\phi \) in \(\mathfrak {L}^*\) such that for every \(\psi \) in \(\mathfrak {L}^{**}\) it holds that \(\not \models \psi \leftrightarrow \phi \). Accordingly, there is no formula in \(\mathfrak {L}^{**}\) that is logically equivalent to \(\phi \).
To chart the expressivity landscape of our twenty-seven languages, we introduce three criteria of expressive power. The first two criteria are straightforward. First, consider the obvious inclusion criterion for \(\mathfrak {L}^*\succeq \mathfrak {L}^{**}\):
Lemma 1
(Inclusion Criterion) Let \(\mathfrak {L}^*,\mathfrak {L}^{**}\in \mathbf {L}\). Then
Secondly, consider the transitivity criterion for \(\mathfrak {L}^*\not \succeq \mathfrak {L}^{**}\). It follows from the transitivity of \(\succeq \):
Lemma 2
(Transitivity Criterion) Let \(\mathfrak {L}^*,\mathfrak {L}^{**},\mathfrak {L}^{***},\mathfrak {L}^{****}\in \mathbf {L}\). Then
The third criterion is a criterion for \(\mathfrak {L}^*\not \succeq \mathfrak {L}^{**}\) that is defined in terms of pointed deontic game models. The criterion applies if two pointed deontic game models validate exactly the same formulas from \(\mathfrak {L}^*\) but give different truth-values to a formula from \(\mathfrak {L}^{**}\). Any ordered pair (M, a) that consists of a deontic game model M and one of its action profiles a is a pointed deontic game model. Two pointed deontic game models are equivalent on \(\mathfrak {L}^*\) if and only if they validate exactly the same formulas from \(\mathfrak {L}^*\):
Definition 6
(Equivalence on \(\mathfrak {L}^*\)) Let \(\mathfrak {L}^*\in \mathbf {L}\). Let (M, a) and \((M',a')\) be pointed deontic game models. Then (M, a) and \((M',a')\) are equivalent on \(\mathfrak {L}^*\) (notation: \((M,a)\equiv _{\mathfrak {L}^*}(M',a')\)) iff for all \(\phi \in \mathfrak {L}^*\) it holds that \((M,a)\models \phi \) if and only if \((M',a')\models \phi \).
We can now formulate the equivalence criterion for \(\mathfrak {L}^*\not \succeq \mathfrak {L}^{**}\):
Lemma 3
(Equivalence Criterion) Let \(\mathfrak {L}^*,\mathfrak {L}^{**}\in \mathbf {L}\). Let (M, a) and \((M',a')\) be pointed deontic game models. Suppose \((M,a)\equiv _{\mathfrak {L}^*}(M',a')\). Then
Proof
Assume \((M,a)\equiv _{\mathfrak {L}^*}(M',a')\). Suppose \((M,a)\models \psi \) and \((M',a')\not \models \psi \) for some \(\psi \in \mathfrak {L}^{**}\). Suppose \(\mathfrak {L}^*\succeq \mathfrak {L}^{**}\). Because \(\psi \in \mathfrak {L}^{**}\), there is a \(\phi \) in \(\mathfrak {L}^*\) such that \(\models \psi \leftrightarrow \phi \). Then \((M,a)\models \phi \) and \((M',a')\not \models \phi \) and \(\phi \in \mathfrak {L}^*\). Contradiction. Therefore, \(\mathfrak {L}^*\not \succeq \mathfrak {L}^{**}\). \(\square \)
The inclusion criterion, the transitivity criterion, and the equivalence criterion help to classify the twenty-seven sublanguages of \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\) in terms of their expressive power. We start with the sublanguages that have precisely the same expressive power.
4 Equally expressive sublanguages
Any obligation modality can be given an Andersonian–Kangerian definition in terms of the universal modality and the relevant deontic admissibility constant:
Lemma 4
Let \(\mathcal {G}\subseteq \mathcal {N}\) be a non-empty set of individual agents. Let \(\phi \in \mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}\). Then
The Andersonian–Kangerian definitions of obligation modalities are central to the proofs that some of the sublanguages of \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\) are equally expressive.
Lemma 5
Let \(x\in \{\star _\mathcal {G},\star _i,\epsilon \}\), \(y\in \{[\mathcal {G}],[i],\epsilon \}\), and \(z\in \{(\mathcal {G}),(i),\epsilon \}\). Then
Proof
(i) We show that for every \(\psi \in \mathfrak {L}_{x,y,(\mathcal {G})}\) there is a \(\phi \in \mathfrak {L}_{\star _\mathcal {G},y,z}\) such that \(\models \psi \leftrightarrow \phi \) by structural induction on \(\psi \).
Basis: we check cases \(\psi =p\), \(\psi =\star _i\) (if \(x=\star _i\)), and \(\psi =\star _\mathcal {G}\) (if \(x=\star _\mathcal {G}\)). Because all of them are also elements of \(\mathfrak {L}_{\star _\mathcal {G},y,z}\), there is a \(\phi \in \mathfrak {L}_{\star _\mathcal {G},y,z}\) such that \(\models \psi \leftrightarrow \phi \).
Induction Hypothesis: for all \(\chi \in \mathfrak {L}_{x,y,(\mathcal {G})}\) with fewer operators than \(\psi \) there is a \(\phi _\chi \in \mathfrak {L}_{\star _\mathcal {G},y,z}\) such that \(\models \chi \leftrightarrow \phi _\chi \).
Induction Step: we check case \(\psi =(\mathcal {G})\chi \). By Lemma 4, \(\models (\mathcal {G})\chi \leftrightarrow \Box (\star _\mathcal {G}\rightarrow \chi )\). By the Induction Hypothesis, there is a \(\phi _\chi \in \mathfrak {L}_{\star _\mathcal {G},y,z}\) such that \(\models \chi \leftrightarrow \phi _\chi \). Hence, \(\models (\mathcal {G})\chi \leftrightarrow \Box (\star _\mathcal {G}\rightarrow \phi _\chi )\). Note that \(\Box (\star _\mathcal {G}\rightarrow \phi _\chi )\in \mathfrak {L}_{\star _\mathcal {G},y,z}\). Hence, there is a \(\phi \in \mathfrak {L}_{\star _\mathcal {G},y,z}\) such that \(\models \psi \leftrightarrow \phi \).
The other cases are similar.
(ii), (iii), and (iv) are proved analogously. \(\square \)
Theorem 1
Each of the following holds:
Proof
(i) By Lemma 5(ii), we have \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\succeq \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(i)}\). By the inclusion criterion, it holds that \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(i)}\succeq \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\). Hence, \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\equiv \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(i)}\). By Lemma 5(i), we have \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\succeq \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\). By the inclusion criterion, it holds that \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\succeq \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\). Hence, \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\equiv \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\). The transitivity of \(\succeq \) gives us \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\equiv \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(i)}\equiv \mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\).
Claims (ii) through (vi) are proved analogously. \(\square \)
Because our focus is on charting the expressivity relations between our twenty-seven sublanguages, we refer to any class of equally expressive languages by the language in that class with the shortest name. Hence, we use the six languages in the first column in Theorem 1 to refer to the six classes of equally expressive languages that were identified in this theorem. Accordingly, \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\) refers to the class of the languages in \(\mathbf {L}\) that are equally expressive as the full language \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\).
5 The full picture of the expressivity relations
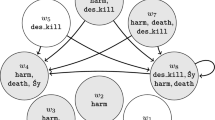
The eighteen sublanguages that remain to be classified are the six languages of the first column of Theorem 1 and the sublanguages in \(\mathbf {L}\) that were not mentioned in this theorem. No two of these eighteen sublanguages are equally expressive. If we represent \(\mathfrak {L}^*\succ \mathfrak {L}^{**}\) by an arrow from \(\mathfrak {L}^*\) to \(\mathfrak {L}^{**}\), the expressivity relations between the eighteen languages can be pictured as in Fig. 1.
Accordingly, \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}]}\) is the most expressive language in \(\mathbf {L}\) and \(\mathfrak {L}\) is the least expressive language in \(\mathbf {L}\). To prove that this picture adequately represents the expressivity relations among the eighteen sublanguages, we think of the picture as a three-dimensional prism and decompose it in the left front face (Fig. 2), the right front face (Fig. 9), and the horizontals (Fig. 10).
6 Bisimulations and Hennessy–Milner theorems
To prove that some sublanguage \(\mathfrak {L}^*\) is not at least as expressive as another sublanguage \(\mathfrak {L}^{**}\), we apply the equivalence criterion to specific pairs of pointed deontic game models. The equivalence criterion can only be applied if the pointed deontic game models in the pair are \(\mathfrak {L}^*\)-equivalent. To prove that they are \(\mathfrak {L}^*\)-equivalent, we develop a suitable concept of \(\mathfrak {L}^*\)-bisimulation and show that the two languages are \(\mathfrak {L}^*\)-bisimilar. All of this is standard practice in modal logic.Footnote 5
An \(\mathfrak {L}^*\)-bisimulation between two pointed deontic game models (M, a) and \((M',a')\) is a relation \(R\subseteq A\times A'\) linking the models’ action profiles that satisfies a specific set of structural conditions associated with the logical operators in \(\mathfrak {L}^*\). For every language \(\mathfrak {L}^*\) in \(\mathbf {L}\) we present such a set of structural conditions on R that characterizes \(\mathfrak {L}^*\)-equivalence. Accordingly, for every language \(\mathfrak {L}^*\) in \(\mathbf {L}\) we show that two given pointed deontic game models are \(\mathfrak {L}^*\)-bisimilar if and only if they are \(\mathfrak {L}^*\)-equivalent. Such theorems are known as Hennessy–Milner theorems. We prove a general claim that summarizes the Hennessy–Milner theorems for all sublanguages in \(\mathbf {L}\) (Theorem 2). To establish this general claim, we use a technique from Van Benthem et al. (2017, § 3) and first prove a general lemma on sublanguages in \(\mathbf {L}\). (Note that this technique is also called upon in our proof of the general claim itself.)
Lemma 6
Let \(\mathfrak {L}^*\in \mathbf {L}\). Let \(M=\langle \mathcal {N},(A_i),d,v\rangle \) and \(M'=\langle \mathcal {N},(A'_i),d',v'\rangle \) be deontic game models. Let \(b\in A\) and \(b'\in A'\). If \((M,b)\equiv _{\mathfrak {L}^*}(M',b')\), then for every \(c\in A\) there is a \(c'\in A'\) such that \((M,c)\equiv _{\mathfrak {L}^*}(M',c')\).
Proof
Assume \((M,b)\equiv _{\mathfrak {L}^*}(M',b')\). Take an arbitrary \(c\in A\). For every \(d\in A\), let \(\phi _{c,d}=p\vee \lnot p\) if \((M,c)\equiv _{\mathfrak {L}^*}(M,d)\); otherwise, let \(\phi _{c,d}=\psi \) for some \(\psi \in \mathfrak {L}^*\) for which it holds that \((M,c)\models \psi \) and \((M,d)\not \models \psi \). Let \(\phi _c=\bigwedge _{d\in A}\phi _{c,d}\). The finiteness of A ensures that \(\phi _c\) is well defined. Note that (\(\dagger \)) for every \(d\in A\) it holds that if \((M,d)\models \phi _c\), then \((M,c)\equiv _{\mathfrak {L}^*}(M,d)\).
Because \((M,c)\models \phi _c\), it holds that \((M,b)\models \Diamond \phi _c\). By our assumption, \((M',b')\models \Diamond \phi _c\). Then there is a \(c'\in A'\) such that \((M',c')\models \phi _c\). Suppose \((M,c)\not \equiv _{\mathfrak {L}^*}(M',c')\). Then there is a \(\chi \in \mathfrak {L}^*\) such that \((M,c)\models \chi \) and \((M',c')\not \models \chi \). Then \((M',c')\models \phi _c\wedge \lnot \chi \) and hence \((M',b')\models \Diamond (\phi _c\wedge \lnot \chi )\). By our assumption, \((M,b)\models \Diamond (\phi _c\wedge \lnot \chi )\). Then there is a \(d\in A\) such that \((M,d)\models \phi _c\wedge \lnot \chi \). By (\(\dagger \)), the first conjunct entails that \((M,c)\equiv _{\mathfrak {L}^*}(M,d)\). However, we have \((M,c)\models \chi \) and \((M,d)\not \models \chi \). Contradiction. Hence, \((M,c)\equiv _{\mathfrak {L}^*}(M',c')\). Therefore, because \(c\in A\) was arbitrary, for every \(c\in A\) there is a \(c'\in A'\) such that \((M,c)\equiv _{\mathfrak {L}^*}(M',c')\). \(\square \)
We now present a list of nine structural conditions on relations R that link the action profiles of two given deontic game models. Each of the twenty-seven languages in \(\mathbf {L}\) is assigned a specific subset of these nine structural conditions. Because all of these subsets include at least three basic structural conditions, we set these three conditions apart. The relations that satisfy them are basic bisimulations:
Definition 7
Let \(M=\langle \mathcal {N},(A_i),d,v\rangle \) and \(M'=\langle \mathcal {N},(A'_i),d',v'\rangle \) be deontic game models. A relation \(R\subseteq A\times A'\) is a basic bisimulation between M and \(M'\) if R satisfies each of the following clauses:
-
(i)
for all \((b,b')\in R\) and all \(p\in \mathfrak {P}\) it holds that \(b\in v(p)\) iff \(b'\in v'(p)\)
-
(ii)
for all \(b\in A\) there is a \(b'\in A'\) such that \((b,b')\in R\)
-
(iii)
for all \(b'\in A'\) there is a \(b\in A\) such that \((b,b')\in R\).
The other six structural conditions on relations R are specified as follows:
Definition 8
Let \(M=\langle \mathcal {N},(A_i),d,v\rangle \) and \(M'=\langle \mathcal {N},(A'_i),d',v'\rangle \) be deontic game models. Let \(R\subseteq A\times A'\) be a relation between M and \(M'\). The six optional structural conditions on R are the following:
-
\(C_{\star _{\mathcal {G}}}\):
for all \((b,b')\in R\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that \(b^{}_\mathcal {G}\in { Adm}_M(\mathcal {G})\) iff \(b'_\mathcal {G}\in { Adm}_{M'}(\mathcal {G})\)
-
\(C_{\star _i}\):
for all \((b,b')\in R\) and all \(i\in \mathcal {N}\) it holds that \(b^{}_i\in { Adm}_M(i)\) iff \(b'_i\in { Adm}_{M'}(i)\)
-
\(C_{[\mathcal {G}]}\):
-
(i)
for all \((b,b')\in R\) and all \(c\in A\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that if \(b^{}_\mathcal {G}=c^{}_\mathcal {G}\), then there is a \(c'\in A'\) such that \(b'_\mathcal {G}=c'_\mathcal {G}\) and \((c,c')\in R\)
-
(ii)
for all \((b,b')\in R\) and all \(c'\in A'\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that if \(b'_\mathcal {G}=c'_\mathcal {G}\), then there is a \(c\in A\) such that \(b^{}_\mathcal {G}=c^{}_\mathcal {G}\) and \((c,c')\in R\)
-
(i)
-
\(C_{[i]}\):
-
(i)
for all \((b,b')\in R\) and all \(c\in A\) and all \(i\in \mathcal {N}\) it holds that if \(b^{}_i=c^{}_i\), then there is a \(c'\in A'\) such that \(b'_i=c'_i\) and \((c,c')\in R\)
-
(ii)
for all \((b,b')\in R\) and all \(c'\in A'\) and all \(i\in \mathcal {N}\) it holds that if \(b'_i=c'_i\), then there is a \(c\in A\) such that \(b^{}_i=c^{}_i\) and \((c,c')\in R\)
-
(i)
-
\(C_{(\mathcal {G})}\):
-
(i)
for all \(c\in A\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that if \(c^{}_\mathcal {G}\in { Adm}_M(\mathcal {G})\), then there is a \(c'\in A'\) such that \(c'_\mathcal {G}\in { Adm}_{M'}(\mathcal {G})\) and \((c,c')\in R\)
-
(ii)
for all \(c'\in A'\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that if \(c'_{\mathcal {G}} \in { Adm}_{M'}(\mathcal {G})\), then there is a \(c\in A\) such that \(c^{}_{\mathcal {G}}\in { Adm}_{M}(\mathcal {G})\) and \((c,c')\in R\)
-
(i)
-
\(C_{(i)}\):
-
(i)
for all \(c\in A\) and all \(i\in \mathcal {N}\) it holds that if \(c^{}_i \in { Adm}_M(i)\), then there is a \(c'\in A'\) such that \(c'_i\in { Adm}_{M'}(i)\) and \((c,c')\in R\)
-
(ii)
for all \(c'\in A'\) and all \(i\in \mathcal {N}\) it holds that if \(c'_i \in { Adm}_{M'}(i)\), then there is a \(c\in A\) such that \(c^{}_i\in { Adm}_{M}(i)\) and \((c,c')\in R\).
-
(i)
Each of the twenty-seven sublanguages in \(\mathbf {L}\) is assigned a specific subset of these six structural conditions in the following way (\(C_\epsilon \) is the empty condition that is satisfied trivially):
Definition 9
Let \(M=\langle \mathcal {N},(A_i),d,v\rangle \) and \(M'=\langle \mathcal {N},(A'_i),d',v'\rangle \) be deontic game models. Let \(x\in \{\star _\mathcal {G},\star _i,\epsilon \}\), \(y\in \{[\mathcal {G}],[i],\epsilon \}\), and \(z\in \{(\mathcal {G}),(i),\epsilon \}\). A relation \(R\subseteq A\times A'\) is an \(\mathfrak {L}_{x,y,z}\)-bisimulation between M and \(M'\) if R is a basic bisimulation that satisfies conditions \(C_x\), \(C_y\), and \(C_z\).
Consequently, an \(\mathfrak {L}\)-bisimulation is just a basic bisimulation, and an \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\)-bisimulation is a basic bisimulation that also satisfies conditions \(C_{\star _i}\) and \(C_{[\mathcal {G}]}\). We write \((M,a)\rightleftarrows _{\mathfrak {L}_{x,y,z}}(M',a')\) if there is an \(\mathfrak {L}_{x,y,z}\)-bisimulation R between M and \(M'\) such that \((a,a')\in R\).
We can now establish our general claim:
Theorem 2
(Hennessy–Milner) Let \(\mathfrak {L}^*\in \mathbf {L}\). Then for all pointed deontic game models (M, a) and \((M',a')\) it holds that \((M,a)\rightleftarrows _{\mathfrak {L}^*}(M',a')\) if and only if \((M,a)\equiv _{\mathfrak {L}^*}(M',a')\).
Proof
Although the general claim is in fact a conjunction of claims on twenty-seven individual cases, the proofs of all these claims are very similar. Because the left-to-right direction is always proved by a straightforward structural induction on \(\phi \), we omit it here. As for the right-to-left direction, we will only give a full proof for the case where \(\mathfrak {L}^*=\mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}\). Suppose \((M,a)\equiv _{\mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}}(M',a')\). Let \(R=\{(b,b')\in A\times A':(M,b)\equiv _{\mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}}(M',b')\}\). We prove that R is an \(\mathfrak {L}_{\star _{\mathcal {G}},[\mathcal {G}],(\mathcal {G})}\)-bisimulation between M and \(M'\). We first show that R is a basic bisimulation. Clause (i) of Definition 7 follows from the definition of R. Clauses (ii) and (iii) of Definition 7 follow from Lemma 6. Hence, R is a basic bisimulation. Next, we show that R satisfies conditions \(C_{\star _\mathcal {G}}\), \(C_{[\mathcal {G}]}\), and \(C_{(\mathcal {G})}\).
- \(C_{\star _\mathcal {G}}\)::
-
Take an arbitrary \((b,b')\in R\) and an arbitrary non-empty \(\mathcal {G}\subseteq \mathcal {N}\). Suppose \(b^{}_\mathcal {G}\in { Adm}_M(\mathcal {G})\). Then \((M,b)\models \star ^{}_\mathcal {G}\). By the definition of R, we have \((M',b')\models \star ^{}_\mathcal {G}\). Hence, \(b'_\mathcal {G}\in { Adm}_{M'}(\mathcal {G})\). The proof of the converse is analogous.
- \(C_{[\mathcal {G}]}\)::
-
We prove clause (i) of condition \(C_{[\mathcal {G}]}\). Take an arbitrary pair \((b,b')\in R\), an arbitrary \(c\in A\), and an arbitrary non-empty \(\mathcal {G}\subseteq \mathcal {N}\). Suppose \(b^{}_\mathcal {G}=c^{}_\mathcal {G}\). Define \(\phi _c\) as in the proof of Lemma 6. Then \((M,c)\models \phi _c\). Because \(b^{}_\mathcal {G}=c^{}_\mathcal {G}\), it follows that \((M,b)\models \langle \mathcal {G}\rangle \phi _c\). By supposition and the definition of R, it must be that \((M',b')\models \langle \mathcal {G}\rangle \phi _c\). Then there is a \(c'\in A'\) such that \(b'_\mathcal {G}=c'_\mathcal {G}\) and \(M',c'\models \phi _c\). By the same reasoning as in the proof of Lemma 6, it must be that \((M,c)\equiv _{\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}}(M',c')\). Hence \((c,c')\in R\). Because \((b,b')\) and c and \(\mathcal {G}\) were arbitrary, for all \((b,b')\in R\) and all \(c\in A\) and all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that if \(b^{}_\mathcal {G}=c^{}_\mathcal {G}\), then there is a \(c'\in A'\) such that \(b'_\mathcal {G}=c'_\mathcal {G}\) and \((c,c')\in R\). The proof of clause (ii) of condition \(C_{[\mathcal {G}]}\) is analogous.
- \(C_{(\mathcal {G})}\)::
-
We prove clause (i) of condition \(C_{(\mathcal {G})}\). Take an arbitrary \(c\in A\) and an arbitrary non-empty \(\mathcal {G}\subseteq \mathcal {N}\). Suppose \(c^{}_\mathcal {G}\in { Adm}_{M}(\mathcal {G})\). Define \(\phi _c\) as in the proof of Lemma 6. Then \((M,c)\models \phi _c\). Hence, \((M,c)\not \models (\mathcal {G})\lnot \phi _c\) and therefore \((M,a)\not \models (\mathcal {G})\lnot \phi _c\). By supposition, it must be that \((M',a')\not \models (\mathcal {G})\lnot \phi _c\). Then there is a \(c'\in A'\) such that \(c'_\mathcal {G}\in { Adm}_{M'}(\mathcal {G})\) and \((M',c')\models \phi _c\). By the same reasoning as in the proof of Lemma 6, it must be that \((M,c)\equiv _{\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}} (M',c')\). Hence, \((c,c')\in R\). Because c and \(\mathcal {G}\) were arbitrary, for all \(c\in A\) and all \(\mathcal {G}\in \mathcal {N}\) it holds that if \(c^{}_{\mathcal {G}}\in { Adm}_M(\mathcal {G})\), then there is a \(c'\in A'\) such that \(c'_{\mathcal {G}}\in { Adm}_{M'}(\mathcal {G})\) and \((c,c')\in R\). The proof of clause (ii) of condition \(C_{(\mathcal {G})}\) is analogous.
Hence, R is an \(\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}\)-bisimulation between M and \(M'\). Because \((a,a')\in R\), we conclude that \((M,a)\rightleftarrows _{\mathfrak {L}_{\star _\mathcal {G},[\mathcal {G}],(\mathcal {G})}}(M',a')\).
The proofs of the other twenty-six cases are simple variations of the above proof. Consider the language \(\mathfrak {L}_{x,y,z}\). If \(x=\star _i\), \(y=[i]\), or \(z=(i)\), then replace each occurrence of \(\mathcal {G}\) in the corresponding part of the above proof with i. If \(x=\epsilon \), \(y=\epsilon \), or \(z=\epsilon \), then leave out the corresponding part of the above proof. \(\square \)
7 The left front face
To chart the expressivity relations among the twelve sublanguages of the left front face of the full expressivity picture (Fig. 2), it suffices to prove five theorems. Using these five theorems, the inclusion criterion, the transitivity criterion and Lemma 5(i), we can easily find the expressivity relations between every pair from the twelve sublanguages of Fig. 2. The labels of the arrows in Fig. 2 indicate the theorem that can be used to establish the corresponding expressivity relation. The five theorems are the following:
Theorem 3
\(\mathfrak {L}_{\star _{\mathcal {G}},[i]}\not \succeq \mathfrak {L}_{[\mathcal {G}]}\).
Proof
Because \(\mathcal {N}\) contains at least three elements, there are \(i,j,k\in \mathcal {N}\) such that \(i\ne j\) and \(j\ne k\) and \(i\ne k\). We define two pointed deontic game models that are \({\mathfrak {L}_{\star _{\mathcal {G}},[i]}}\)-bisimilar (and hence validate exactly the same \({\mathfrak {L}_{\star _{\mathcal {G}},[i]}}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{[\mathcal {G}]}\)-formula [i, k]p.
Let \(M^{}_1=\langle \mathcal {N},(A_i),d,v\rangle \) be such that \(A^{}_i=\{a^{}_i,b^{}_i\}\) and \(A^{}_j=\{a^{}_j,b^{}_j\}\) and \(A^{}_k=\{a^{}_k,b^{}_k\}\) and \(A^{}_l=\{a^{}_l\}\) for all \(l\in \mathcal {N}-\{i,j,k\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j,k\}}=\{a^{}_{-\{i,j,k\}}\}\).) Let \(d(c)=1\) for all \(c\in A\). Lastly, let v(p) \(=\) \(\{(a^{}_i,a^{}_j,a^{}_k,a^{}_{-\{i,j,k\}}),\) \((a^{}_i,a^{}_j,b^{}_k,a^{}_{-\{i,j,k\}}),\) \((a^{}_i,b^{}_j,a^{}_k,a^{}_{-\{i,j,k\}}),\) \((b^{}_i,a^{}_j,a^{}_k,a^{}_{-\{i,j,k\}})\}\) and let \(v(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M^{}_1\) can be pictured as in Fig. 3 (the group action \(a^{}_{-\{i,j,k\}}\) is not represented).
Let \(M'_1=\langle \mathcal {N},(A'_i),d',v'\rangle \) be such that \(A'_i=\{a'_i,b'_i\}\) and \(A'_j=\{a'_j,b'_j\}\) and \(A'_k=\{a'_k\}\) and \(A'_l=\{a'_l\}\) for all \(l\in \mathcal {N}-\{i,j,k\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j,k\}}=\{a'_{-\{i,j,k\}}\}\).) Let \(d'(c')=1\) for all \(c'\in A'\). Lastly, let \(v'(p)=\{(a'_i,a'_j,a'_k,a'_{-\{i,j,k\}}),\) \((b'_i,b'_j,a'_k,a'_{-\{i,j,k\}})\}\) and \(v'(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{q\}\). Model \(M'_1\) can be pictured as in Fig. 4 (the group action \(a'_{-\{i,j,k\}}\) is not represented).
Let \(R=\{(c,c')\in A\times A':c\in v(p) \text{ iff } c'\in v'(p)\}\). Because for all non-empty \(\mathcal {G}\subseteq \mathcal {N}\) it holds that \(M^{}_1\models \star _\mathcal {G}\) and \(M'_1\models \star _\mathcal {G}\), the relation R satisfies bisimulation condition \(C_{\star _{\mathcal {G}}}\). For every \(i\in \mathcal {N}\) and every \(c\in A\) there are \(c^*_{-i},c^{**}_{-i}\in A^{}_{-i}\) such that \((c^{}_i,c^*_{-i})\in v(p)\) and \((c^{}_i,c^{**}_{-i})\not \in v(p)\). Likewise, for every \(i\in \mathcal {N}\) and every \(c'\in A'\) there are \(c''_{-i},c'''_{-i}\in A'_{-i}\) such that \((c'_i,c''_{-i})\in v(p)\) and \((c'_i,c'''_{-i})\not \in v(p)\). From these observations, it follows that R satisfies bisimulation condition \(C_{[i]}\). Therefore, R is an \(\mathfrak {L}_{\star _{\mathcal {G}},[i]}\)-bisimulation between \(M^{}_1\) and \(M'_1\). Hence, \((M^{}_1,(a^{}_i,a^{}_j,a^{}_k,a^{}_{-\{i,j,k\}}))\rightleftarrows _{\mathfrak {L}_{\star _{\mathcal {G}},[i]}}(M'_1,(a'_i,a'_j,a'_k,a'_{-\{i,j,k\}}))\). By Theorem 2, we obtain \((M^{}_1,(a^{}_i,a^{}_j,a^{}_k,a^{}_{-\{i,j,k\}}))\equiv _{\mathfrak {L}_{\star _{\mathcal {G}},[i]}}(M'_1,(a'_i,a'_j,a'_k,a'_{-\{i,j,k\}}))\). However, note that it holds that \((M^{}_1,(a^{}_i,a^{}_j,a^{}_k,a^{}_{-\{i,j,k\}}))\models [i,k]p\) and also that \((M'_1,(a'_i,a'_j,a'_k,a'_{-\{i,j,k\}}))\not \models [i,k]p\). By Lemma 3, \(\mathfrak {L}_{\star _{\mathcal {G}},[i]}\not \succeq \mathfrak {L}_{[\mathcal {G}]}\). \(\square \)
Theorem 4
\(\mathfrak {L}_{\star _{\mathcal {G}}}\not \succeq \mathfrak {L}_{[i]}\).
Proof
Because \(\mathcal {N}\) contains at least two elements, there are \(i,j\in \mathcal {N}\) such that \(i\ne j\). We define two pointed deontic game models that are \(\mathfrak {L}_{\star _{\mathcal {G}}}\)-bisimilar (and hence validate exactly the same \(\mathfrak {L}_{\star _{\mathcal {G}}}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{[i]}\)-formula [i]p.
Let \(M^{}_2=\langle \mathcal {N},(A_i),d,v\rangle \) be such that \(A^{}_i=\{a^{}_i,b^{}_i\}\) and \(A^{}_j=\{a^{}_j\}\) and \(A^{}_k=\{a^{}_k\}\) for all \(k\in \mathcal {N}-\{i\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j\}}=\{a^{}_{-\{i,j\}}\}\).) Let \(d(c)=1\) for all \(c\in A\). Lastly, let \(v(p)=\{(a^{}_i,a^{}_j,a^{}_{-\{i,j\}})\}\) and \(v(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M_2\) can be pictured as in Fig. 5 (left; the group action \(a^{}_{-\{i,j\}}\) is not represented).
Let \(M'_2=\langle \mathcal {N},(A'_i),d',v'\rangle \) be such that \(A'_i=\{a'_i,b'_i\}\) and \(A'_j=\{a'_j,b'_j\}\) and \(A'_k=\{a'_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j\}}=\{a'_{-\{i,j\}}\}\).) Let \(d'(c')=1\) for all \(c'\in A'\). Lastly, let \(v'(p)=\{(a'_i,a'_j,a'_{-\{i,j\}}),(b'_i,b'_j,a'_{-\{i,j\}})\}\) and \(v'(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M'_2\) can be pictured as in Fig. 5 (right; the group action \(a'_{-\{i,j\}}\) is not represented).
Let \(R=\{(c,c')\in A\times A':c\in v(p) \text{ iff } c'\in v'(p)\}\). It is easy to check that R is an \(\mathfrak {L}_{\star _{\mathcal {G}}}\)-bisimulation between \(M^{}_2\) and \(M'_2\). Hence, \((M^{}_2,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\rightleftarrows _{\mathfrak {L}_{\star _{\mathcal {G}}}}(M'_2,(a'_i,a'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M^{}_2,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{\star _{\mathcal {G}}}}(M'_2,(a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M^{}_2,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\models [i]p\) and \((M'_2,(a'_i,a'_j,a'_{-\{i,j\}}))\not \models [i]p\). By Lemma 3, it must be that \(\mathfrak {L}_{\star _{\mathcal {G}}}\not \succeq \mathfrak {L}_{[i]}\). \(\square \)
Theorem 5
\(\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}\not \succeq \mathfrak {L}_{\star _\mathcal {G}}\).
Proof
Because \(\mathcal {N}\) contains at least two elements, there are \(i,j\in \mathcal {N}\) such that \(i\ne j\). We define two pointed deontic game models that are \(\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}\)-bisimilar (and hence validate exactly the same \(\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{\star _\mathcal {G}}\)-formula \(\star _{\{i,j\}}\).
Let \(M_3=\langle \mathcal {N},(A^{}_i),d,v\rangle \) be such that \(A^{}_i=\{a^{}_i\}\) and \(A^{}_j=\{a^{}_j\}\) and \(A^{}_k = \{a^{}_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j\}}=\{a^{}_{-\{i,j\}}\}\).) Let \(d(a^{}_i,a^{}_j,a^{}_{-\{i,j\}})=1\). Lastly, let \(v(p) = \emptyset \) for all \(p\in \mathfrak {P}\). Model \(M_3\) can be pictured as in Fig. 6 (left; the group action \(a^{}_{-\{i,j\}}\) is not represented).
Let \(M_3'=\langle \mathcal {N},(A_i'),d',v\rangle \) be such that \(A'_i=\{a_i',b_i'\}\) and \(A'_j=\{a'_j,b'_j\}\) and \(A'_k=\{a'_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j\}}=\{a'_{-\{i,j\}}\}\).) Let \(d'(a'_i,b'_j,a'_{-\{i,j\}})=d'(b'_i,a'_j,a'_{-\{i,j\}})=1\) and \(d'(a'_i,a'_j,a'_{-\{i,j\}})=d'(b'_i,b'_j,a'_{-\{i,j\}})=0\). Lastly, let \(v(p)=\emptyset \) for all \(p\in \mathfrak {P}\). Model \(M'_3\) can be pictured as in Fig. 6 (right; the group action \(a'_{-\{i,j\}}\) is not represented).
Let \(R=A\times A'\). It is easy to check that R is an \(\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}\)-bisimulation between \(M_3\) and \(M'_3\). Hence, \((M_3, (a_i,a_j,a^{}_{-\{i,j\}}))\leftrightarrows _{\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}}(M'_3, (a'_i,a'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M_3, (a_i,a_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}}(M'_3, (a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M_3, (a_i,a_j,a^{}_{-\{i,j\}}))\models \star _{\{i,j\}}\) and \((M'_3, (a'_i,a'_j,a'_{-\{i,j\}}))\not \models \star _{\{i,j\}}\). By Lemma 3, \(\mathfrak {L}_{\star _i,[\mathcal {G}],(\mathcal {G})}\not \succeq \mathfrak {L}_{\star _\mathcal {G}}\). \(\square \)
Theorem 6
\(\mathfrak {L}_{\star _i,[\mathcal {G}]}\not \succeq \mathfrak {L}_{\star _i,(\mathcal {G})}\).
Proof
Because \(\mathcal {N}\) contains at least two elements, there are \(i,j\in \mathcal {N}\) such that \(i\ne j\). We define two pointed deontic game models that are \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\)-bisimilar (and hence validate exactly the same \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{\star _i,(\mathcal {G})}\)-formula (i, j)p.
Let \(M^{}_4=\langle \mathcal {N},(A_i),d,v\rangle \) be such that \(A^{}_i=\{a^{}_i,b^{}_i\}\) and \(A^{}_j=\{a^{}_j,b^{}_j\}\) and \(A^{}_k=\{a^{}_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j\}}=\{a^{}_{-\{i,j\}}\}\).) Let \(d(a^{}_i,a^{}_j,a^{}_{-\{i,j\}})=d(b^{}_i,b^{}_j,a^{}_{-\{i,j\}})=1\) and \(d(a^{}_i,b^{}_j,a^{}_{-\{i,j\}})=d(b^{}_i,a^{}_j,a^{}_{-\{i,j\}})=0\). Lastly, let \(v(p)=\{(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}),\) \((b^{}_i,b^{}_j,a^{}_{-\{i,j\}})\}\) and \(v(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M_4\) can be pictured as in Fig. 7 (left; the group action \(a^{}_{-\{i,j\}}\) is not represented).
Let \(M'_4=\langle \mathcal {N},(A'_i),d',v'\rangle \) be such that \(A'_i=\{a'_i,b'_i\}\) and \(A'_j=\{a'_j,b'_j\}\) and \(A'_k=\{a'_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j\}}=\{a'_{-\{i,j\}}\}\).) Let \(d'(a'_i,b'_j,a'_{-\{i,j\}})=d'(b'_i,a'_j,a'_{-\{i,j\}})=1\) and \(d'(a'_i,a'_j,a'_{-\{i,j\}})=d'(b'_i,b'_j,a'_{-\{i,j\}})=0\). Lastly, let \(v'(p)=\{(a'_i,a'_j,a'_{-\{i,j\}}),\) \((b'_i,b'_j,a'_{-\{i,j\}})\}\) and \(v'(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M'_4\) can be pictured as in Fig. 7 (right; the group action \(a'_{-\{i,j\}}\) is not represented).
Let \(R=\{(c,c')\in A\times A':c\in v(p) \text{ iff } c'\in v'(p)\}\). It is easy to check that R is an \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\)-bisimulation between \(M^{}_4\) and \(M'_4\). Hence, \((M^{}_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\rightleftarrows _{\mathfrak {L}_{\star _i,[\mathcal {G}]}}(M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M^{}_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{\star _i,[\mathcal {G}]}}(M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M^{}_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\models (i,j)p\) and \((M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\not \models (i,j)p\). By Lemma 3, \(\mathfrak {L}_{\star _i,[\mathcal {G}]}\not \succeq \mathfrak {L}_{\star _i,(\mathcal {G})}\). \(\square \)
Theorem 7
\(\mathfrak {L}_{[\mathcal {G}]}\not \succeq \mathfrak {L}_{\star _i}\).
Proof
Because \(\mathcal {N}\) contains at least two elements, there are \(i,j\in \mathcal {N}\) such that \(i\ne j\). We define two pointed deontic game models that are \({\mathfrak {L}_{[\mathcal {G}]}}\)-bisimilar (and hence validate exactly the same \({\mathfrak {L}_{[\mathcal {G}]}}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{\star _i}\)-formula \(\star _i\).
Let \(M^{}_5=\langle \mathcal {N},(A_i),d,v\rangle \) be such that \(A^{}_i=\{a^{}_i,b^{}_i\}\) and \(A^{}_j=\{a^{}_j\}\) and \(A^{}_k=\{a^{}_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j\}}=\{a^{}_{-\{i,j\}}\}\).) Let \(d(c)=1\) for all \(c\in A\). Lastly, let \(v(p)=\{(b^{}_i,a^{}_j,a^{}_{-\{i,j\}})\}\) and \(v(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M_5\) can be pictured as in Fig. 8 (left; the group action \(a^{}_{-\{i,j\}}\) is not represented).
Let \(M'_5=\langle \mathcal {N},(A'_i),d',v'\rangle \) be such that \(A'_i=\{a'_i,b'_i\}\) and \(A'_j=\{a'_j\}\) and \(A'_k=\{a'_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j\}}=\{a'_{-\{i,j\}}\}\).) Let \(d'(a'_i,a'_j,a'_{-\{i,j\}})=0\) and \(d'(b'_i,a'_j,a'_{-\{i,j\}})=1\). Lastly, let \(v'(p)=\{(b'_i,a'_j,a'_{-\{i,j\}})\}\) and \(v'(q)=\emptyset \) for all \(q\in \mathfrak {P}-\{p\}\). Model \(M'_5\) can be pictured as in Fig. 8 (right; the group action \(a'_{-\{i,j\}}\) is not represented).
Let \(R=\{(c,c')\in A\times A':c\in v(p) \text{ iff } c'\in v'(p)\}\). It is easy to check that R is an \(\mathfrak {L}_{[\mathcal {G}]}\)-bisimulation between \(M^{}_5\) and \(M'_5\). Hence, \((M^{}_5,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\rightleftarrows _{\mathfrak {L}_{[\mathcal {G}]}}(M'_5,(a'_i,a'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M^{}_5,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{[\mathcal {G}]}}(M'_5,(a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M^{}_5,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\models \star _i\) and \((M'_5,(a'_i,a'_j,a'_{-\{i,j\}}))\not \models \star _i\). By Lemma 3, \(\mathfrak {L}_{[\mathcal {G}]}\not \succeq \mathfrak {L}_{\star _i}\). \(\square \)
8 The right front face
To chart the expressivity relations among the nine sublanguages of the right front face of the full expressivity picture (Fig. 9), it suffices to prove four theorems. Using these four theorems, the inclusion criterion, and the transitivity criterion, we can easily find the expressivity relations between every pair from the nine sublanguages in Fig. 9. The labels of the arrows in Fig. 9 indicate which theorem must be used to establish the corresponding expressivity relation. The four theorems are the following:
Theorem 8
\(\mathfrak {L}_{[i],(\mathcal {G})}\not \succeq \mathfrak {L}_{[\mathcal {G}]}\).
Proof
By Lemma 5(i), it holds that \(\mathfrak {L}_{\star _\mathcal {G},[i]}\succeq \mathfrak {L}_{[i],(\mathcal {G})}\). Theorem 3 states that \(\mathfrak {L}_{\star _{\mathcal {G}},[i]}\not \succeq \mathfrak {L}_{[\mathcal {G}]}\). By the transitivity criterion, \(\mathfrak {L}_{[i],(\mathcal {G})}\not \succeq \mathfrak {L}_{[\mathcal {G}]}\). \(\square \)
Theorem 9
\(\mathfrak {L}_{(\mathcal {G})}\not \succeq \mathfrak {L}_{[i]}\).
Proof
By Lemma 5(i), it holds that \(\mathfrak {L}_{\star _\mathcal {G}}\succeq \mathfrak {L}_{(\mathcal {G})}\). Theorem 4 states that \(\mathfrak {L}_{\star _\mathcal {G}}\not \succeq \mathfrak {L}_{[i]}\). By the transitivity criterion, \(\mathfrak {L}_{(\mathcal {G})} \not \succeq \mathfrak {L}_{[i]}\). \(\square \)
Theorem 10
\(\mathfrak {L}_{[\mathcal {G}]}\not \succeq \mathfrak {L}_{(i)}\).
Proof
Consider models \(M_5\) and \(M'_5\) from the proof of Theorem 7. Recall that \((M_5,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}})) \leftrightarrows _{\mathfrak {L}_{[\mathcal {G}]}}(M'_5, (a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M_5,\) \((a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\not \models (i)p\) and \((M'_5,(a'_i,a'_j,a'_{-\{i,j\}}))\models (i)p\). By Lemma 3, \(\mathfrak {L}_{[\mathcal {G}]}\not \succeq \mathfrak {L}_{(i)}\). \(\square \)
Theorem 11
\(\mathfrak {L}_{[\mathcal {G}],(i)}\not \succeq \mathfrak {L}_{(\mathcal {G})}\).
Proof
Consider models \(M_4\) and \(M'_4\) from the proof of Theorem 6. Let \(R=\{(c,c')\in A\times A':c\in v(p) \text{ iff } c'\in v'(p)\}\). It is easy to check that R is an \(\mathfrak {L}_{[\mathcal {G}],(i)}\)-bisimulation between \(M^{}_4\) and \(M'_4\). Hence, \((M^{}_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\rightleftarrows _{\mathfrak {L}_{[\mathcal {G}],(i)}}(M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M^{}_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{[\mathcal {G}],(i)}}(M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\). However, observe that \((M_4,(a^{}_i,a^{}_j,a^{}_{-\{i,j\}}))\models (i,j)p\) and \((M'_4,(a'_i,a'_j,a'_{-\{i,j\}}))\not \models (i,j)p\). By Lemma 3, \(\mathfrak {L}_{[\mathcal {G}],(i)}\not \succeq \mathfrak {L}_{(\mathcal {G})}\). \(\square \)
9 The horizontals
To chart the six horizontal expressivity relations among the twelve sublanguages of Fig. 10, it suffices to prove one theorem. Using this theorem, the inclusion criterion, the transitivity criterion and Lemma 5(iv), we can easily prove the six horizontal expressivity relations. The theorem we need is the following:
Theorem 12
\(\mathfrak {L}_{[\mathcal {G}],(\mathcal {G})}\not \succeq \mathfrak {L}_{\star _i}\).
Proof
Because \(\mathcal {N}\) contains at least two elements, there are \(i,j\in \mathcal {N}\) such that \(i\ne j\). We define two pointed deontic game models that are \(\mathfrak {L}_{[\mathcal {G}],(\mathcal {G})}\)-bisimilar (and hence validate exactly the same \(\mathfrak {L}_{[\mathcal {G}],(\mathcal {G})}\)-formulas) but give different truth-values to the \(\mathfrak {L}_{\star _i}\)-formula \(\star _i\).
Let \(M_6=\langle \mathcal {N},(A^{}_i),d,v\rangle \) be such that \(A^{}_i = \{a_i\}\) and \(A^{}_j = \{a_j\}\) and \(A^{}_k=\{a^{}_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set A of action profiles is \(\times ^{}_{i\in \mathcal {N}}A^{}_i\). (Note that \(A^{}_{-\{i,j\}}=\{a^{}_{-\{i,j\}}\}\).) Let \(d(a_i,a_j,a^{}_{-\{i,j\}})=1\). Lastly, let \(v(p) = \emptyset \) for all \(p\in \mathfrak {P}\). Model \(M_6\) can be pictured as in Fig. 11 (left; the group action \(a^{}_{-\{i,j\}}\) is not represented).
Let \(M_6'=\langle \mathcal {N},(A_i'),d',v\rangle \) be such that \(A'_i=\{a_i',b_i'\}\) and \(A'_j=\{a'_j,b'_j\}\) and \(A'_k=\{a'_k\}\) for all \(k\in \mathcal {N}-\{i,j\}\). The set \(A'\) of action profiles is \(\times ^{}_{i\in \mathcal {N}}A'_i\). (Note that \(A'_{-\{i,j\}}=\{a'_{-\{i,j\}}\}\).) Let \(d'(a'_i,a'_j,a'_{-\{i,j\}})=1\) and \(d'(a'_i,b'_j,a'_{-\{i,j\}})=d'(b'_i,a'_j,a'_{-\{i,j\}})=d'(b'_i,b'_j,a'_{-\{i,j\}})=0\). Lastly, let \(v(p)=\emptyset \) for all \(p\in \mathfrak {P}\). Model \(M'_6\) can be pictured as in Fig. 11 (right; the group action \(a'_{-\{i,j\}}\) is not represented).
Let \(R=A\times A'\). It is easy to check that R is an \(\mathfrak {L}_{(\mathcal {G}),[\mathcal {G}]}\)-bisimulation between \(M_6\) and \(M'_6\). Hence, \((M_6, (a_i,a_j,a^{}_{-\{i,j\}}))\leftrightarrows _{\mathfrak {L}_{(\mathcal {G}),[\mathcal {G}]}}(M'_6, (b'_i,b'_j,a'_{-\{i,j\}}))\). By Theorem 2, it must be that \((M_6, (a_i,a_j,a^{}_{-\{i,j\}}))\equiv _{\mathfrak {L}_{(\mathcal {G}),[\mathcal {G}]}}(M'_6, (b'_i,b'_j,a'_{-\{i,j\}}))\). However, observe that \((M_6, (a_i,a_j,a^{}_{-\{i,j\}}))\models \star _i\) and \((M'_6, (b'_i,b'_j,a'_{-\{i,j\}}))\not \models \star _i\). By Lemma 3, \(\mathfrak {L}_{(\mathcal {G}),[\mathcal {G}]}\not \succeq \mathfrak {L}_{\star _i}\). \(\square \)
10 Weaker assumptions on models and languages
Before concluding the paper, we briefly discuss two assumptions on our models and languages: (a) the assumption that \(\mathcal {N}\) is a fixed finite set of individual agents that contains at least three elements, and (b) the assumption that each sublanguage in \(\mathbf {L}\) includes the universal modality. How would the expressivity relations be affected if we were to weaken these assumptions? (Because these assumptions are not central to the philosophical debate on reductionism in the social sciences, the following considerations are largely technical in nature.)
Throughout the paper, we assumed that \(\mathcal {N}\) is a fixed finite set of individual agents that contains at least three elements. Note that only Theorems 3 and 8 rely on the assumption that \(\mathcal {N}\) contains at least three agents. There are two cases to consider:
-
(i)
If \(\mathcal {N}\) were to contain exactly one agent, then the full language would not contain statements about (non-singleton) groups. Consequently, we would need to consider only eight sublanguages. The expressivity relations for these eight languages are given by the subfigure of Fig. 1 that contains only those languages in \(\mathbf {L}\) that exclude collective admissibility constants, modalities for collective agency, and modalities for collective obligations.
-
(ii)
If \(\mathcal {N}\) were to contain exactly two agents, then the only statements about (non-singleton) groups would be of the form \(\star ^{}_\mathcal {N}\), \([\mathcal {N}]\phi \), and \((\mathcal {N})\phi \). Note that our models validate \([\mathcal {N}]\phi \leftrightarrow \phi \). Consequently (and unlike the case where \(\mathcal {N}\) contains at least three agents), for every language \(\mathfrak {L}^*\) in \(\mathbf {L}\) it holds that \(\mathfrak {L}^*\) is equally expressive as the language \(\mathfrak {L}^{**}\) that is obtained from \(\mathfrak {L}^*\) by adding modalities for collective agency. Hence, under these circumstances, modalities for collective agency could be added without an increase of expressive power. Our results concerning the sublanguages that exclude modalities for collective agency rely only on the assumption that \(\mathcal {N}\) contains at least two agents, and hence the expressivity relations among these sublanguages are given by Fig. 1.
Finally, each sublanguage in \(\mathbf {L}\) includes the universal modality. What can we say about the expressivity relations between languages that exclude the universal modality? Note that because \(\mathcal {N}\) contains at least two distinct individual agents i and j, our models validate \(\Box \phi \leftrightarrow [i][j]\phi \). Accordingly, in each language in \(\mathbf {L}\) that has modalities for individual agency, the universal modality is definable in terms of modalities for individual agency. (Note that for every language \(\mathfrak {L}^*\) in \(\mathbf {L}\) it holds that if \(\mathfrak {L}^*\) has modalities for collective agency, then \(\mathfrak {L}^*\) has also modalities for individual agency.) Hence, in each language in \(\mathbf {L}\) that has modalities for individual agency, the universal modality could be left out without losing expressive power. This does not hold true for those languages in \(\mathbf {L}\) that lack modalities for individual agency. These languages lose expressive power if the universal modality is left out. As a consequence, some expressivity relations no longer obtain: in languages in \(\mathbf {L}\) without modalities for individual agency and without the universal modality, modalities for obligations cannot be defined in terms of the universal modality and the relevant deontic admissibility constant.
11 Conclusion
We classified the twenty-seven sublanguages in \(\mathbf {L}\) in terms of their expressive power. To achieve this classification, we first proved twenty-seven Hennessy–Milner theorems: for every language \(\mathfrak {L}^*\) in \(\mathbf {L}\) it holds that two pointed deontic game models are equivalent on \(\mathfrak {L}^*\) if and only if there is a bisimulation relation between the two pointed models that satisfies a set of structural conditions that are specific to \(\mathfrak {L}^*\). The Hennessy–Milner theorems are central to our proofs that a given sublanguage is strictly more expressive than another.
The expressivity landscape we charted in this paper strongly suggests that the answers to the two philosophical questions in the introduction are negative. Because \(\mathfrak {L}_{[\mathcal {G}]}\succ \mathfrak {L}_{[i]}\) and \(\mathfrak {L}_{(\mathcal {G})}\succ \mathfrak {L}_{[\mathcal {G}],(i)}\), there are statements about collective agency that are not logically equivalent to any statement about individual agency, and there are statements about collective obligations that are not logically equivalent to any statement about collective agency and individual obligations. Naturally, these are not the only reducibility questions that are answered by our current study. For example, because \(\mathfrak {L}_{(\mathcal {G})}\succ \mathfrak {L}_{[i]}\) and \(\mathfrak {L}_{[\mathcal {G}]}\succ \mathfrak {L}_{[i],(\mathcal {G})}\), there are statements about collective obligations that are not logically equivalent to any statement about individual agency, and there are statements about collective agency that are not logically equivalent to any statement about individual agency and collective obligations.
Have we refuted reductionism about collective agency and collective obligations? No, we have not. Our main philosophical contribution to the debate on reductionism about collective agency and collective obligations is methodological: our study indicates that logical methods can be used to find precise answers to the questions we raised in the introduction. To vindicate reductionism, the philosophical interpretation of our logical results must be contested. This can be done in various ways. For instance, the modelling considerations that lie at the basis of our semantics might be criticized. The reductionist might specify alternative models and/or truth-conditions for statements about collective and individual deontic admissibility, statements about collective and individual agency, and statements about collective and individual obligations. Then, she might prove that her alternative modelling supports reductionism about collective agency and collective obligations. Our methodological contribution therefore highlights the fruitfulness of logical methods for the study of reductionism in the philosophy of the social sciences.
Notes
The deontic logic of collective agency is a logic in the tradition of stit (‘sees to it that’) logics of agency. Seminal works include Kanger (1957), Pörn (1970), von Kutschera (1986), and Horty and Belnap (1995). See Belnap et al. (2001) for a textbook presentation of stit logic. There are other formal accounts of agency and normativity. Rather than using stit logic, Meyer (1988) and Segerberg (2012) use dynamic logic to analyse individual actions and obligations. Czelakowski (2020) uses formal linguistics as a basis for a deontic logic of consecutive individual actions.
On admissibility, see Arrow (1951, p. 429), Luce and Raiffa (1957, pp. 287 and 307), Savage (1972, p. 21), and Kohlberg and Mertens (1986, § 2.7.A). Horty (2001, p. 130) relies on collective deontic admissibility to define group obligations, and Tamminga and Duijf use collective deontic admissibility to analyse collective rationality (2017, pp. 200–201) and backward-looking collective moral responsibility (2017, § 6).
We adopt the notational conventions of Osborne and Rubinstein (1994, § 1.7).
Other metalogical investigations of these languages are scarce. Xu (1998), Wansing (2006), and Balbiani et al. (2008) prove completeness for \(\mathfrak {L}_{[i]}\), and Murakami (2005) proves completeness for \(\mathfrak {L}_{[i],(i)}\). Kooi and Tamminga (2008) characterize the possibility of moral conflicts in \(\mathfrak {L}_{[\mathcal {G}],(\mathcal {G})}\). Balbiani et al. (2008) and Herzig and Schwarzentruber (2008) study the complexity of \(\mathfrak {L}_{[i]}\), and the latter study also the complexity of \(\mathfrak {L}_{[\mathcal {G}]}\). Duijf et al. (ms.) define a new and stronger concept of inexpressivity based on nomological equivalence and prove that there are no statements \(\phi \) and \(\psi \) in \(\mathfrak {L}_{\star ^ {}_i,[i]}\) such that \(\phi \) and \(\star ^{}_\mathcal {G}\) are equivalent modulo \(\psi \) (where \(\psi \) specifies a set of individualistic background laws).
Blackburn et al. (2001, § 2.2) provide a textbook presentation of bisimulation in modal logic.
References
Arrow, K. J. (1951). Alternative approaches to the theory of choice in risk-taking situations. Econometrica, 19, 404–437.
Balbiani, P., Herzig, A., & Troquard, N. (2008). Alternative axiomatics and complexity of deliberative stit theories. Journal of Philosophical Logic, 37, 387–406.
Belnap, N., Perloff, M., & Xu, M. (2001). Facing the future: Agents and choices in our indeterminist world. New York: Oxford University Press.
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic. Cambridge: Cambridge University Press.
Czelakowski, J. (2020). Deontology of compound actions. Studia Logica, 108, 5–47.
Duijf, H., Tamminga, A., & Van De Putte, F. (ms.). An impossibility result on methodological individualism.
Herzig, A., & Schwarzentruber, F. (2008). Properties of logics of individual and group agency. In C. Areces & R. Goldblatt (Eds.), Advances in modal logic (Vol. 7, pp. 133–149). London: College Publications.
Horty, J. F. (1996). Agency and obligation. Synthese, 108, 269–307.
Horty, J. F. (2001). Agency and deontic logic. New York: Oxford University Press.
Horty, J. F., & Belnap, N. (1995). The deliberative stit: A study of action, omission, ability, and obligation. Journal of Philosophical Logic, 24, 583–644.
Kanger, S. (1957). New foundations for ethical theory. In R. Hilpinen (Ed.), Deontic logic (pp. 36–58). Dordrecht: D. Reidel Publishing Company. 1971.
Kohlberg, E., & Mertens, J.-F. (1986). On the strategic stability of equilibria. Econometrica, 54, 1003–1037.
Kooi, B., & Tamminga, A. (2008). Moral conflicts between groups of agents. Journal of Philosophical Logic, 37, 1–21.
Luce, R. D., & Raiffa, H. (1957). Games and decisions. New York: Wiley.
Meyer, J.-J. Ch. (1988). A different approach to deontic logic: Deontic logic viewed as a variant of dynamic logic. Notre Dame Journal of Formal Logic, 29, 109–136.
Murakami, Y. (2005). Utilitarian deontic logic. In R. Schmidt, I. Pratt-Hartmann, M. Reynolds, & H. Wansing (Eds.), Advances in modal logic (Vol. 5, pp. 211–230). London: College Publications.
Osborne, M. J., & Rubinstein, A. (1994). A course in game theory. Cambridge, MA: The MIT Press.
Pörn, I. (1970). The logic of power. Oxford: Basil Blackwell.
Savage, L. J. (1972). The foundations of statistics (2nd ed.). New York: Dover Publications Inc.
Segerberg, K. (2012). D\(\Delta \)L: A dynamic deontic logic. Synthese, 185, 1–17.
Tamminga, A., & Duijf, H. (2017). Collective obligations, group plans and individual actions. Economics and Philosophy, 33, 187–214.
Tamminga, A., & Hindriks, F. (2020). The irreducibility of collective obligations. Philosophical Studies, 177, 1085–1109.
van Benthem, J., Bezhianishvili, N., Enqvist, S., & Yu, J. (2017). Instantial neighbourhood logic. Review of Symbolic Logic, 10, 116–144.
von Kutschera, F. (1986). Bewirken. Erkenntnis, 24, 253–281.
Wansing, H. (2006). Tableaux for multi-agent deliberative-stit logic. In G. Governatori, I. Hodkinson, & Y. Venema (Eds.), Advances in modal logic (Vol. 6, pp. 503–520). London: College Publications.
Xu, M. (1998). Axioms for deliberative stit. Journal of Philosophical Logic, 27, 505–552.
Acknowledgements
Allard Tamminga and Hein Duijf gratefully acknowledge financial support from the ERC-2013-CoG project REINS, No. 616512. Hein Duijf gratefully acknowledges funding from the ERC-2017-CoG project SEA, No. 771074. Frederik Van De Putte’s research is funded by a Marie Skłodowska-Curie Fellowship, No. 795329, and by the Research Foundation – Flanders (FWO-Vlaanderen). We thank the anonymous referees at this journal for their valuable suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tamminga, A., Duijf, H. & Van De Putte, F. Expressivity results for deontic logics of collective agency. Synthese 198, 8733–8753 (2021). https://doi.org/10.1007/s11229-020-02597-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-020-02597-0