Two traditions in abstract valuational model theory

Abstract

We investigate two different broad traditions in the abstract valuational model theory for nontransitive and nonreflexive logics. The first of these traditions makes heavy use of the natural Galois connection between sets of (many-valued) valuations and sets of arguments. The other, originating with work by Grzegorz Malinowski on nonreflexive logics, and best systematized in Blasio et al. (Bull Sect Log 46(3/4): 233–262, 2017), lets sets of arguments determine a more restricted set of valuations. After giving a systematic discussion of these two different traditions in the valuational model theory for substructural logics, we turn to looking at the ways in which we might try to compare two sets of valuations determining the same set of arguments.

Appendix: Least sets of valuations in the Set-Set framework

Recall that, given a set A of arguments, there is a set $Mod({A}) = \{V : {\mathcal {A}}V = A\}$. Consider $Mod({A})$ as ordered by $\subseteq$. No matter whether we’re working Set-Set or Set-Fmla, and no matter whether we’re considering ${\mathfrak {V}}_4$, ${\mathfrak {V}}_3^t$, ${\mathfrak {V}}_3^r$, or ${\mathfrak {V}}_2$, $Mod({A})$ has a greatest element: ${\mathcal {V}}A$. This follows from Theorem 1. What we want to answer in this appendix is the following question: under what conditions does it have a least element? In the body of the paper we dealt with the four Set-Fmla cases, and in this appendix we’ll look at the remaining four Set-Set cases.

As above, we begin by looking at what happens when we are considering bivaluations, since this is the best-known and best-explored area, and we can largely answer our question by appealing to or adapting existing results. Second, we turn to the general situation involving tetravaluations. We follow up by considering in turn both reflexive, as well as transitive trivaluations.

1.1 Bivaluations

It is known [for example (Dunn and Hardegree 2001, p. 202)] that for any monotonic reflexive completely transitive set of Set-Set arguments A there is exactly one set V of bivaluations such that ${\mathcal {A}}_{\textsc {ss}}V = A$. That suffices to answer our question for this case: there is always a least such V, since there is always exactly one such V.

1.2 Tetravaluations

Things get trickier when we go to the tetravaluational case. Here, there can be multiple distinct Vs with ${\mathcal {A}}_{\textsc {ss}}V = A$. For example, for any nonempty V, ${\mathcal {A}}_{\textsc {ss}}V = {\mathcal {A}}_{\textsc {ss}}(V \cup \{v_{\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}\})$, where $v_{\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ is the valuation assigning ${\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ to every formula. (This is because $v_{\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ is a counterexample only to the empty argument , and every valuation is a counterexample to this argument.)

We will show that when A is a compact monotonic set of Set-Set arguments, then there is a least set V of valuations with ${\mathcal {A}}_{\textsc {ss}}V = A$. To do this, we first show that there are certain valuations that must be in any V with ${\mathcal {A}}_{\textsc {ss}}V = A$; then we show that, so long as A is compact, these valuations alone are enough to determine A precisely. The needed valuations are the exact counterexamples to those arguments that are maximally out of A. We define each of these notions in what follows, proving needed results along the way. (We earlier defined the notion of exact counterexample for Set-Fmla arguments, but here we need it for Set-Set.)

Definition 9

Given a Set-Set argument , its exact counterexample $v_{a}$ is the valuation such that $v_{a}(\phi ) =$

• $\top$ iff $\phi \in \Gamma {\setminus } \Delta$,

• $\bot$ iff $\phi \in \Delta {\setminus } \Gamma$,

• iff $\phi \in \Gamma \cap \Delta$, and

• ${\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ iff $\phi \not \in \Gamma \cup \Delta$.¹³

Proposition 8

For any arguments a, b, we have iff $b \sqsubseteq a$.¹⁴

Proposition 9

For any argument a and any valuation v, we have iff $v_{a} \sqsubseteq v$.

Proof

Unpacking definitions, in both cases. $\square$

It follows from each of these results that ; an argument’s exact counterexample is indeed a counterexample. Proposition 8 gives us one sense in which this counterexample is ‘exact’: it is a counterexample to all and only subsequents of a. Proposition 9 gives us a different sense: it is information-least among counterexamples to a.

Now, to arguments that are maximally out:

Definition 10

An argument is maximally out of a set A of arguments iff: it is not in A and any proper superargument of it is in A.

Lemma 6

If A is a set of Set-Set arguments, and the argument c is maximally out of A, then for any set V of valuations with ${\mathcal {A}}V = A$ it must be that $v_{c} \in V$.

Proof

Take any such c, A, V, to show $v_{c} \in V$. Since $c \not \in A$ and ${\mathcal {A}}V = A$, there must be some $v \in V$ with . By Proposition 9, $v_{c} \sqsubseteq v$. Suppose towards a contradiction that $v \ne v_{c}$. Then there must be some formula $\phi$ receiving a different value in v than in $v_{c}$. Since $v_{c} \sqsubseteq v$, there are five possibilities:

• (1) $v_{c}(\phi ) = {\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ and $v(\phi ) = \top$

• (2) $v_{c}(\phi ) = {\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ and $v(\phi ) = \bot$

• (3) $v_{c}(\phi ) = {\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$ and

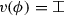
• (4) $v_{c}(\phi ) = \top$ and

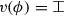
• (5) $v_{c}(\phi ) = \bot$ and

But on any of these possibilities, v is a counterexample to some proper superargument of c: in the first, third, and fifth cases, the argument adds $\phi$ to the conclusions of c, while in the first, second, and fourth, it adds $\phi$ to the premises. These are indeed proper superarguments: Definition 9, plus what we know about $v_{c}(\phi )$ in each case, suffices for this. But since c is maximally out of A, this superargument is in A, and so ${\mathcal {A}}V \ne A$, which is a contradiction. Thus, $v = v_{c}$, and so $v_{c} \in V$. $\square$

So every $V \in Mod({A})$ must include all the exact counterexamples to those arguments maximally out of A. This matters when A is compact because there are enough arguments maximally out of it:

Proposition 10

If A is compact, then every argument $a \not \in A$ is contained in some argument c that is maximally out of A.

Proof

Take a compact A and some $a \not \in A$. Consider the set $B = \{b \;|\; a \sqsubseteq b \; \& \; b \not \in A\}$ of all superarguments of a that are not in A. Every $\sqsubseteq$-chain in B has an upper bound in B: if the chain is finite, its maximum member will do; and if it is infinite, its sequent join will do. (Note that Compactness is needed at this step to ensure that these joins are $\not \in A$). But then by Zorn’s lemma, B has a maximal element c. Since $c \in B$, we know $a \sqsubseteq c$ and $c \not \in A$.

To show that c is maximally out of A, it remains only to show that any proper superargument d of c is in A. But if there were some where $d\not \in A$, then d would have to have been in B, and so c would not be maximal in B after all. $\square$

This is enough now for the theorem.

Theorem 13

If A is a compact monotonic set of Set-Set arguments, then there is a least $V \in Mod({A})$.

Proof

By Lemma 6, any $V \in Mod({A})$ must be such that $V_{0} = \{ v_{c}~|~c \text { is maximally}~\text {out of } A \} \subseteq V$. So if ${\mathcal {A}}V_0 = A$, then $V_0 \in Mod({A})$ and we’re done. Showing this has two phases: that ${\mathcal {A}}V_0 \subseteq A$ and that $A \subseteq {\mathcal {A}}V_0$.

First, that ${\mathcal {A}}V_0 \subseteq A$. Take any $a \not \in A$. By Proposition 10, there is some c maximally out of A with $a \sqsubseteq c$. Since c is maximally out of A we have $v_{c} \in V_0$, and by one direction of Proposition 8 we have . So $a \not \in {\mathcal {A}}V_0$.

Second, that $A \subseteq {\mathcal {A}}V_0$. Take any $a \not \in {\mathcal {A}}V_0$; this has some counterexample $v_{c} \in V_0$. By the other direction of Proposition 8, $a \sqsubseteq c$. But since c is maximally out of A, it is at least out of A; and since A is monotonic, $a \not \in A$. $\square$

1.3 Reflexive trivaluations

If A is a reflexive set of arguments, then the general story carries over immediately, owing to Lemma 5. So when A is reflexive and compact, the least set of tetravaluations determining A (which exists by Theorem 13) is a set of reflexive trivaluations by Lemma 5, and thus a least set of reflexive trivaluations determining A.

1.4 Transitive trivaluations

For transitive trivaluations, the reasoning is not so immediate, because there is no result analogous to Lemma 5 available for complete transitivity and transitive trivaluations.¹⁵ But we can still make our way to the corresponding result; restricting our attention to completely transitive sets of arguments gives us extra tools to work with.

Proposition 11

If A is monotonic and completely transitive, and is maximally out of A, then $\Gamma \cup \Delta = {\mathcal {L}}$.

Proof

Suppose A is monotonic and completely transitive, and is maximally out of A, but that $\Gamma \cup \Delta \ne {\mathcal {L}}$. Then there must be some $\phi \in {\mathcal {L}}$ with $\phi \not \in \Gamma \cup \Delta$. So both and are proper superarguments of . Since is maximally out of A, both of these superarguments must be in A. But then since A is completely transitive, ; contradiction.¹⁶$\square$

This is now enough to proceed.

Theorem 14

If A is a monotonic, completely transitive, and compact set of Set-Set arguments, then there is a least set V of transitive trivaluations determining it.

Proof

As in the proof of Theorem 13, the desired set is the set of exact counterexamples to those arguments maximally out of A. As we have seen in that proof, this set is the least set of tetravaluations determining A. So as long as it is itself a set of transitive trivaluations, we’re done. By Proposition 11, every maximally out of A is such that $\Gamma \cup \Delta = {\mathcal {L}}$. Consulting Definition 9 reveals that the exact counterexample to any such argument cannot use the value ${\mathop {\mathchoice{*\displaystyle }{*\textstyle }{*\scriptstyle }{*\scriptscriptstyle }}}$, and so is a transitive trivaluation. $\square$