Tracking and managing deemed abilities

Abstract

Information about the powers and abilities of acting entities is used to coordinate their actions in societies, either physical or digital. Yet, the commonsensical meaning of an acting entity being deemed able to do something is still missing from the existing specification languages for the web or for multi-agent systems. We advance a general purpose abstract logical account of evidence-based ability. A basic model can be thought of as the ongoing trace of a multi-agent system. Every state records systemic confirmations and disconfirmations of whether an acting entity is able to bring about something. Qualitative inductive reasoning is then used in order to infer what acting entities are deemed able to bring about in the multi-agent system. A temporalised modal language is used to talk about deemed ability, actual agency, and confirmation and disconfirmation of deemed ability. What constitutes a confirmation and a disconfirmation is left to the modeller as in general it depends on the application at hand. So to illustrate the methodology we propose two extended examples, one in practical philosophy, the other in system engineering. We first use a logic of agency and ability to obtain a version of Mele’s general practical abilities. Then, we look at the management of abilities in a supervised system.

1 Preliminaries

In open and highly distributed environments like online services, there are many unknown variables. Specifications are typically provided by the services themselves, and their actual implementation may depend on human intervention. Both are prone to error, to misrepresentation bona fide, and possibly, to deception. On a service repository, services join, evolve, and leave. Think about the sellers on Amazon Marketplace or AbeBooks: They start new businesses, modify their business models, go bankrupt, on sick leave, and on holiday.

Scenario Imagine a rare media service repository. Now, a client of the service repository wishes to acquire two original copies of Robinson Crusoe. Upon inspection, the server manager finds that services $\sigma _1$, $\sigma _2$, and $\sigma _3$ each have one copy on offer. This seems like a trivial enough choreography problem; a typical choreography procedure could combine $\sigma _1$ and $\sigma _2$ in order to obtain a complex service function which, one can expect, consists in sending two copies of the book to the client. The function is called. The outcome is that the client receives a confirmation from $\sigma _1$ that the book has been dispatched and an apologetic message from $\sigma _2$ indicating that it cannot fulfil the request. $\sigma _2$ failed its part of the function. After enquiry, the server manager discovers that $\sigma _2$ does not actually have books in store, but instead acquires them from $\sigma _3$ at discount price. The server manager also finds out that $\sigma _3$ has ceased activity temporarily.

We will come back to service science a few times for illustrative purposes, but we are interested in the bigger picture. In settings presenting the same challenges, how do we deal with the inherent openness of such systems? How do we evaluate the abilities of acting entities? Evaluation of power is subjective. It reflects the information possessed and considered relevant by the system manager, and his own logic of knowledge management. How do we maintain the evaluation of abilities in accordance with the perceived changes in the multi-agent system? Confirmation and disconfirmation are crucial notions in this connection. Depending on the application, they can be the actual exercise of some ability, or the omission thereof. The confirmation or disconfirmation of an ability can be a generalised speech-act like a registration, a ban, the signing of a contract, or the registration of a medical file of aptitude or of invalidity. Remarkable work has been done in this direction in trust assessment using numerical models, e.g., Wang and Singh (2010). But at a more abstract level, we are still compelled to understand and capture the logical aspects of these mechanisms.

Logics dedicated to the study of powers have been studied in Theoretical Computer Science and Artificial Intelligence, with Alternating-time Temporal Logic (ATL) (Alur et al. 2002) being probably the foremost representative. ATL and its numerous variants are excellent formalisms to reason about concurrent systems where the distributed components interact in a game theoretical fashion. Judgements about power are derived from unambiguous models that describe the a priori knowledge that a designer has of an interaction set-up. These models are concurrent game structures. Of particular relevance to our illustrative scenario may be their use in service composition (De Giacomo and Felli 2010). In concurrent game structures, an acting entity is able to bring about that $\phi$ at some moment if it possesses a pertinent action/strategy that would ensure that $\phi$ when executed. Of course, a judgement about ability in this setting does not say anything about the same power at earlier or later times. But in less rigid societies of agents, judgements about ability are often less specific and definitive than in game theoretical models. Ability is more often merely discovered from experience: “We really do have an ‘idea’ corresponding to the word ‘power’. [...] Hume saw that recognition must be given to the essential part played by ‘experience of the past’ in our knowledge of the existence of powers.” (Ayers 1968, p. 59). We acknowledge the historical value of the statement, for we aim to propose a logical framework that recognises it as fundamental. In this paper we focus our attention on the “can” of power, and more precisely on the commonsensical meaning of “can” as deemed ability that accounts for present, previous, and future confirmations and disconfirmations of ability. The result is a work of logic that differs greatly from the existing formalisms like ATL.

In a first part, we will present a general purpose formal framework to reason faithfully about deemed ability. We will assume a linear flow of time and the abstract modal notions of confirmation and disconfirmation. We will present a model theory and a formal language to represent and express specifically the following general principles of “being deemed able” (Sect. 2):

• 1. If the current situation provides the confirmation that the acting entity G is able to bring about $\phi$ then G is deemed able to bring about $\phi$;

• 2. If the current situation disconfirms that G is able to bring about $\phi$ then G is not deemed able to bring about $\phi$;

• 3. If an acting entity G is deemed able to bring about $\phi$, it will continue to be deemed able unless and until we encounter a disconfirmation of this ability.

• 4. If an acting entity G is not deemed able to bring about $\phi$, it remains so unless and until we encounter a confirmation for this ability;

• 5. If an acting entity G is deemed able to bring about something, it is so because there is a confirmation of it now, or there has been a confirmation of it in then past and G has been deemed able ever since.

From the five principles above, we can observe that confirmations, disconfirmation, and the flow of time are necessary and sufficient to decide whether an acting entity is deemed able for something at some instant. We consider the assumption of a linear flow of time to be benign for all practical purpose. Then effectively, this means that the task of specifying the powers of the acting entities of a system can focus exclusively on the two empirical notions: confirmation and disconfirmation of ability. Hence, by adopting the simple generic framework of “being deemed able” for a particular system specification, one steers clear from metaphysical debate about what constitutes an ability in the system at hand.

Of course, there is no one-size-fits-all solution to tracking abilities in multi-agent systems. What constitutes a confirmation and what constitutes a disconfirmation must depend on the application at hand. So in a second part we will present more ad hoc groundings of confirmation and disconfirmation. To illustrate the methodology we propose two extended examples, one in practical philosophy, the other in system engineering. First we use a logic of agency and ability to obtain a version of Mele’s general practical abilities (Sect. 3). Then, we look at the management of abilities in a supervised system (Sect. 4).

2 Being deemed able: the core logic

We suppose a finite supply of agents collected in a set Agt. A group is any subset of Agt. We call an acting entity any agent or group. We also suppose an infinite supply of propositional variables collected in a set Prop. The sets $\textsf {Agt}$ and $\textsf {Prop}$ are fixed throughout the paper.

We first define the static core logic. Then, we give a temporalisation of it. Then, we extend it to obtain the core logic of being deemed able.

2.1 The static core logic

In the following we will use three linguistic constructs that are at the core of the logic of being deemed able. $\textsc {can}_{G}\phi$ reads “acting entity G is deemed able to bring about that $\phi$”. $\textsc {conf}_{G}\phi$ reads “the situation confirms that acting entity G is able to bring about that $\phi$”. $\textsc {disc}_{G}\phi$ reads “the situation disconfirms that acting entity G is able to bring it about that $\phi$”. These readings will also often be rephrased throughout the paper into contextually more appropriate wordings.

To talk about the static facts of being deemed able, we extend the language of propositional logic with the three previous modalities. Formally, we obtain the language $L_{ \textsf {sc}}$ (where $p \in \textsf {Prop}$ and $G \subseteq \textsf {Agt}$) with the following grammar in Backus–Naur form:

$$\begin{aligned} \phi \,{::}{=}\, p \ \mid \ \lnot \phi \ \mid \ \phi \wedge \phi \ \mid \ \textsc {can}_{G} \phi \ \mid \ \textsc {conf}_{G} \phi \ \mid \ \textsc {disc}_{G}\phi \end{aligned}$$

Throughout the paper, we use $\phi \vee \psi$ as a notational variant of $\lnot (\lnot \phi \wedge \lnot \psi )$ and $\phi \rightarrow \psi$ as a notational variant of $\lnot \phi \vee \psi$.

A formula in $L_{ \textsf {sc}}$ can contain arbitrary nestings of modalities. As for any expressive enough language, some grammatically correct sentences could be gibberish, or can be difficult to interpret in plain English: e.g., $\textsc {conf}_{G}\textsc {disc}_{G}\textsc {can}_{G} p$. On the other hand, some other combinations can be useful: e.g., $\textsc {can}_{G_1}\textsc {conf}_{G_2}p$ characterises a situation where the group $G_1$ is deemed able to bring about a situation that is confirmation of the fact that the group $G_2$ is able to bring about that p holds.

Table 1 $\vdash _{ \textsf {sc}}$

The static core logic ${ \textsf {sc}}$ is the minimal set of formulas closed under $\vdash _{ \textsf {sc}}$, presented in Table 1. Note that confirmation and disconfirmation with respect to the same ability are mutually exclusive. By axiom sc1, axiom sc2, and classical logic, we have $\vdash _{ \textsf {sc}} \textsc {conf}_{G}\phi \wedge \textsc {disc}_{G}\phi \rightarrow \textsc {can}_{G}{\phi } \wedge \lnot \textsc {can}_{G}{\phi }$ and thus $\vdash _{ \textsf {sc}} \textsc {conf}_{G}\phi \wedge \textsc {disc}_{G}\phi \rightarrow \bot$.

For many practical purposes, we could close the confirmation and disconfirmation operators under conjunctions. But we refrain from doing so, to allow more modelling versatility.

We can provide a model theory for $\vdash _{ \textsf {sc}}$ with very simple structures (we note $\mathcal {P}(W)$ the set of subsets of a set W):

Definition 1

An ${ \textsf {sc}}$-model is a tuple $M =\langle {W, dabl , conf , disc ,V}\rangle$, where for every $w \in W$ and $G \subseteq \textsf {Agt}$, $dabl (w)(G) \subseteq \mathcal {P}(W)$, $conf (w)(G) \subseteq \mathcal {P}(W)$, $disc (w)(G) \subseteq \mathcal {P}(W)$, and $V(w) \subseteq \textsf {Prop}$. In addition, it satisfies the following constraints:

• 1. If $X \in conf (w)(G)$ then $X \in dabl (w)(G)$

• 2. If $X \in disc (w)(G)$ then $X \not \in dabl (w)(G)$

We define the interpretation $\models _{ \textsf {sc}}$ of the language $L_{ \textsf {sc}}$ in an ${ \textsf {sc}}$-model $M = \langle {W,dabl,evid,fals,V}\rangle$ as follows:

• $M, w \models _{ \textsf {sc}} p$ iff $p \in V(w)$

• $M, w \models _{ \textsf {sc}} \lnot \phi$ iff not $M, w \models _{ \textsf {sc}} \phi$

• $M, w \models _{ \textsf {sc}} \phi \wedge \psi$ iff $M, w \models _{ \textsf {sc}} \phi$ and $M, w \models _{ \textsf {sc}}\psi$

• $M, w \models _{ \textsf {sc}} \textsc {can}_{G}\phi$ iff $||{\phi }||^{M} \in dabl (w)(G)$

• $M, w \models _{ \textsf {sc}} \textsc {conf}_{G}\phi$ iff $||{\phi }||^{M} \in conf (w)(G)$

• $M, w \models _{ \textsf {sc}} \textsc {disc}_{G}\phi$ iff $||{\phi }||^{M} \in disc (w)(G)$

where $||{\phi }||^{M} = \{ w \mid M,w \models _{ \textsf {sc}} \phi \}$.

It is routine to prove that the logic ${ \textsf {sc}}$ is sound and complete wrt. the class of ${ \textsf {sc}}$-models (Chellas 1980).

Proposition 1

Let $\phi \in L_{ \textsf {sc}}$. Then, $\vdash _{ \textsf {sc}} \phi$ iff $\models _{ \textsf {sc}} \phi$.

Effectively, the two constraints in Definition 1 correspond to imposing the static principle linking a confirmation in a world to a deemed ability in that world

and the static principle linking a disconfirmation in a world to an absence of deemed ability in that world.

The formula $\lnot \textsc {conf}_{G}\phi \wedge \textsc {can}_{G}\phi$ is consistent in the static core logic. The static core theory is thus insufficient in that it does not explain why a group is deemed able. When it holds, the theory does not say how this deemed ability came to exist, and how it has been maintained before and until now. The theory does not say what this ability becomes after an acting entity is deemed able to do something. If it is not deemed able to do something, our theory does not say what it takes for it to be deemed able at a later stage.

As a matter of fact, we do not even have the means to talk about before and after in the static logic. We remedy this in the remainder of this section.

2.2 Linear until-since logic

To talk and reason about temporal properties, we use a linear until-since logic based on the following language $L_{ \textsf {time}}$:

$$\begin{aligned} \begin{array}{lcccccccccl} \phi&\,{::}{=}\,&p&\mid&\lnot \phi&\mid&\phi \wedge \phi&\mid&\phi \mathcal {U}\phi&\mid&\phi \mathcal {S}\phi \end{array} \end{aligned}$$

The formula $\phi \mathcal {U}\psi$ reads that the property $\phi$ holds at least until $\psi$ is true. With it, one can define the usual “eventually/future” operator $\mathcal {F}\phi = \top \mathcal {U}\phi$ and the “always/globally” operator, $\mathcal {G}\phi = \lnot \mathcal {F}\lnot \phi$. We can also define the “weak until” as $\phi \mathcal {W}\psi = (\phi \mathcal {U}\psi ) \vee \mathcal {G}\phi$, which will be particularly useful in this paper. The “since” operator $\mathcal {S}$ is used to talk about the past. The formula $\phi \mathcal {S}\psi$ reads that the proposition $\phi$ has been holding ever since $\psi$ was true. With it, one can define the “has always been” operator, $\mathcal {H}\phi = \lnot \mathcal {P}\lnot \phi$ and “has been in the past” operator $\mathcal {P}\phi = \top \mathcal {S}\phi$.

Definition 2

A flow of time is a tuple $\langle {T,<}\rangle$ where T is a nonempty set of instants and < is a linear order over T. A model of time is a tuple $F = \langle {T,<,g}\rangle$, where $\langle {T,<}\rangle$ is a flow of time and g is a valuation function such that $g(t) \subseteq \textsf {Prop}$ for all $t \in T$.

The interpretation $\models _{ \textsf {time}}$ of the language $L_{ \textsf {time}}$ in a model of time $M = {\langle {T,<,g}\rangle }$ is defined as follows (Kamp 1971):

• $M,t \models _{ \textsf {time}} p$ iff $p \in g(t)$, when $p \in \textsf {Prop}$

• $M, t \models _{ \textsf {time}} \phi \mathcal {U}\psi$ iff there is an $s \in T$ with $t < s$ and $M,s \models _{ \textsf {time}} \psi$ and for every $u \in T$, if $t< u < s$ then $M,u \models _{ \textsf {time}} \phi$

• $M, t \models _{ \textsf {time}} \phi \mathcal {S}\psi$ iff there is an $s \in T$ with $s < t$ and $M,s \models _{ \textsf {time}} \psi$ and for every $u \in T$, if $s< u < t$ then $M,u \models _{ \textsf {time}} \phi$

Table 2 $\vdash _{ \textsf {time}}$

The tense logic ${ \textsf {time}}$ is the minimal set of formulas closed under $\vdash _{ \textsf {time}}$, presented on Table 2. Axioms ltl11 and ltl12 ensure that the time is linear. Axioms ltl7, ltl8, and ltl9 ensure that time is transitive. Xu (1988) showed that ltl10 is in fact redundant. An axiomatisation of the tense logic ${ \textsf {time}}$ is presented in Xu (1988). The following theorem is due to Burgess (1982), and Xu (1988).

Theorem 1

Let $\phi \in L_{ \textsf {time}}$. Then, $\vdash _{ \textsf {time}} \phi$ iff $\models _{ \textsf {time}} \phi$.

2.3 Temporalisation

We now present the temporalisation of the static core logic of being deemed able with the until-since logic.

Definition 3

A formula $\phi \in L_{ \textsf {sc}}$ is a Boolean combination iff it is built up from other formulas by means of the Boolean connectives $\wedge$ and $\lnot$ or any other connectives defined in terms of those. A formula $\alpha \in L_{ \textsf {sc}}$ is a monolithic formula iff it is not a Boolean combination.

Examples of Boolean combinations are $\lnot p$, or $\textsc {can}_{G_1}p \rightarrow \lnot \textsc {disc}_{G_2}q$. Examples of monolithic formulas are: p, $\textsc {disc}_{G}(q \rightarrow p)$, or $\textsc {can}_{G_1}(\textsc {conf}_{G_1}(p \vee q) \wedge \lnot \textsc {disc}_{G_2}q)$.

Following Finger and Gabbay (1992), we temporalise ${ \textsf {sc}}$ with ${ \textsf {time}}$, and obtain the logic system ${ \textsf {time}}({ \textsf {sc}})$. We need to define its language, proof theory, models, and model theory.

The language $L_{{ \textsf {time}}({ \textsf {sc}})}$ is defined as follows:

$$\begin{aligned} \begin{array}{lcccccccccl} \phi&\,{::}{=}\,&\alpha&\mid&\lnot \phi&\mid&\phi \wedge \phi&\mid&\phi \mathcal {U}\phi&\mid&\phi \mathcal {S}\phi \end{array} \end{aligned}$$

where $\alpha$ is a monolithic formula of $L_{ \textsf {sc}}$.

The proof theory $\vdash _{{ \textsf {time}}({ \textsf {sc}})}$ consists of:

• All the principles of ${ \textsf {time}}$, and

• If $\vdash _{ \textsf {sc}} \phi$ then $\vdash _{{ \textsf {time}}({ \textsf {sc}})} \phi$, when $\phi \in L_{ \textsf {sc}}$

We define the models of ${ \textsf {time}}({ \textsf {sc}})$.

Definition 4

A model of ${ \textsf {time}}({ \textsf {sc}})$ is a tuple $M_{{ \textsf {time}}({ \textsf {sc}})} = \langle {T,<,g}\rangle$ where $\langle {T,<}\rangle$ is a flow of time, and g a function that maps every member of T into a pointed model (M, w), with $M = \langle {W,dabl,evid,fals,V}\rangle$ an ${ \textsf {sc}}$-model and $w \in W$.

The interpretation of $L_{{ \textsf {time}}({ \textsf {sc}})}$ in a model $M_{{ \textsf {time}}({ \textsf {sc}})} = \langle {T,<,g}\rangle$ of ${ \textsf {time}}({ \textsf {sc}})$ is simply:

• $M_{{ \textsf {time}}({ \textsf {sc}})},t \models \alpha$ iff $g(t) \models _{ \textsf {sc}} \alpha$

when $\alpha$ is a monolithic formula, and analogous to $\models _{ \textsf {time}}$ otherwise, while the truth value of the temporal operators is as before.

Fig. 1

Illustration of temporalisation

Figure 1 illustrates the temporalisation of the static core logic of being deemed able with the until-since logic. At time t, the corresponding pointed ${ \textsf {sc}}$-model is $g(t) =(M_s,w)$. The figure represents the fact that $||{\phi }||^{M_s} \in dabl (w)(G)$. It means that $M_s, w \models _{ \textsf {sc}} \textsc {can}_{G}{\phi }$, and since $\textsc {can}_{G}{\phi }$ is a monolithic formula, we also have that $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}{\phi }$. For similar reasons, we also have that $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {conf}_{G}{\psi }$, and $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}{\psi }$. At time $t'$, the corresponding pointed ${ \textsf {sc}}$-model is $g(t') = (M'_s,w')$. The figure represents the fact that $||{\phi }||^{M'_s} \in disc (w')(G)$, and that $||{\psi }||^{M'_s} \in dabl (w')(G)$. We have that $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}{\psi }$ and $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {disc}_{G}{\phi }$.

Hence, when $t \not = t'$, the pointed models g(t) and $g(t')$ can be different (as exemplified in Fig. 1), but not necessarily so. In them, abilities, confirmations, and disconfirmations are possibly given different truth values, but not necessarily so. The models of ${ \textsf {time}}({ \textsf {sc}})$ do not impose any constraints. To the contrary, the models of deemed ability that we introduce in Sect. 2.4 will be models of ${ \textsf {time}}({ \textsf {sc}})$ satisfying specific temporal constraints about abilities, confirmations, and disconfirmations.

The following result is an immediate consequence of Proposition 1, Theorem 1 and the general completeness theorem of temporalisations due to Finger and Gabbay (Finger and Gabbay 1992, Th. 2.3):

Proposition 2

If $\phi \in L_{{ \textsf {time}}({ \textsf {sc}})}$, $\vdash _{{ \textsf {time}}({ \textsf {sc}})} \phi$ iff $\models _{{ \textsf {time}}({ \textsf {sc}})} \phi$.

2.4 The core logic of being deemed able

The static core logic of being deemed able already captures the first two principles listed in Sect. 1. We now extend ${ \textsf {time}}({ \textsf {sc}})$ to capture the temporal principles. Let us call ${ \textsf {lbda}}$ the core logic of being deemed able. We assume:

We can now formalise the last three principles of being deemed able that we listed in the introduction.

The dynamic role of disconfirmation When an acting entity is deemed able to do something, one can maintain this perceived ability until some further evidence disconfirms it. This suggests the following axiom:

In words, if G is deemed able to do $\phi$, it is deemed able until a disconfirming situation occurs. When this situation occurs, we shall have $\lnot \textsc {can}_{G}\phi$ by axiom sc2. Note that we use the weak version of the “until” operator $\mathcal {W}$. This is to capture the fact that $\textsc {can}_{G}\phi$ might never actually be false in the future, which by axiom sc2, would mean that a disconfirmation never actually occurs in the future. An existing deemed ability which is never disconfirmed is after all the best of deemed abilities. Using $\mathcal {U}$, a disconfirmation would necessarily have to occur in the future in order for an acting entity to be able to do something. This would be counter-intuitive.

The dynamic role of confirmation We have just explained how an ability is maintained once it is deemed to exist. If an acting entity is not deemed able to bring about something, how do we maintain this inability? We adopt the following principle, that is symmetrical to lbda1.

In words, if G is not deemed able to do $\phi$, then it will not be deemed able until a situation is reached that shows evidence of its deemed ability. Note the use of a weak “until” again. If this situation showing confirmation of deemed ability is ever reached, we shall have $\textsc {can}_{G}\phi$ by axiom sc1.

It remains to address what must be the past chronicle of an existing ability. An entity G is deemed able to do $\phi$ only if it has been so ever since the occurrence of a situation showing confirmation for it.

Notice that we use here a standard “since” temporal operator $\mathcal {S}$, as opposed to the weak “until” $\mathcal {U}$ in the principles lbda1 and lbda2. By doing so, we commit our theory to the assumption that the existence of a deemed ability has to be grounded on confirmation. It rules out the possibility that it is a priori for some acting entity to be deemed able to bring about a contingent state of affairs. The first disjunction on the right hand of the implication captures the possibility that the current situation is one showing the pertinent evidence.

The models of deemed ability We can now constrain the models of the logic ${ \textsf {time}}({ \textsf {sc}})$ so as to satisfy the principles for the dynamic role of confirmation and of disconfirmation of ability. We define the models of deemed ability.

Definition 5

A model of deemed ability is a model $M = \langle {T,<,g}\rangle$ of ${ \textsf {time}}({ \textsf {sc}})$, that satisfies the following constraints C1, C2 and C3:

C1:

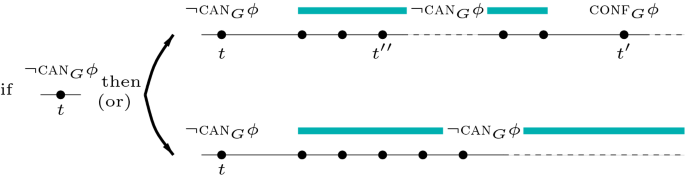
If $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}\phi$ then (i) there is $t < t'$, such that $M,t' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {disc}_{G}\phi$ and $M,t'' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}\phi$ for all $t< t'' <t'$, or (ii) for every $t < t'$ we have $M,t' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}\phi$.

C2:

If $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \lnot \textsc {can}_{G}\phi$ then (i) there is $t < t'$, such that $M,t' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {conf}_{G}\phi$ and $M,t'' \models _{{ \textsf {time}}({ \textsf {sc}})} \lnot \textsc {can}_{G}\phi$ for all $t<t'' < t'$, or (ii) for every $t < t'$ we have $M,t' \models _{{ \textsf {time}}({ \textsf {sc}})} \lnot \textsc {can}_{G}\phi$.

C3:

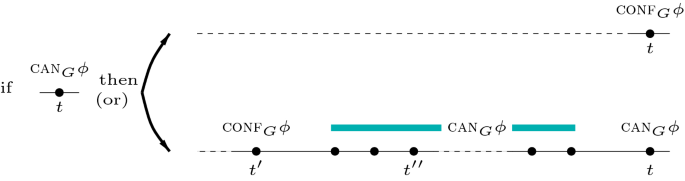
If $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}\phi$ then (i) $M,t \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {conf}_{G}\phi$, or (ii) there is $t' < t$, such that $M,t' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {conf}_{G}\phi$ and $M,t'' \models _{{ \textsf {time}}({ \textsf {sc}})} \textsc {can}_{G}\phi$ for all $t'<t''<t$.

We write $\models _{{ \textsf {lbda}}}\phi$ when for every model of deemed ability $M = \langle {T,<,g}\rangle$, and for every instant $t \in T$, we have that $M, t \models _{{ \textsf {time}}({ \textsf {sc}})} \phi$.

The logic of ${{ \textsf {lbda}}}$ is sound wrt. the class of models of deemed ability.

Proposition 3

If $\vdash _{{ \textsf {lbda}}}\phi$ then $\models _{{ \textsf {lbda}}}\phi$.

This is a simple consequence of Proposition 2 and the fact that the axiom lbda1 (resp. lbda2, lbda3) is sound in the class of models of ${ \textsf {time}}({ \textsf {sc}})$ with the constraint C1 (resp. C2, C3). Moreover, lbdar1 preserves validity: if $\phi$ is true in every model of ${ \textsf {time}}({ \textsf {sc}})$ then it is true in every model of ${ \textsf {lbda}}$.

Notice that the constraints correspond to actual conditions on the frames, using the truth value of monolithic formulas (i.e., of formulas in $L_{ \textsf {sc}}$) as a shortcut.

To see that lbda1 (resp. lbda2, lbda3) is sound in the class of models of ${ \textsf {time}}({ \textsf {sc}})$ with the constraint C1 (resp. C2, C3), it suffices to spell out the truth condition of the axiom, and see that it corresponds to the constraint.

Interdependence of deemed ability and confirmation We say that $\phi$ is true in a model of deemed ability $M = \langle {T,<,g}\rangle$, when for every instant $t \in T$, we have that $M, t \models _{{ \textsf {time}}({ \textsf {sc}})} \phi$. To conclude this section, we verify the simple fact that a deemed ability never occurs in a model of deemed ability if a confirmation for it never occurs, and the other way around. Equivalently, a deemed ability occurs at some instant in a model of deemed ability if and only if a confirmation for this deemed ability occurs at some (possibly different) instant.

Proposition 4

$\lnot \textsc {can}_{G}\phi$ is true in a model of deemed ability M iff $\lnot \textsc {conf}_{G}\phi$ is true in M.

Suppose $\lnot \textsc {can}_{G}\phi$ is true in a model of deemed ability $M = \langle {T,<,g}\rangle$. Hence, $\textsc {can}_{G}\phi$ is not true at any instant $t \in T$. By constraint 1 of Definition 1, this means that $\textsc {conf}_{G}\phi$ is also not true at any instant, and that $\lnot \textsc {conf}_{G}\phi$ is true in M. Suppose $\lnot \textsc {conf}_{G}\phi$ is true in M. Hence, $\textsc {conf}_{G}\phi$ is not true at any instant $t \in T$. Constraint C3 of Definition 5 makes sure that G is deemed able to do $\phi$ only if a situation showing confirmation for it has occurred. Since $\textsc {conf}_{G}\phi$ is not true at any instant, $\textsc {can}_{G}\phi$ is also not true at any instance, and $\lnot \textsc {can}_{G}\phi$ is true in M.

3 Example I: Mele’s general practical ability

Our core logic of being deemed able serves to explain the existence of a general ability extending over some period of time, based on occurrences of confirmations and disconfirmations. But it does not explain what confirmations and disconfirmations are. It is something that depends on a system designer’s choices. To illustrate the abstract framework, we first propose to temporalise the logic of bringing-it-about-that (Pörn 1977; Lindahl 1977), and more specifically, Elgesem’s extension with agents’ ability (Elgesem 1997; Governatori and Rotolo 2005). Effectively, we obtain a temporalised version of Mele’s simple abilities (Mele 2003) that are reminiscent of general practical abilities.

We keep the logic minimal. In Troquard (2014), more conceivable principles of agency and ability are discussed, and many are rejected. However, any sensible principle (e.g., exploiting the set-theoretical relationships between the acting entities) can find its way into a formalization of a more precise particular domain.

We do not present the model theory. This is a straightforward extension of the semantics in the models of deemed ability. We present the extension of the proof theory that we economically signify with $\vdash$ without index. That is, in what follows, for any formula $\varphi$, we adopt $\varphi$ as an axiom of an extension of the logic ${ \textsf {lbda}}$ by stating $\vdash \varphi$.

3.1 Bringing-it-about-that

The bringing-it-about-that (BIAT) modality of agency has been used to model the actions and responsibilities of acting entities. The formula $E_G\phi$ traditionally reads “G brings it about that $\phi$”.

Table 3 Bringing it about that

The principles of the modality $E_G$ are presented in the Table 3. By bringing about the truth of a certain proposition, an acting entity brings about the truth of all equivalent propositions (rule br1). Agency in BIAT reflects some responsibility for a state of affairs. It is stipulated that no acting entity brings about the tautologies (axiom b1). Agency requires achievement of results (axiom b2). Note that as a consequence, it is not possible for a group to bring about the impossible: $\vdash \lnot E_G \bot$. Actions of acting entities aggregate (axiom b3). If at the same instant, an acting entity brings about two propositions, then it also brings the conjunction of these propositions. See some details in Pörn (1977), Elgesem (1997), and Herzig et al. (2018).

3.2 Mele’s abilities

Elgesem’s logic (1997) is an extension of BIAT with an elementary notion of ability. The modality $\textsc {able}_{G}\phi$ reads that “G is able to bring it about that $\phi$”. Elgesem explains at length that when G brings it about that $\phi$, the state of affairs $\phi$ is one concerning a property towards which G has manifested its control. Thus an acting entity only brings about what it is capable of. It is expressed by the axiom $E_G\phi \rightarrow \textsc {able}_{G}\phi$. This is exactly what Mele calls simple ability. He writes “an agent’s A-ing at a time is sufficient for his having a simple ability to A at that time” (Mele 2003, p. 448). This is distinguished from an ability to A intentionally: “being able to A intentionally entails having a simple ability to A and the converse is false.” (Mele 2003, p. 448). A simple ability does not necessarily entail an intentional ability. There can be a simple ability without intention, as doing something, even by accident, is enough ground to have a simple ability.

A major criticism of BIAT is the absence of time, and Elgesem’s extension with abilities is no different. Although we have a means to infer an ability to $\phi$ from an occurrence of $\phi$-ing, this is of little significance since we cannot reason about what will become of the ability in the future; Elgesem’s system deals only with the present, not the future. Also, ability is only partially grounded, because it is consistent that $\lnot E_G\phi \wedge \textsc {able}_{G}\phi$ and we cannot reason about past evidence; again, this system deals only with the present.

However, once integrated in our logic of deemed ability, the problems are easily overcome by grounding confirmations and disconfirmations. The resulting notion of ability is similar to what Mele calls general practical ability. It is an ability which “we attribute to agents even though we know they have no opportunity to A at the time of attribution and we have no specific occasion for their A-ing in mind” (Mele 2006, p. 18).

3.3 Agency grounded confirmations

Using the modalities of bringing-it-out, we are now ready to provide our first axiom of inference of confirmation of an ability.

By axiom sc1, it follows that $\vdash E_G \phi \rightarrow \textsc {can}_{G}\phi$, which corresponds directly to the principle of simple ability discussed before.

Mele says that if an agent $\phi$s, then this is enough to infer that this agent has a simple ability to $\phi$. This is what the principle b4 (with axiom sc1) captures. This is not necessarily an intentional ability; for all we know the agent might have $\phi$-ed by accident.

The logic extending ${ \textsf {lbda}}$ with the principles adopted so far is effectively a temporal extension of Elgesem’s logic of agency and ability.

3.4 Multi-agency ground for confirmations

We can also exploit the agency of groups of agents more finely. In a multi-agent setting, axiom b4 can be generalised. It is argued in Troquard (2014) that when two groups bring about some propositions of their own at the same instant, they show that their actions can be carried out together without conflict. They might not have worked together at the time, but from $E_{G_1} \phi \wedge E_{G_2} \psi$ it is plain that the members of the group $G_1 \cup G_2$ made sure that both $\phi$ and $\psi$ would be true. We can consider that it is a confirmation that they can together bring about the conjunction of these propositions. To acknowledge the superadditive power of groups, we can adopt:

This subsumes axiom b4. Again by axiom sc1, we obtain the theorem $\vdash E_{G_1} \phi \wedge E_{G_2} \psi \rightarrow \textsc {can}_{G_1 \cup G_2} (\phi \wedge \psi )$ which is an axiom in Troquard (2014).

A principle analogous to b5 where the groups’ actions are not simultaneous would not be acceptable. (This could be represented, although indirectly, by the formula $\textsc {can}_{G_1}\phi \wedge E_{G_2}\psi \rightarrow \textsc {conf}_{G_1 \cup G_2}(\phi \wedge \psi )$.) For example, if John brings it about that the light is on at one instant, and Mary brings it about that the light is off one hour later, it is obvious that there is no confirmation of the fact that John and Mary are together able to bring it about that the light is both on and off.

Naturally, other principles of confirmations of group ability can be considered depending on the intended application.

In Troquard (2014), to acknowledge the special character of a group without members, any ability of the empty group is rejected. This is stipulated by the formula $\lnot \textsc {can}_{\emptyset }\phi$ which is adopted as an axiom. In our setting, we can adopt the principle $\lnot \textsc {conf}_{\emptyset }\phi$, saying that no situation confirms that the empty group can bring about that $\phi$. In virtue of Proposition 4, it would also imply that $\lnot \textsc {can}_{\emptyset }\phi$ as a theorem.

In presence of groups of agents as sets, principles of monotonicity are natural candidates. Monotonicity of ability seems even reasonable in some circumstances: if a group G is deemed able to bring it about that $\phi$, then every group $G'$ containing G is also deemed able to bring it about that $\phi$. With $G \subseteq G'$, this could be represented by the formula $\textsc {can}_{G}\phi \rightarrow \textsc {can}_{G'}\phi$. Although a more fundamental principle would be that if a situation confirms that G is able to bring it about that $\phi$ then it also confirms that every group $G'$ containing G is also deemed able to bring it about that $\phi$. With $G \subseteq G'$, this could be represented by the formula $\textsc {conf}_{G}\phi \rightarrow \textsc {conf}_{G'}\phi$.

3.5 Attempt-grounded disconfirmations

Disconfirmations can also be grounded through the use of agentive attitudes that have been studied in the literature of modal logics for agency. One can add an abstract notion of attempt to the bringing-it-about-that framework (Santos et al. 1997). As for the $E_G$ modality, we take $Att_G$ to be a minimal modality:

Following Santos et al. (1997) we could also adopt the axiom (not used in this paper):

It captures the fact that an action is a sort of attempt; a successful one by axiom b2.

Authors such as Kenny (1975), have argued that G’s ability to bring about some proposition $\phi$ is G’s power to bring about $\phi$ when G tries. We can then have an instance of disconfirmation of an ability when an acting entity tries to bring about something but does not actually bring it about. In formula, we have the following axiom:

3.6 A general life cycle of deemed abilities

Take the logical system extending ${ \textsf {lbda}}$ with the principles of this section. The following deductions can be drawn.

• 1. If group G is not deemed able to do $\phi$ at some time, $\lnot \textsc {can}_{G}\phi$, axiom lbda2 makes sure that it is so until some confirmation occurs.

• 2. Suppose at some later time some acting entities $G_1, \ldots , G_k$, where $G = G_1 \cup \cdots \cup G_k$, bring about respectively $\phi _1, \ldots \phi _k$ such that $\vdash \phi _1 \wedge \cdots \wedge \phi _k \leftrightarrow \phi$. By axiom b5 and rule scr2 one can deduce $\textsc {conf}_{G}\phi$.

• 3. By axiom sc1 one can deem G able to bring about $\phi$: $\textsc {can}_{G}\phi$.

• 4. By axiom lbda1, G will be deemed able to do $\phi$ until some disconfirmation occurs.

• 5. Suppose that at some later time, G attempts to bring about $\phi$ but does not actually bring it about, then by axiom b7 one can infer a disconfirmation: $\textsc {disc}_{G}\phi$.

• 6. By axiom sc2, we infer that G is not deemed able to bring about $\phi$: $\lnot \textsc {can}_{G}\phi$, and the life cycle is back to step 1.

4 Example II: supervised management of deemed abilities

In the previous section we have introduced a few notions which allowed us to start grounding confirmations and disconfirmations. We obtained a formalisation of general practical abilities. Leaving the realm of philosophy, we propose further notions to account for when talking about deemed ability. In particular we will consider (i) supervised management, and (ii) agreements between a supervisor and an acting entity to accomplish a task before a specified deadline.

Managing deemed abilities in this setting is related to the problem of assessing trust about the ability of an agent or a group of agents to accomplish a task within a multi-agent system (e.g., Castelfranchi et al. 2006; Wang and Singh 2010). In this section, we introduce a designated agent that we refer to as the manager of the system. The manager can bring it about that a group G is deemed able (within the system of which he is the manager) to bring it about that $\phi$. This can be interpreted as the manager expressing his trust about the ability of the group G to bring about $\phi$. Similarly, the manager can bring it about that a group G is not deemed able to bring it about that $\phi$, effectively expressing his distrust about the ability of the group G to bring it about that $\phi$.

4.1 Supervision-grounded confirmations and disconfirmations

The logical theory so far leaves the concepts of confirmations and disconfirmations under-specified. This allows a more flexible management of deemed abilities. Virtually no real system involving natural agents is a fully autonomous platform. System managers always reserve themselves means to tweak the system to reflect managerial decisions that do not always follow the strict written rules—or logic—of the system.

Let us then assume a special agent $\mathsf{m}$ that is the system manager, or acts on behalf of the system manager. We are not concerned with the nature of the manager. It can be a human being, the management team of a MAS-based business, or a software agent.

In an under-specified system, the manager can make expedient adjustments to the system with information obtained offline concerning the qualifications of acting entities. Hence, we will think of “the manager brings it about that G is deemed able (resp. not deemed able) to bring about $\phi$” as an account of confirmation (resp. disconfirmation) in the information system.

Scenario Suppose our rare media service repository is managed by $\mathsf{m}$. If the manager learns that the service $\sigma _3$ has ceased activity, he can report this information by inserting $E_{\{\mathsf{m}\}} \lnot \textsc {can}_{G \cup \{\sigma _3\}}\phi$ into the system for every currently existing deemed ability $\textsc {can}_{G \cup \{\sigma _3\}}\phi$, for every group G. The rationale for considering every currently existing deemed ability of every group containing $\sigma _3$ is that a group might be deemed able to bring about something but would need the participation of $\sigma _3$ to do so. With $\sigma _3$ out of business, the manager considers that the group $G \cup \{\sigma _3\}$ cannot work together, and this deemed ability should be disconfirmed. Indeed, with axiom t2 it will count as a systematic and systemic disconfirmation.

Symmetrically with axiom t1, the manager can approve a new piece of specification $\phi$ of a service $\sigma _4$ by inserting $E_{\{\mathsf{m}\}} \textsc {can}_{\{\sigma _4\}}\phi$ into the system. E.g., suppose $\sigma _4$ is a vinyl record shop. They inform the manager that they received a few original copies of The Freewheelin’ Bob Dylan; $\phi$ then stands for “sell The Freewheelin’ Bob Dylan”.

In general, using both modes of bringing it about that a coalition is deemed able to $\phi$, and bringing it about that a coalition is not deemed able to $\phi$, the manager can adjust the knowledge of the system to any desired change in service specifications.

4.2 Task-grounded disconfirmations

Task negotiation and attribution are other managerial activities that may occur off-platform in an under-specified system concern. Attribution is worked out by the manager agent, based supposedly on the information contained in the system. Negotiation can follow an arbitrary negotiation protocol.

We use $\textsc {task}_{G}(\phi ,\psi )$ to denote that the group G is assigned the task to bring about the objective $\phi$ before $\psi$ holds. To serve as a criterion of task identity, we must have:

Thus, when the two objectives $\phi _1$ and $\phi _2$ are logically indistinguishable and so are the two deadlines $\psi _1$ and $\psi _2$, then the task of G bringing about the objective $\phi _1$ before $\psi _1$ holds is logically indistinguishable from the task of G bringing about the objective $\phi _2$ before $\psi _2$ holds.

A simple principle then concerns task expiration and completion:

In English, if $\psi$ holds or if G brings it about that $\phi$, then the group G is not assigned the task to bring about $\phi$ before $\psi$ holds. The rational is: if $\psi$ holds, then the task has expired, and if $E_G\phi$ holds then the task has been completed. By contraposition, whenever $\textsc {task}_{G}(\phi ,\psi )$ holds, neither $E_G\phi$ nor $\psi$ do.

The manager can negotiate tasks with possible acting entities. We intend $E_{\{\mathsf{m}\} \cup G} \textsc {task}_{G}(\phi ,\psi )$ to capture the culmination of a negotiation resulting in the manager and the group G agreeing that G will carry the task of bringing about $\phi$ by the time $\psi$ holds. For clarity, we use a dedicated vocabulary to express it:

Observe that an agreement is effective, in the sense that $\vdash \textsc {agree}_{G}(\phi ,\psi ) \rightarrow \textsc {task}_{G}(\phi ,\psi )$ (by axiom b2).

We can now describe mixed temporal properties of agreements, tasks, and disconfirmations.

A task originates from a previous agreement and has existed ever since:

A direct reading is that if G is assigned the task to bring about the objective $\phi$ before $\psi$ holds, then either it has been agreed now, or the task has existed ever since it has been agreed.

An existing task should be maintained at least until it is completed or its deadline is reached:

In fact, together with axiom t3, it follows that an existing task is maintained exactly until it is completed or the deadline is reached.

Finally we can formalise a principle of task-grounded disconfirmation of ability:

If G has uninterruptedly had the task to bring about the objective $\phi$ before $\psi$ holds since a time it was agreed, then if the deadline $\phi$ is reached and G still has not completed the task when $\psi$ becomes true, then the situation is a disconfirmation of G’s being deemed able to bring about $\phi$ in the system. The group G might still be able to bring about $\phi$ eventually. However, having failed to do so under the deadline that was agreed upon with the system’s manager, G is not deemed able from the point of view of the system.

Scenario Suppose now that the service $\sigma _2$ announces to $\mathsf{m}$ that it changed its business model and is able to bring about that $\phi$. We admit that manager $\mathsf{m}$ trusts this information and thus brings it about, say at instant t, that $\textsc {can}_{\{\sigma _2\}}\phi$. This counts as a confirmation $\textsc {conf}_{\{\sigma _2\}}\phi$ by axiom t1. Suppose it is then agreed at instant $t' > t$ for $\sigma _2$ to do $\phi$ before a reasonable $\psi$: $\textsc {agree}_{\{\sigma _2\}}(\phi ,\psi )$. So by axiom t4 and axiom b2, the service $\sigma _2$ is tasked to do $\phi$ before $\psi$. $\textsc {task}_{\{\sigma _2\}}(\phi ,\psi )$ holds at $t'$, and will hold by axiom t6 until the deadline is reached or $\sigma _2$ brings it about that $\phi$, at which time the task will be dropped by axiom t3. Suppose that at the first eventual instant $t'' > t'$ where $\psi$ holds, it has not yet been the case that $E_{\{\sigma _2\}}\phi$. So $\textsc {disc}_{\{\sigma _2\}}\phi$ follows from axiom t7, and $\lnot \textsc {can}_{\{\sigma _2\}}\phi$ follows by axiom sc2. By axiom lbda1, $\textsc {can}_{\{\sigma _2\}}\phi$ held between $t'$ and $t''$.

5 Conclusions

The first contribution is a general framework to track, maintain and reason about the deemed ability of acting entities by taking into account past and future evidence: confirmations and disconfirmations (Sect. 2). The second contribution is a library of principles to ground these confirmations and disconfirmations. These principles permitted us to formalise the philosophically relevant notion of general practical ability (Sect. 3), and to tackle the practically relevant management of abilities in supervised systems (Sect. 4).

We concentrated on providing a rigorous formal foundation for the abstract framework and on providing some intuitions on how to put it to use with some sample instantiations.

As for now, in the proposed instantiations, deemed ability needs only one occurrence of actual agency to exist (axiom b5) and only one failed attempt (axiom b7) or failed task (axiom t7) to disappear. Beyond this first presentation, more realistic judgements about deemed ability could very easily be represented; both more sceptical of confirmation and less hasty in accepting disconfirmation. Quickly, however, we will be confronted with the difficulty of deciding how much evidence is enough to justify the confirmation or the disconfirmation of a deemed ability. There might not be a one-size-fits-all solution that is philosophically correct. Nonetheless, a future extension could offer the possibility to parameterise the temporal models with numerical thresholds to fit specific practical domains.

Another extension would allow one to talk about abilities to bring about that a temporal statement, that is, that a temporal formula is true. As for now, the temporalisation and the temporal language $L_{{ \textsf {time}}({ \textsf {sc}})}$ does not permit to write, say, $\textsc {can}_{G}{\mathcal {F}(\phi \wedge \mathcal {F}\psi )}$ that would capture the fact that the group G is deemed able to bring about that eventually $\phi$ holds and then that $\psi$ holds at a later time. This calls for more expressive temporalisations such as in Finger and Gabbay (1996).

Formal reasoning about deemed ability is already possible with the proposed axioms. The various scenarios that illustrate the paper are examples of it. The ‘supposed’ events in the scenarios are systemic events recorded in the execution trace of the repository system. All the rest is inferred by the logical apparatus to discover new facts in a way that maintains the system’s coherence.

However, our contribution is hardly technical and the formal aspects are so far admittedly rather straightforward. The models describe the trace of a system and are particularly adapted to simulation. Algorithmic solutions will be a step forward towards using the framework for the actual tracking and management of abilities in multi-agent systems.