Abstract
In this paper, I argue that enactivism and computationalism—two seemingly incompatible research traditions in modern cognitive science—can be fruitfully reconciled under the framework of the free energy principle (FEP). FEP holds that cognitive systems encode generative models of their niches and cognition can be understood in terms of minimizing the free energy of these models. There are two philosophical interpretations of this picture. A computationalist will argue that as FEP claims that Bayesian inference underpins both perception and action, it entails a concept of cognition as a computational process. An enactivist, on the other hand, will point out that FEP explains cognitive systems as constantly self-organizing to non-equilibrium steady-state. My claim is that these two interpretations are both true at the same time and that they enlighten each other.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, I argue that enactivism and computationalism—two seemingly incompatible research traditions in modern cognitive science—can be fruitfully reconciled under the framework of the free energy principle (FEP). According to FEP, cognitive systems encode generative models of their niches and cognition can be explained in terms of minimizing free energy (i.e., the prediction error of these generative models).
My argument is as follows. According to FEP, cognition boils down to free energy minimization. According to computationalism, cognition boils down to information processing. According to enactivism, cognition boils down to self-organization under a functional boundary.Footnote 1 Free energy minimization arguably entails Bayesian inference which is supposed to be a computational process. Therefore, FEP entails computationalism. On the other hand, those very computational processes postulated by FEP give rise to self-organization under a functional boundary. Therefore, FEP is a computational enactive theory of mind.
The rest of the paper is structured as follows. In Sect. 2, I introduce FEP and sketch out its two relatively non-controversial interpretations: a biological interpretation (free energy minimization entails being a living system) and a Bayesian one (free energy minimization is a solution to the problem of acting in an uncertain environment). In Sect. 3 I go on to argue that autopoiesis is a special case of FEP, and that FEP fares better than autopoiesis as a conceptual framework for modern enactivism. In Sect. 4 I argue that FEP entails computationalism because free energy minimization is a computational process and I address two possible objections to this computational interpretation. I conclude by arguing that computational enactvism—the view that emerges from my arguments—improves the prospects of both computational and enactive approaches to life and cognition.
2 Mind and life according to the free energy principle
Active inference is a modeling framework in computational neuroscience built upon the assumption that cognitive systems encode a hierarchical generative model of the world and act to minimize their prediction errors. This assumption is known as the free energy principle (henceforth FEP). This approach has received substantial interest in the neuroscience, cognitive science and philosophical communities due to its theoretical appeal, explanatory ambitions and philosophical implications. FEP is theoretically appealing because it is general enough to integrate (absorb as its special case) several well-grounded approaches to cognition and behavior, namely the Bayesian brain hypothesis, maximum entropy principle, utility theory and predictive processing (Friston et al. 2015a, b). A number of cognitive, neurophysiological, clinical and behavioral phenomena can be accounted for in terms of active inference, ranging from EEG rhythms and saccadic eye movement to the emergence of false beliefs in schizophrenia (Friston et al. 2017). Finally, active inference puts forth a radical new image of perception, learning, and action deeply embodied in biological autonomy and intricately coupled while self-organizing around prediction errors (Clark 2016).
2.1 A biological interpretation of FEP
There is also a more general reading of FEP—as the claim that minimizing free energy entails being alive. Formally speaking, FEP pertains any random dynamical system S with state space partitioned into four types of states (or property instances), i.e., internal, external, sensory and action states, in such a way that external and internal states influence each other only though action and sensory states. These are relatively non-controversial assumptions about the causal structure of any physical system. FEP can be then unpacked as the claim that if S manifests certain dynamics (adaptivity), it will necessarily satisfy a non-trivial information–theoretic description, which is satisfied by free energy minimization.
More specifically, for a living system to avoid phase transitions and maintain a non-equilibrium steady-state, the system must behave adaptively, i.e., preserve its physical integrity by maintaining its characteristic variables (determined by the phenotype) within bounds. This bound can be cast in terms of placing an upper bound on information–theoretic entropy of the distribution over sensory states of the system. Entropy (or, the expected or average surprise) is minimized by minimizing the free energy. Therefore, free energy minimization is sufficient for adaptivity and life can be understood in terms of FEP. (For a similar argument, see (Colombo and Wright 2018).)
What is of philosophical interest in this argument is the transition from a biological to a physical (thermodynamic) description, and then from physical to information–theoretic descriptions. Essentially, we arrive at a cybernetic account of life as a self-regulating process (Seth 2015).
2.2 A Bayesian interpretation of FEP
Apart from this transcendental deduction, there is also a more concrete mathematical reason to posit free energy minimization. Let us assume that a cognitive system encodes a generative model of its environment and continues to update it to match sensory evidence. This, however, poses an intractable inference problem and demands some approximation technique to be employed. One way around is a machine learning framework of variational inference, which reduces a Bayesian inference problem to an optimization problem to be solved by minimizing free energy with respect to some parameters defining a proxy distribution approximating our desired posterior (Bishop 2006). Mathematically, the free energy to be minimized is a functional (i.e., a higher-order function) of sensory states and internal states F(action, internal) and can be shown to impose an upper bound on surprise, i.e., the negative log probability of a sensory input given the generative model. Written semi-formally, the free energy minimization is minimized with respect to action and internal states:
where the free energy can be decomposed as
I restrain myself from providing a more detailed derivation of these equations and interpretation of their building blocks; remaining on an intuitive level of understanding is sufficient for our purposes.Footnote 2 What is crucial here is that FEP can be seen as an algorithmic solution to a particular inference problem every living system faces: perceiving and acting in an uncertain environment.
This more concrete, Bayesian perspective on FEP can be argued to follow from a more general biological perspective: the inference problem to be solved is posed by the fact that living systems are adaptive and resist environmental fluctuations. Nevertheless, the fact that there are two readings of FEP is philosophically revealing; later I will argue that this is indeed a major strength of FEP.
2.3 Terminological issues
FEP should be distinguished from active inference itself, predictive coding and predictive processing. FEP is a normative principle asserting that living systems engage in active inference, i.e., free energy minimization, over time. As such, it does not generate quantitative predictions or commit itself to a concrete description of how free energy minimization is implemented. Predictive coding, on the other hand, is a computational model of mammalian visual perception that does commit to some architectural constraints, namely functional asymmetry of information flow in the visual cortex (with one path transmitting predictions down the hierarchy and the other returning precision-weighted prediction errors). A generalization of this model into a research program in neuroscience (applicable to auditory perception, interoception, motor control, mental imagery as well as agency and consciousness) is known as predictive processing.
While predictive coding/processing and FEP are tightly interrelated, there are subtle differences between them. FEP is a principle, while predictive coding is a process theory (or a mechanism sketch) that conforms to the free energy principle. FEP posits an upper bound on the entropy of the probability distribution over sensory states, while predictive coding achieves this by minimizing precision weighted prediction error—where precision weighted prediction error can be regarded as variational free energy, under some simplifying assumptions. FEP itself is transparent about the architecture of computation underlying free energy minimization.
An attempt at going beyond FEP was also recently made by Ramstead et al. (2018), who augment FEP with evolutionary considerations to form a more powerful research framework known as variational neuroethology (VNE).
2.4 The scope of the argument
The arguments mounted in this paper only assume FEP to be true, yet remain compatible with the body of work known as predictive processing (PP), and gain strength when backed up with PP. Importantly, I am not trying to defend FEP as a valid account of life and mind or as a prolific modeling framework in neuroscience; neither do I engage in disputes over the breadth of its explanatory scope (Sims 2016). What I argue is that even if a claim as weak as FEP is true, some non-trivial philosophical conclusions could still be drawn regarding enactive and computational approaches to mind and life.
Though FEP has received significant philosophical attention, the views on the concept of mind to which it is committed are still evolving. (Hohwy 2013) famously argued that it entails a broadly cognitivist account of mind, committing to environmental seclusion over mind extension and intellectualism over the primacy of action. Other authors, however, pursue a different reading, emphasizing parallels between the circular causality induced by FEP and the concept of self-organization at the heart of embodied, enactive approaches in cognitive science. This line of thinking about FEP was furthered by Bruineberg and Rietveld (2014), Kirchhoff (2016) and Kirchhoff and Robertson (2018), who argue for a radical, non-representational and non-computational interpretation of FEP.
A few authors have also argued for the middle ground between cognitivist and enactive accounts of FEP. This approach was pioneered by Allen and Friston (2018) and later developed by Ramstead et al. (2018, 2019) and Allen (2018) under the name of Bayesian enactivism or enactivism 2.0. While Bayesian enactivists overcome the skepticism of classical enactivism about information–theoretic accounts of mind and try to formalize the concept of enactment in terms of active inference, they either remain silent about the computational character of active inference itself (as Allen and Ramstead et al.) or join Kirchoff et al. in rejecting computationalism. The computational enactivism defended in this paper differs in acknowledging and emphasizing active inference being a computational process (as opposed to only being describable as computing), while at the same time entailing a fully-fledged enactive theory of mind.Footnote 3
3 FEP and enactivism
3.1 FEP subsumes autopoiesis
Modern enactive cognitive scientists and philosophers try to tell the story of how the mind works in terms of autonomy, sense-making, emergence and embodiment and experience rather than information processing, representations and mechanisms (Thompson and Stapleton 2009). A number of authors have pointed out similarities between FEP and various flavors of enactive approaches in cognitive science, such as autopoietic enactivism (Kirchhoff 2016), sensorimotor theory (Seth 2015), ecological psychology (Bruineberg and Rietveld 2014) and the extended mind (Clark 2016).
Let us, however, start from the beginning. Historically, enactivism originated from a simple conceptual model of what it takes to be alive: autopoiesis (Maturana and Varela 1980). Being a minimal model of a living creature, an autopoietic system is an organized system characterized by two properties:
-
(a)
It continuously realizes the networks of processes that maintain its existence,
-
(b)
It has a concrete spatial boundary (specified by the topological domain of its realization as a network).
Arguments that FEP subsumes autopoiesis have been put forth by Allen and Friston (2018) and Kirchhoff (2016). As for (a), the network of processes constituting an autopoietic system is usually understood as a particular of topology of the flow of matter and/or energy throughout the system, i.e., each process is maintained by some other process, or more specifically, the system is self-sufficient in the restricted sense that all processes which function to support the system are parts of the system. This property is sometimes known as operational closure and corresponds to what some others call closure to efficient cause (Rosen 1991) or autocatalysis (Kauffman 1993). An active inference agent, described as a directed graphical model (i.e., in terms of distributions over internal, external, action and sensory states, and dependency relations between them), manifests basically the same recursive inter-dependencies.
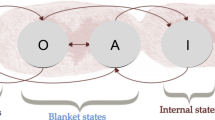
The same is true for (b): the agent is relatively isolated from its environment in the sense that the influence the distribution over external states has on the distribution over internal states is mediated through sensory and action states. Formally, given action and sensory states, internal states are independent of external states. This property is known as a Markov blanket (Pearl 2000). The idea that a (selectively open) boundary of a cognitive system is to be described as its Markov blanket has recently gained popularity among philosophers and neuroscientists (Clark 2017; Kirchhoff et al. 2018).
A few words of caution, though: while Varela and Maturana originally defined autopoiesis as a first-order property of a dynamical system, the FEP claim is probabilistic, formulated in terms of higher-order statistics of a system. What FEP asserts is that for an ensemble of infinitely many copies of a system and empirical distribution over states of these copies, such-and-such information–theoretic relations between distributions over internal, external, action and sensory states hold. For instance, while originally (b) is a statement about concrete spatial boundary (usually interpreted as a cell membrane), when recast in terms of FEP, the boundary is to be understood in terms of conditional independencies between random variables with such-and-such distributions. On one hand, this means that the concept of Markov blanket is much more general than that of spatial boundary and is applicable to a wider class of random dynamical systems. On the other hand, this means that whether FEP is satisfied by a given natural phenomenon depends on how we partition it into states and what distributions over these states we observe or assume.
Interestingly enough, FEP does not only recast the notion of autopoiesis in terms of Bayesian networks. It also tells how to derive constraints (a) and (b) from a more general one: that the organism believes (in the Bayesian sense of the term) in its own survival, or alternatively, believes certain states are more likely to be occupied than others. This prior belief can be seen to be determined by the embodiment of a system and is encoded in the body itself, as for a living system with certain bodily constraints some external states are more viable than others. (Here, viability is cast as sensory surprisal, i.e., the negative log probability of appropriate sensory states). Therefore, if the organism believes it should occupy a certain subset of states, it will engage in active inference to minimize its surprisal with unexpected states (i.e., induce circular interdependencies in (a)). While self-evidencing this belief in its survival, the organism will try to maintain its statistical integrity against environmental fluctuations, equivalent to maintaining a Markov blanket in (b).
3.2 FEP enhances autopoiesis
Modern enactivists very well recognize the need to go beyond mere autopoiesis. To avoid the risk of mounting easy-to-address straw-man arguments, let us borrow a large quotation from Froese and Stewart (2010), avowed enactivists themselves, as they point out shortcomings of the original autopoietic model (dubbed “MV-A”):
(i) Constructive requirements: MV-A is too static and abstract to distinguish the living from the non-living (e.g., Sheets-Johnstone 2000; Fleischaker 1988); it is lacking all consideration of material and energetic conditions for self-organization, emergence, and individuation (e.g., Collier 2004, 2008; Bickhard 2008), as well as being generally silent on the implications and requirements of self-production under far-from-equilibrium conditions (e.g., Ruiz-Mirazo and Moreno 2004; Moreno and Etxeberria 2005; Christensen and Hooker 2000).
(ii) Interactive requirements: MV-A is too isolated; it thus ignores possible incorporation of environment (e.g., Virgo et al. 2011) and dependence on other living systems (e.g., Ruiz-Mirazo et al. 2004; Hoffmeyer 1998); it also lacks consideration of functional interaction cycles (e.g., Arnellos et al. 2010; Di Paolo 2009; Barandiaran and Moreno 2008; Moreno and Etxeberria 2005).
(iii) Normative requirements: MV-A cannot account for normative activity such as adaptivity and goal-directed action (e.g., Barandiaran et al. 2009; Di Paolo 2005; Barandiaran and Moreno 2008; Bickhard 2009), as well as sensorimotor action and cognition (e.g., Barandiaran and Moreno 2006; Bourgine and Stewart 2004; Christensen and Hooker 2000).
(iv) Historical requirements: MV-A is lacking a capacity for memory, learning, and development (e.g., Hoffmeyer 2000), as well as for genetic material (e.g., Hoffmeyer 1998; Emmeche 1997; Brier 1995), and is thus unsuitable for open-ended evolution (e.g., Ruiz-Mirazo et al. 2004).
(v) Phenomenological requirements: MV-A is insufficient for grounding a lived perspective of concern (e.g., Di Paolo 2005), desire (e.g., Barbaras 2002), and thus of lived experience more generally. (pp. 9–10)
Objections (i) and (ii) express a well-known worry, that in its pursuit for self-sufficiency autopoiesis abstracts too much from the environment in terms of the resources it provides and threats it brings. What needs to be acknowledged is that living systems must be energetically, materially and informationally open systems, actively exploring their environments. The concept of a (selectively open) Markov blanket seems to be better suited to capture this trade-off between operational closure and being a world-involving system.
One other problem for autopoiesis is the difficulty of accounting for the fine structure of living systems as complex adaptive systems composed of multiple functionally differentiated subsystems. Autopoiesis, taking a single cell to be a paradigmatic model of life, does not straightforwardly scale up to multi-cellular organisms and multi-organism ecosystems. On the other hand, an ensemble of Markov blankets engaged in active inference can be shown to engage in collective active inference (so that no Markov blanket surprises another) and induce a higher-level Markov blanket around them. In principle, cellular morphogenesis can thus be accounted for in terms of FEP (Friston et al. 2015) and by applying this idea recursively we can model the emergence of hierarchical adaptive systems. The concept of nested Markov blankets is in line with recent work in evolutionary systems theory (e.g., Ramstead et al. 2018) and extended cognition (e.g., Clark 2017).
As for objection (iii), contrary to autopoiesis, FEP is essentially a normative theory of what an organism should do to maintain its integrity in a changing environment (the answer is, obviously, that it should act to minimize its free energy). Intrinsic (organism-level) value can be easily accommodated in this framework in terms of generative models (or, probability distribution over sensory states). This approach is reasonably standard in utility theory or reinforcement learning, and by expressing the utility function as a prior belief, every control-theoretic problem can be formulated in terms of Bayesian inference (Botvinick and Toussaint 2012). Selecting optimal behavior, then, is equivalent to computing a posterior. The notion of value can be thus explicated simply as log evidence (or, negative surprise) and the notion of goal-oriented behavior serves as evidence for an embodied generative model. (For an extended argument, consult Friston, Adams and Montague (2012).)
Objection (iv) is even simpler to address: the optimization of internal states via gradient descent on variational free energy is simply equivalent to learning or, on a longer time-scale, to development or evolution.
Finally, FEP seems to have conceptual resources to at least pose the problem (v) of consciousness and phenomenal aspects of experience in terms of generative modeling. Consciousness arises as the agent engages in inferences involving future or possible consequences of the immediate action and can be framed in terms of the depth of the generative model of the agent. This straightforwardly entails that living systems will vary in temporal thickness or counter-factual depth of their generative models, i.e., how (self-)conscious they are. For instance, a sleeping person and a bacterium have temporally thin models, as they are capable of only reflexive behaviors (Friston 2018). Furthermore, the notion of phenomenal aspects of experience can be understood in terms of counter-factual inference (Seth 2015).
Note that while addressing each of these issues we restricted ourselves to a broadly understood active inference framework. A framework is not supposed to entail specific answers to empirical questions; it is supposed to provide resources for concrete computational models to answer empirical questions. What I argue is that active inference does a better job here than the original autopoiesis and is better suited for grounding an enactivist account of mind.
4 FEP and computationalism
4.1 Free energy minimization as a computational process
In this section, I will argue that FEP entails computationalism, i.e., the claim that cognition is a computational process. For the sake of our argument, I assume a mechanistic account of computation and computational explanation.Footnote 4 According to this account, to compute is to be an organized, functional mechanism that acts on information vehicles according to some model of computation independent of the mechanism’s description (Miłkowski 2013, 2016a). The mechanistic account of computation embraces transparent computationalism (Chrisley 2000), i.e., does not assume a canonical mathematical model for describing the computation or a canonical medium. Analog computers, digital computers, as well as exotic computing systems composed of molecular machines or colliding particles are all classes of computational mechanisms. Moreover, it does not presuppose semantic properties of a computational mechanism; such constraints do not follow from models of computation used in computability theory and therefore should not be imposed by a scientifically informed account. Specifically, representation is not necessary for computation.
The mechanistic account of computation is informed by and closely related to modern accounts of computational explanation in cognitive and life sciences. It requires that a mechanistic model of computation, apart from an abstract specification of a computation, must be complemented with an instantiation blueprint of the mechanism at all relevant levels of organization (Miłkowski 2013). As mentioned before, FEP itself does not provide a mechanistic computational explanation of cognition but can inform concrete computational models as a functional principle. It can also entail that every living system is a computational process while abstracting away from its computational architecture. As I will argue, this entailment is valid.
Recall that FEP interpreted in a Bayesian manner mandates an upper bound on the entropy of sensory states; all that is required is to minimize free energy with respect to action and internal states. Therefore, active inference is just a statistical inference process and FEP is a high-level algorithm for a particular statistical inference procedure. Since statistical inference is an instance of computation, free energy minimization must be a computational process. Now, according to FEP, cognition boils down to free energy minimization, and according to computationalism, cognition boils down to information processing. If free energy minimization is a computational process, then FEP entails computationalism.
Let us provide some additional evidence that even embodied statistical inference in the wild, as in the case of active inference, still counts as computation. To do that, let us unpack the equations governing active inference into a piece of pseudocode describing a particular, naive implementation:

where the actual free energy minimization is delegated to a routine:

Algorithmically, active inference can be decomposed into four steps. First, we sample action states (take an action) and/or sample the generative model encoded by internal states (i.e., infer the state of the world). Second, we evaluate the current free energy with respect to current sensory, action and internal states.Footnote 5 Then, we compute the gradient of action and internal states with respect to free energy. The gradient computed tells us in which direction to adapt in order to be less surprised by a given sensory input in the future. Finally, we update action and internal states using the computed gradient.
The algorithm depicted above is more or less how actual computational models of active inference are implemented (e.g., Baltieri and Buckley 2017). The particular steps should not be taken too seriously, however; there is no biological equivalent of a single CPU or of RAM in a biological system. On the contrary, we should allow an arbitrary degree of redundancy and concurrency in hypothesized biological implementations of active inference. Biologically realistic active inference is no turn-taking game: the computation underlying action and perception is inextricably coupled. Furthermore, each cell of an organism can be seen as executing the algorithm on its own, engaging in inference of its own milieu when playing its role in a metabolic network; the computations composing the behavior of a whole organism are executed asynchronously at various temporal and spatial scales. Yet despite these exotic implementation details, the computations still satisfy a familiar description and could, in principle, be performed by hand on paper.
To be more concrete, let us consider how this computation could be implemented in a plant. Following Calvo and Friston (2017) I will analyze salt-avoidance in pea roots. High concentrations of salt in the soil disrupts the metabolic processes of peas, so pea roots grow in the direction of minimal salt concentration. Under the framework of FEP, this preference means that salt is surprising according to the generative model of sensory states encoded by the plant’s internal states, i.e., there is a phenotypic strong prior for saltless soil. This prediction determines the action to be taken (the direction of root growth) and subsequent stimuli (concentration of salt in a new region); the stimuli are compared against the generative model. The model is then updated relative to its prediction errors.
Growing roots in a particular direction is equivalent to proactively sampling sensory states that are expected to be predictable (i.e., adaptive). As Calvo and Friston remark,
If the reader finds plant examples along these lines a hard pill to swallow, just think of animal vision, where saccades bring about the sampling of sensory states. In the same way that evidence can be gathered by visual saccading to make predictions about visual input (…), a full-fledged active-inferential theory of root nutation states that nutations constitute the sampling of sensory states, and that by taking in different parts of the soil structure roots may gather evidence for predictions (…). Nothing other is called for. (p. 4)
While there is no known mechanism of how generative models and the flow of prediction error is implemented in a non-neural medium, plants seem to have sufficient physiological machinery to implement the message passing needed for active inference. Electrical events can propagate along the vascular system in the membranes of non-neural plant cells. One important difference is that plants did not evolve a central nervous system; we could hypothesize the computation to be heavily distributed across the body of a plant and beyond, involving the rich ecosystem the plant is embedded in. Importantly, apart from electric events, information processing can be delegated to physical movements subject to spatial constraints, as in the case of vines climbing up a host tree for photosynthetic purposes. Using Friston and Calvo’s own phrase, plants can “compute with their bodies in the service of adaptive flexible behaviour” (p. 6). Thus, active inference can be largely implemented by offloading the computations to primary and secondary growth (as in the case of sampling the generative model and action states) and metabolism (as in the case of generative model optimization). We can expect active inference to be implanted by a truly heteromorphous computational architecture, simultaneously computing its posteriors by electric, chemical and mechanical means.
The following two conditions are usually deemed necessary for a physical process to count as computation: producing usable outputs and producing them reliably. The plant example teaches that these conditions are met in the case of free energy minimization. Both partial (the gradients) and final (parameters of the generative model) results of sampling the environment are clearly usable for (by definition) minimizing the free energy and therefore (by the biological interpretation of FEP) contributing to the adaptivity of a system. Similarly, under the biological interpretation of FEP, reliability of the process is equivalent to the adaptivity of the organism, which is self-evident (should the organism remain maladaptive, it would cease to exist).
A mechanist computationalist imposes an additional set of constraints for a physical process to be computational: the computation must be bottomed out by a complete causal description of what happens underneath the computational level of description. Obviously, there is no mechanism description satisfiable by all cognitive processes. FEP, as a functional principle, provides a rough blueprint of mechanism involved in free energy minimization to be specified by concrete models of concrete phenomena. It imposes, however, some modest constraints on possible mechanism, most clearly seen in the graphical model formulation of an active inference agent: there must be a Markov blanket, spanned over sensory and action states, that mediates causal interactions between internal and external states. A formal approach for brigading this constraint with more informative mechanism descriptions is the Hierarchically Mechanistic Mind framework, which boils down to recursively nesting the aforementioned causal network at different spatiotemporal scales (Ramstead et al. 2018).
Some disagree with the outlined interpretation of active inference as a computational process. There are three broad strategies of arguing against the computational interpretation. First, one can deny that all the necessary conditions for a process to be computational are satisfied by all active inference agents. Secondly, one can mount a reductio ad absurdum objection, by pointing out that, according to our conditions, (almost) all physical systems are computers. Finally, some maintain that the computational description of active inference, while technically true, is superfluous and distracting. I will review both of these strategies in the three subsequent subsections.
4.2 The ontological objection against the computational interpretation of FEP
According to the ontological objection, the computational interpretation of FEP is simply false, because at least some instances of free energy minimization fail to satisfy a property supposedly necessary for a computational process, namely possessing semantic content. This worry was recently non-directly voiced by Kirchhoff and Froese (2017) who defend mind–life continuity, which leads them—prematurely—to reject computationalism on the grounds that computation requires semantic content which is not available for basic minds. Obviously, this reasoning can be inverted to argue that, assuming mind–life continuity, the computational interpretation of FEP is troublesome because FEP could only apply to minds capable of dealing with semantic content.
Let us further unpack this argument:
-
(1)
A physical process must have semantic properties to count as computational,
-
(2)
Basic minds are contentless,
-
(3)
For FEP to be an enactive account of mind and life, it must satisfy the mind–life continuity thesis,
-
(4)
For FEP to satisfy the mind–life continuity thesis, it must pertain basic minds as well as higher-order cognition,
-
(5)
Therefore, were active inference necessarily computational, basic minds would not engage in active inference, and FEP would not be a true enactive theory of life and mind.
The controversial premises here are (1) and (2). Assuming a mechanistic account of computation, it is not clear whether semantic properties are really necessary for a process to count as computational. Unlike proponents of the semantic account, mechanist computationalists individuate computational states non-semantically, based on their role in a mechanism rather than supposed content. One may argue, however, that requiring usable output of a computation and correctness conditions (i.e., allowing for miscomputation) entails some crude of satisfaction conditions for the computation results. I will remain agnostic on this matter, since it turns out that modest content-involving computationalism can still defend itself against the ontological objection. This is because premise (2) is false.
Premise (2) assumes the existence of the so-called Hard Problem of Content (Hutto and Myin 2012), the problem of giving a non-circular naturalist account of how content emerges in early cognition. The hard problem of content is purportedly hopeless and makes a case for antirepresentationalism in cognitive science; according to its proponents, all naturalist theories of content fail to explain how it emerges in simple cognitive systems unless scaffolded on social learning. This argument, however, is highly questionable, as there are a few good theories of how complex regulatory systems give rise to semantic information (Korbak 2015). Basically, the process can be formally understood as a sender–receiver game, and the content of a message (semantic information) is determined by how the message (information vehicle) affects the distribution over actions taken by the receiver (Skyrms 2010).
Notice the Bayesian flavor of this account: the content is understood in terms of (a transformation of) the probability distribution over actions the receiver may take. Assuming the graphical model formulation of active inference, the content of a given sensory stimulus S is determined by the gradient of action and internal states in an update step with respect to surprise S brings about. Since content depends on previous priors of a generative model (receiver-specificity) and influences future actions (action guidance), it basically fits the standard teleosemantic account (Millikan 2005).
One additional worry one may have is whether the scope of active inference isn’t broader that the class of systems manifesting the outlined sender–receiver dynamics. I will proceed to address this problem in the next section.
4.3 The pancomputationalism objection
As the class of system engaged in active inference is relatively broad, one related worry arises. There are physical systems that can be argued to be active inference agents, but probably are not living systems, e.g., societies or hurricanes. If that is so, doesn’t it entail a weak form of pancomputationalism (the claim that every self-regulating system is a computer) and thus render computationalism (almost) trivial?
Along these lines, Kirchhoff et al. (2018) formulated a distinction between ‘mere active inference’ and ‘adaptive active inference’. A system engages in mere adaptive inference when it adaptively responds to its environment, maintaining high mutual information (as in the case of two coupled pendulums). A system engages in adaptive active inference when it possesses a
generative model with temporal depth, which, in turn, implies that it can sample among different options and select the option that has the greatest (expected) evidence or least (expected) free energy. The options sampled from are intuitively probabilistic and future oriented. Hence, living systems are able to ‘free’ themselves from their proximal conditions by making inferences about probabilistic future states and acting so as to minimize the expected surprise. (Kirchhoff et al. 2018, p. 7)
While adaptive active inference can be thought to be coextensive with being a living system, mere active inference pertains a much broader class of systems. That’s why coupled pendulums do not compute each other’s position. First, we probably would not ascribe a functional description to parts of a system of pendulums engaging in mere active inference. Since such a system (by definition) is not adaptive, i.e., it does not support second-order, future-oriented regulation; we cannot define the function of any element as contributing to the autonomy of a system. To be fair, we should probably restrict our claim to assert only that all adaptive active inference agents are computers. It feels like an insignificant correction, though: as far as systems of interest for cognitive science and life sciences are concerned (or, after reaching of certain minimal level of complexity of a system under scrutinization), the claim that FEP entails computationalism remains true.
4.4 The epistemological objection against the computational interpretation of FEP
Another argument against the computational interpretation of FEP, voiced most prominently by (Bruineberg et al. 2016), targets the epistemological claim: that the theory-laden language of statistical modelling and Bayesian inference brings a value to FEP. Bruineberg et al. argue that the exact constraints that FEP imposes on cognitive systems can be equivalently formulated in much simpler language, purely in terms of (stochastic) differential equations, without any appeal to Bayesian inference whatsoever.
This deflationary approach is nicely illustrated by the example of Huygens’ clocks. In his influential Horoloqium Oscilatorium, Huygens famously observed that two oscillating clocks hanging on a suspension beam will synchronize through tiny movements of the beam from which they are suspended. This phenomenon is known as generalized synchrony. But should we ascribe “an inferential interpretation of the coupling of the two clocks, in which one clock ‘infers’ the state of the other clock hidden behind the veil of the connecting beam” (Bruineberg et al. 2016)? And if the computational interpretation of FEP is true, should we consider the system a computer? According to Bruineberg et al., the Bayesian and (by extension) the computational accounts are unnecessary and distracting. The story of free energy minimization is better told in terms of coupled dynamics of an agent-environment dynamical system resolving around an unstable equilibrium (or, a dynamic attractor). It is, according to the dynamical interpretation, a story of an agent trying to keep its essential variables within certain bounds by adjusting to environmental dynamics and modulating the environmental dynamics.
There are reasons, however, why the computational interpretation of active inference is warranted and enlightening. The example of Huygens’ clocks is slightly misleading here, being too simple to call for a richer vocabulary to describe it; it engages in mere active inference as opposed to adaptive active inference. But it seems that when a certain threshold of complexity is exceeded, the tools of dynamical systems theory provide less and less insight, and a model builder could use some additional constraints to guide their effort. In the case of more complex systems, the computational interpretation is not exactly equivalent to the dynamical one, because it imposes those constraints. For the purposes of our argument, four types of additional constraints can be distinguished: (1) normative constraints, (2) complexity constraints, (3) energetic constraints and (4) mechanistic constraints.
The (1) normative constraints arise from the fact that the graphical model formulation of active inference agent as Markov blankets and the free energy objectives were derived using the laws of probability calculus. While the variational inference formulation of the problem of inferring hidden causes is largely about reframing it as an optimization problem, there are a number of arbitrary decisions a modeler must make on her own, even after employing the active inference framework; for instance, how to sample from the generative models and what assumptions about its parameterization to make (i.e., assuming mean-field or Laplace approximations). Bayesian statistics offers principled guidance on making these decisions. Further, once we admit it is (also) an inference problem we are solving, the assumption of Bayesian rationality of the agent gives rise to a richer, normative level of description (Oaksford and Chater 2007). This is especially useful when modeling pathological behavior as violations of Bayesian rationality. A great deal of recent work in the field of computational psychiatry accounts for psychiatric diseases in terms of suboptimal inference (Huys et al. 2016). Usually, this reduces to some suboptimal priors over the precision of sensory evidence or prior beliefs.
Computational complexity constraints (2) emerge because, unlike coupled high-dimensional dynamical systems (which usually requires qualitative analysis of numerical simulations rather than analytic treatment to yield any insights), formal models of computation are relatively well-understood mathematically. Specifically, it is usually straightforward to determine a computational complexity class of an algorithm and computational complexity imposes concrete empirical constraints on what living systems compute. Tractability (i.e., being computable in a reasonable, usually polynomial, time) is a powerful constraint of this type (van Rooij 2008), especially in the context of Bayesian modelling (van Rooij et al. 2018). The very reason for employing the variational formulation of FEP is the intractability of exact inference. Moreover, since minimizing the model complexity term (present in certain formulations of the free energy) entails reducing the computational costs, this constraint is implicitly present in FEP.
In a similar vein, every computation comes with a concrete energetic cost. While general energetic bounds of computation (such as Landauer’s limit) are probably too loose to be empirically interesting for a neuroscientist, there is a significant amount of work in physics on the thermodynamic correlates of computations and inferences, which may be empirically relevant in the context of origin of life studies (Bennett 1982; Still et al. 2012). Again, assuming Landauer’s principle the penalty for metabolic costs is inherent in FEP, therefore minimizing the free energy automatically produces the most computationally and energetically efficient scheme (for minimizing the free energy).Footnote 6
Finally, the algorithm describes a certain (linear, recurrent, or concurrent) structure of computation that can be mapped onto the causal structure of an implementation. While FEP, even when interpreted computationally, is indeed quite implementation-agnostic, the dynamical interpretation does not do any better. At least when coupled with predictive processing, FEP entails the existence of two distinct, functionally asymmetric streams of information flow and a hierarchy of message-passing mechanisms. The dynamical account of FEP and radical predictive processing, on the other hand, do not provide a single sketch of a mechanism.
One may object that constraints (1)–(4), while useful in cognitive science, are still better interpreted as model-building heuristics rather than real patterns. Defending such an antirealist stance seems troublesome: the simplest explanation of why these model building constraints hold is that there are corresponding ontological constraints in the world. Just as I assert that active inference agents are computers (as opposed to just being describable as computing), I assert their computations give rise to norms, have certain complexity and energetic costs and are implemented by a concrete mechanism (as opposed to just being describable as if they gave rise to norms etc.).
Finally, one may point out that constraints (1)–(4) can, in principle, be included in a dynamical system model, while dropping the appeal to computation. For instance, we can always add a new state variable tracking energetic expenses or modeling an action-state value function. Even side-stepping the fact that we arrive at these constraints by computational considerations, it would be a Pyrrhic victory. There is hardly any value in distancing from complementary approaches rather than including them. It is indeed a major power of FEP (and predictive processing) that it is able to integrate multiple perspectives on life and cognition and weave models by convolving varied constraints.Footnote 7
5 Conclusions
I argued that FEP is an account of mind and life that both a computationalist and an enactivist could agree upon. This is because the computationalist commitment to explaining cognition in terms of information processing is satisfied by the notion of Bayesian inference underlying action, learning and perception, and because the enactivist commitment to explaining cognition in terms of self-organization under a functional boundary is satisfied by the notion of self-evidencing under a Markov blanket. A hard-core enactivist might still object that the two approaches are fundamentally at odds with each other, for instance by maintaining that the claim that cognition is not computational is part of the enactivist agenda. That would certainly be a valid argument, but one an explanatory naturalist should not make. It is quite a loss to reject the rich Bayesian picture (including all the connections to machine learning, information theory, psychiatry and statistical physics) just because it does not fit a narrowly understood enactivist agenda.
But our claim is stronger than just asserting that enactivism and computationalism are both true under FEP. It is not just that the truth of enactivism and computationalism happens to coincide, assuming FEP. The computations postulated by FEP are there because of the enactivist imperative of self-organization, and, epistemologically, FEP owes its enactivist implications to computations it postulates. Since—as I argued—FEP does a better job as a conceptual model of self-organization than autopoiesis does, solving some of enactivism’s problems, it is the computational perspective that provides much-needed insights for enactivist accounts of mind and life. On the other hand, the enactive perspective—as argued elsewhere (Clark 2016)—imposes ecological constraints on the computations and points our attention to the variety of forms information processing in living systems may take. Thus, computational enactivism is stronger than either computationalism or enactivism on their own.
Notes
Enactivism is not a monolithic camp yet appeal to the concept of self-organization seems to be the unifying trait of most prominent varieties, i.e., sensorimotor, autopoietic (both classical and contemporary) and radical enactivism.
For a derivation of these equations, an outline of the mathematical framework under which FEP is formulated and its relations to models of hierarchical message passing in the brain, consult (Buckley et al. 2017).
One notable attempt at marrying enactivism and computationalism with equal rights was made by Villalobos and Dewhurst (2018), who argue that a computational system can be autonomous. Assuming a more or less classical concept of autopoietic system (as opposed to active inference) as a model of enactment leads to a slightly weaker claim that the view defended here.
The argument should also work under the assumption of a semantic account of computation (e.g., Shagrir 2018). I focus on the mechanistic account, because it is dominant in the philosophy of cognitive science.
Strictly speaking, one does not need to evaluate free energy in order to minimize free energy. A more efficient implementation would just compute the gradients of free energy (with respect to internal and action states) and indeed most of the message passing involved in vanilla perception does not actually evaluate free energy—only its gradients. The pseudocode above is meant for illustration only. I am grateful to the anonymous reviewer for pointing this out.
This is at the heart of mathematical formulations of universal computation. Clear examples here include Solomonoff induction (Solomonoff 1964), based upon the minimization of Kolmogorov complexity. Indeed, some formulations of variational free energy minimization appeal explicitly to algorithmic complexity and the same sort of mathematics that underlies universal computation.
Following Miłkowski (2016b), I distinguish between integration and unification. Unification is the process of developing general (in the sense of an unbounded scope), simple, elegant explanations, while integration is the process of combining multiple explanations in a coherent manner. FEP is not a unified framework in this sense, but it seems to do a particularly good job in integrating various approaches to life and cognition.
References
Allen, M. (2018). The foundation: Mechanism, prediction, and falsification in Bayesian enactivism. Physics of Life Reviews, 24, 17–20. https://doi.org/10.1016/j.plrev.2018.01.007.
Allen, M., & Friston, K. J. (2018). From cognitivism to autopoiesis: Towards a computational framework for the embodied mind. Synthese, 195(6), 2459–2482. https://doi.org/10.1007/s11229-016-1288-5.
Arnellos, A., Spyrtou, T., & Darzentas, I. (2010). Towards the naturalization of agency based on an interactivist account of autonomy. New Ideas in Psychology, 28(3), 296–311.
Baltieri, M., & Buckley, C. L. (2017). An active inference implementation of phototaxis. In Proceedings of the 14th European conference on artificial life ECAL 2017 (pp. 36–43). https://doi.org/10.7551/ecal_a_011
Barandiaran, X. E., Di Paolo, E., & Rohde, M. (2009). Defining agency: Individuality, normativity, asymmetry, and spatio-temporality in action. Adaptive Behavior, 17(5), 367–386. https://doi.org/10.1177/1059712309343819.
Barandiaran, X., & Moreno, A. (2006). On what makes certain dynamical systems cognitive: A minimally cognitive organization program. Adaptive Behavior, 14(2), 171–185. https://doi.org/10.1177/105971230601400208.
Barandiaran, X., & Moreno, A. (2008). Adaptivity: From metabolism to behavior. Adaptive Behavior, 16(5), 325–344. https://doi.org/10.1177/1059712308093868.
Barbaras, R. (2002). Francisco Varela: A new idea of perception and life. Phenomenology and the Cognitive Sciences, 1(2), 127–132. https://doi.org/10.1023/A:1020332523809.
Bennett, C. H. (1982). The thermodynamics of computation—A review. International Journal of Theoretical Physics, 21(12), 905–940. https://doi.org/10.1007/BF02084158.
Bickhard, M. H. (2008). Emergence: Process organization, not particle configuration. Cybernetics and Human Knowing, 15(3–4), 57–63.
Bickhard, M. H. (2009). The biological foundations of cognitive science. New Ideas in Psychology, 27(1), 75–84. https://doi.org/10.1016/j.newideapsych.2008.04.001.
Bishop, C. M. (2006). Pattern recognition and machine learning. New York: Springer.
Botvinick, M., & Toussaint, M. (2012). Planning as inference. Trends in Cognitive Sciences, 16(10), 485–488. https://doi.org/10.1016/j.tics.2012.08.006.
Bourgine, P., & Stewart, J. (2004). Autopoiesis and cognition. Artificial Life, 10(3), 327–345. https://doi.org/10.1162/1064546041255557.
Brier, S. (1995). Cyber-semiotics: On autopoiesis, code-duality and sign games in bio-semiotics. Cybernetics & Human Knowing, 3(1), 3–14.
Bruineberg, J., Kiverstein, J., & Rietveld, E. (2016). The anticipating brain is not a scientist: The free-energy principle from an ecological-enactive perspective. Synthese. https://doi.org/10.1007/s11229-016-1239-1.
Bruineberg, J., & Rietveld, E. (2014). Self-organization, free energy minimization, and optimal grip on a field of affordances. Frontiers in Human Neuroscience. https://doi.org/10.3389/fnhum.2014.00599.
Buckley, C. L., Kim, C. S., McGregor, S., & Seth, A. K. (2017). The free energy principle for action and perception: A mathematical review. Journal of Mathematical Psychology, 81, 55–79. https://doi.org/10.1016/j.jmp.2017.09.004.
Calvo, P., & Friston, K. (2017). Predicting green: Really radical (plant) predictive processing. Journal of the Royal Society, Interface, 14(131), 20170096. https://doi.org/10.1098/rsif.2017.0096.
Chrisley, R. (2000). Transparent computationalism. In M. Scheutz (Ed.), New computationalism: Conceptus-Studien 14 (pp. 105–121). Sankt Augustin: Academia Verlag.
Christensen, W. D., & Hooker, C. A. (2000). Autonomy and the emergence of intelligence: Organised interactive construction. Communication and Cognition-Artificial Intelligence, 17(3–4), 133–157.
Clark, A. (2016). Surfing uncertainty: Prediction, action, and the embodied mind. Oxford: Oxford University Press.
Clark, A. (2017). How to knit your own Markov blanket: Resisting the second law with metamorphic minds. In T. Metzinger & W. Wiese (Eds.), Philosophy and Predictive Processing, 3. Frankfurt am Main: MINDGroup. https://doi.org/10.15502/9783958573031.
Collier, J. (2004). Self-organization, Individuation and Identity. Revue Internationale de Philosophie, 2, 151–172.
Collier, J. (2008). A dynamical account of emergence. Cybernetics and Human Knowing, 15(3–4), 75–86.
Colombo, M., & Wright, C. (2018). First principles in the life sciences: The free-energy principle, organicism, and mechanism. Synthese. https://doi.org/10.1007/s11229-018-01932-w.
Di Paolo, E. A. (2005). Autopoiesis, adaptivity, teleology, agency. Phenomenology and the Cognitive Sciences, 4(4), 429–452. https://doi.org/10.1007/s11097-005-9002-y.
Di Paolo, E. (2009). Extended life. Topoi, 28(1), 9–21. https://doi.org/10.1007/s11245-008-9042-3.
Emmeche, C. (1997). Defining life, explaining emergence. http://www.nbi.dk/~emmeche/cePubl/97e.defLife.v3f.html.
Fleischaker, G. R. (1988). Autopoiesis: The status of its system logic. Biosystems, 22(1), 37–49. https://doi.org/10.1016/0303-2647(88)90048-2.
Friston, K. (2018). Am I self-conscious? (Or does self-organization entail self-consciousness?). Frontiers in Psychology. https://doi.org/10.3389/fpsyg.2018.00579.
Friston, K., Adams, R., & Montague, R. (2012). What is value—Accumulated reward or evidence? Frontiers in Neurorobotics. https://doi.org/10.3389/fnbot.2012.00011.
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., & Pezzulo, G. (2017). Active inference: A process theory. Neural Computation, 29(1), 1–49. https://doi.org/10.1162/NECO_a_00912.
Friston, K., Levin, M., Sengupta, B., & Pezzulo, G. (2015a). Knowing one’s place: A free-energy approach to pattern regulation. Journal of the Royal Society, Interface, 12(105), 20141383. https://doi.org/10.1098/rsif.2014.1383.
Friston, K., Rigoli, F., Ognibene, D., Mathys, C., Fitzgerald, T., & Pezzulo, G. (2015b). Active inference and epistemic value. Cognitive Neuroscience, 6(4), 187–214. https://doi.org/10.1080/17588928.2015.1020053.
Froese, T., & Stewart, J. (2010). Life after Ashby: Ultrastability and the autopoietic foundations of biological autonomy. Cybernetics and Human Knowing, 17(4), 7–49.
Hoffmeyer, J. (1998). Surfaces inside surfaces. On the origin of agency and life. Cybernetics & Human Knowing, 5(1), 33–42.
Hoffmeyer, J. (2000). The biology of signification. Perspectives in Biology and Medicine, 43(2), 252–268. https://doi.org/10.1353/pbm.2000.0003.
Hohwy, J. (2013). The predictive mind. Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199682737.001.0001.
Hutto, D. D., & Myin, E. (2012). Radicalizing enactivism: Basic minds without content. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/9780262018548.001.0001.
Huys, Q. J. M., Maia, T. V., & Frank, M. J. (2016). Computational psychiatry as a bridge from neuroscience to clinical applications. Nature Neuroscience, 19(3), 404–413. https://doi.org/10.1038/nn.4238.
Kauffman, S. A. (1993). The origins of order: Self-organization and selection in evolution. New York: Oxford University Press.
Kirchhoff, M. D. (2016). Autopoiesis, free energy, and the life–mind continuity thesis. Synthese. https://doi.org/10.1007/s11229-016-1100-6.
Kirchhoff, M. D., & Froese, T. (2017). Where there is life there is mind: In support of a strong life-mind continuity thesis. Entropy, 19(4), 169. https://doi.org/10.3390/e19040169.
Kirchhoff, M., Parr, T., Palacios, E., Friston, K., & Kiverstein, J. (2018). The Markov blankets of life: Autonomy, active inference and the free energy principle. Journal of the Royal Society, Interface, 15(138), 20170792. https://doi.org/10.1098/rsif.2017.0792.
Kirchhoff, M. D., & Robertson, I. (2018). Enactivism and predictive processing: A non-representational view. Philosophical Explorations, 21(2), 264–281. https://doi.org/10.1080/13869795.2018.1477983.
Korbak, T. (2015). Scaffolded minds and the evolution of content in signaling pathways. Studies in Logic, Grammar and Rhetoric. https://doi.org/10.1515/slgr-2015-0022.
Maturana, H. R., & Varela, F. J. (1980). Autopoiesis and cognition: The realization of the living. Dordrecht: D. Reidel Pub. Co.
Miłkowski, M. (2013). Explaining the computational mind. Cambridge, MA: MIT Press.
Miłkowski, M. (2016a). A mechanistic account of computational explanation in cognitive science and computational neuroscience. In V. C. Müller (Ed.), Computing and philosophy (pp. 191–205). Cham: Springer. https://doi.org/10.1007/978-3-319-23291-1_13.
Miłkowski, M. (2016b). Unification strategies in cognitive science. Studies in Logic, Grammar and Rhetoric, 48(1), 13–33. https://doi.org/10.1515/slgr-2016-0053.
Millikan, R. G. (2005). Language: A biological model. Oxford: Oxford University Press.
Moreno, A., & Etxeberria, A. (2005). Agency in natural and artificial systems. Artificial Life, 11(1–2), 161–175. https://doi.org/10.1162/1064546053278919.
Oaksford, M., & Chater, N. (2007). Bayesian rationality: The probabilistic approach to human reasoning. Oxford: Oxford University Press.
Pearl, J. (2000). Causality: Models, reasoning, and inference. New York: Cambridge University Press.
Ramstead, M. J. D., Badcock, P. B., & Friston, K. J. (2018). Answering Schrödinger’s question: A free-energy formulation. Physics of Life Reviews, 24, 1–16. https://doi.org/10.1016/j.plrev.2017.09.001.
Ramstead, M. J. D., Kirchhoff, M. D., Constant, A., & Friston, K. J. (2019). Multiscale integration: Beyond internalism and externalism. Synthese. https://doi.org/10.1007/s11229-019-02115-x.
Rosen, R. (1991). Life itself: A comprehensive inquiry into the nature, origin, and fabrication of life. New York: Columbia University Press.
Ruiz-Mirazo, K., & Moreno, A. (2004). Basic autonomy as a fundamental step in the synthesis of life. Artificial Life, 10(3), 235–259. https://doi.org/10.1162/1064546041255584.
Ruiz-Mirazo, K., Peretó, J., & Moreno, A. (2004). A universal definition of life: Autonomy and open-ended evolution. Origins of Life and Evolution of the Biosphere: The Journal of the International Society for the Study of the Origin of Life, 34(3), 323–346.
Seth, A. (2015). The cybernetic Bayesian brain — from interoceptive inference to sensorimotor contingencies. In T. Metzinger & J. M. Windt (Eds.), Open MIND: 35(T). Frankfurt am Main: MIND Group. https://doi.org/10.15502/9783958570108.
Shagrir, O. (2018). In defense of the semantic view of computation. Synthese. https://doi.org/10.1007/s11229-018-01921-z.
Sheets-Johnstone, M. (2000). The formal nature of emergent biological organization and its implications for understandings of closure. Annals of the New York Academy of Sciences, 901, 320–331.
Sims, A. (2016). A problem of scope for the free energy principle as a theory of cognition. Philosophical Psychology, 29(7), 967–980. https://doi.org/10.1080/09515089.2016.1200024.
Skyrms, B. (2010). Signals: Evolution, learning, & information. Oxford: Oxford University Press.
Solomonoff, R. J. (1964). A formal theory of inductive inference. Part I. Information and Control, 7(1), 1–22. https://doi.org/10.1016/S0019-9958(64)90223-2.
Still, S., Sivak, D. A., Bell, A. J., & Crooks, G. E. (2012). Thermodynamics of Prediction. Physical Review Letters. https://doi.org/10.1103/PhysRevLett.109.120604.
Thompson, E., & Stapleton, M. (2009). Making sense of sense-making: Reflections on enactive and extended mind theories. Topoi, 28(1), 23–30. https://doi.org/10.1007/s11245-008-9043-2.
van Rooij, I. (2008). The tractable cognition thesis. Cognitive Science: A Multidisciplinary Journal, 32(6), 939–984. https://doi.org/10.1080/03640210801897856.
van Rooij, I., Wright, C. D., Kwisthout, J., & Wareham, T. (2018). Rational analysis, intractability, and the prospects of ‘as if’-explanations. Synthese, 195(2), 491–510. https://doi.org/10.1007/s11229-014-0532-0.
Villalobos, M., & Dewhurst, J. (2018). Enactive autonomy in computational systems. Synthese, 195(5), 1891–1908. https://doi.org/10.1007/s11229-017-1386-z.
Virgo, N., Egbert, M. D., & Froese, T. (2011). The role of the spatial boundary in autopoiesis. In G. Kampis, I. Karsai, & E. Szathmáry (Eds.), Advances in artificial life. Darwin Meets von Neumann (Vol. 5777, pp. 240–247). New York: Springer. https://doi.org/10.1007/978-3-642-21283-3_30.
Acknowledgements
The author thanks Marcin Miłkowski and two anonymous reviewers for helpful comments on earlier versions of this paper.
Funding
This research was funded by the Ministry of Science and Higher Education (Poland) research Grant DI2015010945 as part of “Diamentowy Grant” program.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Korbak, T. Computational enactivism under the free energy principle. Synthese 198, 2743–2763 (2021). https://doi.org/10.1007/s11229-019-02243-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02243-4