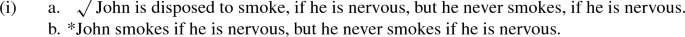Natural kinds and dispositions: a causal analysis

Abstract

Objects have dispositions. Dispositions are normally analyzed by providing a meaning to disposition ascriptions like ‘This piece of salt is soluble’. Philosophers like Carnap, Goodman, Quine, Lewis and many others have proposed analyses of such disposition ascriptions. In this paper we will argue with Quine (‘Natural Kinds’, 1970) that the proper analysis of ascriptions of the form ‘x is disposed to m (when C)’, where ‘x’ denotes an object, ‘m’ a manifestation, and ‘C’ a condition, goes like this: (i) ‘x is of natural kind k’, and (ii) the generic ‘ks are m (when C)’ is true. For the analysis of the generic, we propose an analysis in terms of causal powers: ‘ks (when C) have the causal power to m’. The latter, in turn, is analyzed in a very precise way, making use of Pearl’s probabilistic graphical causal models. We will show how this natural kind-analysis improves on standard conditional analyses of dispositions by avoiding the standard counterexamples, and that it gives rise to precise observable criteria under which the disposition ascription is true.

1 Introduction

Talk of dispositions is omnipresent, not only in our everyday life, but also in scientific discourse. Ellis and Lierse (1994) argue that almost all fundamental properties in science are dispositional. Whether a particle is an electron, for instance, can only be determined in terms of how it is disposed to interact with fields and with other particles. Dispositions can be ascribed making use of predicates with explicit signs such as the suffixes ‘-able’ or ‘-ible’. However, many ordinary predicates whose morphology contains no such suffix have nevertheless a dispositional meaning, like ‘fragile’, or ‘poisonous’. Some examples of disposition ascriptions are given below:

Goodman (1954) even claims that almost all predicates have a dispositional meaning, including examples like ‘is red’. In contrast to episodic sentences like ‘This piece burns now’ or ‘This cube is dissolving in water now’, disposition sentences ascribe stable and enduring properties to objects. Whether or not an object has a dispositional property cannot be easily verified or falsified by simple observation, for something can be water soluble though it never comes into contact with water. Partly for that reason they have received a lot of attention in philosophy.¹ Nonetheless, philosophers like Carnap (1936), Ryle (1949) and Goodman (1954) proposed to analyze disposition ascriptions in terms of observable, or behavioral, terminology after all, suggesting a conditional analysis. Carnap (1936–1937) proposed that a sentence like (1-c) ‘This cube is water soluble’ should be analyzed in terms of a stimulus and a manifestation condition. The manifestation condition is what you can, or will, observe, while the stimulus condition states the condition under which the observational property will be manifested. The manifestation condition for ‘This cube is water soluble’, for example, is the cube’s’ dissolution, and the stimulus condition is ‘being immersed in water’.

In Sect. 2 of this paper we will see that such a conditional analysis is anything but straightforward. Our own analysis will be based on the fact that many disposition ascriptions are about (natural) kinds, rather than about individual objects. In fact, to each of the individual disposition statements in (1-a)–(1-e), there corresponds a disposition statement involving natural kinds:

This gives rise to another intuition, going back to Quine (1970):

Intuitively, what qualifies a thing as soluble though it never gets into water is that it is of the same kind as the things that did or will dissolve. (Quine 1970, ‘Natural Kinds’, p. 16)

According to Quine’s suggestion, x has a certain disposition if and only if x is of natural kind k and objects of kind k show manifestation m (under condition C). We will argue in Sect. 3 in favor of such an analysis, following authors like Fara (2005) and Manley and Wasserman (2007, 2008) making use of habituals, or generics, to account for disposition ascriptions. In Sect. 4 we want to go beyond the latter analyses by basing our proposal on a very precise comparative analysis of generic sentences. In Sect. 5 we will ground this analysis of disposition ascriptions on a causal relation between the natural kind and the manifestation. We will do this by making use of Pearl’s (2000) causal model theory, relating our analysis to the traditional idea that dispositions are, or involve, causal powers. In the end, our analysis proposes to analyze sentences like (1-a) and (1-b) as follows:

We will argue that such an analysis will be less mysterious than it may look at first by showing how, and under which circumstances, dispositional ascriptions can be empirically tested after all.

2 A conditional analysis

Carnap (1936–1937) proposed a conditional analysis of disposition ascriptions. According to it, ‘This cube is water soluble’ is true just in case this cube dissolves, if, or when, it is immersed in water. It was soon recognized that this conditional analysis cannot be worked out making use of the material conditional (because this conditional is true if the antecedent is false), or any other extensional connective (e.g. Burks 1955). Goodman (1954) suggested the natural alternative: making use of counterfactual conditionals: x is soluble iff x would dissolve if it were immersed in water. Similarly, this sample of liquid is poisonous, means that someone would die, if she would drink it. Following Lewis’ (1973a) analysis of counterfactual conditionals, this would mean that x has the disposition of being soluble iff x dissolves in all most similar worlds to the actual one where x is immersed in water.

2.1 Standard worries involving mimicking and masking

Unfortunately, Goldman (1970), Martin (1994), Johnston (1992) and others show that this simple conditional analysis has some immediate counterexamples. First, although the object intuitively doesn’t have the relevant disposition, the conditional could still be true. This is a case where the behavior of an object that does have the disposition is mimicked.² A fish deep in the ocean that is blue, for instance, doesn’t have the disposition to look red. But the fish could be such that if you shine a light on it, it changes such that it looks red. Other examples can be constructed showing that the true disposition can be masked. Although this sample of liquid is poisonous, that doesn’t mean that you always would die when you drank it. It could be that if you water down this sample enough, you would survive. Lewis (1997) proposed to rescue the simple conditional analysis by excluding cases where the internal structure of the object changes during the process of inducing the manifestation. He excludes such changes roughly as follows, by appealing to intrinsic properties of the object:

• x is disposed to m when C iff x has an intrinsic property B such that, if it were the case that C, and if x were to retain B for a sufficient time, then x would have property m.

Whether or not Lewis’s proposal gets rid of the above counterexamples, Johnston (1992) and others show that this more sophisticated conditional analysis still won’t do, because not only internal, but also external conditions can change. Although intuitively this liquid is poisonous because it would normally kill you by drinking it, it does not do so if you have taken an antidote before (Bird 1998). Again, there exist counterexamples of the opposite nature as well, examples showing that some dispositional properties could be mimicked (cf. Smith 1977) by external circumstances. Although diamonds aren’t considered to be flammable, and neither is this one, with extreme heat diamonds will burn after all.³

When confronted with such counterexamples, there are always two ways to go. First, one can try to save the analysis by providing more specific conditions under which the to be observed effect, or manifestation, will show. As observed by Fara (2005) and others, however, this move is problematic for two closely related reasons: (i) it is doubtful whether it possible to spell out the content of this more specific ceteris paribus clause; (ii) if it is possible at all, the challenge is how to save the resulting analysis from being vacuous, or circular. An alternative strategy would be to weaken the conditional analysis.

One way to weaken the conditional analysis is to appeal to normality. Instead of demanding that x would be, or show, m in all most similar worlds where C would be true, one only demands that x would be m in all most normal worlds where C would be true (Mourreau 1997; Bonevac et al. 2011).⁴ In this way, all of the counterexamples could be explained away as being abnormal. Although formally appealing, and in line with much work on non-monotonic logic, we find this proposal conceptually wanting. Without a more elaborate story of what it means to be a normal C-world it is unclear what will be predicted. The danger of spelling out the appropriate normality conditions is obvious: how to avoid the analysis from becoming vacuously true?⁵ A, we feel, more attractive way to weaken the conditional analysis will be discussed in the next section.

2.2 Towards a generic conditional analysis, with natural kinds

How do we know, or believe, that this mushroom is edible, given that it was never eaten before? Most naturally because of an inductive inference: this mushroom is like other mushrooms from which people did not die, when they ate it. So, you wouldn’t die from eating this mushroom either. How come that this mushroom is like these other mushroom? Here we appeal to Lewis’s (1997) intuition: because they share the same intrinsic property. For reasons like this, Fara (2005) argues for the following analysis:

• x is disposed to m when C if and only if x has an intrinsic property in virtue of which it ms when C.

We think that at least for the examples discussed in the introduction, the intrinsic property is always a natural kind.⁶ This mushroom is like these other mushrooms, because they are of the same natural kind: being a chanterelle. Thus, ‘This mushroom is edible’ is true because, (i) it is a chanterelle and (ii) one doesn’t die because of eating a chanterelle. As a result, the analysis reduces to

• x is disposed to m when C iff x is of natural kind k such that x ms when C in virtue of belonging to kind k.

Something close to this was proposed as well by Lowe (2001). Also his analysis relies on the meaning of ‘A k ms when C’, or more explicitly on ‘An object of natural kind k shows manifestation m when C’. According to Lowe (2001), the generic ‘Benzene is flammable’ means that benzene burns when put to fire, which holds because this is a natural law. Lowe argues that although ‘Benzene burns when put to fire’ is (or follows from) a law, this doesn’t mean that all samples of benzene always burn if put to fire, it only means that such samples tend to burn in these circumstances. In this way he claims to have saved his analysis from the standard counterexamples of the conditional analysis involving mimicking and masking. Although we are not unsympathetic to such a proposal, we would like to see a more insightful answer to the question what it means that, for instance, benzene burns when put into fire, or that one doesn’t die from eating a chanterelle, if these laws allow for exceptions.

Fara (2005) provides such a more principled answer by proposing that ‘ks are m when C’ should be analyzed as an habitual, or a generic. For instance, for the habitual ‘John smokes, if he is nervous’ to be true, it is not required that John always smokes when he is nervous. The same holds for habituals, or generics, involving natural kinds, like ‘Benzene burns when put into fire’. Fara argues that because habituals and generics tolerate exceptions, such an analysis can account for the counterexamples involving mimicking and masking. Unfortunately, Fara (2005) doesn’t provide any specific treatment of generics his analysis depends on. We agree with Fara that an analysis of dispositional statements in terms of generics is promising. But we also agree with Yli-Vakkuri (2010) and others that without a specific treatment of generics, or without one that is sufficiently different from an analysis of counterfactuals, we can’t be satisfied with Fara’s proposal as it stands.

2.3 Structural worries about the conditional analysis

Whether or not an appeal to normality, habituals and generics can save a conditional analysis from the standard masking and mimicking counterexamples, we agree with Manley and Wasserman (2007, 2008) and Vetter (2013) that the conditional analysis faces other problems that cannot be ‘solved’ so easily. First, as noted by Manley and Wasserman (2007), disposition ascriptions can be stated in comparative form, (4-a), and they can involve gradability, (4-b).

They note that this is a problem for conditional approaches, because the truth-conditions of counterfactual conditionals don’t allow for the consequent to hold to more or less of a degree.

One might think that comparative and gradable disposition statements are easy to account for on a conditional analysis. After all, Lewis (1973b) makes use of a notion of comparative similarity to account for his counterfactuals. Although for counterfactuals he uses only the most similar worlds that make the antecedent true, one might think that less similar worlds could still be used to interpret comparative dispositional statements, or disposition statements involving degrees. Likewise for an analysis in terms of normality. Example (4-a) can then be analyzed as being true, for instance, because when it would be put into fire, x would burn in more similar worlds to the actual one, or in more ‘normal’ worlds, than y would. Unfortunately, such an analysis would give rise to the consequence that because (4-a) is considered to be true, ‘y is flammable’ is predicted to be false, because the counterfactual ‘y would burn, if put into fire’ would then be false. But this prediction seems much too strong, which falsifies the straightforward proposal under discussion.⁷

But perhaps this seemingly false conclusion could be saved by an appeal to context. Perhaps all that comparative and gradable disposition ascriptions show is that the truth of disposition statements are context dependent. Indeed, as pointed out by Vetter (2013), in the context of aeronautics, many more things will be seen as ‘fragile’ than in more ordinary contexts. Some linguists have proposed (cf. Kamp 1975; Klein 1980) to reduce gradability to comparatives, and the analysis of comparatives, in turn, to context dependence. So perhaps the conditional analysis may be saved in this way from the threat of comparative and graded dispositions statements. Perhaps—but we feel that this kind of savior would be rather unnatural.

Another possible way to account for comparative and gradable disposition ascriptions on a conditional analysis would be to make use of probabilities. Just like many authors feel it is natural to account for indicative conditionals making use of standard conditional probabilities, one might make use of counterfactual conditional probabilities to account for the intuition that if an antecedent would hold, then one consequent would be more likely than another. On such a proposal, the acceptance of (4-a) ‘x is more flammable than y’ need not give rise to the counterintuitive conclusion that y is not flammable. Indeed, we will make a related proposal ourselves later in this paper. But what, on such a proposal, would make it the case that ‘x is flammable’ is accepted? It cannot be that x would burn in all relevant worlds where it would be put in fire, for then the undesirable consequence that y is not flammable would follow after all. Perhaps one can get rid of the problem if one rejects the idea that counterfactual conditionals have truth conditions in the first place, or by proposing that a counterfactual is true if the probability that the consequent would be true if the antecedent would hold is greater than the probability that the consequent is not true. Perhaps—but we wonder how many proponents of the conditional analysis of dispositions would accept any of these consequences for the analysis of counterfactual conditionals.

A natural idea would be to (i) argue with Fara (2005) that a disposition statement like ‘x is flammable’ should be analyzed in terms of a generic, and (ii) that generics should be accounted for in terms of (counterfactual) conditional probabilities. This is a natural proposal, because generics allow for exceptions. It is thus only natural to propose that a generic can be true even though the relevant conditional probability is less than 1. We will see later that, indeed, a proposal along these lines was given by Manley and Wasserman (2007, 2008) and will be given by us as well. But before we come to that, let us first discuss an additional motivation for a treatment of disposition statements like this: the fact that dispositions don’t seem to come with a single stimulus condition. Manley and Wasserman (2007, 2008) suggest that this is another structural problem for the conditional analyses, and this point is strengthened by arguments due to Vetter (2013, 2014).

2.4 Multi- and zero-track dispositions

Ellis and Lierse (1994) already pointed out that most dispositions cannot be characterized by a single conditional:⁸

In the simplest cases, dispositions are said to be single-track. That is, they can manifest themselves in only one kind of circumstance, and then only in one kind of way. Such dispositions are characterized by a single subjunctive conditional. More often than not, however, dispositions are multi-track. That is, they can reveal their presence in a range of antecedent circumstances, yielding a range of different consequent events. Fragility is obviously a multi-track disposition, for a fragile object can manifest this disposition in a wide range of antecedent circumstances: for instance, after being dropped, knocked, struck, stretched, or compressed, resulting in such effects as shattering, cracking, splintering, rupturing, or cleaving. Consequently, to specify fully the meaning of a multi-track dispositional term like ’fragility’, it is necessary to enumerate the full list of subjunctive conditionals which operationally define the term.

Multitrack-dispositions pose a problem—independent of the problems of mimicking and masking—for the thought that the disposition of x can be characterized by the single conditional ‘If x were in condition C, then x would have, or show manifestation m’, because it falsely predicts that x has m only if C. Manley and Wasserman argue that to save the conditional analysis (that doesn’t make use of probabilities), we would need to think of a disposition as correlated with a non-denumerably infinite number of conditionals, each of which specifies in its antecedent a ‘fully specific scenario that settles everything causally relevant to the manifestation of the disposition’ (Manley and Wasserman 2007, p. 72). It is hard to imagine that such an infinite set of conditionals could state the meaning of disposition statements. But the problem is worse. As noted by Fara (2005) , some disposition statements do not mention conditions at all:

I may be disposed to stutter, my drainpipe disposed to leak, and Mr. Magoo disposed to bump into things. Conditional accounts do not even apply to such cases, since they contain nothing to serve as antecedents to a conditional. (Fara 2005, p. 70)

According to Manley and Wasserman (2008) this is so, because the dispositions themselves are non-conditional:

there are plenty of dispositions that do not have any particular stimulus condition. Suppose someone is highly disposed to talk, but there is no particular kind of situation that elicits this response in him. He is disposed to talk when happy, when sad, with others or by himself—he is just generally loquacious [...]. We are not given an ascription of the form ‘x is disposed to give m in C’, we are only given ‘x is disposed to m’ [...]. So with nothing to put in place of ‘C’, how can we construct a conditional of the form ‘x would m if C’? (Manley and Wasserman 2008, pp. 72f)⁹

Vetter (2013) argues that the problem is more general: all dispositions are multi-track dispositions. Even if there seems to be only one condition, the condition is, in fact, still multi-track. Consider the disposition of being fragile as analyzed by ‘to break if struck’. The problem is that one can strike the vase with more or less power. If we want to analyze fragility in terms of a single condition, we have to make a choice on the desired power with which it should be struck. But, intuitively, we don’t associate one strength of hitting with fragility, or the predicate ‘fragile’, in general: for different types of objects we think of different strengths.

Vetter (2013) convincingly argues that there is no way to reduce ‘apparent’ multi-track dispositions to single-track dispositions, such that they could be analyzed by a single condition. In case one specific stimulus condition is singled out as the defining one for manifestation, it is wrongly predicted that x does not manifest the disposition in case x shows m in any of the other conditions. And in case all the conditions are combined in one large disjunctive condition, the condition might be too weak. Because fragility might have different stimulus conditions for different types of objects, it might be that this vase will not break under condition $c_1$, but only under conditions $c_2$ and $c_3$, although $c_1$ does make the disjunctive condition $c_1 \vee c_2 \vee c_3$ true.

3 Manley and Wasserman’s and Vetter’s proposals

Having argued against the standard conditional analysis, Manley and Wasserman (2007, 2008) and Wasserman (2011) propose that the conditional analysis should be restated in a radically different way, while Vetter (2013, 2014) proposes that dispositions are not conditional at all. We will now discuss these proposals in turn.

Manley and Wasserman’s (2008) first suggest to change the standard conditional analysis of disposition statements as follows:

• x is disposed to m when C if and only if x would m in most C-cases.

The use of ‘most’, obviously, helps to account for the standard counterexamples to conditional analyses: mimics and masks are only counterexamples if it is demanded that x is m in all selected C-cases. To account for multi-track dispositions, this analysis requires that x satisfies most of a huge list of counterfactuals of the form ‘x would m if it were in c-$\hbox {case}_n$’, rather than that it demands that ‘x would mostly m if it were in a $c_1 \vee \cdots c_n$-case’. Thus, ‘most’ has wide scope over the disjunction of C-cases. Notice that this analysis differs from a seemingly similar analysis that they criticized before (as discussed in the previous section): their own proposal does not demand that each of the $c_n$ cases ‘fully specifies a scenario that settles everything causally relevant to the manifestation of the disposition’. Their use of ‘most’, they argue, allows them to do so. However, they argue that this analysis is still too strong: an illness can be disposed to spread upon contact, even if in most situations of contact with an afflicted it would not be contracted. They argue that different dispositional predicates may require different proportions of the relevant C-cases in which the dispositional property manifests itself. For this reason, they instead make the following proposal:

• x is disposed to m when C if and only if x would m in some suitable proportion of C-cases.

In Wasserman (2011)a very similar proposal is made:

• x is disposed to m when C if and only if x would m in many C-cases.

Manley and Wasserman (2008) and Wasserman (2011) show that with such an analysis, not only multi-track dispositions can be accounted for, but that comparative and gradable dispositions ascriptions can be handled in this way easily too. The ascription ‘x is more disposed to m than y’, for instance, is true just in case x would m in more C-cases than y would. We agree with the latter claim, and also think that standard disposition ascriptions should be accounted for along the lines that they suggest. However, we also think that their analyses by themselves are not very insightful. Their (closely related) proposals of disposition statements are just too vague for that. They claim that the analysis is less vague than it sounds, because what counts as a ‘suitable proportion’, or what counts as ‘many’, can be determined by context. Unfortunately, nearly nothing is said about how these suitable proportions, or of what counts as ‘many’, depend on context. This underspecification makes the proposals not only hard to falsify, but also hard, if not impossible, to evaluate. In any case, their reliance on context-dependence is somewhat surprising, given that they claimed before that what counts as a suitable proportion might depend on the dispositional predicate. Indeed, we think this is what should be taken into account more seriously.

Whereas Manley & Wasserman’s (2008) and Wasserman’s (2011) proposals are still conditional in form, and rather vague, Vetter (2014) derives a drastic conclusion from the arguments given in the previous section, and comes up with a specific proposal. The drastic conclusion she proposes is to radically reject the conditional analysis: we should not analyze dispositions conditionally like ‘x is disposed to m, if C’, but we should analyze them non-conditionally, simply as ‘x is disposed to m’. Thus, she proposes that dispositions are individuated by their manifestations alone. But how many times, or under which circumstances, do they have to show their manifestations for the disposition statement to be true? Her specific proposal is to count ‘x is disposed to m’ as true exactly if it is possible for x to m.¹⁰ She proposes to account for comparative disposition ascriptions as follows: x would m in more of the relevant situations than y would. A similar analysis is proposed for dispositions involving gradability.

Vetter’s (2013, 2014) proposal is much less demanding than any analysis of dispositions discussed so far. She provides several arguments for this weak analysis. First, in this way the standard counterexamples to conditional analyses can easily be accounted for: mimics and masks are only counterexamples if it is demanded that in all relevant cases x is m, not if it is only required that x is m in at least some relevant case. Second, she notes that in lexicography, the most natural paraphrases of disposition suffixes like ‘-able’ and ‘-ible’ is not in terms of conditionals, but rather in terms of possibility statements like ‘can’. According to the Oxford English Dictionary, for instance, ‘soluble’ is described as ‘able to be dissolved’ and ‘fragile’ as ‘liable to break or be broken’.

Even if some disposition ascriptions can be analyzed appropriately in terms of the mere possibility of its manifestation, it appears to be much too weak to account for all disposition ascriptions. As Manley and Wasserman (2011) imagined a similar proposal, they rejected it on these grounds.

For example, there will be contexts in which an atom does not count as disposed to remain stable even though it would remain stable in some much-higher-than-negligible proportion of nomologically possible situations. (Manley and Wasserman 2011, p. 1223)

Vetter (2014) argues, however, that this is not a good counterexample, because her analysis applies in the first instance to the disposition of being unstable. An analysis of this latter disposition in terms of possibility results in a necessarily-like analysis of its unnegated form stable, which seems appropriate. Moreover, she notes that what counts as relevant possibilities is context dependent. She agrees, though, that counterexamples to her analysis would be possible:

To pose a real threat to the possibility conception, an opponent would need to adduce a disposition which (i) is not plausibly construed as just the negative of some disposition, as (I have argued) stability or robustness is, and (ii) comes with a modality that is clearly stronger than a (mere or graded) possibility, and closer to necessity, of its manifesting. (Vetter 2014, p. 152)

We think counterexamples are easy to find. Take ‘soluble’. Whatever the Oxford English Dictionary tells us, it certainly is not the case that substance x is soluble already if it can be dissolved. If we would say that, just about any substance is soluble. Just consider a metal heated to the (almost) extreme. It will be a liquid, just about any substance will dissolve into. Or take fragile: just about any (kind of) object will break, if you struck it hard enough, etc.. Of course, Vetter (2014) could argue that these examples could be explained away, making use of the context dependence of what counts as a relevant possibility. But that reaction would make Vetter’s proposal much less specific than it seemed at first sight, and thus much less attractive. Moreover, the Oxford English Dictionary states something more about the meaning of dispositions like ‘fragile’ and ‘irascible’ than the mere possibility of its manifestation. It also claims, for instance, that something is ‘fragile’ if it can be ‘easily destroyed’. Similarly for someone being ‘irascible’, or ‘hot-tempered’: he or she has to be ‘easily provoked to anger or resentment’. But the demand that something is easily destroyed, or provoked, is something quite different from the demand that it can be destroyed or provoked. For members of kind k to be easily destroyed it has to be the case that they will, or would, be destroyed in more situations than members of alternative kinds $k', k^{''}, \cdots$ would be destroyed. What this suggests is that dispositions like being fragile and being hot-tempered demand a comparative analysis.

But we don’t have to rely on the ambiguity of what is claimed about the meaning of predicates like ‘fragile’ and ‘irascible’ in the Oxford English Dictionary to argue in favor of a comparative analysis of disposition ascription. First, as acknowledged by Vetter (2014) herself, there are dispositions that at least seem to pose a threat to her proposed analysis. Negative charge seems to be the disposition to attract positively charged particles and repel negatively charged ones. The opposite of being negatively charged is most naturally being positively charged. But to characterize any of those opposites in terms of what it can attract and repel seems much too weak. But there is a deeper worry. Disposition statements are not just statements that ascribe arbitrary properties to objects. Instead, they appear to ascribe characteristic properties of (kinds of) objects. A characterizing property of a (kind of) object is a property which sets it apart from other (kinds of) objects. At first one might think that a characteristic property of a kind of object is a property that all and only all objects of this natural kind possess. But that would be much too strong a requirement. Intuitively, one of the characterizing properties of fish, for instance, is that they (can) swim. But we all know that some other (kind of) animals can swim as well: humans and whales. Similarly, ‘flying’ is one of the characterizing properties of birds, even though some kinds of birds, i.e., penguins, don’t fly. In fact, for f to be a characteristic feature of natural kind k, not even the majority of ks have to have the property. Although ‘having manes’ is a characteristic property of lions, only adult male lions it them.

Characterizing sentences like ‘Fish swim’, ‘Birds fly’ and ‘Lions have manes’ that ascribe characteristic properties to groups of individuals are normally called ‘generic sentences’. If disposition statements ascribe characterizing properties to objects, it seems only natural to analyze such statements in terms of generics. We have seen above that Fara (2005) already proposed to do so, but that his analysis could not deal with the structural worries of other conditional analyses of dispositions. Manley and Wasserman (2008) and Wasserman (2011) proposed an analysis in terms of generics as well, that was constructed explicitly to account for the structural worries. But their accounts were much too unspecific.

In sum, we believe that Vetter’s (2013, 2014) possibility-based analysis of dispositions is too weak. x has the disposition to m not just because it can show manifestation m. Rather, it has this disposition because it shows this manifestation easily, i.e., more easily than other types of objects. We concluded from our discussion of her proposal that we should go for a comparative analysis of disposition statements. The proposals of Manley and Wasserman (2008) and Wasserman (2011), on the other hand, are too vague, or unspecific. Although we think that their analyses are on the right track, we would like to have a more specific proposal. We think it is possible to come up with such a more specific proposal when we take the conclusion from our discussion of Vetter’s proposal into serious account: the analysis has to be comparative. In the ideal case, we would like to have an analysis that is specific enough even to allow disposition statements to become empirically testable, as originally demanded by Carnap (1936). In the next sections we will propose a specific analysis that, we argue, not only can account for the various problems other analyses of dispositions face, but also is empirically testable under many circumstances.

4 A generic analysis using natural kinds

We propose that (1-a) ‘This drop of liquid is flammable’ is true, not just because this drop can burn when put in contact with fire, or that it would burn in suitably many occasions where one put it in contact with fire, but because this drop of liquid is of a kind such that it would burn under (significantly) more circumstances than a drop of (most) alternative types of liquid because of being of this kind. We will come to this analysis in three steps, which will be given below. The first step involves the semantics of characterizing, or generic, sentences.

Step one. Dispositions and characteristic properties We believe that disposition statements ascribe characteristic properties to (kinds of) objects. This feature they share with habitual and generic sentences. This already suggests that the proper analysis of disposition statements should be closely related with the proper analysis of generic sentences. The following are typical examples of generic sentences:

Although (most) generic sentences express inductive generalizations, the generic sentences (5-a) and (5-b) are true, even if not all birds fly, and less than half of the lions have manes. We believe that a property is characteristic of an object, or a natural kind, if we (have learned to) link the property with the object, or natural kind. Psychological research on learning shows that we (but also animals like rats, and pigeons) come to link a feature, or manifestation, m with a group of objects of natural kind k exactly if we observe that comparatively, or relatively, many ks have feature m. Relatively many ks have feature m exactly if the conditional probability of m given k, $P(m\mid k)$, is higher than the conditional probability of m given the set of individuals of all (relevant) alternative kinds, i.e.. $P(m\mid \bigcup Alt(k))$. Here Alt(k) stands for the natural kinds alternative to k, and $\bigcup Alt(k)$ thus for all individuals of these alternative natural kinds. Even though we will assume that Alt(k)—and thus $\bigcup Alt( k)$ as well—might depend on context, the kind dog will almost always be an alternative to the kind cat. Most naturally, alternative kinds to ‘kerosene’ for the interpretation of (2-a) are other kinds of liquids, and something similar holds for alternative kinds for the examples (2-b)–(2-e). In the rest of the paper we will abbreviate $\bigcup Alt(k)$ by $\lnot k$. Our above condition can thus be stated as $P(m\mid k) > P(m\mid \lnot k)$, which is equivalent with $P(m\mid k) - P(m\mid \lnot k) > 0$. In psychological learning theory, the measure $P(m\mid k) - P(m\mid \lnot k)$, is called the contingency of m given k, and denoted by $\Delta P^m_k$:

• $\Delta P^m_k \quad = \quad P(m\mid k) - P(m\mid \lnot k)$.

Vetter (2013) convinced us that some dispositions are non-conditional. Nevertheless, we feel that other dispositions should be given a conditional analysis after all. We believe that contingency counts for characteristic non-conditional dispositions. For conditional dispositions, it is conditional contingency that counts, i.e., the contingency with respect to condition C. This can be straightforwardly determined as follows:

• $\Delta P^m_{k,C} \quad = \quad P(m\mid k,C) - P(m\mid \lnot k,C)$.

On the basis of these considerations, it is natural to give a comparative analysis of characterizing, or generic, sentences. On our first go, (5-a) and (5-b) are true because compared to other types of animals, many birds fly and many lions have manes. Similarly, (5-c) is true, because compared to other people, John smokes many times when he is nervous. We have also argued above that dispositions statements should be analyzed in terms of generics. This brings us to the following provisional proposal (to be replaced in steps 2 and 3) for non-conditional and conditional dispositions, respectively:

• x is disposed to m iff x is of (some) natural kind k and (ii) ks are m.

• x is disposed to m if C iff x is of (some) natural kind k and ks are m, if C.

Intuitively, ‘ks are m’ and ‘ks are m, if C’ are true if ks relatively easily show manifestation m, or relatively easily show it under condition C, like we argued we should in the previous section. More formally, we propose that:

• ks are m just in case $\Delta P^m_k> \!\!> 0$, and

• ks are m, when C just in case $\Delta P^m_{k,C}> \!\!> 0$.         (where $x>\!\!> 0$ iff x is significantly above 0)

The analyses of non-conditional and conditional dispositions are obviously closely related, and we will discuss them from now on simultaneously. We can economically talk about both using parentheses:

• ks are m (when C) just in case $\Delta P^m_{k,(C)}> \!\!> 0$.

Our (provisional) proposal to analyze disposition ascription in terms of generics is not new. We have seen that Fara (2005) and Wasserman (2011), among others, proposed it as well to account for mimicking and masking dispositions. Indeed, just like these alternative proposals, ours also doesn’t have a problem with the standard counterexamples to conditional analyses of dispositions. What is new on our proposal is that (i) we also allow for non-conditional dispositions, (ii) our analysis of generics is comparative in nature, and (iii) our proposal is more specific. Our proposal is more specific because it provides a specific meaning of what it means to show m in many (C) situations: $P(m\mid k, (C))>\!\!> P(m\mid \lnot k, (C))$.

Because our proposed analysis of generics is explicitly comparative in nature, it is able to account for disposition statements involving comparatives and degrees. According to the analysis of generics in terms of $\Delta P^m_{k, (C)}$, the generic ‘ks are m (when C)’ is true if comparatively many ks have property m (when C). This, in turn, means that the conditional probability of individuals having property m given that they are of kind k, i.e. $P(m\mid k, (C))$, is significantly higher than the conditional probability of individuals having property m given that they are of an alternative natural kind, $P(m\mid \lnot k, (C))$. In terms of this it is easy to account for a comparative disposition statement as ‘x is more flammable than y’. The analysis would come down to the claim x is of a natural kind $k_1$ and y of a kind $k_2$ such that $k_1$s are more flammable than $k_2$s, i.e., $P(f\mid k_1, (C)) > P(f\mid k_2, (C))$.¹¹

Step two: A more sophisticated analysis Above we have made use of the experimental observation from learning theory that we learn to link m with ks, or with natural kind k, if, and only if $P(m\mid k)>\!\!> P(m\mid \lnot k)$. However, the stated condition sometimes gives rise to the wrong prediction: if $P(m\mid k) = 1$ and $P(m\mid \lnot k) \not = 1$, then the generic should intuitively be perfect, whatever the value of $P(m\mid \lnot k)$ will be, but this is not what comes out. This wrong prediction is a special case of another empirical observation that the proposal of step one cannot account for: that for learning there to be a link between k and m, $P(m\mid k)$ counts for more than $P(m\mid \lnot k)$. A natural way to account for that is to make use of Shep’s (1958) notion of ‘relative difference’, and assume that ‘ks are m (when C)’ is true iff $\Delta \!^* P^m_{k, (C)}$ is high, where the latter notion of relative difference is defined as follows:

• $\Delta \!^* P^m_{k, (C)} \,= \,\frac{\Delta P^m_{k, (C)}}{1 - P(m\mid \lnot k, (C))}$.

Notice that if, for instance, $P(m\mid k) = 1$ and $P(m\mid \lnot k) = 0.9$, then $\Delta \!^* P^m_k = \frac{P(m\mid k) -P(m\mid \lnot k)}{1 - P(m\mid \lnot k)} = \frac{1 - 0.9}{1 - 0.9} = 1$ which is the maximal value $\Delta \!^* P^m_k$ can receive. But also if $P(m\mid k) \not = 1$, the value of $\Delta \!^* P^m_k$ can be very high, accounting for the idea that generics allow for exceptions. Making use of measure $\Delta \!^* P^m_{k, (C)}$, we can now account for disposition statements as follows:

• x has the disposition to m (when C) iff x is of kind k, and $\Delta \!^* P^m_{k,(C)}$ is high.

Just like the analysis stated in step one, also the new analysis can immediately account for disposition statements involving comparatives and degrees. The reason is that $\Delta \!^* P^m_{k, (C)}$ is defined in terms of $\Delta P^m_{k, (C)}$, which is explicitly comparative.

Although we believe that the new proposal improves on the proposal stated in step one, it is still problematic for at least two closely related reasons. First, there is the problem of accidental patterns (Fara, 2005, 2011): the fact that disposition statements don’t seem to correspond exactly with habitual or generic sentences. On the one hand, the truth of a habitual statement doesn’t mean that the corresponding explicit disposition statement is true as well. According to Fara (2005) and Wasserman (2011), if a sorcerer makes it the case that every time that John is nervous, he will smoke, the habitual (6-a) is true, but the disposition statement (6-b) is not.¹²

Intuitively, the difference between the generic sentence (6-a) and the explicit dispositional sentence (6-b) is that the former is already true if there exists a regular pattern, while for the latter it needs to be the case that the pattern is caused by something within John internally. In fact, Fara (2005) and Wasserman (2011) argue that for the disposition statement there does not even have to exist a pattern.¹³ What this suggests is that an analysis of dispositions cannot be grounded solely on a frequency-based analysis of generics. The second problem of our second provisional proposal is that it does not predict that generics, or disposition ascriptions, support counterfactuals. But this seems to be required for a proper analysis. Indeed, in section 2.2 we argued that x is disposed to m (when C) not just when (i) x of kind k, and (ii) the generic ‘ks show m, when C’ is true, but rather when x of kind k such that x ms when C in virtue of belonging to kind k. What is missing of our analysis so far is an explication of what it means to show m (when C) in virtue of belonging to kind k.

We believe that our analysis of dispositions in terms of generics is appropriate only if the generic that it makes use of expresses a ‘principle connection’. Indeed, ‘This sugar lump dissolves in water’ is true, intuitively, because of, or in virtue of, what it is to be sugar, which involves the capacity, or power to dissolve in water, an inherent stable property of this sugar lump. Thus, we would reformulate our analysis as follows:

• x has the disposition to m iff x is of natural kind k, and the generic ‘ks are m (when C)’ is true because of a principle connection between (being of) kind k and manifestation m.

What remains to be done is to give an analysis of what it means for there to exist a ‘principle connection’. In the next section, in which we will describe the final step of our proposal, we will argue that this connection is normally a causal one.

5 A causal analysis

An analysis of dispositions in terms of the measures $\Delta P^m_{k, (C)}$ or $\Delta \!^* P^m_{k, (C)}$ is very Humean, built on frequency data and probabilistic dependencies and the way we learn from those. Many linguists and philosophers feel that there must be something more: something hidden underlying these actual dependencies that explains them. A most natural explanation is a causal one: the probabilistic dependencies exist in virtue of objective kinds which have causal powers, capacities or dispositions.¹⁴ Indeed, traditionally philosophers have assumed that the natural world is objectively divided into natural kinds, which have essences, a view that has gained popularity in the 20th century again due to the work of Kripke and Putnam. This is much in accordance with the neo-Aristotelean position—defended by psychologists like Keil (1989) and Gelman (2003)—that people (and children especially) have an essentialist view of the world. A closely associated modern view that has gained popularity recently has it that causal powers (Harré and Madden 1975) or capacities (Cartwright 1989) are that in virtue of which many generalities exist. Although any view that makes use of causal powers or capacities has been for a long time unpopular in modern analytic philosophy,¹⁵ the above authors paved the way to current proponents of such views in philosophy (Ellis, Molnar, Mumford & Anjum, and Bird) and in psychology (Cheng). In this paper we want to provide a down to earth analysis of these concepts making use of causal Bayesian models (cf. Pearl 2000). Our analyses will be closely related to that of Cheng (1997), who derived the measure $\Delta \!^* P^m_k$ from the assumption that generalities are (taken to be) due to unobservable causal powers.

There is a closely related way why we should be unsatisfied with our (still provisional) analysis of disposition ascriptions in terms of the measures $\Delta P^m_{k, (C)}$ or $\Delta \!^* P^m_{k, (C)}$. These measures are essentially population data, data about the members of kind k seen as a whole. But many disposition ascriptions are about individual objects, and we want to be able to account for these as well. A causal counterfactual analysis can make a connection between the two.

5.1 Causal models and Carnap’s testability criterion

We will use causal models to represent causal and counterfactual relationships. With Pearl (2000) we assume that such models represent a collection of ‘mechanisms’, a set of stable and autonomous relationships, represented by equations. A causal model, ${{\mathcal {M}}}$, is a triple, $\langle U,V,F\rangle$, where U and V are disjoint sets of exogenous and endogenous variables, respectively, and F is a set of mappings. While the values of the exogenous variables U are determined by factors outside the model, the values of the endogenous variables V are determined by the values of variables in the model, i.e., by $U \cup V$. What U represents depends on the application of the causal model. It can represent a set of situations, but also, for instance, a set of objects. Depending on the application, an assignment to U, i.e, $U = u$, can thus represent, for instance, a particular situation, or object. Such an assignment of U uniquely determines the values of all the endogenous variables. Thus, if X is an endogenous variable, X(u) gives the value of X if $U = u$. The value of X(u) can, for instance, be the temperature in u, if u is a situation, or the length of u, if u is an object. But X(u) could also be the truth-value of p, if u is a situation, and X stands for the issue whether p. The set of mappings F, finally, represent the mechanisms, or causal dependencies. Each $f_i \in F$ is a mapping which gives the value of $V_i$ given the values of all other variables in $U \cup V$. More particularly, each function $f_i$ can be written as an equation

where $pa_i$ denotes the values of the endogenous variables that are the parents of $V_i$, and where the $u_i$ are the set of exogenous variables on which $f_i$ depends.

What the parents of $V_i$ are can be directly seen in the directed acyclic graph (DAG) associated with the causal model ${{\mathcal {M}}}$. Such a directed graph represents the casual dependencies between the members of V graphically. In such a graph, the members of V are represented by nodes, and if in ${{\mathcal {M}}}$ there exists a mapping f from $pa_i$ (the members of V that are the parents of i) to $V_i$, this will correspond to directed edges from the nodes corresponding to the members of $pa_i$ to $V_i$.

To illustrate, consider the following Firing Squad example. In this example we have the following (binary) random variables: A, B, C, D and U that are represented as nodes. A and B are riflemen (that shoot, a, b or not, $\lnot a, \lnot b$), C is the squad’s captain (that orders c, or not $\lnot c$) who waits for the court’s order U (yes, or no). D, finally is the variable standing for death (or not) of the condemned prisoner. We assume that all variables are endogenous, except for U, which is exogenous. The laws can be stated as follows: $\{C := U, A := C, B := C, D := A \vee B\}$. Notice that we assume for simplicity that there are no separate exogenous variables related to A, B, C and D, representing the assumption that A and B are perfectly accurate and alert marksmen, and that they are, just as C, law-abiding. Moreover, we assume that D won’t die from fear, a heart attack, or anything else but a shot. This situation, together with the causal relations, can be displayed by the following DAG.

Notice that the value of the exogenous variable U determines the value of all other variables immediately: if $U = 1$, all endogenous variables will receive value 1 as well, and similarly when $U = 0$. But at many cases we are interested in what would be the case if something went different from how they actually went. Given that the prisoner is dead and that rifleman A shot him, we would like to know, for instance, whether the prisoner would still be dead had rifleman A not shot him. To answer such a counterfactual question, Pearl makes use of interventions.

For the representation of local actions, or hypothetical changes (i.e., interventions), Pearl (2000) makes use of submodels. A submodel ${{\mathcal {M}}}_x$ of ${{\mathcal {M}}}$ is the causal model $\langle U,V, F_x\rangle$, where x is a particular value of endogenous variable(s) X, and where $F_x$ is just like F, except that all functions $f_x$ that correspond to members of X are replaced by constant function $X = x$. Intuitively, ${{\mathcal {M}}}_x$ represents the minimal change from ${{\mathcal {M}}}$ required to make $X = x$ true for any $u \in U$. If X and Y are variables in V, the counterfactual ‘The value that Y would have obtained, had X been x’ is interpreted as denoting $Y_x(u)$. Intuitively, this will just be $f_y(x, u)$, in case X is the only parent of Y in the graphical model. In our Firing Squad example, the intervention of A can be represented by (i) breaking the causal link between the captain’s order and the decision of A whether to shoot, and (ii) setting the value of A to 0.

The counterfactual can now be handled as follows: First we use abduction: given that the prisoner is dead and that rifleman A actually shot him, we can conclude that the captain ordered a shooting, which means, in turn, that the court ordered this as well. Then, we make use of intervention (break the law $A := C$, and replace this by $A = 0$). Finally, we make use of prediction: what follows in the new imagined situation? Obviously, rifleman B is still ordered to shoot, so the prisoner would still be dead.

In this paper we will make use of a probabilistic causal model. This is a pair $\langle {{\mathcal {M}}}, P(u)\rangle$, where $\mathcal{M}$ is a causal model, and P(u) is a probability function defined over the domain U. Because each endogenous variable is a function of U, P(u) completely defines the probability distribution over the endogenous variables as well. If Y is a variable in V, we will abbreviate $P(Y = y)$ from now on by P(y). The latter is determined as follows:

Similarly, if X is also a variable in V, we will abbreviate $P(Y_x = y)$ by $P(y_x)$. The latter is determined as follows:¹⁶

Notice that if $P(y_x) > \frac{1}{2}$, this won’t be due to the fact that most situations where x were true, y would hold, but rather due to the fact that in most situations, y would hold after an intervention with x. Thus, like in the proposal made by Manley and Wasserman (2007), the ‘quantifier’ most has wide scope over the counterfactual conditional. Alternatively, if we think of u as an object and x and y as properties, $Y_x(u) = y$ represents the ‘fact’ that after an imagined (minimal) change of u such that it will become an x (or will have property x), it will have property y. $P(y_x)$, then, measures the relative amount of objects that would be y after ‘becoming’ x due to an intervention.

One of the most appealing features of calculating $P(y_x)$ as proposed by Pearl is that in this way we can also determine the probability $Y = y$ would have after an invention that would make x true, if x is, in fact, not true. Thus, on Pearl’s analysis one can easily determine $P(y_x\mid \lnot x)$. This latter notion is calculated as follows:¹⁷

It is interesting to realize that to determine the counterfactual probability $P(y_x\mid \lnot x)$ we will make use of (i) abduction, (ii) intervention, and (iii) prediction, just like in the above Fire Squad example. Abduction is used to determine from the assumed $\lnot x$ what is the probability of u. Intervention is used to set the value of X to x, from which we calculate, by prediction, the probability of $Y = y$.

Pearl (2000) defines the ‘probability of causal sufficiency’ of x to generate y as $P(y_x\mid \lnot x, \lnot y)$. Another notion of power —what Pearl calls the ‘probability of causal necessity and sufficiency’—he defines as $P(y_x, \lnot y_{\lnot x})$. The former is defined in terms of interventions as follows:

The latter is defined in terms of two interventions:

Because $P(y_x\mid \lnot x, \lnot y)$ measures to what extent x can generate y, it can be thought of as a notion of causal power. Indeed, we will see that this measure corresponds closely with what Cheng (1997) calls ‘the causal power of x to generate y’.

Observe that in the Fire Squad example, $P(d_a\mid \lnot a, \lnot d)$ will be 1. Indeed, the shooting of A suffices to cause the death of the prisoner. On the other hand, $P(d_a, \lnot d_{\lnot a})$ depends on the initial probability of $U = 1$. Suppose that $P(U = 1) = \frac{3}{4}$, then $P(d_a, \lnot d_{\lnot a}) = P(d_a, \lnot d_{\lnot a}| U = 1) \times P(U = 1) + P(d_a, \lnot d_{\lnot a}| U = 0) \times P(U = 0) = 0 \times \frac{3}{4} + 1 \times \frac{1}{4} = \frac{1}{4}$, where $P(d_a, \lnot d_{\lnot a}| U = 1) = 0$ because $P(\lnot d_{\lnot a}| U = 1) = 0$.

The effects of interventions are observable by making explicit experiments. One of the most striking consequences of Pearl’s causal analysis is, however, that the effect of interventions can in many circumstances be predicted from non-experimental data alone, i.e., in case only observational data are available! We take this to be very relevant for the analysis of unobservable dispositions. Pearl (2000) shows that if a condition that he calls ‘monotonicity’ is assumed (the assumption that from a change from $\lnot x$ to x, y cannot change into $\lnot y$, or formally, $\forall u \in U: Y_x(u) \ge Y_{\lnot x}(u)$), $P(y_x\mid \lnot x, \lnot y)$ reduces to $\frac{P(y_x) - P(y)}{P(\lnot y, \lnot x)}$. It is easy to show that $\frac{P(y_x) - P(y)}{P(\lnot y, \lnot x)}$ is equal to $\frac{P(y_x) - P(y \mid \lnot x)}{1- P(y\mid \lnot x)}$, and thus that $P(y_x\mid \lnot x, \lnot y) = \frac{P(y_x) - P(y \mid \lnot x)}{1 - P(y \mid \lnot x)}$. Likewise, $P(y_x, \lnot y_{\lnot x})$ comes, under these circumstances, down to $P(y_x, \lnot y_{\lnot x}) = P(y_x) - P(y_{\lnot x})$. From this it follows that the measures $P(y_x\mid \lnot x, \lnot y)$ and $P(y_x, \lnot y_{\lnot x})$ can be tested by observational data only when the causal effects $P(y_x)$ and $P(y_{\lnot x})$ can be empirically tested in this way. Pearl (2000) famously shows that this can be done by taking the confounding factors (taken to be Z) into account and condition on their various values and averaging over the results: $P(y_z) = \sum _{z \in Z}P(z) \times P(y| x,z)$.

A major simplification can be established when we assume that $P(y_x, \lnot y_{\lnot x} \mid x) = P(y_x,\lnot y_{\lnot x})$ (what Pearl calls ‘X is exogenous relative to Y’, intuitively, that X and Y don’t have common parents, i.e., no common cause). In that case, the causal influence of X on Y is reduced to conditional probability: $P(y_x) = P(y_x\mid x) = P(y\mid x)$. If in addition monotonicity is assumed, the two probabilistic notions of causation come down to the notions in terms of which we previously proposed to analyze generic sentences, i.e., $\Delta P^y_x$ and $\Delta \!^* P^y_x$:

It should be noted that Cheng (1997) derives $\Delta \!^* P^y_x$ as being the ‘causal power’ of x to induce y on similar, though still somewhat different, causal assumptions.

5.2 A causal analysis of dispositions

Before we will discuss our final proposal, let’s first see how to think of the variables in the causal model to make sense of it. We have seen above that it depends on the application of a causal model how we should think of the exogenous and endogenous variables. In some applications, the set of exogenous variables U should be thought of as a set of situations, while in others it could be, for instance, a set of objects. We will think of the set of endogenous variables, V, as functions from U to truth values. If U would be a set of situations, any binary endogenous variable X would be thought of as a propositional variable. If U would be a set of objects, an endogenous variable X would be thought of as a property object u does or does not have. We propose that for our purposes it is best to think of the exogenous variables as situations, or better, of being an arbitrary object in one of these situations. If we think of x as this arbitrary object,¹⁸ an intervention of u with condition c or with natural kind k, in turn, should be thought of as the imagined (minimal) change such that c would be true in the new situation, or that object x would be of kind k. If u is a value of an exogenous variable thought of as a particular situation, and M an endogenous variable in the graphical model, M(u) states whether object x has property m in situation u. Similarly, $M_k(u)$ states whether x would have property m or not, after an intervention of x in situation u with kind k, i.e., whether x in u would have property m or $\lnot m$ when x were of natural kind k. A related interpretation should be given to $M_c(u)$, when c is a condition. Because we assume in this paper that the variables can normally take only two values, we will write $M_{(k)}(u) = m$, instead of $M_{(k)}(u) = 1$, and similarly for $M_{(k)}(u) = \lnot m$. As a result, $P(m_k)$ would measure the proportion of circumstances in which x would have property m if it were of kind k.

The most straightforward use of causal models to provide a counterfactual analysis of dispositions would be as follows:

Natural and familiar as the use of $P(m_c\mid \lnot m, \lnot c, k)$ might seem (because the condition c can be thought of as the antecedent of the counterfactual), analysis (15) is not what we will propose. There are several reasons for this. First of all, we have argued above that condition (ii), stated in terms of a counterfactual, should correspond with a generic. Although there is one—‘Things in situation c, when of kind k, show manifestation m’—it is not the one we thought of earlier: ‘Things of kind k, when in situation c, show manifestation m’. Second, and related, the use of $P(m_c\mid \lnot m, \lnot c, k)$ doesn’t really appeal to the desired principle connection. Intuitively, the principle connection should be between natural kind k and manifestation m. But on the above formulation, a principle connection is assumed between condition c and m. Third, on this analysis it is completely unclear how to account for non-conditional dispositions, things that we have argued in Sect. 2.4 exist as well. Finally, on this analysis it is unclear how to account for Vetter’s (2013) observation that all dispositions are multi-track: the manifestation of the condition can vary with the strength of the condition (one type of stuff can be bent if heated under less high temperatures than other stuff). The proposal under discussion doesn’t allow for this.

In Sect. 4 we proposed the following account of disposition statements:

• x has the disposition to m (when C) iff (i) x is of natural kind k and (ii) ks are m (when C), in virtue of a principle connection between k and m.

In Sect. 4 we argued that the generic ‘ks are m (when C)’ is true just in case $\Delta \!^* P^m_{k, (C)}$ is high. In Sect. 5.1 we provided an explanatory analysis of why $\Delta \!^* P^m_{k, (C)}$ is high, showing that the latter can be derived making use of Pearl’s (2000) graphical causal models. Let us get precise about this now.

We have seen in the previous section that the measures $\Delta P^m_{K, (C)}$ and $\Delta \!^* P^m_{K, (C)}$ can be derived from $P(m_k, \lnot m_{\lnot k}\mid (C))$ and $P(m_k\mid \lnot m, \lnot k, (C))$, respectively. Measure $P(m_k\mid \lnot m, \lnot k, C)$ can be thought of as the proportions of C-situations in which x (which is neither of kind k nor has property m) would have property m if it were of natural kind k. Something similar holds for $P(m_k, \lnot m_{\lnot k}\mid C)$. Observe that $P(m_k\mid \lnot m, \lnot k, C)$ is high just in case being an object of kind k one has a high causal power of being able to show manifestation m in a circumstance in which C holds.

We saw in Sect. 4 that if we analyze disposition statements in terms of $\Delta P^m_{K, (C)}$ or $\Delta \!^* P^m_{K, (C)}$, the familiar masking and mimicking problems of analyses of dispositions can be accounted for. Because these measures can be derived from $P(m_k, \lnot m_{\lnot k}\mid (C))$ and $P(m_k\mid \lnot m, \lnot k, (C))$ we can state our own proposal as follows:

Notice that by analyzing dispositions in terms of $P(m_k \mid \lnot k, \lnot m, (C))$, we can account not only for masking and mimicking counterexamples to the conditional analysis, we can also make sense of the desired ‘principle connection’, thought of in a causal way. Given the intuitive meaning of $P(m_k\mid \lnot m, \lnot k, (C))$, the above proposal reduces to:

Analysis (16)–(17) can account for comparative disposition statements like ‘Things of kind $k_1$ are more disposed to m than things of kind $k_2$’. Indeed, $P(m_{k_1}\mid \lnot m, \lnot k_2, (C)) > P(m_{k_2}\mid \lnot m, \lnot k_2, (C))$ will be the case if there are more situations u such that $M_{k_1}(u) = m$ than situations where $M_{k_2}(u) = m$. Take, for instance, the dispositions of being malleable or of being ductile. The manifestation condition for both dispositions is (can be) ‘bent’. Rubber is more ductile than iron, even if iron can be bent as well, at least under high temperature. Think of $u_1$ and $u_2$ as situations of x being of a particular temperature. Say that $T(u_2) > T(u_2)$, meaning that the temperature in $u_2$ is higher than that of $u_1$. Suppose for simplicity that $P(u_1) = P(u_2)$. Still, it will be the case that $P(Bent_{rubber}\mid \lnot rubber, \lnot bent) > P(Bent_{iron}\mid \lnot iron, \lnot bent)$ although also iron can be bent when heated (enough). The reason is that rubber can be bent easier when heated. It could be that $Bent_{iron}(u_2) = 1$ and $Bent_{iron}(u_1) = 0$, but that rubber could be bent in both situations: $Bent_{rubber}(u_1) = 1 = Bent_{rubber}(u_2)$. It is obvious that gradable disposition statements can be accounted for in a similar way. The same example also shows that this analysis can account for non-conditional dispositions: Rubber can be bent in much more situations than other type of stuff. We take this all to be in support of our analysis of disposition statements in terms of $P(m_k\mid \lnot m, \lnot k, (C))$.

We think that our causal power analysis (16)–(17) of dispositions and/or disposition statements is appropriate. We have also shown that this analysis is far less obscure than it might seem at first, because the clause ‘members of natural kind k have a relatively high causal power to show manifestation m’ can be tested by observational data alone, because it can be reduced to an observable criterium under various circumstances. Thus, it satisfies Carnap’s desire for a testable analysis of dispositions, at least under many circumstances.

It is standardly assumed that disposition statements, just like laws, support counterfactuals. This comes out naturally if one analyses disposition statements in terms of counterfactuals, as proponents of the conditional analyses do. Because we didn’t, it gives rise to the question whether dispositions are predicted to support counterfactuals on our analysis as well. Thus, is it the case that if ‘x is flammable’ is true, it supports a counterfactual? Given that x consists of, say, kerosene, the question is whether the disposition would, on our analysis, support the counterfactual ‘If x is in contact with fire, it would burn, if it were kerosene’. But that would hold exactly if $P(b_k\mid f)$ would be high. To see what the latter means, let us write it out:

$P(b_k\mid f)$ is high just in case if x were kerosene that would be in contact with fire, it would burn in the vast majority of those circumstances. For our analysis, however, we didn’t demand that $P(b_k\mid f)$ is high. Instead, we demanded that what has to be high is $P(b_k\mid \lnot b, \lnot k, f)$:

Fortunately, because in most situations where something is in contact with fire, it either is not kerosene, or it burns, it will hold that $P(b_k\mid \lnot b, \lnot k, f)$ is high because $P(b_k{\mid } f)$ is high. In this way we have explained why the disposition statement supports the counterfactual.

6 Final thoughts

This paper was about dispositions, and disposition statements, that involve natural kinds. The examples we concentrated on were natural kinds like kerosene, sugar, and arsenic. That was no accident, because these are natural kinds the members of which are very similar to one another. Of course, we make disposition statements as well about objects that are of a natural kind where the members of that kind are not all that similar. And for such disposition statements, our analysis seems false: ‘This dog is dangerous’ can be true, even though this dog is a St. Bernard dog, and most of such dogs are not dangerous.¹⁹ Similarly, ‘This dog is not dangerous’ can be true, even though this dog is a Pit bull, a kind of dog we generally take to be dangerous. Would this mean that our analysis works only for an extremely limited type of disposition statements?

Perhaps. But that doesn’t mean that our analysis is useless for all these other cases. In fact, our argumentation for the analysis proposed in the previous two sections still holds, except that we should not limit ourselves to natural kinds. Following Quine (1970) , our analysis was based on natural kinds, making use of the idea that if two objects are of the same natural kind, they are very similar. It is this similarity that allowed us to inductively infer unobservable features of this object of natural kind k from observed features of other objects of natural kind k. But this inductive inference crucially relies on a close similarity between the members of natural kind k. For natural kinds that allow for a larger variation, the precise analysis as given in the previous section doesn’t work, and a somewhat more specific analysis must be provided. But because objects and individuals can be members of several (natural) kinds—due to the fact that kinds are hierarchically ordered (animal, dog, pit bull)—we implicitly assumed a more detailed analysis anyway. In fact, the following comes to mind immediately (see also Wasserman 2011for a similar proposal): the generic that should be true must be one involving a group of objects G that are all extremely similar to one another (in all types of ways). The more general account then goes like this:

• ‘x is disposed to m’ (when C) iff (i) x is extremely similar to all members of group G and (ii) the generic ‘Gs are m, (when C)’ is true because of a principle connection between being a G and m (when C).

Notice the close similarity between this new analysis and the one we proposed in the previous section: although condition (i) is somewhat adapted, the crucial condition (ii) is exactly as it was. The proposal is still based on an analysis of generics that are true because of a principle (mostly) causal connection.

This paper was concerned with the semantic analysis of disposition ascriptions. We have not dealt with the metaphysical question whether dispositions are basic, or whether they should be reduced to categorical properties. In principle, we take it that our analysis is independent of this issue. But that by itself is already noteworthy: our analysis is compatible with the view that dispositions are basic! Let us explain.

In the previous section we argued that on our analysis, disposition ascriptions support counterfactuals. Thus, we assumed there to be a link between dispositional statements and counterfactuals, just like traditional conditional analyses did. However, we don’t necessarily share the original motivation for a counterfactual or conditional analysis of dispositions. The standard conditional analyses define the meaning of disposition statements, and perhaps of dispositions themselves, in terms of these conditionals. Dispositions should be explained away, or reduced to something else that fits a Humean metaphysics. Proponents of such a metaphysics normally allow for categorial properties, but not for dispositional ones.

It is well-known that Lewis (1973b) attempted to reduce causality to counterfactual dependencies for similar metaphysical reasons. Making use of causal models, Pearl (2000), instead, suggests to take causality as a primitive in terms of which counterfactuals can be defined. Similarly, the previous section suggests that we have assumed the existence of causality, or of causal powers, as basic, in terms of which we analyze the meaning of (certain type of) generic and dispositional sentences. On such a reading of our previous section, one can (though need not) think of dispositions as being these primitive causal powers, and thus as basic properties themselves. Our semantic analysis of disposition ascriptions is then not an analysis of the relevant dispositions, in the sense that the analyses do not define the dispositions. Instead, on this reading, our analysis ascribes basic properties to (kinds of) objects, and provides criteria under which the existence of these properties can be tested.

Although we make use of causal models, we don’t feel committed to the above metaphysical stance. In fact, we are quite attracted to Pearl’s earlier, more modest, position concerning causality. In Pearl (1988), he takes the view that humans, when facing complex phenomena, interpret these phenomena almost automatically into structures of cause-and-effect relationships for computational reasons. A causal view of the world, including the assumption of hidden causes, allows us to represent and make use of empirical knowledge in an effective way. Whether this means that these assumed hidden causes actually exist is beyond our grasp. Whether a similar computationally motivated position should be taken with respect to the age-old question whether natural kinds are real, or are concepts that exist only due to our urge to view the world in an organized way, we must leave to the reader.