Abstract
Information exchange can be viewed as a process of asking questions and answering them. While dynamic epistemic logic traditionally focuses on statements, recent developments have been concerned with ways of incorporating questions. One approach, based on the framework of inquisitive semantics, is inquisitive dynamic epistemic logic (\(\textsf {IDEL}\)). In this system, agents are represented with issues as well as information. On the dynamic level, it can model actions that raise new issues. Compared to other approaches, a limitation of \(\textsf {IDEL}\) is that it can only encode public announcements. \(\textsf {IDEL}\) can be refined to encode private questions, by merging its static basis, inquisitive epistemic logic (\(\textsf {IEL}\)), with action model logic (\(\textsf {AML}\)). This can be done in two ways, namely by enriching action models with questions as possible actions or with issues concerning which action takes place. This paper describes the corresponding dynamic logics, which are conservative extensions of both \(\textsf {AML}\) and \(\textsf {IEL}\), and a sound and complete axiomatization is given for both.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Dynamic epistemic logics are used to analyse the process of information exchange: they describe situations in which agents learn facts about the world or about each other’s knowledge. These systems are often interpreted as describing communication or scientific inquiry. However, typical information exchange is not just about uttering statements. Rather, it is a process of asking questions and answering them. In a similar way, scientific inquiry is not just about making observations, but also about asking the right questions.
Recently, these insights have led to the development of dynamic epistemic logics with questions (Baltag 2001; Peliš and Majer 2009; Minică 2011; van Benthem and Minică 2012; Ciardelli and Roelofsen 2015Footnote 1) with an eye to applications in epistemology, philosophy of science and linguistics (see the introduction in Hamami and Roelofsen (2015) for an overview).
Two prominent approaches are the Dynamic Logic of Questions (\(\textsf {DELQ}\), van Benthem and Minică 2012; Minică 2011) and Inquisitive Dynamic Epistemic Logic (\(\textsf {IDEL}\), Ciardelli and Roelofsen 2015; Ciardelli 2016). These systems are generalizations of Public Announcement Logic (\(\textsf {PAL}\), Plaza 1989): they are used to reason about epistemic events of which all agents are fully aware.Footnote 2 In contrast to \(\textsf {PAL}\), a public announcement in these systems can not only be a statement, but also a question. In both \(\textsf {DELQ}\) and \(\textsf {IDEL}\), statements convey information, while questions raise issues. But there are also important differences between these systems:
-
1.
The formal notion of issues. Issues in \(\textsf {DELQ}\) are modelled as an equivalence relation on the set of worlds, following Groenendijk and Stokhof (1984). This relation induces a partition, of which each cell represents an answer to the issue. \(\textsf {IDEL}\) adopts a more general notion of issues from inquisitive semantics (Ciardelli et al. 2013; Ciardelli and Roelofsen 2011), in which alternatives need not be mutually exclusive and can overlap. As a consequence, \(\textsf {IDEL}\) can encode conditional questions like ‘If John comes to the party, will Mary come?’ and alternative questions like ‘Does John speak English, German or French?’, while these are beyond the scope of \(\textsf {DELQ}\).
-
2.
The way in which questions are expressed. In \(\textsf {DELQ}\), all formulas are statements. Questions are encoded as a special type of action. In \(\textsf {IDEL}\), formulas can be questions as well as statements, and there is only one type of action. The latter setting allows for question-embedding sentences such as ‘John wonders whether Mary will come to the party’.
These differences show that compared to \(\textsf {DELQ}\), \(\textsf {IDEL}\) widens the scope of expressions that can be encoded.Footnote 3 However, this comparison is not the full story, since both \(\textsf {IDEL}\) and \(\textsf {DELQ}\) are limited to a special kind of actions, namely public ones.
In standard \(\textsf {DEL}\), the generalization from public actions to general actions, of which not every agent is equally aware, is made by describing actions using action models, resulting in Action Model Logic (\(\textsf {AML}\), Baltag et al. 1998). The same technique can be applied in a setting with questions, to reason about scenarios in which participants are not fully aware of what is being stated or asked. When this happens, they become uncertain about each other’s knowledge and issues. In the framework of \(\textsf {DELQ}\), there exists such a variant of \(\textsf {AML}\), called \(\textsf {ELQm}\) (where m stands for multi-agent, see van Benthem and Minică (2012, Sect. 5) and Minică (2011, Sect. 2.4)).Footnote 4 As of yet, such a variant is lacking for \(\textsf {IDEL}\).
Table 1 shows in a schematic way how the logics discussed so far are related. The goal of this paper is to develop an action model variant of \(\textsf {IDEL}\), thereby filling the empty space on the bottom right of the table. Doing this amounts to merging the static Inquisitive Epistemic Logic (\(\textsf {IEL}\), Ciardelli and Roelofsen 2015) with \(\textsf {AML}\). However, we will see that there is more than one natural way in which this can be done.
One option is to enrich action models in such a way that an action can represent the event of a question being asked. This is a natural extension if we think of actions as speech acts. A second option is to enrich action models in such a way that they encode issues agents have about which action takes place. This is more natural if we think of actions as observations. These two strategies lead to two slightly different systems, which will both be worked out in this paper.
The rest of this paper is structured as follows: I will start with an introduction to \(\textsf {IEL}\) and some relevant notions in Sect. 2. I will then explain in greater detail how the two approaches to merging \(\textsf {IEL}\) and \(\textsf {AML}\) differ. The first approach is worked out in detail in Sect. 3 and I sketch the second one in Sect. 4. I will compare and discuss the approaches in Sect. 5 and conclude in Sect. 6.
2 Background
2.1 Inquisitive epistemic logic
2.1.1 Introducing \(\textsf {IEL}\)
In inquisitive logic, questions and statements are treated in a uniform way, by shifting the evaluation of formulas from single worlds to sets of worlds. Sets of worlds are information states and the meaning of formulas is viewed in terms of the information states that support them, rather than the worlds in which they are true.
For instance, the question ‘Is John home?’ is supported by the information states that specify whether John is home. All of these states specify either that John is home or that he is not. Thus, there are two maximal supporting states (states that are not contained by some other state), namely the state consisting of all the worlds in which he is home and the one consisting of all the worlds in which he is not. In this way, the meaning of the sentence presents alternative ways of supporting it. Because of this, it is called a question.
Inquisitive epistemic models are enrichments of standard epistemic models. To see how, let us first look at the definition of standard epistemic models.
Definition 1
(Standard Epistemic Model)Footnote 5 Let \({\mathscr {P}}\) be a set of propositional atoms. A standard epistemic model is a triple \(M = \langle W, \{\sigma _a ~|~ a \in {\mathscr {A}}\}, V\rangle \) where:
-
W is the domain of worlds;
-
\({\mathscr {A}}\) is the domain of agents;
-
\(\sigma _a : W \rightarrow \wp (W)\) is a function that assigns to each world w an information state \(\sigma _a(w)\);
-
\(V : {\mathscr {P}} \rightarrow \wp (W)\) is a valuation function that specifies for each atomic formula in which worlds it is true.
In standard epistemic models, the information available to an agent a is represented by assigning to each world w an information state \(\sigma _a(w) \subseteq W\). This is the set of worlds that are candidates for the actual world to a in w.Footnote 6
Inquisitive epistemic models enrich these standard epistemic models by adding an inquisitive state on top of this information state. This inquisitive state is the set of information states that count as resolving the agent’s issues. It is always downward closed, which means that for each information state s it contains, it also contains any \(t\subseteq s\). The intuition behind this requirement is that if some body of information is enough to resolve an agent’s issues, then so is any more specific body of information. The formal definition of inquisitive epistemic models is as follows.
Definition 2
(Inquisitive Epistemic Model) Let \({\mathscr {P}}\) be a set of propositional atoms. An inquisitive epistemic model is a triple \(M = \langle W, \{\varSigma _a ~|~ a \in {\mathscr {A}}\}, V\rangle \) where:
-
W, \({\mathscr {A}}\) and V are defined as in Definition 1;
-
\(\varSigma _a\) is the inquisitive state map. It assigns to each world w an inquisitive state \(\varSigma _a(w)\), a non-empty downward closed set of information states. These are the states where the agent’s issues are resolved.
We assume that the information states in \(\varSigma _a(w)\) (that resolve a’s issues in w) are subsets of her current information state in w, and, conversely, that every world in her information state is part of some issue resolving state. This means we can define the information state of a at w as follows:
In this paper, we will assume knowledge is factive: agents always consider the actual world as one of the possible worlds.
Additionally, in \(\textsf {IEL}\) it is assumed that agents are introspective with respect to their knowledge and issues. Formally, this amounts to requiring that the state maps satisfy the following two conditions:
Although it is not necessary for our purposes to require introspection, it does make it easier to represent inquisitive states in diagrams. Therefore, the examples in this paper will rely on full introspection, but nothing hinges on this choice.
As an example, let us define the inquisitive epistemic model M with \(W = \{w_1,w_2,w_3,w_4\}\), \(V(p) = \{w_1,w_3\}\), \(V(q) = \{w_1,w_2\}\) and two agents a and b. Their inquisitive state maps are defined as follows:Footnote 7
-
\(\varSigma _a(w_1) = \varSigma _a(w_3) = \{\{w_1,w_3\}\}^\downarrow \)
-
\(\varSigma _a(w_2) = \varSigma _a(w_4) = \{\{w_2,w_4\}\}^\downarrow \)
-
\(\varSigma _b(w_1) = \varSigma _b(w_2) = \varSigma _b(w_3) = \varSigma _b(w_4) = \{\{w_1,w_2\},\{w_3,w_4\}\}^\downarrow \)
The model M is depicted in Fig. 1. Here and elsewhere, diagrams will depict inquisitive epistemic models as follows. For each world w, the worlds within the same dashed line are the worlds that the agent considers as possible worlds in w. The solid lines represent the issues within each epistemic state: these states and their subsets are the ones that count as resolving the agent’s issues. Only the maximal elements of inquisitive states are shown. The labels p and \({\overline{p}}\) indicate that the worlds below them make p true and false respectively, similar for worlds to the right of q and \({\overline{q}}\).
In worlds \(w_1\) and \(w_3\), p is true and a knows this, because all accessible worlds (within the dashed line) are p-worlds. However, in these worlds a does not know the truth value of q (both \(w_1\) and \(w_3\) are within the same dashed line). In worlds \(w_2\) and \(w_4\), p is false and again a knows this, but here too she does not know the truth value of q. Hence, we can conclude based on a’s inquisitive state map that, no matter which world is the actual one, a knows whether p is true, but not whether \(q\) is true.
In all worlds w, a’s information state is a member of \(\varSigma _a(w)\), the set of states which count as resolving her issues in w. This means she has no non-trivial issues. In the diagram, this corresponds to the solid lines and dashed lines marking the same areas.
The situation is different for b: in all her worlds, all other worlds are within the same dashed line. This means she has no information with respect to the truth of p or q. We can also see that her current information state does not count as resolving her issues. The maximal states that do resolve her issues are \(\{w_1,w_2\}\) and \(\{w_3,w_4\}\). Resolving her issues requires being in a more informative state that determines either that q is true or that q is false. Hence, based on b’s inquisitive state map, we can conclude that b does not know whether p or q are true, and that her issues are only resolved by finding out whether q is true.
We can express these descriptions of information and issues in the language of \(\textsf {IEL}\). Questions are formed by means of inquisitive disjunction:  is supported in a state just in case it supports one of the disjuncts. The semantics of the knowledge modality \(K_a\) generalizes the standard semantics of epistemic logic: this modality can now also operate directly on questions. Furthermore, a new modality \(E_a\) is introduced, which allows us to talk about the issues that the agent entertains.
is supported in a state just in case it supports one of the disjuncts. The semantics of the knowledge modality \(K_a\) generalizes the standard semantics of epistemic logic: this modality can now also operate directly on questions. Furthermore, a new modality \(E_a\) is introduced, which allows us to talk about the issues that the agent entertains.
Definition 3
(Syntax of \({\mathscr {L}}^{\textsf {IEL}}\))

I use the following abbreviations:

As formulas of \(\textsf {IEL}\) are evaluated relative to information states rather than single worlds, the semantics are defined in terms of support rather than truth.
Definition 4
(Support conditions in \(\textsf {IEL}\)) Let s be an information state in inquisitive epistemic model M.

Truth in a world is defined as support in the corresponding singleton information state.
Definition 5
(Truth) Let M be an inquisitive epistemic model and w a world.
This means that the truth conditions for the language are as follows:
Fact 1
(Truth conditions in \(\textsf {IEL}\)) Let w be a world in inquisitive epistemic model M.

Inspecting the truth conditions, we notice two things: first, the truth conditions for the propositional fragment are classical. Second, the truth conditions of the modal formulas are dependent on support conditions.
The relations of support and truth allow us to define the following two sets:
Definition 6
(Support set and truth set) Let \(\varphi \) be a formula and M an inquisitive epistemic model with W as its domain of worlds. Then the support set \([\varphi ]_M\) is the set of all information states in M where \(\varphi \) is supported:
The truth set \(|\varphi |_M\) is the set of all worlds in M in which \(\varphi \) is true:
Fact 2
(Properties of the support relation) For all models M and formulas \(\varphi \in {\mathscr {L}}^{\textsf {IEL}}\), we have the following properties:
-
Persistence property: if \(M,s\models \varphi \) and \(t\subseteq s\), then \(M,t\models \varphi \)
-
Empty state property: \(M,\emptyset \models \varphi \)
This means that \([\varphi ]_M\) is always downward closed and never empty.
An important notion in support-conditional semantics is that of truth-conditionality. A formula is truth-conditional just in case its meaning is completely determined by its truth conditions.
Definition 7
(Truth-conditionality) A formula \(\varphi \) is truth-conditional iff for all models M and states s:
Examples of truth-conditional formulas are  -free formulas and negated formulas. Following Ciardelli (2016), we will regard truth-conditional formulas as statements and all other formulas as questions. As a convention, statements are denoted by \(\alpha \) or \(\beta \) and questions by \(\mu \) or \(\nu \).
-free formulas and negated formulas. Following Ciardelli (2016), we will regard truth-conditional formulas as statements and all other formulas as questions. As a convention, statements are denoted by \(\alpha \) or \(\beta \) and questions by \(\mu \) or \(\nu \).
We have the following fact:
Fact 3
(Double negation and truth conditions) For all \(\varphi \in {\mathscr {L}}^{\textsf {IEL}}\):
-
\(\lnot \lnot \varphi \) is truth-conditional
-
\(M,w\models \varphi \iff M,w\models \lnot \lnot \varphi \)
This means that for any formula \(\varphi \), we can always find a statement \(\alpha \) that has the same truth conditions as \(\varphi \).
2.1.2 Modalities and questions
As we have seen, there are two epistemic modalities, \(K_a\) and \(E_a\), and a third one, \(W_a\), defined in terms of the first two. Just as in standard epistemic logic, the \(K_a\)-modality expresses knowledge, but its semantics is generalized to questions. For instance, \(K_a\mathord {?}p\) is true just in case a knows whether p is the case, that is, if she either knows that p or that \(\lnot p\). An example is shown in Fig. 2a, where the dashed line indicates that a knows which world is the actual one. This means that her information state is such that it resolves the question \(\mathord {?}p\). Therefore, \(K_a\mathord {?}p\) is true in both worlds.
The \(E_a\)-modality is used to express the issues an agent entertains. We say that a entertains \(\mu \) (\(E_a\mu \)) in a world w if a’s issues at w are such that all information states that resolve it also resolve the question \(\mu \). In other words, a’s issues are only resolved by knowing \(\mu \).
Notice that \(K_a\varphi \) implies \(E_a\varphi \): if a knows \(\varphi \), then her information state supports \(\varphi \), so the information states that resolve her issues (which are more informative) must also support \(\varphi \). Furthermore, if \(\alpha \) is a statement, then \(E_a\alpha \) is equivalent to \(K_a\alpha \): if the information states that settle a’s issues all support a truth-conditional formula \(\alpha \), then so does its union, since it only contains worlds in which \(\alpha \) is true.
The wonder modality, \(W_a\), is an abbreviation of not knowing and entertaining. That is, \(W_a\mu \) is true just in case a does not know the answer to the question \(\mu \), but does entertain it. An example is shown in Fig. 2b, where the dashed line indicates that \(w_1\) and \(w_2\) are both considered by a as candidates for the actual world. Therefore, her information state does not resolve the question \(\mathord {?}p\). However, the solid lines indicate that the information states that resolve her issues are \(\{w_1\}\), \(\{w_2\}\) and \(\emptyset \). All these information states resolve the question \(\mathord {?}p\). Therefore, we say that a wonders \(\mathord {?}p\): \(W_a\mathord {?}p\). Since for all statements \(\alpha \), \(E_a\alpha \) and \(K_a\alpha \) are equivalent, \(W_a\alpha \) is always a contradiction. This means that the wonder modality is only meaningful when applied to questions.
Because questions can be embedded under epistemic modalities in \(\textsf {IEL}\), we can express not only the knowledge and issues agents have about general facts, but also the knowledge and issues they have about each other’s knowledge and issues. For instance, that a knows that b wonders whether p: \(K_a W_b\mathord {?}p\); or that b wonders whether a knows p: \(W_b \mathord {?} K_a p\).
2.1.3 Dynamics
The dynamic variant of \(\textsf {IEL}\), called \(\textsf {IDEL}\) (Ciardelli and Roelofsen 2015; Ciardelli 2016), extends \(\textsf {IEL}\) with public announcements, analogous to the way \(\textsf {PAL}\) extends standard epistemic logic (Plaza 1989). The novelty of \(\textsf {IDEL}\) is that both questions and statements can be announced. In the former case, the model will be transformed in such a way that agents will typically come to entertain the question. The language \({\mathscr {L}}^{\textsf {IDEL}}\) extends \({\mathscr {L}}^{\textsf {IEL}}\) with a dynamic modality, \([\varphi ]\), which allows us to talk about the situation after the public utterance of \(\varphi \).
The following definition contains the procedure by which we update a model.
Definition 8
(Update in \(\textsf {IDEL}\)) Let \(M = \langle W,\{\varSigma _a~|~a\in {\mathscr {A}}\},V\rangle \) be an inquisitive epistemic model and \(\varphi \in {\mathscr {L}}^{\textsf {IDEL}}\). Then the model updated with \(\varphi \) is \(M^\varphi = \langle W^\varphi ,\{\varSigma ^\varphi _a~|~a\in {\mathscr {A}}\},V^\varphi \rangle \), defined as follows.
-
\(W^\varphi = W \cap |\varphi |_M\)
-
\(V^\varphi = V\upharpoonright _{|\varphi |_M}\)
-
\(\varSigma ^\varphi _a(w) = \varSigma _a(w) \cap [\varphi ]_M\)
This definition says that updating an inquisitive epistemic model with a formula \(\varphi \) has two effects. First, the worlds in which \(\varphi \) is false are dropped from the model. Second, for each agent a and world w, the information states that count as resolving the issues of a in w become restricted to the ones that support \(\varphi \). See Fig. 3 for an illustration of the effect of a public utterance of a statement and a question (note that the solid lines should be understood as the maximal information states in the downward closed set).
The public utterance operator \([\varphi ]\) has the following support condition:
Definition 9
(Support condition for dynamic modalities)
This means that \([\varphi ]\psi \) is supported in information state s of model M just in case \(\psi \) is supported in the information state s, restricted to the worlds in which \(\varphi \) is true, in the updated model \(M^\varphi \). In other words, our information state s is such that it would come to support \(\psi \) after a public utterance of \(\varphi \).
2.2 Action model logic
As I mentioned before, utterances in \(\textsf {IDEL}\) are always public, whereas in reality agents may not always be sure about what was announced. A common way to encode epistemic events that are not public is by means of action models (Baltag et al. 1998). These are Kripke structures containing the actions considered possible. What the agents know about these actions is encoded by an accessibility relation (or equivalently, as I will do in this paper, by assigning a set of actions to each action). For each action considered, the information that it conveys is given by its precondition: a formula that says what has to be true for the action to be executable.
Definition 10
(Action Model) (van Ditmarsch et al. 2007) An action model is a triple \(\textsf {M} = \langle \textsf {S} ,\{\delta _a ~|~ a \in {\mathscr {A}}\},\textsf {pre} \rangle \) where:
-
\(\textsf {S} \) is a finite domain of actions;
-
\(\delta _a : \textsf {S} \rightarrow \wp (\textsf {S} )\) is a function that assigns to each action \(\textsf {x} \in \textsf {S} \) a set of actions \(\delta _a(\textsf {x} )\);Footnote 8
-
\(\textsf {pre} : \textsf {S} \rightarrow {\mathscr {L}}\) is a function that assigns a formula \(\textsf {pre} (\textsf {x} ) \in {\mathscr {L}}\) to each action point \(\textsf {x} \in \textsf {S} \).
A new epistemic model, which encodes the situation after the epistemic action, is constructed by taking the product update of the original epistemic model and the action model.
Definition 11
(Product update) (van Ditmarsch et al. 2007) Let M be an epistemic model and \(\textsf {M} \) an action model. Then \(M' = (M \otimes \textsf {M} )\) is the product update of M and \(\textsf {M} \), defined as follows.
\(M' = \langle W', \{\sigma _a' ~|~ a \in {\mathscr {A}}\}, V'\rangle \), where:
-
\(W' = \{\langle w, \textsf {x} \rangle ~|~ w\in W, \textsf {x} \in \textsf {S} \text { and } M,w\models \textsf {pre} (\textsf {x} )\}\)
-
\(\langle w, \textsf {x} \rangle \in \sigma '_a(\langle w', \textsf {x} '\rangle )\) iff \(w \in \sigma _a(w')\) and \(\textsf {x} \in \delta _a(\textsf {x} ')\)
-
\(\langle w, \textsf {x} \rangle \in V'(p)\) iff \(w\in V(p)\)
The language of \(\textsf {AML}\) extends epistemic logic with dynamic modalities referring to an action in an action model.Footnote 9 A formula with a dynamic modality (\([\textsf {M} ,\textsf {x} ]\varphi )\) is evaluated in a world w of model M by constructing the product update \(M' = M\otimes \textsf {M} \) and then checking whether if \(\textsf {x} \) is executable at w, \(\varphi \) is true in the world \(\langle w, \textsf {x} \rangle \) of this new model. Formally:
The goal of this paper is to generalize this action model approach, using \(\textsf {IEL}\) instead of standard epistemic logic as the static basis. To achieve this, we need to define a suitable notion of action models and product update. As we will see, action models based on the static logic \(\textsf {IEL}\) can be defined in different ways, depending on the interpretation we give to epistemic actions. In standard \(\textsf {DEL}\), two interpretations are common.
Consider the action model in Fig. 4. We might interpret this model as follows: \(\textsf {x} \) is the announcement ‘Peter will come to the party’. Although a heard the announcement, b did not. She considers it equally possible that the announcement was ‘Peter will not come to the party’. But we might also interpret the model as describing a coin flip: in this scenario, \(\textsf {x} \) could be the observation that it turned up heads. While a has seen this, b has only seen that a has seen it, but has not seen it herself. In the first story, we interpreted the actions as announcements, and in the second story as observations. The same model fits both kinds of stories equally well.
If we interpret actions as announcements, an action represents a speech act. The accessibility relation in the action model encodes which speech acts are indistinguishable to the agent, and the precondition of each speech act encodes what is being uttered. Enriching action models with questions then amounts to considering not just the speech act of stating, as in \(\textsf {AML}\), but also that of asking. Thus, we can enrich action models by allowing questions as the content of actions.
Under the interpretation of actions as observations, things are different.Footnote 10 An observation reveals information, which can be expressed by a statement, but not by a question. The action model contains all observations held possible, and the precondition of each observation expresses the information it reveals. The accessibility relation encodes what each agent knows about what is being observed. Adopting this interpretation, we can enrich action models by not just considering the knowledge agents have about which observation is made, but also their issues. For instance, we can think about a scientific experiment in which several researchers are involved, who have different goals.
Note that when there are no questions in the static language, the two different interpretations do not require a different treatment. This is why they are often not explicitly distinguished and used interchangeably.
To summarize, we consider two approaches to the integration of \(\textsf {IEL}\) and \(\textsf {AML}\):
-
Add questions to action models: allow non truth-conditional formulas to serve as the content of actions.
-
Add issues to action models: change the structure of the action models to encode issues about actions, just like an inquisitive epistemic model encodes issues about worlds.
I will work out both approaches in turn, in Sects. 3 and 4, respectively.
3 Action models with questions
In this section, the first approach to the integration of \(\textsf {IEL}\) and \(\textsf {AML}\) will be worked out in detail. I will start by defining a new type of action models and the logical language this gives rise to, which will be called Action Model Logic with Questions (\(\textsf {AMLQ}\)).
After a demonstration of the way updates work in \(\textsf {AMLQ}\), I will discuss some relevant properties of the system. In the rest of this section I will give an axiomatization based on reduction to \(\textsf {IEL}\).
3.1 Definitions
3.1.1 Action models and logical language
As we have seen above, in \(\textsf {AML}\) the preconditions of actions determine what they convey. In this way we can specify the information associated with the action. However, in our generalized setting we want to encode actions in which a question is asked, which raises an issue. The content of such actions is not truth-conditional, while preconditions are. Hence, while an action’s content is completely determined by its precondition in \(\textsf {AML}\), this is not possible in a setting with questions.
Therefore, one crucial modification to the original definition of action models has to be made: action content and preconditions have to be separated. The function \(\textsf {content} \) assigns a formula from our inquisitive logic, \({\mathscr {L}}^{\textsf {AMLQ}}\), to each action. We give the following two definitions simultaneously.Footnote 11
Definition 12
(Syntax of \({\mathscr {L}}^{\textsf {AMLQ}}\)) Let \({\mathscr {L}}^{\textsf {AMLQ}_0}= {\mathscr {L}}^{\textsf {IEL}}\). For natural numbers \(i > 0\), \({\mathscr {L}}^{\textsf {AMLQ}_i}\) is defined as follows, where \(\textsf {s} \) is a set of actions within the \(\textsf {AMLQ}\) action model \(\textsf {M} \) of at most level \(i - 1\) (defined below).

The full language is the union of all \({\mathscr {L}}^{\textsf {AMLQ}_i}\) for all natural numbers i.
Abbreviations:
-
\([\textsf {s} ]\varphi {:}{=} [\textsf {M} ,\textsf {s} ]\varphi \) (whenever \(\textsf {M} \) is clear from the context)
-
\([\textsf {x} ]\varphi {:}{=} [\{\textsf {x} \}]\varphi \) (where \(\textsf {x} \) is a single action)
Definition 13
(Action Model with Questions) For natural numbers \(i \ge 0\), an \(\textsf {AMLQ}\) action model of level i is a triple \(\textsf {M} = \langle \textsf {S} , \{ \delta _a ~|~ a \in {\mathscr {A}}\}, \textsf {content} \rangle \), where:
-
\(\textsf {S} \) is a finite domain of actions;
-
\(\delta _a : \textsf {S} \rightarrow \wp (\textsf {S} )\) is a function that assigns to each action \(\textsf {x} \in \textsf {S} \) a set of actions \(\delta _a(\textsf {x} )\);
-
\(\textsf {content} : \textsf {S} \rightarrow {\mathscr {L}}^{\textsf {AMLQ}_i}\) is a function that assigns a formula \(\textsf {content} (\textsf {x} ) \in {\mathscr {L}}^{\textsf {AMLQ}_i}\) to each action \(\textsf {x} \in \textsf {S} \).
In what follows, the term ‘action model’ will refer to an action model of some arbitrary level i.
The content of an action is a formula of \({\mathscr {L}}^{\textsf {AMLQ}}\), which means it can be a statement or a question. Like in \(\textsf {AML}\), we will also assign preconditions to our actions. In case the content is a statement, the precondition is equivalent to the statement itself. Whenever the content is a question, the precondition is a statement which we regard as capturing the question’s presupposition that one of the proposed alternatives is true.Footnote 12 This means that the precondition of an action is determined by its content. We make use of the fact that double negation turns any formula into a statement with the same truth conditions (Fact 3).
Definition 14
(Precondition of an action) Given an action \(\textsf {x} \), its precondition \(\textsf {pre} (\textsf {x} )\) is defined as:
Thus, \(\textsf {content} (\textsf {x} )\) expresses what the action conveys, while \(\textsf {pre} (\textsf {x} )\) expresses what has to be true in order to guarantee that the action can be performed. For instance, the precondition of an action with content p is equivalent to p, because it can only be truthfully performed in worlds where p is true. An action with content \(\mathord {?}p\) can be truthfully performed in any world, as it contains no information. Therefore its precondition is \(\lnot \lnot \mathord {?}p\equiv \top \). We have the following proposition, which will play an important part in the rest of the proofs.
Proposition 1
(Action content and precondition have equal truth conditions) For all actions \(\textsf {x} \), for every inquisitive epistemic model M and world w:
Proof
Immediate from Definition 14 and Fact 3.\(\square \)
3.1.2 Update procedure
Next, we need a procedure that describes how to compute the product update of an \(\textsf {IEL}\) model and an \(\textsf {AMLQ}\) action model. The result of an update should be a new \(\textsf {IEL}\) model, which encodes the updated knowledge and issues of the agents.
We need the following two projection operators to take us from a state s in the updated model to a state \(\pi _1(s)\) in the original model and a state \(\pi _2(s)\) in the action model.
Definition 15
(Projection operators) If \(s \subseteq W \times \textsf {S} \), then:
Like in standard action model logic, the domain of the updated model is the cartesian product of that of the original model and the action model, restricted to pairs of which the world satisfies the precondition of the action.
The crucial part of the definition is that of the updated state map. We formulate four conditions for an information state s to belong to the inquisitive state of some agent in a world \(\langle w, \textsf {x} \rangle \). These conditions are as follows:
-
(i)
The knowledge and issues an agent had before the action have to be preserved. Hence, a state can only count as resolving the agent’s new issues if it resolves her old issues. This means that \(\pi _1(s) \in \varSigma _a(w)\);
-
(ii)
The agent’s knowledge about the action should be preserved. Thus, the actions associated with this state have to be indistinguishable from \(\textsf {x} \). Formally, \({\pi _2(s)\subseteq \delta _a(\textsf {x} )}\);
-
(iii)
The state specifies exactly which action has occurred (we assume agents at least want to know this). This means that \(\pi _2(s)\) contains exactly one action \(\textsf {y} \), or it is empty (in case s is the empty state);
-
(iv)
The information state should support the content of the action it specifies. This is trivial for statements, but not for questions, since in this case an information state is not necessarily informative enough to resolve the question it specifies. This requirement has the effect that agents will typically come to entertain a question if they are sure that it was asked.Footnote 13 Formally, we require that \(M,\pi _1(s)\models \textsf {content} (\textsf {y} )\), where \(\textsf {y} \) is the unique action in \(\pi _2(s)\), if present.
Definition 16
(Product update) Let M be an inquisitive epistemic model and \(\textsf {M} \) an \(\textsf {AMLQ}\) action model. Then \(M' = (M \otimes \textsf {M} )\) is the product update of M and \(\textsf {M} \), defined as follows.
\(M' = \langle W', \{\varSigma _a' ~|~ a \in {\mathscr {A}}\}, V'\rangle \), where:
-
\(W' = \{\langle w, \textsf {x} \rangle ~|~ w\in W, \textsf {x} \in \textsf {S} \text { and } M,w\models \textsf {pre} (\textsf {x} )\}\)
-
\(s \in \varSigma '_a(\langle w, \textsf {x} \rangle )\) iff
-
(i)
\(\pi _1(s) \in \varSigma _a(w)\)
-
(ii)
\(\pi _2(s)\subseteq \delta _a(\textsf {x} )\)
-
(iii)
There is at most one \(\textsf {y} \in \pi _2(s)\)
-
(iv)
\(\forall \textsf {y} \in \pi _2(s) : M,\pi _1(s)\models \textsf {content} (\textsf {y} )\)
-
(i)
-
\(\langle w, \textsf {x} \rangle \in V'(p)\) iff \(w\in V(p)\)
3.1.3 Semantics
Notice that we have extended \(\textsf {IEL}\) with dynamic modalities for sets of actions \(\textsf {s} \). We interpret these set modalities as expressing information about which action is executed: it may be any action \(\textsf {x} \in \textsf {s} \). We then recover the execution of a single action as a special case, namely the case where \(\textsf {s} \) is a singleton.
The semantics of \(\textsf {AMLQ}\) consists of the support conditions of \(\textsf {IEL}\), extended with a new support condition for dynamic modalities. Before we can define this support condition, we need a way to connect states in the original model to the corresponding states in the updated model. Let M be an inquisitive epistemic model and s an information state in that model. Let \(\textsf {M} \) be an \(\textsf {AMLQ}\) action model and \(\textsf {s} \) a set of actions in that model. Furthermore, let \(M' = M \otimes \textsf {M} \).
Definition 17
(Updated state) \(s[\textsf {M} ,\textsf {s} ]\) is the information state in \(M'\) such that:
We allow omission of the action model \(\textsf {M} \) in the notation of updated states. Notice that by the above definition, the set \(s[\textsf {s} ]\) consists of all the pairs \(\langle w, \textsf {x} \rangle \in s\times \textsf {s} \) such that \(M,w\models \textsf {pre} (\textsf {x} )\). Using the notion of updated states, we can now give the support condition for dynamic modalities.
Definition 18
(Support condition for dynamic modalities) The support condition for dynamic modalities is the following:
Like in \(\textsf {IEL}\), truth in a world is defined as support in the corresponding singleton state. We therefore have the following truth condition for dynamic modalities.
Fact 4
(Truth condition for dynamic modalities) Let \(w[\textsf {M} ,\textsf {s} ] = \{ \langle w, \textsf {x} \rangle \in W' ~|~ {\textsf {x} \in \textsf {s} } \}\). Then the truth condition for dynamic modalities is the following:
Because \(\textsf {s} \) may contain multiple actions, \(w[\textsf {s} ]\) may be an information state consisting of more than one world. This means that, for \([\textsf {s} ]\varphi \) to be true in w, \(\varphi \) must be supported in \(w[\textsf {s} ]\). Giving a characterization of truth of dynamic formulas only in terms of truth is only possible for modalities of a single action:
This formulation makes it clear that \([\textsf {x} ]\varphi \) is true in w just in case either the action \(\textsf {x} \) is incompatible with w (making the formula vacuously true) or \(\varphi \) is true in the corresponding world \(\langle w, \textsf {x} \rangle \) in the product update. This corresponds exactly to the truth condition of dynamic modalities in \(\textsf {AML}\).
Intuitively, a formula of the form \([\textsf {x} ]\varphi \) expresses that \(\varphi \) is supported after action \(\textsf {x} \) is executed. A formula with a dynamic modality that contains a set \(\textsf {s} \) of actions, like \([\textsf {s} ]\varphi \), can be read as: ‘after getting the information that some action of \(\textsf {s} \) is executed, \(\varphi \) is supported’. This means we can think of sets of actions \(\textsf {s} \) in the same way as we think of information states s. Namely, as encoding the information that the actual world (action) is one of the worlds (actions) in the set.
In \(\textsf {AMLQ}\), entailment amounts to preservation of support, just as in \(\textsf {IEL}\):
Definition 19
(Entailment) Let \(s\models \varPhi \) be short for ‘\(s \models \varphi \) for all \(\varphi \in \varPhi \)’. Then entailment is defined as follows:
3.1.4 Epistemic states and state maps in updated models
The following lemma tells us that the information state of a in world \(\langle w, \textsf {x} \rangle \) of the updated model is simply the information state of a in world w of the original model updated with the set of actions which a considers possible, \(\delta _a(\textsf {x} )\).
Lemma 1
(Epistemic states in updated models) Let w be a world in an inquisitive epistemic model M, \(\textsf {x} \) an action in action model \(\textsf {M} \) and \(M' = M\otimes \textsf {M} \). Let \(\langle w, \textsf {x} \rangle \) be a world in \(M'\). Then we have the following:
Proof
By unpacking Definitions 16 and 17.\(\square \)
This shows that epistemic states in the updated model are obtained as in standard action model logic. The next lemma shows how inquisitive states in the original and updated models are related.
Lemma 2
(State maps in updated models) Let w be a world in an inquisitive epistemic model M, \(\textsf {x} \) an action in action model \(\textsf {M} \) and \(M' = M\otimes \textsf {M} \). Suppose \(\langle w, \textsf {x} \rangle \in W'\). Then we have the following:
Proof
By unpacking Definition 16.\(\square \)
The above lemma may be viewed as an alternative formulation of the definition of \(\varSigma '_a\).
3.2 Example
Let us now look at a simple example to see the mechanisms at work. Suppose Anna and Bob have invited their friends Peter and Quinn to their party. Initially, both Anna (a) and Bob (b) have no knowledge or issues about whether Peter is attending (p) or Quinn is attending (q), as illustrated in Fig. 5a.
Then, Anna gets a call from Peter. He asks whether Quinn is attending (\(\mathord {?}q\)). However, Bob considers it possible that Peter calls to say whether he himself is attending (p) or not (\(\lnot p\)). We encode this epistemic action in an action model with three actions: \(\textsf {x}\), \(\textsf {y}\) and \(\textsf {z}\), where \(\textsf {content} (\textsf {x}) = p\), \(\textsf {content} (\textsf {y}) = \lnot p\) and \(\textsf {content} (\textsf {z}) = \mathord {?}q\) (Fig. 5b).
We can then calculate the product update (Fig. 5c and d). We know that the actual world in the updated model is one of the \(\textsf {z} \)-worlds. Thus, after the phone call, Anna entertains the issue whether Quinn is attending (all information states in the original model support \([\textsf {z} ]E_a \mathord {?}q\)), but Bob does not (\([\textsf {z} ]\lnot E_b\mathord {?}q)\).
3.3 Properties of \(\textsf {AMLQ}\)
In this section I will discuss some interesting properties of \(\textsf {AMLQ}\), which will be used in proofs in later sections.
3.3.1 Persistence and empty state
Let me start by noting that the support relation of \(\textsf {AMLQ}\) has the persistence property and the empty state property, which are the hallmark of inquisitive logics.
Proposition 2
(Properties of the support relation) For all models M and formulas \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\), we have the following properties:
-
Persistence property: if \(M,s\models \varphi \) and \(t\subseteq s\), then \(M,t\models \varphi \)
-
Empty state property: \(M,\emptyset \models \varphi \)
Proof
By unpacking the support conditions.\(\square \)
The persistence property corresponds to the intuitive idea that if some body of information is enough to support a formula, than so is any more specific body of information. The empty set is interpreted as the inconsistent state and thus supports every formula.
3.3.2 Declaratives
As in \(\textsf {IEL}\), we can syntactically define a fragment of our language, the declaratives, and prove that all of its members are truth-conditional.
Definition 20
(Declarative fragment of \({\mathscr {L}}^{\textsf {AMLQ}}\)) The set of declarative formulas \({\mathscr {L}}^{\textsf {AMLQ}}_!\) is defined inductively as follows, where \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\):
Although \(K_a\varphi \) and \(E_a\varphi \) are truth-conditional even if \(\varphi \) is not, this is not the case for \([\textsf {s} ]\varphi \), as can be seen from the support condition of the dynamic modality. For instance, \([\textsf {s} ]\mathord {?}p\) will typically not be truth-conditional (although this depends also on \(\textsf {s} \)). Therefore, I will call \([\textsf {s} ]\alpha \) a declarative just in case \(\alpha \) is.
Proposition 3
Any \(\alpha \in {\mathscr {L}}^{\textsf {AMLQ}}_!\) is truth-conditional
Proof
By induction on the complexity of \(\alpha \). All steps of the proof proceed as in \(\textsf {IEL}\) (Ciardelli 2016, p. 260). We only add the step for the dynamic modality. By the induction hypothesis, \(\alpha \) is truth-conditional. Then we use the support condition of the dynamic modality and the definition of a state in an updated model to obtain:
By Definition 7, \([\textsf {s} ]\alpha \) is truth-conditional. \(\square \)
3.3.3 Resolutions and normal form
An important result, familiar from \(\textsf {IEL}\), is that every formula of \({\mathscr {L}}^{\textsf {AMLQ}}\) is equivalent to an inquisitive disjunction of declarative formulas, namely its resolutions.
Definition 21
(Resolutions) (based on Ciardelli 2016) For any formula \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\), its set of resolutions \({\mathscr {R}}(\varphi )\) is defined inductively as follows:
-
\({\mathscr {R}}(\alpha ) = \{\alpha \}\) if \(\alpha \) is an atom, \(\bot \) or a modal formula \(K_a\varphi \) or \(E_a\varphi \)
-
\({\mathscr {R}}(\varphi \wedge \psi ) = \{\alpha \wedge \beta ~|~ \alpha \in {\mathscr {R}}(\varphi )\text { and } \beta \in {\mathscr {R}}(\psi )\}\)
-
\({\mathscr {R}}(\varphi \rightarrow \psi ) = \{\bigwedge _{\alpha \in {\mathscr {R}}(\varphi )}(\alpha \rightarrow f(\alpha ))~|~ f \text { is a function from } {\mathscr {R}}(\varphi )\text { to } {\mathscr {R}}(\psi )\}\)
-
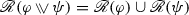
-
\({\mathscr {R}}([\textsf {s} ]\varphi ) = \{[\textsf {s} ]\alpha ~|~ \alpha \in {\mathscr {R}}(\varphi )\}\)
Proposition 4
(Resolution support) For all \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\), for every inquisitive epistemic model M and state s:
Proof
By induction on the complexity of \(\varphi \). All steps of the proof proceed as in \(\textsf {IEL}\) (Ciardelli 2016, p. 261). We only add the step for the dynamic modality. By the induction hypothesis, \(M,s\models \varphi \iff M,s\models \alpha \text { for some }\alpha \in {\mathscr {R}}(\varphi )\). Then we use the support condition of the dynamic modality and Definition 21 to obtain:
\(\square \)
Proposition 5
(Normal form) For all \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\),  .
.
Proof
Resolution sets are by definition finite. Hence, this proposition follows immediately from Proposition 4 and the support condition of inquisitive disjunction.\(\square \)
3.3.4 Set modalities and non-deterministic actions
In \(\textsf {AML}\) there are dynamic modalities not just for simple actions, but also for complex actions, e.g. we have formulas of the form \([\textsf {x} \cup \textsf {y} ]\alpha \). Like in \(\textsf {PDL}\) (Fischer and Ladner 1979), the action \(\textsf {x} \cup \textsf {y} \) is taken to be the single action of non-deterministically executing the action \(\textsf {x} \) or \(\textsf {y} \). This seems very similar to \([\{\textsf {x} ,\textsf {y} \}]\alpha \) in \(\textsf {AMLQ}\), which we take to mean that our information implies that \(\alpha \) is true after getting the information that either of \(\textsf {x} \) and \(\textsf {y} \) is executed.
These two interpretations of dynamic modalities are in fact interchangeable, as long as the language does not contain questions. Thus, the informational interpretation I give to these modalities is also available in \(\textsf {AML}\). However, the two interpretations come apart when we consider questions. If \(\mu \) is a question, \([\textsf {s} ]\mu \) expresses something stronger than support of \(\mu \) after any \(\textsf {x} \in \textsf {s} \).
To see this, consider the example depicted in Fig. 6. The original information state of agent a supports both \([\textsf {x} ]p\) and \([\textsf {y} ]\lnot p\), as can be seen from Fig. 6c: given the information that \(\textsf {x} \) is occurring, it supports p, while given the information that \(\textsf {y} \) is occurring, it supports \(\lnot p\). So, after any action in the set \(\{\textsf {x} ,\textsf {y} \}\), \(\mathord {?}p\) is supported. However, a’s original information state does not support \([\{\textsf {x} ,\textsf {y} \}]\mathord {?}p\): the information that one of \(\textsf {x} \) and \(\textsf {y} \) is executed is not enough to settle \(\mathord {?}p\), since the information state in the updated model that corresponds to this information (\(\{\langle w_1, \textsf {x} \rangle ,\langle w_2, \textsf {y} \rangle \}\)) does not support \(\mathord {?}p\).
This shows the following:
Proposition 6
\([\{\textsf {x} ,\textsf {y} \}]\varphi \not \equiv [\textsf {x} ]\varphi \wedge [\textsf {y} ]\varphi \)
This is a fundamental difference between dynamic modalities in support-conditional semantics and in truth-conditional semantics. In logics based on the latter, like \(\textsf {AML}\), this equivalence does hold (van Ditmarsch et al. 2007, p. 152). As one would expect, this equivalence also holds in \(\textsf {AMLQ}\) whenever \(\varphi \) is truth-conditional. We can even be a bit more general and prove this for all sets \(\textsf {s} \).Footnote 14
Proposition 7
If \(\alpha \) is truth-conditional, then \([\textsf {s} ]\alpha \equiv \bigwedge _{\textsf {x} \in \textsf {s} }[\textsf {x} ]\alpha \)
Proof
As dynamic modalities and conjunction preserve truth-conditionality (see the proof of Proposition 3), \([\textsf {s} ]\alpha \) and \(\bigwedge _{\textsf {x} \in \textsf {s} }[\textsf {x} ]\alpha \) are truth-conditional. This means that it suffices to show that they have the same truth conditions. From the fact that \(\alpha \) is truth-conditional, the definition of \(s[\textsf {s} ]\) and the support conditions of the dynamic modality and conjunction we can obtain:
\(\square \)
3.4 Reduction
We can axiomatize \(\textsf {AMLQ}\) using the same strategy as is used for \(\textsf {AML}\) (van Ditmarsch et al. 2007) and \(\textsf {IDEL}\) (Ciardelli 2016), namely by showing that the dynamic logic is not more expressive than the static logic it extends (in this case, \(\textsf {IEL}\)).
3.4.1 Atom and \(\bot \)
Like in \(\textsf {AML}\), the following equivalences hold for formulas in which a dynamic modality precedes an atom or \( \bot \). As usual, \(\textsf {x} \) denotes a single action.
Proposition 8
\([\textsf {x} ]p \equiv \textsf {pre} (\textsf {x} )\rightarrow p\)
Proof
As both formulas are declaratives, we only need to show that they have the same truth conditions. We can show this using the truth condition of the dynamic modality, the definition of a state in an updated model and the truth condition of implication.
\(\square \)
In a similar way we can obtain a reduction equivalence for \(\bot \).
Proposition 9
\([\textsf {x} ]\bot \equiv \lnot \textsf {pre} (\textsf {x} )\)
Proof
Again both formulas are declaratives, so we can show this with a proof similar to the previous one.\(\square \)
3.4.2 Conjunction and inquisitive disjunction
Whenever a dynamic modality precedes a conjunction, we can distribute it over the conjunction, just like in \(\textsf {AML}\) and \(\textsf {IDEL}\). This goes for dynamic modalities of single actions as well as sets.
Proposition 10
\([\textsf {s} ](\varphi \wedge \psi ) \equiv [\textsf {s} ]\varphi \wedge [\textsf {s} ]\psi \)
Proof
By unpacking the support conditions of the dynamic modality and conjunction.\(\square \)
With dynamic modalities that precede an inquisitive disjunction, we can do the same.
Proposition 11

Proof
Analogous to Proposition 10.\(\square \)
3.4.3 Implication
Although one might expect that we can have a similar reduction equivalence for implication, this is in fact not the case, as the following proposition shows.
Proposition 12
\([\textsf {s} ](\varphi \rightarrow \psi ) \not \equiv [\textsf {s} ]\varphi \rightarrow [\textsf {s} ]\psi \)
Proof
Consider the original state map, action model and updated state map in Fig. 7. Let \(s = \{w_1,w_2\}\) and \(\textsf {s} = \{\textsf {x} ,\textsf {y} \}\). Then \(s[\textsf {s} ]\) is the information state consisting of all the worlds in the updated model. This information state does not support \(\lnot K_a p\), because it contains a world \(\langle w_1, \textsf {x} \rangle \) in which a does know that p. So \(s[\textsf {s} ]\not \models K_a p\rightarrow \bot \), which in turn means that \(s\not \models [\textsf {s} ](K_a p\rightarrow \bot )\).
However, the only subset of s that supports \([\textsf {s} ]K_a p\) is the empty set, and the empty set supports \([\textsf {s} ]\bot \). Thus, \(s\models [\textsf {s} ]K_a p\rightarrow [\textsf {s} ]\bot \).\(\square \)
The problem with the right to left direction is that to show from any assumption that a state s supports \([\textsf {s} ](\varphi \rightarrow \psi )\), we need to show that any \(t'\subseteq s[\textsf {s} ]\) that supports \(\varphi \), supports \(\psi \) as well. However, this \(t'\) may be any subset, meaning that \(t'\) may not be equal to \(t[\textsf {t} ]\) for any t and \(\textsf {t} \). Therefore, there is no way we can use the support conditions of the dynamic modality and implication to find a reduction equivalence for \([\textsf {s} ](\varphi \rightarrow \psi )\).
This problem does not occur when \(\textsf {s} \) is a singleton: any subset of \(s[\textsf {x} ]\) is in fact equal to some \(t[\textsf {x} ]\) where \(t\subseteq s\). We can use this to show the following equivalence.
Proposition 13
\([\textsf {x} ](\varphi \rightarrow \psi ) \equiv [\textsf {x} ]\varphi \rightarrow [\textsf {x} ]\psi \)
Proof
- \((\Rightarrow )\) :
-
Assume \(M,s\models [\textsf {x} ](\varphi \rightarrow \psi )\). Then by the support condition of the dynamic modality, \(M',s[\textsf {x} ]\models \varphi \rightarrow \psi \). Take any \(t\subseteq s\) such that \(M,t\models [\textsf {x} ]\varphi \). Then \(M',t[\textsf {x} ]\models \varphi \). As \(t[\textsf {x} ]\) is a subset of \(s[\textsf {x} ]\), \(M',t[\textsf {x} ]\models \psi \) by the support condition of implication. This means that \(M,t\models [\textsf {x} ]\psi \). By the support condition of implication we have \(M,s\models [\textsf {x} ]\varphi \rightarrow [\textsf {x} ]\psi \).
- \((\Leftarrow )\) :
-
Assume \(M,s\models [\textsf {x} ]\varphi \rightarrow [\textsf {x} ]\psi \). Take any \(t'\subseteq s[\textsf {x} ]\) such that \(t'\models \varphi \). Let \(t=\pi _1(t')\). Then by the definition of updated states, \(t[\textsf {x} ] = t'\). As \(M',t[\textsf {x} ]\models \varphi \), \(M,t\models [\textsf {x} ]\varphi \). By the support condition of implication, \(M,t\models [\textsf {x} ]\psi \). So \(M',t[\textsf {x} ]\models \psi \). As \(t'\) was an arbitrary subset of \(s[\textsf {x} ]\), by the support condition of implication, \(M',s[\textsf {x} ]\models \varphi \rightarrow \psi \). Therefore \(M,s\models [\textsf {x} ](\varphi \rightarrow \psi )\). \(\square \)
As we will see, this equivalence suffices to guarantee that any formula of \(\textsf {AMLQ}\) is equivalent to a static formula of \(\textsf {IEL}\). However, it will pose a challenge for the proof.
3.4.4 Knowledge modality
It might be tempting to think that \([\textsf {x} ]K_a \alpha \) is equivalent to \(K_a[\textsf {x} ]\alpha \), but it is not: even if a knows that after \(\textsf {x} \) it is the case that \(\alpha \), a may still fail to know after \(\textsf {x} \) that \(\alpha \) is the case, because she was ignorant of the fact that \(\textsf {x} \) occurred. We have to keep track of the knowledge of a with respect to which action is occurring. Doing so, we will find that \([\textsf {x} ]K_a\alpha \) is equivalent to \(\textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}K_a[\textsf {y} ]\alpha \), just as in \(\textsf {AML}\). Indeed, for statements \(\alpha \), knowing \(\alpha \) after \(\textsf {x} \) is (given that the precondition of \(\textsf {x} \) is met) the same as knowing that after any action indistinguishable from \(\textsf {x} \), \(\alpha \) will be the case. However, this equivalence does not generalize to questions:
Proposition 14
\([\textsf {x} ]K_a\varphi \not \equiv \textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}K_a[\textsf {y} ]\varphi \)
Proof
Consider the following counterexample, illustrated in Fig. 8: agent a has no non-trivial knowledge or issues in the original model and no knowledge about which action is taking place, which is in fact action \(\textsf {x} \).
Clearly, in the updated model, a still does not know whether p is true or false. So \([\textsf {x} ]K_a\mathord {?}p\) is false in \(w_1\). However, \(\textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}K_a[\textsf {y} ]\mathord {?}p\) is true in \(w_1\), because a does know that \([\textsf {x} ]p\) and \([\textsf {y} ]\lnot p\), which together make the consequent true.\(\square \)
Since \(\varphi \) can be a question, knowing \(\varphi \) after some action \(\textsf {x} \) is not the same as knowing that after \(\textsf {y} \), \(\varphi \), for each action \(\textsf {y} \) indistinguishable from \(\textsf {x} \).
In fact, for \([\textsf {x} ]K_a\mathord {?}p\) to be true, it is required that either \(K_a([\textsf {x} ]p \wedge [\textsf {y} ]p)\) or \(K_a([\textsf {x} ]\lnot p \wedge [\textsf {y} ]\lnot p)\). This means we could come up with an equivalence for \([\textsf {x} ]K_a\varphi \) by quantifying over the resolutions of \(\varphi \). However, we get a more concise equivalence if we use the set modality to express the uncertainty about which action is the actual one. We can show that after \(\textsf {x} \), a knows \(\varphi \) just in case \(\textsf {pre} (\textsf {x} )\) is false or a’s current information state is such that learning that one of \(\delta _a(\textsf {x} )\) is executed is enough to settle \(\varphi \).
Proposition 15
\([\textsf {x} ]K_a\varphi \equiv \textsf {pre} (\textsf {x} ) \rightarrow K_a[\delta _a(\textsf {x} )]\varphi \)
Proof
As both formulas are declaratives, we only need to show that they have the same truth conditions.
- \((\Rightarrow )\):
-
Assume \(M,w\models [\textsf {x} ]K_a\varphi \). Then \(M',w[\textsf {x} ]\models K_a\varphi \). Assume \(M,w\models \textsf {pre} (\textsf {x} )\). Then \(\langle w, \textsf {x} \rangle \) exists in \(M'\). We have \(M',\sigma '_a(\langle w, \textsf {x} \rangle )\models \varphi \) and by Lemma 1, \(\sigma '_a(\langle w, \textsf {x} \rangle ) = \sigma _a(w)[\delta _a(\textsf {x} )]\). So \(M',\sigma _a(w)[\delta _a(\textsf {x} )]\models \varphi \). We use the truth condition of the dynamic modality to obtain \(M,\sigma _a(w)\models [\delta _a(\textsf {x} )]\varphi \). By the truth condition of the knowledge modality, \(M,w\models K_a[\delta _a(\textsf {x} )]\varphi \). We can then drop our assumption that \(M,w\models \textsf {pre} (\textsf {x} )\) to obtain \(M,w\models \textsf {pre} (\textsf {x} ) \rightarrow K_a[\delta _a(\textsf {x} )]\varphi \).
- \((\Leftarrow )\):
-
Assume \(M,w\models \textsf {pre} (\textsf {x} ) \rightarrow K_a[\delta _a(\textsf {x} )]\varphi \). Either \(M,w\models \textsf {pre} (\textsf {x} )\) or \(M,w\not \models \textsf {pre} (\textsf {x} )\). In the latter case, we immediately have \(M,w\models [\textsf {x} ]K_a\varphi \), since \(w[\textsf {x} ] = \emptyset \). In the former case, we have \(M,w\models K_a[\delta _a(\textsf {x} )]\varphi \). By the truth condition of the knowledge modality, \(M,\sigma _a(w)\models [\delta _a(\textsf {x} )]\varphi \). Then by the truth condition the dynamic modality, \(M',\sigma _a(w)[\delta _a(\textsf {x} )]\models \varphi \). Since by Lemma 1, \(\sigma '_a(\langle w, \textsf {x} \rangle ) = \sigma _a(w)[\delta _a(\textsf {x} )]\), that means \(M',\sigma '_a(\langle w, \textsf {x} \rangle )\models \varphi \). Hence, \({M',w[\textsf {x} ]\models K_a\varphi }\) and \(M,w\models [\textsf {x} ]K_a\varphi \). \(\square \)
3.4.5 Entertain modality
We now move on to the reduction equivalence for the entertain modality.
Proposition 16
\([\textsf {x} ]E_a\varphi \equiv \textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\varphi )\)
Proof
As both formulas are declaratives, we only need to show that they have the same truth conditions.
- \((\Rightarrow )\):
-
Assume \(M,w\models [\textsf {x} ]E_a\varphi \). Then \(M',w[\textsf {x} ]\models E_a\varphi \). Assume \(M,w\models \textsf {pre} (\textsf {x} )\). Then \(\langle w, \textsf {x} \rangle \) exists in \(M'\). By the truth condition of the entertain modality, we have for all \(s'\in \varSigma '_a(\langle w, \textsf {x} \rangle ) : M',s'\models \varphi \). Take any action \(\textsf {z} \in \delta _a(\textsf {x} )\) and some \(s\in \varSigma _a(w)\). Then take any \(t\subseteq s\) such that \(M,t\models \textsf {content} (\textsf {z} )\). By Lemma 2, \(t[\textsf {z} ]\in \varSigma '_a(\langle w, \textsf {x} \rangle )\). This means that \({M',t[\textsf {z} ]\models \varphi }\). By the support condition of the dynamic modality, we have \(M,t\models [\textsf {z} ]\varphi \). By the support condition of implication, we have \(M,s\models \textsf {content} (\textsf {z} )\rightarrow [\textsf {z} ]\varphi \). As s was an arbitrary state in \(\varSigma _a(w)\), we have \(M,w\models E_a(\textsf {content} (\textsf {z} )\rightarrow [\textsf {z} ]\varphi )\). As \(\textsf {z} \) was an arbitrary action indistinguishable by a from \(\textsf {x} \), we have \(M,w\models \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\varphi )\). Then, finally, we drop our assumption that \(M,w\models \textsf {pre} (\textsf {x} )\) to obtain \(M,w\models \textsf {pre} (\textsf {x} )\rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\varphi )\).
- \((\Leftarrow )\):
-
Assume \(M,w\models \textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\varphi )\). Either \(M,w\models \textsf {pre} (\textsf {x} )\) or \(M,w\not \models \textsf {pre} (\textsf {x} )\). In the latter case, we immediately have \(M,w\models [\textsf {x} ]E_a\varphi \), since \(w[\textsf {x} ]=\emptyset \) and we are done, so assume the former. Then we have \(M,w\models \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\varphi )\). As \(M,w\models \textsf {pre} (\textsf {x} )\), we have a world \(\langle w, \textsf {x} \rangle \) in the updated model. Take any \(s'\in \varSigma '_a(\langle w, \textsf {x} \rangle )\). Then by Lemma 2, \(s' = s[\textsf {z} ]\) for some \(s,\textsf {z} \) such that \(s\in \varSigma _a(w)\), \(\textsf {z} \in \delta _a(\textsf {x} )\) and \(M,s\models \textsf {content} (\textsf {z} )\). It follows from \(\textsf {z} \in \delta _a(\textsf {x} )\) that \(M,w\models E_a(\textsf {content} (\textsf {z} )\rightarrow [\textsf {z} ]\varphi )\). Then by \(s\in \varSigma _a(w)\) we have that \(M,s\models \textsf {content} (\textsf {z} )\rightarrow [\textsf {z} ]\varphi \). As \(M,s\models \textsf {content} (\textsf {z} )\), we obtain \(M,s\models [\textsf {z} ]\varphi \). By the support condition of the dynamic modality, \(M',s'\models \varphi \). As \(s'\) was an arbitrary state in \(\varSigma '_a(\langle w, \textsf {x} \rangle )\), we have \(M',\langle w, \textsf {x} \rangle \models E_a\varphi \), which means that \(M',w[\textsf {x} ]\models E_a\varphi \). Hence \(M,w\models [\textsf {x} ]E_a\varphi \). \(\square \)
Since any formula of the form \(K_a\varphi \) or \(E_a\varphi \) is a declarative, the reduction equivalences for \([\textsf {x} ]K_a\varphi \) and \([\textsf {x} ]E_a\varphi \) can be combined with Proposition 7 to reduce formulas of the form \([\textsf {s} ]K_a\varphi \) and \([\textsf {s} ]E_a\varphi \). We now have all the reduction equivalences we need to prove the following theorem.
Theorem 1
(Every formula of \(\textsf {AMLQ}\) is equivalent to some formula of \(\textsf {IEL}\))
For any \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\), there is some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\varphi \equiv \varphi ^*\).
Proof sketch The challenge for the proof is the lack of a reduction equivalence for formulas of the form \([\textsf {s} ](\varphi \rightarrow \psi )\), where \(\textsf {s} \) contains more than one action and \(\varphi \rightarrow \psi \) is a question, since neither Proposition 7 nor Proposition 13 can be used in this case.
However, we can use the fact that \([\textsf {s} ](\varphi \rightarrow \psi )\) is equivalent to its normal form: the inquisitive disjunction of its resolutions. The resolutions of \([\textsf {s} ](\varphi \rightarrow \psi )\) are guaranteed to be declaratives, which means they can be reduced using Proposition 7. The full proof is given in the Appendix.
3.5 Axiomatizing \(\textsf {AMLQ}\)
A sound and complete proof system for \(\textsf {AMLQ}\) can be obtained by combining all the inference rules for \(\textsf {IEL}\)Ciardelli (2014) and the rules in Fig. 9.Footnote 15 The rules in this figure are reduction rules that correspond to the equivalences we proved in Sect. 3.4, together with a rule of replacement of equivalents.Footnote 16 The relation of derivability in this system is denoted by \(\vdash \) and the relation of inter-derivability by \(\dashv \vdash \).
Theorem 2
(\(\textsf {AMLQ}\) is sound and complete)
For any \(\varPhi \cup \{\psi \}\subseteq {\mathscr {L}}^{\textsf {AMLQ}}, \varPhi \vdash \psi \iff \varPhi \models \psi \).
The proof is given in the Appendix.
4 Action models with issues
I will now turn to the second approach of merging \(\textsf {IEL}\) and \(\textsf {AML}\). This time we will interpret actions as possible observations and add issues as to what is observed.
Standard action models assign to each action \(\textsf {x} \) an information state \(\delta _a(\textsf {x} )\), which is the set of actions held possible by a relative to \(\textsf {x} \). If a rolls a die and observes this herself, then we can say that \(\delta _a(\textsf {x} _1) = \{\textsf {x} _1\}, \delta _a(\textsf {x} _2) = \{\textsf {x} _2\}\), etc. In this way, the information a has will depend on what actually happened.
We can treat issues in a similar way. Suppose b made a bet that the die would land on 6. Because she observes the die from a distance, she can only tell if the number is lower than 4 or not. Her issue will then depend on what happened: if the die landed on 1, 2 or 3, she does not require any more specific information. But if any other action occurred, then she needs to know whether the actual action is in \(\{\textsf {x} _6\}\) or in \(\{\textsf {x} _4,\textsf {x} _5\}\).
We can encode this by giving action models the structure of inquisitive epistemic models: we equip each agent in the action model with an inquisitive state map. This state map assigns to each action an inquisitive state: the set of information states (in this case, sets of actions) that count as resolving the agent’s issue with respect to the observations. Thus, the state map does not just encode the indistinguishability of actions (uncertainty about what is observed) but also the agent’s issues about what is being observed.
Like in the previous section, I will also introduce a new logical language that extends \(\textsf {IEL}\) with dynamic modalities. This will be referred to as Action Model Logic with Issues (\(\textsf {AMLI}\)).
4.1 Definitions
The contents of actions will be formulas of \({\mathscr {L}}^{\textsf {AMLI}}_!\), the declarative fragment of \({\mathscr {L}}^{\textsf {AMLI}}\), defined as in Definition 20. The syntax of the language is defined in the same way as in Definition 12. The definition of the models is given below.Footnote 17
Definition 22
(Action Model with Issues) For natural numbers \(i \ge 0\), an \(\textsf {AMLI}\) action model of level i is a triple \(\textsf {M} = \langle \textsf {S} , \{ \varDelta _a ~|~ a \in {\mathscr {A}}\}, \textsf {pre} \rangle \), where:
-
\(\textsf {S} \) is a finite domain of actions;
-
\(\varDelta _a\) is a function that maps each action to a non-empty downward closed set of sets of actions;
-
\(\textsf {pre} : \textsf {S} \rightarrow {\mathscr {L}}^{\textsf {AMLI}_i}_!\) is a function that assigns a precondition \(\textsf {pre} (\textsf {x} ) \in {\mathscr {L}}^{\textsf {AMLI}_i}_!\) to each action \(\textsf {x} \in \textsf {S} \).
Let \(\delta _a(\textsf {x} ) {:}{=} \bigcup \varDelta _a(\textsf {x} )\), the set of actions indistinguishable from \(\textsf {x} \) to a.
I define a new update procedure, which is much more straightforward than the one for \(\textsf {AMLQ}\), since this only needs to take care of two things:
-
(i)
Preserve the knowledge and issues from the original epistemic model (i.e. with respect to worlds). Formally, \(\pi _1(s) \in \varSigma _a(w)\).
-
(ii)
Preserve the knowledge and issues from the action model (i.e. with respect to actions). Formally, \(\pi _2(s) \in \varDelta _a(\textsf {x} )\).
Definition 23
(Product update) Let M be an inquisitive epistemic model and \(\textsf {M} \) an \(\textsf {AMLI}\) action model. Then \(M' = (M \otimes \textsf {M} )\) is the product update of M and \(\textsf {M} \), defined as follows.
\(M' = \langle W', \{\varSigma _a' ~|~ a \in {\mathscr {A}}\}, V'\rangle \), where:
-
\(W'\) and \(V'\) are defined as in Definition 16.
-
\(s \in \varSigma '_a(\langle w, \textsf {x} \rangle )\) iff
-
(i)
\(\pi _1(s) \in \varSigma _a(w)\)
-
(ii)
\(\pi _2(s) \in \varDelta _a(\textsf {x} )\)
-
(i)
Since we require factivity of \(\varSigma _a\), we need to require that the agent’s knowledge about the actions is also factive (for all \(\textsf {x} \in \textsf {S} \), \(\textsf {x} \in \delta _a(\textsf {x} )\)), to make sure that factivity is preserved by the update. Similarly, whenever introspection is assumed in \(\varSigma _a\), it is preserved by the update procedure as long as \(\varDelta _a\) satisfies introspection.
As for the semantics, the support condition for dynamic modalities is defined analogous to \(\textsf {AMLQ}\). The facts and definitions I discussed in Sect. 3.3 (persistence and empty state properties, declarative fragment, resolutions and normal form) carry over to \(\textsf {AMLI}\).
4.2 Example
Let us look at a simple scenario that we can model in this system. Suppose there is a disease for which no cure is known yet. In order to find out whether two newly developed medicines cure this disease, an experiment takes place. However, the experiment is designed in such a way that for each medicine, the outcome can only be positive or indeterminate.
Thus, the experiment has four possible results: both medicines work (\(p\wedge q\)), one of them works (p or q) or the result is indeterminate for both medicines (\(\top \)). The action model contains four actions, one for each of these results.
The experiment is performed by a laboratory technician (agent a), who is not involved in the development of the medicines and has no prior knowledge or non-trivial issues about whether the medicines work (Fig. 10a). Being the observer herself, she knows exactly what is observed (Fig. 10d).
There are also two other agents involved, who are not present when the experiment is performed, but are interested in the outcome. Agent b is a doctor, who wants to have a medicine to cure the disease. This means she already has an issue before the experiment, which is resolved either when one such medicine is found or when it becomes clear that neither of them works (Fig. 10b).Footnote 18 Because information about q cannot be disclosed to medical professionals immediately after the experiment, the doctor only gets information about p, and not about q (Fig. 10e).
Agent c is another laboratory technician and a colleague of a. In case the result of the experiment is indeterminate, she will be given the task to design a new experiment. Initially, she has no information about the outcome. Her issue is resolved by finding out whether or not observation \(\textsf {x} _\textsf {4}\) was made (Fig. 10f).
Example of an update in \(\textsf {AMLI}\). a State map of a before action, b state map of b before action, c state map of c before action, d state map of a in action model, e state map of b in action model, f state map of c in action model, g state map of a after action, h state map of b after action and i state map of c after action
As can be seen in the updated model (Fig. 10g–i), the update results in state maps that combine the state maps from the original model and the action model. We can express the effects of the experiment on the knowledge and issues of the agents using dynamic modalities. Let s be the set of worlds in the original model and \(\textsf {s} \) the set of actions.
Agent a will not develop any issues. She will find a medicine just in case what she observes is not \(\textsf {x} _\textsf {4}\). Thus, if we let \(\textsf {t} = \{\textsf {x} _\textsf {1},\textsf {x} _\textsf {2},\textsf {x} _\textsf {3}\}\), then we have  , while
, while  .
.
Because of the limited information agent b gets, her issue is resolved just in case the experiment shows that p is the case. This can be expressed as follows. Let  . Then, before the experiment, agent b wonders what the answer to this question is: \(s\models W_b \mu \). Let \(\textsf {t} = \{\textsf {x} _\textsf {1},\textsf {x} _\textsf {3}\}\) and \(\textsf {t} ' = \{\textsf {x} _\textsf {2},\textsf {x} _\textsf {4}\}\). Then, \(s\models [\textsf {t} ]\lnot W_b \mu \) and \(s\models [\textsf {t} '] W_b \mu \).
. Then, before the experiment, agent b wonders what the answer to this question is: \(s\models W_b \mu \). Let \(\textsf {t} = \{\textsf {x} _\textsf {1},\textsf {x} _\textsf {3}\}\) and \(\textsf {t} ' = \{\textsf {x} _\textsf {2},\textsf {x} _\textsf {4}\}\). Then, \(s\models [\textsf {t} ]\lnot W_b \mu \) and \(s\models [\textsf {t} '] W_b \mu \).
For agent c, the experiment generates an issue which is resolved by finding out whether the result was indeterminate or not. We can express this in terms of the knowledge of a. Let  . Then \(\alpha \) is true just in case a knows of at least one medicine that it works. Thus, \(s \models [\textsf {s} ] W_c \mathord {?} \alpha \).
. Then \(\alpha \) is true just in case a knows of at least one medicine that it works. Thus, \(s \models [\textsf {s} ] W_c \mathord {?} \alpha \).
4.3 Reduction and axiomatization
We have seen in Sect. 3.4 that every formula of \(\textsf {AMLQ}\) can be reduced to a formula of \(\textsf {IEL}\). The same is the case for \(\textsf {AMLI}\). All reduction equivalences we formulated for \(\textsf {AMLQ}\) carry over to \(\textsf {AMLI}\), with one exception: the reduction equivalence for the entertain modality is different.
Proposition 17
\([\textsf {x} ]E_a\varphi \equiv \textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {s} \in \varDelta _a(\textsf {x} )}E_a[\textsf {s} ]\varphi \)
Proof
I give a sketch of the proof. First, by unpacking Definition 22 it is easy to show that, instead of Lemma 2, we now have:

With this fact, we can prove the equivalence by unpacking the formulas by the support conditions of the connectives, similar to the proof for Proposition 16.\(\square \)
This characterizes the fact that the two systems are the same, except for the way in which new issues can be raised by an action. The proof system for \(\textsf {AMLI}\) is the same as the one for \(\textsf {AMLQ}\), but with a different reduction axiom for the entertain modality, corresponding to the equivalence above. The completeness proof is analogous.
5 Comparison
In this section, I will compare the systems \(\textsf {AMLQ}\) and \(\textsf {AMLI}\) with the systems we discussed in the introduction and with each other.
5.1 Comparing \(\textsf {AMLQ}\) with \(\textsf {AML}\) and \(\textsf {IDEL}\)
Let us first see how \(\textsf {AMLQ}\) relates to \(\textsf {AML}\). We have seen that the update procedure of \(\textsf {AMLQ}\) is standard with respect to knowledge. Furthermore, we can check that all connectives of the language of \(\textsf {AML}\) have the same truth conditions as those of \(\textsf {AMLQ}\) and that all \(\alpha \in \textsf {AML}\) are truth-conditional. It follows that the semantics of these formulas remains standard in our setting, and so does the notion of entailment restricted to these formulas. This makes \(\textsf {AMLQ}\) a conservative extension of \(\textsf {AML}\).
We have seen how \(\textsf {IDEL}\) extends \(\textsf {IEL}\) with public announcements. In \(\textsf {AMLQ}\), the public announcement of a formula \(\varphi \) can be encoded in an action model with \(\textsf {pub}^\varphi \) as its only action and \(\textsf {content} (\textsf {pub}^\varphi ) = \varphi \). It can be shown that the effect of updating with this model in \(\textsf {AMLQ}\) is the same as the effect of the public announcement of \(\varphi \) in \(\textsf {IDEL}\). Thus, if we define \([\varphi ]\psi \) as an abbreviation of \([\textsf {pub}^\varphi ]\psi \), \(\textsf {AMLQ}\) is a conservative extension of \(\textsf {IDEL}\). Like \(\textsf {IDEL}\), it is then also a conservative extension of \(\textsf {IEL}\) and \(\textsf {PAL}\). See Fig. 11 for a visual representation of how these logics relate. Arrows to the left stand for an extension of the dynamic possibilities in the system; arrows to the right stand for making the logic inquisitive.
5.2 Comparing \(\textsf {AMLI}\) with \(\textsf {AMLQ}\)
I will now compare the two systems developed in this paper. First, I will show that actions in \(\textsf {AMLQ}\) can be simulated in \(\textsf {AMLI}\), while the converse is not the case. Then, we will see that combining the two systems poses a challenge.
5.2.1 Simulating \(\textsf {AMLQ}\) in \(\textsf {AMLI}\)
Let us consider once again the scenario from Sect. 3.2, in which our agents considered three speech acts to be possible: two of stating and one of asking. If we change our perspective slightly, we will see that this scenario can be simulated in \(\textsf {AMLI}\). We have to allow actions to not just be observations, but also future observations. Then, the asking of a question \(\mathord {?}q\) can be modelled by two actions which represent future observations that resolve \(\mathord {?}q\): thus, one action for each resolution, q and \(\lnot q\), and an issue over them (Fig. 12a and c). This is the same way that questions enter the system in \(\textsf {ELQm}\) (van Benthem and Minică 2012).
Example from Sect. 3.3 in \(\textsf {AMLI}\). a State map of a in action model, b state map of a after action, c state map of b in action model and d state map of b after action
As can be seen, the resulting product update is isomorphic to the product update in the same example in \(\textsf {AMLQ}\). Thus, it does not matter for the outcome whether we encode our scenario in \(\textsf {AMLQ}\) or \(\textsf {AMLI}\).
Recall that in \(\textsf {AMLQ}\), we made the assumption that uncertainty about epistemic actions is always an issue to the agents: if they don’t know which action is the actual one, then their issues can only be resolved by finding this out. Now, let us add a third agent c, who is aware of the phone call, but not interested (Fig. 13a). As we can see in the updated state map (Fig. 13b), this agent will not develop any new issues. Thus, contrary to \(\textsf {AMLQ}\), agents who are uninterested in the action can be encoded in an \(\textsf {AMLI}\) action model.
The example above is not just a special case: in fact, it turns out that any action model of \(\textsf {AMLQ}\) can be translated to an \(\textsf {AMLI}\) action model that gives an isomorphic product update. Let us see how.
Definition 24
(Translation of \(\textsf {AMLQ}\)action model to \(\textsf {AMLI}\)action model) Let \(\textsf {M} = \langle \textsf {S} , \{ \delta _a ~|~ a \in {\mathscr {A}}\}, \textsf {content} \rangle \) be an \(\textsf {AMLQ}\) action model. We will define a corresponding \(\textsf {AMLI}\) action model \(\textsf {M} ^*\).
First, we define a function C that maps each action to the set of all combinations of resolutions of its content. For every action \(\textsf {x} \in \textsf {S} \), let \(\varphi ^\textsf {x} \in {\mathscr {L}}^{\textsf {IEL}}\) be a formula that is equivalent to \(\textsf {content} (\textsf {x} )\).Footnote 19
By definition, every member of \(C(\textsf {x} )\) is a set of statements. For each set \(C(\textsf {x} )\), let \(C(\textsf {x} ) = \{\varGamma ^\textsf {x} _1,\ldots ,\varGamma ^\textsf {x} _n\}\). Then let \(\overline{\varGamma ^\textsf {x} _i}\) = \({\mathscr {R}}(\varphi ^\textsf {x} )-\varGamma ^\textsf {x} _i\) be the set of resolutions of the content of \(\textsf {x} \) that are not in \(\varGamma ^\textsf {x} _i\) for this particular i.
Then we define the \(\textsf {AMLI}\) action model \(\textsf {M} ^* = \langle \textsf {S} ^*, \{ \varDelta ^*_a ~|~ a \in {\mathscr {A}}\}, \textsf {pre} ^* \rangle \) as follows:
-
\(\textsf {S} ^* {:}{=} \{\textsf {x} _i ~|~ \textsf {x} \in \textsf {S} \text { and } \varGamma ^\textsf {x} _i \in C(\textsf {x} ) \}\)
-
\(\textsf {s} \in \varDelta ^*_a(\textsf {x} _i)\) iff
-
For all \(\textsf {y} _j\in \textsf {s} \) : \(\textsf {x} \in \delta _a(\textsf {y} )\)
-
For all \(\textsf {y} _j,\textsf {y} '_k\in \textsf {s} \) : \(\textsf {y} =\textsf {y} '\)
-
There is some \(\alpha \) such that for all \(\textsf {y} _j\in \textsf {s} : \alpha \in \varGamma ^\textsf {y} _j\)
-
-
For every \(\textsf {x} _i\in \textsf {S} ^*\), \(\textsf {pre} ^*(\textsf {x} _i) {:}{=} \bigwedge \varGamma ^\textsf {x} _i\wedge \bigwedge _{\alpha \in \overline{\varGamma ^\textsf {x} _i}}\lnot \alpha \)
It is easy to check that \(\textsf {M} ^*\) is indeed an action model with issues according to Definition 22. We now show that updating any inquisitive epistemic model with either \(\textsf {M} \) or \(\textsf {M} ^*\) gives us the same updated model.
Proposition 18
(Isomorphism between updated models) For every \(\textsf {AMLQ}\) action model \(\textsf {M} \) and its \(\textsf {AMLI}\) counterpart \(\textsf {M} ^*\), for every inquisitive epistemic model M : \(M\otimes \textsf {M} \) is isomorphic to \(M\otimes \textsf {M} ^*\).
Proof
Take any \(\textsf {AMLQ}\) action model \(\textsf {M} = \langle \textsf {S} , \{ \delta _a ~|~ a \in {\mathscr {A}}\}, \textsf {content} \rangle \). Now take any inquisitive epistemic model \(M = \langle W, \{\varSigma _a ~|~ a \in {\mathscr {A}}\}, V\rangle \). We claim that \(M\otimes \textsf {M} = \langle W', \{\varSigma '_a ~|~ a \in {\mathscr {A}}\}, V'\rangle \) is isomorphic to \(M\otimes \textsf {M} ^* = \langle W'', \{\varSigma ''_a ~|~ a \in {\mathscr {A}}\}, V''\rangle \).
First, observe that \(\langle w, \textsf {x} \rangle \in W'\) just in case \(\langle w, \textsf {x} _i\rangle \in W''\) for some i. To guarantee that we can make a bijection between any world \(\langle w, \textsf {x} \rangle \in W'\) and \(\langle w, \textsf {x} _i\rangle \in W''\), we also need to show that for any \(\langle w, \textsf {x} \rangle \in W'\), there is exactly one \(\langle w, \textsf {x} _i\rangle \in W''\). That is, for every \(\langle w, \textsf {x} _i\rangle ,\langle w, \textsf {x} _j\rangle \in W''\), it must be that \(i=j\). To see that this is the case, suppose that \(i\ne j\). Then by the definition of \(W''\), \(M,w\models \textsf {pre} ^*(\textsf {x} _i)\) and \(M,w\models \textsf {pre} ^*(\textsf {x} _j)\). However, as \(\varGamma ^\textsf {x} _i\ne \varGamma ^\textsf {x} _j\), there must be some \(\alpha \) that is in one of these sets and not in the other. But then from the definition of \(\textsf {pre} ^*\) we can see that w supports both this \(\alpha \) and its negation. We have obtained a contradiction, so \(i=j\).
From this we can conclude that if we let \(f(\langle w, \textsf {x} _i\rangle ) = \langle w, \textsf {x} \rangle \), then f is a bijection between \(W''\) and \(W'\). Now let us show that it is indeed an isomorphism. For this, we need to show two things:
-
(i)
The mapping preserves the structure of the state maps. That is, if we write \({\{ f(w) ~|~ w\in s \}}\) as f(s), then we have:
$$\begin{aligned} s\in \varSigma ''_a(\langle w, \textsf {x} _i\rangle ) \iff f(s) \in \varSigma '_a(f(\langle w, \textsf {x} _i\rangle ) \end{aligned}$$ -
(ii)
The mapping preserves the valuation: \(V''(\langle w, \textsf {x} _i\rangle )=V'(f(\langle w, \textsf {x} _i\rangle ))\)
Given the definition of valuation, the latter is trivial, so we only show (i). Take any world \({\langle w, \textsf {x} _i\rangle \in W''}\) and any state \(s''\subseteq W''\). Let \(s' = f(s'')\). Then we need to show that \({s''\in \varSigma ''_a(\langle w, \textsf {x} _i\rangle )\iff s'\in \varSigma '_a(\langle w, \textsf {x} \rangle )}\).
- \((\Rightarrow )\):
-
Assume \(s''\in \varSigma ''_a(\langle w, \textsf {x} _i\rangle )\). Then \(s''\) satisfies conditions (i) and (ii) of Definition 23 to be in \(\varSigma ''_a(\langle w, \textsf {x} _i\rangle )\). We need to show that \(s'\) satisfies conditions (i)–(iv) of Definition 16 to be in \(\varSigma '_a(\langle w, \textsf {x} \rangle )\). Since \(\pi _1(s') = \pi _1(s'')\) and the first condition is the same, we only need to check conditions (ii), (iii) and (iv). If \(s'\) is empty we are done, so assume it is not. From the fact that \(s''\) satisfies condition (ii) of Definition 23 we know that \(\pi _2(s'')\) satisfies the three conditions to be in \(\varDelta ^*_a(\textsf {x} )\) formulated in the definition of \(\textsf {M} ^*\). From the first condition of that definition we have that \(\forall \textsf {y} \in \pi _2(s') : \textsf {x} \in \delta _a(\textsf {y} )\), which means condition (ii) is satisfied. We know that there is exactly one \(\textsf {y} \in \pi _2(s')\) because for all \(\textsf {y} _j,\textsf {y} '_k\in \pi _2(s'')\) : \(\textsf {y} =\textsf {y} '\), so condition (iii) is satisfied. By definition there is some \(\alpha \) such that for all \(\textsf {y} _j\in \pi _2(s'')\), \(\alpha \in \varGamma ^\textsf {y} _j\). Now take any \(\langle v, \textsf {y} _j\rangle \in s''\). Then \(M,v\models \textsf {pre} ^*(\textsf {y} _j)\), so \(M,v\models \alpha \). As \(\langle v, \textsf {y} _j\rangle \) was chosen arbitrarily, this goes for all \(v\in \pi _1(s'')\), so \(M,\pi _1(s'')\models \alpha \) by the truth-conditionality of \(\alpha \). As \(\alpha \in {\mathscr {R}}(\varphi ^\textsf {y} )\), we have \(M,\pi _1(s'')\models \varphi ^\textsf {y} \) and therefore \(M,\pi _1(s'')\models \textsf {content} (\textsf {y} )\). So condition (iv) is satisfied too. As s satisfies conditions (i)-(iv) of Definition 16, \(s\in \varSigma '_a(\langle w, \textsf {x} \rangle )\).
- \((\Leftarrow )\):
-
Assume \(s'\in \varSigma '_a(\langle w, \textsf {x} \rangle )\). Then \(s'\) satisfies conditions (i)-(iv) of Definition 16 to be in \(\varSigma '_a(\langle w, \textsf {x} \rangle )\). We need to show that \(s''\) satisfies conditions (i) and (ii) of Definition 23 as well. As the first condition is the same, we only need to check that \(\pi _2(s'')\in \varDelta ^*_a(\textsf {x} )\). In our definition of \(\textsf {M} ^*\), we formulated three conditions for a set of actions to be in \(\varDelta ^*_a(\textsf {x} )\). These are all satisfied if \(s''\) is empty, so suppose it is not. We have for all \(\textsf {y} _j\in \pi _2(s'') : \textsf {x} \in \delta _a(\textsf {y} )\) by condition (ii) of Definition 16. By condition (iii) there is just one \(\textsf {y} \in \pi _2(s')\). This guarantees us that for all \(\textsf {y} _j,\textsf {y} '_k\in \pi _2(s'')\): \(\textsf {y} =\textsf {y} '\). That leaves only the third condition. By condition (iv), \(M,\pi _1(s')\models \textsf {content} (\textsf {y} )\). This means that \(M,\pi _1(s'')\models \alpha \) for some \(\alpha \in {\mathscr {R}}(\varphi ^\textsf {y} )\). Now take any world \(\langle v, \textsf {y} _j\rangle \) in \(s''\). Suppose for reductio that \(\alpha \notin \varGamma ^\textsf {y} _j\). By definition, \(\alpha \in \overline{\varGamma ^\textsf {y} _j}\). Then from \(M,v\models \textsf {pre} ^*(\textsf {y} _j)\) we obtain \(M,v\models \lnot \alpha \). But as v is in \(\pi _1(s'')\) and \(M,\pi _1(s'')\models \alpha \), we have \(M,v\models \alpha \), so we have a contradiction. This means \(\alpha \in \varGamma ^\textsf {y} _j\). Because the world was chosen arbitrarily, this goes for all worlds in \(s''\). Hence, \(\pi _2(s'')\) satisfies the third condition. As \(\pi _2(s'')\) satisfies all three conditions to be in \(\varDelta ^*_a(\textsf {x} )\), \(s''\) satisfies condition (ii) of Definition 23, which means \(s''\in \varSigma ''_a(\langle w, \textsf {x} _i\rangle )\).
We have thereby shown that f is an isomorphism between \(M\otimes \textsf {M} \) and \( M\otimes \textsf {M} ^*\).\(\square \)
This means that every action in \(\textsf {AMLQ}\) can be simulated in \(\textsf {AMLI}\). However, the converse is not the case, as we have already seen, because in \(\textsf {AMLI}\) we can encode agents who are uninterested about which action was performed, while these cannot be encoded in \(\textsf {AMLQ}\).
5.2.2 Combining \(\textsf {AMLI}\) with \(\textsf {AMLQ}\)
As we have seen, the system \(\textsf {AMLI}\) is similar to \(\textsf {AMLQ}\). The fact that there is a translation from \(\textsf {AMLQ}\) to \(\textsf {AMLI}\) means the latter inherits the conservativity results of the former with respect to \(\textsf {AML}\) and \(\textsf {IDEL}\). What makes \(\textsf {AMLI}\) more general than \(\textsf {AMLQ}\) is that issues about actions are encoded in an explicit way, allowing for agents that do not develop new issues as to which action was performed. Another advantage is that the update procedure of \(\textsf {AMLI}\) is symmetric in its treatment of worlds and actions.
However, we have also seen that if we interpret actions as speech acts, the \(\textsf {AMLQ}\) approach is more natural, since asking a question is treated in the same way as uttering a statement. This is especially relevant considering our initial goal of generalizing \(\textsf {IDEL}\), because one of its key features is the way it treats statements and questions on a par.
It is therefore natural to ask whether we can combine the two approaches to obtain a system with both advantages. At first glance, it seems this would simply amount to interpreting actions as speech acts again, and thus allowing questions to be the contents of actions in \(\textsf {AMLI}\). Let me sketch why this is more complicated than it may seem. In such a combined system, a new class of scenarios can be encoded: namely, scenarios in which an agent does not know which of two questions was asked, and does not care either. In such scenarios, there is a conflict between the issue raised by the content and the issue raised by the structure of the action model. The questions demand an issue, while the structure of the action model does not allow for one.
Although a combined system that is backwards compatible with both \(\textsf {AMLQ}\) and \(\textsf {AMLI}\) is surely possible, such conflicts make it difficult to have clear intuitions about what it should produce in cases that go beyond the scope of the two systems we have discussed in this paper. A principled solution to this problem, that does not require ad hoc conditions, is not yet available. It seems therefore that \(\textsf {AMLQ}\) and \(\textsf {AMLI}\) remain two separate systems. Both encode almost the same things, but in a different way. Depending on the interpretation we have in mind, we will either need questions on the level of actions (what was asked) or issues with respect to actions (what the agent wants to know). If we think about actions as speech acts, which is also the intended interpretation of \(\textsf {IDEL}\), then \(\textsf {AMLQ}\) is the more natural choice.
5.3 Comparing \(\textsf {AMLI}\) with \(\textsf {ELQm}\)
In the introduction I mentioned the Dynamic Logic of Questions (\(\textsf {DELQ}\)) and I noted some differences between this system and \(\textsf {IDEL}\). I mentioned that there is a non-public variant of \(\textsf {DELQ}\) called \(\textsf {ELQm}\), developed in van Benthem and Minică (2012). This system is similar to \(\textsf {AMLI}\), but has some important differences as well, which I will briefly review.
The static systems \(\textsf {IEL}\) and \(\textsf {ELQ}\), which form the basis of \(\textsf {AMLI}\) and \(\textsf {ELQm}\), respectively, have already been compared extensively in Ciardelli and Roelofsen (2015). The most important differences, as I mentioned in the introduction, are the notion of issues, which is strictly more general in \(\textsf {IEL}\), and the way questions enter the logical system. While in \(\textsf {IEL}\) there is a direct way of talking about the questions an agent entertains (\(E_a\mu \)), in \(\textsf {ELQ}\) a paraphrase is required. For instance, \(U(Q_a\varphi \vee Q_a\lnot \varphi )\) expresses that agent a entertains the question \(\mathord {?}\varphi \) (see van Benthem and Minică 2012, p. 637). This paraphrase uses the universal modality U. As a consequence of this approach, issues are always common knowledge, and it is impossible to express uncertainty about issues or issues about issues. These two differences between the static systems are inherited by their dynamic extensions \(\textsf {AMLI}\) and \(\textsf {ELQm}\).
Another difference between \(\textsf {IEL}\) and \(\textsf {ELQ}\) is that in the latter framework, cells of issue partitions may extend beyond the boundaries of cells of epistemic partitions, as is the case in Fig. 14a. In this model, the issue relation encodes that the agent is indifferent as to whether p is the case. According to the epistemic indistinguishability relation, she knows whether p is the case. In this way, the model keeps track of what the agent’s issues were prior to knowing whether p.
If we are interested in the agent’s current issues, taking into account what she already knows, we only have to look at the issue cells within the boundaries of epistemic cells. The dynamic extension of \(\textsf {ELQ}\) (van Benthem and Minică 2012) provides an issue refinement action, which transforms the issue relation in such a way that the agent’s current issues become represented. The issue relation depicted in Fig. 14a would be like Fig. 14b after such a refinement action.
Although it is natural to keep track of prior and current issues in a setting in which information is treated as defeasible (for such a strategy in a doxastic version of \(\textsf {IEL}\), see Sparkes 2016), in \(\textsf {AMLI}\) and \(\textsf {ELQm}\) it is assumed that when we obtain new information, the contrary is ruled out irreversibly. Thus, it does not seem necessary to keep issues about this information around. Furthermore, it is not clear what the issue refinement action in \(\textsf {ELQm}\) corresponds to from a cognitive point of view.
In contrast, in \(\textsf {IEL}\) models, alternatives cannot include epistemically distinguishable worlds, which means that issues are always refined. Hence, obtaining new information can affect issues directly. This difference is also present on the level of action models. This means that, unlike in \(\textsf {AMLI}\), \(\textsf {ELQm}\) action models can have unrefined issues. It is not entirely clear how we should think of such issues.
In one respect, action models of \(\textsf {AMLI}\) are more general, because they allow non-partition issues. In another respect, \(\textsf {ELQm}\) action models are more general, since they allow for unrefined issues. Setting the differences between issues in \(\textsf {ELQm}\) and \(\textsf {AMLI}\) aside, we find that they share a common core, namely, refined partition models. Restricting ourselves to epistemic models and action models of this kind, we can compare the update procedures of \(\textsf {ELQm}\) and \(\textsf {AMLI}\), by asking when it is the case that two worlds \(\langle w, \textsf {x} \rangle \) and \(\langle w', \textsf {x} '\rangle \) are in the same issue cell in the product update. This is the case if and only if in the original model, w and \(w'\) are in the same issue cell and in the action model, \(\textsf {x} \) and \(\textsf {x} '\) are.Footnote 20 Thus, in this common core, the updates in \(\textsf {ELQm}\) and \(\textsf {AMLI}\) coincide.
6 Conclusion and further work
The objective of this paper was to generalize \(\textsf {IDEL}\) in such a way that private actions can be encoded, by merging its static basis \(\textsf {IEL}\) with \(\textsf {AML}\). I have shown that this can be done in at least two ways: \(\textsf {AMLQ}\) and \(\textsf {AMLI}\). The former is a very natural extension of \(\textsf {IDEL}\) in which asking a question is an epistemic action, just like uttering a statement. This is not the case in \(\textsf {AMLI}\), but this system has different advantages, namely the fact that it can explicitly encode issues with respect to actions and its symmetric treatment of worlds and actions. Which of the two is more natural depends in part on the intended interpretation of epistemic actions. Both are conservative extensions of \(\textsf {AML}\) and \(\textsf {IEL}\). I gave a sound and complete axiomatization for both, based on reduction axioms that allow us to turn each formula into a formula of the static language of \(\textsf {IEL}\).
I have illustrated a challenge to the integration of these systems. I leave it to further work to find other approaches to action models with issues over actions and questions as content. In addition, there are several other directions for further research that can be considered.
So far, we have restricted ourselves to cases in which agents always consider the actual world (and action) possible. Doxastic cases, in which agents can be mislead, are often more exciting. This requires an integration with doxastic logic and belief revision. A first step in this direction is Sparkes (2016).
The logics developed in this paper only describe single actions of stating and asking. Much more can be said when looking at sequences of utterances in a temporal setting. Insights from this paper may enhance existing frameworks that investigate question-answer protocols (cf. van Benthem et al. 2009; van Benthem and Minică 2012 for a system based on \(\textsf {ELQ}\) and Hamami (2014) for an inquisitive approach). In such a setting, we would want to incorporate notions of common knowledge and common issues (Ciardelli 2016). Common issues can be taken to explain why certain utterances are appropriate in some context.
Another interesting line of research is that of question-answer games, either among agents (Ågotnes et al. 2011), between an inquirer and nature (the Interrogative Model of Inquiry, Hintikka 1981, 1999), or among nature and several agents (\(\textsf {DEL}_\textsf {IMI}\), Hamami 2015). We may be able to model similar situations in a setting based on \(\textsf {AMLQ}/\textsf {AMLI}\), benefiting from the inquisitive view on issues and questions.
We may also investigate pragmatics in the \(\textsf {AMLQ}/\textsf {AMLI}\) setting, by taking appropriateness conditions for making statements and asking questions into account (cf. Ciardelli 2016, Sect. 8.5). We can extend the preconditions of a question \(\mu \) to incorporate pragmatic assumptions about the speaker a, such as the fact that the speaker wonders about the question (\(W_a\mu \)).
With this paper, I hope to have provided a suitable logical foundation for these enterprises.
Notes
A related line of work focuses specifically on questions embedded under ‘know’. See Wang (2018) for an overview.
A non-public variant of \(\textsf {DELQ}\) is also developed in van Benthem and Minică (2012), as we will see later. I will use the name \(\textsf {DELQ}\) to refer specifically to the public variant.
For an extensive discussion, see Ciardelli and Roelofsen (2015). As an anonymous reviewer pointed out, a full comparison should not just consider expressive power, but also the trade-off in terms of complexity of reasoning tasks. As far as I am aware, such a comparison between the systems is not yet available.
Although, as we will see in Sect. 5.3, the language of \(\textsf {ELQm}\) does not provide an adequate way to express that an agent is uncertain about another agent’s issues.
It is common to encode an agent’s information by means of an accessibility relation between worlds, in such a way that \(w\sim _a w'\) just in case w and \(w'\) are indistinguishable to a. I use information states for ease of comparison with inquisitive epistemic models, but the two notions are interchangeable: \({w \sim _a w' \iff w' \in \sigma _a(w)}\).
\(S^\downarrow \) is the downward closure of S, the set of all subsets of elements of S.
For the sake of uniformity with epistemic models, I use a function from actions to sets of actions instead of an accessibility relation. Again, the accessibility relation can be retrieved: \(\textsf {x} \sim _a \textsf {y} \iff \textsf {y} \in \delta _a(\textsf {x} )\).
This means that the syntax of \(\textsf {AML}\) contains names for action models. For a discussion about whether action models are semantic or syntactic objects, see van Ditmarsch et al. (2007, Sect. 6.1.1).
Such an interpretation is suggested, for instance, by Pacuit (2013).
These definitions refer to levels in order to prevent dynamic modalities from being circular. For instance, there should be no action model with an action \(\textsf {x} \) such that \(\textsf {content} (\textsf {x} ) = [\textsf {x} ]p\). This is also the case in standard \(\textsf {AML}\), although the levels are often left implicit.
Note that the precondition of \(\textsf {x} \) is not the presupposition of \(\textsf {x} \) in general: for \(\textsf {x} \) to take place in a world, \(\textsf {pre} (\textsf {x} )\) does not have to be known, it only has to be true.
This is not always the case: because questions can be about the knowledge and issues of agents, they might have a presupposition that becomes false once uttered.
Notice that \(\textsf {s} \) can be empty. In that case, we have an empty conjunction, which we take to be \(\top \).
Note that some axioms refer to the properties of particular action models, which means that information about the action models is required to be able to use the axiomatic system. This is true about action model logic in general (see also footnote 9).
An axiomatization without the rule RE can be obtained by adding a rule based on the monotonicity of dynamic modalities. See van Gessel (2016) for the details and completeness proof.
Since the content of an action is always a statement in \(\textsf {AMLI}\), content and precondition are always equivalent. Therefore, we do not need a separate function \(\textsf {content} \) here.
Notice that by this experiment it cannot be discovered that neither of the medicines work.
Recall that \(\textsf {content} (\textsf {x} )\) may contain dynamic modalities of \(\textsf {AMLQ}\) action models. As we define an \(\textsf {AMLI}\) action model, they cannot be part of the content of our actions here. However, we can always find an equivalent formula \(\varphi ^\textsf {x} \in {\mathscr {L}}^{\textsf {IEL}}\) using Theorem 1.
The update procedures of \(\textsf {ELQm}\) and \(\textsf {AMLI}\) can only be compared in such a way because of the restriction to refined partition models. If \(\textsf {AMLI}\)-models are allowed to be non-partition models, they cannot be characterized by just looking at pairs of worlds. Analogously, if \(\textsf {ELQm}\)-models are allowed to be unrefined, then looking at just the issue relation is not enough.
Here \(|{\mathscr {R}}(\varphi )|\) is the number of resolutions of \(\varphi \). By definition, this is always a finite number.
References
Ågotnes, T., van Benthem, J., van Ditmarsch, H., & Minică, Ş. (2011). Question-answer games. Journal of Applied Non-Classical Logics, 21(3–4), 265–288.
Baltag, A. 2001. Logics for insecure communication. In: Proceedings of the 8th conference on Theoretical aspects of rationality and knowledge, pp. 111–121. Morgan Kaufmann Publishers Inc.
Baltag, A., Moss, L.S., Solecki, S. (1998). The logic of public announcements, common knowledge, and private suspicions. In: Proceedings of the 7th conference on theoretical aspects of rationality and knowledge, pp. 43–56. Morgan Kaufmann Publishers Inc.
Ciardelli, I. (2014). Modalities in the realm of questions: Axiomatizing inquisitive epistemic logic. In B. K. R. Goré & A. Kurucz (Eds.), Advances in modal logic (pp. 94–113). London: College Publications.
Ciardelli, I. 2016. Questions in logic. Ph.D. thesis, ILLC, University of Amsterdam.
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2013). Inquisitive semantics: A new notion of meaning. Language and Linguistics Compass, 7(9), 459–476.
Ciardelli, I., & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40(1), 55–94.
Ciardelli, I., & Roelofsen, F. (2015). Inquisitive dynamic epistemic logic. Synthese, 192(6), 1643–1687.
Fischer, M. J., & Ladner, R. E. (1979). Propositional dynamic logic of regular programs. Journal of computer and system sciences, 18(2), 194–211.
Groenendijk, J., Stokhof, M. 1984. Studies on the semantics of questions and the pragmatics of answers. Ph.D. thesis, University of Amsterdam.
Hamami, Y. (2014). Inquiry in conversation: Towards a modelling in inquisitive pragmatics. Logique et Analyse, 228, 637–661.
Hamami, Y. (2015). The interrogative model of inquiry meets dynamic epistemic logics. Synthese, 192(6), 1609–1642.
Hamami, Y., & Roelofsen, F. (2015). Logics of questions. Synthese, 192(6), 1581–1584.
Hintikka, J. (1981). On the logic of an interrogative model of scientific inquiry. Synthese, 47(1), 69–83.
Hintikka, J. (1999). Inquiry as inquiry: A logic of scientific discovery. Alphen aan den Rijn: Kluwer Academic Publishers.
Minică, Ş. 2011. Dynamic logic of questions. Ph.D. thesis, ILLC, University of Amsterdam.
Pacuit, E. (2013). Dynamic epistemic logic ii: Logics of information change. Philosophy Compass, 8(9), 815–833.
Peliš, M., Majer, O. 2009. Logic of questions from the viewpoint of dynamic epistemic logic. The logica yearbook, pp. 157–172.
Plaza, J.A. 1989. Logics of public communications. In: Proceedings of the 4th International Symposium on Methodologies for Intelligent Systems, pp. 201–216.
Sparkes, B. 2016. Inquisitive conditional-doxastic logic. MSc thesis, University of Amsterdam.
van Ditmarsch, H., van Der Hoek, W., & Kooi, B. (2007). Dynamic epistemic logic. Berlin: Springer Science & Business Media.
van Benthem, J., Gerbrandy, J., Hoshi, T., & Pacuit, E. (2009). Merging frameworks for interaction. Journal of Philosophical logic, 38(5), 491–526.
van Benthem, J., & Minică, Ş. (2012). Toward a dynamic logic of questions. Journal of Philosophical Logic, 41(4), 633–669.
van Gessel, T. 2016. Action models in inquisitive logic. MSc thesis, University of Amsterdam.
Wang, Y. 2018. Beyond knowing that: A new generation of epistemic logics. In: Jaakko Hintikka on Knowledge and Game-Theoretical Semantics, pp. 499–533. Springer.
Acknowledgements
I am grateful to Ivano Ciardelli, Floris Roelofsen, Matthijs Westera, Aybüke Özgün, Gianluca Grilletti, Tom Schoonen and three anonymous reviewers for their comments on earlier versions of this paper. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 680220). The results in this paper have been presented in a preliminary form in van Gessel (2016).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Theorem 1
As mentioned before, the lack of a reduction equivalence for formulas of the form \([\textsf {s} ](\varphi \rightarrow \psi )\) can be overcome by the fact that \([\textsf {s} ](\varphi \rightarrow \psi )\) is equivalent to its normal form,  . Since the resolutions of \([\textsf {s} ](\varphi \rightarrow \psi )\) are guaranteed to be declaratives, they can be reduced using Propositions 7 and 13.
. Since the resolutions of \([\textsf {s} ](\varphi \rightarrow \psi )\) are guaranteed to be declaratives, they can be reduced using Propositions 7 and 13.
However, as can be seen from the definition of resolutions, the resolutions of a question of the form \(\varphi \rightarrow \psi \) are more complex than \(\varphi \rightarrow \psi \) itself. This means a straightforward induction on the structure of formulas is not possible. To be able to perform induction, we require a complexity measure \(\textsf {c} \) that has the following properties:
-
1.
If \(\psi \) is a proper subformula of \(\varphi \), then \(\textsf {c} (\varphi ) > \textsf {c} (\psi )\)
-
2.
If \(\varphi \) is a not a declarative, then \(\alpha \in {\mathscr {R}}(\varphi )\) implies \(\textsf {c} (\varphi ) > \textsf {c} (\alpha )\)
The standard measure of complexity has the first property, but not the second. The following non-standard complexity measure does have both properties:Footnote 21
-
\(\textsf {c} (p) = \textsf {c} (\bot ) = 1\)
-
\(\textsf {c} (\varphi \circ \psi ) = 1 + \textsf {max} (\textsf {c} (\varphi ),\textsf {c} (\psi ))\) for
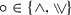
-
\(\textsf {c} (\blacksquare \varphi ) = 1 + \textsf {c} (\varphi )\) for \(\blacksquare \in \{K_a,E_a,[\textsf {s} ]\}\)
-
\(\textsf {c} (\varphi \rightarrow \psi ) = {\left\{ \begin{array}{ll} 1 + \textsf {max} (\textsf {c} (\varphi ),\textsf {c} (\psi )) &{} \text {if }\varphi \rightarrow \psi \text { is a declarative;}\\ 1 + |{\mathscr {R}}(\varphi )| + \textsf {max} (\textsf {c} (\varphi ),\textsf {c} (\psi )) &{} \text {otherwise.} \end{array}\right. }\)
By inspecting the definition, it is immediate that \(\textsf {c} \) has the first property. The second property can be shown by induction on the standard complexity of formulas.
Proof
(\(\textsf {c} \)has property 2) We give only the crucial step, namely the one for implication. Take an arbitrary resolution of \(\varphi \rightarrow \psi \). By the definition of resolutions, this will be a formula of the form \(\bigwedge _{\alpha \in {\mathscr {R}}(\varphi )}(\alpha \rightarrow \beta _\alpha )\) where, for each \(\alpha \), \(\beta _\alpha \in {\mathscr {R}}(\psi )\). By the definition of \(\textsf {c} \), its complexity is, at most, the amount of conjuncts minus 1, plus the complexity of some declarative implication \(\alpha \rightarrow \beta \) where \(\alpha \in {\mathscr {R}}(\varphi )\) and \(\beta \in {\mathscr {R}}(\psi )\). Thus, at most, \(|{\mathscr {R}}(\varphi )| - 1 + 1 + \textsf {max} (\textsf {c} (\alpha ),\textsf {c} (\beta ))\) = \(|{\mathscr {R}}(\varphi )| + \textsf {max} (\textsf {c} (\alpha ),\textsf {c} (\beta ))\).
By the induction hypothesis it holds for both \(\varphi \) and \(\psi \) that, if they are not declaratives, their resolutions are strictly less complex. We also know that if a formula is a declarative, it has itself as its only resolution. Therefore, \(\textsf {c} (\alpha ) \le \textsf {c} (\varphi )\) and \(\textsf {c} (\beta ) \le \textsf {c} (\psi )\). Hence, the complexity of our arbitrary resolution cannot be bigger than \(|{\mathscr {R}}(\varphi )| + \textsf {max} (\textsf {c} (\varphi ),\textsf {c} (\psi ))\). By definition of \(\textsf {c} \), \(\textsf {c} (\varphi \rightarrow \psi ) = 1 + |{\mathscr {R}}(\varphi )| + \textsf {max} (\textsf {c} (\varphi ),\textsf {c} (\psi ))\). Thus \(\varphi \rightarrow \psi \) has property 2. \(\square \)
We proceed by showing that all formulas of \({\mathscr {L}}^{\textsf {AMLQ}_1}\) can be reduced. Take any \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}_1}\). We need to show that there is some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\varphi \equiv \varphi ^*\). We perform an induction on the structure of \(\varphi \). All steps are immediate, except for the one where \(\varphi \) is \([\textsf {s} ]\psi \). By the induction hypothesis we have a \(\psi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\psi \equiv \psi ^*\), so \(\varphi \equiv [\textsf {s} ]\psi ^*\). Therefore, what we need to show is that \([\textsf {s} ]\psi ^*\equiv \varphi ^*\) for some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\). This we do by induction on \(\textsf {c} (\psi ^*)\).
- Base case:
-
\(\psi ^*\) is an atom p or \(\bot \). Take any set of actions \(\textsf {t} \). Then by Proposition 7 and Proposition 8 or 9 we have:
$$\begin{aligned}{}[\textsf {t} ]\psi ^*\equiv {\bigwedge }_{\textsf {x} \in \textsf {t} }(\textsf {pre} (\textsf {x} )\rightarrow \psi ^*) \end{aligned}$$which means that in case of \([\textsf {s} ]\psi ^*\) we can let \(\varphi ^* {:}{=} \bigwedge _{\textsf {x} \in \textsf {s} }\textsf {pre} (\textsf {x} )\rightarrow \psi ^*\).
- Inductive step:
-
Induction hypothesis: for all \(\chi \) less complex than \(\psi ^*\), for all sets of actions \(\textsf {t} \), there is some \(\chi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \([\textsf {t} ]\chi \equiv \chi ^*\).
- \((\wedge )\):
-
Suppose \(\psi ^*\) is \(\chi \wedge \chi '\). Then by Proposition 10, \([\textsf {s} ]\psi ^*\equiv [\textsf {s} ]\chi \wedge [\textsf {s} ]\chi '\). By the induction hypothesis, we have some \(\chi ^*,\chi '^*\in {\mathscr {L}}^{\textsf {IEL}}\) which are equivalent to \([\textsf {s} ]\chi \) and \([\textsf {s} ]\chi '\) respectively. So we can let \(\varphi ^* {:}{=} \chi ^*\wedge \chi '^*\).
 :
:-
Analogous to conjunction.
- \((\rightarrow )\):
-
Suppose \(\psi ^*\) is \(\chi \rightarrow \chi '\). Then \(\chi \rightarrow \chi '\) is either a declarative or it is not. Let us first consider the former. Then by Proposition 7 and 13 , \([\textsf {s} ]\psi ^*\equiv \bigwedge _{\textsf {x} \in \textsf {s} }([\textsf {x} ]\chi \rightarrow [\textsf {x} ]\chi ')\). Take any \(\textsf {x} \in \textsf {s} \). By the induction hypothesis, we have some \(\chi ^*,\chi '^*\in {\mathscr {L}}^{\textsf {IEL}}\) which are equivalent to \([\textsf {x} ]\chi \) and \([\textsf {x} ]\chi '\) respectively. Let \(\theta _\textsf {x} {:}{=} \chi ^*\rightarrow \chi '^*\). Then \(\theta _\textsf {x} \equiv [\textsf {x} ]\chi \rightarrow [\textsf {x} ]\chi '\). As we can define such a \(\theta _\textsf {x} \) for all \(\textsf {x} \in \textsf {s} \), we can let \(\varphi ^* {:}{=} \bigwedge _{\textsf {x} \in \textsf {s} }\theta _\textsf {x} \). Now suppose \(\chi \rightarrow \chi '\) is not a declarative. In that case, the strategy above is not available, since there is no reduction equivalence for \([\textsf {s} ](\chi \rightarrow \chi ')\). However, we can use the fact that all formulas are equivalent to their normal form. Take any \(\alpha \in {\mathscr {R}}([\textsf {s} ]\psi ^*)\). By definition, this \(\alpha \) will be of the form \([\textsf {s} ]\beta \). Since \(\beta \) is a resolution of \(\psi ^*\), by the induction hypothesis we have some \(\alpha ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\alpha ^*\equiv [\textsf {s} ]\beta \). Thus, we let
 .
. - (K):
-
Suppose \(\psi ^*\) is \(K_a\chi \). Then by Proposition 7 and 15 we have \([\textsf {s} ]\psi ^*\equiv \bigwedge _{\textsf {x} \in \textsf {s} }(\textsf {pre} (\textsf {x} ) \rightarrow K_a[\delta _a(\textsf {x} )]\chi )\). By the induction hypothesis we have some \(\chi ^*_\textsf {x} \in {\mathscr {L}}^{\textsf {IEL}}\) equivalent to each \([\delta _a(\textsf {x} )]\chi \). So we can let \(\varphi ^* {:}{=} \bigwedge _{\textsf {x} \in \textsf {s} }(\textsf {pre} (\textsf {x} ) \rightarrow K_a\chi ^*_\textsf {x} )\).
- (E):
-
Suppose \(\psi ^*\) is \(E_a\chi \). Then by Proposition 7 and 16 we have \([\textsf {s} ]\psi ^*\equiv \bigwedge _{\textsf {x} \in \textsf {s} }(\textsf {pre} (\textsf {x} ) \rightarrow \bigwedge _{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow [\textsf {y} ]\chi ))\). By the induction hypothesis we have some \(\chi ^*_\textsf {y} \in {\mathscr {L}}^{\textsf {IEL}}\) equivalent to each \([\textsf {y} ]\chi \). So we can let \(\varphi ^*\) be defined as:
$$\begin{aligned} {\bigwedge }_{\textsf {x} \in \textsf {s} }(\textsf {pre} (\textsf {x} ) \rightarrow {\bigwedge }_{\textsf {y} \in \delta _a(\textsf {x} )}E_a(\textsf {content} (\textsf {y} )\rightarrow \chi ^*_\textsf {y} )) \end{aligned}$$
This concludes the proof for the claim that we can find a \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) equivalent to \([\textsf {s} ]\psi ^*\). As this was the only step which was left to prove, we have thereby shown that for every \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}_1}\), there is some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\varphi \equiv \varphi ^*\).
We can now generalize this claim to all formulas of \({\mathscr {L}}^{\textsf {AMLQ}}\), by an induction on the natural numbers.
-
Base case By definition \({\mathscr {L}}^{\textsf {AMLQ}_0}\) is just \({\mathscr {L}}^{\textsf {IEL}}\), and we have already shown that the claim holds for \({\mathscr {L}}^{\textsf {AMLQ}_1}\).
-
Inductive step For \({\mathscr {L}}^{\textsf {AMLQ}_i}\), the proof for the base case can be repeated. However, this time when we want to use \(\textsf {pre} (\textsf {x} )\) or \(\textsf {content} (\textsf {x} )\) of some action \(\textsf {x} \) in our reduction, it might be the case that these are not formulas of \(\textsf {IEL}\). But then they are formulas of at most \({\mathscr {L}}^{\textsf {AMLQ}_{(i-1)}}\), which means that by the induction hypothesis we can obtain an equivalent formula from \(\textsf {IEL}\) that we can use instead.
1.2 Proof of Theorem 2
We start by showing that every formula of \({\mathscr {L}}^{\textsf {AMLQ}}\) is inter-derivable with an equivalent formula in \({\mathscr {L}}^{\textsf {IEL}}\). As our inference rules for dynamic modalities correspond to the reduction equivalences shown in Sect. 3.4, we can follow the same strategy as in the proof for Theorem 1. However, this proof relies on the equivalence between formulas and their normal form, so we first need to show that every formula is also inter-derivable with its normal form.
Lemma 3
(Provability of normal form) For any \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\),  .
.
Proof
By induction on the complexity of \(\varphi \). We can repeat the base case and the inductive step for  , \(\wedge \) and \(\rightarrow \) from Ciardelli (2016, p. 86). The steps for the modalities \(K_a\) and \(E_a\) are trivial: by definition, for all modal formulas \(\alpha \), \({\mathscr {R}}(\alpha ) = \{\alpha \}\). We only need to add the inductive step for dynamic modalities. Suppose \(\varphi \) is \([\textsf {s} ]\psi \). By the induction hypothesis, we have
, \(\wedge \) and \(\rightarrow \) from Ciardelli (2016, p. 86). The steps for the modalities \(K_a\) and \(E_a\) are trivial: by definition, for all modal formulas \(\alpha \), \({\mathscr {R}}(\alpha ) = \{\alpha \}\). We only need to add the inductive step for dynamic modalities. Suppose \(\varphi \) is \([\textsf {s} ]\psi \). By the induction hypothesis, we have  . We can use RE to obtain:
. We can use RE to obtain:

Also, using  in both directions we can get:
in both directions we can get:

By the definition of resolutions, we have the following equivalence:

This means we can combine the two inter-derivabilities to:

This concludes the inductive step for the dynamic modality, which was all we needed to show that  .\(\square \)
.\(\square \)
Now that we have provability of normal form, we can move on to the proof for the following theorem.
Theorem 3
(Every formula of \(\textsf {AMLQ}\) is inter-derivable with a formula of \(\textsf {IEL}\)) For any \(\varphi \in {\mathscr {L}}^{\textsf {AMLQ}}\), there is some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\varphi \dashv \vdash \varphi ^*\).
Proof
The proof for this claim is analogous to the proof for Theorem 1, but using the relation of inter-derivability instead of logical equivalence. Instead of the reduction equivalences, we use the corresponding deduction rules from Fig. 9 and RE for substitution of equivalents under dynamic modalities. We use Lemma 3 instead of Proposition 5.\(\square \)
Note that for all \(\varphi \), the formula \(\varphi ^*\) obtained from Theorem 3 is the same as the one obtained from Theorem 1. Now, notice that we have conservativity of entailment in \(\textsf {AMLQ}\) over \(\textsf {IEL}\):
Proposition 19
(Entailment in \(\textsf {AMLQ}\) is conservative over \(\textsf {IEL}\))
For all \(\varPhi \cup \{\psi \}\subseteq {\mathscr {L}}^{\textsf {IEL}}\), \(\varPhi \models _{\textsf {AMLQ}}\psi \iff \varPhi \models _{\textsf {IEL}}\psi \).
Proof
This is immediate from the fact that \(\textsf {AMLQ}\) has standard support conditions for all the connectives that are in the syntax of \({\mathscr {L}}^{\textsf {IEL}}\).\(\square \)
This means that we can use the entailment relation \(\models \) for entailment in \(\textsf {IEL}\) and \(\textsf {AMLQ}\) interchangeably. Now we can finally prove the soundness and completeness of \(\vdash \).
- \((\Rightarrow )\):
-
The inference rules consist of the inference rules in Fig. 9 and the ones of \(\textsf {IEL}\). The former are sound by Propositions 7 and 8–16 and the latter by Proposition 7.3.11 of Ciardelli (2016, p. 283).
- \((\Leftarrow )\):
-
Suppose \(\varPhi \models \psi \). Then by Theorem 1, for every \(\varphi \in \varPhi \) there is some \(\varphi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\varphi ^*\equiv \varphi \) and some \(\psi ^*\in {\mathscr {L}}^{\textsf {IEL}}\) such that \(\psi ^*\equiv \psi \). Let \(\varPhi ^*\) be a set containing for each \(\varphi \in \varPhi \) a formula \(\varphi ^*\) equivalent to \(\varphi \). Then we have \(\varPhi ^*\models \psi ^*\). We obtain \(\varPhi ^*\vdash \psi ^*\) by the completeness of the proof system for \(\textsf {IEL}\). Theorem 3 guarantees that \(\varPhi \vdash \varphi ^*\) for all \(\varphi ^*\in \varPhi ^*\) and \(\psi ^*\vdash \psi \). This means that \(\varPhi \vdash \psi \).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van Gessel, T. Action models in inquisitive logic. Synthese 197, 3905–3945 (2020). https://doi.org/10.1007/s11229-018-1886-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-018-1886-5










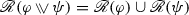









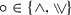
 :
: .
.