No evidence amalgamation without evidence measurement

Abstract

In this paper we consider the problem of how to measure the strength of statistical evidence from the perspective of evidence amalgamation operations. We begin with a fundamental measurement amalgamation principle (MAP): for any measurement, the inputs and outputs of an amalgamation procedure must be on the same scale, and this scale must have a meaningful interpretation vis a vis the object of measurement. Using the p value as a candidate evidence measure, we examine various commonly used approaches to amalgamation of evidence across similar studies, including standard forms of meta-analysis. We show that none of these methods satisfies MAP. Thus an underlying measurement problem remains. We argue that a successful approach to evidence amalgamation necessitates a solution to the problem of evidence measurement, and we suggest some lines of reasoning that might guide further work towards this end.

1 Introduction

Formal methods for amalgamating evidence are of importance in a variety of settings, from basic research to policy making. In the biological, biomedical and social sciences, increasing reliance on statistical analysis of individual studies increases the need for quantitative methods for rigorous evaluation of the totality of evidence across multiple studies. Similarly, evidence-based policy decisions require policy makers to integrate the outputs of what are often diverse study designs and complex mathematical analyses across multiple sources of information. While this integration of evidence across sources can be, and generally is, done informally, rigorous quantitative methods would carry obvious advantages.

Evidence amalgamation is important for another reason as well: it is tethered to the question of how to measure evidence based on a single study. This latter, seemingly simpler, issue remains unresolved, even in the narrow context of statistical analysis (our main focus here; see below). Most scientists and lay people alike treat the p value as a measure of evidence, but among statisticians other options are often preferred. These include the likelihood ratio (Barnard 1949; Good 1950; Edwards 1992; Royall 1997; Zhang 2009; Bickel 2010) and the Bayes factor (Jeffreys 1939; Kass and Raftery 1995), both widely used, as well as some more recent alternatives (Stern and Pereira 2014; Evans 2015; Vieland and Seok 2016). These various outcome measures differ from one another in substantive ways, and they can lead to quite different conclusions. Thus they cannot all be measures of the same thing. How do we decide which if any of them represent the evidence?

Here we are going to consider the problem of per-study evidence measurement by focusing on evidence amalgamation. We start with a simple and general measurement amalgamation principle (MAP): for any measurement, the inputs and outputs of an amalgamation procedure must be on the same scale, and this scale must be meaningfully interpretable with respect to the underlying object of measurement. MAP provides a mechanism for evaluating candidate evidence measures, in terms of the relationship between the inputs and output of the appropriate amalgamation procedure. We consider some examples in detail below.

In order to keep the discussion as focused as possible, we will restrict the scope of the argument in several ways. First, as already mentioned, we will consider only statistical evidence. While not all evidence is statistical in nature, statistical analyses provide a substantial proportion of the inputs to data amalgamation efforts, which means that it will not be possible to solve the evidence amalgamation problem in general unless our solution includes amalgamation in the context of statistical analyses. Additionally, as a mathematical subtype of evidence, statistical evidence is a somewhat more specific concept, and therefore more amenable to formal analysis, than is evidence considered simultaneously in all its myriad contexts of use.

Second, we will focus on the most familiar and commonly used measure of statistical evidence: the (empirical) p value.¹ The p value is all too often interpreted as the strength of the evidence against the null hypothesis, with very small values taken to mean that the evidence against the null is very strong. The p value also shows up in amalgamation settings, e.g., as the central outcome measure in meta-analysis, or as the basis for classifying studies as “positive” or “negative” as inputs to amalgamation algorithms. Thus the p value is important from a practical point of view. Focusing on the p value also allows us to structure the main arguments with a minimum amount of technical detail.

Finally, we will assume throughout that we are attempting to amalgamate evidence across multiple studies of the same type and design, for instance, multiple randomized clinical trials (RCTs) of a single drug, or, multiple psychological studies of the same correlational effect. In other words, we will restrict attention to situations in which one may reasonably view the set of studies as constituting multiple independently conducted replicates of one another. A full treatment of what constitutes an independent replicate would involve subtleties beyond the scope of this paper, but the following somewhat loose, common sense understanding will suffice for our purposes here: replicate studies utilize the same design to address the same research question, but based on separately generated or newly collected data; in order to simplify the statistical discussion, we additionally assume throughout that the replicate studies all have the same sample size. Amalgamation of evidence is obviously more complicated when the individual studies are diverse in nature, but nothing about these more difficult situations will change the logic of our argument. If difficulties appear already in the simplest case, the complicated case is unlikely to prove more tractable.

The remainder of the paper is organized as follows. We will expand upon MAP as a principle regarding measurement in general, and its relevance to measurement of evidence in particular, in Sect. 2. Then in Sects. 3 and 4 we will consider established amalgamation options for p values, and argue that they violate MAP. In Sect. 5 we consider some of the broader implications of our results and speculate regarding steps needed to solve the evidence measurement problem.

2 Evidence amalgamation and evidence measurement

2.1 Evidence as data versus evidence as relationship

Before proceeding a terminological clarification is in order. In common parlance and throughout the philosophical literature, the word “evidence” is used to indicate the facts or propositions at hand. These are the inputs to epistemic operations. We say that a lawyer presents the evidence to the jury, meaning, the facts, or items of information, that that the jury is asked to consider.

But then the jury is asked to weigh the evidence. This weighing operation involves a relationship between the facts and a judgment that the jury is asked to render, say, regarding the defendant’s guilt or innocence. In practice there is slippage between the idea of the facts per se and this “weighing” relationship, and the sense of evidence as facts blends into the concept of evidence as a relationship. The jury may well end its deliberations by agreeing that the evidence is overwhelming. They are not being overwhelmed merely by facts, say by their number or their complexity, but rather by the bearing of those facts upon the verdict.

Indeed, the facts per se are not evidence; facts constitute evidence only in the context of specific deliberations. The prosecutor does not present just any facts, but only facts chosen for their relevance to the matter at hand. A DNA match between the suspect and a sample taken from the crime scene is only a bit of evidence after we specify the topic of deliberation. It may be evidence of responsibility, but it is not evidence of, say, prior intent to commit the crime. If the jury is deliberating over responsibility, then the fact of the DNA match is evidence; if the jury is deliberating over intent, then that very same fact is not evidence. Moreover, the fact is evidence only in the context of a pair of outcomes. The DNA match is evidence in deliberating guilt versus innocence, but not in deliberating guilt versus the existence of prior intent; and it may have different evidential bearing on the question of guilt versus innocence than it does on the question of the suspect’s presence versus absence from the crime scene. There is a presumption that when a fact serves as evidence, it does so insofar as it bears meaningfully upon some judgment, and this already imbues the facts with a quality involving their relationship to the alternatives under consideration.²

Insofar as the term “evidence” is used to refer to the facts, it already packs quite a bit of additional meaning in on top of the fact in itself. More properly, the DNA match should be described as evidence only in context. That the context may be tacit, and the relevance of the fact to the deliberation taken for granted, does not change the point. Facts are not evidence in and of themselves, but only insofar as they participate in a particular kind of relationship to the objects of deliberation. Indeed, there is another common usage of the word “evidence,” in which it explicitly refers to this relationship rather than the raw inputs to deliberation. As soon as one talks about the weight or strength of evidence, we have slipped into this second usage. Facts themselves have no strength in the intended sense. Insofar as evidence can be strong, this strength is itself a relational quality.

We stress this point because it is particularly important to disambiguate these two different senses of evidence in connection with evidence amalgamation. There is a sense in which the amalgamation problem addresses the assembly of facts drawn from different sources. However, the output of an amalgamation procedure is not merely a concatenation of these facts, but rather, an assessment of the overall bearing of these facts on the deliberation at hand. The question is not merely how to combine the fact of a DNA match with the fact of, say, an eyewitness report. The question is how to arrive at the combined strength of evidence, that is, the bearing of the totality of these facts upon the question of, say, guilt or innocence. This suggests that what we really intend to combine is the strength of the DNA match with the strength of the eyewitness report, insofar as these facts bear upon our deliberation. And indeed, amalgamation procedures do not merely concatenate facts; rather, they take as inputs quantities that already represent a projection of the facts onto a representation of evidence strength, e.g., the p value.

One problem with allowing the word “evidence” to refer both to the data and to the relationship between the data and a specified hypothesis contrast, is that this obscures the measurement issue inherent in the amalgamation operation. Facts are not things that require measurement, they are (in the current context) givens.³ Thus when we equate evidence with facts or data themselves, it appears that we can treat evidence amalgamation operations as purely logical relationships among these givens. But if we intend to interpret the amalgamation output as some kind of summary of the combined evidence strength, then the inputs to amalgamation cannot be the facts alone. Amalgamation in this context is more than the mere concatenation of disparate facts; it involves combining the evidential bearing of those facts. And this raises the question of how we measure this evidential bearing.

Thus, while there is no question that “evidence” has (at least) two distinct meanings in ordinary usage, to avoid confusion in what follows we propose to adopt a narrower, more technical usage for the remainder of the paper. Statisticians refer to the inputs to their analyses as “data” and to the objects of deliberation as “hypotheses.” Then a particular kind of relationship between the data and a given hypothesis contrast is called the evidence.⁴ In order to avoid ambiguity, from here out we will use the word “evidence” in this relational sense, and the word “data” to refer to the inputs. The evidence amalgamation problem, then, becomes the problem of how to arrive at the total strength of evidence in contexts involving multiple sets of data, each yielding some degree or strength of evidence on its own with respect to some hypothesis contrast.

2.2 Evidence and evidence amalgamation as measurement

We have already stated MAP as the guiding principle for our argument: evidence measurement scales for inputs and amalgamation outputs need to be on the same scale, and also, on a scale that is meaningfully interpreted as representing the thing we set out to measure, viz., in the present context, the evidence. At the risk of belaboring the obvious, an analogy will clarify what we have in mind.

Suppose we are interested in the total length of a set of rods, made of different metals and of varying diameters. The obvious way to obtain the total length would be to measure the length of each rod in turn, say, in feet, and then add these lengths to arrive at the total, which would then be in the same units (in this case, feet) used to measure the individual rods.By contrast, a quite problematic way to obtain the total length would be to add the individual weights. This would be a fine procedure for arriving at the total weight, but it would only provide a measure of total length if we knew a one-to-one mapping between weight and length for each type of rod—say, as a function of diameter and density—and took this information into account in our calculations.

What makes the measure of total length meaningful is the fact that we have properly measured the length of each individual rod and used the appropriate amalgamation operation, in this case, addition. We could equally well express this by saying that what makes the measure of each individual rod meaningful is the fact that we have a rigorous arithmetic operation for amalgamating these measures to find the total length. Proper measurement is equally about the per-unit operation and the across-unit amalgamation rule.⁵

As a general point about measurement, this may seem barely worth mentioning. But we belabor the point because, in connection with evidence amalgamation, it seems to us to underscore a crucial lacuna in statistical discussions. For instance, as we will argue, not all methods for combining p values across similar studies (say, multiple RCTs) preserve scale between the inputs and amalgamation outputs. And even rigorous scale-preserving amalgamation procedures, which de facto constitute good procedures for arriving at the “total” p value, may not lend themselves to an interpretation in terms of the total evidence. Current statistical practice largely ignores this elementary tenet of measurement, seriously compromising the evidential interpretation of both the inputs to and outputs of familiar statistical amalgamation procedures. Even a universally accepted amalgamation procedure, such as meta-analytic calculation of the combined p value across multiple RCTs of the same drug, will fail as a technique for ascertaining the total evidence if it violates MAP.

2.3 Summary of Sect. 2

In connection with evidence amalgamation, the word “evidence” has two meanings. It is used to refer to the raw facts which are the inputs to amalgamation. But it is also used to refer to the relationship between those facts and specified hypothesis contrasts. Going forward, we will refer to the former as “data” and only the latter, relational quality as “evidence.” We argued that evidence amalgamation is a measurement procedure, and as such, it requires preservation of measurement units between inputs and outputs along with cogent interpretability in terms of the underlying object of measurement, the evidence.

3 p values, evidence and evidence amalgamation

3.1 The p value

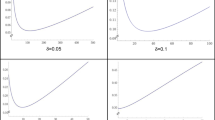
The p value is defined as the probability of what was observed or an even more extreme observation, assuming that the null hypothesis $\hbox {H}_{0}$ is true.⁶ To illustrate, suppose we are interested in the true effect size R (where R might be, e.g., a correlation coefficient). We take as our null hypothesis $\hbox {H}_{0} : R = 0$ (no correlation). We draw a random sample of individuals, on the basis of which we calculate the observed correlation r in this particular sample. Let’s say we obtain $r = 0.5$. Then by definition the (two-sided) $p\,\hbox {value} = \textit{Pr}[{\vert }r{\vert } \ge 0.5 {\vert } R = 0]$ (Fig. 1). The calculation of this probability requires a model, or distribution; the Figure illustrates a case in which the distribution of r under $\hbox {H}_{0}$ is normal. This model determines the shape of the curve with respect to which the “tail” probability (that is, the area in the shaded “tails” of the distribution) is computed.

Fig. 1

Illustration of the (two-sided) p value calculation, assuming a normally distributed random variable R, an observed value $r = 0.5,$ and the null hypothesis $\hbox {H}_{0} : R = 0$. The p value is by definition the area under the shaded portions of the graph

A small p value is generally interpreted as evidence against $\hbox {H}_{0}$. Large p values, on the other hand, are not interpreted as evidence for $\hbox {H}_{0}$. A large p value could correspond to (possibly weak) evidence against $\hbox {H}_{0}$, or to evidence supporting $\hbox {H}_{0}$. The p value does not provide a mechanism for distinguishing between these two possibilities. This point is related to the fact that calculation of the p value is based on the specification of only one hypothesis, $\hbox {H}_{0}$. Recall, however, that evidence with respect to any single hypothesis can differ depending on the alternative. We interpret a small p value as evidence against $\hbox {H}_{0}$ compared to any alternative, in the sense that the data are incompatible (to some degree) with $\hbox {H}_{0}$ regardless of which alternative is entertained; but we allow for the fact that a large p value might correspond to evidence in favor of $\hbox {H}_{0}$ against some alternatives but not others.

The p value is commonly used not only to assess the per-study evidence, but also to assess the evidence amalgamated across multiple studies. One approach to doing this is formal meta-analysis, which comes in a variety of flavors, all of which provide a single, summary p value across the input studies; another approach is based on the binary classification of individual studies as either “positive” (statistically significant) or “negative” (not statistically significant), and a set of heuristic procedures for combining results classified in this way. In the remainder of this section we will consider two meta-analytic approaches.⁷ We’ll return to the classification-based approach in Sect. 4.⁸

3.2 Meta-analysis I: Combining p values

Suppose we have two studies, $\hbox {S}_{1}$ and $\hbox {S}_{2}$, which are replicates in the sense defined above. Say we obtain p values $\hbox {P}_{1}, \hbox {P}_{2}$ for studies $\hbox {S}_{1}, \hbox {S}_{2}$, respectively. How do we obtain the combined evidence across the two studies?

We might reason as follows: Let’s assume that the p value, which is the probability of an event (e.g., the event $e_{1} : [{\vert }r{\vert } \ge 0.50]$, or the event $e_{2} : [{\vert }r{\vert } \ge 0.10]$), is also a measure of the evidence. Because the two studies are conducted independently of one another, the probability of both events (say, $e_{1}$ in $\hbox {S}_{1}$ and $e_{2}$ in $\hbox {S}_{2})$ is the product of their individual probabilities. Therefore, $\hbox {P}_{1} \times \hbox {P}_{2}$ should represent the combined evidence. The logic seems unassailable, but there is an obvious problem with this approach. By virtue of being a probability, we have $0 \le \hbox {P}_{i} \le 1$ for all studies i. Thus $\hbox {P}_{1} \times \hbox { P}_{2} \le$ minimum $(P_{1},\hbox { P}_{2})$, that is, the product of the p values is always smaller than the smaller of the initial p values. If we were to interpret the result of multiplying p values as itself being a measure of evidence, we would have to conclude that the evidence always increases (or stays the same) upon consideration of a second study, regardless of the second study’s data. This is clearly wrong. Thus $\hbox {P}_{1} \times \hbox { P}_{2}$ cannot be interpreted as a measure of the combined evidence.

In fact, the product of p values is not itself a p value. This seemingly technical detail is important here because it illustrates the need for care in considering the input-output relationship inherent in any statistical amalgamation procedure. The product of the probabilities of two independent events is indeed the probability of the intersection of the events. But as it happens, the distribution of the product of two p values has a somewhat more complicated relationship to the distributions of the individual p values. Recall that the p value is defined as a particular (tail) probability, which is calculated with respect to the distribution of the variable(s) of interest. In our example, in order to find the p value in each of the individual studies, we needed to specify the distribution, assuming $\hbox {H}_{0}$ to be true, of r. Similarly, if we wish to compute the amalgamated p value, then we need to find the functional form of the distribution, again under H$_{0}$, of the statistic computed by the amalgamation procedure. This explains the apparent paradox of the preceding paragraph: $\hbox {P}_{1 }\times \hbox {P}_{2}$ is the correct joint probability, but it does not have the same interpretation as the input p values, because they are tail probabilities under a particular distribution, while $\hbox {P}_{1 }\times \hbox {P}_{2}$ is not.

In the present case, the amalgamation statistic at hand is the product of the per-study p values, or equivalently, the sum of their natural logarithms. In order to compute the p value corresponding to this sum, one needs to determine the functional form of its distribution. This functional form was derived by Fisher (1925), who showed that $-\,2\mathop \sum \nolimits _{i=1}^k \ln P_i \sim \chi _{2k}^2$, where k is the number of studies being considered and $\hbox {P}_{i}$ is the p value for the ith study. If one wishes to interpret the amalgamation output as a p value, the proper statistical procedure is to sum the logarithms of the per-study p values, multiply this quantity by −2, and then to look up the corresponding tail probability in a table of $\chi ^{2}$ quantiles with the appropriate degrees of freedom.

To be concrete, let’s consider a numerical example. Let $\hbox {S}_{1}$ have $n_{1} = 40$ and $r_{1} = 0.5.$ This yields a p value of $\hbox {P}_{1} = 0.002.$⁹ Let S$_{2}$ have $n_{2} = 40$ and $r_{2} = 0.1$, yielding $\hbox {P}_{2} = 0.527.$ Then to amalgamate these input p values to obtain the “total” p value $\hbox {P}_{12}$, we look up the tail probability associated with $-\,2[\ln (0.002) + \ln (0.527)] = 13.71$ on a $\chi _{4}^{2}$ table. This amalgamated p value turns out to be 0.008. Note that, unlike the product $\hbox {P}_{1 }\times \hbox { P}_{2}$ itself, $0.008 > \hbox {minimum}(\hbox {P}_{1},\hbox { P}_{2})$. Fisher’s method returns, in this particular example, an amalgamated p value that is intermediate between the two input per-study p values, and therefore less significant than the smaller of the two considered on its own.

One way to think about Fisher’s method is in terms of a type of averaging procedure. An average is obtained by summing a set of quantities and dividing by the total number of quantities in the summation. Fisher’s method sums the (logarithms of) the p values, but rather than directly dividing this sum by k, the number of terms in the summation is accounted for by the degrees of freedom (d.f., in this $\hbox {case} = 2{k} = 4$) of the $\chi _{d.f.}^2$ distribution. This operation is related to averaging, insofar as it will often return a result intermediate between the extremes of the per-study p values. But it is not simple averaging, and there is no guarantee that it will always return an intermediate result. E.g., when both $\hbox {P}_{1}$ and $\hbox {P}_{2}$ are large, $\hbox {P}_{12}$ will tend to be larger than maximum($\hbox {P}_{1}$, $\hbox {P}_{2})$, and when $\hbox {P}_{1}$ and $\hbox {P}_{2}$ are both small, $\hbox {P}_{12}$ will tend to be smaller than minimum$(\hbox {P}_{1}, \hbox {P}_{2})$. But in those cases where meta-analysis is most needed—situations in which not all studies show extreme results in the same direction—Fisher’s method tends to return something akin to an average p value.¹⁰ Let’s call the arithmetic operation underlying this approach to meta-analysis paveraging (related to, but not the same as P-averaging).

Paveraging p values across our two studies is a correct method for obtaining $\hbox {P}_{12}$. The inputs are the per-study p values, and the output is a p value interpreted in exactly the same way as the inputs: $\hbox {P}_{12}$ is the probability of obtaining a test statistic (viz., the sum of the log p values from the input studies) equal to or greater than the observed statistic, assuming $\hbox {H}_{0}$ is true. But this establishes only that Fisher’s method is a correct amalgamation procedure for something, not necessarily for the evidence. It could turn out that Fisher’s method is the analogue of a correct procedure for ascertaining the total weight of our metal rods, without any explicit procedure for mapping this weight onto the intended object of our measurement, that is, the total length.

Insofar as we are interested solely with the p value per se, we need only be concerned with ascertaining the correct sampling distribution under $\hbox {H}_{0}$ for any given statistic (including the product of p values), that is, the question of evidential interpretation is irrelevant. But if we are genuinely interested in amalgamation of evidence, then the question of interpretation is crucial. If the per study p values are in fact measures of evidence, then Fisher’s method might plausibly be construed as giving us the amalgamated evidence. But if they are not, there is no basis for assigning an evidential interpretation to the amalgamation result. By the same token, if we cannot justify an evidential interpretation for the amalgamated p value obtained via Fisher’s method, then we must conclude that the per-study p values themselves should not be interpreted as measures of the evidence. We will return to the question of evidential interpretation below, after considering another and far more popular approach to meta-analysis.

3.3 Meta-analysis II: Combining parameter estimates

The second approach to meta-analysis employs an amalgamation operation that is related to but not the same as paveraging. It probably owes its popularity both to its flexibility in handling complications beyond the scope of this paper (in particular, extensions to random effects models), but also, to a pleasing intuitive connection with parameter estimation, as we will explain. But as we will see, parameter-based meta-analysis turns out to lack the impeccable logical rationale underlying Fisher’s method, leading to even thornier measurement issues.

We continue with the same example: two studies, each of which summarizes the data in terms of the observed correlation r between the same two things, and each of which tests the null hypothesis $R = 0$ based on a sample size of n. It is well established by classical statistical theory that (under some broad regularity conditions), the more data we have, the better will be our estimate of R. In this simple setting, the best estimate of R across our two studies is the weighted average $r_{12}$ of the estimates obtained in each of the two studies, $r_{1}$ and $r_{2}$, where (in our simple example with equal sample sizes) $r_{12} = (1/2)(r_{1}+r_{2})$. Standard meta-analysis across the studies proceeds in two steps: (1) Calculate $r_{12}$, then (2) find the p value on the combined studies, that is, based on the “combined ” estimate $r_{12}$ and the combined sample size, which enters through the standard error (s.e.) of the combined estimate.¹¹

Continuing with the numerical example from above $(n_{1} = 40, r_{1} = 0.5, \hbox {P}_{1} = 0.002; n_{2} = 40, r_{2} = 0.1, \hbox {P}_{2} = 0.527)$, we first calculate $r_{12} = (1/2)(0.5 + 0.1) = 0.3.$ Based on this new estimate and the combined sample size, the combined p value $\hbox {P}_{12} = 0.007$. Two things about this result are noteworthy. First, this is not the same as the result we obtained from Fisher’s method $(\hbox {P}_{12} = 0.008)$.¹² This is not surprising, given that one technique considers only the per-study p values and the other explicitly takes parameter estimates and sample sizes into account. But it does raise the question of which p value, if either, represents the actual strength of evidence. The second noteworthy feature of this result is that, just as with Fisher’s method, we have $\hbox {P}_{1}< \hbox {P}_{12} < \hbox {P}_{2}$.¹³

As with Fisher’s method, this form of meta-analysis involves an operation related to averaging in going from the per-study p values to the combined p value. In this case, however, it is not the p values themselves that are averaged (that is, paveraged), but rather, the per-study estimates of r. Let’s call this new operation raveraging. Raveraging takes the (weighted) average estimate of r and calculates the amalgamated p value based on this average and the new sample size under an appropriate null distribution.¹⁴

In using raveraging as its amalgamation operation, meta-analysis in effect acknowledges that the study-wise p values are not themselves measures of evidence: if they were, then paveraging would seem to be the correct procedure. Raveraging has baked into it the premise that mapping study-wise results onto the amalgamated evidence must involve some function of $\left( {r_1 ,n_1 } \right)$ and $\left( {r_2 ,n_2 } \right)$. This suggests that, while the study-wise p values are not themselves measures of evidence, they should be transformable into evidence measures as a function of r and n. Just as with the need for a mapping function from weight to length in our length amalgamation analogy, it seems that one needs to invoke $\left( {r_i ,n_i } \right)$ to map the p value of the ith study onto the evidence. This is the only explanation that allows us to simultaneously interpret the meta-analytic p value in terms of evidence while justifying an amalgamation procedure based on something other than the per-study p values themselves. But it precludes consideration of the per-study p value per se as an evidence measure in the absence of an explicit formal procedure for mapping it onto the evidence as a function of r and n.

Thus the inputs and outputs of parameter-based meta-analysis are, apparently, not on the same scale, that is, if we interpret the meta-analytic p value itself to be a measure of evidence. Moreover, turning to the question of interpretability vis a vis the underlying evidence, the situation is really quite logically perplexing. This form of meta-analysis appears to allow us to directly interpret its outcome measure—the meta-analytic p value—as an evidence measure, without further consideration of $r_{12}$ and N, even while it entails a tacit acknowledgment that the per-study p values share no such quality. In fact, the statistical literature tends to support the idea that the p value per se, or taken on its own, is not a measure of evidence, but that it can be interpreted as a measure of evidence if one is careful to take various aspects of context into consideration (Wasserstein and Lazar 2016). Crucial aspects of context are often said to include effect-size (or, more generally, parameter) estimates and sample sizes, which bear on the power of a p value based test to reject $\hbox {H}_{0 }$ when it is false.¹⁵ However, there is no explicit rule for these per-study p value transformations in the literature; rather, investigators are instructed to use judgment in taking extraneous factors into consideration when interpreting p values in evidential terms.

3.4 Does meta-analysis measure amalgamated evidence?

Let’s first consider raveraging (we will return to paveraging below). If the p value is not a direct measure of evidence, but requires transformation as a function of r and n (and perhaps other things) in order to represent the evidence, then some way of validating the transformation operation is needed. Parameter-based meta-analysis is ingenious in this regard, because raveraging itself incorporates a formal transformation rule at the amalgamation level, without committing to any particular transformation rule at the per-study level. Rather than providing a mechanism for directly transforming a p value onto the evidence scale, it builds a mapping function into the amalgamation procedure itself. Therefore, in order to assess whether r and n are in fact being properly taken into account, one needs to consider whether raveraging is returning the correct amalgamated evidence. Without a formal measure of per-study evidence on the table to begin with, this is a particularly challenging task. But there are some things we can say about it.

In our example, in which the second study yields a parameter estimate with the same sign but smaller than the estimate from the first study, as noted above raveraging leaves us with $\hbox {P}_{12}$ intermediate between $\hbox {P}_{1}$ and $\hbox {P}_{2}$. When $\hbox {P}_{1}$ and $\hbox {P}_{2}$ are from studies carried out one after the other, this result implies that the evidence grows weaker (yields a larger p value), relative to the original study, when we take the second study into account. Given the numbers used in this example, we think almost everyone will agree that this result is at least plausible. The reasoning seems to go like this: the true evidence should be the evidence corresponding to the best estimate of r. Since the estimate of r improves with sample size, the fact that $r_{12} < r_{1}$ indicates that our initial estimate $r_{1}$ was an overestimate. Then once this number is appropriately adjusted downward (indicating less correlation than we had originally supposed), it seems correct that the evidence against H$_{0}$ should decrease (that is, correspond to a larger p value) when we take S$_{2}$ into account. We tend to share the intuition that a decrease in r should produce a reduction in the strength of the evidence.¹⁶

But at the same time, all other things being equal, we think we can all agree that evidence gets stronger with increasing sample size. Imagine that we had obtained $r_{2}=r_{1} = 0.5$. Clearly in this case, having doubled the sample size while maintaining the same estimated effect size, we would expect the evidence against $\hbox {H}_{0}$ to have grown stronger. Returning to the original example, two things are happening simultaneously: we have a change from $r_{1}$ to $r_{12}$, which, all other things being equal, might suggest a reduction in the evidence; and we have a change from n to 2n, which, all other things being equal, might entail an increase in the evidence. Intuition stops short of determining whether or not the dampening effect on the evidence of the decrease in r was sufficient to overcome the augmenting effect of the increase in sample size. Intuition may instruct us that the evidence might decrease going from $r_{1} = 0.5$ to $r_{2} = 0.1$, but there is no clear basis for an intuition that it did decrease, given the simultaneous doubling of the sample size. Appealing to intuition does not provide us with a means to decide whether raveraging is behaving correctly in this case or not as an evidence amalgamation procedure.

Indeed, we have a third intuition that further complicates things. Consider a legal argument which first points out an exact DNA match between the suspect and a sample taken from the crime scene, and then afterwards notes a blood type match. The first finding gives us relatively strong evidence that the suspect was present at the scene, while the second gives us weaker evidence since blood type matches are far more common. But we do not mentally adjust our original (DNA match based) assessment of the evidence strength downward after hearing about the blood type match. Here strong evidence followed by weak evidence in favor of the same conclusion increases (though perhaps only by a very small increment) the evidence relative to its initial state. By contrast, if the second piece of information had been an eye-witness report of seeing the suspect somewhere other than the crime scene at the time of the crime (which might only be weak evidence, depending on the reliability of the witness, but still evidence in favor of innocence), then the initially strong evidence would be tempered. Whether the evidence goes up or down when we receive the second bit of information seems to be a matter of whether the second bit favors guilt or innocence, rather than the strength of the evidence of the second bit of information relative to the strength of the initial evidence.¹⁷

It is unclear whether this line of reasoning carries over to the statistical case, but if it does, we would have to say that whether $\hbox {P}_{1} < \hbox {P}_{12}$ is correct or not ought to depend upon whether $\hbox {P}_{2}$ is (possibly weak) evidence against$\hbox {H}_{0}$, or whether $\hbox {P}_{2}$ is actually evidence for$\hbox {H}_{0}$. In the former case, it would seem that the total evidence goes up; and only in the latter case does it go down. But remember, as noted at the outset, that based on the p value alone we cannot tell the difference. The larger p value in $\hbox {S}_{2}$ could correspond to either (possibly weak) evidence against $\hbox {H}_{0}$ or evidence in favor of $\hbox {H}_{0}$. This again leaves us with no way to verify whether raveraging is doing the right thing when we interpret it as a measure of total evidence across the two studies.

Note too that all arguments in this section apply equally, if in a somewhat modified form, to meta-analysis based on direct combining of p values. Recall that, for our selected example, Fisher’s method also yielded $\hbox {P}_{1}< \hbox {P}_{12} <\hbox { P}_{2}$. If we decide in the end that this pattern does not accurately reflect the behavior of the evidence, then this poses as big a challenge to an evidential interpretation of $\hbox {P}_{12}$ under paveraging as it does to the outcome of raveraging. Since the paveraged p value is demonstrably on the same scale as the input per-study p values, and since the amalgamation operation is logically and mathematically impeccable, we would have to conclude that the per-study p value is not a measure of evidence.

Raveraging, on the other hand, produces as the amalgamation output a p value that apparently has a scale that differs from that of its inputs, that is, if we are to interpret the raveraged p value itself as a direct measure of evidence. Raveraging produces a p value that is fundamentally different from the p value produced by paveraging, not merely because its numerical value may be different given the same set of input studies (arguably a problem in its own right), but because it bears a different relationship to the per-study p values corresponding to its inputs. Both approaches agree that, given the numbers in our example, the p value is larger after consideration of $\hbox {S}_{2}$. But it is not clear that the evidence has gone down. Which method, if either, is correct? We are left up to this point in a bit of a muddle.

3.5 Summary of Sect. 3

We considered two forms of meta-analysis. One combines per-study p values to obtain an amalgamated p value; the other combines parameter estimates to arrive at an appropriately weighted average value, and then obtains an amalgamated p value by referring the new estimate to an appropriate distribution using the combined sample size. We called the former procedure paveraging and the latter raveraging. Raveraging, though the more popular of the two approaches in practice, is mysterious insofar as it provides a measure of evidence that adjusts the total p value as a function (sticking to the example considered in this section) of $r_{12}$ and the total sample size N, even in the absence of a corresponding procedure for similarly transforming per-study p values into evidence measures.¹⁸ And we are left with no way to confirm whether the raveraged p value is correctly reflecting the total evidence. The arguments that suggest that the raveraged p value may not be reflecting the total evidence apply to paveraging as well. As this latter method is unarguably a correct way to produce an overall p value, this further undermines interpretation of the per-study p value as an evidence measure in the first place.

4 Amalgamation using classification rather than measurement

4.1 Amalgamation based on binary evidence outcomes

A different approach to statistical evidence involves eschewing quantitative assessment altogether in favor of binary outcomes, with each study simply classified as “positive” or “negative.” At first blush, this may appear to be a change of topic, because we seem no longer to be talking about evidence measurement at all. But the assignment of a study to one class or the other does require some underlying evidence assessment, along with a choice of threshold for the classification procedure. Moreover, binary-based classification procedures lead to their own forms of evidence amalgamation, including the “independent replication” requirement as widely imposed throughout the social and biological sciences, as we will discuss.

By far the most common approach is to use the p value for purposes of this classification, so that “positive” and “negative” are simply other names for “statistically significant” and “non-significant.” The reasoning goes something like this: The p value represents sufficiently strong evidence against $\hbox {H}_{0}$ if it is smaller than some predetermined threshold; therefore we can use the p value to classify a study as positive or negative by checking whether its value is less than or greater than this threshold. Let’s say that we have set the per-study significance threshold at p value $\hbox {P} \le 0.05.$¹⁹ In many cases, when an initial study yields $\hbox {P}_{1} \le 0.05$ but a follow-up (replicate) study yields $\hbox {P}_{2} > 0.05$, we say that the initial finding failed to replicate, and conclude that it was likely to have been a mistake, or formally, a false positive result (Type 1 error).

On the other hand, when we find both $\hbox {P}_{1} \le 0.05$ and $\hbox {P}_{2} \le 0.05$, we conclude that the evidence in consideration of both studies is compelling in a way that it could never be based on any one study considered on its own. Although no quantitative assessment is made of how much stronger the evidence is at the conclusion of the two studies, we interpret the result of “positive” plus “positive” as something stronger than a “positive” based on any single study. Indeed, this is the basis of the now ubiquitous requirement of independent replication, as imposed by journals and funding agencies throughout the social and biological sciences. The independent replication requirement is a kind of evidence amalgamation rule, but one that proves difficult to defend.

On first blush, it seems safe to say that when both $\hbox {P}_{1}$ and $\hbox {P}_{2}$ equal, say, 0.05, we have stronger evidence than we could have obtained from any single study on its own. From a psychological point of view, this feels like stronger evidence than a small p value in a single study. After all, what are the chances of getting statistically significant results twice if $\hbox {H}_{0 }$ is actually true? But in fact, Fisher’s method provides the corresponding p value, $\hbox {P}_{12} = 0.018$.²⁰ Now suppose that the actual p value in the first study had been $\hbox {P}_{1 }= 0.018$. The logic of independent replication instructs us to treat this as a “positive” result, since $0.018 < 0.05$, and to look for corroboration in the form of $\hbox {P}_{2} \le 0.05$. But this suggests that a p value of 0.018 is stronger evidence if it was obtained from two studies than if it was obtained directly as 0.018 in a single study.

We must admit to a bit of magical thinking here. Obtaining $p= 0.05$ twice might feel like stronger evidence against $\hbox {H}_{0}$ than $p= 0.018$ in a single study, but from a purely mathematical point of view this notion is indefensible.²¹ We may be justified in concluding that a second positive study leaves the evidence as “positive,” but our practice of considering the combined evidence to be a stronger kind of “positive” than can be obtained in any single study considered on its own—regardless of the magnitude of its p value—is without mathematical justification.²²

The amalgamation operation implicit in the independent replication requirement reveals the confusion underlying the seemingly innocuous practice of binary evidence classification. In fact, common practice does ascribe some sort of ordering of evidence strength, considering some “positive” results—in particular, those based on two independent studies—to be more “positive” than others, although nothing about the p value itself supports this practice. But this is by no means the only problem with binary evidence classification.

4.2 Thresholds for binary decisions

Binary evidence classification requires an underlying threshold for per-study significance. This threshold must be chosen based on considerations of utilities, costs and benefits. And these in turn depend upon what one is trying to do. To use another analogy: Is $180\,{^{\circ }}\hbox {F}$ hot enough? There is no single answer to this question. It depends on whether, say, one is trying to boil water (“no”) or ethanol (“yes”). In either case one relies upon a reliable method for ascertaining the temperature, but the temperature itself cannot make the decision for us as to whether or not it is hot enough. Just so for p value thresholds. Whether one chooses 0.05 or 0.0005 as the significance threshold depends upon what one is trying to accomplish, and the costs, in that context, of erroneously rejecting $\hbox {H}_{0}$, among other things.²³ For this reason alone we cannot substitute the threshold for an evidence measure. If the evidence measure is to serve as a meaningful input to decision making about what to do, then it needs to have ontological status separate from the pragmatic particulars of any given decision. Binary classification based on the threshold does not eliminate the evidence measurement problem, it simply obscures it.

Moreover, recall the mainstream statistical view that the p value can be interpreted as a measure of evidence only when r and n (and possibly other things) are properly taken into account, even in the absence of a formal mechanism for so doing. This stance acknowledges that the p value does not have constant evidential meaning across applications. Then in what sense can we say that a threshold of, say, $P \le 0.05$ always rejects $\hbox {H}_{0}$ at the same level of evidence, even though individual studies may involve different values of r and n? Imagine a situation in which we were measuring length using a ruler that contracted and expanded by inches unpredictably. What would happen if we used this ruler to sort objects into length classes, say, $< 12''$ versus $> 12''$? Any such procedure would be seriously compromised by our inability to get a stable reading of length. This same logic applies to evidence. If we cannot reliably establish the strength of the evidence, then sorting p values by whether or not they cross some threshold is an evidentially compromised procedure.

Thresholds have their place in setting or evaluating performance characteristics for alternative statistical procedures. But in connection with evidence, they cannot get us around the underlying measurement problem. Unless we have a well-calibrated measure of evidence in the first place, the threshold value itself is evidentially indefinite. This problem also impinges upon any attempt to formalize evidence amalgamation procedures when the inputs are the result of a Y/N comparison between each p value and a significance threshold. If the threshold does not have constant evidential meaning across studies, then there is no justification for interpreting the amalgamation result as a measure of total evidence.²⁴

This remains the case in the face of our craving for an answer to the question “How strong is strong enough when it comes to evidence?” It might be nice to have a single reliable rule (or at least, rule of thumb) in answer to the question, but it is no more reasonable to expect this in connection with evidence than it would be in connection with any other type of measurement. Is $180\,{^{\circ }}\hbox {F}$ hot enough? If you are an experimental physicist you simply have to live with the fact that there is no single answer to that question. Measurement of statistical evidence is no different, and we simply have to learn to live with this.

4.3 Asymmetry between positive and negative evidence

There is another problem with evidence thresholds as well. Recall that, even were we to grant an evidential interpretation to very small p values, the p value still could not distinguish weak evidence against $\hbox {H}_{0}$ from evidence in favor of $\hbox {H}_{0}$. This complicates the notion of a “negative” study (that is, one that fails to reject $\hbox {H}_{0})$. The nomenclature is fine, as long as we bear in mind that the class of “negative” studies includes both studies that provide (perhaps weak) evidence against$\hbox {H}_{0}$ along with studies that might be providing evidence in favor of $\hbox {H}_{0}$. All we can do using the p value is to divide studies into those that are “positive” (i.e., statistically significant) and those that “failed to be positive.” But these latter studies are not truly “negative,” in the usual understanding of the word in which it stands in antithesis to “positive.” There is a built-in asymmetry in the nature of “positive” versus “negative” results when we use the p value as the basis of the classification.

It seems plain that in view of this asymmetry, the classification procedure is going to be insufficient for amalgamation purposes, since it will lead us to enter (perhaps weakly) supportive studies on the “negative” side of the ledger. No matter how sophisticated an amalgamation procedure may be, as long as it accepts as inputs the binary outcomes, “positive” or “negative,” based on per-study p values, the fundamental asymmetry between these two outcomes undermines any evidential interpretation of the amalgamation result.

4.4 Is the problem simply the p value?

At this point, it might be tempting to simply conclude that the p value itself is not a measure of evidence, and indeed, we intend the arguments put forward above as a novel critique of the p value. But there are independent, and in some ways far simpler, ways to critique the p value as an evidence measure. Two of the most compelling lines of argument involve the role of the alternative hypothesis, and the “irrelevance of the sample space” (see, e.g., Royall 1997 on both counts). Is it possible that a candidate evidence measure that appropriately considers the alternative hypothesis and/or depends solely on the data at hand (rather than the sampling distribution of all possible data) would be more amenable to proper amalgamation?

One such candidate is the log maximum likelihood ratio (log MLR). Consider for simplicity an LR with no free parameters in the denominator (e.g., $\hbox {H}_{\mathrm{DEN}} : R = 0$), and one or more free parameters in the numerator (e.g., $\hbox {H}_{\mathrm{NUM}} : R \ne 0$). The corresponding log MLR can indicate evidence for $\hbox {H}_{\mathrm{NUM}}$ (log MLR > 0), or it can fail to indicate evidence for $\hbox {H}_{\mathrm{NUM}}$ (log $\hbox {MLR} = 0$), depending on the data; but by virtue of the additional maximization in the numerator, the ratio can never be less than 0 and as a result the log MLR can never indicate evidence in favor of $\hbox {H}_{\mathrm{DEN}}$. This mirrors the asymmetric behavior of the p value, so that “positive” and “negative” results are not the complements of one another. Additionally, in practice the magnitude of the log MLR is usually evaluated by comparison with some conventional threshold. For instance, longstanding convention in human genetics has been to consider the evidence to be strong if the $\hbox {log}_{10}$ MLR $\ge 3.0$. This benchmarking against an evidentially indeterminate threshold is problematic for the same reasons discussed above in connection with the p value.

The log MLR also shares some features with raveraging. Its associated amalgamation operation, which derives from basic likelihood theory, involves “pooling” the data from $\hbox {S}_{1}$ and $\hbox {S}_{2}$, estimating (via maximum likelihood) $r_{12}$ based on the pooled data, and then calculating the corresponding log likelihood ratio at $r_{12}$ (implicitly taking into consideration the augmented sample size). This operation introduces a dependence of the amalgamated log MLR on $r_{12}$, in much the same way that raveraging ties the amalgamated p value to the weighted average parameter estimate. This can cause the log MLR to in effect “average” the evidence across two studies under certain circumstances, just as raveraging does for p value. Finally, calibration of the scale of the log MLR across studies requires considerations of “degrees of freedom,” or the number of parameters being maximized over, raising distinct measurement issues.

Thus the log MLR does not appear to satisfy MAP any more than does the p value. This is true despite the fact that the log MLR is, arguably, a better candidate for an evidence measure on the face of things, per arguments put forward by Barnard (1949), Hacking (1965), Edwards (1992) and Royall (1997), among many others.

4.5 Summary of Sect. 4

In the end, attempts to amalgamate evidence based on the dichotomous classification of studies into “positive” versus “negative” do not offer us a way to circumvent the evidence measurement problem. Instead, amalgamation of binary outcomes reveals confusion regarding the logical underpinnings of some common statistical practices. Mainstream statistical norms eschew formal evidence measurement in favor of requiring independent replication, which can be viewed as a form of amalgamation, understood in this context to be a method for weeding out false positive findings. But when examined carefully, the replication requirement is seen to be predicated on magical thinking, logically unsupportable practices involving thresholds of indeterminate meaning and a wholly inadequate notion of negative studies. Using a p value (or log MLR) based classification of studies as “positive” or “negative” as the inputs to any evidence amalgamation procedure merely obscures the measurement issue, and it undercuts any connection between the amalgamation output and the evidence.

5 Conclusions and directions for further work

We have focused in this paper on assessing the total or overall strength of statistical evidence based on multiple replicate studies, using some familiar and widely used statistical evidence amalgamation procedures. We began by noting that a rigorous amalgamation procedure requires a shared measurement scale between its inputs and its outputs, along with cogent interpretation for this scale in terms of the underlying object of measurement. We hope to have shown that, when viewed through this lens, standard statistical practice ties us in logical and conceptual knots.

Neither attempts to quantify amalgamated evidence via commonly used forms of meta-analysis, nor attempts at characterizing the total evidence using binary classification of studies, seem to be consistent with a cogent approach to per-study evidence measurement via the p value. This is true even under idealized circumstances, in which our study designs perfectly satisfy all assumptions of the underlying statistical model. But in practice, (at least) one relevant aspect of this model is routinely violated.

Meta-analysis presupposes a method for selecting input studies that does not introduce bias with regard to the per-study p values. Obviously, any method of selecting studies that systematically favors those with particularly small p values will tend to return smaller meta-analytic p values than a sampling method without such a bias. As is well known, meta-analyses of published studies tend to violate this assumption in exactly this manner, because studies that yield small p values tend to be preferentially published over studies that do not. We mentioned above that examples such as the one we considered, with $\hbox {P}_{1}< \hbox {P}_{12} <\hbox { P}_{2}$, were more the rule than the exception in many fields. This can occur as a consequence of publication bias, which may impact initial reports more than studies aimed at replicating those reports. In some fields, it is difficult to publish a new result that does not carry a small p value, but once a published result is deemed important, attempts to replicate that result may tend to be considered worth publishing whether or not the replication is successful. If $\hbox {S}_{1}$ is selected for a notably small p value, but $\hbox {S}_{2}$ is not, then $\hbox {P}_{2}$ will tend to be larger than $\hbox {P}_{1}$, and both paveraging and raveraging will tend to return an intermediate $\hbox {P}_{12}$, that is, a value closer to what one would have expected without the initial bias in selection. This is simply a form of regression to the mean.

But the problem here is not publication bias per se. Any experimental activity (including but not limited to publication) that involves preferentially following up on one’s most statistically promising initial results presents the same challenge. For example, a standard study design in genetics is to scan the genome, one position at a time, for statistical evidence of a genetic variant with an effect on some phenotype in one or more families, in order to find the best-supported genomic position; and then to follow up with additional data, e.g., using a new set of families, in order to corroborate the result at that position. This procedure seems scientifically unassailable, but any attempt at evidence amalgamation across the two stages of the study violates the same statistical assumption as does publication bias. When following up on our most promising findings, we can expect the p value to regress to the mean regardless of whether the evidence is going up or down, by virtue of having selected a location for follow-up on the basis of a notably small p value.

It seems that if there’s one thing evidence measurement should be good for, it would be allowing us some mechanism for determining whether the evidence is getting stronger or weaker as we accumulate data. And to be useful, any such measure must be meaningfully interpretable not only when following up on randomly selected studies or experiments, but especially, when following up on those studies or experiments that provided the best evidence in the first place.

But we see little hope of developing an evidence measure for use in such circumstances until we confront (at least) one foundational aspect of the standard statistical model, namely, the tight coupling (under broad regularity conditions) between effect size estimates (such as r, as considered above) and p values. For given sample size n, the larger is the value of r, the smaller is the p value, and vice versa, in a one-to-one manner. Thus, when we preferentially publish studies with small p values, we therefore also preferentially publish studies with inflated values of r, because those are precisely the studies with the smaller p values. When we go to replicate a study, however, we are likely (although not guaranteed) to obtain a value of r closer to R (the true value) so that $r_2 <r_1$. This immediately implies $\hbox {P}_{2} >\hbox {P}_{1}$. This phenomenon is sometimes referred to as “the winner’s curse.”

Intuitively, a correspondence between the parameter estimate and the p value may seem quite natural. But our tendency to blend the two things might be an artifact of the historical development of statistics, with much of modern theory grounded in Fisher’s development of likelihood as a foundation for the theory of parameter estimation, and various other objectives—such as testing and evidence measurement—layered on top (see, e.g., Gorroochurn 2016, for an overview of Fisher’s shaping of modern statistics). Perhaps a cogent approach to evidence measurement requires us to rethink the connection to parameter estimation.

To begin with, it is clear that effect size estimation and evidence measurement are simply not the same thing. One can have weak evidence for a large effect size or strong evidence for a small one, although the latter may require a larger sample size. Moreover, as Hacking (1965) pointed out, a general’s best estimate of the number of her troops may be an underestimate, while the opposing general’s best estimate of that same number may be an overestimate. What constitutes the best estimate depends on the context and judgments regarding the intended use of the estimate. But evidence is different. How well a hypothesis is supported by the data should be independent of pragmatic appeals of this type.²⁵ Indeed, $r_{12}$ will be a better estimate than $r_{1}$ under almost any pragmatic criteria, simply by virtue of being based on twice the sample size.²⁶ But, as we argued above, observing that the better estimate $r_{12}$ is smaller than the original $r_{1}$ does not guarantee that the evidence has gone down, or up. By coupling evidence measurement to parameter estimation we virtually guarantee that in situations where the parameter estimate regresses to the mean, the evidence measure will do the same. This precludes the possibility of correctly ascertaining whether the evidence is in fact going up or down on the acquisition of new data, precisely in those situations in which an evidence measure is most needed. The coupling of the p value to parameter estimation is therefore a feature (or perhaps we should say, bug) of the standard statistical model that fundamentally confounds measurement of evidence.

In this regard, an undue focus on extremely simple examples, while facilitating discussion, can also blur an important distinction. For instance, we considered above an example in which interest was in a single quantity, the correlation coefficient. In such settings, a common response to the problem of evidence measurement is to eschew p values altogether in favor of a focus on the parameter estimate itself, say, simply reporting the estimate along with a confidence interval.²⁷ But hypotheses are not necessarily limited to questions regarding specific parameter values. The legal case considered above had this flavor: the hypotheses were “guilt” versus “innocence,” but the data were related to different aspects of those hypotheses, including DNA results matching the suspect to the scene of the crime and eye witness accounts placing the suspect at the scene at a particular time. Scientific hypotheses too often have this flavor. For instance, our genetic hypotheses may be “gene X is causing disease Y” versus “gene X is not causing disease Y.” There is no single underlying parameter of interest here, but rather, a set of parameters which can be assayed using different experimental designs (DNA sequencing, gene expression experiments, etc.). Indeed these sorts of cases seem to be the more interesting ones in the context of evidence amalgamation, because they require us to assemble the aggregate evidence based on multiple types of data.

Our premise here has been that rigorous amalgamation of evidence in these more complex settings presupposes a solution in the simpler case, in which interest is focused on assessment of statistical evidence regarding the value of a parameter. One might argue that in fact the simpler case is different in kind: that statistical inference can be used to amalgamate evidence regarding the value of a single parameter based on multiple studies of the same type, but that this task is fundamentally different from amalgamation of evidence in the general case, in which the different studies may have different designs and/or involve different parameters. We have tried to illustrate some difficulties for evidence amalgamation in the simplest case. The apparent connection between these difficulties and the tethering of evidence measures such as the p value to parameter estimation seems to us to be a clue to solving this problem. Perhaps starting with the general case—in which we are forced to decouple estimation from evidence from the outset—will be a better strategy. In this case, we may yet find that the solution in the simple case is of a type with the general solution.

Recall too that, while we have used the p value to illustrate underlying measurement issues, our conclusions are by no means restricted to just this one statistic. Our central point is not merely that the p value fails as an evidence measure (although we believe that it does). Rather, our point is that as soon as we talk about evidence measurement, it behooves us to invoke MAP both as a tool for critiquing existing candidate measures and, ideally, as a guide in developing better ones.

Statistical theory has yet to provide a good methodology for addressing evidence measurement questions. This point applies equally—and for exactly the same reasons—to per-study evidence measures and to evidence amalgamation procedures. While it may be possible to make progress on the general evidence amalgamation problem before a complete measurement solution is available, no amalgamation algorithm will fully succeed in capturing the totality of evidence until the underlying evidence measurement problem has been resolved.