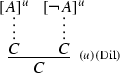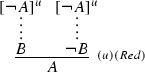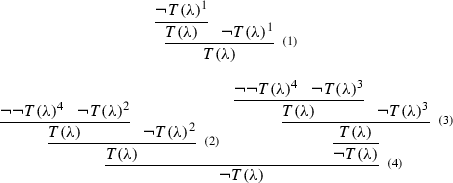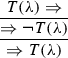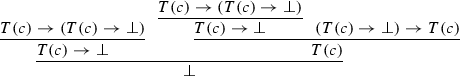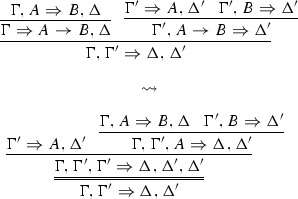Abstract
Nonclassical theories of truth have in common that they reject principles of classical logic to accommodate an unrestricted truth predicate. However, different nonclassical strategies give up different classical principles. The paper discusses one criterion we might use in theory choice when considering nonclassical rivals: the maxim of minimal mutilation.
Similar content being viewed by others
Notes
The maxim, at least by this name, is introduced in Quine (1970).
See for example French (2016), (Ripley 2012, 2013a, b, 2015), Zardini (2011, 2015) and further references below. I hasten to add that these advocates of substructural theories do not use MMM when arguing for their theories. What is more, they have other—and I believe better—arguments (e.g. unification of solutions to paradoxes). None of what follows here will deal directly with these advantages.
In what follows I will use the term ‘inference rule’ as a label for informal rules, in contrast to various proof rules, e.g. natural deduction rules or sequent calculus rules. I will also occasionally talk about inference rules or proof rules in zero-premise cases, i.e. for principles such as the law of excluded middle. The inference rules will be known by various natural language sobriquets such as ‘proof by cases’, ‘modus (ponendo) ponens’, ‘ex falso quodlibet’, and so on. The proof rules will have labels depending on the system in question, for example, \(\rightarrow I\) for the conditional introduction rule in natural deduction, or \(L\vee \) for the left-rule for disjunction in sequent calculus. Typically, an inference rule will have many proof rules as formal counterparts, and it is precisely this feature that makes the revisions harder to track. A familiar case is modus ponens, an inference rule that corresponds to a variety of different proof rules, including axioms, single-premise rules, multiple-permise rules, and meta-rules. Finally, I will apply the term ‘logical principle’ in an even wider sense to include principles such as tertium non datur, the principle of bivalence, the principle of truth preservation, etc.
However, see Halbach and Nicolai (2017) for an interesting argument against the idea that nonclassical theories can recapture classical arithmetic.
Recall, I treat LEM as a zero-premise proof rule. I will treat \(\bot \) as the conjunction of all formulas.
The naming device is rather coarse compared to introducing the theory of syntax via arithmetic and coding, but it suffices for our purposes. Note that the technique requires that the domain is infinite in every model (since it contains every formula of the language). See Ripley (2012) for further discussion and comparison.
The paradoxical derivation also shows why the classical dilemma ND rule (Dil) leads to paradox (together with \(\lnot E\)):
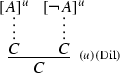
Other negation rules are problematic for both paraconsistent and paracomplete theories. Consider the following version of classical reductio:
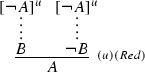
The paradox returns since the instance of Red with vacuous discharge of assumptions is simply \(\lnot E\) (given that \(\bot \) lets us derive B):
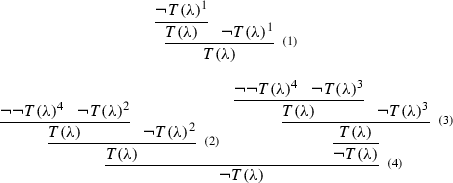
I will assume that the three-valued logics are well-known. See Priest (2008) for details.
For details of multiple conclusion consequence relations for \(\mathbf {LP}\) and \(\mathbf {K3}\), see Beall (2011).
We could equally well define the Curry sentence with an arbitrary formula p as the consequent. The result is that Curry-style sentences can give us a derivation of any formula.
Alternatively, a theory of truth with a negation defined in terms of \(\bot \) and \(\rightarrow \) might limit the revisions to inference rules for the conditional.
See Feferman (1984, p. 96) for a similar conclusion.
Granted, the rejection of weakening is independently motivated since \(\mathbf {BX}\) is after all a relevant logic, but it is still significant for MMM if the purpose is only to block the paradoxes of truth.
See especially Field (2008, Ch. 17.4).
Horsten says that the natural deduction rules for his system (\(\mathbf {PKF}\)) are just those of classical logic with the exception of \(\rightarrow I\). It is unclear what he takes the inference rules for negation to be. On pain of paradox they cannot be classical (or even intuitionistic), but perhaps Horsten has in mind a natural deduction system with a negation defined in terms of the conditional and \(\bot \). But in any case, even for formulas where LEM hold, the system won’t have the full power of the classical conditional (e.g. Peirce’s law) without some further principle.
Field actually advocates the same restricted version of \(\rightarrow I\) for his primitive conditional (cf. Field 2008, p. 269).
In the context of sequent rules, the (sequent) premises and (sequent) conclusion will be the sequents occurring above and below the line, while the antecedent and succedent are the left- and right-hand side of the sequents respectively.
See Troelstra and Schwichtenberg (2000, pp. 61–62). I will omit the sequent rules for quantifiers as they won’t play any role in what I have to say.
The structural rules in sequent calculus don’t have straightforward counterparts in natural deduction. Instead, the structural rules are embedded as various structural properties in natural deduction systems. Two of these—weakening and contraction—are represented as policies for discharge of assumptions (vacuous discharge and multiple discharge respectively). Identity is represented by assumptions themselves, that is, the labels of top nodes of natural deduction derivation trees. Finally, cut is represented by the transitivity of natural deduction derivations. See von Plato (2001) for further details on translations between natural deduction and sequent calculus.
LK and RK allows a derivation of \(\Gamma \Rightarrow \Delta \) for any \(\Gamma , \Delta \).
It won’t help to blame the paradoxes on the fact that the operational rules in \(\mathbf {G1c}\) are multiple conclusion. The result of restricting the sequent rules to empty or singleton succedents leads to the intuitionistic calculus \(\mathbf {G1i}\). Both paradoxical sentences will still lead to triviality in \(\mathbf {G1i}\), however. For the Curry sentence this is trivial since the derivation doesn’t rely on multiple conclusion. See also footnote 29.
Unification is a criterion that is accepted by most parties in the debate. Priest (1998, 2002, 2010) has championed a principle of uniform solution to paradoxes. See also Smith (2000). Field (2008, p. 15) says that ‘[I]t is important that we not just deal with each paradox piecemeal, but provide a systematic account that can be shown to handle them all’.
Some authors also motivate substructural theories by arguing that they handle related paradoxes such as the validity Curry paraodx (cf. Shapiro 2010; Beall and Murzi 2013) and the set-theoretic Hinnion–Libert paradox (cf. Hinnion and Libert 2003; Restall 2008). These paradoxes have in common that they don’t rely on any of the operational rules for standard connectives. The result is that revision of negation or the conditional has no traction.
Incidentally, it won’t help to reject only one contraction rule. Suppose we have LW but not RW. Then we can still derive \(T(\lambda ) \Rightarrow \), and the following derivation gives us \(\Rightarrow T(\lambda )\):
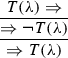
Here is an example using the slightly weaker rule form of absorption (and instances of the T-schema):
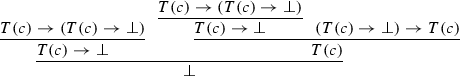
The double line indicates that we potentially apply more than one instance of LW and RW. The derivation of the other \(L\sqsupset \) rule is almost identical.
Zardini’s theory also has multiplicative quantifiers, but I will set aside that complication here. See Ripley (2015) for some discussion.
Zardini (2011, p. 514) makes the case that this is an improvement on the paracomplete and paraconsistent theories.
A sequent rule is admissible if adding the rule to a calculus won’t extend the class of derivable sequents. A derivable sequent rule is therefore admissible, but it is not always the case that admissible rules are derivable. The famous example is the cut rule itself.
Interestingly, Gentzen’s (1934) own \(\mathbf {LK}\) system has the multiplicative rules for the conditional, and the additive rules for conjunction and disjunction. Troelstra and Schwichtenberg (2000, p. 87) attributes the \(\mathbf {G1c}\) formulation to Kleene (1952). Thanks to an anonymous referee for the observation.
Thanks to an anonymous referee for this point.
Although Rosenblatt (2017) develops a noncontractive theory with mixed connectives, but where a restriction on cut avoids structural contraction from being reintroduced. I bracket this development here since the theory is both noncontractive and nontransitive.
Note that the noncontractivist can still accept additive connectives (i.e. connectives with context-sharing left- and right-rules). Mares and Paoli (2014) defends a noncontractive theory that includes both additive and multiplicative connectives.
There is another subtle way to argue against the mixed connectives. The additive \(\sqsupset \) and multiplicative \(\multimap \) conditionals have left and right rules whose reduction conversion in a cut elimination proof yields the very same sequent as the original proof, without applications of additional structural rules. The same is not the case for the mixed conditional \(\rightarrow \). Here is the conversion step (with the standard multiplicative cut rule):
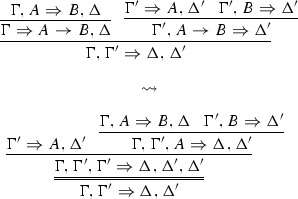
The final step in the redux derivation might require one or more applications of LW and RW. In effect, the redux derivation has to compensate for the contraction made admissible by the rules for \(\rightarrow \). The noncontractivist could argue that a permissible connective should have sequent rules that have a reduction conversion that doesn’t require additional applications of structural rules. That would be a step towards distinguishing the additive and multiplicative connectives from the mixed connectives.
See also Barrio et al. (2015) for a connection between nontransitive theories and \({\mathbf {LP}}\).
For simplicity I use the connective \(\rightarrow \) here as well, but it shouldn’t be confused with the mixed connective discussed in Sect. 5.1. Ripley gives the rule the name CFMPP since it is a context-free modus (ponendo) ponens rule. I will use the labels from ND rules (\(\rightarrow E\)) for sequent style rules as well, but with an SC superscript.
The added contexts \(\Gamma , \Gamma '\) simply indicate open assumptions (top nodes) in the derivation. Note that the multiple conclusions are not innocuous. Together with an appropriate multiple conclusion conditional proof rule, it axiomatizes the full classical conditional (as opposed to the intuitionistic conditional axiomatized by \(\rightarrow I\) and \(\rightarrow E\) in the absence of negation). See Read (2000, pp. 144–146) for details and further references.
See also Negri and von Plato (2001).
Note that the sequent calculus derivation of Curry’s paradox derives both \(\Rightarrow T(c)\) and \(\Rightarrow T(c) \rightarrow \bot \).
Adding the axiom \(\bot \Rightarrow \) is just one particularly simple way of regaining full cut. In fact, \(\mathbf {G1c}\) sometimes has the axiom instead of the ordinary negation rules. Alternatively, if \(\Delta \) or \(\Delta '\) is nonempty, we can let the right-most sequent premise be \(B \Rightarrow B\), for \(B \in \Delta \cup \Delta '\). We then use RW to contract the instance in the final step of the derivation, thus deriving a restricted form of cut.
Since the \(\mathbf {G1c}\) rule \(R\wedge \) is additive, the derivation is of additive cut. But note that this makes no difference in a nontransitive calculus with both contraction and weakening.
Recall that in a ND proof system, reflexivity is represented by the assumptions labelling the leaf nodes of the derivations.
See Troelstra and Schwichtenberg (2000, p. 66).
On my account \(\lambda \) is a distinguished name and cannot occur as a formula in a sequent. Thus there is no sequent of the form \(\lambda \Rightarrow \lambda \). In contrast, French (2016) uses \(\lambda \) as a sentence.
See Takeuti (1975, pp. 75–76) for details of the system.
Of course, recapture of classical arithmetic is not exclusive to nonreflexive theories. It works for the nontransitive and noncontractive theories as well, but with different technical solutions.
Shapiro (2016) has recently argued for a stronger conclusion. He maintains that there is ‘no useful explication of the idea of a substructural approach to paradox’ (ibid.). Although I agree with Shapiro that some fully structural logics can be formalized as substructural, and vice versa, I don’t agree that going substructural contributes nothing to the solution to the paradoxes. In fact, abductivism suggests that two theories containing equivalent but differently formalized logics can be distinguished by various selection criteria, for example, MMM, simplicity, unification, etc.
French (2016) also suggests that his nonreflexive theory is connected to \(\mathbf {K3}\).
Ripley gives two different proof systems: the disjunctive reading and the negated-conjunctive. Here we have only considered the former. See also Barrio et al. (2015) for a discussion of the connection between the nontransitive system and \(\mathbf {LP}\).
Admittedly this assumes that we can make sense of the connection between 3-sided sequents and inference. For some discussion see Hjortland (2014).
I only include the rules for \(\lnot \) and \(\wedge \) for reasons of brevity. The operational rules for \(\vee \) simply dualize those of \(\wedge \). See Baaz et al. (1993) for details. Note that the \(\mathbf {3G}\) rules are additive. Again, given the presence of weakening and contraction these are equivalent to the multiplicative counterparts.
This is the logic \(\mathbf {TS}\) (tolerant-strict) from Cobreros et al. (2011).
Cf. Cobreros et al. (2011, Lem. 9). Thanks to Rohan French and David Ripley for making this connection clear.
References
Anderson, A. R., & Belnap, N. D. (1975). Entailment (Vol. 1). Princeton: Princeton University Press.
Baaz, M., Fermuller, C., & Zach, R. (1993). Systematic construction of natural deduction systems for many-valued logics. In Proceedings 23rd international symposium on multiple-valued logic (pp. 208–213). IEEE Press.
Barrio, E., Rosenblatt, L., & Tajer, D. (2015). The logics of strict-tolerant logic. Journal of Philosophical Logic, 44(5), 551–571.
Beall, J. (2009). Spandrels of Truth. Oxford: OUP.
Beall, J. (2011). Multiple-conclusion LP and default classicality. Review of Symbolic Logic, 4(2), 326–336.
Beall, J. (2013). LP+, K3+, FDE+, and their ‘classical collapse’. The Review of Symbolic Logic, 6(04), 742–754.
Beall, J. (2015). Free of detachment: Logic, rationality, and gluts. Noûs, 49(2), 410–423.
Beall, J., & Murzi, J. (2013). Two flavors of Curry paradox. Journal of Philosophy, CX(3), 143–165.
Caret, C. R., & Weber, Z. (2015). A note on contraction-free logic for validity. Topoi, 34(1), 63–74.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2011). Tolerant, classical, strict. Journal of Philosophical Logic, 41(2), 347–85.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2014). Reaching transparent truth. Mind, 122(488), 841–66.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2015). Vagueness, truth and permissive consequence. In T. Achourioti, H. Galinon, J. Martínez Fernández, & K. Fujimoto (Eds.), Unifying the philosophy of truth (pp. 409–430). Berlin: Springer.
Feferman, S. (1984). Toward useful type-free theories. I. Journal of Symbolic Logic, 49, 75–111.
Field, H. (2008). Saving truth from paradox. Oxford: OUP.
Fjellstad, A. (2016). Naive modus ponens and failure of transitivity. Journal of Philosophical Logic, 45(1), 65–72.
French, R. (2016). Structural reflexivity and the paradoxes of self-reference. Ergo, An Open Access Journal of Philosophy, 3(05), 113–31.
Gentzen, G. (1934). Untersuchungen über das logische Schliessen. Mathematische Zeitschrift, textit39, 405–431. (Translated in The Collected Papers of Gerhard Gentzen, ed. by M. E. Szabo. North Holland, 1969).
Gentzen, G. (1936). Die Widerspruchsfreiheit der reinen Zahlentheorie. Mathematische Annalen, 112, 493–565.
Grišin, V. N. (1981). Predicate and set-theoretic calculi based on logic without contractions. Mathematics of the USSR. Izvestija, 18, 41–59.
Halbach, V., & Nicolai, C. (2017). On the costs of nonclassical logic. Journal of Philosophical Logic, 1–31. https://doi.org/10.1007/s10992-017-9424-3.
Hinnion, R., & Libert, T. (2003). Positive abstraction and extensionality. The Journal of Symbolic Logic, 68(03), 828–836.
Hjortland, O. T. (2012a). Harmony and the context of deducibility. In C. D. Novaes & O. T. Hjortland (Eds.), Insolubles and consequences: Essays in honour of Stephen Read. London: College Publications.
Hjortland, O. T. (2012b). Logical pluralism, meaning-variance, and verbal disputes. Australasian Journal of Philosophy, 91(2), 355–373.
Hjortland, O. T. (2014). Speech acts, categoricity, and the meanings of logical connectives. Notre Dame Journal of Formal Logic, 55(4), 445–467.
Hjortland, O. T. (2017). Anti-exceptionalism about logic. Philosophical Studies, 174(3), 631–58.
Horsten, L. (2009). Levity. Mind, 118(471), 555–581.
Horsten, L. (2011). The Tarskian turn: Deflationism and axiomatic truth. Cambridge, MA: MIT Press.
Humberstone, L. (2007). Investigations into a left-structural right-substructural sequent calculus. Journal of Logic, Language and Information, 16(2), 141–171.
Kleene, S. C. (1952). Permutability of inferences in Gentzen’s calculi LK and LJ. Memoirs of the American Mathematical Society, 10, 1–26.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72(19), 690–716.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43(2), 439–469.
McGee, V. (1990). Truth, vagueness, and paradox: An essay on the logic of truth. Cambridge: Hackett.
Murzi, J., & Shapiro, L. (2015). Validity and truth-preservation. In T. Achourioti, H. Galinon, J. Martínez Fernández, & K. Fujimoto (Eds.), Unifying the philosophy of truth (pp. 431–459). Dordrecht: Springer.
Negri, S., & von Plato, J. (2001). Structural proof theory. Cambridge: Cambridge University Press.
Petersen, U. (2000). Logic without contraction as based on inclusion and unrestricted abstraction. Studia Logica, 64(3), 365–403.
Priest, G. (1980). Sense, entailment and modus ponens. Journal of Philosophical Logic, 9(4), 415–435.
Priest, G. (1987/2006b). In contradiction (2nd Ed.). OUP, Oxford.
Priest, G. (1991). Intensional paradoxes. Notre Dame Journal of Formal Logic, 32(2), 193–211.
Priest, G. (1998). The import of inclosure: Some comments on grattan-guinness. Mind, 107(428), 835–840.
Priest, G. (2002). Beyond the limits of thought. Oxford: Oxford University Press.
Priest, G. (2006a). Doubt truth to be a liar. Oxford: OUP.
Priest, G. (2008). An introduction to non-classical logic (2nd ed.). Cambridge: Cambridge University Press.
Priest, G. (2014). Revising logic. In P. Rush (Ed.), The metaphysics of logic, Chapter 12 (pp. 211–223). Cambridge: CUP.
Priest, G. (2016). Logical disputes and the a priori. Logique et Analyse, 59(236), 347–66. Forthcoming.
Priest, G., et al. (2010). Inclosures, vagueness, and self-reference. Notre Dame Journal of Formal Logic, 51(1), 69–84.
Quine, W. V. (1951). Two dogmas of empiricism. Philosophical Review, 60(1), 20–43.
Quine, W. V. (1970). Philosophy of Logic. Oxford: Oxford University Press.
Read, S. (2000). Harmony and autonomy in classical logic. Journal of Philosophical Logic, 29(2), 123–154.
Read, S. (2010). General-elimination harmony and the meaning of the logical constants. Journal of Philosophical Logic, 39(5), 557–576.
Restall, G. (2000). An introduction to substructural logics. London: Routledge.
Restall, G. (2008). Assertion, denial and non-classical theories. In K. Tanaka, F. Berto, E. Mares, & F. Paoli (Eds.), Paraconsistency: Logic and applications (pp. 81–100). Berlin: Springer.
Ripley, D. (2012). Conservatively extending classical logic with transparent truth. Review of Symbolic Logic, 5(2), 354–378.
Ripley, D. (2013a). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–164.
Ripley, D. (2013b). Revising up: Strengthening classical logic in the face of paradox. Philosophers’ Imprint, 13(5), 1–13.
Ripley, D. (2015). Comparing substructural theories of truth. Ergo: An Open Access Journal of Philosophy, 2(13), 299–328.
Rogerson, S. (2007). Hirokawa on right weakening and right contraction. In J.-Y. Béziau & A. Costa-Leite (Eds.), Perspectives on universal logic (pp. 237–263). Monza: Polimetrica.
Rosenblatt, L. (2017). Noncontractive classical logic. Manuscript.
Russell, G. (2015). The justification of the basic laws of logic. Journal of Philosophical Logic, 44(6), 793–803.
Schroeder-Heister, P. (2012). Paradoxes and structural rules. In C. D. Novaes & O. T. Hjortland (Eds.), Insolubles and consequences: Essays in honour of Stephen Read (pp. 203–212). London: College Publications.
Shapiro, L. (2010). Deflating logical consequence. The Philosophical Quarterly, 61(243), 320–342.
Shapiro, L. (2016). The very idea of a substructural approach to paradox. Synthese, 1–20. https://doi.org/10.1007/s11229-016-1230-x.
Smith, N. J. (2000). The principle of uniform solution (of the paradoxes of self-reference). Mind, 109(433), 117–122.
Standefer, S. (2016). Contraction and revision. The Australasian Journal of Logic, 13(3), 58–77.
Takeuti, G. (1975). Proof theory. Amsterdam: North-Holland.
Tennant, N. (1982). Proof and paradox. Dialectica, 36(2–3), 265–296.
Troelstra, A. S., & Schwichtenberg, H. (2000). Basic proof theory. Cambridge: Cambridge University Press.
Visser, A. (1984). Four valued semantics and the liar. Journal of Philosophical Logic, 13(2), 181–212.
von Plato, J. (2001). Natural deduction with general elimination rules. Archive for Mathematical Logic, 40, 541–567.
Weber, Z. (2016). On closure and truth in substructural theories of truth. Synthese, 1–15. https://doi.org/10.1007/s11229-016-1226-6.
Weir, A. (2015). A robust non-transitive logic. Topoi, 34(1), 99–107.
Williamson, T. (2013). Modal logic as metaphysics. Oxford: Oxford University Press.
Williamson, T. (2015). Semantic paradoxes and abductive methdology. In B. Armour-Garb (Ed.), The relevance of the liar. Oxford: OUP.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4(4), 498–535.
Zardini, E. (2013). Naive modus ponens. Journal of Philosophical Logic, 42(4), 575–593.
Zardini, E. (2015). Getting one for two, or the contractors’ bad deal. Towards a unified solution to the semantic paradoxes. In T. Achourioti, H. Galinon, J. Martínez Fernández, & K. Fujimoto (Eds.), Unifying the philosophy of truth (pp. 461–493). Dordrecht: Springer.
Acknowledgements
Acknowledgements: This research is funded by the Research Council of Norway (RCN), Grant 251218. I am grateful to the audiences at the Munich Center for Mathematical Philosophy (Buenos Aires–MCMP workshop), the University of Oslo (‘Critical Views on Logic’ workshop), and the Kyoto University (Logic and Metaphysics Workshop) for excellent discussions of the paper. I am very grateful to Pål Antonsen, Rohan French, Lavinia Picollo, Dave Ripley, Lucas Rosenblatt, and Shawn Standefer, who have all given me invaluable comments. Finally, I need to thank Elia Zardini and two anonymous referees for generous and insightful comments on an earlier draft of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hjortland, O.T. Theories of truth and the maxim of minimal mutilation. Synthese 199 (Suppl 3), 787–818 (2021). https://doi.org/10.1007/s11229-017-1612-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1612-8




 to be intersubstitutable. See for example Beall (
to be intersubstitutable. See for example Beall (