Abstract
This paper defends the naïve thesis that the method of experiment has per se an epistemic superiority over the method of computer simulation, a view that has been rejected by some philosophers writing about simulation, and whose grounds have been hard to pin down by its defenders. I further argue that this superiority does not come from the experiment’s object being materially similar to the target in the world that the investigator is trying to learn about, as both sides of dispute over the epistemic superiority thesis have assumed. The superiority depends on features of the question and on a property of natural kinds that has been mistaken for material similarity. Seeing this requires holding other things equal in the comparison of the two methods, thereby exposing that, under the conditions that will be specified, the simulation is necessarily epistemically one step behind the corresponding experiment. Practical constraints like feasibility and morality mean that scientists do not often face an other-things- equal comparison when they choose between experiment and simulation. Nevertheless, I argue, awareness of this superiority and of the general distinction between experiment and simulation is important for maintaining motivation to seek answers to new questions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
If we are thinking within our system, then it is certain that no one has ever been on the moon. Not merely is nothing of the sort ever seriously reported to us by reasonable people, but our whole system of physics forbids us to believe it. For this demands answers to the questions “How did he overcome the force of gravity?” “How could he live without an atmosphere?” and a thousand others which could not be answered. – Ludwig Wittgenstein, c. 1950 (published 1969)
It is madness and a contradiction to expect that things which were never yet performed should be effected, except by means hitherto untried.
— Sir Francis Bacon (1620, Part 1, Sec. 1, Aphorism 6)
1 Introduction
The method of experiment, in which we compel nature, under controlled conditions, to answer the questions we ask, has long been seen as what distinguishes modern science from its ancestors. The method of computer simulation first showed its effectiveness through its indispensable role in the design of the thermonuclear bomb (Galison 1997, pp. 689–780), still perhaps the most spectacular demonstration of Francis Bacon’s dictum that knowledge is power. Contemporary science and life are suffused with computer simulation, but for all the usefulness of this method there remains a steady strain of the opinion that was there from the beginning, that computer simulation is inferior to experiment for gaining knowledge of the world. In recent times many philosophers have denied this thesis that experiment is superior to computer simulation, and supporters have had difficulty defending the intuition.
I will argue that grounding a thesis about the superiority of experiment requires clarity about the purpose for which the methods are compared, and the quantificational structure of the claim, and that it can, and can only, be supported by an explicitly other-things-equal argument. Both defenders and detractors of the superiority of experiment are mistaken, I will argue, in the assumption that it depends on the study sample in an experiment being materially similar to the target in the world that the investigator is trying to learn about. The relevant factor is not material similarity but a kindhood with which nature is replete, but that can also be found in manufacturing, and for which material similarity is neither sufficient nor necessary. Practical constraints like feasibility and morality mean that scientists do not often face an epistemically other-things-equal comparison when they choose between experiment and simulation. Nevertheless, I argue, awareness of this superiority and of the general distinction between experiment and simulation is important for maintaining motivation to seek answers to new questions.
Scientists have all sorts of reasons to do simulations, and all sorts of purposes to which they put experiments. The superiority thesis I will defend concerns simulations that aim to answer a specific, determinate question about the actual world, a question of the sort an experiment is often used to answer. The scope of the claim does not include the use of simulation to “explore a topic”, and does not include its use for heuristic purposes—to discover hypotheses worth testing or experiments worth doing, or what is possible as opposed to actual. It does not include the use of simulation to explore the dynamical dimensions and potential of a model, or as a method of design, or as a tool to aid classic experimentation—for example for preselecting setups, simulating data, or analyzing the results of experiments—or for discovering possible explanations of a known phenomenon, or for pedagogical purposes.Footnote 1 The thesis does not claim that there is something that no simulation could ever do, such as discover novelties (cf. Parke 2014).
The existence of hybrids that display elements of both experiment and simulation does not undermine my appeal to a difference between the methods since there exists a recognizable distinction between the two, discussed below, that applies to enough clear cases to make a claim of principled advantage important. The considerations in this paper will make it clear that there is no need to abandon wholesale the common practice of judging the epistemic value of cases by among other things their status as simulation or experiment, as has been urged by Parke (2014). We can continue with these judgments provided we keep in mind the conditions under which the status reveals anything, and what it does and does not reveal. As I argue below, this practice has a positive role in maintaining motivation to seek answers to new questions.
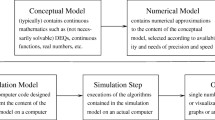
2 Materials and methods
There is a persistent intuition that experiments are more direct than simulations, that they are in a more direct relationship to the object of study, the material world, and that this is what makes them superior. This intuition surely has a role in the concern that has been expressed among some experimental physicists that simulations will come to be preferred because they are generally cheaper, and that this will inhibit discovery of new facts about the world (Humphreys 2004, pp. 133–134). After all, it has been said, a simulation can only reveal the consequences of knowledge we already possess, or, as Herbert Simon put it, “a simulation is no better than the assumptions built into it” (Simon 1969, p. 18).
This latter intuition is supported by the idea that a computer simulation is merely calculating the consequences of a set of theoretical assumptions. There would thus be no information in the results of the simulation that were not already present in the theoretical assumptions—garbage in, garbage out. However there are two problems with this idea about why computer simulations are inferior at bringing new knowledge. First, even “mere” calculation can give us new knowledge, for the fact that information is present in theoretical assumptions does not mean that we know what it is. Analogously, the fact that what determines the outcome of an experiment is already present in the substrate it is performed on does not mean we know what it is, and no one thinks that makes an experiment trivial or unable to bring new knowledge. Moreover, to the extent that we know that theoretical assumptions are accurate about the world, a surprising result of calculation from them gives us some new purchase on the world. It has been argued further that simulations can yield surprises and novel discoveries in the same ways that experiments can (Parke 2014; cf. Morgan 2005), and I will not dispute that point. My interest here is not in the possibility of discovery, of possibilities or actualities, but in the strength of the justification the two methods can yield for answers to questions about the actual world.
In trying to locate an inferiority for simulation one might think that even if a simulation surprises us, the epistemic value or justification of the new beliefs about the world that we form on the basis of the simulation’s results is no better than that of the theory from which it produced the calculations, since the simulation has no grounds independent of our trust in the theory. However, in fact a computer simulation’s results do have sources independent of the theory, since it is a long road from theoretical assumptions to a “solver,” the computer program that will give the final results (Morgan 2002, 2003, 2005; Humphreys 2004; Winsberg 2010). The solver is the product of theoretical ideas, analogies, approximation techniques, replacement, pre-existing pieces of code, ingenuity, and necessity. It has a life of its own; its credentials are evaluated independently of the theory and it is typically the solver, not the theory, that is revised when predictions resulting from a simulation face recalcitrant experience.
The multiple sources from which a simulation is constructed could even bring a positive epistemic advantage; their carrying support independently of the theoretical assumptions and of each other could form the basis for an abductive inference to the best explanation, from the fact that a simulation “works” in mimicking an effect to the deeper resemblance of its model to the way the world is. At least, it is not clear why such an inference would be any worse off than the analogous inference for a theory or hypothesis. That at least some evaluation of a simulation is done independently of evaluation of the theory is the second problem with viewing a simulation as merely calculating the consequences of theoretical assumptions.
If a simulation has enough distance from the theoretical assumptions to give it an independent status, perhaps a difference in status between simulation and experimentation can be located in the former having too much distance from the target system, the part of the world that the two methods can be used to tell us something about. On one such view, whereas in an old-fashioned experiment one is “controlling the actual object of interest, ..., in a simulation one is experimenting with a model rather than the phenomenon itself.” (Gilbert and Troitzsch 1999) An immediate problem with this view is that the actual object of interest of a scientist conducting an old-fashioned experiment to test a hypothesis often extends beyond the sample that can be manipulated in the lab. When Ernest Rutherford first argued that the atom has a nucleus, he used experiment on gold samples to draw a conclusion about the structure of all atoms, including those in gold outside the lab, and also those in lead, and hydrogen, and phosphorus.
In order to draw conclusions about the world from a model one must make assumptions about its similarities to the target system, so a model may be thought to be epistemically further from the wide world’s atoms than a sample of gold is because a model cannot have the degree of similarity to the world that a chunk of the world has. But as evident to us as it may be, the claims that the gold in the lab is similar to all other gold and to lead, and hydrogen, and phosphorus, in the relevant respects are also assumptions that must have been justified if the results on the sample of gold were to be generalized to all atoms. In both simulations and experiments the object acted upon is separated from the world that one often wants to learn about by a layer of assumptions of relevant similarity. The strength of justification that we have for those assumptions depends on the case and is not determined by whether the study is an experiment or a simulation (Parker 2009; Winsberg 2009, 2010).Footnote 2
Another popular way of attempting to make out the intuition that experiment is more direct than simulation focuses on the kind of similarity that obtains between study system and target system. A gold sample is materially similar to all other gold, and to lead, hydrogen, and phosphorus, in the relevant respects, whereas a computer model is similar to the target system only in virtue of its form (Morgan 2002, 2003, 2005; Guala 2005). This, according to what is called the Materiality Thesis, makes generalization of the study’s results to the target more justified. Both defenders and detractors of the superiority of experimentation take it to depend on some version of the Materiality Thesis (Durán 2013).
Some critics of this approach have said that the distinction between formal and material similarity is confused (Winsberg 2010, p. 62), because for any two material objects one can find a formal similarity. All objects have both sorts of properties, of course, and the fact that living things and petroleum are not only both self-identical but also both composed largely of carbon and hydrogen atoms would not incline us to experiment on petroleum in order to learn about mice. However, this does not mean that material properties are not specially important or distinct from formal properties, but only that any property, material or formal, may be insufficiently relevant to a given question for a similarity with respect to that property to be helpful. Among the relevant properties a distinction, albeit vague at the boundary, can be made between those that are material and those that are formal. A wooden table and chair are materially but not formally similar. A wooden camshaft is formally but not materially similar to a steel camshaft. And a theoretical model of a physical process may be formally but is definitely not materially similar to the thing it models.
The material-formal distinction is clear enough, and tracks something in the difference between experimentation and simulation. The real challenge for the view that material similarity makes an experiment superior is to explain why this distinction makes any principled difference to the strength of justification of conclusions. Several authors claim that material similarity is always relevant:
We are more justified in claiming to learn something about the world from the experiment because the world and experiment share the same stuff. In contrast, inference from the model experiment is much more difficult as the materials are not the same—there is no shared ontology, and so the epistemological power is weaker. (Morgan 2005, p. 323; cf. Guala 2002, 2005; Harré 2003, pp. 27–8.)
but the claim that “ontological equivalence provides epistemological power” (Morgan 2005, p. 326) gives no guidance as to why this special similarity matters to justification.
One might think that material similarity has more to offer because it offers a greater degree of similarity than formal similarity does, and thereby more strongly justifies the “back inference” to the target (Harré 2003, pp. 27–28). However a material similarity claim cannot justify our back inference to the target unless it is itself justified. If a claim of material similarity is strictly stronger than a claim of formal similarity then that would suggest it is more difficult to justify.Footnote 3 At least, it would be the burden of the advocate of the Materiality Thesis to say why not. If the material similarity claim more strongly supports the back inference because of its logically stronger content, what we trade for this is the claim’s own level of justification. From this it seems that reliance on a claim of material similarity could put the experimenter at a justificational disadvantage.
Even if a claim of material similarity is justified, it is hard to see why we should think material similarity is strictly stronger than formal similarity. Clearly material similarity does not imply formal similarity. Animal fur can be made into a cap or a coat, ceramic into a plate or a cup. The different objects rendered in fur and in ceramic respectively are not only formally different but topologically different. You cannot put your arm through a cap without tearing it. Grabbing a plate with a curled finger would be challenging. Two objects being materially similar does not even make it more likely that they are formally or topologically similar.
The most compelling and popular suggestion about why material similarity makes experiment stronger comes from what Francesco Guala calls “blackboxing” (Guala 2002). Having a chunk of the world in the lab appears to let the experimenter get away with less commitment than the simulator.Footnote 4 Experimenter and simulator must both insure that their study systems are dynamically similar to the target system. The simulator does this by making in her study system a model of the dynamics of the target system. By contrast operating on a sample of the target system relieves the experimenter of the need to make a model of that system. On this way of defending the superiority thesis, if the experimenter has reason to believe his sample is made of the same stuff as the target, that entitles him to assume it will behave the same way as the target, without making commitments about how it does so. Rutherford could suppose that the sample gold behaves like all other gold in the relevant respects—whatever they are—because they all are gold. The experimenter’s claim that object and target are the same stuff must be justified, of course, but the simulator must go further, to make specific commitments about what the dynamics of the target system are. Thus the simulator seems to be strictly further out on a limb. Her claim is not merely a generic one of formal or dynamical similarity of her system and the world but similarity with respect to, say, A, B, C, D, and E. With this in mind it is no longer obvious that the same-stuff similarity claim the experimenter makes is harder to justify than the similarity claims of the simulator; the latter are more specific and so logically stronger.
Though Eric Winsberg rejects the idea that experiment has a principled superiority over simulation, he concludes on the basis of careful analysis of real cases that the fact that simulators model the target system and experimentalists do not have to is the defining difference between the two methods (Winsberg 2010, pp. 64–70). Nevertheless, as a way of defending superiority for experiment Guala’s blackboxing idea faces problems. One is that the argument appears not to show superiority in principle or in every case, for there are many cases where we have models that are well accurate enough to do the simulations we need to answer the intended question. The experimenter may be able to blackbox in these cases and avoid commitments, but it would give him no epistemic advantage.
A second problem is Guala’s assumption that material similarity is what makes black-boxing legitimate.Footnote 5 Material similarity is supposed to underwrite the legitimacy of assuming that the lab sample of gold will behave as all other gold does. We saw above that little follows from similarity of material properties, and this would seem also to apply to behavior: rubber can be made into a tire or a ball, which are formally, topologically, and dynamically different. Guala’s blackboxing requires that similarity with respect to material properties be a reason to expect similarity with respect to other, unknown properties, and it is unclear what that would be based on. A higher degree of similarity with regard to any given set of properties does not by itself imply more reliable projections on unknown properties. Green jadeite and green nephrite are more similar to each other with regard to color and other properties detectable by the senses than either of these rocks is to lavender jadeite. However, lavender jadeite would give more reliable projections of green jadeite’s specific gravity than green nephrite would.
The other-things equal argument that follows identifies why, and the conditions under which, black-boxing implies epistemic advantage. I also argue that the justification of black-boxing does not depend on material similarity, and cannot be defended on the basis of material similarity, but depends on properties of kinds. Thus, we will see that though detractors of the superiority of experiment are right to deny the Materiality Thesis, they are wrong to think that that undermines the case for an epistemic superiority of experimentation over simulation.
3 Other things equal
Morrison (2009), Parker (2009), Winsberg (2009), and Parke (2014)) have denied that the difference between material and formal similarity has epistemic significance per se, and for that reason denied the generalization that experiment is a superior method. In partial support of these claims, Parker and Winsberg point out that some simulations are better than the experiments that we are able to do in pursuit of the same question, despite the fact that the experiments would be much more materially similar, for example, same-stuff models of weather and same-stuff models of black holes (Parker 2009, p. 492; Winsberg 2010, p. 61). However, this point is not probative for two reasons. One is the qualification to experiments that we are able to do. That there are questions for which the simulation we are able to do is more reliable than any experiment we can do gives no reason to deny the superiority of a comparable experiment that we cannot, or cannot yet, do. Even when methods cannot be carried out they can often be compared for what information and justification they would give if they could be carried out, and the superiority claimed here is epistemic, not pragmatic. The fact that we do not have the ability to experiment on black holes is not relevant to what an experiment would give us if it could be done.
Secondly, the claim “experiment is superior to simulation”, as the thesis is often stated, is ambiguous, not only between epistemic and practical yardsticks of comparison but also between several different quantificational structures and scopes. It could mean that all simulations are inferior to the kind of knowledge and justificational status one can get from any good experiment, or that for every simulation there exists a possible experiment that is superior to it. The first claim is too strong to be defensible, the second too weak to be very significant. We have the capability, surely, to make a simulation of a simple, familiar system that could achieve as good a justification for its conclusion as a good experiment on some more complex, unfamiliar system can achieve for its. And though for every simulation on something there exists a possible experiment on something else that would get us more or higher quality epistemic goods, this is surely also true in reverse.
Winsberg (2010, pp. 70–71) admits what he calls the epistemological priority of experiment to simulation, by which he means that since the knowledge you need in order to simulate is always quite sophisticated, the ability to construct a simulation at all depends on a history of learning things from observation and experiment, from manipulating the world itself when you did not already know how it works. This is the claim that if no experiment had existed no simulation would exist, overall and in a given domain, and Winsberg is right to think that it is not strong enough to support a thesis that current simulations are inferior to experiments, now that we do have a great deal of background knowledge. But that is partly because the claim is very weak and the superiority thesis is still unclear.
All of the blank generalities considered above as possible statements of the superiority thesis will fail because whether one method is superior to another depends on the question they are to be used to address. Thus, a superiority thesis with plausibility and significance will be relativized to the question, rather than comparing simulations on some questions to experiments on other questions. Given a question about the actual world that you don’t know the answer to, which method should you ideally choose for answering it? I will argue that if the answer to your question is determined in part by something you do not know, then, under a condition identified below as what justifies blackboxing, you are always epistemically better off with an experiment. This is all under the assumption that what you do not know is also something you do not need to know in order to know that an experimental result answers the question (internal validity), a qualification I will take as understood and omit repeating. The priority thesis allows that we now know enough to answer some questions by simulation, but the fact that we know enough to answer some questions by simulation does not mean that we know enough to answer any given question as well as an experiment on that question could.
To achieve generality in the superiority claim it must be made relative to the question; no one should expect that an experiment on question p will be superior to a simulation on q, for all p and q. Analogously, no one should expect that an experiment carried out by a novice will always be superior to a simulation carried out by a master, so we will assume that both the experimenter and the simulator have equal and adequate skill for their tasks. It is not possible to evaluate whether there is a general, principled advantage to experiment unless we isolate the epistemic difference that being an experiment or a simulation makes. That is, we must compare the two methods holding other things equal on a given case, holding everything the same except the fact that one study is an experiment and the other a simulation. The other-things-equal comparison will allow us to see the significance of the ability to blackbox and that its justification does not rest on material similarity.
Parker recognizes the need for an other-things-equal comparison but despairs of defining this phrase in the current context since it seems impossible to make the ““same” intervention or make the “same” observations in two experiments [studies] in which the systems being intervened on and observed are quite different in material and structure” (Parker 2009, p. 492).Footnote 6 However, the equality needed is not material or structural; it is epistemic. The crucial and neglected factor that must be held equal for our purposes is the background knowledge the two investigators have. There is no reason to expect, for example, that an experiment will be superior to a simulation made by a scientist who already knows the answer, but that does not undermine a claim of superiority. My strategy in what follows will be to make explicit some of the epistemic properties that do not distinguish the methods of experimentation and simulation, of which there are many. Then, the relevant difference will emerge when we consider an actual experiment and constructively imagine the best possible simulation for addressing the same question, that is similar to the experiment in every epistemic respect that a simulation can be.
For all their material and structural differences, the methods of experiment and simulation are remarkably similar epistemically, in ways that Galison (1997), Parker (2008), and Winsberg (2010) have brought out. Both methods in the uses I am focused on employ a stand-in, a study system whose results are to be generalized to a target system. In experiments this is typically a hunk of the world. In computer simulations it is a formal computational model. In both cases the justification for that generalization goes by way of establishing relevant similarity between the study and target systems, of whatever sort, by whatever means. Both experiments and simulations are run. That is, they are dynamical processes initiated by the functional equivalent of an ON switch. In both experimentation and computer simulation these processes are concrete. In experiment this is obvious; for example, Rutherford’s alpha particles are shot at thin gold foil and follow a trajectory dictated by physical law. In computer simulation, the process is a computation governed by dynamical laws encoded in a program. A computation is a physical process. That is, in perfect analogy to an experiment the computer program constitutes a set of dynamical laws that govern the time evolution of hunks of hardware, typically made of silicon. A program is not a concrete entity, but neither are the laws of physics. What both sets of laws govern are concrete processes. Both methods are interventions in a broad sense. When the switch is flipped on, an initial state—whether this is flying alpha particles and a sheet of gold, or numerical inputs and their associated silicon—is set free to do its work according to the laws.
Both kinds of studies have outputs at the end of the process that are typically called “data”, and in both methods the data must be interpreted in order to have results. To do this, one must verify that the intended intervention (physical process, computation) was actually performed, that the data actually reports the desired quantity, and that control for irrelevant factors was achieved. Debugging a program is epistemically analogous to tinkering with a concrete experimental apparatus to make it intervene or measure as intended. In both methods, the claim that the apparatus or program does what is intended is verified by benchmarking, that is, comparing the results to known endpoint values, and to the results of other studies. Results so certified can be used to justify conclusions about the target system, provided a claim of relevant similarity between study- and target- system is justified.
That there is such a raft of important similarities may be surprising but it should not mislead us; that two things have many similarities does not show they have no relevant difference. To compare the powers of the aspects of the two methods that are different, we must imagine them to be aiming to answer the same question. Even if a given climate simulation is just as good, or better, at answering its questions as economics experiments on crowds of people are at answering theirs, it is not to the point of the superiority thesis. Moreover, the question addressed must be determinate. Such a question would be, for example, what the scattering pattern of a type of particles is under a particular set of conditions, or what the trajectory and evolution of a particular hurricane will be, and epistemic success is finding the correct answer or having strong grounds for believing you have.
Simulations and experiments are also used to do things like “study phenomenon X” and “explore topic Y” but the aim of activities so described is diffuse and what would count as success is not sufficiently specified to make a comparison ahead of time of the two methods’ ability to achieve it. Experiments and simulations are both used to study dynamics and to explore the evolution of organisms, and both have the capacity to teach us things, but this does not tell us what goal a superiority claim would be about in such cases. Finally, the question I will assume both methods are supposed to answer is about the actual world. It has been argued convincingly that simulations can be superior in some contexts for discovering possibilities that had not, and perhaps could not, be exposed in experiments on actual stuff, but that is not the topic here.
The epistemic difference between the two methods that is salient to my superiority claim is best developed through an example. Rutherford’s (1911) paper that explained a variety of scattering results via a nuclear model of the atom is remembered as decisive (Rutherford 1911). The experiments by Hans Geiger and Ernest Marsden (Geiger and Marsden 1909; Geiger 1910) showing back deflection of alpha particles which are remembered as particularly well explained by Rutherford’s nuclear interpretation provide examples of a comprehensible and significant type of experiment. It answered the clear question of what is the deflection pattern of alpha particles shot at gold foil a few atoms thick. At the time of Rutherford’s nuclear interpretation, physicists knew about electrons, their mass and single negative charge, and that the atom was electrically neutral, and so, that because it contained electrons the atom must also contain positive charge. However, they did not know how the positive charge was distributed. J. J. Thomson’s “plum-pudding” model dominated, and in this picture the positive charge was uniformly distributed over the atom.
In the short version of the story, the fact that some alpha particles were scattered through a wide angle when they were shot at a very thin gold foil, and sometimes even deflected almost all the way back, could only be explained by supposing the atom had a nucleus, because otherwise nothing in the atom would have enough density or charge to deflect the hefty alpha particle that strongly. In the more detailed version, this experiment, even when combined with all of the other scattering phenomena Rutherford’s model could explain, was not taken to be decisive, in part because investigation of the atom via scattering had multiple unknowns concerning the structure of the atom, and the scattering properties of the projectiles. Other aspects of the structure of the atom than the distribution of its matter and charge also affected how it would scatter alpha particles. For example, Thomson’s model, which had only compound scattering, could explain the back deflection if the radius of the atom as a whole was exceedingly tiny, and while Rutherford evidently thought this was implausible, atomic radii had not yet been measured.Footnote 7 Unknowns that affect the results are among the chief reasons experiments are conducted, and we will see that they are crucial to the difference between what our two methods can possibly achieve in a given case.
To see the difference between one of the alpha-scattering experiments and an other-things-equal simulation we distinguish knowns and unknowns in the former. Many relevant matters in addition to those listed above were already settled. In addition to knowing the mass and charge of electrons, they knew that alpha particles were helium atoms stripped of their electrons and having a \(+2\) charge and 8000 times the mass of an electron. Experimenters had the ability to collimate beams of alphas to shoot at very high speed at small targets, and to make a foil of gold thin enough that an alpha should be meeting atoms only a few at a time. By the time of Rutherford’s interpretation, atoms were known to have a number of electrons that was, conservatively, no more than ten times the atomic weight of the atom, a matter relevant to whether electrons sprinkled over the atom would have the heft in mass to deflect an alpha strongly.
The first step in constructing a simulation that is epistemically equal to an alpha-scattering experiment is to take all of the things the experimenters knew and did not know and suppose that the simulator has the same epistemic status toward those matters. Since the simulator knows those things the experimenter knows, ideally she can program her model to fulfill them, to work the same way. For example, she can program simulacra alphas with the right “charge” properties, where that means they respond to simulacra positive and negative charge by changing the analog of their positions in the way that physical charges do, according to the Coulomb force. This programming requires skill, but so do the tasks of control and isolation of variables that prepare the experiment. We hold the skill levels of the two investigators equal, and of a level adequate to take advantage of all of the background knowledge we have supposed they both have. We hold equal the tools that the two have at their disposal by supposing both have whatever they need. For example, we suppose the simulator has as much computing power as she needs, and the experimenter has the best materials and devices.
The key question in constructing this simulation is what the programmer is to do about the experimenter’s unknowns. Experimenters did not know the radius of the atom, its distribution of positive charge, or number of electrons, among other things. These unknown matters play a role in determining the deflection pattern for alpha particles, and can do so, and be known to do so, without becoming known in the process. When alphas are shot at thin gold foil something happens in the foil and consequently to a circular scintillation screen surrounding the foil, which records the hits and yields the raw data of where the alphas landed, and the experimenters do not need to know the structure of the atom in order for this evolution to occur, or in order to interpret the results as wide-angle deflection of alphas by atoms. In the simulation there has to be an analogous computation or evolution, yielding numbers as data. What should that part of the program look like, and what will the programming decisions be based on? Assumptions will need to be incorporated, corresponding to the structure of the atom. Otherwise there will simply be no data about what an “alpha” does in response to an “atom.”Footnote 8
No experimenter at the time could be confident about these features of the atom, so the other-things-equal simulator could not piggy-back on them. An arbitrary choice about them would make the data resulting from the simulation meaningless. One could program multiple simulations based on a variety of different hypotheses about atomic structure, and this would be a fine thing, but this would be the epistemic analog of what Rutherford and Thomson actually did in constructing their theoretical models and determining what followed from them mathematically.Footnote 9 Those types of calculations could give no answer at all to what alphas actually will do when shot at a thin metal foil.
Whatever an experiment does give us in this case, an other-things-equal simulation on the same question would seem to have nothing comparable to offer. If the simulator were to program something to determine the scattering pattern of “alphas” she would be either begging the question of how alphas scatter when shot at atoms or, at least indirectly, making use of results of previous experiments on that question. At a later point in history, previous experiments would give support for a hypothesis about the structure of the atom, which then could be relied on in the programming of subsequent simulations. There is a possible simulation that gives a non-question-begging answer to the question, but the programmer would have to help herself to more background knowledge than the experimenter needed, or actually existed in 1910, so that simulation would not be other-things-equal to the experiment epistemically.
4 Blackboxing and background knowledge
The kind of unknown that the advantage of experiment over simulation rests on is a key to explaining how an experiment can teach us anything at all about the world.Footnote 10 These are unknowns that play a role in determining the result, but do not themselves need to be known ahead of time or even described, or even learned via the experiment, in order for us to interpret the results of the experiment as giving an answer to the set question. Geiger and Marsden could be non-committal about the structure of the atom during and after their experiments, as long as they knew that what was determining the scattering result was the structure of the atom, which they could know in part by insuring that the sheet of metal was made of atoms and was only a few atoms thick. The ability to so interpret the results while yet refraining from assumptions about some things in the structure of the atom is indeed what allows the results of the experiment to independently test a variety of models of that structure.
The results of an other-things-equal simulation that posited assumptions for the unknowns about the structure of the atom would obviously not provide a test of those assumptions that was independent of them, since the results would be in part determined by those assumptions. Interpreting the results of the corresponding experiment depends on assumptions too, of course, the assumptions about what I have called “knowns”. But these are assumptions to which the simulator also helps herself, and they do not get her to the finish line. Holding other things equal, the simulator must make more specific commitments about the unknown structure and dynamics of the world in order to give an answer to the question.
The conditions under which experiments are and are not epistemically superior to simulations divide neatly along the lines of whether there is or is not a particular kind of unknown in the question being investigated. Neither the experimenter nor the simulator has knowledge of the unknown matters that affect the results, but at least the experimenter will witness their consequences in his results. It looks like this argument can be run for the epistemic superiority of an experiment over the other-things-equal simulation for any case in which there are elements in the experimenter’s study system that affect the results and are unknown.
In contrast, in the extreme case, if there are no such unknowns then there is nothing epistemic to point to that the simulation corresponding to the experiment lacks. If there were nothing unknown to us about the structural properties of the atom or alpha particles that played a role in determining the deflection of alphas, then since we would ipso facto have true beliefs about these matters, the simulator would—assuming as we are sufficient programming and modeling skills—have the means to construct a program based on those beliefs that would yield the same results that the world, as acted on in the experiment, would give. But then, in this case no one would expect an experiment to be superior. This addresses the first difficulty with Guala’s blackboxing idea, that it does not show a superiority in every case. There is no reason that it should show a superiority in every case; if the simulator has a good enough model of the study system to answer a given question, then the ability to refrain from making assumptions gives no advantage, and we should not have thought it would. A superiority claim need not hold in all possible cases in order to be general and principled.
One might think it would always be reassuring to do the experiment, even if a simulation apparently has all of the background information it needs and has been benchmarked (Guala 2002; Morgan 2005). This can also be explained, because even if you do actually have enough background knowledge to make a simulation that will answer your question, it is a different thing to know that you know. An experiment on the same question can provide an independent check that you do.
A good way to test whether my view agrees with our experience is to consider the following implication of my point. If I am right then it should be that in cases where you do trust that a simulation is good enough to answer a question about the actual world, then you believe that we have enough knowledge of what determines the answer to write a program that will compute it (assuming again the required programming skill). Many of the questions that scientists actually use simulations to answer are cases that they regard as falling well enough into this category, where our beliefs about the determinants of the behavior of interest are already so well justified that doing an experiment would have no marginal benefit. A mixed example that illustrates this point, and that includes a variety of questions whose answers do and do not depend on unknown factors, is the way that simulations and experiments are used to understand the principles governing protein folding (Freddolino et al. 2010; Piana et al. 2011, 2014).
Protein folding is studied by both experiment and simulation, with simulation studies pushing the envelope on space and time scales that experiments currently cannot reach. Experimental techniques have reached an impressive capacity for direct examination of this process, but they have not yet advanced to a degree that enables scientists to follow trajectories at an atomic level of resolution, and at a time resolution high enough to capture intermediate states of the faster folding proteins. However, we know enough about the physical fields generated by the individual constituents of an amino-acid chain, the atoms and molecules, to build computational models. The folding of a protein is determined by the molecular and atomic properties of each amino acid and its parts, the sequence of the amino acids in a chain, and the properties of the environment, e.g. the temperature, and the pH and other properties of the solvent, usually water, and these are all factors we know a great deal about taken individually.
How the forces brought by individual atoms add up to a field of forces when they are combined into amino-acid molecules, linked in a chain, and placed in water is not feasibly calculable from differential equations, but one way it can be modeled is by numerically solving Newtonian equations of motion for systems of interacting particles, in a method called molecular dynamics (MD). The forces and potential energies of the protein are calculated from molecular mechanics force fields that are hypothesized based on known properties of the constituent atoms and molecules. Thus, what we do know allows scientists to narrow the possible force fields substantially and non-arbitrarily; in making simulations scientists are not wasting computer time with stabs in the dark. Among other outputs these models generate values for some general quantities relating to the kinematics and thermodynamics of folding, such as rates and free energies of folding, that are among the things that can be measured experimentally. Whether the two match is used to test how well the computational models capture the dynamics and the physical force field of a protein, and new validations of this sort are seen as required for every new development in a simulation.
Besides the computational challenge of the sheer volume of sampling required for protein folding simulations the limiting factor currently is the accuracy of the model of the force field that a chain of amino acids creates, because the atomic-resolution trajectories depend sensitively on these fields. We do not know by experimental examination what the force fields are at the atomic level of resolution, but simulators are essentially doing an inference to the best explanation of the success of the computational model’s outputs in matching features that are antecedently known, such as the structure of the fully folded protein, and quantities that can be measured in experiment, to the hypothesis that their model correctly captures that field, hence that the intermediate states of folding that the simulation produces can be trusted.
The writing and reasoning of authors in this field betrays no doubt at all that if we had the techniques to examine the process, and the field of forces of such molecules, at the atomic level via experiments on actual proteins that would give us better evidence of the dynamics and intermediate folding states than we can gain from simulations they have built so far. To see why, we must hold other things than the method equal by supposing that the experimenter and simulator are equally skilled relative to their tasks, and that the experimenter is as justified in his claim to be measuring atomic structure of intermediate folding states in his sample (internal validity), as the simulator is in her claim that given outputs of her program are solutions to the intended equations (verification). If so then an experimenter would not need to do what the simulator does, inventing and adding in to the computational template features that will mimic hydrogen bonding and atomic polarization, and hoping that they work like the real thing in the respects that are relevant to the time evolution of the protein’s structure. Experimenters would not have to do this modeling because the protein molecules would be producing the intermediate folding states on their own. If experimenters could examine the intermediate states then they could blackbox the dynamics and sit back and watch.
There could come a point where the simulator’s inference to the best explanation is so strong that we take the simulation as reliable for predicting or depicting protein folding in general, its use saving us the cost of molecule preparation and subtle physical equipment. But that would be because, or if, the simulation has reproduced many properties that can be directly measured in experiments. The more features on which the experiment validates the simulation the more we can trust the simulation on its own. In the limit we could trust the simulation to identify an intermediate protein structure accurately just as much as we would an experiment, for any purpose at all, but that would only be because experimentation would have validated it on every dimension.
An other-things-equal simulation can be just as good as an experiment if there is nothing in the experimental system that affects the results and is unknown to us, and we can know that it is just as good if we know this. There are any number of questions for which this condition is not fulfilled, cases like how a protein folds and the deflection pattern of alpha particles at the time the answers were still unknown, and they exceed our current imagination; to imagine them would require imagining everything we do not know. Though there are questions we haven’t even formulated on which experiment is superior to simulation, there are also any number of questions on which it is not. This second set contains questions that are not only possible for us to answer by simulation, but also often easier for us to know how to ask. It is obviously valuable to answer many of those questions, but if the superiority argued for here is denied, then it follows that science would be no worse off for knowledge if we ignored the first kind of question. That does not seem plausible.
Winsberg’s priority thesis admits that we have to have some knowledge gained by experiment in order to succeed in constructing any simulation at all. The other-things-equal argument has exposed a stronger and more specific sense in which the priority of experiment never goes away. On a given question posed in an experiment, and with a given set of background knowledge sufficient for the experimenter to get the study system to answer the question, the simulator cannot get the answer unless we suppose that the background knowledge includes the relevant determinants of the experimental result, in which case no one would think we would need to do an experiment in order know the answer. To get the answer to a given question the simulator must be given more background knowledge than the experimenter needs. Epistemically, the method of simulation is always one step behind.Footnote 11
5 Matter doesn’t matter
Blackboxing allows the experimenter to get by with less background knowledge than the simulator needs in order to get an answer, but justifying blackboxing also requires background knowledge, and it is here that one might think material similarity between the study and target systems gives an advantage. Geiger and Marsden had the gold itself, where the simulator has nothing. However, material similarity per se is not essential to the argument, because material similarity is neither sufficient nor necessary to justify black-boxing. We will see that what is essential to a case in which the simulator is one step behind is not only (1) as above, that the outcome of the experiment is in part determined by facts that are not known to the scientist, but that do not need to be known in order to interpret the outcome as answering the set question, but also (2) that the sample and the target are of a kind whose kindhood can be legitimately projected into the unknown properties that determine the answer to the question. In many cases this will be a natural kind, but artefactual kinds can be just as good. However we will see that material similarity is not even extensionally equivalent to the concept that must be used to justify blackboxing.
For blackboxing to be justified we must be justified in believing that the sample is similar to the target in the unknown properties that determine the answer to the question. In our example, we need to be justified in believing that the sample gold is similar to other gold and other elements in the unknown feature that determines the deflection pattern of alphas: the distribution of positive charge in the atom. As we saw above, material similarity is inadequate to insure such a thing. Material similarity does not make formal, topological, or dynamical similarity more probable. It does not per se make any other kind of similarity of properties more probable. In our case all atoms of gold could be materially similar in having the same quantity of positive charge; that does not imply that the charge is distributed the same in all of them.
What justified believing that all of the gold atoms had their positive charge distributed in the same way, and hence justified blackboxing, was that the experimenters were justified in believing that gold is a natural kind. All atoms of gold (modulo isotopes) share not only their known non-relational properties but also all of their unknown non-relational properties. The intuition about the superiority of experiment in the case of Rutherford scattering is so strong because the elements (and sub-atomic particles) are the strongest natural kinds in the scientific pantheon. They are model natural kinds.
Something weaker but similar obtains for molecules like proteins. They are made of atoms, and have characteristic behaviors and fields that depend systematically on the properties of the particular atoms the amino acids are made of, and the order in which the latter molecules fall in the sequence. Every carbon atom under the same conditions is the same, and will, other things equal, react the same way to changes in environment, e.g. in pH, and in what other atoms it is exposed to or attached to. If there is something we do not know about the protein and that the answer to our question depends on, then the sample in the lab can nevertheless be trusted to behave just as other instances of the protein would under the same conditions.
What natural kinds are, how to define them, and whether particular cases in science count are all rich and complex questions that cannot be settled here. However, we need not take a stand on every question for the notion to serve our purposes. For example, for our purposes natural kinds may but need not have essences—necessary and sufficient conditions for membership in the kind—because not all properties need to be projectible for a particular question that an experiment seeks to answer. We need not be natural kind realists for whom natural kinds are entities; we may be naturalists, who simply think that some classifications are genuinely more natural than others. We need not agree on an account of what it is that makes something a natural kind, either, for example, whether there are universals. The one feature that is crucial here is that natural kinds support inductive inference, a property that everyone accepts natural kinds have, whatever one might think the metaphysical basis for this is (Bird and Emma 2017; Quine 1969).
The elements (modulo isotopes) and sub-atomic particles are special cases of natural kinds because we think members of these classes share every non-relational property. For that reason their kindhood will be projectible to the non-relational properties relevant to any question at all about them, and this extreme feature explains the strength of the intuition that experiment is superior in cases involving the elements and sub-atomic particles essentially. We will see below that study and target systems sharing natural kindhood to that extreme degree is not necessary to justify blackboxing on a given question, and sharing natural kindhood merely in some respect or other is not sufficient. We will also see that the kind need not be natural but may be artefactual. However, this special case of strong natural kindhood gives us guidance toward what the needed condition is.
That study and target system merely share a natural kind is not sufficient to justify blackboxing because being members of a natural kind does not imply that two things are the same in every property, or indeed in any property relevant to a given question. Superficially, human being is some kind of natural kind, but that does not mean we can assume that the liver of every human being will respond the same way to a drug. We know that the natural kind human being does not provide similarity to a level of specificity sufficient to insure this. We must pick more specific kinds—e.g., human men aged 40–55 with or without hepatitis, and otherwise random—in order to be able to project that the liver response in the study population is the same as what the target population would have. To justify blackboxing the kind must be projectible in particular to the unknown properties on which the answer to the experiment’s question depends.
The members of a justifying kind must be similar in the unknown properties on which the answer depends, but the members of a justifying kind need not share all properties. It is possible to have a kind projectibility that justifies blackboxing even if the study and target populations are also members of different kinds. This is because two things can simultaneously be members of one kind and members of different kinds. A red ball and a red cube provide a toy example. For a realistic example, scientists have sometimes judged it appropriate to draw conclusions about the toxicity of chemicals for human beings on the basis of experiments on mice.Footnote 12 This is because, or to the extent that, they are justified in believing that human beings and mice belong to a kind, perhaps mammal, some of whose organs will respond similarly to chemicals when appropriately adjusted for dosage. The similarity of two species in known properties can justify a projection to their similarity in the unknown properties that determine reactions, despite the fact that the two species are also different kinds, and different in many other properties, known and unknown, that are not relevant to the reaction. Which properties we need to project the kind to depends on the question, and that projectibility can co-exist with a great deal of difference in other properties. Shared relevant kindhood is necessary to justify blackboxing, but not extreme natural kindhood of the sort we have with the elements.
Material similarity is not sufficient for shared relevant kindhood – as we saw above with examples like the rubber ball and tire with their different dynamical properties—and so not sufficient to justify blackboxing. Material similarity is also not necessary, because it is not necessary in order for two things to be members of a projectible kind. Hollow cylindrical solid objects are all of a kind, as are cubical solid objects. A cubical solid object whose side is the same length as the diameter of a hollow cylindrical object will not fit into the latter, and this can be expected in every sample whether the objects are made of wood, plastic, or melamine. Two different isotopes of an element are materially different, having different numbers of neutrons, but many chemical experiments on one isotope will be generalizable to the other isotopes. Or imagine that aliens who were visually indistinguishable from humans but made of some other material arrived unannounced and assimilated into human communities over generations, none of them ever exhibiting behavior outside the human statistical norm. The results of behavioral experiments on a random sample of the population that included aliens, would be projectible to the human population, because the relevant type is abstract, behavioral, and shared. Shared kindhood is necessary to justify blackboxing, but material similarity per se would be necessary for blackboxing only if the world were entirely lacking in multiple realization.
Though natural kinds provide the easiest way to see the point about experiments, the kinds that justify blackboxing can also be artefactual, for example when mass manufacturing produces artefactual kinds that are projectible because of the uniformity of the production process over all of its instances. The Continental ExtremeContact DW is a model of tire, all instances of which have the same material and formal properties, within manufacturing tolerances. Controlled tests on samples of such a type are used to rate all members of the type, and the ratings are published to help consumers make informed decisions. This particular tire model has good dry traction, but less steering-responsiveness than its close rivals in the market, according to the testers at tirerack.com. We trust that the tests on a sample of tires indicate how other tokens of the tire type will perform because even if we do not know the structure or composition of the rubber—it may be a proprietary secret—we have good reason to believe properties relevant to performance are the same in the samples as in the tires the consumer might buy. In this case, rather than being a gift from nature this follows from the consistency of manufacturing that survival in a competitive market requires. Either way, we have reason to believe that study sample and target are of the same kind in the properties we don’t know that determine the result.
One might suspect that with artefactual kinds we have come around to simulation and are not seeing an advantage for experiment. However, the performance of that tire type is not being simulated in these road tests. A simulation of tire performance would involve making a model of the tire and watching how it fares in simulated conditions. If there is anything we do not know about what makes the tire have the behavior it does on the road, then we are much better off testing tires that are samples of the type—that is, doing the road test—than we are with simulation tires on simulation roads. Maybe the manufacturer knows exactly the structure of the rubber in its tire, down to the microlevel, and exactly how that will affect its response to turning and wet and dry surfaces, in which case a computer simulation should be entirely satisfying. But even if the manufacturer could satisfy itself of this—which is doubtful—consumers and independent testers do not have the knowledge to make a simulation. It is fortunate for the consumer, then, that a test on a sample tire is at least as good as anything the manufacturer can do to determine its performance properties. The fact that a tire is an artefactual rather than natural object doesn’t make a test of the tire a simulation.
Because I have argued that whether in a given case experiment is superior depends on whether there are unknown features that determine the answer to the question, one might have the impression that a key to the superiority of experiment is its ability to pick up on unknown unknowns. Whatever the unknown features are, whether we are aware of them or not, they will act in a sample in the same way as they do in the target of the same kind.Footnote 13 However, the existence of unknown unknowns is not necessary for justifying the blackboxing that makes an experiment superior on a given question. There did not need to be unknown unknowns relevant to the question what the deflection pattern of alphas would be. The known unknown of distribution of positive charge was sufficient to give experiment the advantage.
Whether we think there are unknown unknowns does affect our judgment in a given case that a simulation is good enough, because for that judgment, on this view, one must judge that there are no unknowns—known or unknown—that affect the phenomenon of interest enough to make a difference to the outcome for our purposes. But one can make the negative judgment that there are too many unknowns to make a simulation adequate, without any of those being unknown unknowns. The existence of unknown unknowns is not necessary for experiment to be superior. It is also not sufficient, since even when unknown unknowns exist they may play no role in determining the outcome of an experiment. In comparison of experiment and simulation invocation of unknown unknowns can be misleading.
6 The possibility of experiment
Supposing I am right that experiment is epistemically superior other things equal, under the specified conditions, why does it matter when our options in practice actually are constrained pragmatically and our choices are not typically between otherwise equal studies? Obviously, we cannot do a total climate experiment that will tell us what we want to know in time for it to be helpful, and should not detonate nuclear missiles when we have signed a test ban treaty, or deliberately infect human beings with a disease. Why does it matter that these experiments would have higher epistemic value if it is not possible or ethical to do them anyway?
Keeping in mind the epistemic advantage that experiment has matters because it affects our consideration of what is possible, and even what is possible itself. Our only option is indeed to do the best we can within our budget, abilities, and moral commitments, but budgets and the boundaries of what is possible for us also change in response to our actions. After driving a rental sports car one might decide that owning one is worth economizing in the rest of one’s life in order to save up for it. An analogous point holds for funding science; reducing the number of simulation studies funded might make an experiment on a harder question affordable. It might not be easy to take this consideration into account in pairwise comparison of the quality and significance of proposed studies, but it could be applied at a more global level of choices among funding strategies and incentive structures. It’s no use denying that the sports car performs better in acceleration, speed, and handling. The only question is the practical one whether that added value is affordable and worth it given your goals.
Not only budgets, but the boundaries of what is possible for us can change, shrinking or expanding in response to our actions. There are cases in which we face the choice of whether to act to make future experimentation on a subject matter impossible. Since smallpox was eradicated in 1980 it has regularly been proposed that the official remaining stockpiles of the variola virus that causes it be destroyed in order to reduce the risk of future infections.Footnote 14 (Butler 2014) In recent years studies by the World Health Organization and the American Academies of Arts and Sciences have identified specific, medically beneficial research that we could not do if we destroyed the last known stockpiles of this virus, because we do not have sufficient knowledge of the virus to answer them by simulation. As long as there remain matters about how the virus works that are unknown to us there will exist questions that we can only answer by experiment, even if we cannot formulate them. Guessing whether these are important questions when you do not know what they are is challenging. However, destroying the virus would make it impossible for us to answer any of them, whatever they are. Thus, given that the stakes in this case involve the possible death of millions of people, it would be rational to take the kind of superiority of experiment argued for here into account in any decision about whether to destroy all of the virus we have.
What is possible for us can not only shrink by our own hand, but also expand in response to our efforts. The boundaries for this cannot always be established a priori. It is easy to think that they can because as Hume pointed out, habitual assumptions can masquerade as necessary truths:
Such is the influence of custom, that, it not only covers our natural ignorance, but even conceals itself, and seems not to take place, merely because it is found in the highest degree. (Hume 1999, p. 110)
There are many experiments it seems we cannot do, but it also once seemed impossible to see the surface of the moon—until Galileo used a telescope—or to measure the speed of light or the density or rotation of the earth. And who would have thought we could do an experiment in which the structural properties of an invisible entity like DNA would make observable differences? One would not have thought it was possible for Michelson and Morley to move the earth relative to the sun, and one would have been right, but by being clever they did not have to move the earth in order to do an experiment that would expose relative speeds of light if they existed. Once we have become accustomed to these as actualities it can be easy to forget that they once seemed impossible or even absurd. If experiments are superior in the way argued here, then avoiding classification of epistemic value by means of the categories of experiment and simulation could discourage us from maximizing our potential to gain knowledge, by discouraging us from asking questions that, given our current state of knowledge, could only be answered by experiment. Scientific progress depends on a healthy suspicion toward our current perceptions of the boundaries of the possible.
Presumption that the boundaries of the possible are clear has in turn a practical effect on those boundaries through the psychological mechanism of motivation. Belief that something is impossible does not imply that it is impossible, but it does mean that one has no subjective reason to make the effort, and thereby that a rational person will not actually make the effort. We may even be attracted to believing that a thing is impossible in order to excuse ourselves from making the effort. You can’t win if you don’t play, as the lottery people tell us, so belief that a thing is impossible prevents us from achieving it, at least with the kind of possibility-making in science that does not come by luck. Surely, it will be objected, one cannot deny that there are experiments that will never be possible for us, and questions that we cannot answer. Surely there are, and there is no need to deny it, but a hazard lies in being sure that we know what they are.
7 Conclusion
Experiment is superior to simulation, other things equal, on a given question where (1) the answer depends on a feature of the world that is unknown and does not need to be known in order to know that the experiment answers the question, and (2) the sample an experimenter uses is of the same kind as the target such that the kindhood is projectible to that unknown feature. In cases where (1) is not fulfilled, where what we do not know does not affect the answer to the question, a simulation is just as good as an experiment. In cases where we know that unknown factors do not affect the answer to the question, we know that the simulation is just as good. The superiority that experiment has in cases where both (1) and (2) hold comes from the experimenter being able to blackbox, and refrain from making a model, hence assumptions about, the unknown feature that affects the result, and puts the simulator one step behind. The legitimacy of that blackboxing depends on the sample and the target in the experiment sharing a kindhood that is projectible to the relevant unknown property. Material similarity is neither sufficient nor necessary for this. Critics are right that the Materiality Thesis is false, but wrong to think the superiority of experiment depends on it.
The superiority of experiment defended here implies that, given our current background knowledge, and assuming the world is replete with kinds, there are any number of questions that possible experiments could answer but no currently epistemically possible simulation could. Experiments on these matters would likely be more difficult and costly than simulations that are epistemically possible for us, which would be on other, better known, matters. Keeping in mind the distinction between experiment and simulation, and judging their value accordingly, so far as and in the ways that that is appropriate, has an important role to play in helping us to avoid narrowing of our attention to the questions we already have the tools to answer.
Notes
A variety of these uses of simulation can be seen in the process of designing the first thermonuclear bomb, and in experiments to detect “golden events” in particle physics (Galison 1997, pp. 689–780).
I say “often” because sometimes the goal of an experiment is primarily to learn something about the sample in the lab rather than to generalize the results or test a more general hypothesis.
It does not imply this, of course, since in mathematics it can be easier to prove a logically stronger theorem than a weaker one due to the way the content is stated. But even in mathematics we would not expect this to be true in every case or every type of case.
Cf. Bogen and Woodward (1988, pp. 326–336), who argued that experimenters need not make a model that explains the data in order to evaluate the reliability of that data, which is important for understanding experiments generally.
But one does not have to specify the full set of structural equations governing the target system. The trick is to make sure that the target and the experimental system are similar in most relevant respects, so as to be able to generalise the observed results from the laboratory to the outside world. Experimenters make sure that this is the case by using materials that resemble as closely as possible those of which the parts of the target system are made (Guala 2002, p. 12).
In this context she is using the term “experiment” broadly to encompass both traditionally-styled experiments and simulations.
Rutherford was proposing a model that included multiple innovations: a nucleus, treatment of the alpha as a point mass, and single collisions rather than only compound scattering. Thus, despite his obvious confidence, his argument took the form of an inference to the simplest explanation of a variety of experimental results, rather than an argument that his was the only possible explanation. After his 1911 paper was largely ignored he recognized that he would not persuade his colleagues until he derived and tested radioactive, chemical, and spectroscopic predictions of his model. Maybe this period of obscurity for his nuclear hypothesis is largely forgotten because it was so short. Rutherford got the project of deriving further predictions started soon after when Niels Bohr joined him in Manchester in 1912 (Heilbron 1968, pp. 300–305).
It may be objected that simulators do not always go about programming by attempting to mimic literally the parts and properties of the natural system. This is true but makes no difference in the kind of case we are considering. The simulator needs to program something non-arbitrary in order to get a non-arbitrary answer to the question, and the fact that the world determines the answer in part by the atom either having or lacking a nucleus is all that anyone had to go on at that point. Programming something that mimics the behavior without an effort at a realistic model is not possible because no one knows what the behavior will be.
Note that this comparison does not assume that the solver in a simulation is a theoretical model. It is what it is, but just as for a theoretical model, when initial conditions or inputs are inserted, mathematical computation, whether human or machine, will yield values or outputs. Those values are relative to the model or solver.
See fn. 5.
This does not imply that simulation is always behind temporally, that a simulation cannot be done until the experiment is done, or that we cannot go very far without actually doing the experiment. We may never actually be able to do a full weather experiment, but we have simulations that can predict it with impressive reliability. This is possible in part because we have a strong understanding of the fluid dynamics and of many of the other physical processes involved, and partly because simulators can do abductive inferences as described above. But though in this way simulations can become reliable enough for our purposes, it is still the case that if we lack full knowledge of the determinants of the behavior the other-things-equal experiment would be superior.
The claim that animal testing is predictive of human response has come under criticism in recent years. (See, e.g., Davis et al. 2013; Shanks et al. 2009). It is clear that whether an animal model is predictive depends on the species and on the question. The point here is only that it is possible for members of two quite different kinds to also belong to a kind that makes projection on the relevant feature justified.
This point is also sometimes used to argue against a general superiority for experiment because the unknowns may interfere with the experiment getting the right answer. However, while, as I argue in the text, the existence of unknown unknowns does not automatically make experiment superior, it also does not undermine the superiority claim. A simulator who puts factors in by hand indeed avoids unknown factors that might interfere in an experiment, precisely because she does not know about them. But whether this general fact is significant depends on the particular case and must be subjected to an other-things-equal comparison. An interfering factor may be a known unknown, such as a magnetic field opposite the gold foil that re-collimates the alphas before they reach the scintillation screen. But known unknowns are down to the skill of the experimenter—if he does not check for such a magnetic field, which is easy to do, then he does not have master skills, as we have supposed both investigators do. If an interfering factor is an unknown unknown, then this affects the set of target cases that the experimenter’s result can be extrapolated to, but it does nothing to remove the advantage that the experimenter has by operating on the same natural kind: the simulator’s study is not affected by unknown unknown features of the world, but she still lacks a non-arbitrary answer to the question because nobody knows the distribution of charge in the nucleus.
The range of considerations is complex. One might think that eradication of the official stockpiles would make medical and bio-terrorism research unnecessary, but there has never been an attempt to verify that there are no unofficial stocks, and some even think it likely that there are. Anyway, say retentionists, the DNA sequence of variola is now in the public domain, so a terrorist could make his own. So also could vaccine researchers, say destructionists, if the need ever arose. Might there be unknown differences between manufactured and natural viruses? If so then the researchers without the natural virus would be behind terrorists with the natural virus.
References
Bacon, F. (1620). Novum organum. In The Works of Francis Bacon (1815), Vol. 4, p. 4.
Bird, A., & Emma, T. (2017) Natural kinds. In The Stanford Encyclopedia of Philosophy (Spring 2017 Ed.), E. N. Zalta (Ed.). https://plato.stanford.edu/archives/spr2017/entries/natural-kinds/.
Bogen, J., & Woodward, J. (1988). Saving the phenomena. Philosophical Review, XCVII(3), 303–352.
Butler, D. (2014). WHO postpones decision on destruction of smallpox stocks—Again. Nature News Blog.
Davis, M., et al. (2013). The new revolution in toxicology: The good, the bad, and the ugly. Annals of the New York Academy of Sciences, 1278, 11–24.
Durán, J. M. (2013). The use of the “Materiality Argument” in the literature on computer simulations. In J. M. Durán & E. Arnold (Eds.), Computer simulations and the changing face of scientific experimentation (pp. 76–98). Newcastle-upon-Tyne: Cambridge Scholars Publishing.
Freddolino, P. L., Harrison, C. B., Liu, Y., & Schulten, K. (2010). Challenges in protein-folding simulations. Nature Physics, 6, 751–758.
Galison, P. (1997). Image & logic: A material culture of microphysics. Chicago: University of Chicago Press.
Geiger, H. (1910). The scattering of the \(\alpha \) particles by matter. Proceedings of the Royal Society of London A, 83, 492–504.
Geiger, H., & Marsden, E. (1909). On a diffuse reflection of the \(\alpha \) particles. Proceedings of the Royal Society of London A, 82, 495–500.
Gilbert, N., & Troitzsch, K. (1999). Simulation for the social scientist. Philadelphia, PA: Open University Press.
Guala, F. (2002). Models, simulations, and experiments. In: Magnani et al. (Ed.), 2002, pp. 59–74.
Guala, F. (2005). The methodology of experimental economics. Cambridge: Cambridge University Press.
Harré, R. (2003). The materiality of instruments in a metaphysics for experiments. In Radder (Ed.), 2003, pp. 19–38.
Heilbron, J. L. (1968). The scattering of \(\alpha \) and \(\beta \) particles and Rutherford’s Atom. Archive for History of Exact Sciences, 4(4), 247–307.
Hume, D. (1999). An enquiry concerning human understanding. T. L. Beauchamp (Ed.). Oxford: Oxford University Press.
Humphreys, P. (2004). Extending ourselves: Computational science, empiricism, and scientific method. New York: Oxford University Press.
Magnani, L., & Nersessian, N. (Eds.). (2002). Model-based reasoning: Science, technology, values. New York: Kluwer.
Morgan, M. (2002). Model experiments and models in experiments. In: Magnani et al. (Ed.), 2002, pp. 41–58.
Morgan, M. (2003). Experiments without material intervention: Model experiments, virtual experiments and virtually experiments. In Radder (Ed.), 2003, pp. 216–235.
Morgan, M. (2005). Experiments versus models: New phenomena, inference, and surprise. Journal of Economic Methodology, 12(2), 317–329.
Morrison, M. (2009). Models, measurement and computer simulation: The changing face of experimentation. Philosophical Studies, 143(1), 33–57.
Parke, E. (2014). Experiments, simulations, and epistemic privilege. Philosophy of Science, 81, 516–536.
Parker, W. S. (2008). Franklin, Holmes, and the epistemology of computer simulation. International Studies in the Philosophy of Science, 22(2), 165–183.
Parker, W. S. (2009). Does matter really matter? Computer simulations, experiments, and materiality. Synthese, 169, 483–496.
Piana, S., Lindorff-Larsen, K., & Shaw, D. (2011). How robust are protein folding simulations with respect to force field parameterization? Biophysical Journal, 100, L47–L49.
Piana, S., Klepeis, J. L., & Shaw, D. E. (2014). Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Current Opinion in Structural Biology, 24, 98–105.
Quine, W. V. O. (1969). Natural kinds. Ontological relativity and other essays. New York: Columbia University Press.
Radder, H. (Ed.). (2003). The philosophy of scientific experimentation. Pittsburgh, PA: University of Pittsburgh Press.
Rutherford, E. (1911). The scattering of \(\alpha \) and \(\beta \) particles by matter and the structure of the atom. Philosophical Magazine, 21(125), 669–688.
Shanks, N., Greek, R., & Greek, J. (2009). Are animal models predictive for humans? Philosophy, Ethics, and Humanities in Medicine, 4(2), 2.
Simon, H. A. (1969). The sciences of the artificial. Boston: MIT Press.
Winsberg, E. (2009). A tale of two methods. Synthese, 169, 575–592.
Winsberg, E. (2010). Science in the age of computer simulation. Chicago: University of Chicago Press.
Wittgenstein, L. (1969). On certainty, G. E. M. Anscombe & G. H. von Wright (Eds.). New York: HarperCollins.
Author information
Authors and Affiliations
Corresponding author
Additional information
I would like to thank Paul Humphries, David Teplow, Brian Keeley, Jim Bogen, Ken Waters, Nancy Cartwright, Jordi Cat, and Clark Glymour for helpful discussions of this material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Roush, S. The epistemic superiority of experiment to simulation. Synthese 195, 4883–4906 (2018). https://doi.org/10.1007/s11229-017-1431-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1431-y
Keywords
- Experiment
- Simulation
- Computer simulation
- Computation
- Unknown
- Unknown unknown
- Possibility
- Verification
- Validation
- Internal validity
- External validity
- Feasibility
- Rutherford scattering
- Protein folding
- Black-boxing
- Natural kind
- Other things equal
- Ceteris paribus
- Method
- Justification
- Reliability
- Material similarity
- Projectibility