Abstract
The existence of non-local correlations between outcomes of measurements in quantum entangled systems strongly suggests that we are dealing with some form of causation here. An assessment of this conjecture in the context of the collapse interpretation of quantum mechanics is the primary goal of this paper. Following the counterfactual approach to causation, I argue that the details of the underlying causal mechanism which could explain the non-local correlations in entangled states strongly depend on the adopted semantics for counterfactuals. Several relativistically-invariant interpretations of spatiotemporal counterfactual conditionals are discussed, and the corresponding causal stories describing interactions between parts of an entangled system are evaluated. It is observed that the most controversial feature of the postulated causal connections is not so much their non-local character as a peculiar type of circularity that affects them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction: entanglement and non-local correlations
The phenomenon of quantum entanglement does not cease to intrigue and inspire scientifically-oriented philosophers. The discovery of entangled systems has made a lasting impression on our understanding of the inner workings of the world at the fundamental level. Many authors insist that the ubiquity of quantum entanglement forces us to revise some of the basic concepts with which we attempt to describe the fundamental features of reality. Among these affected are the notions of locality, separability, individuality, causality, property and relation. Furthermore, it is quite common for contemporary metaphysicians of the naturalistic stripe to use arguments from quantum entanglement in strictly philosophical debates, such as discussions on the status of the laws of nature and modality, or on reduction and emergence.Footnote 1 In this essay I am going to limit myself to discussing some metaphysical consequences of the existence of perfect non-local correlations, which are one of the most recognizable features of entangled states. My primary goal will be to investigate possible causal explanations of this phenomenon, and to ascertain what amendments to the ordinary concept of causation have to be made in order for these explanations to be successful.
An entangled state of two or more quantum systems is formally defined as a state which cannot be factorized into the product of individual states. A generic example of an entangled state of two particles can look like this:
- (1.1):
-
\(\frac{1}{\sqrt{2}}\left( {| 0\rangle |0\rangle +| 1\rangle |1\rangle } \right) \),
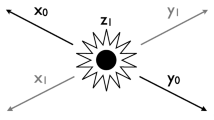
where \({\vert }0\rangle \) and \({\vert }1\rangle \) are two orthogonal vectors in the appropriate one-particle Hilbert space. Let us now select an observable O whose eigenvectors are \({\vert }0\rangle \) and \({\vert }1\rangle \), corresponding respectively to the values 0 and 1 for this observable.Footnote 2 The standard experimental setup that is used in this scenario involves two measurements of observable O performed on individual components of this system at two distant locations L and R.Footnote 3 It is assumed that the locations of the two measurements are space-like separated, i.e. no signal travelling at or below the speed of light can connect these two events (see Fig. 1). Given the form (1.1) of the initial state of the two-particle system, each measurement can reveal the values 0 or 1 with equal probabilities; however, the outcomes obtained in both measurements have to be perfectly correlated, meaning that the values revealed in distant locations must be either two 1’s, or two 0’s. This correlation does not appear to depend on the spatial distance between the two experiments; it is supposed to hold regardless of how far away from each other the two particles are. The insensitivity of the quantum correlations to the space-like separation between the correlated systems is what justifies the use of the adjective “non-local”.
The spatiotemporal layout of measurement events in the case of two entangled particles (“L” and “R” stand for “left” and “right”, respectively). Grayed areas represent the future and past light cones of respective measurements. Dotted lines indicate two selected hyperplanes of simultaneity relative to some frames of reference. Two curved lines designate the wordlines of the individual particles
Given the enormous variety of the different conceptions of causal relations proposed in the literature, we have to decide which philosophical analysis of causation to use in our discussion of quantum non-local correlations. It seems that the counterfactual analysis of causation, gaining so much popularity in recent years, would be the best choice.Footnote 4 The main reason for this decision is that the counterfactual definition of causation, as opposed to alternative approaches, does not rely on persistent and easily identifiable features of common causal links that nevertheless may not be essential for all forms of causality. These features include the spatiotemporal contiguity of the cause and the effect (as per Hume’s version of the regularity approach), or the presence of a transfer of energy, mass, or other conserved quantity. The counterfactual account is flexible enough to accommodate causal links whose physical mechanisms and external appearance may differ radically from ordinary, everyday causation, and therefore seems well suited to deal with non-classical cases, to which the case of quantum entanglement belongs. An alternative option which some may find attractive, given the enormous variety of competing conceptions of causality, is to altogether abandon an analysis of quantum correlations in terms of causation, but we will not follow this radical approach.
Stripped of all embellishments, the main question that will occupy us now is whether there is a causal link between distant components of an entangled quantum system. However, this question cannot be properly addressed without first discussing the intricate connections between causation, counterfactuals, and spatiotemporal relations. Thus we will have to ascertain some consequences of the existence of non-local correlations between quantum events for our understanding of counterfactual dependence and causal dependence. While engaging in this conceptual analysis we have to keep in mind that there are fundamentally two directions in which inferences can be made here. First and foremost, one can simply apply their favorite theories of counterfactuals and causality to draw whatever their metaphysical implications may be regarding the case of nomological correlations between space-like separated events. However, one could equally well use the case in question as a testing ground for various philosophical theories of counterfactual causality, and as a result pick those conceptions that deliver preferred answers concerning the quantum case of non-local correlations. In our subsequent analysis we will to a certain extent adopt both approaches, first eliminating those philosophical analyses of counterfactuals/causality that deliver implausible verdicts with respect to the case at hand, and then applying the remaining conceptions to find the sought-after answers to the metaphysical questions concerning the nature of quantum non-local phenomena.
The principal factual premise that we will accept in subsequent investigations is that there exist perfect correlations of a nomological kind (and thus not merely accidental) between outcomes of measurements carried out in distant locations. These correlations may be expressed for instance in the form of the following law-like generalization:Footnote 5
-
(1.2)
If a system of two particles is prepared in the state (1.1), and measurements of quantity O are performed for both subsystems, then the outcome of one such measurement is 0 (1) iff the outcome of the other measurement is 0 (1).
Given this assumption, we are going to address the following two questions:
-
(1.3)
Does the correlation expressed in (1.2) support the counterfactual conditional “If the outcome of one measurement was 1 (0), the outcome of the other measurement would be 1 (0)”?
-
(1.4)
Does the truth of the counterfactual stated in (1.3) imply that there is a causal link between the actually obtained outcomes of experiments performed in distant locations?
The structure of the paper is as follows. In Sects. 2 and 3 we will focus on discussing problem (1.3). We will start off with presenting the basics of David Lewis’s approach to counterfactuals, and we will identify the main difficulty that this semantic analysis encounters in the context of non-local correlations set out in a relativistic framework. Section 3 introduces three main alternative semantics of relativistically-invariant counterfactuals: one frame-dependent and two frame-independent, based on the assumption of the fixity of the relativistic past. The frame-independent interpretations further split into variants with and without miracles, which brings the overall count up to six. It turns out that not all considered interpretations of counterfactuals support the conditional stated in (1.3). In Sect. 4 we will limit ourselves to those semantics of the counterfactual that imply the existence of counterfactual dependence between distant outcomes, and we will proceed to consider question (1.4). We will identify the main challenge for proponents of the causal character of the non-local correlations, in the form of the circularity problem. Section 4 also briefly discusses and rejects an attempt to disconnect causation from counterfactual dependence by adopting a modified variant of Lewis’s influence theory. In Sect. 5 we will shift attention to the different yet related question of whether a local measurement can causally affect the distant part of the entangled system by altering its physical state. Adopting a dispositional interpretation of quantum states together with a counterfactual reading of dispositional properties, we will propose three causal models of non-local interactions occurring as a result of measurements performed on one part of an entangled system. The last section sums up the main results of the paper and highlights the non-standard character of the three causal models developed in the paper.
2 Lewis’s counterfactual orthodoxy and its problems
It has become commonplace to explicate the meaning of counterfactual conditionals in terms of possible worlds and the comparative relation of closeness (similarity). The celebrated Lewisian truth conditions for counterfactuals can be spelled out as follows: for a counterfactual conditional \(P\square \rightarrow Q\) to be non-vacuously true there has to be an antecedent-world \(w_{P}\) such that Q is true in all antecedent-worlds at least as close to the actual world as \(w_{P}\) (Lewis 1973a). We will adopt this generic reading of counterfactuals in subsequent discussions (with some exceptions of which more later). However, we should stress that the precise meaning of counterfactual statements is not determined until we decide how to interpret the requisite notion of closeness (similarity) with respect to the actual world. Depending on the adopted criteria of similarity we may end up accepting significantly divergent valuations of counterfactual conditionals.
Lewis’s semantic analysis of counterfactuals is intimately connected with his preferred theory of causation. As he was an ardent proponent of the counterfactual theory of causation, his main goal was to give a reductive analysis of a causal link between two distinct events c and e in terms of the counterfactual “If event c hadn’t occurred, event e wouldn’t have occurred”. But achieving this goal requires first and foremost the elimination of so-called backtracking counterfactuals, i.e. counterfactuals whose evaluation is based on some adjustments of the past events. Backtracking counterfactuals not only seem to imply the possibility of causally affecting the past, but also muddle the distinction between genuine causal links and non-causal correlations due to the existence of a common cause (see Lewis 1973b). There are basically two ways to avoid backtracking counterfactuals. One is to stipulate, using brute force, as it were, that the antecedent-worlds closest to the actual world have to retain the same past of the antecedent-event as in the actual world. In other words, we fix the past, add the antecedent-event, and then evolve the world according to the actual laws. In this approach all backtracking counterfactuals with no exceptions are eliminated “by fiat”.
Another option is to come up with some criteria of similarity that would imply that the majority of backtracking counterfactuals get rejected as a matter of fact (given some contingent features of the actual world). This is the strategy pursued by Lewis himself, who stresses that he would like to leave open the (unlikely) possibility that some past events could counterfactually depend on the present facts (and thus that backward causation is not conceptually impossible, even though it is most probably non-existent in our world). Lewis’s well-known criterion of similarity consists of an intricate, multi-tiered mix of comparisons with respect to the violation of laws and the differences in particular facts. In order to decide which of two given possible worlds is more similar to the actual world we have to consider first whether there are “big and widespread” violations of laws (“miracles” in Lewis’s terminology) in one of them. If this criterion does not offer a definitive answer, we should then take into account regions of perfect match of particular facts. Subsequent comparisons include small violations of laws, and finally approximate similarity of particular facts (Lewis 1986, pp. 47–48). Lewis claims that, given the de facto temporal asymmetry of our world, the majority of backtracking counterfactuals are expunged by his criteria.Footnote 6 That is, in typical situations the closest antecedent-worlds will be those in which just before the antecedent-event a small miracle happens, while all later events arise in accordance with the usual laws. Such worlds are arguably closer to the actual one than the worlds in which the past is adjusted for a lawful occurrence of the contrary-to-fact antecedent-event, and also closer than the worlds in which the future is made identical to the actual one by inserting miracles right after the antecedent-event.
In order to assess the suitability of Lewis’s counterfactual semantics as a conceptual tool in our analysis of non-local correlations, we have to take into account both its inherent strengths and weaknesses, and the way it performs when applied to the case at hand. As many critics have observed, Lewis’s conception is controversial, to say the least. In particular, it is not true that his criteria of similarity eliminate all backtracking counterfactuals. As a matter of fact, we are forced to accept highly dubious backtracking counterfactuals of the form “If a occurred at t, then there must have been a small miracle just before t” (see Maudlin 1994, ft. 5, p. 159). And it is not only the fact that the consequent-event happens before the antecedent-event that raises the red flag here. It is perhaps even more unsettling that virtually all counterfactual scenarios we wish to contemplate must involve violations of the actual laws of nature. But to insist for example that if Hillary Clinton had dropped out of the presidential race in May of 2015, the law of gravity would have to have been temporarily suspended, sounds at best like a bad joke.Footnote 7
Problems with Lewis’s analysis only mount up when we consider the case of perfect correlations between events that are space-like separated. It turns out that Lewis’s combined criteria, when applied within the framework of special relativity, deliver a surprising verdict with respect to the possibility of counterfactual dependence between such events. The verdict is that such dependence is virtually excluded out of hand. Without going into detailsFootnote 8 we can only observe that for the counterfactual “If the outcome of measurement L had been 0, the outcome of measurement R would have been 0” to be true in the world where both actual outcomes were 1, the world with the two outcomes switched from 1 to 0 should be closest to the actual one of all antecedent-worlds. However, it may be argued that the antecedent-world in which the R-measurement still has the actual outcome 1 is closer according to Lewis’s criteria. Even though a small miracle that breaks the correlation between the outcomes happens in this world, the gain is in the form of a much larger spatiotemporal area of perfect match with the actual world (the additional area of match is the future light cone of the R-measurement minus the future light cone of the L-measurement—see Fig. 1). This argument is perfectly analogous to the relativistic variant of Lewis’s own argument against backtracking, where admitting one small miracle was worth more than adjusting an event in the past, because the latter strategy commits us to a world with a much more widespread area of differences in particular facts.
Why should we take the verdict delivered by Lewis’s theory with respect to the case of non-local correlations as speaking against its viability? After all, we will see in the subsequent section that one of the alternative semantics for counterfactuals proposed there has precisely the same consequence. The conclusion that there is no counterfactual dependence between the distant outcomes in spite of them being perfectly correlated may be slightly surprising, but in itself does not seem to be sufficient to reject Lewis’s approach.Footnote 9 However, the case at hand reveals a deeper problem with Lewis’s truth criteria for counterfactuals. I claim that his method of comparing the areas of (mis-)match with respect to particular facts was introduced specifically in the context of the pre-relativistic conception of space-time and causation, and is therefore ill-suited to deal with relativistic cases. In classical mechanics there is no upper limit on the speed at which causal influences propagate, thus a change of a particular fact at a moment t is in principle associated with some changes (however minute) in the entire spatiotemporal region at all moments after t. Consequently, inserting a small miracle in order to ‘erase’ some of the consequences of a contrary-to-fact event does not seem to result in diminishing the area of mismatch with respect to particular facts. Thus, in the case of two spatially separated, correlated and simultaneous events, keeping the distant event unchanged while the local event was changed does not offer any advantages in terms of the area of the perfect match of particular facts. Lewis’s theory applied in the pre-relativistic framework predicts that the counterfactual connecting alternative outcomes of distant measurements will be true. In the light of this observation, the opposite evaluation of the same counterfactual obtained in the relativistic context looks more like a fluke than a genuine prediction of the theory.Footnote 10 Taking this into account, we should probably look for alternative semantics for counterfactuals that would be tailor-made to work in the relativistic framework from the outset.
3 Fixing the past: with and without miracles
The alternative to Lewis’s analysis that was already mentioned earlier is the method of evaluating counterfactuals based on the assumption of the fixity of the past. This method can be easily made relativistically invariant, which leads to its splitting into two distinctive versions (for more details and a philosophical background see Bigaj 2004, 2006, chap. 5). One version is the following: in order to evaluate the counterfactual \(P \square \rightarrow Q\), where P describes a well-localized event, we should consider possible worlds which are identical with the actual world within the past light cone of the P-event, in which P occurs, and which otherwise evolve according to the actual laws of nature. Let us label this interpretation “the narrow fixed past”. The second variant is essentially based on the same strategy, except now we “keep fixed” the entire complement of the future light cone of the P-event (and, consequently, we can call this approach “the broad fixed past”).Footnote 11 It should be noted that both approaches admit (and in some situations require) the possibility of violations of the laws (“miracles”); however, these violations are limited to one specific instance only, namely to ensure the occurrence of the counterfactual P-event in cases when a lawful occurrence of this event would require adjustments in the absolute past (or the absolute elsewhere, in the second strategy) of this event. Thus, for instance, if we assumed that our world is strictly deterministic, all counterfactual suppositions would be analyzed in possible worlds in which some laws are violated, as there is no other way to keep the absolute past fixed while introducing a new event that doesn’t occur in reality. However, in an indeterministic world, such as the world governed by the laws of quantum mechanics under the collapse interpretation, a contrary-to-fact event may be introduced without the need for miracles.Footnote 12 In any case, the semantic analysis offered in this section does not require any presupposition regarding the deterministic or indeterministic character of the world.
When we apply the above relativistic interpretations of counterfactuals to the case of non-local correlations, it is straightforward to observe that in the narrow fixed past variant the counterfactual connecting the alternative outcomes becomes true, while under the broad fixed past interpretation it turns out false.Footnote 13 This difference can be intuitively explained by noting that in the first approach events space-like separated from a given antecedent-event are treated as if they belonged to the open future, whereas in the second variant they are included in the already fixed past.Footnote 14 Of course each decision can be seen as somewhat arbitrary, since technically events located at a space-like separation from us are neither in our past nor in our future; they are “elsewhere”. Thus perhaps a third approach is needed; and indeed such an approach can be afforded in the form of the decision to relativize counterfactual valuations to a particular inertial frame of reference. More specifically, the proposal is to consider a given counterfactual as true in a particular frame of reference if the consequent is true in all antecedent-worlds which are identical with the actual world at all times preceding the antecedent-event relative to this frame, and which do not contain any law-violating events after the antecedent-event.Footnote 15 Applying this simple strategy to the case of non-local correlations we can immediately see that the counterfactual “If the outcome of measurement L had been 0, the outcome of measurement R would have been 0” is true in all frames of reference in which the L-measurement temporarily precedes the R-measurement, and false in frames where the temporal order between measurements is reversed (see Fig. 1). The case when both measurements are simultaneous relative to a particular frame can be conventionally included in either category.
We will postpone a discussion of the admissibility of the concept of frame-dependent counterfactuals until the next section, devoted to the issue of causality. For now let us note that all the fixed past approaches share with the original Lewisian analysis the controversial feature resulting from the fact that in order to evaluate typical counterfactuals in deterministic scenarios we have to invoke law-violating worlds. The only difference is that the fixed past approach assumes only one, “antecedent-introducing” miracle, whereas Lewis keeps open the possibility of considering worlds with more miraculous events, as long as this is compensated by a substantial increase in matching particular facts. Regardless of this difference, the need for law-breaking events may be seen as a shortcoming, as we have argued in the previous section. As it turns out it is possible to come up with semantic analyses that eliminate law-breaking worlds altogether; however, such analyses are slightly more complicated than the above-mentioned “fixing the past” strategies. Basically, the idea is to come up with natural extensions of the two non-frame-dependent “fix the past” strategies described earlier, in the sense that the new approaches would reduce to the old ones when the considered antecedent-event is not determined by its past (where the past is identified with either the past light cone, or the complement of the future light cone, depending on the original approach). However, if there is a necessary nomological connection between past events and the antecedent-event, we are not allowed to keep the whole past of this event intact. The main premise of this approach is that the only acceptable comparisons between alternative possible worlds should be with respect to the spatiotemporal regions where differences in particular facts might occur.
The details of the no-miracle versions of the fixed past approaches need not concern us. It should suffice to say that in the case of the broad fixed past analysis it is relatively simple to come up with a similarity relation based entirely on the comparison of areas of perfect match with respect to particular facts (for more on that see Finkelstein 1999; Bigaj 2004).Footnote 16 This similarity relation implies that when the antecedent-event of a given counterfactual is not nomologically connected with any event outside its future light cone, the valuation of this counterfactual will be precisely the same as under the broad fixed past analysis. On the other hand, if the introduction of the antecedent-event requires a modification of its (broad) past, the no-miracle approach to counterfactuals will diverge from the miracle-based analysis. The appropriate similarity relation will force us to consider possible worlds which lawfully accommodate the contrary-to-fact antecedent event, and which diverge from the actual world at the latest possible moment (in a suitable relativistic sense of the word).Footnote 17 One consequence of this analysis is that the relation of similarity between possible worlds is no longer a linear ordering but only a partial one (see Lewis 1981, p. 230; Bigaj 2004, p. 5 for details).
The task of finding a suitable extension of the narrow fixed past semantics presents us with a greater challenge. I have proven in Bigaj (2004) that there is no similarity relation of the Lewisian type (even if we admit partially ordering relations) which could reduce to this method of evaluation for indeterministic events. The best we can do is selecting, for each antecedent-event separately, a set of possible antecedent-worlds in which the consequent has to be true in order for the counterfactual to be satisfied. However, it turns out that this selection procedure will strongly depend on what antecedent we consider, and for that reason we cannot rely on a predetermined comparison with respect to the similarity to the actual world (Bigaj 2006, pp. 204–209, 2012a offer a step-by-step explanation of this strategy).
It can be easily verified that both no-miracle semantics produce the same valuation for alternative-outcome counterfactuals connecting space-like separated measurements (under the assumption that these outcomes are truly indeterministic events). While the sets of possible worlds in which we should carry out such an evaluation differ in both cases, the net result is the same: the counterfactual comes out true. This result is to be expected: after all, in the currently considered approaches no law-breaking worlds are permitted, and thus an alteration of the outcome of one measurement must be associated with a corresponding change in the other outcome.Footnote 18
The price we have to pay for eliminating law-violating possible worlds is that counterfactual dependence no longer implies causal dependence. It is now possible to have two events such that if one did not occur, the other would not occur either, without any causal link connecting the two. This may happen if both events have a common cause in their joint past, in which case the relevant-antecedent worlds will have a divergence point in the past, and the counterfactual will be evaluated as true. In order to derive conclusions regarding the existence of a causal link we have to make sure that such a situation is excluded. Thus, if we have two events A and B, and there is a non-A-world such that B does not occur in it either, and moreover both absolute pasts of the locations of A and B are exactly as in the actual world, we can conclude that there is a causal link between A and B. Unfortunately, the very fact that there is no such world does not conversely imply that there is no causal link—it is still possible that either event is separately caused by some occurrence in their joint past without there being a common cause. Thus the currently considered conceptions of counterfactuals can supply us with a sufficient, but not necessary condition for causality.
To sum up our analysis so far: we have come up in total with six possible variants of counterfactual semantics that could be potentially applied to the case of non-local quantum correlations. These are: Lewis’s original semantics based on the multi-tiered set of comparisons, the three “fixed past” approaches (the frame-dependent approach, the narrow fixed past and the broad fixed past semantics), and the two no-miracle approaches (broad and narrow). Table 1 below lists all these approaches together with their main features for quick reference.
In the next section we will shift our attention to the problem of causation within quantum entangled systems.
4 From counterfactual dependence to causality
As we have seen, the jury is still out regarding the truth of the counterfactual connecting alternative outcomes of space-like separated measurements. Even though the majority of the considered interpretations of counterfactuals imply that the distant outcomes are indeed counterfactually dependent on each other, still there are available conceptions that can cast doubt on this conclusion. In this section we will limit ourselves to the interpretations that imply the existence of counterfactual dependence between distant outcomes, in order to be able to discuss question (1.4) regarding the causal character of this dependence.Footnote 19 Can we confidently say that (given an appropriate reading of counterfactuals) the outcome obtained in one wing of the apparatus causally influences the other, distant wing and contributes to the creation of the outcome revealed there? Are we ready to embrace the conclusion that causation in quantum mechanics can overcome the limitations imposed by the requirements of special relativity and can connect events that are too far away from each other to send and receive “conventional” signals? Before we can attempt to formulate even tentative answers to these questions, we should revisit the relevant facts.
We know that counterfactual dependence entails causality only for the right type of counterfactual statements. Are the counterfactuals in question of the “right” type? It seems that indeed they are. In the narrow fixed past approach we’ve made sure that no backtracking is permitted, and hence non-causal counterfactual dependencies (via a common cause) are excluded. In the two remaining “no-miracle” approaches backtracking is allowed, and this means that generally speaking counterfactual dependence does not guarantee the existence of a direct causal link. However, in the specific case that we are considering, an additional assumption is believed to be satisfied: no adjustment of the joint absolute past of both measurements is necessary in order to introduce alternative outcomes of the experiments. Therefore no explanation of the outcome-to-outcome counterfactual dependence in terms of a common cause is available, and the path to direct causation stands wide open.Footnote 20
But are we sure that there is no common cause? Here the verdict is up to physics, not philosophy. Given the existence of perfect correlations between outcomes, the only possibility for a local, common-cause explanation is in the case when an event in the joint past of the measurements determines both outcomes beforehand. But we know from Bell’s theorem that any deterministic theory which is also local produces experimentally testable consequences that are not borne out by experience.Footnote 21 Standard quantum mechanics (in the form of the collapse interpretation) rejects determinism, and therefore avoids the clash with experiment, while its main contender, Bohmian mechanics, embraces non-local influences as a price for its determinism. But either way, it seems that non-local causal links are unavoidable in both approaches.
Or are they? Here philosophers are likely to make the following complaint. We have proven so far that according to several compelling accounts of counterfactuals, the alternative-outcome counterfactuals come out true in a way that makes it almost inevitable that their truth should be underpinned by a legitimate causal link. But we have ignored one inconvenient fact: the counterfactual outcome-outcome dependence goes in both directions. The situation is entirely symmetric: we may equally well say that had the L-outcome been 0, the R-outcome would have been 0, or vice versa. Consequently, we have to accept the fact that the L-outcome causes the R-outcome, and the latter reciprocates, causing the former in turn. But is this even intelligible? Isn’t it part of how we understand the words “cause” and “effect” that an effect cannot cause its own cause? And when we add to that the additional assumption of transitivity (which, it has to be admitted, has been questioned by several authors), we end up with a clear case of causa sui, so dreaded by all metaphysicians.Footnote 22
Some authors try to skirt this problem by doing a bit of terminological maneuvering. Instead of talking about causal links, let us say that distant outcomes in an entangled system are causally implicated with one another.Footnote 23 The relation of being causally implicated is assumed to be symmetric from the outset, so no harm is done. However, this solution strikes me as being rather disingenuous. I can see two legitimate reasons for using the “directionally-neutral” causal terminology. One is when the events in question are not directly causally linked, but are part of a broader causal network. A clear example of such a case is the common cause scenario, and of course there can be more complex causal connections involving the events in question. But clearly there is no reason to hedge our bets in such a way in the case of quantum non-local correlations between outcomes. We know for sure that there is a direct (and bidirectional) counterfactual dependence here, and we don’t know of any other events that would participate in a broader causal network together with the outcome-events. The second possible justification for the use of the non-directional term “causally implicated” is that we don’t know yet which event is a cause and which an effect—all we know is that one of them caused the other one. But again the ignorance scenario does not apply to our case, as we already know (given all the required assumptions) that one event causes the other, while the other causes the first event back.
At this moment we should recall one particular interpretation of counterfactuals that may be able to break the impasse here. Namely, it is the interpretation which relativizes the truth value of a given counterfactual to a frame of reference. According to this approach, it is never the case that both counterfactuals connecting alternative outcomes are true in the same frame. If we select a particular frame of reference in which the L-measurement temporarily precedes the R-measurement, the counterfactual dependence goes from the former to the latter, and so does the causal link. However, in a different frame where the temporal relation between measurements is reversed, it is the outcome of the R-measurement that causes the other outcome. So there is no description of the entire system which would require us to admit that there is a causal loop there. Causality is always unidirectional, only it can change its direction when we move from one “perspective” to another one.
Promising as this strategy may be, it is nevertheless far from being entirely immune from legitimate objections. The most controversial aspect of this approach is associated with the commonly accepted view that features which are frame-dependent do not reflect the objective nature of reality but are mere “artefacts” of our description. And yet causation seems to be one of the most fundamental, objective relations that constitute the metaphysical “ground floor”, so to speak. It is difficult to accept that the fact that one event causes another should depend on one’s adopted perspective. One may try to rebut this objection by pointing out that in the current approach it is not the causal link but merely its direction that is frame-dependent (see Laudisa 2001, p. 229 for a similar view). But this is a mere word-play. It remains the case that in one frame of reference event A causes event B, while in another frame A is no longer a cause of B. We can cut this any way we want, but we can’t deny that according to the current proposal the causal link leading from A to B can be made to disappear by simply switching from one conventional description of reality to another.
Given these quandaries, it may be advisable to look again at the purported connection between counterfactual dependence and causality. Aren’t we missing something here? Is there perhaps a third factor that has to be thrown in in order to get from the former to the latter? Is counterfactual dependence really sufficient for causality? As it turns out, there is an alternative conception of causation that seeks to explicate this notion in terms of a relation more intricate than simple counterfactual dependence. This relation, introduced in Lewis (2000, 2004), is known as “influence”. Without going into unnecessary details we can characterize influence broadly as follows. An event A influences an event B, if small counterfactual variations of A are associated with small variations of B. By small variations Lewis means changing some properties of a given event without actually affecting its identity, or replacing the event with its non-identical and yet similar variant, or finally eliminating the event altogether.Footnote 24 All such changes of the cause should be accompanied by similar changes in the effect. Typical examples of counterfactual variations of everyday-life causes include changing the time and location of the cause, changing the manner in which the cause is brought about, or changing some of the quantitative parameters characterizing the cause (such as the strength and/or direction of the applied force).
Lewis insists that counterfactual dependence constitutes a special case of the relation of influence (Lewis 2004, pp. 91–92), and if we agree with this assessment, then the cases of counterfactual dependence between distant outcomes of measurements will be immediately classified as instances of influence. However, it is debatable whether the notion of influence defined as above indeed covers counterfactual whether-whether dependence as its special case.Footnote 25 At any rate, we can always specify the relation of influence in such a way as to exclude the case of pure counterfactual dependence. We will then interpret Lewis’s theory as follows: we demand that for an event A to influence an event B there has to be a non-empty set \(R_{A}\) of alterations of A not limited to its total elimination, and a non-empty set \(R_{B}\) of alterations of B such that each element of \(R_{B}\) counterfactually depends on an element in \(R_{A}\). Moreover, we stipulate that \(R_{A}\) contains arbitrarily small alterations which are nevertheless mapped onto non-zero alterations from \(R_{B}\). Thus no matter how small an alteration of A is, it will be accompanied by a non-zero alteration of B.
It may be interesting to check whether the relation of influence thus defined holds between outcomes of measurements in the case of quantum entangled systems. And it is not difficult to observe that most likely there is no influence in the quantum case. Changing slightly the time and/or location of one measurement-and-outcome event clearly does not affect the corresponding characteristics of the other measurement and its outcome. Similarly, insignificant changes in the manner in which one experiment is performed (as long as the outcome stays the same) are not associated with the same types of changes in the other experiment. It is difficult if not outright impossible to think of any measurable parameter characterizing one measurement and its outcome whose alteration would change the corresponding parameter of the distant measurement. It is true that the special alteration of one outcome in the form of substituting in its place an alternative result will counterfactually change the distant outcome. However, this alteration amounts to the total elimination of the actual outcome, and we need more subtle alterations as well in order to talk about influence in the above-defined sense. Hence we may confidently say that one outcome of measurement does not influence the other in the technical sense of the term. And if we accept the proposed version of Lewis’s latest theory of causation, there can be only one conclusion: no causal link connects distant outcomes of experiments in the quantum-mechanical case of entangled systems.
As always, this is a big “if”. Lewis’s influence theory of causation has met with a barrage of criticism.Footnote 26 The main accusation leveled is that there are cases of undeniable causal links which nevertheless fail to satisfy the conditions of influence. One prominent category of such counterexamples involves cases in which a condition is created that later enables some independent chain of events to come to its conclusion. Clearing a forest can causally contribute to a much later avalanche’s destroying a village, and yet there is no relation of influence that connects the act of clearing with the event of destroying the village, apart from ordinary counterfactual dependence (if the forest had not been cleared, the avalanche would have been stopped and the village would have been saved). Can this run-of-the-mill example throw some light on the bizarre case of quantum entangled systems? I claim that it can.
Actually, it may be argued that quantum non-local correlations are underpinned precisely by the sort of causal links that serve as counterexamples to Lewis’s theory of influence. According to the collapse interpretation of quantum mechanics (whether in the orthodox, Copenhagen version, or in the modern GRW guise) the local measurement initiates an (almost) instantaneous reduction of the global state of the system which, given the entangled form of the initial state, results in a change of the state of the distant part of the system. The distant subsystem acquires a state which is the eigenstate of the relevant observable, and this state in turn is responsible for revealing the precise value of the observable that is correlated with the outcome obtained locally. Thus we have here a clear case of creating the right conditions which enable the faraway system to reveal the expected outcome in an independent process of measurement. No wonder, then, that there is no relation of influence between the two outcomes. But this fact does not prove that non-local causality is absent in the whole experimental setup.
At this point it should become clear that we can’t expect to make any further progress without delving deeper into the physical mechanism responsible for the occurrence of the experimentally verified perfect correlations between distant outcomes of measurements. In the next section we will look closer into how standard quantum mechanics describes the process of measurement and its effects on systems in entangled states.
5 Quantum dispositions and non-local causation
Let us now shift our attention from the correlations between outcomes of two space-like separated measurements to an even simpler setup involving only one local measurement. Suppose that a measurement of observable O with eigenstates \({\vert }0\rangle \) and \({\vert }1\rangle \) has been performed on the L-subsystem of the entire system prepared in state (1.1). According to the collapse interpretations of quantum mechanics, immediately after the measurement the entire system rapidly changes its state from the initial entangled state (1.1) to one of the two product states \({\vert }0\rangle {\vert }0\rangle \) or \({\vert }1\rangle {\vert }1\rangle \). This, in turn, means that both subsystems acquire new states that haven’t been possessed earlier. In particular, as a result of the local L-measurement the distant R-system finds itself in one of the two eigenstates for observable O. Our task now will be to assess whether this process deserves to be categorized as a non-local causal interaction between the local measurement and the distant system.Footnote 27
It can be useful to clarify some potentially confusing issues first. Somebody could object that we can’t speak about genuine non-local causality here, since the purported effect is not an observable event. Indeed, quantum-mechanical states are not directly observable, so there is no way for us to experimentally verify if (and when) the state of the distant subsystem collapsed into an eigenstate of O. But we are engaged here in doing metaphysics of science, not epistemology. As long as our theory uses the concept of states to characterize physical systems, we have the right to at least consider the possibility of interpreting the state of a system as one of its objective properties. And any process that changes an objective property of an entity can be potentially treated (barring possible arguments to the contrary, of which more later) as a causal one, regardless of whether the property in question is observable or not. The above-mentioned confusion may have something to do with the emphasis that is sometimes put on non-local signaling rather than non-local causality. Indeed, no superluminal signal can be sent using local measurements in quantum entangled systems, precisely because the purported change in the state of the distant system is not directly observable. But this should not be mistaken for the impossibility of non-local causation.
The central problem that we should zero in on now is the nature of a quantum-mechanical state. Various interpretations of this key concept abound. In some approaches states (encompassed in wave functions) are objectified as some sort of physical fields that can interact with other objects, while in other conceptions states merely serve as computational devices for calculating expectation values for different observables. However, one possible interpretation of quantum mechanical states stands out prominently. Several authors have noted that quantum states display a striking dispositional nature: they tell us what would happen, had we decided to perform such and such measurements.Footnote 28 Dispositions associated with a given state are typically probabilistic, but in special cases when the state is an eigenstate of a given observable, the corresponding disposition is deterministic (“sure-fire”). This is precisely the case in our example: the distant system seems to acquire a deterministic disposition to reveal a particular value (1 or 0) in an appropriate measurement.
A detailed analysis of the metaphysical controversies surrounding the concept of dispositional properties is beyond the scope of this article. However, I would like to put at ease those who are ill-disposed to dispositions by pointing out that the only substantial assumption that we will borrow from the standard approach to dispositions is the conditional analysis of dispositional properties in terms of their stimulus and manifestation, plus the additional premise that the link between the stimulus and the manifestation is expressed by the counterfactual conditional (in one of the available interpretations discussed earlier). In particular, we don’t need to enter the heated debate on the existence of fundamental irreducible dispositions and their purported role in grounding the laws of nature. Essentially, we are here following the lead of Ghirardi and Grassi (1994, p. 404) who propose to explicate possessing a definite value a of a given observable O by a physical system p with the help of the counterfactual conditional “If O was measured on system p, the result would be a”. Ghirardi and Grassi don’t even use the word “disposition” in their analysis, while I resort to this term of art as a mere convenience (shorthand for “counterfactually interpreted definite value of an observable”).
After these explanations we can now deploy the formalism of counterfactual semantics in order to asses some intuitive claims regarding entangled systems and their properties, starting with the seemingly unassailable assumption that the local measurement indeed causes the occurrence of the corresponding disposition at a space-like separated location. Under closer scrutiny it turns out that this claim is not as ironclad as it may seem, and the reason again is the ambiguity inherent in our concept of counterfactuals. To see this, we should consider the truth of the disposition-expressing counterfactual “If the R-measurement was performed, the outcome would be 0” under the assumption that in the actual world the L-measurement has been done at a space-like separated location, and its revealed outcome has been 0. In order to accomplish that we have to take into account appropriate possible worlds in which the R-measurement is carried out, but of course the exact form of these worlds depends on the adopted semantics. As we recall, there are basically three options here: we can keep fixed the past light cone of the R-measurement, or we can fix the complement of its future light cone, or we can relativize counterfactuals to a particular frame of reference.Footnote 29 It is easy to observe that only in one of these three approaches the considered counterfactual comes out true, namely when we decide to keep the complement of the future light cone fixed. In contrast to that, when we fix the past light cone only, the actual L-outcome, and indeed the very measurement on the L-system, cannot be guaranteed to occur (as they are not determined by the absolute past of the R-location). The third solution is to admit that the appropriate disposition exists only in those frames of reference in which the L-measurement temporarily precedes the moment of time at which we consider the disposition of the R-system. Again, as we have already indicated, the problem with this approach is that it treats as perspective-dependent facts that are typically seen as objective (in this case the existence or non-existence of a dispositional property of a system).
But how can we take seriously a conception that flat-out denies that a measurement on one subsystem of an entangled system must be accompanied by the change of the state on the other, space-like separated subsystem? Doesn’t this contradict the assumed principles of quantum mechanics (under the collapse interpretation)? And, even worse, doesn’t this approach imply the possibility of the violation of perfect law-like correlations between outcomes? As we will see, these worries are entirely unfounded. First of all, no violation of perfect correlations is implied by denying the existence of the deterministic disposition of the distant system. The lack of the appropriate disposition means that the measurement on the R-system can reveal an outcome other than 0 (i.e. 1), but in possible worlds in which this happens the L-measurement will not yield the value 0. Actually, there may not even be a measurement on the L-system at all! As for the collapse postulate that we have explicitly adopted in current discussions, its precise implementation depends on additional assumptions regarding the spatiotemporal relations between two measurements: the actual measurement performed on the L-system, and the possible R-measurement aimed at actualizing the (purported) disposition. No-one would question the fact that if we selected a spatiotemporal point on the world-line of the R-system that is located absolutely earlier than the L-measurement (in the intersection of the two past light cones of L and R—see Fig. 1), no deterministic disposition would be present there, since at this point the collapse has not yet occurred. Similarly, it is unquestionable that the appropriate disposition must be present at all points that are located in the absolute future of the L-measurement. But the controversial case is precisely when the selected point is assumed to be space-like separated from the L-measurement. The intuition behind the narrow fixed past approach is such that from the perspective of the counterfactually considered R-measurement, the actual L-measurement has not yet taken place (it’s still in the “future”, metaphorically speaking). Thus there are two possible outcomes at location R, and therefore the disposition is not present. Needless to say, the alternative broad fixed past approach sees things differently.
However, an interesting question remains. How can we explain the existence of perfect correlations between space-like separated outcomes of measurements, if the L-measurement does not produce a sure-fire disposition of the R-system to reveal the same outcome? An off-the-cuff answer may be that because, as we have observed above, the L-measurement seems to happen “later” than the counterfactual R-measurement, it would be the R-measurement which would (if performed) produce an appropriate disposition at the location of the L-measurement, thereby securing the required correlation. But this is incorrect. The entire situation is completely symmetric. No measurement can produce any sure-fire disposition at a space-like separated location, since from the perspective of this location the measurement is non-existent. Under the considered interpretation of counterfactuals the correlations cannot be explained by the action of one measurement on the pre-measurement state of the other subsystem.
I can see only one way out of this predicament if we insist on finding causal explanations of observable phenomena, as we do throughout the paper. We have to admit that indeed the perfect correlation between outcomes is a result of a spooky, unmediated, non-local and bidirectional causal link connecting the two events. This suggestion is confirmed by the fact that under the very same interpretation of counterfactuals the alternative-outcome counterfactuals come out true, strongly hinting at the existence of direct causation between distant outcomes. Thus the story offered under one possible resolution of the ambiguity of spatiotemporal counterfactuals is that immediately before the R-measurement the particle is not in an eigenstate for the measured observable O, so when we limit ourselves to the local situation only, two outcomes of the measurement are possible. However, the outcome revealed in the distant L-measurement has the capability to causally and non-locally affect the R-outcome precisely at the moment of the R-measurement, hence the perfect correlation is secured without the need to adjust the quantum state of the R-system before the measurement.Footnote 30
On the other hand, the story given by the alternative broad fixed past approach is different. Here measurements are capable of creating sure-fire dispositions at distant locations; however the counterfactual connecting alternative outcomes is false. Thus the causal explanation for correlations is as follows: one measurement creates the sure-fire disposition to reveal the correlated outcome on the distant system, and subsequently the other measurement confirms this outcome. There is no direct counterfactual dependence between outcomes. However, there is a chain of counterfactual dependencies, first between the L-measurement (together with its outcome) and the disposition of the R-system, and next between the disposition and the revealed outcome.Footnote 31 Thus if we accepted Lewis’s definition of causation as the transitive closure of the relation of counterfactual dependence, we would have to admit that ultimately the distant outcomes are causally connected with, albeit not counterfactually dependent on, one another.
Let us finally note that each story suffers from a singular case of causal (or explanatory) circularity. The circularity affecting the causal interpretation of the non-local correlations under the narrow fixed past approach has been already identified earlier in the text. As in this approach each outcome is counterfactually dependent on the other one, the causal link between distant outcomes is symmetric and thus clearly circular. Under the alternative, broad fixed past interpretation the circle is perhaps less conspicuous, but no less worrisome. In the scenario when two measurements are performed we can pick any measurement (let’s say R) and its outcome o and verify that this measurement causes the occurrence of the L-system disposition to reveal the same value o. On the other hand, the L-disposition together with the local measurement are causally responsible for the actualization of the outcome o. The circularity comes to the surface when we note that there is an alternative and equally acceptable causal story that starts with the L-measurement and its outcome and proceeds through the creation of the appropriate R-disposition to the occurrence of the R-outcome. The ensuing circle can be then expressed as follows: in order to explain why the outcome of the R-measurement was o we can first point out to the existence of the corresponding disposition (eigenstate), which in turn was brought into being by the distant L-measurement and its outcome. However, the L-outcome is similarly explained by the chain of events starting with the R-measurement and its outcome. This closes the explanatory and causal circle.
6 Conclusion: three causal stories
The main goal of this article was to offer an analysis of causal interactions within entangled quantum systems under the counterfactual interpretation of causality. The first step of this analysis was a search for a semantics of counterfactual conditionals with the help of which we could properly evaluate counterfactuals connecting space-like separated events. We have distinguished no less than six inequivalent interpretations of counterfactuals that could be used to describe the observed correlations between distant parts of an entangled system. Of these six interpretations three have been selected as the most promising candidates for explicating counterfactual and causal dependence between space-like separated measurement events. All three approaches follow the intuition that in order to evaluate a counterfactual whose antecedent refers to a localized event, we have to keep the past of this event exactly as in the actual world. But they differ in how we are supposed to define the past in accordance with the principles of relativity. This can be done as follows: we can define the relativistically-invariant past of an event as the interior of its past light cone (the narrow fixed past), as the exterior of its future light cone (the broad fixed past), or as the region consisting of all spatiotemporal points temporarily preceding the selected event in a particular frame of reference (the frame-dependent approach).
The three alternative interpretations of counterfactuals diverge with respect to their verdict regarding the counterfactual dependence between distant outcomes of measurements in an entangled system. One of them (the narrow fixed past) implies that the outcomes are counterfactually dependent, the second (broad fixed past) that they are not dependent, and the third that their counterfactual dependence is frame-relative. Consequently, under the standard Lewisian approach to causation the first of the above semantics implies that there is a direct causal link between distant outcomes of measurements. However this link displays some non-standard features, such as symmetricity, and (arguably) reflexivity. Faced with this challenge, we have explored an alternative to the standard counterfactual analysis of causation in the form of a modified version of Lewis’s theory of influence. Though it may be argued that the relation of influence does not hold between distant outcomes of measurements, it is too hasty to draw from this fact the conclusion that there is no causality involved here, since there are many legitimate instances of causation that similarly lack the required features of influence. Hence the holding of the relation of influence does not seem to be a necessary condition for causation. On the other hand, the lack of counterfactual dependence between distant outcomes under the broad fixed past interpretation does not exclude the possibility of a causal link, since causation is typically defined as the transitive closure of the relation of counterfactual dependence.
Continuing our search for causal mechanisms responsible for the non-local correlations in quantum entangled systems, we have posed the question of whether a measurement performed on one subsystem of an entangled system can have an effect on the state of the other subsystem even when this subsystem is not subject to any measurement. In order to make this question more tractable, we have made several interpretational assumptions. In addition to adopting the postulate to reduce the cause and effect link to counterfactual dependence, we have also decided to interpret an eigenstate of a particular observable in terms of the sure-fire disposition of a system to reveal the corresponding value of the observable under measurement. The dispositional properties, in turn, are assumed to be analyzed in terms of counterfactual conditionals “If a measurement was performed, the outcome would be such-and-such”. Under these assumptions the broad fixed past approach to counterfactuals predicts that revealing a particular outcome in one measurement is followed by a change in the state of the other subsystem. On the other hand, under the narrow fixed past analysis the local measurement does not affect the state of the distant subsystem. The frame-dependent approach to counterfactuals relativizes the existence of an appropriate disposition to the inertial frame of reference in which the counterfactual is evaluated.
The key result of our investigation into the causal underpinnings of quantum non-local correlations seems to be that there are three alternative causal stories that can be given here, each associated with a particular way of resolving the ambiguity of relativistically-invariant counterfactuals. Each of these causal explanations violates, in its own unique way, some classical intuitions pertaining to the notion of causality. Relativization of counterfactual statements to a particular inertial frame of reference has the immediate consequence that the causal nexus itself loses its status of an objective, perspective-independent feature of the world. The remaining two stories retain the objective and relativistically-invariant sense of causality, but imply that the causal connections present in quantum entangled systems possess some rather non-standard properties. According to the narrow fixed past approach the causal nexus directly connects the outcomes revealed in space-like separated parts of the entangled system. However, the most controversial aspect of this analysis, apart from the obvious non-local character of the causal link involved, is that it entails that each outcome-event plays two distinct roles: that of a cause and an effect of the other event. Due to this symmetric character, the relation between both events looks more like an instance of a common cause rather than direct causation. However, as the existence of a common cause is excluded by the Bell-type arguments, we are left with a case of causal bidirectional correlations between space-like separated and indeterministic events. Speaking metaphorically, distant outcomes appear to be mutually coordinated in a causal way rather than causing one another or being caused by an external factor.
The third causal analysis of the quantum non-local correlations is even more complex. When we identify the counterfactually fixed past of an event with the complement of its future light cone, the consequence of this assumption is that each measurement non-locally causes the emergence of a sure-fire disposition of the distant correlated system, which in turn is responsible (in an entirely local way) for revealing a unique outcome of measurement. This story works in an almost perfectly intuitive way when limited to each measurement separately, but when these measurements are analyzed jointly, inevitable circularity ensues. That is, the L-measurement, together with its outcome, creates the sure-fire disposition to reveal the correlated outcome on the R-system. The R-measurement, in turn, actualizes this disposition by producing the appropriate outcome, but in addition to that it also creates non-locally the requisite disposition of the L-system, actualized in its measurement. Nowhere in this looped chain of events can we identify a point at which it can be said that an indeterministic selection of an outcome of measurement is taking place, as prescribed by the rules of ordinary quantum mechanics. Each measurement seems to reveal a preexisting value of the considered observable, whose presence is causally explained by the non-local influence of the other measurement and its outcome. While this story does not immediately appear to be internally inconsistent (nor, as it seems, does it directly contradict any principle of quantum mechanics or relativityFootnote 32), it certainly leaves us with the uneasy feeling of not completely understanding the causal mechanism behind the observed phenomena. Unfortunately, it is doubtful that a more satisfactory story can be told without leaving the confines of the standard collapse interpretation of quantum mechanics.
Notes
To keep the discussion general, I am not making any specific assumption regarding the physical interpretation of observable O and its eigenstates \({\vert }0\rangle \) and \({\vert }1\rangle \). This approach to quantum states and properties is commonly adopted in quantum information theory (see e.g. Barnett 2009). The reader used to philosophical discussions of entangled states involving spin of electrons or polarization of photons can reinterpret the given formulas to make them more familiar.
To be entirely correct, the entangled state given in (1.1) should contain spatial degrees of freedom in order to properly describe this experimental situation. I’ll ignore this complication for the sake of simplicity.
I gauge the popularity of the counterfactual theory of causation by the number of papers on this subject (including critical ones) that have been published in the last two decades. This is not to say that this approach is without serious issues or formidable opponents. Collins et al. (2004) is a collection of the most influential articles highlighting various philosophical aspects of the counterfactual approach to causation.
The assumption of the existence of perfect correlations between experimental outcomes is obviously an idealization, as all realistic measurements are prone to various inaccuracies and experimental errors. However, I take it that the biconditional expressed in (1.2) is a consequence of the quantum-mechanical rules applied to state (1.1) which predict that the joint probability of the results (0, 1) and (1, 0) is zero. Under the idealized assumption that the detectors used are perfectly accurate and efficient, this implies conditional (1.2).
It may be objected that the alternative no-miracle semantics leads to equally implausible backtracking counterfactuals of the kind “If Clinton had dropped out of the race, the past would have been different ten million years ago”. I admit that the last counterfactual sounds strange, even though it is debatable which of the two types of backtrackers is more offensive to our intuitions (I, for one, am perfectly happy with accepting the latter kind). However, I believe that the discomfort associated with the counterfactuals of the second kind can be explained away by pointing out that their truth is based on the doctrine of strict determinism, which itself is not a common-sense view. If we are ready to accept the controversial thesis that what happened millions of years ago predetermines Clinton’s current decision, small wonder that we end up with an equally controversial-looking counterfactual pronouncement. On the other hand, the no-miracle semantics produces no such aberrant counterfactuals once the assumption of determinism is dropped. So the problem (if at all) seems to be caused not by the semantics but by the metaphysical doctrine of determinism.
Fenton-Glynn and Kroedel (2015) insist that our intuitions regarding the counterfactual dependence between space-like separated events are indecisive, and that our preferred theory of counterfactuals and causation should reflect this indecisiveness. Similar thoughts are also expressed in Skyrms (1984) and Butterfield (1992a).
Fenton-Glynn and Kroedel point out yet another peculiar feature of Lewis’s analysis (Fenton-Glynn and Kroedel 2015, p. 59). They correctly observe that if we considered an entangled state involving a multitude of space-like separated components, and not just two, then the number of miracles required to ensure the perfect match outside the future light cone of the antecedent-event would be too big to be compensated for by the gain in the match of particular facts. Consequently, in this case Lewis’s theory predicts that there is a counterfactual dependence between space-like separated events. But it is rather strange to admit that the existence of non-local counterfactual dependences is contingent on the number of objects involved.
Strictly speaking, we should further split the considered interpretations into distinct variants depending on whether we elect to include or exclude the surface of the past (or future) light cone in the fixed region. But these subtle distinctions will have no significant impact on subsequent discussions. For the sake of completeness we will adopt the convention according to which in the broad fixed past approach we don’t fix the surface of the future light cone, while in the narrow fixed past analysis we include the surface of the past light cone in the fixed past (see Bigaj 2006, p. 186 ft 2). This means that in both approaches we treat future events that can be reached from us via a light signal as “ontologically open”, and past events that can send us a light signal as already “settled”.
However, we should keep in mind that even in the quantum-mechanical world there are some causal, or nomological links between events, so it may happen that miracles are required in order to consider alternative scenarios.
We are assuming here, in accordance with the dominant view, that the non-local quantum correlations cannot be explained by a common cause operating in the joint past of both measurements (see Sect. 4 for further details). If there was a common cause affecting both outcomes of measurements and ensuring their perfect correlations, the valuations of the alternative-outcome counterfactual would look significantly different. In the first approach the counterfactual would not be true, since by keeping fixed the absolute past of one measurement we also keep fixed the common cause which ensures that the other outcome is exactly as in the actual world. However, under the second reading of counterfactuals the valuation of the alternative-outcome counterfactual is the same (i.e. false) both with and without a common cause.
It may be argued that the broad fixed past approach trivializes the problem of counterfactual dependence between space-like separated events, since such dependence is excluded from the outset by the stipulation to fix the entire area outside the future light cone of the antecedent-event, regardless of what consequent-event we consider. However, as we will see later in the text, the lack of counterfactual dependence does not exclude the possibility that there may be a causal link connecting space-like separated events. For an extended argument that there is no strong reason to prefer either the broad or the narrow fixed past approach to counterfactuals, see Bigaj (2006, pp. 219–224).
More specifically, the proposed similarity relation takes into account the earliest points at which a given possible world diverges from the actual one, and considers the total area that is the sum of all future light cones originating at these points. A world A is closer to the actual than a world B if the above-defined area for A is properly included in the corresponding area of B. Note that the resulting similarity relation is essentially equivalent to the relation of global comparative closeness defined by Placek and Müller in their proposed semantics for counterfactuals within the framework of Nuel Belnap’s Branching Space-Time theory (Placek and Müller 2007, pp. 182–183). While I have no space here to make a detailed comparison, I would like to acknowledge that there are close analogies between Placek and Müller’s approach and the no-miracle semantics based on the broad fixed past theory. One distinguishing detail, though, is that Placek and Müller prefer to use a ‘local’ version of their theory in which counterfactuals, as well as their components, are evaluated precisely at the same spatiotemporal location. This restriction makes it difficult, if not outright impossible, to consider counterfactuals connecting events that occur at different (e.g. space-like separated) locations.
We should add that the two no-miracle approaches currently discussed sometimes produce different valuations of the same counterfactuals, so they are not generally equivalent. A typical example of such a case is a counterfactual whose consequent refers to an indeterministic event occurring in actuality at a space-like separation from the unrelated antecedent-event. Under the first interpretation the counterfactual is true, but the second interpretation gives the opposite valuation.
The concept of the counterfactual and causal dependence between distant outcomes is reminiscent of the well-known distinction between two types of non-local influences in quantum entangled states: outcome dependence and parameter dependence. Originally introduced (under different names) by Jarrett (1984), the conditions of outcome independence and parameter independence are presented in the form of probabilistic formulas stating that the local outcome is statistically independent from the distant outcome and from the distant measurement setting. As is well known, the joint assumption of outcome independence and parameter independence leads to Bell’s inequality. Quantum mechanics violates outcome independence, but preserves parameter independence. The latter result can be confirmed in our counterfactual analysis, as the counterfactual “If a different observable had been measured at L, the outcome obtained at R would be different” is clearly wrong. For criticism of the philosophical meaning of Jarrett’s distinction see Maudlin (1994, p. 95ff) and Bigaj (2006, pp. 47–58).
To be entirely accurate, the fact that the joint absolute past of the measurements can be fixed does not guarantee that there is no common cause of both outcomes located somewhere outside this area. But in that case we would have a non-local causal influence anyhow, since the purported common cause would have to be space-like separated from at least one measurement (see Maudlin 1994, p. 131).
This point is made in Kistler (2006, pp. 48–49). Among the authors that question the transitivity of the causal relation is Hall (2000). Fenton-Glynn and Kroedel (2015, p. 68) suggest that we should accept a limited version of transitivity which applies to distinct events only, thus forestalling the derivation of self-causation in the quantum case.
The concept of a “small” change is left intentionally vague by Lewis, in keeping with his broad view that the concept of causality itself is vague and admits various inequivalent precisifications.
For an argument against Lewis’s claim regarding the relation between counterfactual dependence and influence see Bigaj (2012b, pp. 10–11).
However, we should keep in mind that so far there is no satisfactory relativistically invariant account of the measurement process in quantum mechanics. See Barrett (2014) for an extensive discussion of this problem.
Dispositional interpretations of quantum states are advocated for various reasons e.g. in Suárez (2007), Dorato (2007) and Bigaj (2012c). However, see Dorato (2011) for a detailed argument for the thesis that the dispositional account of properties can be helpful only in the context of some specific interpretations of quantum mechanics, such as the GRW approach.
As we are dealing here with antecedent-events (i.e. measurements) that are typically assumed to be free-choice occurrences not affected by the past, we don’t have to separately consider counterfactual semantics that do not admit miracles.
This causal story displays a striking resemblance to cases of so-called finkish dispositions known from the literature on the metaphysics of dispositional properties (see Bird 2007, pp. 25–26 for an overview). Finkish dispositions provide counterexamples to the “naïve” conditional analysis of dispositions in the form of cases in which either there is a particular disposition which cannot be manifested due to a fink, or there is no disposition but the entire setup guarantees that the appropriate manifestation will be present. The above-discussed story appears to belong to the second category of cases, as we have argued that there is no disposition of the R-system to reveal a given outcome, and yet the L-measurement secures the occurrence of one particular value. However, this case does not necessarily undermine the conditional analysis of dispositions, since the appropriate “local” counterfactual that takes into account only R-measurements is false, in line with the assumption of the non-existence of the underlying dispositions. On the other hand, the counterfactual that includes the occurrence of the L-outcome in its antecedent does come out true, but this counterfactual represents a “global” disposition of the entire system, rather than the local disposition of the R-system. The underlying difference between local and global dispositions can be spelled out in terms of the difference in the spatiotemporal location of the triggering event (stimulus). The local disposition of the R-system involves the local measurement event as the triggering factor, while the global disposition of the entire system makes reference to the stimulus event that consists of both the R-measurement and the L-measurement together with its actual outcome.
I have no space here to discuss one possible objection to the existence of a causal link between a measurement event on one subsystem and the occurrence of an appropriate disposition on the other subsystem. The objection I have in mind is based on the claim, put forward by many authors (e.g. Esfeld 2001, 2004; Ney 2010), that subsystems of an entangled system possess only extrinsic properties, i.e. properties whose possession by an object depends on the existence of other objects in the universe. The extrinsicness argument against the causal link alleges that the change brought about in the distant part of the system by the local measurement is a mere “Cambridge” change, similar to the change I “induce” in the Eiffel tower by moving fifty feet away from it (since now the tower has the property of being fifty feet away from me). I believe that the extrinsicness argument applied to the quantum case is wrong for various reasons, but I have to leave its detailed analysis for another occasion.
It should be stressed that the fact that for each subsystem taken separately the state of this subsystem just before the measurement appears to be an eigenstate of the measured observable does not necessarily violate the rules of standard quantum mechanics, as long as these “collapsed” eigenstates cannot be projected back into the common absolute past of both measurements.
References
Barnett, S. M. (2009). Quantum information. Oxford: OUP.
Barrett, J. (2014). Entanglement and disentanglement in relativistic quantum mechanics. Studies in History and Philosophy of Modern Physics, 48, 168–174.
Bell, J. (1987). Speakable and unspeakable in quantum mechanics. Cambridge: Cambridge University Press.
Bennett, J. (1984). Counterfactuals and temporal direction. The Philosophical Review, 93(1), 57–91.
Bennett, J. (2003). A philosophical guide to conditionals. Oxford: Clarendon Press.
Bigaj, T. (2004). Counterfactuals and spatiotemporal events. Synthese, 142(1), 1–20.
Bigaj, T. (2006). Non-locality and possible worlds: A counterfactual perspective on quantum entanglement. Frankfurt: Ontos.
Bigaj, T. (2008). Making trouble for Lewis in the quantum world. In A. Brożek (Ed.), Filozoficzne Problemy Nauki: Seminarium Lwowsko-Warszawskie [Philosophical problems of science: The Lvov-Warsaw seminar]. Warsaw: Semper.
Bigaj, T. (2012a). Counterfactual semantics and quantum physics. Semiotica, 188, 181–202.
Bigaj, T. (2012b). Causation without influence. Erkenntnis, 76, 1–22.
Bigaj, T. (2012c). Ungrounded dispositions in quantum mechanics. Foundations of Science, 17, 205–221.
Bigaj, T. (2013). How to evaluate counterfactuals in the quantum world. Synthese, 190(4), 619–637.
Bird, A. (2007). Nature’s metaphysics. Oxford: Clarendon Press.
Butterfield, J. (1992a). David Lewis meets John Bell. Philosophy of Science, 59, 26–43.
Butterfield, J. (1992b). Bell’s theorem: What it takes. British Journal for the Philosophy of Science, 43, 41–83.
Collins, J., Hall, N., & Paul, L. A. (Eds.). (2004). Causation and counterfactuals. Cambridge, MA: The MIT Press.
Darby, G. (2012). Relational holism and Humean supervenience. British Journal for the Philosophy of Science, 63, 773–788.
Dorato, M. (2007). Dispositions, relational properties and the quantum world. In M. Kistler & B. Gnassounou (Eds.), Dispositions and causal powers (pp. 249–270). Farnham: Ashgate.
Dorato, M. (2011). Do dispositions and propensities have a role in the ontology of quantum mechanics? Some critical remarks. In M. Suárez (Ed.), Probabilities, causes and propensities in physics, synthese library (pp. 197–219). Berlin: Springer.
Dowe, P. (2000). Is causation influence? Unpublished manuscript.
Elga, A. (2001). Statistical mechanics and the asymmetry of counterfactual dependence. Philosophy of Science, 68, S313–S324.
Esfeld, M. (2001). Lewis’ causation and quantum correlations. In W. Spohn, M. Ledwig, & M. Esfeld (Eds.), Current issues in causation (pp. 175–189). Paderborn: Mentis.
Esfeld, M. (2004). Quantum entanglement and a metaphysics of relations. Studies in the History and Philosophy of Modern Physics, 35B, 601–617.
Esfeld, M. (2014). Quantum Humeanism, or physicalism without properties. The Philosophical Quarterly, 64(256), 453–470.
Fenton-Glynn, L., & Kroedel, T. (2015). Relativity, quantum entanglement, counterfactuals and causation. British Journal for the Philosophy of Science, 66, 45–67.
Field, H. (2003). Causation in a physical world. In M. J. Loux & D. W. Zimmerman (Eds.), The Oxford handbook of metaphysics (pp. 435–460). Oxford: OUP.
Finkelstein, J. (1999). Space-time counterfactuals. Synthese, 119, 287–298.
Ghirardi, G., & Grassi, R. (1994). Outcome predictions and property attribution: The EPR argument reconsidered. Studies in History and Philosophy of Science, 25(3), 397–423.
Hall, N. (2000). Causation and the price of transitivity. The Journal of Philosophy, 97, 198–222.
Jarrett, J. (1984). On the physical significance of the locality condition in the Bell arguments. Nous, 18, 569–589.
Kistler, M. (2006). Causation and the laws of nature. London: Routledge.
Kvart, I. (2001). Lewis’s causation as influence. Australasian Journal of Philosophy, 79(3), 409–421.
Laudisa, F. (1999). A note on nonlocality, causation and Lorentz invariance. Philosophy of Science, 66, S72–S81.
Laudisa, F. (2001). Non-locality and theories of causation. In T. Placek & J. Butterfield (Eds.), Non-locality and modality (pp. 223–234). Dordrecht: Kluwer.
Lewis, D. (1973a). Counterfactuals. Cambridge, MA: Harvard University Press.
Lewis, D. (1973b). Causation. The Journal of Philosophy, 70, 556–567.
Lewis, D. (1981). Ordering semantics and premise semantics for counterfactuals. Journal of Philosophical Logic, 10, 217–234.
Lewis, D. (Ed.). (1986). Counterfactual dependence and time’s arrow (with Postscripts). In Philosophical papers (Vol. II, pp. 32–66). Oxford: OUP.
Lewis, D. (2000). Causation as influence. The Journal of Philosophy, 97(4), 182–197.
Lewis, D. (2004). Causation as influence. In J. Collins, N. Hall, & L. A. Paul (Eds.), Causation and counterfactuals. Cambridge, MA: The MIT Press.
Maudlin, T. (1994). Quantum non-locality and relativity. Oxford: Blackwell.
Maudlin, T. (2007). The metaphysics within physics. Oxford: OUP.
Mumford, S. (1998). Dispositions. Oxford: OUP.
Ney, A. (2010). Are there fundamental intrinsic properties? In A. Hazlett (Ed.), New waves in metaphysics (pp. 219–239). London: Palgrave-Macmillan.
Placek, T., & Müller, T. (2007). Counterfactuals and historical possibilities. Synthese, 154, 173–197.
Ryle, G. (2009). The concept of mind (60th Anniversary ed.). London: Routledge.
Schaffer, J. (2001). Causation, influence, and effluence. Analysis, 61(1), 11–19.
Skyrms, B. (1984). EPR: Lessons for metaphysics. Midwest Studies in Philosophy, 9, 245–255.
Suárez, M. (2007). Quantum propensities. Studies in History and Philosophy of Modern Physics, 38, 418–438.
Acknowledgements
I would like to thank the anonymous referees for this volume for their extensive critical comments to the earlier versions of this paper. The work of this paper was supported by the Marie Curie International Outgoing Grant FP7-PEOPLE-2012-IOF-328285.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bigaj, T. On quantum entanglement, counterfactuals, causality and dispositions. Synthese 197, 4161–4185 (2020). https://doi.org/10.1007/s11229-016-1304-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1304-9