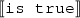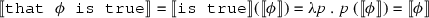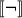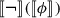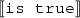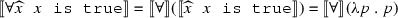Abstract
Renewed worries about the unity of the proposition have been taken as a crucial stumbling block for any traditional conception of propositions. These worries are often framed in terms of how entities independent of mind and language can have truth conditions: why is the proposition that Desdemona loves Cassio true if and only if she loves him? I argue that the best understanding of these worries shows that they should be solved by our theory of truth and not our theory of content. Specifically, I propose a version of the redundancy theory according to which ‘it is true that Desdemona loves Cassio’ expresses the same proposition as ‘Desdemona loves Cassio’. Surprisingly, this variant of the redundancy theory treats ‘is true’ as an ordinary predicate of the language, thereby defusing many standard criticisms of the redundancy theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to an important tradition, there is a common class of entities, propositions, that can be both thought and asserted. A thought or assertion is correct only if the proposition thought or asserted is true. But a proposition does not have its truth-value all by itself, independently of the world at large. For example, Richard said and Margaret believes (q) that Richard killed Henry. This proposition is true because Richard did indeed kill Henry. On the other hand, Iago said and Othello believes (p) that Desdemona loves Cassio. This proposition is false because Desdemona does not love Cassio. This co-variation is so familiar that it’s easy to pass without noticing between a simple sentence asserting a proposition such as (1) and a sentence ascribing truth to this proposition such as (2).
-
(1)
Desdemona loves Cassio.
-
(2)
That Desdemona loves Cassio is true.
Though familiar, these transitions should not be overlooked in our theory. Indeed, the familiarity of these inferences is itself perplexing. Why are claims such as (1) so closely connected to claims such as (2) in our inferential practice? What accounts for the necessary connection—in standard, non-paradoxical cases—between a proposition and the seemingly distinct state of the world that determines its truth-value?
Recently, this question has been raised under the guise of a renewed worry about “the unity of the proposition”. Those pushing the worry ask how a proposition manages to have truth conditions. That is, why does the truth-value of the proposition that Desdemona loves Cassio necessarily co-vary with whether she loves him?Footnote 1 The need to associate a proposition with its truth condition is meant to be an important check on the theory of what propositions are. Standard theories of the nature of propositions are judged inadequate because they cannot explain why a proposition has truth conditions. So, it is contented that what Othello believes cannot be (a) a structured whole, (b) a primitive abstract entity, or (c) a set of possible worlds on pain of failing to deliver a crucial explanation.Footnote 2 Some have taken this unity worry to be so severe as to mandate the psychologicstic conclusion that propositions are dependent on mental acts or linguistic vehicles.Footnote 3
In this paper, I isolate two formulations of the new problem of the unity of the proposition. One formulation asks for an explanation of why propositions have truth conditions. Why is the proposition that Desdemona loves Cassio true if and only if Desdemona loves Cassio? The other formulation begins with an attempted explanation. A proposition has truth conditions because it represents in some independent sense. On this view, the proposition that Desdemona loves Cassio represents that Desdemona loves Cassio. This fact purportedly explains why the proposition’s truth-value varies with whether Desdemona loves Cassio. On this formulation of the unity worry, the puzzle is to explain why propositions are representational, whereas mere lists or aggregates are not.
I argue, however, that supposing that propositions are representational in this independent sense is no explanatory advance. Thus, we should prefer a formulation of the problem in terms of truth conditions to a formulation in terms of representation. We need to explain why a proposition and the claim that it is true are, in general, equivalent; that is, why is it that the proposition that Desdemona loves Cassio is true if and only if Desdemona loves Cassio. Since I accept this demand, my position differs significantly from others who deny that propositions are representational such as Speaks (2014a, b, c) and Richard (2014).
The worry is to explain why the truth-value of a proposition varies with the state of the world. Those pushing the unity objection tend to frame this as a problem about contents. They say that there is something about propositions which explains this variation. I propose a change of view: the problem should be solved by our theory of truth and not our theory of content. To this end, I develop a form of the redundancy theory of truth delivering the needed explanation. On this theory, a simple sentence and a corresponding truth-ascription such as (1) and (2) express the same proposition. The claim that Desdemona loves Cassio just is the claim that the proposition that Desdemona loves Cassio is true. This explains why they are equivalent. In other words, the puzzle is to explain why Desdemona’s loving Cassio co-varies with the seemingly distinct state of the world that the proposition that Desdemona loves Cassio is true. The redundancy theory replies that these states of the world are not as distinct as they might seem.
I develop a Compositional Redundancy Theory, which surprisingly treats ‘is true’ as an ordinary predicate. I treat predicates generally as denoting functions from individuals to propositions. The truth predicate is no exception and thus functions as an ordinary predicate. However, the truth predicate denotes a particular function, which maps a proposition to itself and is undefined for other inputs. It is for this reason that a simple sentence and a corresponding truth ascription express the same proposition.
-
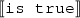
= \(\lambda p\) . p
-
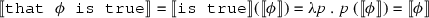
This form of the redundancy theory of truth is novel, though motivated by overlooked remarks of Ramsey. Moreover, I suggest that this new redundancy theory avoids the pitfalls of other broadly deflationary theories of truth by treating the truth predicate on analogy with the other predicates of the language.
Because my explanation is delivered by a theory of truth, and not a theory of content, it is compatible with most accounts of the metaphysics of propositions on offer. In this, I am again in agreement with Ramsey that the metaphysics of propositions is not constrained by the demand that they have truth conditions.
[I]f we have analysed judgment we have solved the problem of truth; [...] the truth or falsity of this depends only on what proposition it is that is judged[.] (Ramsey 1927, p. 158).
As a result, the new problem of the unity of the proposition does not call for the radical revisions to the traditional conception of propositions contemplated in the literature.
2 Unity problems: old and new
The renewed worries about the unity of the proposition arise against the backdrop of more traditional concerns about propositional unity. These more traditional worries tend to target conceptions of propositions as structured wholes. I am attracted to one such conception, deriving from Moore and Russell. This view construes propositions as structured complexes containing objects, properties, and relations as constituents. The proposition that Desdemona loves Cassio is a structured whole containing Love, Desdemona, and Cassio. We may represent this structure as \(\langle \)Love, \(\langle \)Desdemona, Cassio\(\rangle \rangle \), where the set-theoretic relations go proxy for corresponding structural facts about the proposition. Importantly, I assume only that propositions can be represented in terms of set theoretic constructions, not that propositions are identical to n-tuples. Rival theories also identify propositions with structured wholes, but differ as to the constituents of these wholes. According to one alternative picture, due to an interpretation of Frege, propositions are structured wholes containing representations of these objects, properties, and relations.
Advocates of structured propositions have faced a formidable challenge concerning the unity of the proposition. The challenge is to explain how the proposition is a unity. The problem has come in many guises. Some have asked how the diverse constituents—Desdemona, Cassio, and love—come together to make up the structured proposition. Bradley (1893/2002) charged that complexity is itself mysterious. Others have inquired about the relationship between the structured complex and these constituents. Thus, Lewis (1986) and Keller (2014) charge that structured complexes require a mysterious kind of complexity.Footnote 4
In this paper, I will not address these traditional worries, but rather a renewed unity worry that asks why propositions are true or false depending on how things are in the world while mere lists or aggregates are not.Footnote 5 This renewed unity problem purports to show that no traditional conception of propositions can be correct on account of the fact that propositions have truth conditions. As Soames says:
What is special is that propositions must be—inherently and without further interpretation by us—capable of being true or false. (Soames 2014b, p. 32)
The problem we need to solve [...] is not to find some relation born by the constituents of a proposition to one another that ‘holds them together’ as parts of a single complex entity; the problem is to explain the intentionality of propositions. (Soames 2014b, p. 32)
Understood as a problem about truth conditions, the unity of the proposition asks why a proposition’s truth-value varies with the world at large. That is, why is the proposition that Desdemona loves Cassio true just in case Desdemona loves Cassio? Similarly, why is the proposition that Richard killed Henry true just in case Richard killed Henry? The question can be repeated for any non-paradoxical case. One might understand this covariation as a kind of representation.Footnote 6 The proposition that Desdemona loves Cassio represents that Desdemona loves Cassio insofar as it is true just in case Desdemona loves Cassio. The proposition that Richard killed Henry represents that Richard killed Henry insofar as it is true just in case Richard killed Henry.
Of course, a theorist might deny that there is anything to be explained. The connection between a sentence expressing a proposition and a sentence ascribing truth to the proposition is very tight and we often pass over the distinction unnoticed. Given this close connection, one might imagine this theorist as committing to a number of entities, p, q, and so on. Following the magical ersatzer of Lewis (1986/2001, p. 175), the theorist offers the following theory about them:
Necessarily, p is true if and only if Desdemona loves Cassio. Necessarily, proposition q is true if and only if Richard murdered Henry. And so on. End of theory.
But such a theory feels unsatisfactory. This theory is worse—all other things being equal—than a theory that explains these equivalences.
One might conceive of these worries as addressing unity on the grounds that they interrogate why a proposition is true or false while a list or mere aggregate of diverse constituents is not. It is important to keep in mind that while the traditional worries primarily target conceptions of propositions as structured entities uniting diverse constituents, the renewed worries target any view according to which propositions are not linguistic or psychological entities but exist and have truth-values which vary with the state of the world. Thus, the renewed worries equally face alternatives to structured propositions, including:
-
Intensionalism: Propositions are intensions in that (i) they determine functions from points-of-evaluation to truth-values and (ii) two propositions that determine the same functions are identical.Footnote 7
-
Primitivism: Propositions are fine grained, simple objects with no internal structure.Footnote 8
On almost any view of propositions, they have truth-values which vary with how things are in the world. In this respect, the partisans of propositions are called upon to explain this dependence: why does the proposition that Desdemona loves Cassio become true when Desdemona loves Cassio? Thus, they all face renewed worries about propositional unity.Footnote 9
I first examine an approach that attempts to explain this connection in terms of the theory of content. Specifically, the thesis that propositions are representations and that truth is accurate representation. I then argue that the covariation can be explained by our account of truth rather than our account of content. My own proposal will be developed in a framework which identifies propositions with structured wholes composed of objects, properties, and relations. But nothing I say will depend essentially on this framework. Indeed, everything I say could be adopted by proponents of almost any conception of propositions so long as it can be developed in conjunction with certain semantic assumptions that I discuss below.
3 Unity through representation
Sometimes, those pushing the unity objection propose that propositions have distinct representational properties which explain why they have truth conditions. For instance, Soames (2010, p. 56) suggests that “it is only by being representational that anything becomes a candidate for being true or false”. Soames holds that a given proposition has its truth-value because it represents what is—or is not—the case. As Soames (2014a, p. 104) says:
why is the proposition that snow is white true? It is true because (a) it represents snow as white, and (b) snow is white.
Returning to our examples: proposition q—that Richard murdered Henry—represents that Richard murdered Henry. Richard did murder Henry. So q is true. On the other hand, proposition p—that Desdemona loves Cassio—represents that Desdemona loves Cassio. Desdemona did not love Cassio. So p is not true.
On this view, the representational properties of propositions are primary. They explain why the proposition has truth conditions. Truth is representing what is the case. Lewis once described an analogous position about possible worlds, according to which worlds are “elements” that represent things. One of these elements is the actual world (or, as he says, it is “selected”) just in case it represents what is the case.
[S]ome elements have the property: representing that a donkey talks, or being an element according to which a donkey talks. It is in virtue of these representational properties that some elements are selected and some or not. For instance, there is one element that has the aforementioned property of representing that a donkey talks, and no other properties. Necessarily, that one is selected iff a donkey talks. (Lewis 1986/2001, p. 177)
On this view, a certain element is “selected” because it represents that Richard murdered Henry and Richard did murder Henry. The analogous position about propositions—defended by Hanks (2007), Soames (2014a), and Merricks (2015, ch. 6)—says roughly that the proposition that Richard murdered Henry is true because it represents that Richard murdered Henry and Richard did murder Henry.
This position purports to explain why propositions have truth conditions. In doing so, it explains one kind of representation (co-variation) in terms of another, as yet unspecified, kind of representation. The renewed unity objection can then be presented in terms of representation. In virtue of what do propositions possess these representational properties? Lewis pressed this sort of objection against an ersatzer claiming that properties, propositions, or states of affairs had representational properties, but offering no further explanation of why they had them. According to Lewis, such unexplained representation amounts to “magic”.
We have not the slightest idea what the ‘representational properties’ are; except that they are properties whereby a vast flock of abstract simples differ from one another. Lewis (1986/2001, p. 178)
By way of contrast, Lewis allowed that we can understand linguistic or pictorial representation.Footnote 10 He would, presumably, also say the same about mental representation. If we are to have representation (as something beyond co-variation) it must be explained in terms of the same mechanisms by which we explain linguistic, pictorial, or psychological representation. To a certain extent, Soames, Hanks, and King all agree. They attempt to explain representation in psychological or linguistic terms. The representational properties of propositions are due to the abilities of agents, psychological states, or sentences to represent.
I do not believe that the problem of the unity of the proposition should be framed in terms of representation. In particular, I do not believe that propositions represent in any sense other than being true or false depending on how things are in the world. The problem is that any account developed in these terms should answer the question: what does a proposition—say, that Desdemona loves Cassio—represent? This question is answered by constructions of two sorts:
-
Representation-That: The proposition that Desdemona loves Cassio represents that Desdemona loves Cassio.
-
Representation-As: The proposition that Desdemona loves Cassio represents Desdemona as loving Cassio.
I argue that both sorts of answer prompt the complaint that a proposition represents itself or another item which itself has problematic representational features. I take this complaint to be forceful enough to motivate exploring another option. Before I close the section, I will compare my position to others who have denied that propositions are representational.
3.1 Representation-that
Those who think that propositions have their truth conditional properties on account of their representational properties posit an explanatory connection between truth and representation. Namely, a proposition that represents that \(\phi \) is true just in case \(\phi \). Above, we saw Lewis construe his opponents’ view as asserting that a certain primitive element represents that a donkey talks and that this element is selected just in case a donkey talks. The analogous position about propositions says that a certain proposition represents that Desdemona loves Cassio. This proposition is true just in case Desdemona loves Cassio. Many philosophers do indeed use this terminology to refer to the representational properties of propositions or their features, including King (1995, p. 526), Richard (2014, p. 2), and Jago (2015, p. 4). The aim of this section is to suggest that one cannot explain the truth conditional properties of propositions in terms of their representational properties construed as properties of representation-that.
To see the difficulties, we must scrutinize the construction (3).
-
(3)
Proposition p represents that Desdemona loves Cassio.
Such constructions are used in ordinary English with the relevant meaning, when one says—for instance—that placing many occurrences of the sign ‘$’ adjacent to a restaurant review represents that the restaurant is expensive.
Constructions such as (3) do not occur in isolation. They contain verbs followed by ‘that’-clauses, in this case ‘that Desdemona loves Cassio’. Saliently, ‘that’-clauses also appear in propositional attitude ascriptions such as (4) and (5).
-
(4)
Othello believes that Desdemona loves Cassio.
-
(5)
Margaret knows that Richard killed Henry.
I propose that (3) should be construed along the same lines as (4) and (5). In particular, (3) should be construed as ascribing a relationship between the proposition p and some other entity specified by ‘that Desdemona loves Cassio’. Indeed, one of the standard motivations for propositions is the assumption that these sentences assert that an agent stands in a relation to a proposition specified by the ‘that’-clause. Given the similarity of the constructions, construing the ‘that’-clause otherwise takes away much of the motivation for making the analogous claim in the case of (4) and (5).Footnote 11
I have argued that the ‘that’-clause in (3) should be construed as specifying or describing some object just as the analogous ‘that’-clauses do in (4) and (5). One might push the analogy with propositional attitude ascriptions to argue that the entity specified in (3) must be a proposition. But, then, it is hard to see how we have a satisfactory explanation of a proposition’s possession of truth conditions in terms of its being representational. It is unilluminating—from the point of view of explaining why propositions have truth conditions—to say that the proposition has truth conditions because it represents itself.Footnote 12
I will not here go through the entire literature on alternative views as to what the ‘that’-clause in (3) might represent. Rather I divide the potential candidates into two categories. The two options I consider are: (\(\alpha \)) the proposition that Desdemona loves Cassio represents something which may exist regardless of whether Desdemona loves Cassio and (\(\beta \)) this proposition represents something that exists if and only if she loves him.
Suppose (\(\alpha \)) that the proposition that Desdemona loves Cassio represents something which—like the proposition itself—may exist even if Desdemona does not love Cassio. This category includes states of affairs, as some construe them. On these construals, the state of affairs that Desdemona loves Cassio exists regardless of whether she loves him. If she does love him, then the state of affairs has an additional feature: it is the case or obtains. If the proposition that Desdemona loves Cassio represents some entity in this category, then the truth-value of the proposition is explained by both the entity it represents and whether the entity has the additional feature. If propositions represent states of affairs, then the proposition that Desdemona loves Cassio represents the state of affairs that Desdemona loves Cassio. The proposition is true if the state of affairs is the case or obtains.Footnote 13
The problem is that the notion of being the case or obtaining introduces the same sort of worry we had about truth. The state of affairs that Desdemona loves Cassio may be the case or it may fail to be the case. But it does not have these features—being the case or failing to be the case—in isolation from the world at large. In particular, when Desdemona loves Cassio, that Desdemona loves Cassio is the case. And when she fails to love him, it is not the case. It is natural to ask why the obtaining of this state of affairs co-varies with the world at large in this way. Thus, this proposal purports to explain why propositions have truth conditions in terms of the structurally similar fact that states of affairs have obtaining conditions. Given the precise structural similarity, I fail to see how this is a genuine explanatory advance.
Now suppose (\(\beta \)) that the represented entity cannot exist unless the proposition is true. Under this category, we might include states of affairs or facts, as they are sometimes conceived.Footnote 14 On such a view, the proposition that Richard killed Henry represents the fact that Richard killed Henry. And this fact could not exist unless Richard did kill Henry. This approach, then, can provide an account of truth along the lines of classical truth-maker theory.Footnote 15 For a proposition to be true is for it to represent a fact.
Note that on this proposal, false propositions fail to represent anything. The proposition that Desdemona loves Cassio is false. As a result, it represents nothing on this picture. Yet, if Desdemona were to love Cassio, then necessarily there would come into existence a fact F that Desdemona loves Cassio. And the proposition that Desdemona loves Cassio would come to represent F. The proposal, therefore, posits two modal connections where before we only had one. First, whenever Desdemona loves Cassio, F comes into existence.Footnote 16 Second, whenever Desdemona loves Cassio and F comes into existence, the proposition p that Desdemona loves Cassio comes to represent F. It is far from obvious that jointly explaining these two connections will be easier than explaining why the proposition that Desdemona loves Cassio becomes true when Desdemona loves Cassio.Footnote 17
3.2 Representation-as
Recently, it has been popular to offer an alternative formulation of what a proposition represents. Rather than saying that a proposition represents that such and such is the case, proponents of this alternative formulation say that a proposition represents an object as being a certain way. Thus, it might be suggested that the proposition that Desdemona loves Cassio represents Desdemona as loving Cassio.Footnote 18 The proposition that Richard killed Henry represents Richard as killing Henry.
It is then argued that we can explain why a proposition has its truth conditions in terms of what it represents. Thus, Soames argues:
[Propositions] represent things in the world as being certain ways; thus they have truth conditions. Since the proposition that o is red represents a certain object as red (while doing no further representing) it is true iff o is the way it is represented to be—red. (Soames 2014a, p. 95)
The idea is that if something represents an object as having a property, then the representation is true (or accurate) just in case the object has the property.
We might think of this connection as a general law relating representation to truth. Presumably, this law is meant to be part of our pre-theoretic conception of representing an object as having a property. That is, representing a as F is not some new unstructured monadic property P or relational property R(a as F), between a proposition and what it represents. Rather, the notion of representation invoked is meant to be something pre-theoretically available and expressible in natural language using one of these ‘as’ constructions. If it were not, then the purported explanation would be no better than that of a traditional structured propositionalist who says that the fact that the proposition that Desdemona loves Cassio stands in interesting constituency relations to Desdemona, love, and Cassio explains why it has truth conditions.
Therefore, the plausibility of this view turns on how we should understand ‘as’-constructions in English such as (6), (7), and (8).
-
(6)
The proposition that Desdemona loves Cassio represents Desdemona as loving Cassio
-
(7)
The department represented Mary as a syntactician.
-
(8)
The department regarded Mary as a semanticist.Footnote 19
These constructions are widely used in ordinary English. A dean might, for instance, utter (7) to describe how a linguistics department presents a job candidate to the university.
Unfortunately, the exact syntax and semantics of these constructions are controversial.Footnote 20 The important point for my purposes is that many of the proposed analyses of ‘as’-constructions raise the same difficulties that arose in the case of representation-that. In particular, many analyses would treat an ‘as’-clause as a syntactic constituent of a sentence. For instance, these constructions can be coordinated, which is fairly commonly taken as prima facie evidence that an expression is a syntactic constituent.Footnote 21 Thus, one might say:
-
(9)
The linguistics department represented Mary as a syntactician and Sam as a semanticist.
This is evidence that ‘Desdemona as loving Cassio’ is a syntactic constituent of (6). The next question is: how does ‘Desdemona as loving Cassio’ function?
My preferred account has two components. One component is that an ‘as’-clause functions as a small clause, a type of construction containing a noun and an uninflected predicate expression. On this view, a sentence such as (8) ‘The department regarded Mary as a semanticist’ would mean something similar to (10).
-
(10)
The department considered Mary a semanticist.
As a result, the embedded construction ‘Mary as a semanticist’ would mean the same thing as the embedded construction ‘Mary a semanticist’. The other component of my preferred account is that a small clause is a syntactic constituent whose semantic function is similar to that of a complete sentence. On this account, then, ‘as’-clauses including ‘Desdemona as loving Cassio’, ‘Mary as a syntactician’, and ‘Mary as a semanticist’ would simply express propositions. Given the discussion above, this will obviously not do for explaining the truth conditions of a proposition in terms of what it represents.
Of course, any account of the nature of these ‘as’-clauses will be controversial, and my preference is no exception. I don’t need to defend my preference here. Rather, I note that on many accounts ‘as’-clauses will represent something. And whatever they represent will lead to issues similar to those discussed above.Footnote 22 I take this as sufficient motivation to explore another option.
3.3 Properties and representation
I am investigating why propositions have truth-values which vary with the state of the world. One attempted explanation, that propositions represent something further, does not promise to deliver this explanation. Thus far, I agree with Richard (2014, p. 705) that rather than being representational in some robust sense,
Propositions [...] are what is represented. They are representational in the minimal sense that they are true or false[.]Footnote 23
I believe, however, that we still must explain why propositions are representational in this minimal sense: why does their truth-value depend on what happens in the world? Why is the proposition that Desdemona loves Cassio true if and only if she loves him?
Richard and also Speaks (2014a) think that they have a satisfactory explanation that does not derive from any purportedly representational properties of propositions. Richard and Speaks both identify a proposition—say the proposition that Desdemona loves Cassio—with an entity that according to them unproblematically varies with whether Desdemona loves Cassio. In particular, both identify the proposition that Desdemona loves Cassio with a certain property, the property of being such that Desdemona loves Cassio.Footnote 24 This property is instantiated just in case Desdemona loves Cassio. Very roughly, they claim that for a proposition to be true is for it to be instantiated.
Though we agree that propositions are not representational except insofar as they are true or false, I disagree with Speaks and Richard that they have offered a satisfactory explanation of why propositions possess these truth conditions. As I conceive of the worry over truth, it is essentially the same as the one Lewis raises against “magical ersatzism” in Lewis (1986/2001). Why is a certain proposition true—or, why is a given ersatz world “selected”—just in case Desdemona loves Cassio? I conceive of these same worries as applying to complex properties: why is the property of being such that Desdemona loves Cassio instantiated just in case Desdemona and Cassio instantiate the loving relation (in the right order)? The initial explanatory demand concerned why a proposition’s truth-value covaries with what happens to the world at large. It is answered by appealing to properties whose instantiation covaries with the instantiation of other properties. But I believe it is reasonable to ask why the instantiation of these properties covaries with the instantiation of simpler universals. And I believe that this is Lewis’s (1986) worry as well, especially as developed by Hawley (2010). This is why Lewis’s objections to ersatz possible worlds so closely resemble his objections to “structural universals” whose instantiation conditions vary with those of simpler properties. So from my point of view, the shift from propositions to properties makes little explanatory advance.Footnote 25
4 A solution through truth
The task is to explain why the truth-value of a proposition varies with the world at large. Why does the proposition that Desdemona loves Cassio come to be true just in case she loves him? As we have seen, it has recently been popular to attempt to explain this covariation in terms of the nature of contents: there is something special about propositions such that their truth-value varies with the world at large. I suggest an alternative approach. I propose that there is something special about truth such that the ascription of truth to a proposition will necessarily co-vary with the world at large.
The thought that these equivalence derive from the nature of truth is common to many broadly deflationary accounts of truth. For instance, following Horwich (1998) and Lewis (2001, p. 602) suggests a form of minimalism:
The truth about truth, so far as propositions are concerned, is a long but simple story. A proposition is true iff
it is the proposition that a donkey talks, and a donkey talks; or
it is the proposition that pigs fly, and pigs fly; or
it is the proposition that cats purr, and cats purr; or
it is the proposition that servitude to the state is perfect freedom, and servitude to the state is perfect freedom; or....
For Lewis, the easy task is to explain the equivalence between the truth of the proposition that Desdemona loves Cassio and Desdemona’s loving Cassio. The hard task, by way of contrast, is to explain why a given proposition p gets to be named “the proposition that Desdemona loves Cassio”.Footnote 26 This hard task is a version of the traditional problem of unity, and I shall not address it here.
On the other hand, I defend a different solution to the easy task: the redundancy theory of truth. According to this theory, sentences of the form S and \(\ulcorner \)that S is true\(\urcorner \) express the same proposition in context. Thus, the claim that the proposition that Desdemona loves Cassio is true is identical to the claim that Desdemona loves Cassio. This identity explains their equivalence. Although anticipated by Frege (1918), this approach is prominently associated with Ramsey. Ramsey divided truth ascriptions into two classes. In some truth ascriptions, the proposition is explicitly given. These ascriptions are usually of the form \(\ulcorner \)that S is true\(\urcorner \) such as (2) in which the proposition to which truth is ascribed is expressed by the sentence in the ‘that’-clause. On Ramsey’s view, if the proposition is explicitly given in a truth ascription, then the truth ascription expresses the same proposition as a simpler sentence embedded in the ‘that’-clause.
The proposition to which they are ascribed may be either explicitly given or described. Suppose first that it is explicitly given; then it is evident that “it is true that Caesar was murdered” means no more than that Caesar was murdered[.] (Ramsey 1927, p. 157)
The basic idea behind the redundancy theory—that sentences of the form S and \(\ulcorner \)that S is true\(\urcorner \) say the same thing—is shared by distinct views of truth. For instance, some interpreters of Ramsey such as Soames (1999, p. 238) take him to hold that constructions involving ‘is true’ are always eliminable or paraphrasable into constructions that do not involve truth. Advocates of the prosentential theory of truth follow this line, but allow that these paraphrases can be developed in an expanded version of English.Footnote 27 The idea is also present in Strawson’s (1950) performative theory.Footnote 28
In the remainder of this paper, I will defend a particular implementation of Ramsey’s idea, according to which the truth predicate has a definite meaning that can be incorporated into a standard compositional semantics. In what follows, I first explain why I develop a compositional version of the theory. I then sketch a semantics that assigns each sentence (in context) to a Russellian structured proposition. I show how a truth predicate exhibiting these features can be smoothly integrated into this semantics. As I mentioned above, the crucial move is to regard ‘is true’ as expressing an identity function restricted to propositions. This function takes a proposition as argument and returns that very proposition. Although I develop my solution in a broadly Russellian framework, the basic structure of this proposal could be adopted by rival views so long as the semantic value of a predicate is treated as determining a mapping from individuals into propositions, whatever these turn out to be on the theory.Footnote 29
4.1 Why a compositional redundancy theory?
Before proceeding, I briefly explain why I prefer my compositional version of the redundancy theory to other broadly deflationary approaches to propositional truth. Because of the vastness of the literature, I will focus on two views: minimalist and prosentential theories. According to minimalism, the nature of truth is wholly explained by the truth of propositions of the form: the proposition that p is true if and only if p, together with the background non-alethic facts. For instance, Horwich (1998, p. 23) says:
According to the minimalist thesis, all of the facts whose expression involves the truth predicate may be explained in such a way: namely by assuming nothing more about truth than instance of the equivalence schema.
Horwich seems to mean, in particular, that all facts whose expression involves truth are logically entailed by the equivalence theory and background non-alethic facts. However, as Gupta (2005a, b) and Soames (1999, pp. 246–251) point out, many of the theses we might wish to express about truth involve generalizations such as (11).
-
(11)
Everything John said is true.
It is difficult to see how these generalizations could be derived from a collection of propositions about particular truths, no matter how large.
Classical interpretations of the redundancy theory that attempt to make do without assigning a compositional meaning to ‘is true’ have also been charged with these difficulties.Footnote 30 In particular, if the only semantic claim about ‘is true’ is that sentences of the form S and \(\ulcorner \)that S is true\(\urcorner \) express the same proposition, it is unclear what a claim such as (11) might mean.Footnote 31 Prosentential theorists attempt to understand Ramsey as offering a paraphrase of these sentences into a language which allows propositional quantification. The intelligibility of these interpretations is itself hotly disputed.Footnote 32
My version of the redundancy theory, however, sidesteps these worries. I assign a standard predicate meaning to ‘is true’. This standard predicate meaning nonetheless delivers the result that S and \(\ulcorner \)that S is true\(\urcorner \) express the same proposition. I do not hold that all facts whose statement involves ‘is true’ are entailed by propositions expressed in non-alethic terms together with instances of the schema, the proposition that p is true if and only if p. Rather, I hold that I can assign a meaning to every sentence in context containing the predicate ‘is true’. Because ‘is true’ functions analogously to any other predicate of the language, there is no difficulty in understanding quantified claims so long as we have a reasonable understanding of the meaning of the quantifier. I present this theory in the next few sections, beginning with the background propositionalist semantics.Footnote 33
4.2 Propositionalist semantics
As I mentioned above, I take Russellian structured propositions to be the semantic values of sentences in context. Thus, sentence (1) ‘Desdemona loves Cassio’ denotes a structured proposition which I represent as \(\langle \)Love, \(\langle \)Desdemona, Cassio\(\rangle \rangle \). A propositionalist semantics aims to compositionally map the sentences of a language onto their semantic values. Following a proposal briefly mentioned by Dummett (1981, p. 294) and developed in Pagin and Pelletier (2007), Elbourne (2011, pp. 104–107), and Pickel (forthcoming), I suggest—contra some leading proponents of structured propositions—that sentences are functionally compositional: the semantic value of a sentence in context is the result of applying the function denoted by one component in context to the argument denoted by the other component in context.Footnote 34
To see how this works, I begin with simple n-ary predicates. I take these to denote propositional functions, which map individuals to propositions. Consider a first-order regimentation of (1) as (1a).
-
(1a)
Love(Desdemona, Cassio).
The dyadic predicate ‘loves’ denotes a function which takes two individuals and yields the proposition that the first loves the second. That is: \(\llbracket \)Love\(\rrbracket \) = \(\lambda o_1, o_2\)\(\langle \)Love, \(\langle o_1, o_2\rangle \rangle \).
Following standard Montague semantics, I take semantic composition, by and large, to be functional application. So a sentence such as ‘Loves(Desdemona, Cassio)’ will denote the result of applying the function denoted by ‘loves’ to the denotations of ‘Desdemona’ and ‘Cassio’. It follows that:
-
\(\llbracket \)Love(Desdemona, Cassio)\(\rrbracket \) = \(\llbracket \)Love\(\rrbracket \)(\(\llbracket \)Desdemona\(\rrbracket \), \(\llbracket \)Cassio\(\rrbracket )\) = \(\langle \)Love, \(\langle \)Desdemona, Cassio\(\rangle \rangle \).
This delivers the result we want. Sentence (1a) ‘Loves(Desdemona, Cassio)’ is mapped to the structured proposition \(\langle \)Love, \(\langle \)Desdemona, Cassio\(\rangle \rangle \). In Pickel (forthcoming), I show that this approach can be extended to deliver a satisfactory semantics for many natural language constructions.
For the purposes of this paper, I take logical constants to ascribe logical universals and relations to propositions and propositional functions. Consider first the truth functional connectives such as negation. A sentence of the form \(\ulcorner \)it is not the case that \(\phi \urcorner \) (abbreviated \(\ulcorner \lnot \phi \urcorner \)) ascribes the universal, negation (NEG), to the proposition expressed by \(\phi \) in the context.Footnote 35
-
\(\llbracket \lnot \phi \rrbracket \) = \(\langle NEG, \langle \llbracket \phi \rrbracket \rangle \rangle \)
To deliver this result using functional application, I take \(\lnot \) to denote a function which takes a proposition and ascribes NEG to it.
-
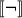
= \(\lambda q \)\(\langle NEG, \langle q \rangle \rangle \)
-
\(\llbracket \lnot \phi \rrbracket \) =
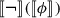
= \(\langle NEG, \langle \llbracket \phi \rrbracket \rangle \rangle \)
The other truth functional connectives will be dealt with similarly. I will examine the function of quantifiers in subsequent sections.
The quantifiers raise additional complications. Let us understand a quantifier as syntactically applying to a complex predicate. That is, a quantified sentence of the form \(\ulcorner \)for each x, \(\phi \urcorner \) (abbreviated \(\forall \widehat{x} \phi \)) will be understood as resulting from composing the quantifier \(\forall \) with the complex predicate \(\widehat{x}\phi \). This predicate itself results from applying the variable binder \(\widehat{x}\) to a formula \(\phi \). Following Soames and Salmon (and ultimately Russell), the complex predicate will be taken as a propositional function which maps individuals to propositions. Essentially, \(\widehat{x} \phi \) denotes the propositional function that maps an object o onto the proposition expressed by the formula \(\phi \), but with x reinterpreted to designate o.Footnote 36
The quantifier \(\forall \) in \(\forall \widehat{x} \phi \) will be taken as attributing the universal, “holding always”, to the propositional function expressed by \(\widehat{x}\phi \).Footnote 37 I denote this universal by ‘ALL’.Footnote 38
-
\(\llbracket \forall \widehat{x} \phi \rrbracket \) = \(\langle ALL, \langle \llbracket \widehat{x} \phi \rrbracket \rangle \rangle \).
To deliver this semantic value for the sentence, I treat the quantifier \(\forall \) as designating a function which takes a propositional function as argument and returns a proposition which attributes the universal, ALL, to this function, yielding:
-

= \(\lambda g \)\(\langle ALL,\langle g \rangle \rangle \)
Having outlined the basic structure of the propositionalist semantics, I turn now to truth.
4.3 The truth predicate
I have proposed a redundancy theory of truth. On this view, S and \(\ulcorner \)that S is true\(\urcorner \) express the same proposition. So the aim is to offer a semantics which compositionality delivers:
-
\(\llbracket \)That\(\phi \)is true\(\rrbracket \) = \(\llbracket \phi \rrbracket \).
To achieve this desideratum, I propose that ‘is true’ expresses a propositional function whose value is the same as the input proposition.
-
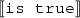
= \(\lambda p\) . p
Given the background semantic framework, assigning this semantic value to ‘is true’ allows us to derive the required identities.
It follows that the propositions expressed by ‘that Desdemona loves Cassio is true’ and ‘that Richard killed Henry is true’ are identical to the propositions expressed by ‘Desdemona loves Cassio’ and ‘Richard killed Henry’, respectively.
From this we can derive a natural explanation of why the truth or falsity of a proposition varies with the state of the world. In particular, we can provide a very natural explanation of (12).
-
(12)
That Desdemona loves Cassio is true if and only if Desdemona loves Cassio
Consider (13) which is an unproblematic logical truth.
-
(13)
Desdemona loves Cassio if and only if Desdemona loves Cassio
(13) stands in no need of explanation. We do not need to explain why Desdemona loves for Cassio whenever she loves him. But on the semantics on offer, (12) and (13) express the same proposition. If the inference from a sentence to a sentence that says the same thing is a licensed, explanation preserving inference, then we can derive (12) from an unproblematic logical truth that itself needs no explanation.
This view delivers a very natural account of quantified contexts. On the standard propositionalist semantics given above, the quantifier ‘everything’ (\(\forall \)) takes a propositional function as argument and yields a proposition predicating being always true (ALL) of a propositional function. There is no obstacle to combining this quantifier with the meaning of ‘is true’.
-

= \(\lambda g \)\(\langle ALL, \langle g \rangle \rangle \)
-
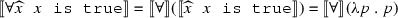
= \(\langle ALL, \langle \lambda p\) . \(p \rangle \rangle \)
Thus, unlike prosentential views, this approach can naturally assign a meaning to quantified claims involving truth without introducing a language that allows for quantification into sentential positions.Footnote 39 Unlike minimalism, it is not part of the theory that the truth of every claim expressed using ‘is true’ can be derived from the non-alethic facts together with instances of the schema p is true if and only if p. As a result, the approach is better poised to explain generality.
While it is not essential, I believe that this approach can also claim Ramseyian pedigree.Footnote 40
[When] the proposition is described and not given explicitly, [...] we get statements from which we cannot in ordinary language eliminate the words “true” and “false.” Thus if I say “he is always right” I mean that the propositions he asserts are always true, and there does not seem to be any way of expressing this without using the word “true.” But suppose we put it thus “For all p, if he asserts p, p is true,” then we see that the propositional function p is true is simply the same as p, as e.g. its value “Caesar was murdered is true,” is the same as “Caesar was murdered.” (Ramsey 1927, p. 158)
So here, Ramsey is saying that the propositional function which I write as ‘\(\lambda p\).p is true’ and the propositional function which I write as ‘\(\lambda p\).p’ are identical. For any input, they give the same output. My view combines this basic insight with a semantics that compositionally assigns structured propositions by treating ordinary predicates as mappings from individuals onto structured propositions. As a result, the truth predicate can be treated as an ordinary predicate of the language.
5 Objections
I have offered a new redundancy theory of truth in order to solve the renewed problem of the unity of the proposition. Traditional redundancy theories have faced a variety of objections. I believe that my implementation is largely immune to these objections. However, in a few cases, I adopt standard solutions to them. In this section, I briefly outline my response to these standard challenges to the redundancy theory.
5.1 Meaning
One charge is that the redundancy theory leaves the truth predicate itself devoid of meaning. As we have seen, however, I offer an explicit semantic value for ‘is true’ so that it functions along the lines of any other predicate in the language. But this charge has been developed by Horwich, who says:
[One] respect in which minimalism improves on the original redundancy theory is not claiming that ‘p’ and ‘The statement (belief,...) that p is true’ have exactly the same meaning. This claim is implausibly strong; for those meanings would appear to be, in some sense, ‘components’ of the meaning of ‘The statement that p is true’ but not of ‘p’. (Horwich 1998, p. 124)
Horwich’s idea seems to be that the meaning of a component of a sentence must be a component of the meaning of the sentence. I believe that this is wrong. On my semantic framework, the semantic value of an expression is generally not a component of the semantic value of a sentence that contains it. Consider, for instance, the predicate ‘loves’ as it occurs in ‘Desdemona loves Cassio’. I suggested that the semantic value of ‘loves’ was a function from pairs of individuals to the proposition that one loves the other: \(\llbracket \)Loves\(\rrbracket \) = \(\lambda o_1, o_2\)\(\langle \)Love, \(\langle o_1, o_2\rangle \rangle \). The semantic value of the sentence ‘Desdemona loves Cassio’ is the value of applying this function to arguments Desdemona and Cassio. In general, a function is not a constituent of its value and this case provides no exception. So, I see no reason to endorse Horwich’s claim.
Künne (2003, §§2.1.3–4) offers a related criticism based on a rather stringent requirement on identity of the propositions expressed by sentences. In particular, Künne argues that if understanding two sentences S and \(S^*\) requires mastery of different concepts, then S and \(S^*\) express different propositions.
-
B-NEC: Two sentences express the same proposition only if there is no concept whose mastery has to be exercised only in understanding utterances of one of them. (Künne 2003, p. 47)
I will grant that one can understand the sentence ‘Desdemona loves Cassio’ without exercising the concept expressed by ‘is true’ but not ‘it is true that Desdemona loves Cassio’. It would follow from B-NEC that these sentences express different propositions. I reject this conclusion, which means I must reject B-NEC as well.
But why should we think that B-NEC is plausible? Künne motivates B-NEC by appealing to propositional attitude reports. In particular, he exhibits pairs of sentences that stand in some strong equivalence relation such as necessary, a priori, or cognitive equivalence, but do not substitute salva veritate in propositional attitude constructions. Künne wants to explain these substitution failures by appeal to B-NEC.
[B-NEC is necessary] if we want to make sense of our practice of ascribing attitudes and reporting speech by means of that-clauses: ‘Our youngest daughter believes (said) that she has ten fingers, but she does not believe (did not say) that the number of her fingers equals ten multiplied by one’ may be a correct report, but if the embedded sentences were to express the same proposition, such a report would be inconsistent. (Künne 2003, p. 48)
Note first that nothing as strong as B-NEC is required to account for the substitution failure Künne considers. That is, Künne’s example may show that B-NEC has an advantage over views saying that necessarily, a priori, or cognitively equivalent sentences express the same proposition. But on its own, it fails to show that B-NEC is required to explain these substitution failures.
Moreover, I deny that B-NEC delivers a good explanation, because I believe it overgeneralizes. In particular, we often report what agents think or say by accessing the same content, but we access this content by means of different concepts. To take just one example, consider complex demonstratives of the form ‘that \(\phi \)’. According to a prominent view, a use of a complex demonstrative in a context refers to the object demonstrated in the context provided that the object satisfies \(\phi \) (Braun 2012, §5.2). On such a view, an utterance of sentence containing a complex demonstrative such as (14) in a context that demonstrates a dog named ‘Fido’ may express the same proposition as (15), even though the former, but not the latter, requires mastery of the concept associated with ‘dog’.
-
(14)
That dog is a cat.
-
(15)
Fido is a cat.
One can use complex demonstratives to ascribe beliefs to agents. Thus, I might report someone who uttered (15) using (16) while pointing at Fido.
-
(16)
Sam said that that dog is a cat.
The sentence (16) seems perfectly apt to ascribe what Sam said, even though the sentence embedded in the ‘that’-clause of the ascription deploys the concept expressed by ‘dog’, which Sam’s sentence does not.
On my view, truth ascriptions very much follow this pattern: we may use them to characterize the beliefs and assertions even of those who would dissent from truth talk. In particular, I believe that a sentence expressing a proposition and a sentence ascribing truth to the proposition are substitutable in even the strictest of hyperintensional contexts. That is, it is easy to substitute a sentence ascribing truth to a proposition for a simple sentence in (18) or—given suitable common ground regarding what Iago said—(19).
-
(17)
Othello believes that Desdemona loves Cassio.
-
(18)
Othello believes that it’s true that Desdemona loves Cassio.
-
(19)
Iago says that Desdemona loves Cassio and Othello believes that it’s true.
I do not believe that we differentiate between these belief ascriptions in ordinary practice. Thus, I do not believe that one can believe a proposition without believing that it is true.
I should note, that this does not mean that everyone must believe that there are propositions. We cannot conclude that an agent thinks that there are propositions from the fact that the agent thinks of a proposition that it is true. Even in the radical case of ascribing beliefs to an agent who denies the existence of propositions, it is natural to substitute a sentence and a corresponding truth ascription. Consider for instance, the following dialogue.Footnote 41
-
A:
Quine thinks that there are no propositions.
-
B:
That’s a striking position. Does anyone else think that’s true?
-
A:
Yes. Davidson does/thinks that’s true as well.
This dialogue is perfectly acceptable and unproblematic as a piece of ordinary language. It characterizes a commitment of Quine’s and of Davidson’s, that there are no propositions, using a piece of language that they would not themselves use.Footnote 42 This is no more problematic than ascribing using (16) to describe what someone who uttered (15) said.Footnote 43
5.2 Truth and singular terms
Following Ramsey, the account given so far addresses two kinds of sentences ascribing truth. In one kind of case, the proposition to which truth is ascribed is the semantic value of an embedded ‘that’-clause. In these cases, the truth ascription expresses the same proposition (in context) as the proposition expressed by the sentence in its embedded that clause. Thus (2) expresses the same proposition as (1)
-
(1)
Desdemona loves Cassio.
-
(2)
That Desdemona loves Cassio is true.
In the other class of cases considered so far, it is asserted that there is a proposition with a certain characteristic which is true or that every proposition with a certain characteristic is true. Thus, the approach provides a natural account of the propositions expressed by (20) and (21).
-
(20)
Something is true.
-
(21)
Everything Mary said is true.
For simplicity, I focus on (20). Let SOME be the universal possessed by propositional functions that hold sometimes. Then, a sentence such as (20) expresses a proposition which attributes SOME to the propositional function denoted by ‘is true’. The semantics for the first-order regimentation of this sentence (‘\(\exists \widehat{x}\)x is true’) can be given as follows.
-
\(\llbracket \exists \widehat{x}\)xis true\(\rrbracket \) = \(\llbracket \exists \rrbracket \)(\(\llbracket \widehat{x}\)xis true\(\rrbracket \)) = \(\langle SOME\), \(\langle \lambda p.p \rangle \rangle \)
As I mentioned above, the ability to assign meanings to quantified sentences allows for an immediate response to challenges about the redundancy theory charging that it requires more sophisticated tools such as quantification into sentential position in order to understand these sentences.Footnote 44
Soames (1999, pp. 48–49) offers a related set of challenges concerning singular terms. The charge is that one can assert a sentence of the form \(\ulcorner \alpha \) is true\(\urcorner \) where \(\alpha \) is a directly referential term for a proposition without thereby asserting the proposition to which \(\alpha \) refers. Let me divide the potentially problematic cases into two. First, \(\alpha \) might be a pronoun that refers to a proposition that is somehow supported by the discourse context, whether by propositional anaphora or propositional deixis. Second, there are cases where \(\alpha \) purportedly refers to a proposition that is absent from discourse context, as when \(\alpha \) is purportedly a proper name.
I tend to assume that when \(\alpha \) is a pronoun that refers to a proposition somehow present in or supported by the discourse context, then \(\alpha \) does so by propositional anaphora. Consider the pronoun ‘he’ in the sequence, ‘John walks. He talks’. This pronoun is anaphoric on its antecedent, ‘John’. It is semantically mandated that these expressions co-refer. I believe that this model naturally applies to occurrences of pronouns referring to propositions, such as ‘that’ in (22b)
-
(22)
-
a.
Desdemona loves Cassio.
-
b.
That’s true.
-
a.
Proponents of the prosentential tradition have also suggested that a proposition is explicitly given in a truth construction when it is specified using an anaphoric pronoun picking up its reference from a prior sentence in the context such as (22b).Footnote 45 Thus, I don’t think it’s a problem to regard (22b) as expressing the same proposition as (22a). Although Soames construes these pronouns as deictic, he seemingly agrees that the treatment by the redundancy theory is adequate.Footnote 46
Soames (1999, pp. 48–49) himself moves to cases of the second type, where a purported singular term refers to a proposition not salient in the context. For instance, ‘Goldbach’s Conjecture’ refers to a mathematical thesis that might be expressed by (23a).
-
(23)
-
a.
Every even natural number greater than 2 is the sum of two primes.
-
b.
Goldbach’s Conjecture is true.
-
a.
It is quite plausible that a truth ascription containing ‘Goldbach’s Conjecture’ such as (23b) expresses a different proposition than (23a). One could, for example, believe that Goldbach’s Conjecture is true without believing that every even natural number greater than 2 is the sum of two primes. Thus, this case poses a potential problem for my view.
However, I agree with those in the prosentential tradition who suggest that we understand the expression ‘Goldbach’s Conjecture’ in (23b) as a description (Grover et al. 1975, p. 95). If it is a description, then the case can be assimilated to that of quantification. The core issue, then, becomes whether expressions such as ‘Goldbach’s Conjecture’ are non-descriptive proper names. Soames would suggest that they are names and that descriptive theories of names have been refuted by Saul Kripke.
If names were equivalent to definite descriptions, this might not be so since they might then be assimilated to the quantificational case. However, the convincing refutation of descriptive theories of names by Saul Kripke and others makes this strategy unpromising. (Soames 1999, p. 49)
The matter is not this simple. Unlike core cases of proper names, the expressions at issue such as ‘Goldbach’s Conjecture’ are morphologically complex, which makes Kripke’s arguments already considerably less forceful. Moreover any of these views deploy constructions whose semantic composition rule is highly underspecified. For instance, ‘Goldbach’s Conjecture’ is a possessive construction which leaves highly underspecified what, if any, connection there is between Goldbach and the conjecture.
Relatedly, there is reason to think that the relevant expressions such as ‘Goldbach’s Conjecture’ do not designate specific propositions. Consider an utterance of (24a). If ‘Goldbach’s Conjecture’ were a singular term, then it should refer to exactly one proposition such as the proposition expressed by (23a).
-
(24)
-
a.
Sam believes Goldbach’s Conjecture.
-
b.
Sam believes that every even natural number greater than 2 is the sum of two primes.
-
c.
Sam believes that every natural number greater than 2 into which 2 divides evenly is the sum of two primes.
-
a.
If this were right, then one must believe the specific proposition referred to by ‘Goldbach’s Conjecture’ in order for (24a) to be true. But, Salmon (2005b) has argued convincingly that there is no single proposition designated by an expression such as ‘Goldbach’s Conjecture’. In particular, it seems that (24a) may be true of a mathematician if she endorses the that-clause of either (24b) or (24c). On the fine-grained account of content I am interested, these classes express different propositions. But regardless of which she endorses, it seems reasonable to say that she believes Goldbach’s Conjecture. I suggest that the best treatment of this is to suppose that ‘Goldbach’s Conjecture’—and almost any other proposition name—is an indefinite description whose semantic value is highly underspecified.
Nothing I have said here is specific to the fact that ‘Goldbach’s Conjecture’ is a possessive construction. Rather, it is a striking fact about propositions that we normally refer to them using morphologically complex expressions. Many of the constructions seem to be some sort of explicit definite description such as ‘The First Law of Thermodynamics’ (Künne 2003, p. 72), ‘The Riemann Hypothesis’, and so on. Other expressions are morphologically complex in a different way, including Soames’s (1999, p. 49) example of a thesis he labels ‘Extensionalism’. The morpheme ‘ism’ attaches to a root node ‘extensional’ to form the name of a thesis or condition. The relation between the thesis and the root is highly underspecified as can be seen by contrasting: ‘Logicism’, ‘Pythagoreanism’, ‘Utilitarianism’, and ‘Extensionalism’. Given that these names are morphologically complex, I have no qualms about positing that they are highly underspecified descriptions of propositions rather than directly referential names. Propositions are rarely given syntactically simple names, except in highly idiosyncratic circumstances, as in the course of a mathematics proof. These simple names rarely seem to stick beyond a local practice, which suggest they function analogously to anaphoric pronouns discussed above.
Still, the proponent of the compositional redundancy theory need not go this far. I am proposing that the proposition expressed by an inexplicit truth attribution such as (i) \(\ulcorner \)something is true\(\urcorner \) or (ii) \(\ulcorner \alpha \) is true\(\urcorner \) may differ from the proposition expressed by a corresponding explicit truth attribution such as \(\ulcorner \)that \(\phi \) is true\(\urcorner \) due to the fact that the quantifier ‘something’ or the singular term \(\alpha \) may specify the proposition expressed by \(\phi \) in an inexplicit manner. I have done so by suggesting that many singular terms purporting to refer to propositions are descriptions.
But to resist Soames’s arguments, it suffices that purported names of propositions are not Millian. They must have semantic contents other than the proposition named. The crucial point is that the proposition to which truth is attributed is only indirectly specified, it does not exhaust the semantic content of the name. Any difference in semantic values of \(\ulcorner \alpha \) is true\(\urcorner \) and \(\ulcorner \)that \(\phi \) is true\(\urcorner \) must be grounded in a difference in the semantic values of \(\alpha \) and \(\ulcorner \)that \(\phi \urcorner \).Footnote 47
6 Conclusion
We began with an explanatory demand: why does the truth-value of a proposition co-vary with what’s happening in the world at large? I have argued that this puzzle is to be solved by our theory of truth and not our theory of content. A redundancy theory purports to explain the covariation by narrowing the gap between the truth of a proposition and the reality that makes it true. The truth of the proposition that Desdemona loves Cassio amounts to nothing more than that Desdemona loves Cassio. Unlike many other broadly deflationist theories of truth, the form of the redundancy theory which I advocate The Compositional Redundancy Theory, predicts this identity of content in the context of a function-argument conception of compositionality and therefore integrates rather smoothly with contemporary formal semantics. There are many avenues left for exploration, however. One important further test will be to see how well The Compositional Redundancy Theory integrates with existing solutions to the semantic paradoxes such as the Liar. Another will be to investigate its relation to other theories of truth. But, insofar as the theory brings a true proposition and the reality that makes it true closer together, it already has one significant advantage: it solves the renewed problem of the unity of the proposition.Footnote 48
Notes
By this, I just mean to ask why the proposition is true or is false depending on whether she loves him. (I do not mean to construe truth-values as objects.) King (2009, p. 258) articulates this worry as follows: “How does [...] the proposition that [Desdemona loves Cassio] manage to have truth conditions and so represent [Desdemona] as [loving Cassio]?”.
A thorough recent presentation of this argument can be found in Soames (2014b).
Hawley (2010) contains an important related discussion concerning complex properties.
MacBride (2013b, p. 212) frames some of the worries about unity in Frege and Russell in essentially similar terms: “Propositions are entities possessed of that distinctive unity that enables them to bear truth-values.”
This is something like the “deflated” sense in which propositions are representational of Richard (2014, p. 716).
Lewis (1986/2001, p. 174).
Dyke (2012) also offers an argument against the idea that propositions are representational. Her conclusions also resonate with those of this paper insofar as we agree that the proposition that it is true that Desdemona loves Cassio is just the proposition that she loves him, though my argument does not lend support to the idea that propositions should be extruded from the world.
Nothing I say here is meant to criticize the identity theory of truth according to which, roughly, a true proposition is identical to a fact. The positive view I develop bears interesting relations to the identity theory that will need to be explored in further work. The view does not require that proposition represent the relevant facts; propositions are the facts. See defenses of the identity theory of truth in McDowell (1994), Hornsby (1997, 1999), and Dodd and Hornsby (1992). Criticism can be found in Baldwin (1991), Candlish (1999a, b), and Johnston (2013).
Hanks (2011) often glosses his view as though he construes propositions as representing states of affairs. For instance, in describing the renewed unity puzzle he says that traditional views face an obligation: “An account has to be given of how these contents represent states of affairs that does not make any appeal to the intentional actions of speakers” (143). Similarly, he describes his own view—that a proposition is a mental act type—as one on which a proposition represents a state of affairs: “Because any instance of a speaker applying the property of tallness to Smith represents a certain state of affairs, the type [=proposition] that unites these instances also represents that state of affairs” (159ff). While I doubt that Hanks would endorse this as the final statement of his view, it is important to see why it is an undesirable stopping place.
We might conjoin this approach with a reductive account of truth: truth just is representing a fact. This view, like my own, attempts to explain why truth co-varies with the world in terms of the theory of truth and not in terms of the theory of representation. There remain, however, worries about explaining why the existence of the represented entity co-varies with the state of the world. For instance, Russell (1913/1992, 144ff) builds toward this sort of picture in his definition of truth for a “non-permutative belief”.
The last two examples are or are based on examples from Bowers (1993).
See, for instance, Radford (1997, p. 105). Bowers (1993, p. 602) presses this argument most clearly when he says: “A powerful empirical argument in support of the theory of clause structure proposed in this article is the fact that phrases each consisting of an object and its complement can, quite generally, be conjoined [‘John regards professors as strange and politicians as creepy’].” Landman (1989, p. 732) offers a similar argument. Szabó (2003) is a forceful critic of the view that ‘as’-phrases are constituents in sentences such as ‘John as a judge makes a lot of money’. He regards the phrase ‘as a judge’ as an adjunct. But, when considering examples of the form (7), Szabó (2003, p. 395) seems to concede that ‘as’ indicates predication. It is unclear to me what his ultimate view is on sentences of this kind.
It might be that the proponents of representation-as mean the clauses of the form \(\ulcorner a\) as \(F\urcorner \) to denote higher-order entities. This would involve them in complications which I avoid in my preferred theory, as I discuss in my discussion of the prosentential theory in §4.1.
Speaks (2014b, pp. 145–146) makes similar claims.
Speaks (2014a, p. 76) responds to those who want to explain the instantiation of the property of being such that Desdemona loves Cassio in terms of the truth of the proposition that Desdemona loves Cassio by suggesting that the order of explanation proceeds the other way. But he offers no explanation, as far as I can tell, for why the property is instantiated just in case Desdemona loves Cassio. I believe that I can offer an explanation for why the truth-value of the proposition that Desdemona loves Cassio co-varies with whether she loves him. I can then offer an explanation of why the property of being such that Desdemona loves Cassio co-varies with whether she loves him as deriving from its connection to the proposition that Desdemona loves Cassio. For this reason, I prefer not to reverse the order of explanation, as Speaks recommends.
Lewis (1986/2001, pp. 177–179, 182).
On Ramsey’s own view, the objects of thought are the diverse entities that the thought is about. So Ramsey’s own view is an implementation of Russell’s multiple relation theory of judgment. But this aspect of his view is motivated by the original problem of the unity of the proposition and related problems about facts and is therefore separable from his account of truth.
The view can be embedded in an intensionalist framework, for instance, if the semantic values of predicates are the compositional intensions of Lewis (1970).
See Soames (1999, pp. 39–49, 232–238).
The strategy resembles an argument of MacFarlane (2014, §4.8) purporting to show that semantic relativism can support the truth schema. A crucial difference is that the underlying semantics of this paper proceeds by assigning only meanings to sentences in contexts, whereas MacFarlane’s semantics appeals to underlying notions of truth at a parameter which demand further explanation.
I take the term from Cresswell (2002). As King and Stanley (2005, p. 134) observe, standard advocates of structured propositions—Soames (1987), Salmon (1986, Appendix C) and King (2007, Appendix)—posit “no significant composition of semantic contents” in the mapping from a sentence to the structured proposition it expresses in context. In particular, King and Stanley observe that in typical cases, the proponents of structured propositions take the semantic value of a complex to be the result of pairing the semantic values of its components. In Pickel (forthcoming), I argue that this result is undesirable, since it threatens to undermine almost the whole of contemporary formal semantics. The semantics, as sketched below, also reveals that the proponent of structured propositions can accept functional composition.
See Pickel (forthcoming, §7) for a discussion of variable binding and the semantics for complex predicates in a propositionalist semantics.
Soames (2010, pp. 122–129) suggests that treating ALL as a universal leads to difficulties in deriving the truth conditions for the propositions expressed by the sentences of a language. For instance, Soames (2010, p. 125) argues that an account as to the nature of propositions must deliver the following equivalence.
-
A proposition that predicates being always true (ALL) of a propositional function g is true iff g assigns a true proposition to every object.
According to the worry, if ALL is a simple universal, then the equivalence is an ad hoc meaning postulate. I believe that the redundancy theory developed below will go some way towards substantiating these equivalences. For instance, the semantics will deliver the following identities.
-
\(\langle ALL\), \(\langle g \rangle \rangle \) = \(\langle ALL\), \(\langle \lambda o. g(o) \rangle \rangle \) = \(\langle ALL\), \(\langle \lambda o. \lambda p.p(g(o)) \rangle \rangle \) = \(\langle ALL\), \(\langle \lambda o. \llbracket \)is true\(\rrbracket ( g(o)) \rangle \rangle \)
Allowing substitution of identical propositions, the identities entail that, concerning a propositional function g, the proposition \(\langle ALL\), \(\langle g \rangle \rangle \) is true if and only if for every o, g applied to o is true.
-
That is, there is no need for such quantification issuing from the theory of truth. I have said nothing foreclosing the need for such quantification to resolve other problems.
Note that Ramsey himself explicitly denied that the truth predicate was similarly eliminable in natural language from cases in which the proposition to which truth is ascribed is not explicitly given). Thus, Ramsey endorsed only what Künne (2003) calls the redundancy thesis and not what he calls the redundancy theory, that truth is everywhere redundant. Given that Ramsey is a prototypical proponent of the redundancy theory, I will call the weaker thesis the redundancy theory.
Thanks to an anonymous referee from Synthese for making me consider this example.
Compare the equally acceptable dialogue:
-
A:
Bealer thinks that there are propositions.
-
B:
Quine thinks that that’s not the case. He thinks that it’s not true that there are propositions.
-
A:
Asay (2013, §§5.2.2–3) offers a nice example defending this “omnipresence” thesis, remarking: “Think to yourself, ‘I wonder whether there are any kangaroos in Africa, though I do not wonder whether it is true that there are any kangaroos in Africa.’ I for one cannot do it” (155).
Soames (1999, pp. 39–43, 232–234).
Soames (1999, pp. 48–49) writes: “There are other, related problems with the redundancy theory. One familiar kind of case in which true is used is one in which we refer demonstratively in a propositioned say, ‘That’s true.’ Typically, in such cases, the proposition said to be true is expressed by an assertive utterance or inscription in the context, so it is transparent what proposition we have referred to. In these cases, the redundancy theory may seem tempting. However, not all cases of referring to a proposition are like this.” The cases Soames considers are those of the second type, to which I now turn.
In a recent paper, Rattan (2015) articulates—but does not defend—a limited redundancy theory that accounts for the cognitive value of “inexplicit” truth attributions as “grounded in the cognitive value of generalization” (22) and other mechanisms of indirect specification. Rattan suggests that there is nonetheless a tension in limited versions of the redundancy theory such as the compositional redundancy theory advocated here. I believe that this challenge can be resisted, but leave this project to future work.
This paper was improved as a result of feedback from Derek Ball, Ray Buchanan, Matthew Chrisman, Manuel García-Carpintero, Ephraim Glick, Bjørn Jespersen, Colin Johnston, John Keller, Lorraine Juliano Keller, Jeff King, Peter Pagin, Brian Rabern, Anders Schoubye, Wolfgang Schwarz, James Shaw, Alex Skiles, Scott Soames, Patrick Todd, Giuliano Torrengo, and anonymous referees for Synthese. It also benefited from feedback from audiences at the Edinburgh Philosophy of Language Reading Group, at the University of Milan, at the University of Stirling, and at the LOGOS Basic Workshop on the Unity and Individuation of Structured Propositions. Research related to this project was partially funded by a project FFI2016-80636-P, supported by the Spanish Ministry of Economy and Competitiveness.
References
Armour-Garb, B., & Beall, J. C. (2005). Deflationary truth. Chicago, IL: Open Court Press.
Armstrong, D. M. (1997). A world of states of affairs. Cambridge: Cambridge University Press.
Asay, J. (2013). The primitivist theory of truth. Cambridge: Cambridge University Press.
Asher, N. (2006). Things and their aspects. Philosophical. Issues, 16, 1–23.
Baldwin, T. (1991). The identity theory of truth. Mind, 100, 35–52.
Bealer, G. (1982). Quality and concept. Oxford: Clarendon Press.
Beaney, M. (1997). The Frege reader. Malden, MA: Blackwell Publishing.
Bowers, J. (1993). The syntax of predication. Linguistic Inquiry, 24, 591–656.
Bradley, F. H. (1893/2002). Appearance and reality: A metaphysical essay. Adegi Graphics LLC.
Brandom, R. (2005). Expressive versus explanatory deflationism about truth. In B. P. Armour-Garb & J. C. Beall (Eds.), Deflationary truth (pp. 237–257). Chicago: Open Court Publishing.
Braun, D. (2012). Indexicals. The stanford encyclopedia of philosophy (Summer 2012 Edition). http://plato.stanford.edu/archives/sum2012/entries/indexicals/.
Candlish, S. (1999a). A prolegomenon to an identity theory of truth. Philosophy, 74, 199–220.
Candlish, S. (1999b). Identifying the identity theory of truth. Proceedings of the Aristotelian Society, 99, 233–240.
Carnap, R. (1947/1988). Meaning and necessity: A study in semantics and modal logic. Midway reprints, University of Chicago Press, Chicago, IL.
Church, A. (1951). A formulation of the logic of sense and denotation. In P. Henle, H. Kallen, & S. Langer (Eds.), Structure, method, and meaning: Essays in honor of Henry M. Sheffer (pp. 3–24). New York, NY: Liberal Arts Press.
Cresswell, M. J. (1985). Structured meanings: The semantics of propositional attitudes. Cambridge, MA: The MIT Press.
Cresswell, M. J. (2002). Why propositions have no structure. Noûs, 36, 643–662.
Davidson, D. (2005). Truth and predication. Cambridge, MA: Harvard University Press.
Dodd, J., & Hornsby, J. (1992). The identity theory of truth: Reply to Baldwin. Mind, 101, 319–322.
Dummett, M. (1981). Frege: Philosophy of language. Cambridge, MA: Harvard University Press.
Dyke, H. (2012). Propositions: Truth vs. existence. In J. Maclaurin (Ed.), Rationis defensor. The Netherland: Springer.
Elbourne, P. (2011). Meaning: A slim guide to semantics. Oxford: Oxford University Press.
Frege, G. (1918), Thought. In M. Beaney (Ed.), The Frege reader. Blackwell Publishing: Malden, MA (1997)
Geach, P. T. (1976). Critical notice on Frege: Philosophy of language. Mind, 85, 436–449.
Gibson, M. I. (2008). Critical notice for truth and predication. Philosophy and Phenomenological Research, 76, 215–219.
Grover, D. L. (1972). Propositional quantifiers. Journal of Philosophical Logic, 1, 111–136.
Grover, D. L. (1976). ‘This is false’ on the prosentential theory. Analysis, 36, 80–83.
Grover, D. L., Kamp, J. L., & Belnap, N. D. (1975). A prosentential theory of truth. Philosophical Studies, 27, 73–125.
Gupta, A. (2005a). A critique of deflationism. In B. P. Armour-Garb & J. C. Beall (Eds.), Deflationary truth (pp. 199–226). Chicago: Open Court Publishing.
Gupta, A. (2005b). Postscript to “A critique of deflationism”. In B. P. Armour-Garb & J. C. Beall (Eds.), Deflationary truth (pp. 227–236). Chicago: Open Court Publishing.
Hanks, P. (2015). Propositional content. Oxford: Oxford University Press.
Hanks, P. W. (2007). The content-force distinction. Philosophical Studies, 134, 141–164.
Hanks, P. W. (2011). Structured propositions as types. Mind, 120, 11–52.
Hawley, K. (2010). Mereology, modality and magic. Australasian Journal of Philosophy, 88, 117–133.
Henle, P. (1951). Structure, method, and meaning: Essays in honor of Henry M. Sheffer. New York, NY: Liberal Arts Press.
Hornsby, J. (1997). The presidential address: Truth: The identity theory. Proceedings of the Aristotelian Society, 97, 1–24.
Hornsby, J. (1999). The facts in question: A response to Dodd and to Candlish. Proceedings of the Aristotelian Society, 99, 241–245.
Horwich, P. (1998). Truth. Oxford: Clarendon Press.
Jago, M. (2015). Hyperintensional propositions. Synthese, 192, 585–601.
Johnston, C. (2013). Judgment and the identity theory of truth. Philosophical Studies, 166, 381–397.
Keller, L. (2014). The metaphysics of propositional constituency. Canadian Journal of Philosophy.
Keller, L. J., & Keller, J. A. (2013). Compositionality and structured propositions. Thought: A Journal of Philosophy, 2, 313–323.
King, J. C. (1995). Structured propositions and complex predicates. Noûs, 29, 516–535.
King, J. C. (2007). The nature and structure of content. Oxford: Oxford University Press.
King, J. C. (2009). Questions of unity. Proceedings of the Aristotelian Society (Hardback), 109, 257–277.
King, J. C. (2013). Propositional unity: What’s the problem, who has it and who solves it? Philosophical Studies, 165, 71–93.
King, J. C. (2014). Naturalized propositions. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 47–70). Oxford: Oxford University Press.
King, J. C., & Stanley, J. (2005). Semantics, pragmatics, and the role of semantic content. In Z. G. Szabó (Ed.), Semantics versus pragmatics (pp. 111–164). Oxford: Oxford University Press.
King, J. C., Soames, S., & Speaks, J. (2014). New thinking about propositions. Oxford: Oxford University Press.
Klement, K. C. (2004). Putting form before function: Logical grammar in Frege, Russell, and Wittgenstein. Philosophers’ Imprint, 4, 1–47.
Künne, W. (2003). Conceptions of truth. Oxford: Oxford University Press.
Lance, M. (2005). The significance of anaphoric theories of truth and reference. In B. P. Armour-Garb & J. C. Beall (Eds.), Deflationary truth. Chicago: Open Court Publishing.
Landman, F. (1989). Groups II. Linguistics and Philosophy, 12, 723–744.
Lepore, E., & Ludwig, K. (2013). A companion to Donald Davidson. Blackwell companions to philosophy. Hoboken: Wiley.
Lewis, D. (1970). General semantics. Synthese, 22, 18–67.
Lewis, D. (1986). Against structural universals. Australasian Journal of Philosophy, 64, 25–46.
Lewis, D. (1986/2001). On the plurality of worlds. Oxford: Wiley.
Lewis, D. (1999a). Papers in metaphysics and epistemology. Cambridge: Cambridge University Press.
Lewis, D. (1999b). A world of truthmakers. Papers in metaphysics and epistemology (pp. 215–220). Cambridge: Cambridge University Press.
Lewis, D. (2001). Truthmaking and difference-making. Noûs, 35, 602–615.
MacBride, F. (2013a). For keeping truth in truthmaking. Analysis, 73, 686–695.
MacBride, F. (2013b). The Russell-Wittgenstein dispute: A new perspective. In M. Textor (Ed.), Judgment and truth in early analytic philosophy and phenomenology (pp. 206–241). London: Palgrave MacMillian.
MacBride, F. (2013c). Truthmakers. Stanford encyclopedia of philosophy. http://plato.stanford.edu/archives/spr2014/entries/truthmakers/.
MacFarlane, J. (2014). Assessment sensitivity: Relative truth and its applications. Oxford: Oxford University Press.
Marsh, R. (Ed.). (1989). Logic and knowledge. New York, NY: Routledge.
McDowell, J. (1994). Mind and world. Cambridge, MA: Harvard University Press.
Merricks, T. (2015). Propositions. Oxford: Oxford University Press.
Moore, G. E. (1927). Facts and propositions. Proceedings of the Aristotelian Society (Supplementary), 7, 171–206.
Pagin, P., & Pelletier, F. J. (2007). Content, context and composition. In G. Preyer & G. Peter (Eds.), Context-sensitivity and semantic minimalism: New essays on semantics and pragmatics (pp. 25–62). Oxford: Oxford University Press.
Pickel, B. (forthcoming). Structured Propositions in a Generative Grammar. Mind.
Preyer, G., & Peter, G. (2007). Context-sensitivity and semantic minimalism: New essays on semantics and pragmatics. Oxford: Oxford University Press.
Radford, A. (1997). Syntactic theory and the structure of english: A minimalist approach. Cambridge: Cambridge University Press.
Ramsey, F. P. (1927). Facts and propositions. Proceedings of the Aristotelian Society (Supplementary), 7, 153–170.
Rattan, G. (2015). Truth incorporated. Noûs, 49.
Richard, M. (2014). What are propositions? Canadian Journal of Philosophy, 43, 702–719.
Ripley, D. (2012). Structures and circumstances: Two ways to fine-grain propositions. Synthese, 189, 97–118.
Russell, B. (1905). On denoting. Mind, 14, 479–493.
Russell, B. (1913/1992). Theory of knowledge: The 1913 manuscript. London: Routledge.
Russell, B. (1918). The philosophy of logical atomism. In R. Marsh (Ed.), Logic and knowledge (pp. 175–282). New York, NY: Routledge.
Salmon, N. (1986). Frege’s puzzle. Atascadero, CA: Ridgeview.
Salmon, N. (2005a). Metaphysics, mathematics, and meaning. Oxford: Oxford University Press.
Salmon, N. (Ed.). (2005b). On content. In Metaphysics, mathematics, and meaning (pp. 269–285). Oxford: Oxford University Press.
Schantz, R. (Ed.). (2007). Current issues in theoretical philosophy: Prospects for meaning. Berlin: Walter de Gruyter.
Soames, S. (1987). Direct reference, propositional attitudes, and semantic content. Philosophical Topics, 15, 47–87.
Soames, S. (1999). Understanding truth. Oxford: Oxford University Press.
Soames, S. (2010). What is meaning?. Princeton: Princeton University Press.
Soames, S. (2014a). Cognitive propositions. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 91–124). Oxford: Oxford University Press.
Soames, S. (2014b). Why the traditional conception of propositions can’t be correct. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 25–44). Oxford: Oxford University Press.
Speaks, J. (2013). Predication. In E. Lepore & K. Ludwig (Eds.), A companion to Donald Davidson. Blackwell companions to philosophy. Hoboken, NJ: Wiley.
Speaks, J. (2014a). Properties of everything or nothing. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 71–91). Oxford: Oxford University Press.
Speaks, J. (2014b). Representational entities and representational Acts. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 147–165). Oxford: Oxford University Press.
Speaks, J. (2014c). Representation and structure in the theory of propositions. In J. C. King, S. Soames, & J. Speaks (Eds.), New thinking about propositions (pp. 215–225). Oxford: Oxford University Press.
Stalnaker, R. (1984). Inquiry. Cambridge: Cambridge University Press.
Strawson, P. F. (1950). Symposium: Truth. Aristotelian Society Supplementary, 24, 129–156.
Szabó, Z. G. (2003). On qualification. Philosophical Perspectives, 17, 385–414.
Szabó, Z. G. (2005). Semantics versus pragmatics. Oxford: Oxford University Press.
Textor, M. (Ed.). (2013). Judgment and truth in early analytic philosophy and phenomenology. London: Palgrave MacMillian.
Van Inwagen, P. (2001). Generalizations of homophonic truth-sentences. In R. Schantz (Ed.), What is truth? Schantz, Richard: Current issues in theoretical philosophy (pp. 205–222). Boston, MA: De Gruyter.
Whitehead, A. N., & Russell, B. (1910/1957). Principia Mathematica. Cambridge: Cambridge University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pickel, B. Unity through truth. Synthese 196, 1425–1452 (2019). https://doi.org/10.1007/s11229-016-1279-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1279-6