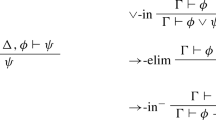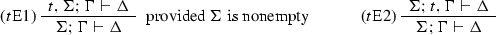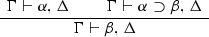Abstract
This paper aims to call into question the customary division of logically revisionary responses to the truth-theoretic paradoxes into those that are “substructural” and those that are “(fully) structural.” I proceed by examining, as a case study, Beall’s recent proposal based on the paraconsistent logic LP. Beall formulates his response to paradox in terms of a consequence relation that obeys all standard structural rules, though at the price of the language’s lacking a detaching conditional. I argue that the same response to paradox can be given using a consequence relation that preserves detachment rules for a conditional, though at the price of restricting structural rules. The question “Is paradox being blocked by invoking a substructural consequence relation?” is thus ill-posed. The lesson of this example, I conclude, is that there is no useful explication of the idea of a substructural approach to paradox.
Similar content being viewed by others
Notes
Avron and Lahav (2011) speak of “fully-structural” proof systems.
In earlier work, I proposed that “contraction-free and detachment-free responses” (which restrict, respectively, structural contraction and modus ponens for the conditional) “need not be in conflict, once they are taken to involve different understandings of the structural comma” used to specify a consequence relation (Shapiro 2013, p. 106n5). Recently, and independently, Field has likewise raised “the possibility that the issue might be largely verbal.” That’s because a contraction-free response typically has a “structuralist analogue,” involving a different understanding of the comma, that retains all structural principles but “restricts Modus Ponens” (Field 2016). I imagine advocates of such responses would reply that the need to restrict modus ponens to recover structural principles reveals that the responses are in fact substructural. The present paper will put pressure on this rejoinder, by showing that it would classify as substructural a response orthodoxy regards as a paradigm non-substructural one.
Though it will play no role in what follows, \(\alpha \vdash \) can be understood as saying that \(\alpha \) is a logical absurdity.
I trust there will be no confusion when I speak of the “premises” of an inference rule and the “premises” collected in the antecedent of a sequent (cf. Zardini 2011, p. 509n25).
For a formal characterization, see Barrio et al. (2015, pp. 556–7). By accepting a rule with no premises, one endorses all instances of a schematic consequence claim.
The more standard term ‘operational’ derives from the English translation in Gentzen (1969), where it means operator-involving. But the truth predicate isn’t an operator.
Such collections may be, e.g., singleton sets, singleton multisets, or sequences of length one, and \(\cup \) may represent, e.g., set union, multiset union, sequence concatenation, or ordered pair formation. Of course, if \(\cup \) is set union, ExchL\(^*\) and ContrL\(^*\) are trivially admissible.
Beall himself cites tableau systems for single-conclusion LP as his model (cf. Priest 2008). I have made minor changes to his presentation.
Again, this is apparent from LPT\('\)s semantics; I omit a derivation in S \(_{LPT}\) in the interest of space.
As described so far, the response to truth-theoretic paradox based on LP doesn’t differ from that based on the logic ST (Cobreros et al. 2013; Ripley 2012). Unlike LP, however, ST yields \(T\langle \lambda \rangle \wedge \lnot T\langle \lambda \rangle \vdash \pi \), and the inference from \(\vdash T\langle \lambda \rangle \supset \pi \) to \(T\langle \lambda \rangle \vdash \pi \). Hence the simple transitivity rule Tran is inadmissible in the ST-based truth theory on pain of paradox.
Beall’s formulation of logic’s “constraint role” in terms of multiple-conclusion consequence builds on Restall (2005).
Of course, LP’s material conditional doesn’t display all classical patterns. For example, neither \(\alpha \wedge (\alpha \supset \beta ) \vdash \beta \) nor \((\alpha \supset \beta ) \wedge (\beta \supset \gamma ) \vdash \alpha \supset \gamma \) holds for LP, so it’s no surprise that a proponent of LP can’t preserve the ordinary ways of reasoning reflected in classical derivations of them. The question, then, is whether we can identify behavior that yields derivations of (say) Importation, Permutation and Prefixing, but doesn’t yield derivations of the above two sequents. Also, I don’t mean to suggest that all conditionals must obey those three classical principles. In the case of each principle, there are well-known substructural logics for which it fails to hold (see e.g. Restall 2000).
The proof system S \(_{LPT}'\) is a close relative of three-sided sequent systems for three-valued logics (see e.g. Paoli 2002, ch. 4). Thus a non-ordinary sequent \(\Sigma ; \Gamma \vdash \Delta \) is derivable iff for all valuations (defined as above), either some sentence in \(\Sigma \) receives 0, or some sentence in \(\Gamma \) receives either 0 or \(\frac{1}{2}\), or some sentence in \(\Delta \) receives either \(\frac{1}{2}\) or 1. However, S \(_{LPT}'\) can also been viewed as using a much simplified version of of the “dual-bunching” structure pioneered for fragments of relevant logics by Dunn and Mints (e.g. Paoli 2002, ibid.). As in such systems, we have two forms of combination of sets of premises, one of which (here set union, and associated with conjunction/disjunction) builds in exchange and contraction while the other (here pair formation, and associated with negation) does not. Given the connection in this case between the two kinds of proof systems, it is interesting that 3-sided systems, unlike Dunn-Mints systems, have not been regarded as “substructural.” (I’m grateful to Dave Ripley for pointing out that my purposes require at most pairs of sets as antecedents, rather than finite sequences of sets.)
As Elia Zardini pointed out, we would circumvent the restriction if we introduced a constant t governed by the rule tE1 below without its requirement that \(\Sigma \) be nonempty. However, the following rules are admissible.
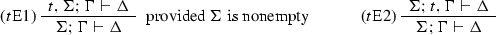
Note also that the restriction to nonempty \(\Sigma \) is necessary in order for Cut\('\) to be admissible, since without this restriction the inadmissible ContrL\(^*\) would be immediately derivable using Id and Weak\('\).
For present purposes, it doesn’t matter whether these sequents express genuine modus ponens. See also my reply to Objection 4 below.
As might be expected, all these claims enjoy parallels for a naive truth theory based on the “paracomplete” consequence relation K3, which is specified model-theoretically by letting 1 be the sole designated value. Here it’s conditional proof, rather than detachment, that’s unsound. For a substructural proof system S \(_{K3T}'\) that recovers conditional proof, simply remove the restriction on the rule \(\lnot \)E\('\) that \(\Sigma \) be nonempty, and instead impose that same restriction on \(\lnot \)I\('\) as well as the left-hand version of Weak\('\). ContrL\(^*\) and Cut\(^*\) now become admissible, while ExchL\(^*\) remains inadmissible.
There may be some looseness in what counts as exemplifying a structure. For instance, a simple sequent \(\alpha \vdash \beta \) should be counted as exemplifying both a set-antecedent and a multiset-antecedent structure. That’s because the representation of the antecedent as a singleton set/multiset, rather than as a sentence, is a mere artifact of convenience.
See e.g. Field (2008, ch. 4).
The proper specification of the “familiar” rules for conjunction and disjunction (context-sharing or context-free) will, however, depend on whether these connectives are to be identified with the additive or multiplicative connectives of the noncontractive system. See also Zardini (2011).
Both systems, however, agree with LPT in rejecting the following rule, which the noncontractive theorist sees as illicitly building in contraction and the nontransitive theorist sees as illicitly building in transitivity:
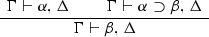
Thus I won’t address the controversy over whether (i) and (ii) are requirements on genuine modus ponens, as Zardini (2013) argues they are. Some theorists who claim to affirm modus ponens have rejected these desiderata. In the presence of a deduction theorem and assuming that \(\wedge \) is tied to the structural comma, the sequents in (i) each yield \(\vdash (\alpha \wedge (\alpha \rightarrow \beta )) \rightarrow \beta \), which Restall (1994, pp. viii–ix, 42) dismisses as the “pseudo modus ponens” axiom. And desideratum (ii) is rejected by Ripley (2012, 2015).
It is rejected in my own previous work (Shapiro 2015).
Here Ripley (2015) is an instructive example. His evaluation of the relative merits of substructural and fully structural theories of truth as responses to paradox doesn’t appeal to any interpretation of sequent structure. Indeed, doing so would complicate his comparison between nontransitive and noncontractive theories. That’s because one natural interpretation of the sequent structure of nontransitive logics, the one advocated in Ripley (2013), is not suitable as an interpretation of the structure of noncontractive logics. This is the interpretation based on Restall (2005) discussed below.
That might appear an unmotivated interpretation of antecedent structure. For a motivation, see Shapiro (2015). On the view defended there, antecedent structure serves to enable useful generalization over patterns of simple sequents involving particular logical vocabulary.
This paper has benefited greatly from discussion with my colleagues Jc Beall and Dave Ripley, as well as from comments by the participants in a graduate seminar (especially Jared Henderson) and audiences at UConn and Logica 2016. Julien Murzi, Lorenzo Rossi and Elia Zardini provided very helpful written comments, as did two referees.
References
Anderson, A., & Belnap, N. (1963). First degree entailments. Mathematische Annalen, 149, 302–319.
Anderson, A., & Belnap, N. (1975). Entailment: The logic of relevance and necessity (Vol. 1). Princeton: Princeton University Press.
Asenjo, F. G. (1966). A calculus of antinomies. Notre Dame Journal of Formal Logic, 16, 103–105.
Avron, A. (1991). Natural 3-valued logics: Characterization and proof theory. Journal of Symbolic Logic, 56, 276–294.
Avron, A., & Lahav, O. (2011). Kripke semantics for basic sequent systems. In K. Brünnler & G. Metcalfe (Eds.), Automated reasoning with analytic tableaux and related methods. New York: Springer.
Barrio, E., Rosenblatt, L., & Tajer, D. (2015). The logics of strict-tolerant logic. Journal of Philosophical Logic, 44, 551–571.
Beall, J. (2009). Spandrels of truth. Oxford: Oxford University Press.
Beall, J. (2011). Multiple-conclusion LP and default classicality. Review of Symbolic Logic, 4, 326–336.
Beall, J. (2015). Free of detachment: Logic, rationality, and gluts. Noûs, 49, 410–423.
Beall, J., & Murzi, J. (2013). Two flavors of Curry’s paradox. Journal of Philosophy, 110, 143–165.
Beall, J., & Ripley, D. (2016). Non-classical theories of truth. In M. Glanzberg (Ed.), The Oxford handbook of truth. Oxford: Oxford University Press (forthcoming).
Caret, C., & Hjortland, O. T. (2015). Logical consequence: Its nature, structure, and application. In C. Caret & O. T. Hjortland (Eds.), Foundations of logical consequence. Oxford: Oxford University Press.
Cobreros, P., Eǵré, P., Ripley, D., & van Rooij, R. (2013). Reaching transparent truth. Mind, 122, 841–866.
Field, H. (2008). Saving truth from paradox. Oxford: Oxford University Press.
Field, H. (2016). Disarming a paradox of validity. Notre Dame Journal of Formal Logic (forthcoming).
Gentzen, G. (1935). Untersuchungen über das logische Schliessen, Mathematische Zeitschrift, 39, 176–210, 405–431. (M. E. Szabo, Trans. in Gentzen 1969, pp. 68–131).
Gentzen, G. (1969). Collected Papers, North Holland. Edited by M. E. Szabo.
Girard, J. Y. (1987). Linear logic. Theoretical Computer Science, 50, 1–102.
Goodship, L. (1996). On dialethism. Australasian Journal of Philosophy, 74, 153–161.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43, 439–469.
Murzi, J., & Carrara, M. (2015). Paradox and logical revision. A short introduction. Topoi, 34, 7–14.
Ono, H. (2003). Substructural logics and residuated lattices—An introduction. In V. Hendricks & J. Malinowski (Eds.), Trends in logic: 50 years of Studia Logica (pp. 177–212). Berlin: Kluwer.
Paoli, F. (2002). Substructural logics: A primer. Berlin: Kluwer Academic Publishers.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Priest, G. (2006). Doubt truth to be a liar. Oxford: Oxford University Press.
Priest, G. (2008). An introduction to non-classical logic: From if to is. Cambridge: Cambridge University Press.
Restall, G. (1994). On logics without contraction, PhD thesis, The University of Queensland.
Restall, G. (2000). An introduction to substructural logics. London: Routledge.
Restall, G. (2005). Multiple conclusions, in Hájek, P., Valdés-Villanueva, L., and Westerståhl, D., (eds). Logic, methodology and the philosophy of science: Proceedings of the Twelfth International Congress (pp. 189–205), King’s College Publications.
Ripley, D. (2012). Conservatively extending classical logic with transparent truth. Review of Symbolic Logic, 5, 354–378.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91, 139–164.
Ripley, D. (2015). Comparing substructural theories of truth. Ergo, 2, 299–328.
Rosenblatt, L. (2015). Two-valued logics for transparent truth theory. Australasian Journal of Logic, 12, 44–66.
Shapiro, L. (2013). Validity curry strengthened. Thought, 2, 100–107.
Shapiro, L. (2015). Naive structure, contraction and paradox. Topoi, 34, 75–87.
Slaney, J. (1990). A general logic. Australasian Journal of Philosophy, 68, 74–88.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4, 498–535.
Zardini, E. (2013). Naive modus ponens. Journal of Philosophical Logic, 42, 575–593.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shapiro, L. The very idea of a substructural approach to paradox. Synthese 199 (Suppl 3), 767–786 (2021). https://doi.org/10.1007/s11229-016-1230-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1230-x