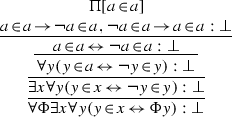Abstract
This is a reply to the considerations advanced by Schroeder-Heister and Tranchini (Ekman’s paradox, Unpublished typescript) as prima facie problematic for the proof-theoretic criterion of paradoxicality, as originally presented in Tennant (Dialectica 36:265–296, 1982) and subsequently amended in Tennant (Analysis 55:199–207, 1995). Countering these considerations lends new importance to the parallelized forms of elimination rules in natural deduction.
Similar content being viewed by others
Notes
Note that the compactifying reduction procedure is not considered by Prawitz. This is why he was able to prove the normalization theorem for intuitionistic logic, despite basing it on the serial forms of elimination for \(\wedge \), \(\rightarrow \) and \(\forall \). Prawitz was considering as eligible reduction procedures only those provided for the logical operators’ introduction-elimination rule-pairs. These reduction procedures are designed to eliminate ‘maximal sentence occurrences’—ones standing as conclusions of introductions, and as major premises of the corresponding eliminations.
Space does not permit any further explanation here of the details of Schroeder-Heister’s and Tranchini’s positive proposal; the interested reader in search of such details is referred to their text. My concern here is to confront the problem they have raised, and to propose a more effective and simpler solution to it.
These are also known as ‘generalized’ elimination rules. They were first introduced in Schroeder-Heister (1984).
The sequent calculus in question is a single-conclusion one (succedents of sequents being at most singletons), whose sequent-antecedents are sets of sentences, not sequences of sentence-occurrences. Thus the Gentzenian structural rules of Contraction and Interchange (or Permutation) are irrelevant, because unnecessary; and modifications of such rules, in the manner of Zardini (2011), for example, are orthogonal to the discussion undertaken here.
A note on notation: we shall use \(\Pi \), \(\Sigma \), \(\Omega \) and \(\Xi \) for proofs, and use \(\Delta \) and \(\Gamma \) for sets of premises.
A similar proof, of \(\lnot ((A\!\rightarrow \!\lnot A)\wedge (\lnot A\!\rightarrow \! A))\), using parallelized elimination rules, but using the definition of \(\lnot \varphi \) as \(\varphi \rightarrow \bot \), was given by von Plato (2000), at p. 123, by way of solution of Ekman’s problem for the serial forms of elimination rules. Note that all applications of (\(\rightarrow \)E) in the proofs that we are giving here are applications of the parallelized form of that rule, even if some of those applications involve degenerate (i.e., single-sentence) major subproofs.
With an eye to the Paradox’s historical (i.e., Fregean) origins, we see also (at second order) that Naïve Abstraction is refutable:
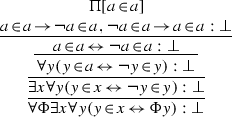
Recall that a free logic is one that is not based on the standard presupposition that all singular terms denote. Put another way: free logic allows for non-denoting singular terms. If in addition the logic is not based on the standard presupposition that the universe is non-empty, then it is called a universally free logic. Such a logic was presented in Tennant (1978), Ch. 7. A completeness proof was also given there for the universally free logic of a first-order language with identity and the familiar primitive variable-binding operator \(\{x|\ldots x\ldots \}\) for forming (singular) set-abstraction terms.
Here I am indebted to Elia Zardini.
See Ramsey (1926), at pp. 352–3.
References
Curry, H. B. (1952). The system LD. Journal of Symbolic Logic, 17, 35–42.
Ekman, J. (1998). Propositions in propositional logic provable only by indirect proofs. Mathematical Logic Quarterly, 44(1), 69–91.
Gentzen, G. (1934, 1935). Untersuchungen über das logische Schliessen. Mathematische Zeitschrift, I, II: (Vol. 176–210, pp. 405–431) (Translated as ‘Investigations into logical deduction’, in The collected papers of Gerhard Gentzen (Vol. 1969, pp. 68–131), edited by M. E. Szabo). Amsterdam: North-Holland.
Prawitz, D. (1965). Natural deduction: a proof-theoretical study. Stockholm: Almqvist & Wiksell.
Ramsey, F. P. (1926). The foundations of mathematics. Proceedings of the London Mathematical Society, 25, 338–384.
Schroeder-Heister, P. (1984). A natural extension of natural deduction. Journal of Symbolic Logic, 49, 1284–1300.
Schroeder-Heister, P., & Tranchini, L. Ekman’s paradox. Unpublished typescript.
Tennant, N. (1978). Natural logic. Edinburgh: Edinburgh University Press.
Tennant, N. (1982). Proof and paradox. Dialectica, 36, 265–296.
Tennant, Neil. (1992). Autologic. Edinburgh: Edinburgh University Press.
Tennant, N. (1995). On paradox without self-reference. Analysis, 55, 199–207.
Tennant, N. (2012). Cut for core logic. Review of Symbolic Logic, 5(3), 450–479.
Tennant, N. (2014). Logic, mathematics, and the a priori, Part II: core logic as analytic, and as the basis for natural logicism. Philosophia Mathematica, 22, 321–344.
Tennant, N. (2015a). A new unified account of truth and paradox. Mind, 123, 571–605.
Tennant, N. (2015b). Cut for classical core logic. Review of Symbolic Logic, 8(2), 236–256.
Tennant, N. (2016). Rule-irredundancy and the sequent calculus for core logic. Notre Dame Journal of Formal Logic, 57(1), 105–125.
von Plato, J. (2000). A problem of normal form in natural deduction. Mathematical Logic Quarterly, 46(1), 121–124.
Yablo, S. (1993). Paradox without self-reference. Analysis, 53, 251–252.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4(4), 498–535.
Acknowledgments
I am grateful to Peter Schroeder-Heister and Luca Tranchini for generously providing a copy of Schroeder-Heister and Tranchini (Unpublished typescript) and thereby provoking this study. I thank the Editor, Elia Zardini, and two anonymous referees for their careful readings and helpful suggestions for improvements. Any defects that remain are my sole responsibility.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tennant, N. Normalizability, cut eliminability and paradox. Synthese 199 (Suppl 3), 597–616 (2021). https://doi.org/10.1007/s11229-016-1119-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1119-8