Abstract
In the section of the Antinomy of pure Reason Kant presents three notions of infinity. By investigating these concepts of infinity, this paper highlights important ‘building blocks’ of the structure of the mathematical antinomies, such as the ability of reason of producing ascending and descending series, as well as the notions of given and givable series. These structural features are discussed in order to clarify Ernst Zermelo’s reading of Kant’s antinomy, according to which the latter is deeply rooted in the tendency of the mind of producing “creative progress” and “inclusive closure”. The aim of this paper is to explain in which sense and why Kant’s treatment of the antinomies attracts the attention of Zermelo in the early 1900s and which aspects of his second axiomatic system have been inspired by Kant’s philosophy. Thus, by reading Kant’s antinomy ‘through Zermelo’s eyes’—with emphasis on the concept of regressive series in indefinitum and on that of regressive series ad infinitum – this paper identifies the echoes of Kant’s work in the making of the ZFC set theory.
Similar content being viewed by others
Notes
Moore (1988) investigates and solves the apparent contrast between the notion of infinity of the Transcendental Aesthetics and that of the Antinomy of pure Reason, according to which space and time are infinite given magnitudes (in the first case), but at the same time cannot be infinitely given (in the second one). In discussing this apparent contrast in Kant’s conception of infinity, Posy (2008) investigates its echoes in Brouwer’s and Hilbert’s 1920s works.
Kant’s system offers a wide range of concepts of infinity related to his philosophy of mathematics, as it is the case for the mathematical sublime in the Critique of the Power of Judgment (Ak 5:248ff). Studies on Kant’s conception of infinity such as Parsons (1964), Carson (1997) and Sutherland (2008) focuse on the doctrine of transcendental idealism of space and time in the Transcendental Aesthetics in the attempt of reconstructing Kant’s philosophy of mathematics and its historical sources. The connection between Kant’s philosophy and the history of axiomatization is discussed in Carson and Huber (2006), but the recognition of Kant’s influence on Zermelo’s work is lacking.
References to Kant’s texts follow the pagination of the Academy edition (Ak). References to the Critique of pure Reason use the standard notation (CPR) followed by the pages of its first (1781) and second (1787) edition (A/B). Translations are from the Cambridge Edition of the Works of Immanuel Kant. For a study on the origin of Kant’s antinomies in relationship to the Leibniz-Clarke correspondence, see Al-Aẓm (1972). For an analysis of Kant’s first antinomy, see Gram (1967), Craig (1979) and Loparic (1990). In particular, Craig focuses on Kant’s first antinomy and the problem of the beginning of the universe. He argues against Russell’s critique of Kant’s concept of infinity, and offers an overview of Whithrow’s reading of Kant and Zeno’s paradoxes. For a study of the second antinomy, see Van Cleve (1981). Fried (1940) proposes a critical logical analysis of the first antinomy, whereas Malzkorn (1999) offers a detailed analysis of all Kant’s antinomies; Falkenburg (2000) illustrates Kant’s cosmology in the pre-critical and critical writings, by taking into account the results of the antinomy.
Kant defines the first two antinomies “mathematical”, whereas the third and the fourth are “dynamical”. This paper will discuss only the first two.
The understanding, for instance, must follow the rule that however far we may have come in the series of empirical conditions, one should never assume an absolute boundary, but rather we should subordinate every appearance as conditioned to another as its condition (CPR A519-520/B547-548). In other words, as it is the case in the first antinomy, a series that goes in indefinitum is allowed.
Kant applies the concept of “antinomy” in different ways throughout the years (Hinske 1965, p. 486; Engelhard 2005, p. 277) and gives a new philosophical meaning to it within the system of transcendental philosophy. For Kant’s seminal definitions of antinomy and antithesis, see Hinske (1965), pp. 494–495. The antinomy also constitutes the nucleus from which the critique of pure reason arises, as Kant admits in a letter to Garve (21st September 1798), see Briefwechsel, Ak 12:257–8.
The section Antinomy of pure Reason occupies a special place in the Transcendental Dialectic, in analogy with the form of the hypothetical syllogism (CPR A405-6/B432-33).
After showing that the causes of Russell’s antinomy are to be ascribed to the field of logic, Fraenkel and Bar-Hillel (1939, p. 227) direct attention to the difference between syntactic and logical antinomies (Fraenkel and Bar-Hillel 1939, pp. 228–229). Russell’s antinomies can be found in Russell (1919, p. 136). For a concise reconstruction of the roots of Russell’s antinomy and its differences with respect to Kant, Hegel and Leibniz, see (Moore 1982, p. 58), 1988.
There are however transcendental conditions to apply concepts of infinity to the idea of the world or to the real in space, i.e. matter, in the resolution of the mathematical antinomies. In the second antinomy, for instance, when matter is taken as a thing in itself, then the whole series of decomposition is taken to be given and complete (abgeschlossen). Kant’s resolution of the second antinomy makes it possible to apply the concept of an infinitum dabile to matter, by taking matter as appearance only. That is why the mathematical antinomies are, in Kant’s view, an indirect proof of transcendental idealism, which discards the principle of complete determination by taking the objects of our sensations as appearances only.
Suppes (1995) remarks that in the first antinomy Kant uses concepts that come close to anticipating Russell’s paradox or the Burali-forti paradox in set theory. Other references to a possible role played by Kant’s antinomy in Zermelo’s work can be found in Falkenburg (2004, p. 190) and Engelhard (2005, pp. 14; 346; 433 footnote).
The definition of the world in terms of totality of a series can be found in Leibniz in a letter to de Bosses (\(20^{\mathrm{th}}\) November 1708). Kant rejects Leibniz’s idea that totality can be objectively given to intuition: only space and time as quanta continua are infinite, but subjectively given, namely in order to be known by the understanding, a composite can be infinite, but it is not the case for an absolute totality.
Kant claims that the infinite, taken as an absolute totality, i.e. God, cannot be given to intuition, but it must be thought of as something necessarily outside the series, as a regulative ideal that orientates them. The idea of God is thus reduced by the regulative use of pure theoretical reason into a focus imaginarius on which the systematic unity of science relies. It is worth noticing here Kant’s move in comparison to Cantor’s studies on the definition of the transfinite. Cantor distinguishes the notion of transfinite from that of absolute infinity: the truly unlimited must be regarded as a class rather than a set, it is not measurable, it has no determinate magnitude or cardinality. This is what Cantor called “the absolute totality” and absolute maximum exceeding our human intellect, see Cantor (1887–1888[1932]). In Mitteilungen zur Lehre vom Transfiniten, he claims that he discovered the principle of difference in the transfinite. Differently from the absolute, the transfinite encompasses a multiplicity of forms inserted in an indefinitely progressing series (see Hallett 1984, 15, 35–36, 39, 44). Priest (2002, pp. 120–121) claims that Kant’s antinomy shows the same structure as Cantor’s paradoxes of absolute infinity and adds that Hessenberg, Zermelo and Fraenkel noticed that similarity (see Sects. 4 and 5 below). Tengelyi (2011, pp. 533–534) also highlights the link between Cantor and Kant’s antinomy. I do not enter into this debate here, but it is worth noticing that even if one rejects the similarity of Cantor’s paradoxes with Kant’s antinomy, yet Cantor’s definition of absolute infinity has the same epistemic status of Kant’s idea of God in the CPR. It would be interesting to show the ground of this similarity, by investigating Cantor’s epistemology rather than his theological views.
This is because, in Kant’s view, we cannot intuit the concept of the world as a whole (CPR A519/B547).
Notice that the regressive and progressive series pertain to the subjective activity of producing them and are recognized as “mine”, as products of my activity. The synthetic activity of producing series is brought back to the unity of apperception. Since apperception is an act of self-consciousness that may accompany any act of representation, it can be related to a temporal dimension (see CPR A418-419/B546-547).
The cosmological principle is also a regulative principle to be applied to cosmology (CPR A509/B537) and prescribes a regress in the series of conditions for given appearances, in which regress it is never allowed to stop with an unconditioned (CPR A508-9/B536-37).
See Metaphysics Mrongovius, Ak 29:834-839; Metaphysik \(\hbox {L}_{2}\), Ak 28:568-569.
The given (datum) concerns space and the givable (dabile) time.
According to Kant, “time is in itself a series (and the formal condition of all series), and hence in it, in regard to a given present, the antecedentia are to be distinguished a priori as conditions (the past) from the consequential (the future)”, see CPR A411-B438.
In the Metaphysics Mrongovius, Kant presents in a clear manner this distinction between composing and decomposing a totality understood as a composite in the second antinomy: “Here the noumenon is thus confused again with the phenomenon. For the world, considered as noumenon, must consists of simple parts, because otherwise it cannot be composed. But as a phenomenon, it is different. The things in themselves have neither finite nor infinite parts (at least we cannot know this), but the regression (regressus) of my decomposition is infinite. For in space and time there is no last (item). They are continuous quanta (quanta continua). Consequently my decomposition of them is infinite, thus also of the remaining one that are found in these. These questions of com- and decomposition in the world concern the totality of the synthesis of appearances insofar as they constitute a composite (compositum), and this is mathematical synthesis” (Ak 29:858–859).
According to Kant, different possible ways of composing and decomposing a composite also depend on the different ways in which we represent space and time, the first being an aggregate whose parts exist simultaneously, for which there is no distinction between progression and regression, and the second being a series whose members can be subordinated to each other, see CPR A412/B439.
In discussing Kant’s notions of infinity, Moore (1988, p. 218) briefly points out the distinction between regress in infinitum and regress in indefinitum, as well as their relevant role, but he does not offer a clear account for them and does not even mention the third kind of regressus that can take place. Kant distinguished these two kinds of infinity in A527/B555 with reference to an infinite division that indicates only the appearance as quantum continuum and to the assumption of an appearance as quantum discretum. When something is assumed as quantum discretum the multiplicity of units in it is determined and it is always equal to a number. This kind of regress ad infinitum reveals a tendency (the suffix ad + accusative in Latin refers to a generic destination or to an approximation), a process that in the empirical regress in the composition is never to be taken as absolutely complete.
One could object that the absolute completeness of the composition of a given whole of all appearances can be part of a regressive series of hypothetical syllogisms, simply because there is no such a distinction between phenomena and noumena. If there is no distinction the absolute completeness represents the maximum of both the ascending and descending series, and this implies that also the whole of the progressive series is given. However, the future is not given yet, which contradicts the concept of absolute completeness. Another solution could be to think of an instantaneous time or that time is just an illusion. However, this position cannot justify any macroscopic change in the world, unless is assumed a possible way, e.g. through pre-established harmony, to think of change without time, or to think of a continuous external divine action on the world.
In the sceptical representation of the cosmological ideas, Kant emphasises that this is because if every appearance in space (matter) consists of infinitely many parts, then the regress of division is always too big for an empirical concept of the understanding. Also if the division of space should cease at any one member of the division (the simple), then it is too small for the idea of the unconditioned. For this member always allows of still another regress to further parts contained in it (CPR A487-488/B515-516).
Also Fraenkel (1919, 133) recognizes the affinity between Kant’s antinomy representing nature as a closed whole (ein abgeschlossenes Ganzes) and Russell’s and the Burali-Forti’s paradoxes.
To his second axiomatic system (ZF-system), Zermelo adds the Axiom Schema of Replacement and the Axiom of Foundation to his former system. He cancels the Axiom of Infinity and does not mention explicitly the Axiom of Choice, because he considers it as a general logical principle, rather than an axiom.
Zermelo also recognizes a pedagogical function to Kant’s antinomy. Martin (1955, p. 54), for instance, reports to be grateful to Zermelo for lecturing on Kant’s antinomy when explaining Russell’s paradoxes. Another reason why Zermelo was forced to work on Kant is the fact that he was editing Cantor’s philosophical writings (published in 1932) and there were a number of references to Kant’s system therein.
Notice the resemblance of Kant’s treatment of the transcendental dialectic as the doctrine of illusion (Schein) and the reference to “the confusion” that leads to an apparent contradiction, as it was the case of the dilemmas exposed by Kant.
Consider Zermelo’s Axiom of Foundation, according to which “every (descending) chain of elements, each member of which is an element of the previous one, breaks up with a finite index into an urelement. Or, what is equivalent: Every subdomain T (of a ZF-model) contains at least one element \(\hbox {t}_{0}\), that has no element t in T” (Zermelo 1930a, p. 31).
Recall here the reference to Cantor’s notion of absolute infinity to be put outside the series, see footnote 14.
The origin of the term “critique” derives from the Greek
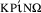 , which means “to judge”, but also “to discern”, “to separate” different domains.
, which means “to judge”, but also “to discern”, “to separate” different domains.According to Kant, only experience and the a priori principles of the understanding can settle how far the organization in an articulated body may go (CPR A527/B555).
The reference to Kant’s distinction between Grenzen (limits) and Schranken (borders) is suggested by Kanamori, though only with reference to §57 of the Prolegomena, see Kanamori (2010, p. 395 footnote). The notion of limits requires the existence of an entity outside a particular place, whereas the notion of borders means negation that pertains to any incomplete magnitude (CPR A767/B795).
For Kant’s definition of a quantum discretum as articulated into members and in which every part is once again articulated encountering always new complex parts in a process of decomposition that goes to infinity, see CPR A526/B554.
For a comparison between Kant’s account of the antinomy in the CPR and in the Prolegomena and the role played by Kant’s doctrine of judgments therein, see Vanzo (2005).
References
Al-Aẓm, Ṣ. J. (1972). The origins of Kant’s arguments in the antinomies. Oxford: Oxford University Press.
Baumanns, P. (1997). Kants Philosophie der Erkenntnis: durchgehender Kommentar zu den Hauptkapiteln der “Kritik der reinen Vernunft”. Würzburg: Königshausen & Neumann.
Cantor, G. (1887–1888[1932]). Mitteilungen zur Lehre vom Transfiniten. In: E. Zermelo (Ed.), Abhandlungen mathematischen und philosophischen Inhalts (pp. 378–451). Berlin: Springer.
Cantor, G. (1895). Beiträge zur Begründung der transfiniten Mengenlehre (Erster Artikel). Mathematische Annalen, 46, 481–512.
Carson, E. (1997). Kant on intuition in geometry. Canadian Journal of Philosophy, 27(4), 489–512.
Carson, E., & Huber, R. (Eds.). (2006). Intuition and the axiomatic method. Dordrecht: Springer.
Craig, W. L. (1979). Kant’s First Antinomy and the Beginning of the Universe. Zeitschrift für philosophische Forschung, 33(4), 553–567.
Engelhard, K. (2005). Das Einfache und die Materie: Untersuchungen zu Kants Antinomie der Teilung. Berlin: de Gruyter.
Falkenburg, B. (2000). Kants Kosmologie: die wissenschaftliche Revolution der Naturphilosophie im 18 Jahrhundert. Frankfurt am Main: Klostermann.
Falkenburg, B. (2004). Kants Naturalismus-Kritik. In K. Engelhard & D. Heidemann (Eds.), Warum Kant heute? (pp. 177–206). Berlin: de Gruyter.
Fraenkel, A. (1919). Einleitung in die Mengenlehre. Berlin: Springer.
Fraenkel, A., & Bar-Hillel, J. (1939). Le problème des antinomies et ses développements récents. Revue de Métaphysique et de Morale, 46(2), 225–242.
Fried, M. (1940). Kant’s first antinomy: A logical analysis. Mind, 49(194), 204–218.
Giaquinto, M. (2002). The search for certainty: A philosophical account of foundations of mathematics: A philosophical account of foundations of mathematics. Oxford: Oxford University Press.
Gram, M. S. (1967). Kant’s first antinomy. The Monist, 51(4), 499–518.
Hallett, M. (1984). Cantorian set theory and limitation of size. Oxford: Clarendon Press.
Hessenberg, G. (1906). Grundbegri?e der Mengenlehre. Abhandlungen der Fries’schen Schule, 4, 479–706.
Hinske, N. (1965). Kants Begriff der Antinomie und die Etappen seiner Ausarbeitung. Kant-Studien, 56(3–4), 485–496.
Kanamori, A. (2010). Introductory note to 1930a. In H.-D. Ebbinghaus, A. Kanamori, & D. Kramer (Eds.), Ernst Zermelo-Collected Works/Gesammelte Werke (pp. 390–399). Berlin: Springer.
Kant, I. ([1781/1787] 1998). In: P. Guyer., & A. W. Wood, (Eds.). Critique of pure reason. Cambridge: Cambridge Univerisity Press.
Kant, I. (1910ff.). Gesammelte Schriften, Königlich-Preußischen Akademie der Wissenschaften (Ed.). Berlin: Reimer/DeGruyter.
Longuenesse, B. (1998). Kant and the capacity to judge. Sensibility and discursivity in the transcendental analytic of the critique of pure reason. Princeton: Princeton University Press.
Loparic, Z. (1990). The logical structure of the first antinomy. Kant-Studien, 81(3), 280–303.
Malzkorn, W. (1999). Kants Kosmologie-Kritik: eine formale Analyse der Antinomienlehre. Berlin: Walter de Gruyter.
Martin, G. (1955). Kant’s metaphysics and theory of science. Manchester: Manchester University Press.
Moore, A. W. (1988). Aspects of the Infinite in Kant. Mind, 97(386), 205–223.
Moore, G. H. (1982). Zermelo’s axiom of choice: Its origins, development, and influence. New York: Springer.
Moore, G. H. (1988). The roots of Russell’s paradox. Russell: The Journal of Bertrand Russell Studies, 8(1), 46–56.
Parsons, C. (1964). Infinity and Kant’s conception of the possibility of experience. The Philosophical Review, 73(2), 182–197.
Peckhaus, V. (2005). Pro and Contra Hilbert: Zermelo’s Set Theories. Philosophia Scientiae, 5, 199–215.
Posy, C. (2008). Intuition and infinity: A Kantian theme with echoes in the foundations of mathematics. Royal Institute of Philosophy Supplement, 63, 165–193.
Priest, G. (2002). Beyond the limits of thought (2 extended ed.). Oxford: Clarendon Press.
Russell, B. (1919). Introduction to Mathematical Philosophy. London: George Allen and Unwin Ltd & New York: The Macmillan Co.
Schulthess, P. (1981). Relation und Funktion. Eine systematische und entwicklungsgeschichtliche Untersuchung zur theoretischen Philosophie Kants. Berlin: De Gruyter.
Suppes, P. (1995). Principles that transcend experience: Kant’s antinomies revisited. In: Proceedings of the 1994 Austrian Philosophy Conference.
Sutherland, D. (2008). Arithmetic from Kant to Frege: Numbers, pure units, and the limits of conceptual representation. Royal Institute of Philosophy Supplement, 63, 135–164.
Taylor, R. G. (2002). Zermelo’s Cantorian theory of systems of infinitely long propositions. Bulletin of Symbolic logic, 8(4), 478–515.
Tengelyi, L. (2001). On absolute infinity in Cantor. In D. Moran & H.-R. Sepp (Eds.), Phenomenology 2010 volume 4: Selected essays from Northern Europe, traditions, transitions and challenges: Traditions, transitions and challenges (pp. 529–550). Bucharest: Zeta Books.
Van Cleve, J. (1981). Reflections on Kant’s second antimony. Synthese, 47(3), 481–494.
Vanzo, A. (2005). Kant’s treatment of the mathematical antinomies in the first critique and in the prolegomena: A comparison. Croatian Journal of Philosophy, 5(3), 505–531.
Weyl, H. (1921). Über die neue Grundlagenkrise der Mathematik. Mathematische Zeitschrift, 10, 37–79.
Wolzogen, C. (1984). Die autonome Relation: zum Problem der Beziehung im Spätwerk Paul Natorps. Amsterdam: Rodopi.
Zermelo, E. (1930a). On boundary numbers and domains of sets. New investigations in the foundations of set-theory. In H.-D. Ebbinghaus, A. Kanamori, & D. Kramer (Eds.), Collected Works/Gesammelte Werke (pp. 400–429). Berlin: Springer.
Zermelo, E. (1930b). Report to the emergency association of german science about my research. In H.-D. Ebbinghaus, A. Kanamori, & D. Kramer (Eds.), Collected Works/Gesammelte Werke (Vol. 1, pp. 434–443). Berlin: Springer.
Zermelo, E.(1932a). In: E. Zermelo (Ed). Georg Cantor. Abhandlungen mathematischen und philosophischen Inhalts. Berlin: Springer.
Zermelo, E. (1932b). Über Stufen der Quantifikation und die Logik des Unendlichen. Jahresbericht der Deutschen Mathematiker-Vereinigung, 41, 85–88.
Zermelo, E. (1932c). Über mathematische Systeme und die Logik des Unendlichen. Forschungen und Fortschritte, 8, 6–7.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
De Bianchi, S. When series go in indefinitum, ad infinitum and in infinitum concepts of infinity in Kant’s antinomy of pure reason. Synthese 192, 2395–2412 (2015). https://doi.org/10.1007/s11229-015-0813-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0813-2




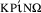 , which means “to judge”, but also “to discern”, “to separate” different domains.
, which means “to judge”, but also “to discern”, “to separate” different domains.