Abstract
This paper studies a generalization of rational choice theory. I briefly review the motivations that Helzner gives for his conditional choice construction (2013). Then, I focus on the important class of conditional choice functions with vacuous second tiers. This class is interesting for both formal and philosophical reasons. I argue that this class makes explicit one of conditional choice’s normative motivations in terms of an account of neutrality advocated within a certain tradition in decision theory. The observations recorded—several of which are generalizations of central results in the standard theory of rational choice—are intended to provide further insight into how conditional choice generalizes the standard account and are offered as additional evidence of the fruitfulness of the conditional choice framework.
Similar content being viewed by others
Notes
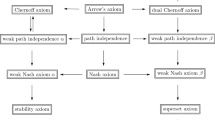
As Helzner points out, while Savage’s work eximplifies the tradition of expected utility most familiar to economists, psychologists, and statisticians, perhaps the tradition descending from Jeffrey (1983) is most well-known among philosophers.
Seidenfeld et al.’s account of coherent choice generalizes Levi’s account by relaxing convexity (2010).
\(\fancyscript{P}(X)\) is the power set of \(X\).
Though we can define a relation \(\ge \) by \(x \ge y\) iff \(\lnot (y >x)\) that rationalizes the choice function in the precise sense specified above. Note that this relation generated from \(>\) is complete, converting incompleteness into indifference.
In the non-standard Faith constraints, \(B\) is intended to represent a set of “absolutely satisfactory options.” Together, the Faith constraints entail that all and only absolutely satisfactory options are in the choice set when present on a menu.
See (Rott 2001, pp. 286–290) for proof.
In Sen (1971), Sen uses \(\beta \) instead of the stronger condition \(\beta ^+\). In the presence of \(\alpha \), however, \(\beta \) and \(\beta ^+\) are equivalent. \(\beta :\) If \(x, y \in C(Y), Y \subseteq Y',\) and \(y \in C(Y')\), then \(x \in C(Y')\).
The sort of expectation intended here is the one of relevance to nonmonotonic logic and not the familiar sort of expectation of decision theory.
This line of response to the epistemic value of the menu enjoys a serious advantage over a response of a different kind. Another way to respond is to insist that the option \(w\) from menu \(\{w,x\}\) is not the same as option \(w\) from the menu \(\{w,x,y,z\}.\) Such a response does forestall counterexamples of the above sort, but at a rather severe cost. If an option changes depending on the other available options (e.g., steak at a bad restaurant versus steak at a good restaurant), it will be quite hopeless to attempt to invoke inter-menu consistency constraints. We risk emptying the theory of real content.
Again, unlike Helzner, we do not make the more standard assumption that choice sets are non-empty.
I owe emphasizing this point to an anonymous referee.
The “whatever the neutral position is” hedge is an important one. With it, I mean to avoid commiting to a particular position on a relevant and disputed philosophical issue. As mentioned earlier, Levi insists that credal states be convex: if \(p_1, p_2 \in \mathbf{P},\) then \(\alpha p_1 + (1 - \alpha ) p_2 \in \mathbf{P}\) for \(\alpha \in [0,1].\) The convex combination of two probability functions represents a compromise, and suspending judgment between two “rival” probability judgments, on his view, requires considering any compromise—and not just \(p_1\) and \(p_2\)—to be permissible to use in computing expectated utility. Levi imposes convexity on states of utility judgment as well. Focusing just on probability judgments, if we endorse convexity, the neutral position, \(e\), for two distinct, determinate states of probability judgment, \(p_1\) and \(p_2,\) will be the convex set generated by these two states. In that case, the admissible options at \(e\) are not just those admissible relative to \(p_1\) and to \(p_2\), but those options deemed admissible relative to any strengthening of the convex set, \(e.\) Similarly, only options ruled out at every strengthening of \(e\)—not just those ruled out at both \(p_1\) and \(p_2\)—will be ruled out at \(e.\) This, according to Seidenfeld, et al., is an unwelcome consequence of convexity (2010). They insist that a neutral position with respect to two, distinct judgments of admissibility ought to preserve the shared agreements in admissibility judgments between those two states. For example, if \(x \notin \mathcal {\tilde{C}}(Y|\{p_1\})\) and \(x \notin \mathcal {\tilde{C}}(Y|\{p_2\}),\) the inadmissibility of \(x\) is a shared agreement that should be preserved at a neutral state, \(e\). Such an agreement is not always preserved under convexity. With an adequate formulation of the conditioning set, \(E,\ \{p_1, p_2\}\notin E\) if convexity is required of credal states. If convexity is relaxed, such a credal state can be legitimate. At issue here is whether we should seek consensus in judgments of admissibility or in reasons for judgments of admissibility (probability, utility, etc.) (Seidenfeld et al. 1989). Conditional judgments of admissibility might be seen as a way of walking a line between these two views, but in any case, we can deliver the right results for either view by suitably constraining \(E\).
Consider the following counterexample for \((I)\), perhaps the most central constraint in the theory of rational choice. Let \(\mathcal {C}\) be a conditional choice function, and let \(X=\{x,y,z\}\) and \(\mathcal {X}=\fancyscript{P}(X)\). Let \(E=\{e,e',e''\}\) with \(e \sqsubseteq e'\), \(e \sqsubseteq e''\), but
 and
and  . Suppose that \(\mathcal {C}_{e'}\) and \(\mathcal {C}_{e''}\) each satisfy \((I)\), and so \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\). Let \(\mathcal {C}_{e''}\) optimize \(z < y < x\). Let \(\mathcal {C}_{e'}\) optimize \(x < y < z\). Let \(\mathcal {C}(\{x,y,z\}|e)=\{x, z\}\) and \(\mathcal {C}(\{x,y\}|e)=\{y\}\). It is clear that \(\mathcal {C}_e\), while satisfying the definition of a conditional choice function, does not satisfy \((I)\). Compare Seidenfeld et al.’s Example 1 (2010, p. 158) and Helzner’s Example 2 (2013, p. 932), both drawing heavily on Levi’s work.
. Suppose that \(\mathcal {C}_{e'}\) and \(\mathcal {C}_{e''}\) each satisfy \((I)\), and so \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\). Let \(\mathcal {C}_{e''}\) optimize \(z < y < x\). Let \(\mathcal {C}_{e'}\) optimize \(x < y < z\). Let \(\mathcal {C}(\{x,y,z\}|e)=\{x, z\}\) and \(\mathcal {C}(\{x,y\}|e)=\{y\}\). It is clear that \(\mathcal {C}_e\), while satisfying the definition of a conditional choice function, does not satisfy \((I)\). Compare Seidenfeld et al.’s Example 1 (2010, p. 158) and Helzner’s Example 2 (2013, p. 932), both drawing heavily on Levi’s work.Helzner shows instead that \(\mathcal {C}\) satisfies \((I^{\star })\) and \((IV^{\star })\) iff \(\mathcal {C}(Y|e) \subseteq \{x :xRy\) for all \(y \in Y\) wrt some weak order \(R \in O_e\}.\)
References
Aizerman, M., & Malishevski, A. (1981). General theory of best variants choice: Some aspects. IEEE Transactions on Automatic Control, 26(5), 1030–1040.
Arló-Costa, H. (2006). Rationality and value: The epistemological role of indeterminate and agent-dependent values. Philosophical Studies, 128(1), 7–48.
Arló-Costa, H. (2011). Indeterminacy and belief change. In H. Arló-Costa (Ed.), Dynamic formal epistemology (pp. 173–195). Dordrecht: Springer.
Arló-Costa, H., & Pedersen, A. P. (2011). Social norms, rational choice and belief change. Belief Revision Meets Philosophy of Science, 2011, 163–212.
Ellsberg, D. (1963). Risk, ambiguity, and the savage axioms. The Quarterly Journal of Economics, 77(2), 327–336.
Fishburn, P. C. (1973). The theory of social choice (Vol. 264). Princeton: Princeton University Press.
Gärdenfors, P., & Sahlin, N. E. (1982). Unreliable probabilities, risk taking, and decision making. Synthese, 53(3), 361–386.
Helzner, J. (2011). Uncertainty in the context of pragmatist philosophy and rational choice theory. In Center on capitalism and society. http://capitalism.columbia.edu/9th-annual-conference-philosophical-foundations-economics-and-good-economy-individual-values-human.
Helzner, J. (2013). Rationalizing two-tiered choice functions through conditional choice. Synthese, 190(6), 929–951.
Helzner, J. (MS) Admissibility in a logical framework, manuscript.
Jeffrey, R. C. (1983). The logic of decision. Chicago: University of Chicago.
Kadane, J. B., Schervish, M. J., & Seidenfeld, T. (1999). Rethinking the foundations of statistics. Cambridge: Cambridge University Press.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica: Journal of the Econometric Society, 47, 263–291.
Keynes, J. M. (1921). A treatise on probability. London: Courier Dover Publications.
Knight, F. H. (1921). Risk, uncertainty and profit. New York: Hart, Schaffner and Marx.
Kyburg, H. E. (1968). Bets and beliefs. American Philosophical Quarterly, 5(1), 54–63.
Levi, I. (1974). On indeterminate probabilities. Journal of Philosophy, 71(13), 391–418.
Levi, I. (1986). Hard choices: Decision making under unresolved conflict. Cambridge: Cambridge University Press.
Levi, I. (1991). The fixation of belief and its undoing: Changing beliefs through inquiry. Cambridge: Cambridge University Press.
Luce, R. D., & Raiffa, H. (1957). Games and decisions: Introduction and critical survey. New York: Courier Dover Publications.
Misak, C. (2004). Truth and the end of inquiry: A Peircian account of truth. Oxford: Clarendon Press.
Moulin, H. (1985). Choice functions over a finite set: A summary. Social Choice and Welfare, 2(2), 147–160.
Nehring, K. (1997). Rational choice and revealed preference without binariness. Social Choice and Welfare, 14(3), 403–425.
Peirce, C. S. (1992). The essential Peirce: Selected philosophical writings (Vol. 1). Bloomington: Indiana University Press.
Rott, H. (2001). Change, choice and inference: A study of belief revision and nonmonotonic reasoning (Vol. 42). Oxford: Oxford University Press.
Rubinstein, A. (2012). Lecture notes in microeconomic theory: The economic agent. Princeton: Princeton University Press.
Savage, L. (1972). originally published in 1954). The foundations of statistics. New York: Wiley.
Seidenfeld, T. (1988). Decision theory without independence or without ordering. Economics and Philosophy, 4(2), 267–290.
Seidenfeld, T., Kadane, J. B., & Schervish, M. J. (1989). On the shared preferences of two bayesian decision makers. The Journal of Philosophy, 86(5), 225–244.
Seidenfeld, T., Schervish, M. J., & Kadane, J. B. (2010). Coherent choice functions under uncertainty. Synthese, 172(1), 157–176.
Sen, A. (1971). Choice functions and revealed preference. The Review of Economic Studies, 38(3), 307–317.
Sen, A. (1993). Internal consistency of choice. Econometrica: Journal of the Econometric Society, 61, 495–521.
Sen, A. (1997). Maximization and the act of choice. Econometrica: Journal of the Econometric Society, 65, 745–779.
Suzumura, K. (1983). Rational choice, collective decisions, and social welfare. Cambridge: Cambridge University Press.
Walley, P. (1991). Statistical reasoning with imprecise probabilities. London: Chapman and Hall.
Acknowledgments
Thanks are due to John Collins, Jeff Helzner, Tobias Lessmeister, Isaac Levi, Yang Liu, Ignacio Ojea, Paul Pedersen, Hans Rott, and two anonymous referees for helpful comments and discussions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix: Proofs
Proof of observation 1
Proof
Let \(\mathcal {C}:\mathcal {X} \times \mathcal {E} \rightarrow \fancyscript{P}(X)\) be a conditional choice function.
\((\Leftarrow )\) Suppose that \(\mathcal {C}\) satisfies \(\nu \) and that \(\succ _e = \emptyset \) for all \(e \in E.\) Let \(x \in \mathcal {C}(Y|e).\) Since \(\mathcal {C}\) is a conditional choice function, it follows immediately that there is an \(f \in E\) such that \(e \sqsubseteq f\) and \(x \in \mathcal {C}(Y|g)\) whenever \(f \sqsubseteq g.\) For the other direction of \((ii'),\) assume that there is an \(f \in E\) such that \(e \sqsubseteq f\) and \(x \in \mathcal {C}(Y|g)\) whenever \(f \sqsubseteq g.\) By \(\nu ,\) we have \(\mathcal {C}(Y|e) \ne \emptyset .\) So there is some \(y \in \mathcal {C}(Y|e).\) Suppose that \(x \notin \mathcal {C}(Y|e).\) It follows that \(y \succ _e x,\) which is a contradiction. So \(x \in \mathcal {C}(Y|e).\) Hence, \(\mathcal {C}\) satisfies \((ii').\)
\((\Rightarrow )\) Suppose that \(\mathcal {C}\) satisfies \((ii').\) Suppose that \(\mathcal {C}(Y|e') \ne \emptyset \) for some \(e' \in E\) such that \(e \sqsubseteq e'.\) Then there is some \(x \in \mathcal {C}(Y|e').\) By \((ii'),\) there is an \(f \in E\) such that \(e' \sqsubseteq f\) and \(x \in \mathcal {C}(Y|g)\) whenever \(f \sqsubseteq g.\) But \(e \sqsubseteq f\) too, so by \((ii'),\ x \in \mathcal {C}(Y|e),\) so \(\mathcal {C}(Y|e) \ne \emptyset .\) Hence, \(\mathcal {C}\) satisfies \(\nu .\) Now suppose that \(\succ _e \ne \emptyset \) for some \(e \in E.\) Then, for some \(Y \in \mathcal {X},\) there are \(x, y \in Y\) such that \(x \in \mathcal {C}(Y|e),\ y \notin \mathcal {C}(Y|e),\) but \(y \in \mathcal {C}(Y|f)\) for some \(f \in E\) such that \(e \sqsubseteq f.\) It follows from \((ii')\) that there is an \(f' \in E\) such that \(f \sqsubseteq f'\) and \(y \in \mathcal {C}(Y|g)\) whenever \(f' \sqsubseteq g.\) But since \(e \sqsubseteq f',\) by \((ii'),\ y \in \mathcal {C}(Y|e),\) which is a contradiction. Thus, \(\succ _e = \emptyset \) for all \(e \in E.\) \(\square \)
Proof of observation 2
Proof
That \(\mathcal {\tilde{C}}(Y|e) \subseteq \bigcup \{\mathcal {\tilde{C}}(Y|e') :e \sqsubseteq e'\}\) holds for all \(Y \in \mathcal {X}\) and \(e \in E\) is easy to see from the fact that \(e \sqsubseteq e.\) For the other inclusion claim, let \(x\) be in \(\bigcup \{\mathcal {\tilde{C}}(Y|e') :e \sqsubseteq e'\}.\) By \(\nu ,\) \(\mathcal {\tilde{C}}(Y|e) \ne \emptyset .\) So there is some \(y \in \mathcal {\tilde{C}}(Y|e).\) Suppose that \(x\) is not in \(\mathcal {\tilde{C}}(Y|e).\) It follows that \(y \succ _e x,\) which contradicts the assumption that the second tier is vacuous. Hence, \(x \in \mathcal {\tilde{C}}(Y|e).\) \(\square \)
Proof of observation 3
Proof
Immediate from condition (i) in the definition of conditional choice, since a conditional choice function is a choice function in its first argument. \(\square \)
Proof of observation 4
Proof
Let \(C\) be a choice function on \(X\). \(C^{\star } :\mathcal {X} \times \mathcal {E} \rightarrow \fancyscript{P}(X)\) since, for all \(Y \in \mathcal {X}\) and \(e \in E\), \(C^{\star }(Y|e)=C(Y)\). For condition (i), \(C^{\star }(Y|e) \subseteq Y\) because \(C(Y) \subseteq Y\) for all \(Y \in \mathcal {X}\). As for condition (ii), first suppose that \(x \in C^{\star }(Y|e)\). Since, for any \(e' \in E \), \(C^{\star }(Y|e)=C^{\star }(Y|e')\), it follows that there is an \(f \in E\) such that \(e \sqsubseteq f\) and \(x \in C^{\star }(Y|g)\) whenever \(f \sqsubseteq g\). Finally, for the other direction, suppose that there is an \(f \in E\) such that \(e \sqsubseteq f\) and \(x \in C^{\star }(Y|g)\) whenever \(f \sqsubseteq g\). Again, since \(C^{\star }(Y|f)=C(Y)=C^{\star }(Y|e')\) for all \(e' \in E\), it follows that \(x \in C^{\star }(Y|e)\). \(\square \)
Proof of observation 5
Proof
Suppose that \(C\) is a choice function on \(X\) and satisfies \(P\). Since \(C^{\star }_e=C\) for all \(e \in E\), it follows that \(C^{\star }\) satisfies \(P^{\star }\). For the other direction, assume that \(C^{\star }\) satisfies \(P^{\star }\). Let \(e \in E\). By assumption, we have it that there is an \(f \in E\) such that \(e \sqsubseteq f\) and, for all \(g \in E\) such that \(f \sqsubseteq g, C^{\star }_g\) satisfies \(P\). But this implies that \(C^{\star }_f\) satisfies \(P\) and \(C^{\star }_f =C\), so \(C\) satisfies \(P\). \(\square \)
Proof of observation 6
Proof
Suppose that \(\mathcal {\tilde{C}}\) satisfies \(P^{\star }\). Let \(x \in \mathcal {\tilde{C}}(Y|e)\). By definition, there is some \(f \in E\) such that \(e \sqsubseteq f\) and \(x \in \mathcal {\tilde{C}}(Y|g)\) when \(f \sqsubseteq g\). From the assumption, we have that there is some \(f' \in E\) such that \(f \sqsubseteq f'\) and \(\mathcal {\tilde{C}}_{g'}\) satisfies \(P\) whenever \(f' \sqsubseteq g'\). It follows that \(x \in \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\ \text {and}\ \mathcal {\tilde{C}}_{e'}\ \text {satisfies}\ P\}\). Now assume that \(x \in \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\ \text {and}\ \mathcal {\tilde{C}}_{e'}\ \text {satisfies}\ P\}\). It follows immediately from Observation 2 that \(x \in \mathcal {\tilde{C}}(Y|e)\). \(\square \)
Proof of observation 7
Proof
Let \(\{C_i: i \in I\}\) be a collection of choice functions, \(C_i: \mathcal {X} \rightarrow \fancyscript{P}(X)\), and define \(C(Y) = \bigcup _{i \in I}C_i(Y)\), for all \(Y \in \mathcal {X}\). It is clear that \(C\) is a well-defined choice function. We check each axiom.
\((I)\) Assume that for all \(i \in I\), \(C_i\) satisfies \((I)\). Suppose that \(Y \subseteq Y'\) and \(x \in Y \cap C(Y')\). Since \(x \in C(Y')\), it follows that \(x \in C_i(Y')\) for some \(i \in I\). By assumption \(C_i\) satisfies \((I)\), so it follows that \(x \in C_i(Y)\). Hence, \(x \in C(Y)\), too. So, \(C\) satisfies \((I)\).
\((I^-)\) Suppose that for all \(i \in I\), \(C_i\) satisfies \((I^-)\). Assume that \(Y \subseteq Y'\), \(C(Y') \subseteq Y\), and \(x \in C(Y')\). Then, for some \(i \in I\), \(x \in C_i(Y')\). Since \(C_i\) satisfies \((I^-)\), it follows that \(x \in C_i(Y)\). Hence, \(x \in C(Y)\). So, \(C\) satisfies \((I^-)\).
\((I')\) Suppose that \(C_i\) satisfies \((I')\) for all \(i \in I\). Assume that \(x \in C(Y \cup Y')\). So, for some \(i \in I\), \(x \in C_i(Y \cup Y')\). By \((I')\), \(x \in [C_i(Y) \cup C_i(y')]\). In either case, it follows that \(x \in [C(Y) \cup C(Y')]\). So \(C\) satisfies \((I')\).
\((III)\) Let \(C_i\) satisfy \((III)\) for all \(i \in I\). Suppose that \(Y \subseteq Y'\) and \(C(Y') \subseteq Y\), and let \(x\) be in \(C(Y)\). It must then be the case that \(C_i(Y') \subseteq Y\) for all \(i \in I\). And, for some \(i \in I\), \(x \in C_i(Y)\). By \((III)\), \(x \in C_i(Y')\). Hence, \(x \in C(Y')\). It follows that \(C\) satisfies \((III)\).
\((IV^+)\) Let \(C_i\) satisfy \((IV^+)\) for all \(i \in I\). Assume that \(Y \subseteq Y'\) and \(x \in C(Y)\). It follows that \(x \in C_i(Y)\) for some \(i \in I\). By \((IV^+)\), \(x \in C_i(Y')\). Thus, \(x \in C(Y')\). \(C\) therefore satisfies \((IV^+)\).
(Faith1) Suppose that (Faith1) is satisfied by \(C_i\) for all \(i \in I\). Assume that \(Y \cap B \ne \emptyset \) (where \(B\) is the set of “absolutely satisfactory” options in \(X\)) and let \(x\) be in \(C(Y)\). It follows that there is an \(i \in I\) such that \(x \in C_i(Y)\). By (Faith1), \(x \in B\). So, \(C\) satisfies (Faith1).
(Faith2) Let \(C_i\) satisfy (Faith2) for all \(i \in I\). Assume that \(x \in Y \cap B\). By (Faith2), \(x \in C_i(Y)\) for all \(i \in I\). Hence, \(x \in C(Y)\). \(C\) therefore satisfies (Faith2).
(Success) Suppose that \(C_i\) satisfies (Success) for all \(i \in I\). Consider some \(Y \ne \emptyset \) in \(\mathcal {X}\). By (Success), \(C_i(Y) \ne \emptyset \) for all \(i \in I\). Hence, \(C(Y) \ne \emptyset \). So, \(C\) satisfies (Success).
\((\emptyset 1)\) Let \(C_i\) satisfy \((\emptyset 1)\) for all \(i \in I\). Suppose that \(Y \subseteq Y'\) and that \(C(Y') = \emptyset \). Then, \(C_i(Y') = \emptyset \) for all \(i \in I\). By \((\emptyset 1)\), it follows that \(C_i(Y) = \emptyset \) for all \(i \in I\). Hence, \(C(Y) = \emptyset \), too. So, \(C\) satisfies \((\emptyset 1)\).
\((\emptyset 2)\) Suppose that \(C_i\) satisfies \((\emptyset 2)\) for all \(i \in I\). Assume that \(Y \subseteq Y'\) and \(C(Y) = \emptyset \). Then, \(C_i(Y) = \emptyset \) for all \(i \in I\). By \((\emptyset 2)\), we have that \(C_i(Y') \cap Y = \emptyset \) for all \(i \in I\). It follows that \(C(Y') \cap Y = \emptyset \). \(C\) therefore satisfies \((\emptyset 2)\). \(\square \)
Proof of observation 8
Proof
(\(\Leftarrow \)) Since, by hypothesis, every local choice function of \(\mathcal {\tilde{C}}\) satisfies property \(P\), it follows that, for every \(e \in E\) there is an \(f \in E\) such that \(e \sqsubseteq f\) and \(\mathcal {\tilde{C}}_g\) satisfies \(P\) for all \(g \in E\) such that \(f \sqsubseteq g\). That is, \(\mathcal {\tilde{C}}\) satisfies \(P^{\star }\).
(\(\Rightarrow \)) Let \(\mathcal {\tilde{C}}\) satisfy \(P^{\star }\). By Observation 6, \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\ \text {and}\ \mathcal {\tilde{C}}_{e'}\ \text {satisfies}\ P\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\). For those constraints, \(P\), that are preserved under unions (Observation 7), it follows that \(\mathcal {\tilde{C}}_e\) satisfies \(P\). Hence, every local choice function of \(\mathcal {\tilde{C}}\) satisfies \(P\). \(\square \)
Proof of observation 9
Proof
Assume that \(\mathcal {\tilde{C}}: \mathcal {X} \times \mathcal {E} \rightarrow \fancyscript{P}(X)\) is a conditional choice with a vacuous second tier that satisfies \((\emptyset 1^{\star })\), and let \(\mathcal {X} = \fancyscript{P}_{fin}(X)\).
\((\Rightarrow )\) Suppose that \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\) and \((II^{\star })\). By Observation 8, every local choice function of \(\mathcal {\tilde{C}}\) satisfies \((\emptyset 1)\) and \((I)\). From Observation 6 it follows that \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) satisfies \((II)\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\). So, \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) satisfies \((\emptyset 1), (I),\) and \((II)\}\). By Theorem 1, \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) is rationalizable \(\} = \{x: xRy\) for all \(y \in Y\) with respect to some rationalizing \(R \in O_e\}\).
\((\Leftarrow )\) Suppose that, for all \(x \in X, Y \in \mathcal {X}\), and \(e \in \mathcal {E},\ \mathcal {\tilde{C}}(Y|e)=\{x :xRy\) for all \(y \in Y\) wrt some rationalizing \(R \in O_e\}\). Let \(\mathcal {E}_e\) be the poset \(\langle \{f|e \sqsubseteq f\}, \sqsubseteq \rangle \), where \(\sqsubseteq \) is the relevant restriction of the partial order from \(\mathcal {E}.\) By the assumption on \(\mathcal {E}\), it follows that every chain in \(\mathcal {E}_e\) has an upper bound in \(\mathcal {E}_e\). Thus, by Zorn’s lemma, \(\mathcal {E}_e\) has a maximal element. Let \(f\) be such a maximal element of \(\mathcal {E}_e\). Either (i) \(\mathcal {\tilde{C}}(Y|f) \ne \emptyset \) for some \(Y \in \mathcal {X}\) or (ii) \(\mathcal {\tilde{C}}_f\) always returns the empty set. Suppose that (i). Then, for some \(Y \in \mathcal {X},\) there is some \(x \in \mathcal {\tilde{C}}(Y|f).\) By assumption, there is a rationalizing \(R \in O_f\) such that \(xRy\) for all \(y \in Y.\) \(f\) is maximal so \(R_{\mathcal {\tilde{C}}_f}\) is rationalizing. Therefore, by Theorem 1, \(\mathcal {\tilde{C}}_f\) satisfies \((I)\) and \((II)\). And because \(f\) is maximal, \(\mathcal {\tilde{C}}_g\) satisfies \((I)\) and \((II)\) for any \(g \in E\) such that \(f \sqsubseteq g\). Now, consider case (ii). \(\mathcal {\tilde{C}}(Y|f) = \emptyset \) for all \(Y \in \mathcal {X}.\) It is straightforward to verify that \(\mathcal {\tilde{C}}_f\) vacuously satisfies constraints \((I)\) and \((II).\) Again, because \(f\) is maximal, \(\mathcal {\tilde{C}}_g\) satisfies \((I)\) and \((II)\) for any \(g \in E\) such that \(f \sqsubseteq g\). It follows that \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\) and \((II^{\star })\). \(\square \)
Proof of observation 11
Proof
Assume that \(\mathcal {\tilde{C}}: \mathcal {X} \times \mathcal {E} \rightarrow \fancyscript{P}(X)\) is a conditional choice with a vacuous second tier that satisfies \((\emptyset 1^{\star })\), and let \(\mathcal {X} = \fancyscript{P}_{fin}(X)\).
\((\Rightarrow )\) Assume that \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\) and \((IV^{\star }).\) By Observation 8, it follows from our assumptions that \(\mathcal {\tilde{C}}\) satisfies \((\emptyset 1)\) and \((I)\) at each of its local choice functions. By Observation 6, \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) satisfies \((IV)\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\). Putting these together, it follows that \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) satisfies \((\emptyset 1), (I),\) and \((IV)\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\). By Theorem 2, this amounts to \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) is weak order rationalizable\(\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\).
\((\Leftarrow )\) Now assume that for all \(e \in E,\ \mathcal {\tilde{C}}_e\) is pseudo-rationalizable by a collection of local choice functions \(\{\mathcal {\tilde{C}}_{e'} :e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) is weak order rationalizable\(\}.\) We establish that \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\) and \((IV^{\star }).\) Let \(\mathcal {E}_e\) be the poset \(\langle \{f|e \sqsubseteq f\}, \sqsubseteq \rangle \), where \(\sqsubseteq \) is the relevant restriction of the partial order from \(\mathcal {E}.\) By the assumption on \(\mathcal {E}\), it follows that every chain in \(\mathcal {E}_e\) has an upper bound in \(\mathcal {E}_e\). Thus, by Zorn’s lemma, \(\mathcal {E}_e\) has a maximal element. Let \(f\) be such a maximal element of \(\mathcal {E}_e\). Either (i) \(\mathcal {\tilde{C}}(Y|f) \ne \emptyset \) for some \(Y \in \mathcal {X}\) or (ii) \(\mathcal {\tilde{C}}_f\) always returns the empty set. Consider case \((i)\) first. Suppose that, for some \(Y \in \mathcal {X}\), \(x \in \mathcal {\tilde{C}}(Y|f)\). By the assumption of the pseudo-rationalizability of each local choice function (i.e., \(\mathcal {\tilde{C}}(Y|e) = \bigcup \{\mathcal {\tilde{C}}(Y|e'): e \sqsubseteq e'\) and \(\mathcal {\tilde{C}}_{e'}\) is weak order rationalizable\(\}\) for all \(Y \in \mathcal {X}\) and \(e \in E\)), it follows that there is a weak order rationalizable local choice function \(\mathcal {\tilde{C}}_{f'}\) such that \(f \sqsubseteq f'\) and \(x \in \mathcal {\tilde{C}}_{f'}(Y).\) \(f\) is maximal so \({\mathcal {\tilde{C}}_{f}}\) must itself be weak order rationalizable. Therefore, by Theorem 2, \(\mathcal {\tilde{C}}_{f}\) satisfies \((I)\) and \((IV)\). And because \(f\) is maximal, \(\mathcal {\tilde{C}}_g\) satisfies \((I)\) and \((IV)\) for any \(g \in E\) such that \(f \sqsubseteq g\). Now consider case \((ii)\), \(\mathcal {\tilde{C}}_f(Y) = \emptyset \) for all \(Y \in \mathcal {X}\). \((I)\) and \((IV)\) are trivially satisfied. Because \(f\) is maximal, \(\mathcal {\tilde{C}}_g\) satisfies \((I)\) and \((IV)\) for any \(g \in E\) such that \(f \sqsubseteq g\). It follows that \(\mathcal {\tilde{C}}\) satisfies \((I^{\star })\) and \((IV^{\star })\). \(\square \)
Rights and permissions
About this article
Cite this article
Stewart, R.T. Conditional choice with a vacuous second tier. Synthese 193, 219–243 (2016). https://doi.org/10.1007/s11229-015-0754-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0754-9



 and
and  . Suppose that
. Suppose that