An unmanned tank combat game driven by FPSO-MADDPG algorithm

Abstract

With the development of artificial intelligence and unmanned technology, unmanned vehicles have been utilized in a variety of situations which may be hazardous to human beings, even in real battle fields. An intelligent unmanned vehicle can be aware of surrounding situations and make appropriate responding decisions. For this purpose, this paper applies Multi-agent Deep Deterministic Policy Gradient (MADDPG) algorithm for vehicle’s of situation awareness and decision making, inside which a Fast Particle Swarm Optimization (FPSO) algorithm is proposed to calculate the optimal vehicle attitude and position; therefore, an improved deep reinforcement learning algorithm FPSO-MADPPG is formed. A specific advantage function is designed for the FPSO portion, which considers angle, distance, outflanking encirclement. A dedicated reward is designed for the MADPPG portion, which considers key factors like angle, distance, and damage. Finally, FPSO-MADPPG is then used in a combat game to operate unmanned tanks. Simulation results show that our method not only can obtain higher winning rate, but also higher reward and faster convergence than DDPG and MADPPG algorithms.

1 Introduction

With the progress of science and technology, unmanned vehicles, like Unmanned Aerial Vehicle (UAV), Unmanned Ground Vehicles (UGV) or Unmanned Surface Vehicles (USV), come to true. In 2016, Russia put forward uranus-9 [1] multi-functional unmanned combat vehicle to international market. In 2017, United States proposed the Next Generation Combat Vehicle (NGCV) [2]. The emergence of unmanned tanks will undoubtedly bring revolution to traditional land warfare.

Many techniques are used for agent decision-making problems, including expert system [3], fuzzy logic [4], genetic algorithm [5], and artificial potential field method [6] and so on. Methods like expert system and fuzzy algorithm are difficult to collect experience or data from game playing on the fly. On contrast, reinforcement learning algorithms can direct agents to make decisions via maximizing reward from their interacting with the environment and therefore, achieve specific goals. Reinforcement learning algorithms have been widely used in agent decision-making problems.

Li Xia et al. applied Deep Q-Network (DQN) algorithm to one vs. one UAV confrontation [7], where a dual network structure and experience replay buffer are used. In this work, an action space with only five discrete actions is assumed. They achieved good results against MinMax and Monte Carlo method. Li Yongfeng proposed a multi-step double depth Q-network algorithm (MS-DDQN) for one vs. one UAV combat [8], where 27 discrete actions are assumed. To overcome the defects of slow training speed and convergence speed in traditional DRL, MS-DDQN adopts a pre-training learning model as the starting point of another to simulate the UCAV aerial combat decision-making process. Piao proposed Multi-agent Hierarchical Policy Gradient algorithm (MAHPG) algorithm for multi-UAV combat [9], where policy gradient network is divided into high level and low level network. The high level portion is in charge of aircraft maneuvering strategy where 14 discrete maneuvering actions are defined, and the low level portion is in charge of firing control. Compared with DQN and MADDPG, MAHPG performs better in UAV combat simulations. MAHPG has the ability of Air Combat Tactics Interplay Adaptation, and sometimes new operational strategies emerge that can surpass human expertise.

Although there are bunches of research works applying reinforcement learning on UAV combat, either single UAV or multi-UAV cases [10], similar research works on unmanned tank combat are very limited. Yung-Ping Fang designed a game, where a human player combats against a Non-Player-Character (NPC) tank. The NPC tank is driven by a combination algorithm of reinforcement learning (SARSA or Q-Learning) and fuzzy logic [11]. The battle field is divided into $5*3$ cells, and each tank can only take four possible movements, i.e., left, right, up, down. Obviously, the scenario is over-simplified. Haoluo Jin extended Advantage Actor-Critic (A2C) to multi-tank combat problem [12], where each agent can only receive its local observations and execute an action based on it, but global states are used for evaluating the impacts of joint actions. This work discretizes the action space, which has only four moving directions, i.e., $(0, 90, 180, 270^{\circ })$. But our algorithm assumes continuous action space.

In this research, we try to study multi-tank confrontation using a combination of MADDPG and PSO algorithms. In our framework, tank maneuvering decision is regarded as an optimization problem, where PSO algorithm is used calculate the best position and attitude for an agent so as to pursue its maximum advantage over its opponents, and then, MADDPG algorithm is used to direct the agents according to the outcome of PSO. Agents can cooperate with each other, launching attack against their opponents at the best advantage position and with the best attitude.

2 Related work

2.1 Reinforcement learning

In this paper, we limit our discussion on reinforcement learning to model free method, which can be divided into three categories:

(1) Value function based methods. This category methods, such as Q-learning [13], SARSA [14] and DQN [15], use value function to evaluate the quality of interacting with the environment. An agent tries to maximize the value function by selecting appropriate action. DQN is continuously being improved in recent years. In DQN, experience replay buffer is introduced to resolve correlation between samples, and the target network [16] effectively improves the updating speed of the neural network and the convergence time of the algorithm. DQN has achieved good results in a variety of games, but it can only be applied in discrete action space, rather continuous action space.

(2) Policy based methods. The most representative one in this category is the policy gradient (PG) [17] algorithm. Unlike DQN which does not allow back-propagation, PG directly selects an action for back-propagation through observation and the policy. And the probability of selecting an action is increased or decreased according to the received reward depending on this selection. The disadvantage of this algorithm is that it is apt to converge to a local optimal value rather than a global one.

(3) Mixed methods. A typical method in this category is actor-critic [18]. The actor selects an action according to the policy, while the critic evaluates the quality of this selection using a value function. The actor will adjust its strategy according to the critic’s evaluation. However, it is difficult to make both actor and critic networks converge at the same time. Later, people derived many other algorithms from actor-critic, such as A3C [19], DDPG [20] and so on.

DDPG uses the target network from DQN to improve the stability of the algorithm, and makes the algorithm easier to converge. Experience replay buffer is also used to break the sample correlation problem. DDPG has good effects in solving the problems where continuous actions are involved. Then MADDPG, a multi-agent version, is proposed based on DDPG. This method adopts centralized training and decentralized execution and has good performance in multi-agent situation.

2.2 Particle swarm optimization

Particle swarm optimization (PSO) is an evolutionary optimization method. The early version of PSO algorithm, invented by Reynolds in 1987 [21], was originally used to simulate birds’ predation behavior. Its basic idea is to find the optimal solution through information sharing and cooperation among individuals in the group.

The performance of PSO can be improved by adjusting inertia weight and learning factor. Shi proposed an inertia weight adjustment approach using linear attenuation [22], which conducts search in larger range at early stage of iteration and conducts local fine search at late stage. Chatterjee proposed a nonlinear adjustment approach on inertia weight [23], tested it on benchmark function set, and proved its good performance. Jiang proposed an adaptive particle swarm optimization algorithm using disturbance acceleration factor [24]. The algorithm uses cosine function to control the change of inertia factor, which decreases across the whole iteration process and tends to be flat at later stage. Yang proposed a particle swarm optimization algorithm based on memory integration [25], which periodically changes the inertia weight during iteration process and repeatedly searches the target area. Dong proposed a reversed particle swarm optimization algorithm with adaptive elite disturbance and inertia weight [26], which increases the inertia weight to cover large search range when most particles in the swarm tend to be consistent. Ratnaweera adopted an adjustment method that changes with the number of iterations [27]. Chen used trigonometric functions to adjust learning factors [28], and test results show that this method can converge fast and has higher accuracy.

3 Background

3.1 MADDPG

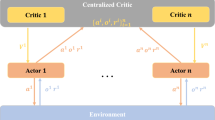
MADDPG is a multi-agent reinforcement learning algorithm [29]. It adopts the actor-critic paradigm, where the actor is responsible for action selection, and the critic evaluates the quality of the actors’ selection. MADDPG adopts the strategy of centralized training and decentralized execution as shown in Fig. 1. During training, global information is fed into the critic network of each agent; therefore, it can make a more reasonable judgment on the action selected by the agent. While during execution, the agent will select actions according to its local information.

During the interaction with the environment, for any specific agent i at time t, its actor will record current state $s_{i}^{t}$ and select an action $a_{i}^{t}$; then, $s_{i}^{t}$ will transfer to the next state $s_{i}^{t+1}$, and the agent will get a reward $r_{i}^{t}$. The tuple $\left( {\textbf {s}},{\textbf {a}}, {\textbf {r}}, {\textbf { s}}^{\prime }\right)$ is named as experience, where $\varvec{s} =\left( s_{1}^{t},s_{1}^{t}...s_{N}^{t}\right)$, ${\textbf {a}} =\left( a_{1}^{t},a_{1}^{t}...a_{N}^{t}\right)$, ${\textbf {r}} =\left( r_{1}^{t},r_{1}^{t}...r_{N}^{t}\right)$, and ${\textbf {s}}^{\prime } =\left( s_{1}^{t^\prime },s_{1}^{t^\prime }...s_{N}^{t^\prime }\right)$. This experience information is collected by each agent, and stored in its replay buffer for subsequent training. During training, S experiences in the replay buffer will be randomly sampled so as to counter correlations between them. The samples will be sent to the critic network for evaluation, so as to guide the agent to select appropriate action. Therefore, the agent can learn certain strategies through its interactions with the environment.

Fig. 1

Network structure of MADDPG

Each agent has its own actor-critic network, and either the actor $\mu$ or the critic Q includes both an online-net and a target-net. The online-net updates utilizing experience from the replay buffer, while the target-net each time updates a small portion of its own parameters from the online-net. For example, agent i’s actor $\mu$ updates its target-net parameters $\theta ^{\mu ^{\prime }}_{i}$ with a learning rate $\tau$ as Eq. (1).

$$\begin{aligned} \theta ^{\mu _{i}^{\prime }}_{i} \leftarrow \tau \theta _{i}^{\mu _{i}} +(1-\tau ) \theta _{i}^{\mu _{i}^{\prime }} \end{aligned}$$

(1)

The actor’s online policy network’s policy gradient $\nabla _{\theta _{i}^{{\mu }}}J$ can be calculated as:

$$\begin{aligned} \nabla _{\theta _{i}^{{\mu _{i}}}}J \approx \frac{1}{S} \sum _{j=1}^{S}\nabla _{\theta _{i}^{\mu _{i}}} {\mu _{i}}\left( s_{i}^{t}\right) \nabla _{a_{i}^{t}}Q_{i} \left( s_{i}^{j},a_{1}^{j},a_{2}^{j},...a_{N}^{j}\right) \bigg |_{a_{k}^{j}={\mu }_{k}\left( s_{k}^{j}\right) } \end{aligned}$$

(2)

For the critic, its online network Q has a loss as defined in (3):

$$\begin{aligned} L( \theta ) = \frac{1}{S} \sum _{j=1}^{S} \left( y_{i}^{j}-Q_{i}\left(\varvec{s}^{j}, \varvec{a}^{j}\right) \right) ^{2} \end{aligned}$$

(3)

where $y_{i}^{j}$ can be regarded as a label in supervised learning.

$$\begin{aligned} y_{i}^{j} = r_{i}^{t^{j}} +\gamma _{i}{Q_{i}^{\prime }} \left( \varvec{s}^{\prime ^{j}},{a_{1}^{t^\prime }}^{j},{a_{2}^{t^\prime }}^{j},...{a_{N}^{t^\prime }}^{j} \right) \bigg |_{{a_{k}^{\prime }}^{j}=\mu _{k}^{\prime }\left( s_{k}^{j}\right) } \end{aligned}$$

(4)

The critic updates its target Q-net parameters in a way similar to the actor.

$$\begin{aligned} \theta ^{Q_{i}^{\prime }}_{i} \leftarrow \tau \theta _{i}^{Q{i}} +(1-\tau ) \theta _{i}^{Q_{i}^{\prime }} \end{aligned}$$

(5)

3.2 PSO

PSO has gone through a variety of modifications after its initial occurrence. Each particle (bird) can remember its own position and speed and can remember the best position it has reached, and its position and speed can be updated during each iteration.

Suppose that each particle i has a speed $v_{i}^{k}$ and a position $x_{i}^{k}$ at current iteration step k, rand1() and rand2() are two separate random numbers between (0, 1), $\omega$ denotes the inertia factor, and $C_{1}$and $C_{2}$ denote learning factors, $pbest_{i}$ denotes the particle’s local optimal solution in current swarm, and $gbest_{i}$ denotes the particle’s global optimal solution in current swarm. Its speed is updated as Eq. (6)

$$\begin{aligned} v_{i}^{k+1} = \omega \times v_{i}^{k} + C_{1} \times {rand1()}\times \left( {pbest_{i}}-x_{i}^{k}\right) + C_{2} \times {rand2()}\times \left( {gbest_{i}}-x_{i}^{k}\right) \end{aligned}$$

(6)

Its position is updated as Eq. (7)

$$\begin{aligned} x_{i}^{k+1} = x_{i}^{k} + v_{i}^{k+1} \end{aligned}$$

(7)

The framework of particle swarm optimization algorithm is shown as in Fig. 2, more details can be seen in [21].

Fig. 2

Flowchart of PSO

3.3 Parameter adjustment method of PSO

PSO is very time consuming, and in our proposed MADDPG framework, PSO is called in each iteration by each agent. Therefore, it is necessary to speedup PSO while without losing accuracy. As shown in Eq. (5), updating $v_{i}$ of each particle is controlled by inertia weight $\omega$ and learning factors $C_{1}$ and $C_{2}$. These parameters have impacts on PSO performance, and they are adjusted during each iteration. Some scholars studied different adjustment methods, trying to balance its global and local searching capabilities. In the following expressions (8) (12), $\omega _\text{max}$ and $\omega _\text{min}$ are constants denoting the maximum and minimum inertia weight; k denotes the current iteration step, and K denotes the total number of iteration steps. There are three different approaches for adjusting Inertia Weight:

1. Adjust inertial weight with linear decreasing function:

$$\begin{aligned} \omega ^{k} = \left(\omega _\text{max} -\omega _\text{min}\right) \times \left( \frac{K-k}{K}\right) + \omega _\text{min} \end{aligned}$$

(8)

2. Adjust inertia weight with nonlinear function:

$$\begin{aligned} \omega ^{k} = \left(\omega _\text{max} -\omega _\text{min}\right) \times \frac{(K-k)^{n}}{K^{n}} + \omega _\text{min} \end{aligned}$$

(9)

3. Adjustment inertial weight with dynamic cosine function:

$$\begin{aligned} \omega ^{k} = \frac{ \left(\omega _\text{max} -\omega _\text{min}\right)}{2} \times \cos {\left( \frac{\pi k}{K}\right) } + \frac{(\omega _\text{max}+\omega _\text{min})}{2} \end{aligned}$$

(10)

Because of $k < K$, the function $\cos \left( \frac{\pi k}{K}\right)$ decreases all the time during the whole iteration process and changes slowly near $k = 0$ and $k =K$ and changes dramatically near $k= \frac{K}{2}$. Therefore, it ensures that the inertia weight changes smoothly at early global search stage and late local fine search stage, which are conducive.

Similarly, there are two adjustment methods for learning factors:

• (1) Adjust learning factors with linear variation:

  $$\begin{aligned} {\left\{ \begin{array}{ll} C_{1}^{k} = \left(C_{1f}-C_{1i}\right) \times \frac{k}{K}+C_{1i} \\ C_{2}^{k} = \left(C_{2f}-C_{2i}\right) \times \frac{k}{K}+C_{2i} \end{array}\right. } \end{aligned}$$

  (11)

  where $C_{1f}$, $C_{1i}$, $C_{2f}$, $C_{2i}$ are constants and $C_{1}\in {[0.5, 2.5]}$, $C_{2} \in {[0.5, 2.5]}$.

• (2) Adjust learning factors with trigonometric function:

  $$\begin{aligned} {\left\{ \begin{array}{ll} C_{1}^{k} = \zeta \times \cos \left[ \left( 1 -\frac{k}{K}\right) \times \frac{\pi }{2} \right] + \delta \\ C_{2}^{k} = \zeta \times \sin \left[ \left( 1 -\frac{k}{K}\right) \times \frac{\pi }{2}\right] + \delta \end{array}\right. } \end{aligned}$$

  (12)

where $\zeta$, $\delta$ are constants, e.g., $\zeta = 2$, $\delta = 0.5$.

In multi-agent reinforcement learning, it may take tens of thousands of episodes for training, or hundreds of thousands of steps before convergence. Therefore, it is necessary to speedup training. We test different combinations of Inertial Weight adjustment and Learning Factors adjustment methods. Finally, we choose linear decreasing method for inertial weight and the linear Variation adjust method for learning factors. This combination can lead to fast convergence and higher advantages, which was named as FPSO. Relevant results will be shown in Sect. 5.

4 FPSO-MADDPG algorithm

In Sect. 4, confrontations between two sides are evaluated under the proposed framework of MADPPG, where each agent using FPSO to select position and attitude to pursue the largest advantage over its opponents. Afterward, each agent is directed to move that position and take appropriate attitude, and then launches attack with high hit probability. In Sect. 4.1, some important concepts and notations are introduced. In Sects. 4.2 and 4.3, the Advantage Function and Reward used in MADPPG are studied, respectively. In Sect. 4.4, the combination of FPSO and MADPPG is introduced in detail, which guides the confrontation.

4.1 Engagement area and life model

A circle area with the tank at the center and a radius of 1.2 km can be defined as a high probability damage zone HPDZ. The hit probability will decrease as the distance increases. However, the hit probability is not very high in the range 1.2~2  km, i.e., the attacker may not win even if it takes an advantage position and attitude. Therefore, we assume that a tank fires its opponents no more than 1.5 km away. The area between 1.2~1.5 km is defined as weapon engagement zone WEZ. Both HPDZ and WEZ are shown in Fig. 3. The line AT denotes the distance between the attacker and the target.

Fig. 3

WEZ and HPDZ of a tank

Fig. 4

Life model of a tank

We assume a simplified damage model, i.e., each tank has an initial life value 1. When the tank enters the WEZ, the two confronting opponents may fire each other. As shown in Fig. 4, if the angle between the line AT and the line at 0 degree is $\theta$ (scaled in radian), the target’s life can be modeled using formula (13).

$$\begin{aligned} {\left\{ \begin{array}{ll} life = life \quad if \quad P < rand(0,1)\\ life = life - \frac{\theta }{2} \quad else \end{array}\right. } \end{aligned}$$

(13)

where P denotes the hit probability. The function rand(0, 1) generates a random numbers between(0, 1). If the random number is greater than P, the target is missed and its life value will not change. If the random number is less than or equal to P, the target T is hit and its life value will reduce. We use $\frac{\theta }{2}$ to simulate the damage degree, and $\theta \in \left( 0,\frac{\pi }{2}\right)$. If the life value is less than zero, the tank is thought to have been destroyed.

4.2 The advantage function

Each particle denotes a possible position and attitude which an agent may take. The quality of each particle is evaluated with the advantage function relative to all possible opponents. The particle with the best quality is selected by the agent.

Fig. 5

Geometric relationship between attacker A and target T

The advantage of one agent over its opponent depends on their relative position and attitude. It can be evaluated in three perspectives, i.e., deviation angle, the departure angle and distance. The relative position and attitude between attacker A and target T are illustrated in Fig. 5, where the line LOS denotes the line of sight, and $\varphi$ denotes the deviation angle and q the departure angle, and D the distance between them.

Let $A_{\varphi }$ represents the attacker’s deviation angle advantage over the target, and it can be expressed as formula (14):

$$\begin{aligned} A_{\varphi }= {\left\{ \begin{array}{ll} \begin{aligned} 1- \frac{\varphi }{5 \varphi _\text{max}} , \quad if \quad 0< \varphi< \varphi _\text{max}\\ 0, \quad if \quad {\varphi _\text{max}}< \varphi < \pi \end{aligned} \end{array}\right. } \end{aligned}$$

(14)

If $\varphi$ is large, the attacker A will expose its side to the target T more, and has less advantages. When $\varphi =0$, the advantage is the largest; when $\varphi$ increases $A_\text{max}$ decreases; when $\varphi > \varphi _\text{max}$, the attacker A exposes its side portion too much to the target and loses the advantage.

Let $A_{q}$ represent the departure angle advantage, it can be expressed as:

$$\begin{aligned} A_{q}= e^{-|{q}|}, \quad {-\pi } \le {q} \le {\pi } \end{aligned}$$

(15)

when $q = 0$ and $\varphi = 0$, the attacker A has the greatest attitude advantage over the target T. Let $A_{D}$ represent the advantage function of distance, and it can be expressed as:

$$\begin{aligned} A_{D}= {\left\{ \begin{array}{ll} \begin{aligned} &{}1,&{} &{} \quad if \quad D< D_{HDPZ}\\ &{}2^{ {\small -\frac{D-D_{HDPZ}}{D_{WDZ}- D_{HDPZ}} }},&{} &{}\quad if \quad D_{HDPZ}< D < D_{ WEZ}\\ &{}0,&{} &{} \quad if \quad D> D_{WEZ} \end{aligned} \end{array}\right. } \end{aligned}$$

(16)

where $D_{HDPZ}$ represents radius of HDPZ, and $D_{WEZ}$ represents the radius of WEZ. If $D< D_{HDPZ}$, it indicates that the target T is in the HDPZ of the attacker A; if $D_{HDPZ}< D < D_{ WEZ}$, it indicates that the target is outside the attacker’s HDPZ, but within its WEZ; if $D> D_{WEZ}$, it indicates that the target is outside the attacker’s WEZ.

The comprehensive advantage ADV is determined by the deviation angle $\phi$, the departure angle q and distance D can be expressed as:

$$\begin{aligned} ADV = A_{\varphi }^{\gamma _{1}} \cdot A_{q}^{\gamma _{}2} \cdot A_{D} \end{aligned}$$

(17)

where $\gamma _{1}$ and $\gamma _{2}$ are weights and with $\gamma _{1}+ \gamma _{2}= 1$.

Suppose that the red side has N agents, the blue side M agents, and $ADV_{i,j}$ is the advantage value of the red agent i over the blue agent j, and it can be expressed as follows:

$$\begin{aligned} ADV{i} = \sum _{i=1}^{N} \left( A_{i,j}-{PD}_{i,j}\right) , \quad i =1,2,...N \end{aligned}$$

(18)

where ${PD}_{i,j}$ represents the penalty suffered by $r_{i}$ when it enters the HDPZ of $b_{j}$, and it can be expressed as:

$$\begin{aligned} {PD}_{i,j}= {\left\{ \begin{array}{ll} \begin{aligned} &{} 0,&{} &{} \quad if \quad D_{i,j} > D_{HDPZ\left(\varphi _{i,j}, q_{i,j}\right)}\\ &{}A_{\varphi }^{\gamma _{1}} \cdot A_{q}^{\gamma _{2}} \frac{D_{i,j}}{D_{HDPZ\left(\varphi _{i,j}, q_{i,j}\right)}},&{} &{}\quad if \quad D_{i,j} < D_{HDPZ\left(\varphi _{i,j}, q_{i,j}\right)} \end{aligned} \end{array}\right. } \end{aligned}$$

(19)

where $\varphi _{i,j}$, $q_{i,j}$ and $D_{i,j}$ are the deviation angle, departure angle and the distance between $r_{i}$ and $b_{j}$, respectively. If $D_{i,j} > D_{HDPZ(\varphi _{i,j}, q_{i,j})}$ it means that $r_{i}$ has not entered the HDPZ of $b_{j}$; If $D_{i,j} < D_{HDPZ(\varphi _{i,j}, q_{i,j})}$, it means that $r_{i}$ has entered theHDPZ of $b_{j}$.

The static advantages of the red side over the blue side can be expressed as follows:

$$\begin{aligned} {ADV}_{static} = \sum _{i=1}^{N} ADV_{i}, \quad i =1,2,...N \end{aligned}$$

(20)

Fig. 6

Illustration of between attacker A and target T

As shown in Fig. 6, both the attacker A and target T sit at the center of a circle. The red circle denotes the WEZ of A, and the black circle the WEZ of target T. When T and A are close enough, an angle $\angle CTB$ (defined as $\theta _{mt}$ ) is formed. The smaller is, the longer the distance between T and A is, the target is more likely to escape from being attacked. When $\theta _{mt}$ is bigger, it is more difficult for T to escape out of A’s attack range. If there are two attackers against one target, the attackers’ joint outflanking encirclement advantage function can be expressed as:

$$\begin{aligned} {ADV}_{\theta _{mt}} = \text{min}\left( \theta _{mt,L},\theta _{mt,R}\right) \end{aligned}$$

(21)

and $\theta _{mt,L}$, $\theta _{mt,R}$ represent the $\theta _{mt}$ of the left and right attacker, respectively.

The red side’s encircling advantage over the blue side can be expressed as follows:

$$\begin{aligned} {ADV}_{encircle} = \sum _{i=1}^{N} {ADV}_{\theta _{mt},j} \end{aligned}$$

(22)

The advantage function of the red side over the blue side can be expressed as:

$$\begin{aligned} {ADV}_{T} = \omega _{1}{ADV}_{static}+ \omega _{2}{ADV}_{encircle} \end{aligned}$$

(23)

$\omega _{1}$ and $\omega _{2}$ are weights on ${ADV}_{static}$ and ${ADV}_{circle}$, respectively, with $\omega _{1}+\omega _{2}=1$.

Suppose that any agent i in those N red agents is facing ${num \_threat}_{j}$ threats from those M blue agents, the red side try to pursue the greatest overall advantage over the blue side by directing each agent to take the best position and attitude, this problem can be expressed as follows:

$$\begin{aligned} \begin{aligned}&\max \quad ADV_{T}\\&\begin{array}{rlll} s.t.&{} 0 \le \varphi _{i} \le \pi \\ &{} {num \_threat}_{j} \le M \\ &{}i=1,2,3\ldots ,N\\ &{}j=1,2,3\ldots ,M \end{array} \end{aligned} \end{aligned}$$

(24)

4.3 Reward function

In the framework of reinforcement learning, reward is used to encourage agents to learn good strategies. In our scenario, the reward is evaluated with three items, i.e., the distance reward, the angle reward and destroy reward. They are defined as the following:

• (1) distance reward $R_{D}$

  $$\begin{aligned} R_{D}= {\left\{ \begin{array}{ll} \begin{aligned} &{}1,&{} &{} \quad if \quad D< D_{HDPZ}\\ &{}2^{ {\small -\frac{D-1200}{2000-1200}}},&{} &{}\quad if \quad D_{HDPZ}< D < D_{ WEZ}\\ &{}-\frac{D}{1000},&{} &{} \quad if \quad D> D_{WEZ} \end{aligned} \end{array}\right. } \end{aligned}$$

  (25)

  where D is the distance between the agent and its opponent.

• (2) angle reward $R_{\alpha }$ In Fig. 6, $\varphi$ is the deviation angle of attacker A, q is the departure angle of target T, and $\alpha$ is the advantage angel which is calculated from FPSO. The attacker’s deviation angle reward and departure angle reward can be expressed as Eqs. (26), (27).

  $$\begin{aligned}{} & {} r_{\varphi }= {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{1-3\varphi }{2\pi },&{} &{} \quad if \quad 0 \le \phi -\alpha< \frac{\pi }{3}\\ &{}\frac{1.5 -3 \varphi }{\pi },&{} &{} \quad if \quad \frac{\pi }{3} \le \phi -\alpha< \frac{\pi }{2} \\ &{}\frac{1-2\varphi }{\pi },&{} &{} \quad if \quad \frac{\pi }{2} \le \phi -\alpha < {\pi } \end{aligned} \end{array}\right. } \end{aligned}$$

  (26)
  $$\begin{aligned}{} & {} r_{q}= {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{1-3q}{2\pi },&{} &{} \quad if \quad 0 \le q< \frac{\pi }{3}\\ &{}\frac{1.5 -3q}{\pi },&{} &{} \quad if \quad \frac{\pi }{3} \le q<\frac{\pi }{2} \\ &{}\frac{1-2q}{\pi },&{} &{} \quad if \quad \frac{\pi }{2} \le q < {\pi } \end{aligned} \end{array}\right. } \end{aligned}$$

  (27)

  The total angle reward of attacker A is:

  $$\begin{aligned} R_{\alpha } = r_{\varphi }+ r_{q} \end{aligned}$$

  (28)

• (3) destroy reward $R_{d}$

If an agent destroys an opponent:

$$\begin{aligned} R_{d} = R_{d}+10 \end{aligned}$$

(29)

If an agent is destroyed:

$$\begin{aligned} R_{d} = R_{d}-10 \end{aligned}$$

(30)

Comprehensive reward function R is therefore:

$$\begin{aligned}{} & {} R =\alpha _{1}R_{D} + \alpha _{2}R_{\alpha } + \alpha _{3}R_{d}, \nonumber \\{} & {} \quad \text {with} \quad \alpha _{1}+ \alpha _{2}+ \alpha _{3} =1, \quad \text {and} \quad \alpha _{1}, \alpha _{2}, \alpha _{3} \ge 0. \end{aligned}$$

(31)

4.4 Selecting the best position and attitude for each agent with FPSO

Given N red agents and M blue agents, each particle in the swarm contains the corresponding position matrix X and attitude matrix H. For a red agent i, it has a position $(x_{i},y_{i})$ and corresponding $\psi _{i}$, which denotes the angle between the forward direction of the agent and the positive direction of the Y axis. Therefore, coordinates of N agents in the red side can be represented with the matrix $X=(x_{1},y_{1},x_{2},y_{2}...x_{N},y_{N})$, and their attitude with the matrix $H=(\psi _{1},\psi _{2}...\psi _{N})$.

To apply particle swarm optimization algorithm to unmanned tank combat, an advantage function defined as Eq. (23) is used to evaluate which can be seen in Sect. 4.2. For example, from the perspective of the red side, the inputs to the advantage function are X, H of the blue side. The outputs of the advantage function include the maximum overall advantage value of the red side over the blue side, positions and attitudes of all red agents corresponding to the maximum overall advantage value.

As shown in Algorithm 1, FPSO is used to evaluate current position and attitude of each agent to pursue the largest advantage. Each agent is then directed to the position with the greatest advantage over its proponents and then, lunches attack with high hit probability. FPSO is specially targeted to real-time decision. Compared with PSO, FPSO has higher performance due to its combination of parameter adjustment approaches, i.e., decreasing inertia weight and linear change of learning factor.

4.5 Fusion of MADDPG and FPSO

Agents of the two side confront each other under the framework of MADPPG, corresponding algorithm is shown in Algorithm 2. Each agent executes distributively, but its critical network is updated by centralized training.

While MADDPG is running, in each iteration in each round the agent will select an action to interact with the current environment according to current states and expected reward R, and then the state S will transfer to the next state. In our scenario, the reward R is defined as in Sect. 4.3.

During training, each agent’s critic network can see all information in the environment, therefore can understand the environment in a comprehensive view. And then it will collect information and put into the experience playback pool for subsequent training.

Algorithm 1

Updating X and H

Algorithm 2

FPSO-MADDPG for N agents

5 Experiments setup

Experiments are conducted on a workstation with a CPU Intel Xeon Gold 6230 with 128 G Memory and a Nvidia GPU Geforce RTX 2080 Super with 8 G memory. All codes are written in Python 3.6.8, TensorFlow 1.1.2. Anaconda 4.9.2, and running under Ubuntu 18.04 LTS. We assume that the confronting two side have the same type of tank, i.e., they have the same weapon configurations, amour protection and maneuvering capability. Therefore, experiments can expose effectiveness of decision making, which is critical to wining the confrontation. In the following experiments, the red side adopts FPSO-MADDPG algorithm, and the blue side adopts MADDPG algorithm.

5.1 Performance comparison between FPSO and DPSO

Some scholars used the combination of discrete particle swarm optimization (DPSO) and formation algorithm to solve the problem of UAV confrontation [30]. Unlike continuous particle swarm optimization (PSO), DPSO divides the whole region into N*N cells. Each cell is flagged as 0 if it contains no agent, or flagged as 1 if it contains any agent. During iteration, the flag of each cell is dynamically updated. DPSO takes a parameter updating method similar to that of PSO.

In the 2 vs.2 confrontation scenario, we tested both DPSO and FPSO. The population of particles is set as 30, and the number of iteration steps is set as 100. Simulation results are summarized in Table 1. It can be seen from Table 1; for DPSO, the finer the battle field is divided, the larger the maximum advantage value is got at the cost of running time.

Table 1 Performance of FPSO and DPSO

Compared with DPSO with N = 40, the maximum advantage value of FPSO is increased by 4.4% and with a speedup of 33.4. Compared with DPSO with N = 20, the maximum advantage value of FPSO is increased by 8.2% and with a speedup of 10.9. Compared with DPSO when N = 10, the maximum advantage value of FPSO is increased by 8.8% and with a speedup of 5. In summarize, the performance of FPSO is far above DPSO, especially it can satisfy real-time requirement.

5.2 Two vs. two tank experiment

Fig. 7

A two vs. two confrontation episode at step 3, 6, 9, 11, 12, 13

Simulation results in one episode of confrontation are shown in Fig. 7. (a) shows current positions and attitudes after some maneuvering. The two red tanks $R_{1}, R_{2}$ stay at the left side of the battlefield, and two blue tanks $B_{1},B_{2}$ stay at the right side. The two red ones are approaching the blue ones. It can be seen from (b) that $R_{2}$ selects the tank $B_{1}$ as the target and keeps approaching, and $R_{1}$ selects $B_{2}$ as the target. The red side takes an X-shaped maneuvering route. As shown in (c) and (d), as $R_{2}$ advances, $R_{2}$ and $B_{1}$ both enter each other’s attack range, i.e., each of them can launch an attack against the other. Therefore, the attitudes they take are very critical. $R_{2}$ is directing its front portion (with strong amour protection) toward $B_{1}$’s side portion (with weak amour protection). Therefore, the red side has certain advantage over the blue side. In figure (e), $B_{1}$ is successfully destroyed by $R_{2}$ and then, is removed from the field of view. Although $R_{2}$ survives due to its advantage attitude, it suffers certain damage. At this time, $B_{2}$ approaches the border where the two red tanks’WEZ range overlap, therefore at a risk of being jointly attacked by the two red tanks. In (f), the two red ones destroy $B_{2}$ in their overlapping WEZ. The red side wins the battle without losing any tank.

The loss function and reward of three algorithms are compared: FPSO-MADDPG, MADDPG and DDPG. As summarized in Figs. 8 and 9, respectively, the average loss or reward in a specific episode is drawn.

Fig. 8

Loss of two vs. two

Fig. 9

Reward of two vs. two

As shown in Fig. 8, the loss of FPSO-MADDPG starts to converge after about 5000 episode and converges to around $-$15 and then, tends to be stable between episode 6000–10,000 with small fluctuations. The loss of MADDPG algorithm can only reach $-$14 after 7000 episodes, with bigger fluctuations between episode 7000–10,000. DDPG’s performance is the worst; its loss can only reach a loss $-$10.7 at around 5000 episodes and then, with even bigger fluctuations after 8000 episodes. In summary, FPSO-MADDPG converges fast with the lowest loss; MADDPG converges slower, with a loss close to that of FPSO-MADDPG, but fluctuates greatly; DDPG cannot converge well, even fluctuates worst at later training stage.

Figure 9 shows that the reward of FPSO-MADDPG increases rapidly, which can reach about 7 after about 2500 episodes. For MADDPG, it takes about 10,000 episodes to reach 7 and for DDPG about 20,000 episodes. After 15,000 episodes, FPSO-MADDPG gets the highest reward compared with the other two algorithms. The maximum reward obtained by DDPG in one episode is 7.62, MADDPG 8.46 and FPSO-MADDPG 9.5.

Fig. 10

Confrontation results of 100 episodes of two vs. two

The red side takes FPSO-MADDPG, MADDPG and DDPG strategy, respectively, and the blue side takes MADDPG. Simulations are conducted for 100 episodes, winning/lose out of each side are summarized in Fig. 10. It can be seen from the figure that FPSO-MADDPG has the highest winning rate 65%, MADDPG is 46%, and DDPG is 34%. Both FPSO-MADDPG and MADDPG have equal draws. In summary, FPSO-MADDPG performs well than the other two, and MADDPG performs well than DDPG.

5.3 Four vs. four tank experiment

In this section, four vs. four confrontation experiments are conducted; both sides have four tanks, i.e., $R_{1}$,$R_{2}$,$R_{3}$,$R_{4}$, on the red side, and $B_{1}$,$B_{2}$,$B_{3}$, $B_{4}$ on the blue side. The red side adopts FPSO-MADDPG algorithm, and the blue side adopts MADDPG algorithm.

Fig. 11

A four vs. four confrontation episode at step 8, 10, 11, 12, 13, 17, A four vs. four confrontation episode at step 22, 25, 29

Figure 11 shows one episode of combat. (a) shows the current position after some maneuvering. $R_{1}$ and $R_{2}$ are approaching the blue side from the northwest, $R_{4}$ is approaching the blue side from the west, and $R_{3}$ is turning to the north of the blue side. They are encircling the blue side from three directions. In (b), $R_{1}$ and $R_{4}$ enter the WEZ of each other. $R_{1}$ directs its front portion toward to $B_{4}$, and $B_{4}$’s side portion is exposed to $R_{1}$. Now, $R_{1}$ has certain advantage over $B_{4}$ and higher chance to destroy. In (c), $R_{1}$ continues to move forward and enters the attack range of $B_{3}$ and $B_{4}$. At this moment, $R_{2}$ also enters the WEZ of $B_{4}$. Now, $R_{1}$ still has better attitude advantage against $B_{3}$ and $B_{4}$, so it is difficult for the blue side to destroy $R_{1}$ from the front. While $B_{3}$ and $B_{4}$ are attacked by $R_{1}$, $R_{2}$ can launch an attack on $B_{4}$ from its side portion. In (d), $B_{3}$ and $B_{4}$ are destroyed by the joint attack from $R_{1}$ and $R_{2}$, and they are removed from the battle field. $R_{1}$ enters WEZ of $B_{1}$ and $B_{2}$. In (e), $R_{1}$ is destroyed by the joint attack from $B_{1}$ and $B_{2}$, and is removed from the battle field. From (e)$\sim$(f), $R_{2}$ is about to enter the WEZ of $B_{1}$ and $B_{2}$, and its side portion is completely exposed to $B_{1}$ and $B_{2}$, so it tries to keep away from their attack, waiting for arrivals of $R_{3}$ and $R_{4}$. In (g), $R_{3}$ enters the WEZ of $B_{1}$ and $B_{2}$ from the north. $B_{3}$ chooses $B_{1}$ as its target whose side portion is exposed, but is attacked by $B_{2}$. In (h), both $R_{3}$ and $B_{1}$ are destroyed. At this moment, $R_{4}$ is approaching from the west of $B_{2}$. In the following simulation steps, $B_{2}$ is destroyed by $R_{4}$, and the red side wins the battle, as shown in (i).

The loss and reward of three algorithms are compared: FPSO-MADDPG, MADDPG and DDPG. The average loss or reward in a specific episode is drawn as summarized in Figs. 12 and 13, respectively.

Fig. 12

Loss of four vs. four

Figure 12 shows that the loss of FPSO-MADDPG starts to converge to around $-$3.7 after 5000 episodes and then, tends to be stable between episode 5000–10,000 with small fluctuations. The loss of MADDPG algorithm can only reach $-$3.5 after 4000 episodes and then, rises to about $-$2.5 and fluctuates dramatically between episode 4000–10,000. DDPG’s performance is the worst; its loss can only reach $-$3 at around 4000 episodes and then, has even bigger fluctuations between episode 4000–10,000. In summary, FPSO-MADDPG performs the best; MADDPG performs better than DDPG.

Figure 13 shows that the reward of FPSO-MADDPG initially converges to about 0.6 after around 5000 episodes, while both MADDPG and DDPG converge to about 0.4 after around 20,000 episodes. From episode 12,000 to 25,000, FPSO-MADDPG always gets higher reward than the other two algorithms. The rewards of FPSO-MADDPG and MADDPG algorithms can keep relatively stable after convergence, while the reward of DDPG fluctuates dramatically between episode 15,000–22,000. FPSO-MADDPG reaches a maximum reward 1.045, while MADDPG and DDPG can only reach a maximum reward about 0.7. In general, FPSO-MADDPG gets the highest reward and proves to be the best strategy out of the three.

Fig. 13

Reward of four vs. four

Fig. 14

Confrontation results of 100 episodes of four vs. four

The red side takes FPSO-MADDPG, MADDPG and DDPG strategy, respectively, and the blue side takes MADDPG. Simulations are conducted for 100 episodes, winning/lose out of each side is summarized in Fig. 14. It can be seen from the figure that FPSO-MADDPG has the highest winning rate $51\%$, MADDPG $42\%$ and DDPG $43\%$. FPSO-MADDPG, MADDPG and DDPG have draws of 36, 42 and 33, respectively, and lose 13, 27, and 24, respectively. In summary, FPSO-MADDPG performs well than the other two, and MADDPG performs well than DDPG.

6 Conclusions and future work

In this research, the FPSO-MADDPG algorithm is proposed, where Fast Particle Swarm Optimization (FPSO) is integrated into traditional MADDPG algorithm. FPSO evaluates the best advantage position and attitude for each agent; MADPPG then directs corresponding agent according to these evaluation results. Simulation experiments are conducted on two vs. two and four vs. four scenarios. Compared with DDPG and MADPPG algorithms, the proposed algorithm performs the best and has the highest wining probability. We notice that our work assumes a flat and no obstacle battle field, and these assumptions are too ideal. In future, we will consider impacts of terrain and obstacles on tank’s movement.