Large neighborhood local search method with MIP techniques for large-scale machining scheduling with many constraints

Abstract

This study addresses the problem of scheduling machining operations in a highly automated manufacturing environment while considering the work styles of workers. In actual manufacturing, many aspects of the operation must be considered, such as constraints related to the works to be machined in the machining schedule and the states of the workers. To derive good solutions for such a large-scale problem with many constraints within a realistic amount of computation time, we develop an optimization technique based on a mixed-integer programming (MIP)-based large neighborhood local search method for the machining scheduling problem. Then, computer experiments on a problem based on actual machining requirements are performed to verify the validity of the proposed method.

1 Introduction

In recent years, production processes at manufacturing sites have been rapidly automated. However, some tasks still need to be performed manually. Thus, operational problems such as complications with production control can occur because of the mixing of humans and machines. These problems can be solved as combinatorial optimization problems; however, at an actual site, there are many requirements to be considered, which increases the number of decision variables and constraints. Many of these optimization problems are solved using meta-heuristics [1]. However, for some problems that are of a large scale or complicated by many constraints, it is difficult to define the solution representation and neighborhood; and even if they could be defined, the search space is large or complex. Therefore, in such cases, it is difficult to derive a good solution even if a considerable amount of time is spent on computation [2]. For such problems, the neighborhood setting should be set according to the constraint structure or variable expression. This study attempts to devise the neighborhood structure of the mixed-integer programming (MIP)-based large neighborhood local search method to derive a good solution for a large-scale problem with many constraints within a realistic amount of computation time. In recent years, such methods that incorporate the MIP model into a local search method have been proposed [3, 4].

For this study, we target a machining scheduling problem for a real automated manufacturing site. In our previous study, we proposed an optimization technique based on an MIP model [5] for the problem. However, that study had a limitation in that the optimization requires considerable computation time. For our targeted problem, this would be an infeasible solution because in a real manufacturing site, there are many constraints involved in machining objects (hereinafter referred to as “workpieces") or performing tasks. Some cases even require a long-term schedule, which would increase the number of workpieces.

For our newly proposed optimization technique, which is intended to derive a good solution within a realistic amount of computing time, we incorporate the use of filters into the MIP neighborhood local search method to obtain good solution efficiency. Then, we perform computer experiments on problems based on actual processing requirements to verify the validity of the proposed method. We also verified the effect of using filters.

2 Overview of target machining scheduling problem

2.1 Target process

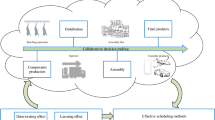
The target of this study is a real machine tool manufacturer of automobile manufacturing facilities. In this company, there are approximately 1,000 employees, and all processes are controlled by computers. In addition, the machine tools are worked all day. The person in charge of each process creates the schedule manually every morning. Thus, the lead time to completion for each workpiece remains unclear. This study focuses on the machining processes performed using a machining center in such a factory and attempts to improve the efficiency of these production processes.

A machining center (MC) is a processing machine tool that machines different types of workpieces. It is used for manufacturing molds or machining metal parts. The machining processes follow procedures (a)–(c) as follows. In the target site, a facility called an automatic pallet system works between the operator and the MC (Fig. 1).

• (a) Install the workpiece and jig.

• (b) Machine the workpiece.

• (c) Remove the workpiece.

Fig. 1

Machining process using a pallet system

A pallet is a table on which workpieces are installed. There are a total of 12 pallets, and the operator can install workpieces in any order. The MC sequentially machines workpieces that have already been installed on the pallet (regardless of the installation order). Then, the machined workpieces are returned from the MC, and the operator removes the workpieces from the pallet in any order, similar to in the installation step.

The pallet requires the installation of a jig to fix the workpieces. Although there are supported and unsupported jigs that can be used for each workpiece, this type of setup requires supported jigs to be attached.

Some workpieces require multiple machining processes. If all the required machining is not completed after the removal of the workpiece, the workpiece is reinstalled and worked on again.

Each workpiece has a part number. If the part numbers differ before and after the workpieces are on the pallet, it takes 10 min for the changeover.

Although the MC can work continuously without a break, the operator, as a human being, needs breaks periodically, especially during the night. This study assumes the derivation of a multi-day schedule, and therefore, it is important to deal with the scenario in which only MCs operate during the night.

Although there are various ways to evaluate the schedule, this study focuses on the sum of the delivery time margin for each workpiece.

2.2 Modeling of target problem

The target problem indicated in Sect. 2.1 has the following features.

• The work order of the operator and MC can be determined independently.

• Limited time is available for the operator to work.

Such a problem can be considered a job-shop scheduling problem (JSP [6]) for two machines: an operator and an MC. In this case, work corresponds to the workpiece, and tasks correspond to the three types of processes involved, as follows (parentheses indicate the subject who does the work).

• Installation of the workpiece and jig (Operator).

• Removal of the workpiece and jig (Operator).

• Machining of the workpiece (MC).

An example of a scheduling problem is as follows.

• Workpiece A, B, and C:

  • A: Completed after one processing (Work A$_1$).

  • B: Completed after two processes (Work B$_1$, B$_2$).

  • C: Completed after three processes (Work C$_1$, C$_2$, C$_3$).

An example schedule is shown in Fig. 2. According to the schedule, the operator first installs workpiece A$_1$. Then, as the operator installs workpiece B$_2$ on another pallet, the MC simultaneously starts machining workpiece A$_1$.

Fig. 2

Example schedule

The decisions and constraints of pallet and jig selection are as follows.

• Pallet:

  • (a) Multiple workpieces cannot be simultaneously installed on a single pallet. In other words, the operator can install only one workpiece at a time.

  • (b) There is a limit to the number of pallets available.

• Jig:

  • (A) The type of jig required for each workpiece is defined.

  • (B) Installation/removal of the jig is performed by the operator and requires 45 min. The jig may remain installed onto the pallet or may be removed and reinstalled as necessary.

  • (C) The number of available jigs has an upper limit for each type.

In our previous study, we proposed an MIP model [7] for such a problem. The model is shown as follows. This model includes a deadline constraint, and therefore, only a realistic schedule is derived.

Definitions
$\bullet$ Machine ID: $\textrm{M}_i$	$\left\{ \begin{array}{cc} i=1: \hbox {Operator}\\ i=2: \hbox {MC} \end{array} \right.$
$\bullet$ Workpiece ID: $\textrm{J}_j$	($j \in \{1,...,W\}$)
$\bullet$ Number of $\textrm{J}_j$ tasks: $n_j$	($j \in \{1,...,W\}$)
$\bullet$ Task set $\mathcal {W}$:	($\mathcal {W}=\{ N_{j-1}+1,...,N_{j}\ |\ N_{j} = \sum _{m=1}^{j}N_{m}\ ;\ N_{0} = 0\}$)
$\bullet$ Installation task set: $\mathcal {B}$
$\bullet$ Break task set: $\mathcal {R}$
$\bullet$ Task ID for all tasks: $\textrm{O}_{k}$	($k \in \mathcal {W} \cup \mathcal {R}$)
$\bullet$ Jig ID: $\textrm{H}_h$	($h \in \{1,\ldots ,F$})
$\bullet$ Jig set corresponding to $\textrm{O}_{k}$: $\mathcal {G}_k$	$(k \in \mathcal {W})$
$\bullet$ Machine ID for machinable $\textrm{O}_{k}$: $\mu _{k}$	$(k \in \mathcal {W})$
$\bullet$ Pallet ID: $\textrm{L}_l$	($l \in \{1,\ldots ,12$})
Constants
$\bullet$ Number of workpieces: W
$\bullet$ Number of all jigs: F
$\bullet$ Processing time of $\textrm{O}_{k}$: ${P}_{k}$	$(k \in \mathcal {W} \cup \mathcal {R})$
$\bullet$ Nighttime period: T
$\bullet$ Day: s	$(s \in \{1,\ldots ,D \})$
$\bullet$ Start time of night on day s: $t^{\textrm{NS}}_{s}$	$(s \in \{1,\ldots ,D \})$
$\bullet$ Start time of break: $t^{\textrm{RS}}_k$	$(k \in \mathcal {R})$
$\bullet$ Show the noncommon item numbers between $\textrm{O}_k$ and $\textrm{O}_{k^{\prime }}$: $\omega _{kk^{\prime }} \in \{0,1\}$
$\bullet$ Deadline of workpiece $\textrm{J}_j$: $E_j$	$(j \in \{1,\ldots ,\textrm{W}\})$
$\bullet$ Big real number: A
Decision variables
$\bullet$ Start time of $\textrm{O}_{k}$: $t^{\textrm{S}}_{k}$	$(k \in \mathcal {W} \cup \textrm{R})$ (A.1)
$\bullet$ Processing order of tasks: $x_{kk^{\prime }}$	$(k \in \mathcal {W} \cup \mathcal {R})$ (A.2)
$\bullet$ Date assignment of a task: $y^{s}_{k}$	($s \in \{1,\ldots ,D\}\ ;\ k \in \mathcal {W}$) (A.3)
$\bullet$ Pallet assignment of a task: $v_{kl}$	($k \in \mathcal {W}\ ;\ l \in \{1,\ldots ,12\}$) (A.4)
$\bullet$ Jig assignment of a task: $u_{kh}$	($k \in \mathcal {W}\ ;\ h \in \{1,\ldots ,F\}$) (A.5)

Dependent variables
$\bullet$ Completion time of $\textrm{O}_{k}$: $t^{\textrm{F}}_{k}$	($k \in \mathcal {W} \cup \textrm{R}$)
$\bullet$ Delivery time of margin for $\textrm{J}_j$: $\psi _j$	($j \in \{1,\ldots ,W\}$)
$\bullet$ Sharing the pallet l or not between tasks: $\rho _{kk^{\prime }l}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12\}$)
$\bullet$ Sharing a pallet or not between tasks: $\Delta _{kk^\prime },\Delta ^{\textrm{R}}_{kk^\prime }$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Sharing the jig h or not between tasks: $\varepsilon _{kk^{\prime }h}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ h \in \{1,\ldots ,F\}$)
$\bullet$ Sharing a jig or not between tasks: $\alpha _{kk^\prime },\alpha ^{\textrm{R}}_{kk^\prime }$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Recent processing order of tasks on a pallet: $x^{\textrm{P}}_{kk^{\prime }}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Processing order on a jig: $x^{\textrm{J}}_{kk^\prime }$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Pallet sharing or not between tasks on a jig: $\kappa _{kk^{\prime }}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Jig sharing or not between tasks on a pallet: $\lambda _{kk^{\prime }}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Jig sharing or not on a pallet: $\gamma ^{\textrm{B}}_k,\gamma ^{\textrm{A}}_k$	($k \in \mathcal {B}$)
$\bullet$ Pallet sharing or not on a jig: $\pi ^{\textrm{B}}_k,\pi ^{\textrm{A}}_k$	($k \in \mathcal {B}$)
$\bullet$ Jig use or not: $\tau _{h}$	($h \in \{1,\ldots ,F\}$)
$\bullet$ Jig replacement or not: $\phi ^{\textrm{B}}_{k},\phi ^{\textrm{A}}_{k}$	($k \in \mathcal {B}$)
$\bullet$ Setting up or not between tasks: $\eta _{kk^{\prime }}$	($k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}$)
$\bullet$ Setting up or not: $\theta _{k}$	($k \in \mathcal {B}$)

Objective
$\textrm{Maximize} \ \sum ^{W}_{j=1}{\psi _j}$	(B.1)
Constraints
$E_{j} - t^{\textrm{F}}_{k} \ge {\psi _j}$	$(j \in \{1,\ldots ,W\}\ ;\ k = \sum _{m=1}^{j}N_{m})$ (B.2)
$t^{\textrm{S}}_{k} \ge C_j$	$(k \in \mathcal {B}\ ;\ j \in \{1,\ldots ,W\}\})$ (B.3)
$t^{\textrm{F}}_{k} \le E_j$	$(k = \sum _{m=1}^{j}N_{m}\ ;\ j \in \{1,\ldots ,W\})$ (B.4)
$t^{\textrm{S}}_{k} \ge t^{\textrm{F}}_{k-1}$	$(k \in \{N_{j-1}+2,\ldots ,N_j\ |\ j \in \{1,\ldots ,W\}\})$ (B.5)
$t^{\textrm{S}}_{k^{\prime }} \ge t^{\textrm{F}}_{k} - A(1 - x_{kk^{\prime }})$	$(k,k^{\prime } \in \{\mathcal {W} \cup \mathcal {R}\ |\ k \ne k^{\prime },\ \mu _k = \mu _{k^{\prime }} \})$ (B.6)
$t^{\textrm{S}}_{k} \ge t^{\textrm{F}}_{k^{\prime }}- Ax_{kk^{\prime }}$	$(k,k^{\prime } \in \{\mathcal {W} \cup \mathcal {R}\ |\ k \ne k^{\prime },\ \mu _k = \mu _{k^{\prime }} \}$ (B.7)
$\sum _{s=1}^{D}y^{s}_{k} = 1$	$(k \in \{\mathcal {W}\ |\ \mu _k = 1\})$ (B.8)
$t^{\textrm{S}}_{k} \ge 0$	$(k \in \mathcal {W})$ (B.9)
$t^{\textrm{S}}_{k} = t^{\textrm{RS}}_k$	$(k \in \mathcal {R})$ (B.10)
$t^{\textrm{F}}_{k} \ge t^{\textrm{S}}_{k} + P_{k}$	$(k \in \mathcal {W} \cup \mathcal {R})$ (B.11)
$t^{\textrm{S}}_{k} \ge (t^{\textrm{NS}}_{s-1}+T)y^{s}_{k}$	$(k \in \{\mathcal {W}\ |\ \mu _k = 1\}\ ;\ s \in \{2,\ldots ,D\})$ (B.12)
$t^{\textrm{NS}}_{s} + A(1-y^{s}_{k}) \ge t^{\textrm{F}}_{k}$	$(k \in \{\mathcal {W}\ |\ \mu _k = 1\}\ ;\ s \in \{1,\ldots ,D\})$ (B.13)
$\sum _{l=1}^{12}v_{kl}=1$	$(k\in \mathcal {B})$ (B.14)
$t^{\textrm{S}}_{k^{\prime }} \ge t^{\textrm{F}}_{k+2}+A(v_{kl}+v_{k^{\prime }l}+x_{kk^{\prime }}-3)$	$(k,k^{\prime } \in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12 \})$ (B.15)
$\sum _{h \in \mathcal {G}_{k}}{u_{kh}}=1$	$(k\in \mathcal {B})$ (B.16)
$u_{kh} = 0$	$(k\in \mathcal {B}\ ;\ h \in \{1,\ldots ,F\ | \ \overline{\mathcal {G}_k}\})$ (B.17)
$t^{\textrm{S}}_{k^{\prime }} \ge t^{\textrm{F}}_{k+2} + A(u_{kh}+u_{k^{\prime }h}+x_{kk^{\prime }}-3)$	$(k,k^{\prime } \in \{ \mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ h \in \mathcal {G}_k)$ (B.18)
$t^{\textrm{F}}_k \ge t^S_k + P_k + 22.5 \phi ^{\textrm{B}}_{k}$	$(k\in \mathcal {B})$ (B.19)
$t^{\textrm{F}}_{k+2} \ge t^S_{k+2} + P_{k+2} + 22.5 \phi ^{\textrm{A}}_{k}$	$(k\in \mathcal {B})$ (B.20)
$t^{\textrm{F}}_{k} \ge t^S_{k} + P_{k} + 10 \theta _{k}$	$(k\in \mathcal {B})$ (B.21)
$x_{kk^\prime } \in \{0,1\}$	$(k,k^{\prime } \in \{\mathcal {W} \cup \mathcal {R}\ |\ k \ne k^{\prime },\ \mu _k = \mu _{k^{\prime }} \})$ (B.22)
$y^s_k \in \{0,1\}$	$(k \in \{\mathcal {W}\ |\ \mu _k=1\}\ ;\ s \in \{1,\ldots ,D\})$ (B.23)
$v_{kl} \in \{0,1\}$	$(k\in \mathcal {B}\ ;\ l\ \in \{1,\ldots ,12\})$ (B.24)
$u_{kh} \in \{0,1\}$	$(k\in \mathcal {B}\ ;\ h \in \{1,\ldots ,F\})$ (B.25)
$\rho _{kk^{\prime }l} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12\})$ (B.26)
$\rho _{kk^{\prime }l} \ge v_{kl} + v_{k^{\prime }l} - 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12\})$ (B.27)
$\rho _{kk^{\prime }l} \le \frac{v_{kl} + v_{k^{\prime }l}}{2}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12\})$ (B.28)
$\Delta _{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.29)
$\Delta _{kk^{\prime }} \ge v_{kl} + v_{k^{\prime }l} - 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ l \in \{1,\ldots ,12\})$ (B.30)
$\Delta _{kk^{\prime }} = \sum ^{12}_{l}{\rho _{kk^{\prime }l}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.31)
$\Delta ^{\textrm{R}}_{kk'} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.32)
$\Delta ^{\textrm{R}}_{kk'} = 1 - \Delta _{kk'}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.33)
$\varepsilon _{kk^{\prime }h} \in \{0,1\}$	$(k ,k^{\prime } \in \{ \mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ h \in \mathcal {G}_k)$ (B.34)
$\varepsilon _{kk^{\prime }h} \ge u_{kh} + u_{k^{\prime }h} -1$	$(k ,k^{\prime } \in \{ \mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ h \in \mathcal {G}_k)$ (B.35)
$\varepsilon _{kk^{\prime }h} \le \frac{u_{kh} + u_{k^{\prime }h}}{2}$	$(k,k^{\prime } \in \{ \mathcal {B}\ |\ k \ne k^{\prime }\}\ ;\ h \in \mathcal {G}_k)$ (B.36)
$\alpha _{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.37)
$x_{k+2\ k^\prime } \ge x_{kk^\prime } + \alpha _{kk^\prime } - 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.38)
$\alpha _{kk^{\prime }} = \sum _{h \in \mathcal {G}_k}{\varepsilon _{kk^{\prime }h}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.39)
$\alpha ^{\textrm{R}}_{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.40)

$\alpha ^{\textrm{R}}_{kk^{\prime }} = 1 - \alpha _{kk^{\prime }}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.41)
$x^{\textrm{P}}_{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.42)
$x^{\textrm{P}}_{kk^{\prime }} \le \Delta _{kk^{\prime }}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.43)
$x^{\textrm{P}}_{kk^{\prime }} \le x_{kk^{\prime }}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.44)
$t^{\textrm{S}}_{k^{\prime }} \ge t^{\textrm{F}}_{k+2} - A(1-x^{\textrm{P}}_{kk^{\prime }})$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.45)
$x^{\textrm{P}}_{kk^{\prime }} + x^{\textrm{P}}_{k^{\prime }k} \le 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.46)
$\sum _{k^{\prime }\in \mathcal {B}}{x^{\textrm{P}}_{kk^{\prime }}} \le 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.47)
$\sum _{k\in \{0,\mathcal {B}\}}{x^{\textrm{P}}_{kk^{\prime }}} = 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.48)
$\sum _{k\in \mathcal {B}}{x^{\textrm{P}}_{0k}} \le 12$	(B.49)
$x^{\textrm{J}}_{kk^\prime } \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.50)
$x^{\textrm{J}}_{kk^\prime } \le \alpha _{kk^\prime }$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.51)
$x^{\textrm{J}}_{kk^\prime } + x^{\textrm{J}}_{k^{\prime }k} \le 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.52)
$x^{\textrm{J}}_{kk^\prime } \le x_{kk^{\prime }}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.53)
$\sum _{k^\prime \in \mathcal {B}}{x^{\textrm{J}}_{kk^\prime }} \le 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.54)
$\sum _{k\in \{0,\mathcal {B}\}}{x^{\textrm{J}}_{kk^\prime }} = 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.55)
$\lambda _{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.56)
$\lambda _{kk^{\prime }} \ge x^{\textrm{P}}_{kk^{\prime }} + \alpha ^{\textrm{R}}_{kk^{\prime }} - 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.57)
$\lambda _{kk^{\prime }} \le \frac{x^{\textrm{P}}_{kk^{\prime }} + \alpha ^{\textrm{R}}_{kk^{\prime }}}{2}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.58)
$\kappa _{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ | \ k \ne k^{\prime }\})$ (B.59)
$\kappa _{kk^{\prime }} \ge x^{\textrm{J}}_{kk^{\prime }} + \alpha _{kk^{\prime }} - 1$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.60)
$\kappa _{kk^{\prime }} \le \frac{x^{\textrm{J}}_{kk^{\prime }} + \alpha _{kk^{\prime }}}{2}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.61)
$\gamma ^{\textrm{B}}_{k} \in \{0,1\}$	$(k \in \mathcal {B})$ (B.62)
$\gamma ^{\textrm{B}}_{k} \ge \sum _{k^{\prime } \in \mathcal {B}}{\lambda _{k^{\prime }k}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.63)
$\gamma ^{\textrm{A}}_{k} \in \{0,1\}$	$(k \in \mathcal {B})$ (B.64)
$\gamma ^{\textrm{A}}_{k} \ge \sum _{k^{\prime } \in \mathcal {B}}{\lambda _{kk^{\prime }}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.65)
$\pi ^{\textrm{B}}_{k} \in \{0,1\}$	$(k \in \mathcal {B})$ (B.66)
$\pi ^{\textrm{B}}_{k} \ge \sum _{k^{\prime } \in \mathcal {B}}{\kappa _{k^{\prime }k}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.67)
$\pi ^{\textrm{A}}_k \in \{0,1\}$	$(k\in \mathcal {B})$ (B.68)
$\pi ^{\textrm{A}}_{k} \ge \sum _{k^{\prime } \in \mathcal {B}}{\kappa _{kk^{\prime }}}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.69)
$\tau _{h} \in \{0,1\}$	$(h \in \{1,\ldots ,F\})$ (B.70)
$\tau _{h} \ge \frac{\sum _{k \in \mathcal {B}}{u_{kh}}}{A}$	$(h \in \mathcal {G}_k)$ (B.71)
$\tau _{h} \le \sum _{k \in \mathcal {B}}{u_{kh}}$	$(h \in \mathcal {G}_k)$ (B.72)
$\phi ^{\textrm{B}}_{k} \in \{0,1\}$	$(k\in \mathcal {B})$ (B.73)
$\phi ^{\textrm{B}}_{k} \ge \frac{\pi ^{\textrm{B}}_k + \gamma ^{\textrm{B}}_k}{2}$	($k\in \mathcal {B})$ (B.74)
$\phi ^{\textrm{A}}_{k} \in \{0,1\}$	$(k\in \mathcal {B})$ (B.75)
$\phi ^{\textrm{A}}_{k} \ge \frac{\pi ^{\textrm{A}}_k + \gamma ^{\textrm{A}}_k}{2}$	$(k\in \mathcal {B})$ (B.76)
$\sum _{k\in \ \mathcal {B}}{x^{\textrm{J}}_{0k}} = \sum _{h\in \{1,\ldots ,\textrm{F}\}}{\tau _h}$	$(k\in \mathcal {B})$ (B.77)
$\eta _{kk^{\prime }} \in \{0,1\}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.78)
$\eta _{kk^{\prime }} \ge \omega _{kk^{\prime }} + x^{\textrm{P}}_{kk^{\prime }} + \alpha _{kk^{\prime }} - 2$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.79)
$\eta _{kk^{\prime }} \le \frac{\omega _{kk^{\prime }} + x^{\textrm{P}}_{kk^{\prime }} + \alpha _{kk^{\prime }}}{3}$	$(k,k^{\prime }\in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.80)
$\theta _{k} \in \{0,1\}$	$(k\in \mathcal {B})$ (B.81)
$\theta _{k} = \sum _{k^\prime \in \mathcal {B}}{\eta _{kk^{\prime }}}$	$(k \in \{\mathcal {B}\ |\ k \ne k^{\prime }\})$ (B.82)

3 Optimization technique based on MIP neighborhood local search method

3.1 Overview

To solve the problem, we apply meta-heuristics based on a local search. A local search is an approximation algorithm that starts with any feasible solution, changes part of the solution, and by looping the step, improves the solution [1].

We apply the MIP neighborhood local search method to the problem to derive a good solution within a realistic amount of computation time. This method generates a neighborhood solution using mathematical programming. Therefore, it enables an efficient search, while defining the neighborhood more widely than does the normal local search method, to derive an optimal solution from within the neighborhood. This method is called a large neighborhood search because of the large neighborhood encompassed by the local search [8].

In this study, we apply a local search method, using any feasible solution as the initial solution. A neighborhood solution is derived using mathematical programming in each iteration of the local search method. Then, we divide the decision variables of the MIP model into free and fixed variables to define a neighborhood. The free variables are derived using MIP, whereas the fixed variables are fixed as the tentative solution. The search space of the neighborhood is larger than that of a typical local search. In addition, the MIP derives an optimal solution from within the neighborhood. Therefore, this method can derive a good solution within a realistic amount of computation time. Some research studies have already applied MIP to large neighborhood searches [1, 3].

Selecting an appropriate combination of free and fixed variables is important for this method. It is presumed that quality improvement can be obtained by selecting variables that have a relationship based on constraints in the MIP model as free variables. Further, we introduce the use of filters to select the combination of free and fixed variables. A filter shrinks the search space by fixing some variables with any feasible solution; therefore, it is expected to reduce the computation time. In addition, a good solution can be derived within a short amount of time by looping this process many times and updating the solution.

This is an overview of the MIP neighborhood local search method; the use of filters establishes the originality of this study. Some case studies have used the MIP neighborhood local search method on lot-size problems [9]. The structure of a lot-size problem is comparatively simple, and usually, the free variables are selected in a very clear manner. However, by contrast, this study considers a target problem that has many variables and constraints. Therefore, this problem is more complex and large-scale than lot-size problems. Finding appropriate filter settings for such problems is the target of this study.

3.2 Procedure

In our proposed method, applying a filter corresponds to narrowing down the neighborhood, whereas solving the subproblem obtained from applying the filter corresponds to selecting a neighborhood solution.

The steps of the proposed method in the solution space are shown in Fig. 3. A feasible solution to the original problem is derived using mathematical programming to generate the initial solution. In each iteration of the local search method, a filter is applied to the tentative solution and to obtain a sub-solution space (corresponding to the neighborhood). The sub-solution space is defined by fixing some variables with a tentative solution; the other variables are free variables. The solution obtained by solving the subproblem using mathematical programming is then the tentative solution of the next iteration. The solution is updated by repeating these steps.

Fig. 3

Search methods in solution space

In summary, a solution is derived via the following steps. Based on the application of the proposed method described earlier, the following procedure is used to derive a quasi-optimal solution for the target problem. The solution is updated by repeating steps 2–4 to derive a good solution.

• 1. Any feasible solution can be derived as an initial solution using mathematical programming. This is the first tentative solution.

• 2. A filter is applied to the tentative solution, and the decision variables are divided into free and fixed variables.

• 3. A subproblem is generated with only free variables based on the applied filter.

• 4. A new tentative solution is derived using mathematical programming.

3.3 Filter settings

We introduce a filter in each iteration to divide decision variables into free and fixed variables. In the local search method, a larger neighborhood improves the solution quality. However, it increases the computation time [1]. Therefore, considering the problem scale and structure, setting filters enables a good solution to be derived efficiently.

Further, in setting the filters, it is presumed that selecting a combination of related variables in the MIP model as free variables increases the solution efficiency. If independent variables are selected as free variables, the solution would be assumed to be the same as that from individually selecting each variable as a filter. Considering the constraints of the MIP model, we introduce five types of filters for the target problem. Filters A, B, C, D, and E are for selecting assignment variables as free variables, for selecting assignment variables for tasks, for selecting the order variables for tasks, a combination of filters B and C, and for selecting variables for any workpieces, respectively. If the start time is fixed, the objective value does not change. Thus, the start time is selected as a free variable for all filters.

• Filter A Starting time $t^{\mathrm S}_k$ of decision variable ${\mathrm O}_k$ Pallet assignment variables for work $v_{kl}$

  Jig assignment variables for work $u_{kh}$

• Filter B Starting time $t^{\mathrm S}_k$ of decision variable ${\mathrm O}_k$ Work-date assignment variables $y^s_k$

• Filter C Starting time $t^{\mathrm S}_k$ of decision variable ${\mathrm O}_k$ Work-processing order variable $x_{kk'}$

• Filter D Starting time $t^{\mathrm S}_k$ of decision variable ${\mathrm O}_k$ Work-date assignment variables $y^s_k$

  Work-processing order variable $x_{kk'}$

• Filter E Starting time $t^{\mathrm S}_k$ of decision variable ${\mathrm O}_k$ Decision variables for some work

4 Computer experiment

4.1 Problem solving

Computer experiments are conducted on problems based on real situations to verify the validity of the optimization techniques presented in Sect. 3. Two problems of different scales were solved using mathematical programming and the proposed method; the quality of the solutions and the computation time are compared. Table 1 lists the number of workpieces and deadlines in the target problems. Problem A and B are small- and large-scale problems, respectively.

Table 1 Numbers of workpieces and deadlines in target problems

For the initial condition of the pallet, all workpieces must be removed the previous day, and the pallet must start with mounting workpieces. The available working time of the operator is 9:00–17:00 (480 min), of which 10:00–10:10, 12:00–12:45, and 15:00–15:15 are rest periods, during which the operator cannot work. The night period is 17:00–9:00 (960 min).

The specifications of the computer used are as follows.

• Apple Mac Studio

• CPU: M1 Max

• RAM: 64 GB

• IBM Cplex version 20.1.0.0

The experimental setups for the mathematical programming and proposed method for deriving a schedule for the experimental problem are as follows.

Mathematical programming Based on the scale of the problem, it is practically difficult to derive an optimal solution, and therefore, the maximum computation time for mathematical programming is set to 86,400 s (24 h), which excludes the computation time required to generate the initial solution. We must create the daily schedule by morning, and thus, the maximum computation time can be 24 h from the last scheduling session. If the optimal solution cannot be found within the set maximum computation time, the tentative solution at that time is considered the best solution; it is the result of sufficient CPU time. For further comparison, an additional solution is derived using mathematical programming within the same duration as the average time used for the MIP neighborhood local search method.

MIP neighborhood local search method The target problem is solved using mathematical programming, and the obtained feasible solution is used as the initial solution. The computation time for deriving an initial solution is set based on the approximate time to obtain any solution from preliminary experiments. In accordance with a filter selected randomly from among the several filters prepared, the variables constituting the solution are divided into free and fixed variables; a small-scale subproblem with only free variables is generated. For filter E, we divide the workpieces in advance, and each one of them is considered a filter E. Thus, for problems A and B, there are three and four types of filter E, respectively. One filter is selected from among the seven or eight filters (Filters A–D and three or four filters E) randomly with equal probability. If the same filter is selected as the previous iteration, the filter selection is redone. A series of operations for solving the generated subproblems using mathematical programming are repeated a certain number of times. If the optimal solution cannot be found within the set time, the solution at that point is considered the best solution, and the next filter is applied. If the total delivery margin of the derived feasible solution is smaller than that of the previous solution, the solution is not updated.

In this experiment, because the filter is selected randomly, the final solution will differ depending on the selected filter. Therefore, 10 computer experiments are performed on the target problems. The mean of the sum of the delivery time margins and computation time required to find the solution, and the maximum and minimum values of the sum of the final delivery margins and computation time are obtained.

4.2 Experimental results

Table 2 outlines the sum of the delivery margins and computation time obtained by mathematical programming and the proposed method for the target problems. The CPU time in parentheses represents the computation time when the initial solution is generated.

Table 2 Sum of delivery time margins and computation time obtained by each method for the target problems

For problem A, which is the small-scale problem, the sum of the delivery time margins derived within the same computation time shows that, in these terms, mathematical programming is approximately 0.6% superior to the proposed method. However, the proposed method was able to derive a close solution using mathematical programming. Further, the differences in (a) and (b) for mathematical programming are small. These differences indicate that the proposed method can still be applicable to a small-scale problem.

On the other hand, for problem B, which is the large-scale problem, the sum of the delivery time margins derived within the same computation time shows that, in these terms, the proposed method is approximately 27% superior to mathematical programming, which, by contrast, required 24 h computations. These results show that the proposed method reduces computational complexity and improves the solution for a large-scale problem.

For each problems, proposed method is equal or better than mathematical programming. It shows that proposed method is operational in real site.

Filters A–D select free variables according to the types of variables. By contrast, filter E selects free variables according to the workpieces. Therefore, we verify the effectiveness of the filters via experiments with different filters applied to problem B; one experiment uses filters A–D, and the other uses filter E.

Filter D is a combination of filters B and C. Therefore, we verify its effectiveness using a case that excludes filters B and C.

Table 3 shows the sum of the delivery time margins for each applied filter. When filter E is applied, the results are inferior to those when filters A–D are applied. However, the result after applying filters A–D is also inferior to that when all filters are applied. Thus, fewer applications of filter E are required.

The result obtained from applying filters A, D, and E is better than that when all filters are applied. This is attributed to filter D including both filters B and C. Therefore, the number of applications of filters can be decreased. Then, the efficiency of search is increased for the same iteration count. However, the computation time increased compared to when all filters are applied. Therefore, for a larger-scale problem, more time may be required to obtain a solution. This result shows that applying filters B and C decreases the computation time.

Table 3 Results of applying filters to problem B

In Tables 2 and 3, the selection probability between all filters A–D and three or four filters E is equalized. For problem B, filter E includes four filters. Then, filters E has a 1 in 8 chance of being selected for problem B. Therefore, the selection probability of filter E is higher than filter A–D when equalize selection probabilities between all filters.

Table 4 shows the result when equalize the selection probabilities between filter types. It means each filter of filter type E has a 1 in 4 chance of being selected. The sum of delivery margin is a little worse than that of Table 2b. It indicates that it needs to be set up selection probabilities of filters appropriately for the problem.

Table 4 Results obtained equalizing selection probabilities between filter types

This computer experiment focused on machining scheduling using the proposed method based on a local search method. Thus, the proposed method is applicable to many types of problems for which the local search method can be used. The difference is that the proposed method needs an MIP model because the neighborhood is defined by decision variables on the MIP model. According to the filter concept, the proposed method is effective for solving problems in which the decision variables are related to each other.

5 Conclusion

We developed an optimization technique based on the MIP neighborhood local search method for deriving good solutions to large-scale, multi-constrained problems within a realistic amount of computation time. We focused on a machining scheduling problem that considers the work styles of workers in a highly automated manufacturing facility.

The results of the computer experiments on problems based on real situations demonstrated that the proposed method can derive good-quality solutions within a realistic amount of computation time. In this computer experiment, the initial solution is derived using mathematical programming. When using any meta-heuristics, the proposed method can have a short computation time. Additionally, the proposed method can be applied to more large-scale problems.