1 Introduction

Data analysis workflows (DAWs) consist of tasks with control or data dependencies. The use of DAWs to help scientists organize the steps involved in large-scale, complex scientific processes is a well-known paradigm [1, 2]. Generally, the structure of a DAW is represented with a directed acyclic graph (DAG). Some workflows are known as bag-of-tasks (BoT) workflows which consist of a set of concurrent bags; each includes a large number of independent homogeneous tasks [3]. Scientists often use a heterogeneous cluster infrastructure to run their DAWs where a set of computing nodes are interconnected with a high-speed network. This choice is due to privacy and financial issues and because it provides high-performance computing environments. Hence, large-scale scientific workflows can be run within a reasonable time [4]. In such an environment, the main goal is to schedule the tasks of the DAW to the computing resources so that the total run time (makespan) is minimized. Generally, scheduling a DAG in heterogeneous systems is a well-known problem in scheduling theory and is NP-Hard [5] because of the heterogeneity within the computing system and the precedence constraints between tasks.

The current research investigates the problem of BoT DAWs scheduling in heterogeneous cluster infrastructures by using mathematical programming. Mathematical models are applicable in scientific and engineering problems, especially those related to optimization. The main advantages of a mathematical model can be highlighted as follows [3, 6]:

  • In a mathematical model, the objective function, decision variables, and the problem constraints are expressed using mathematical expressions. These models provide insight into the problem structure. Some critical information, such as post-optimality analysis or trade-offs, can be derived explicitly.

  • The model can be adapted when the problem conditions change. Modifying the key features of the model (decision variables, constraints, or objective functions) is possible since the underlying mathematical programming engine and algorithms always remain the same. Therefore, maintaining mathematical optimization applications is easier than using heuristics.

  • When we construct a mathematical optimization model for a scientific approach, this approach improves as related optimization algorithms improve.

The model adopted in this work is a Mixed Integer Linear Programming (MILP) model. It provides comprehensive, clear, and flexible descriptions of our assignment problem. This model, because of its linear structure, is also one of the simplest mathematical models that can be solved in a reasonable time through efficient algorithms [7]. A proper combination of compute nodes is selected for the DAW execution so the objective function is minimized, and problem constraints are satisfied. After solving the model, some post-optimality analyses are performed.

The contributions of the current study are highlighted as follows:

  • The problem of DAW scheduling in a heterogeneous cluster environment is formulated as a MILP model to minimize makespan. We compared our approach to five well-known and novel approaches on three different cluster sizes for four different scientific workflows. Comparative results show that our approach outperforms related approaches in \(75\%\) of cases.

  • As a part of the post-optimality analysis, choosing a preferred solution among the set of (possible) alternative optimal solutions is investigated.

  • Relaxation of the makespan in the hope of significantly reducing the number of consumed nodes is probed in another post-optimality analysis.

The paper is organized as follows: Sect. 2 presents a review of the related work, and Sect. 3 illustrates the system model consisting of the infrastructure model, the workflow model and the problem statement. Section 4 introduces the proposed mathematical model. Section 5 discusses the numerical results, and Sect. 6 provides concluding remarks and plans for further studies.

2 Related works

Much research has been done on the problem of scientific DAW scheduling. In a cloud infrastructure, the objective is cost minimization because cloud providers offer a pay-as-you-go model for leasing resources, while in a cluster infrastructure the main goal is makespan minimization [4, 8].

Generally, workflows are scheduled using static or dynamic methods [9, 10]. Static scheduling approaches address the problem of assigning a set of tasks to compute resources in advance. It is assumed that accurate information about workflow and infrastructure resources can be obtained before scheduling, while dynamic scheduling approaches don’t require such assumptions. In this paper, we propose a static scheduling approach for scientific DAWs.

Since obtaining an optimal solution for the DAWs scheduling problem is difficult within a reasonable time in most cases, heuristic-based algorithms have been widely used in the past few decades [8, 9]. Heuristics provide approximate solutions within polynomial time periods. These algorithms for the workflow resource allocation problem in an HPC system can be classified into three groups: list-based, clustering-based, and duplication-based scheduling [11, 12].

A list scheduling algorithm has two phases. The first phase consists of giving a priority to each task of the workflow. The second phase selects the computing node that will execute the task. List-based algorithms are superior to the other groups of heuristic algorithms [13]. HEFT [14] computes the priority or rank of each task \(t_i\) using an upward rank value which indicates the length of the critical path from task \(t_i\) to the exit task. In the task assignment phase, HEFT assigns each task to a node that allows completing the task the earliest. HEFT uses an insertion policy in which tries to insert a task at the earliest idle time between two already scheduled tasks on a computing node, if the slot is large enough to accommodate the task. The PEFT algorithm [15] is an effective list-based scheduling technique with a look-ahead feature. It predicts the impact of an assignment for all successor tasks of the current task without sacrificing the time complexity. This prediction is based on an "optimistic cost table (OCT)" which is used to rank tasks of the workflow, and to select a processor for a task. The IPPTS algorithm [16] introduced the "looking ahead" as a new feature in the task prioritization phase while considering the "out-degree" of a task, and used "downward-upward" approach to look ahead in the computing node selection phase. The IPEFT algorithm [17] calculates the priority of the tasks based on a pessimistic cost table and uses a critical node cost table to predict features. In [18], an estimation of distribution algorithm (EDA) enhanced by path relinking is proposed to minimize makespan. To describe the relative position relationships between two tasks, a specific probability model is created and the task processing permutations are generated by sampling such a model.

In our proposed method, it is assumed that the workflows are in the form of BoT; however, there is no such assumption in heuristic methods (e.g., HEFT) and they can be used in the most general form of workflows. Therefore, it is expected that heuristic methods provide a lower makespan allocation than the proposed method, but because the heuristic methods obtain sub-optimal solutions, this does not happen in some cases. On the other hand, the proposed method has other advantages over heuristic methods. Firstly, despite accepting the above-mentioned limitation, because the proposed method obtains an optimal solution, its solutions are competitive with the solutions of heuristic methods that operate without the above-mentioned limitation and obtain sub-optimal solutions. Secondly, the proposed method has a very important advantage that the heuristic method lacks. By using mathematical models, one can apply secondary criteria to the set of optimal solutions (expertise) and provide post-optimality analysis. For this purpose, we need an explicit representation of all optimal solutions. In mathematical models, this can be done by adding a constraint that guarantees optimality, whereas heuristic methods lack this capability. More precisely, in mathematical programming, the optimality condition is imposed by adding an equality or inequality to the set of constraints of the problem. Thus, the feasible space of the augmented problem is the same as the set of all the optimal solutions to the original problem. Therefore, any type of secondary preference can be applied to this set; equivalently, any secondary objective function can be optimized on it.

A clustering algorithm has three phases [19, 20]: clustering, cluster-merging, and task-ordering within clusters. In the clustering phase, the highly communicating tasks are grouped into clusters. Then, the clusters are merged to be mapped to the bounded number of computing nodes (cluster-merging phase). In the task-ordering phase, task priority is determined to obtain a schedule. The CMWSL algorithm [21] calculates the lower bound of the total execution time for each node by taking into account both the system and application characteristics. As a result, the number of nodes used for actual execution is adjusted to minimize the Worst Schedule Length (WSL). The actual task assignment and task clustering are then performed to minimize the schedule length until the total execution time in a task cluster exceeds the lower bound. The RBCA and DBCA algorithms [22] addressed runtime and dependency imbalance problems, respectively. The dependency imbalance may occur when a task requires data from other tasks clustered in different task clusters; thus, this delays the release of subsequent tasks and increases the overall makespan. The runtime imbalance occurs when the tasks are assigned to the different task clusters with a significant difference in execution time; thus, the execution of task clusters on the next level of the workflow will be delayed and it affects the overall makespan of the workflow. To avoid the dependency imbalance, DBCA clusters the tasks with high dependency correlation(similarity of two tasks in terms of data dependency) together while RBCA clusters the tasks into multiple task clusters with roughly equal workload summation.

Most clustering-based algorithms (e.g. DBCA and RBCA) select the optimal number of task clusters equal to the number of computing nodes. Furthermore, they try to reduce data transfer time by grouping highly communicating tasks into a common task cluster. Employing all computing nodes may not lead to minimum makespan. In our proposed approach, the highly communicating tasks are implicitly grouped by considering the data transfer time in the objective function. Moreover, unlike clustering-based algorithms, the proposed approach does not necessarily use all of the computing nodes. Notably, as a post-optimality analysis, the proposed approach can yield the minimum number of consumed nodes with the minimum makespan (See Sect. 5.2.1).

In duplication-based algorithms, the main idea is to duplicate tasks on multiple computing nodes so that the results of the duplicated tasks are available on multiple nodes to trade computation time for communication time[11, 13]. At first, the TDCA algorithm [23] assigns tasks to computing nodes to generate several initial clusters. In the next step, a task duplication method is applied to modify the initial clusters to reduce the makespan iteratively, so new clusters are added if necessary. Then, TDCA merges some clusters and decreases the number of occupied computing nodes to obtain a preliminary schedule. Finally, a task insertion scheme is adopted which inserts a task to an idle time slot located before its successor tasks if this insertion could make the successor start earlier.

It is concluded from the above-mentioned discussion that achieving a low value of makespan requires a large number of iterations, which leads to a large amount of running time for the algorithm. As is expected the experimental results show that the proposed approach outperforms the TDCA method for all cases in the viewpoint of makespan.

3 System model

This section describes the infrastructure model and the workflow model. At the end, it introduces the problem statement.

3.1 Infrastructure model

We assume that the target computing environment is a heterogeneous cluster, which is a common configuration used for workflow execution [24, 25]. A heterogeneous cluster consists of multiple compute nodes that are different in the amount of cores, memory, and performance characteristics. Also, nodes are usually connected to a distributed file system via a fast interconnection network. We assume that each node k of the cluster is connected to the network via a dedicated link characterized by its bandwidth \(BW_k\). Notably, our model takes data transfer between tasks into account, in addition to the individual task run times themselves (see Sect. 4). However, we do not model the effects of potential network contention due to too many concurrent data transfers (see, e.g., [26]). We plan to extend our model to include such effects as future work.

3.2 Workflow model

As previously stated, a workflow consists of a set of computational tasks with specific inter-dependencies represented by a DAG. Dependencies indicate data flow and execution priority between tasks. We consider the following four scientific workflows from various applied scientific fields:

  • Epigenome: Biology

  • LIGO: Gravitational physics

  • Montage: Astronomy

  • CyberShake: Earthquake science

The specifications of these workflows can be found in the Pegasus Workflow Generator.Footnote 1 A small structure of the workflows is shown in Fig. 1. Some task distribution patterns are commonly used in scientific workflows: pipeline, scatter, gather, broadcast, reuse, and distribute [27, 28]. In these patterns, every level of the DAG contains a group of parallel homogeneous tasks or a single task namely a Bag-of-Task(BoT). A bag includes tasks located in the same level of DAG which have approximately the same characteristics (e.g. runtime and required memory). Studies of the real-world characteristics of parallel workloads show that between 34% and 89% of applications running on parallel systems have a BoT structure [29]. Given that no data dependency exists between the tasks in a bag, they can be executed parallelly. In this study, we propose a model that is applicable to those workflows that have BoT structures. Such partitioning enables us to consider a few bags instead of many tasks individually [3, 30].

Fig. 1
figure 1

The general structure of scientific DAWs [27]

Full size image

3.3 Problem statement

This study addresses the scheduling of scientific workflow applications in heterogeneous cluster environments through mathematical programming with an objective of makespan minimization. We assumed that m computing nodes are available in a cluster environment and that the workflow application consists of n bag-of-tasks at the n levels. We formulated this scheduling problem as an MILP model.

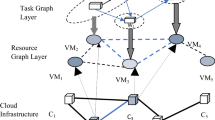
Figure 2 provides an overview of the system model. During the first step, specifications of the cluster infrastructure and the workflow are collected. It can be done by existing approaches to profile the cluster nodes performance [4, 24] and analyzing existing task performance metrics from historical workflow executions. In the second step, these specifications are submitted to the scheduler as input for an MILP mode. Then, by solving the MILP model, optimal assignment is obtained. Finally, the optimal assignment is used to run the DAW in the cluster.

Fig. 2
figure 2

Overview of the system model

Full size image

4 The proposed mathematical model

A mathematical planning study involves: providing a mathematical model for the problem being evaluated, solving the model, and performing a post-optimality analysis. In the proposed model, the objective function and constraints are expressed by linear functions of decision variables. The decision variables contain non-negative integer, binary, and real variables. Thus, the proposed model is an MILP model. Due to the simple structure of the model, efficient computational algorithms and software programs are available to solve it. In the following, we explain how to create constraints and express the objective function as a function of decision variables.

The input data for the mathematical model are described in Table 1. Also, this table explains decision variables existing in the proposed model. The workflow characteristics (e.g., number of levels and tasks in each level) and the infrastructure specifications (e.g., number of cores and size of memory) are available.

Table 1 Models parameters/variables and their description
Full size table

The makespan of a workflow includes executional and data transfer times and the objective function minimizes the makespan. The model has binary and real decision variables. For example, assignment of tasks to computing nodes of the cluster is determined by binary variables. Also, some other auxiliary variables have been used in the proposed model. In addition, the model fulfills constraints on the workflow requirements and infrastructure resource limitations. For example, it ensures that each task is assigned to only one computing node and the memory requirement is fulfilled, etc. The objective function, constraints, and decision variables are as follows:

$$\begin{aligned}&\text {(MILP model)}~~~~ \text {Total Run-Time}\,=\min MS_n \end{aligned}$$
(1)
$$\begin{aligned}&\text {subject to:}\nonumber \\&\sum _{k=1}^{m} {x_{ijk}}=1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} ,\forall j\in J_i \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{j \in J_i}{x_{ijk}} \le \gamma _{ik} \cdot \delta _{i}~~~~~~~~~~~~~~~~~~~~\forall i\in \{1,2,\ldots ,n\}, \forall k\in \{1,2,...,m\} \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{j \in J_i}{x_{ijk}} \ge \gamma _{ik}~~~~~~~~~~~~~~~~~~~~~~~~~\forall i\in \{1,2,\ldots ,n\}, \forall k\in \{1,2,\cdots ,m\} \end{aligned}$$
(4)
$$\begin{aligned}&\gamma _{ik} \cdot Mem_{i}\le mem_k ~~~~~~~~~~~~~~~~~\forall i\in \{1,\ldots ,n\}, \forall k\in \{1,\cdots ,m\} \end{aligned}$$
(5)
$$\begin{aligned}&Z_{i} \ge \gamma _{i-1,k} - \gamma _{i,k} ~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{2,\ldots ,n\}, \forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(6)
$$\begin{aligned}&Z_{i} \ge \gamma _{i,k} -\gamma _{i-1,k} ~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{2,\ldots ,n\}, \forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(7)
$$\begin{aligned}&\Theta _{ik} \le \frac{1}{2} (\gamma _{ik}+ Z_i) ~~~~~~~~~~~~~~~~~~~~\forall i\in \{2,\ldots ,n\}, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(8)
$$\begin{aligned}&\Theta _{ik} \ge (\gamma _{ik}+ Z_i) -1 ~~~~~~~~~~~~~~~~~\forall i\in \{2,\ldots ,n\}, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(9)
$$\begin{aligned}&y_{ijk} \le \frac{1}{3} (x_{ijk}+\gamma _{ik}+ Z_i) ~~~~~~~~~~~\forall i\in \{2,\ldots ,n\},\forall j\in J, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(10)
$$\begin{aligned}&y_{ijk} \ge (x_{ijk}+\gamma _{ik}+ Z_i) -2 ~~~~~~~~\forall i\in \{2,\ldots ,n\},\forall j\in J, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(11)
$$\begin{aligned}&u_{ijk} \le \frac{1}{3} (x_{ijk}+\gamma _{ik}+ Z_{i+1}) ~~~\forall i\in \{1,\ldots ,n-1\},\forall j\in J, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(12)
$$\begin{aligned}&u_{ijk} \ge (x_{ijk}+\gamma _{ik}+ Z_{i+1}) -2 ~~~~~\forall i\in \{1,\ldots ,n-1\},\forall j\in J, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(13)
$$\begin{aligned}&R_i \ge \frac{IDS_i}{BW_k} \cdot \Theta _{ik} ~~~~~~~~~~~~~~~~~~~~~~\forall i\in I_1, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(14)
$$\begin{aligned}&R_i \ge \frac{IDS_i}{BW_k} \cdot \sum _{j \in J_i}y_{ijk} ~~~~~~~~~~~~~~~~\forall i\in I_2,\forall k\in \{1,\ldots ,m\} \end{aligned}$$
(15)
$$\begin{aligned}&WR_i \ge \left( \frac{ODS_{i}}{BW_k} \cdot \Theta _{ik}\right) ~~~~~~~~~~~~~~~\forall i\in I_1,\forall j\in J, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(16)
$$\begin{aligned}&WR_i \ge \left( \frac{ODS_{i}}{BW_k} \cdot \sum _{J}u_{ijk} \right) ~~~~~~~~~~\forall i\in I_2, \forall k\in \{1,\ldots ,m\} \end{aligned}$$
(17)
$$\begin{aligned}&ET_{i} \ge \frac{\left( \sum _{j \in J_i}{x_{ijk}}\right) \cdot W_i}{P_k \cdot C_k}~~~~~~~~~~~~~~~\forall i\in \{1,2,\ldots ,n\} ,\forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(18)
$$\begin{aligned}&ST_{i+1}=ST_i + ET_{i} + R_i + WR_i ~~~~~ \forall i\in \{1,\ldots ,n-1\} \end{aligned}$$
(19)
$$\begin{aligned}&{MS}_i \ge ST_i + ET_{i} + R_i + WR_i ~~~~~~~ \forall i\in \{1,\ldots ,n\} \end{aligned}$$
(20)
$$\begin{aligned}&x_{ijk} \in \{0,1\} ~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} ,\forall j\in J, \forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(21)
$$\begin{aligned}&y_{ijk} \in \{0,1\} ~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} ,\forall j\in J, \forall k\in \{1,2,\ldots ,m\}\end{aligned}$$
(22)
$$\begin{aligned}&u_{ijk} \in \{0,1\} ~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n-1\} ,\forall j\in J, \forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(23)
$$\begin{aligned}&\gamma _{ik} \in \{0,1\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} ,\forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(24)
$$\begin{aligned}&\Theta _{ik} \in \{0,1\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} ,\forall k\in \{1,2,\ldots ,m\} \end{aligned}$$
(25)
$$\begin{aligned}&Z_i \in \{0,1\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(26)
$$\begin{aligned}&MS_i \in \mathbb {R}^+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(27)
$$\begin{aligned}&ST_i \in \mathbb {R}^+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(28)
$$\begin{aligned}&ET_{i} \in \mathbb {R}^+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(29)
$$\begin{aligned}&WR_i \in \mathbb {R}^+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(30)
$$\begin{aligned}&R_i \in \mathbb {R}^+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \forall i\in \{1,2,\ldots ,n\} \end{aligned}$$
(31)

Below, the roles of the constraints and objective function of the model are explained in detail:

  • The objective function, presented in Eq. (1), indicates the makespan of the last bag which is equal to the makespan of the workflow, including execution and data transferring times. The model minimizes this objective function.

  • Constraints (2) state that each task must be assigned to only one node of the cluster.

  • Constraints (3) and (4) guarantee that all tasks in \(B_i\) must be assigned. Precisely, \(\gamma _{ik}=1\) ( \(\gamma _{ik}=0\)) iff \(\sum x_{ijk} > 0\) (\(\sum x_{ijk}=0\)).

    If multiple tasks are assigned to a node, the node will execute them sequentially. Therefore, the memory constraint should be satisfied for each task individually. Constraints (5) guarantee that each task of each bag is assigned to the nodes that can satisfy its memory requirements.

  • Constraints (6) and (7) show that if all tasks of \({B_i}\) and \({B_{i-1}}\) are assigned to a common node of the cluster, then \(Z_{i}=0\). Thus, data transfer time must be disregarded from the analysis.

    Remark: Constraints (6) and (7) can guarantee \(Z_{i}=1\) when tasks of \(bag_i\) and \(bag_{i-1}\) are assigned to different nodes and if they are assigned to the same node, both constraints lead to \(Z_{i} \ge 0\). In mathematical models, some constraints are intentionally ignored because they are automatically satisfied in optimality, since the mathematical models obtain global optimal solution. In addition, this ignoring leads to a simplification of the problem and reduces the number of computations. The proposed model takes advantage of this property of mathematical models. More precisely, the constraints (8)– (13) are linearized forms of the decision variables \(\Theta _{ik}\), \(y_{ijk}\), and \(u_{ijk}\). On the other hand, the constraints (14)–(17) show the effect of the decision variable \(Z_i\) in the calculation of the data transfer time. Since \(makespan=execution~ time+ data~ transfer~ time\), the optimal value of the objective function leads to the minimization of data transfer time. Therefore, in order to keep optimality, when two bags i and \(i-1\) are assigned to the same node, \(Z_i\) must be zero.

  • Constraints (8) and (9) determine the value of decision variable \(\Theta _{ik}\). Indeed, \(\Theta _{ik}=1\) iff \(Z_i\)=1 and \(\gamma _{ik}=1\), otherwise \(\Theta _{ik}=0\). Precisely, these constraints are equivalent to the nonlinear equation: \(\Theta _{ik}=\gamma _{ik} \cdot Z_i\).

  • Constraints (10) and (11) determine the value of decision variable \(y_{ijk}\). Indeed, \(y_{ijk}=1\) iff \(Z_i=1\) and \(\gamma _{ik}=1\) and \(x_{ijk}=1\), otherwise \(y_{ijk}=0\). Precisely, these constraints are equivalent to the nonlinear equation: \(y_{ijk}= Z_i \cdot \gamma _{ik} \cdot x_{ijk}\).

  • Constraints (12) and (13) determine the value of decision variable \(u_{ijk}\). Indeed, \(u_{ijk}=1\) iff \(Z_{i+1}\)=1 and \(\gamma _{ik}=1\) and \(x_{ijk}=1\), otherwise \(u_{ijk}=0\). Precisely, these constraints are equivalent to the nonlinear equation: \(u_{ijk}=Z_{i+1} \cdot \gamma _{ik} \cdot x_{ijk}\).

  • Constraints (14) determine the value of data transfer time of input data for \(B_i\) which i is in I1. We divide the bag’s index into two groups, I1 and I2—I1 for the bags that tasks have a same input data and I2 for others bags.

  • Constraints (15) determine the value of data transfer time of input data for \(B_i\) which i is in I2.

  • Constraints (16) determine the value of data transfer time of output data for \(B_i\) which i is in I1.

  • Constraints (17) determine the value of data transfer time of output data for \(B_i\) which i is in I2.

  • Constraints (18) determine the value of execution time of \(B_i\). The tasks of \(B_i\) can be assigned to different nodes of the cluster simultaneously. \(\frac{(\sum _{j \in J_i}{x_{ijk}}) \cdot W_i}{P_k \cdot C_k}\) denotes just the execution time of those tasks assigned to \(CN_k\). Thus, the execution time of \(B_i\) is max \(\frac{(\sum _{j \in J_i}{x_{ijk}}) \cdot W_i}{P_k \cdot C_k}\).

  • Constraint (19) determines the value of start time of \(B_i\) and guarantees that the model fulfills the sequence of two sequential bags.

  • Constraint (20) calculates the makespan of \(B_i\).

A mathematical model related to a decision-making problem includes decision variables that represent the number of certain resources for use or the level of certain activities. The value of decision variables is specified during the problem-solving process. The decision variables in the model are defined in Eqs. (21)–(31).

For a cluster node having \(C_k\) processors(cores), parallel execution time \(T_p\) of a task \(t_i\) can be calculated using Amdahl’s law [31]:

$$T_p(t_i, C_k)=\left(\alpha + \frac{1-\alpha }{C_k}\right)\cdot T_p(t_i,1)$$

where \(T_p ( t_i, 1 )\) is the execution time of \(t_i\) in single processor and, \(\alpha\) is the fraction of \(t_i\) that cannot be parallelized. We assume that tasks of the workflow can be parallelized completely, so: \(T_p(t_i, C_k)=\frac{T_p(t_i,1)}{C_k}\)

5 Experimental results

The proposed mathematical model was implemented by CPLEX SolverFootnote 2 version 20.1.0. To perform experiments, we used a system with an \(Intel\,core\) i7-6500U CPU, a 2.5 GHz 8 GB RAM. We performed numerical experiments for the Epigenome, LIGO, Montage, and CyberShake workflows, whose specifications were taken from the Pegasus Workflow Generator.

In this section, the proposed approach is compared with related ones. We presented an example to illustrate the performance of the proposed MILP model and other related approaches. Then, two post-optimality analysis scenarios were presented. Finally, the running time of the MILP model and other related works were reported.

5.1 Comparing the proposed approach with related methods

For evaluating performance, we compare our approach to several related approaches. As previously stated, heuristic-based algorithms have been widely proposed to address the problem of DAWs scheduling in the past few decades [8, 9], therefore we selected well-known, efficient (HEFT, CPOP) and state-of-the-art (RBCA, DBCA, TDCA) heuristic algorithms to evaluate our approach. Moreover, these algorithms have been selected from all three groups of heuristic-based scheduling algorithms (list-based, clustering-based, and duplication-based).

For the comparison fairly, we assume the following for all approaches:

  • The communication time is zero when two dependent task \(t_i\) and \(t_j\) are scheduled on the same node.

  • Any task can be started only after completing all precedent tasks and receiving input data.

  • Any tasks must be assigned to one node only once.

  • All tasks are non-preemptive tasks.

  • A computing node of the cluster can run only one single task at any time.

In the following, the algorithms HEFT, CPOP, RBCA, DBCA and TDCA are briefly described for comparison with our proposed MILP approach.

  • Heterogeneous Earliest Finish Time (HEFT): The HEFT [14] algorithm is a well-known static and list-based algorithm for the workflow scheduling problem. It has two main phases: task prioritization phase and task assignment phase. In the task prioritization phase the algorithm computes the priority or rank of each task \(t_i\) using an upward rank value. \(rank_u(t_i)\) calculated by Eq. 32 which indicates the length of the critical path from task \(t_i\) to the exit task where \(\bar{W_i}\) is the average execution time of task \(t_i\) on all nodes, \(\bar{C_{i,j}}\) is the average communication time between tasks \(t_i\) and \(t_j\) across all pairs of nodes and \(rank_u(t_\mathrm{{exit}})=\bar{W_\mathrm{{exit}}}\). In the task assignment phase, HEFT assigns each task to a node that allows completing the task the earliest. It is mentionable that the HEFT algorithm also uses an insertion policy in which tries to insert a task in at the earliest idle time between two already scheduled tasks on a computing node, if the slot is large enough to accommodate the task.

    $$\begin{aligned} rank_u(t_i)= \bar{W_i} + \max _{t_j \in successor (t_i)} \{{rank_u(t_j)+\bar{C_{i,j}}}\} \end{aligned}$$
    (32)

  • Critical Path on Processor(CPOP): The CPOP algorithm [14] has the same phases as the HEFT algorithm with different strategies. In the task prioritization phase, both the upward and downward rank values are considered. \(rank_d(t_i)\) calculated by Eq. 33 represents the longest distance from the entry task to the task \(t_i\), not including the computation cost of the \(t_i\). The priority of each task \(t_i\) is assigned with the summation of upward and downward ranks (\(rank_d(t_i)+rank_u(t_i)\)). The length of the critical path is equal to the priority value of the entry task, and the entry task is selected as the first critical task. Then, the immediate successor task of the selected task that has the highest priority value is selected as the next critical task. This process continues until the exit task. In the computing node selection phase, the critical path node is the node that minimizes the computation time of all tasks on the critical path. A non-critical task is assigned on a node that minimizes the earliest execution finish time of the task with considering the insertion scheduling policy.

    $$\begin{aligned} rank_d(t_i)= \max _{t_j \in predecessor (t_i)} \{{rank_d(t_j)+\bar{W_j}+\bar{C_{i,j}}}\} \end{aligned}$$
    (33)

  • Runtime Balance Clustering Algorithm (RBCA): The RBCA algorithm [22] is one of the most novel static and cluster-based algorithms for the workflow scheduling problem. Although cloud computing is considered as the infrastructure, this approach is comparable with our approach, because, like our approach, the objective of RBSA is minimizing the overall makespan of the workflow. It also applies horizontal task clustering for a workflow that merges the tasks of the same horizontal level in a workflow into a specific number of task clusters. In [22], it has been explained that runtime imbalance occurs when the tasks are assigned to the different task clusters with a large difference in execution time. In such a status, the execution of task clusters on the next level of the workflow will be delayed, thus affecting the overall makespan of the workflow. RBCA tries to balance the run time of defined task clusters using a backtracking strategy. It minimizes the value of TBM(Time Balance Measurement) metric. TBM is calculated by Eq. 34 which represents the maximum summation of runtime among defined task clusters where the tasks of a level of the workflow are clustered into m task cluster \((C_1,\ldots ,C_m)\); \(taskTimeSum(C_i)\) represents the sum of runtime of all tasks in cluster \(C_i\). RBCA chooses the number of compute nodes as the number of task clusters.

    $$\begin{aligned} TBM = \max {\{taskTimeSum(C_i)}\} ~~~~~~ i=1,\ldots ,m \end{aligned}$$
    (34)

  • Dependency Balance Clustering Algorithm (DBCA): The DBCA algorithm is a new static and cluster-based algorithm presented in [22] like RBCA. It also applies horizontal task clustering and considers the number of compute nodes as the number of task clusters. DBCA tries to tackle over dependency imbalanced problem. The dependency imbalance may occur when a task requires the data from other tasks clustered in different task clusters. This delays the release of following tasks and thus increases the overall makespan. To avoid the dependency imbalance, DBCA clusters the tasks with high dependency correlation(similarity of two tasks in terms of data dependency) together.

    The dependency correlation between two tasks \(t_i\) and \(t_j\) is calculated by Eq. 35 where \(succ(t_i)\) represents the set of immediate successors of task \(t_i\), and \(|succ(t_i)|\) represents the number of immediate successors of task \(t_i\).

    $$\begin{aligned} cor(t_i,t_j)= & {} \frac{|succ(t_i)\cap succ(t_j) |}{\sqrt{|succ(t_i) \cdot succ(t_j) |}} \nonumber \\= & {} \sqrt{\frac{|succ(t_i)\cap succ(t_j) |}{|succ(t_i)|}} \cdot \sqrt{\frac{|succ(t_i)\cap succ(t_j) |}{|succ(t_j)|}} \end{aligned}$$
    (35)

  • Task Duplication-based Clustering Algorithm (TDCA): The TDCA algorithm [23] includes four phases which is an improved extension of the TANH algorithm [32]. In the first phase, it assigns tasks to computing nodes to generate several initial clusters. In the second phase, a task duplication method is applied to modify the initial clusters to reduce the makespan, so new clusters are added if necessary. In the third phase, TDCA merges some clusters and decreases the number of occupied computing nodes to obtain a preliminary schedule. Finally, in the last phase, a task insertion scheme, introduced in DCPD [33], is adopted which inserts a task to an idle time slot located before its successor tasks if this insertion could make the successor start earlier.

5.1.1 An illustrative example

To illustrate the performance of the proposed approach compared to related work, we use the workflow in Fig. 3, which is roughly similar in structure to the Epigenome workflow. Assume that the cluster infrastructure consists of three compute nodes N1, N2, and N3 with different computing power. The average data transfer time required between two tasks is shown by the values on the edges. The execution time of the tasks on each of the nodes in the cluster is also shown. Figure 4 shows how our MILP approach and the heuristic algorithms schedule the workflow of Fig. 3. It also shows the scheduling length (makespan).

Regarding the upward ranking of the HEFT, tasks of the same level have the same priority. Therefore, the tasks of a level can be prioritized in ascending order of their number. So, the scheduling order of the tasks for the HEFT algorithm is \(T_1\), \(T_2\), \(T_3\), \(T_4\), \(T_5\), \(T_6\), \(T_7\), \(T_8\), \(T_9\), \(T_{10}\).

The CPOP algorithm identifies four critical paths of equal weight which are {\(T_1-T_2-T_6-T_{10}\)}, {\(T_1-T_3-T_7-T_{10}\)}, {\(T_1-T_4-T_8-T_{10}\)}, and {\(T_1-T_5-T_9-T_{10}\)}. On the other hand, the critical node is \(N_3\) because it minimizes the execution time of the tasks on the critical path. All tasks are scheduled on \(N_3\) and the makespan is 270 if all four paths are considered critical path. If only one of them is considered the critical path, the makespan is 225.

The DBCA and RBCA algorithms give the same result. This is because the levels in the DAG are completely homogeneous. This homogeneity covers both the runtime and the dependencies of the tasks. Since they cluster and assign the tasks of each level of the DAG based on the number of nodes, all nodes are used.

The TDCA algorithm assigns all tasks to node N3. Since N3 is better than the other nodes for all tasks, all schedules from the other nodes are merged onto the best node. The algorithm may work better for cluster infrastructures where no single node is best for all tasks, so different tasks may have different preferred nodes.

Fig. 3
figure 3

A workflow with 10 tasks and computation time of tasks on three nodes of a cluster

Full size image
Fig. 4
figure 4

Scheduling of workflow in Fig. 3 with a MILP (makespan=211), b HEFT(makespan=222), c CPOP (makespan=225), d RBCA (makespan=242), e DBCA (makespan=242), f TDCA (makespan=270)

Full size image

5.1.2 Comparison results

To compare the MILP model with other approaches, we performed experiments on the Epigenome, LIGO, Montage, and CyberShake workflows with four workflow sizes (about 30, 50, 100, and 1000 tasks). We looked into three cluster sizes, namely small, medium, and large (consist of 4, 8, and 16 computing nodes, respectively) with the following parameters:

  • The small cluster:

    \(P[CN_k]=\{15,10,25,20\}\)

    \(C[CN_k]=\{10,6,4,8\}\)

    \(BW[CN_k]=1000\)

    \(mem[CN_k]=\{5000,2000,4000,8000\}\)

  • The medium cluster:

    \(P[CN_k]=\{10,25,15,15,30,12,10,30\}\)

    \(C[CN_k]=\{14,4,10,8,4,12,16,6\}\)

    \(BW[CN_k]=1000\)

    \(mem[CN_k]=\{1000,1050,5000,2000,4000,8000,6000,3000\}\)

  • The large cluster:

    \(P[CN_k]=\{10,25,15,15,30,12,10,30,25,10,15,30,25,12,10,20\}\)

    \(C[CN_k]=\{14,4,10,8,14,12,16,6,4,12,8,6,8,10,14,8\}\)

    \(BW[CN_k]=1000\)

    \(mem[CN_k]=\{1000,1050,5000,2000,4000,8000,6000,3000,1100,1250, 5500,2300,4300,8100,6200,3900\}\)

The numerical results are provided in Tables 2, 3, 4 and Figs. 5, 6, 7. It should be noted that the all bars in Figs. 5, 6, 7 are extracted from the data in Tables 2, 3, 4 which are normalized using the maximum value of makespan for different workflow sizes.

As previously stated in Sect. 2, in contrast to heuristic methods, we assumed that the workflows are in the form of BoT. Therefore, the heuristic methods are expected to give a lower makespan than that of our proposed method. But as seen in the experimental results of makespan reported in Tables 2, 3 and 4, in \(75\%\) of cases, our approach outperforms to other approaches. It should be noted that in almost all other cases (except one), our approach is ranked second in terms of makespan.

Table 2 Obtained makespan of different approaches for scientific workflows on the small cluster
Full size table
Fig. 5
figure 5

Normalized makespan for the workflows with different sizes on the small cluster

Full size image
Table 3 Obtained makespan of different approaches for scientific workflows on the medium cluster
Full size table
Fig. 6
figure 6

Normalized makespan for the workflows with different sizes on the medium cluster

Full size image
Table 4 Obtained makespan of different approaches for scientific workflows on the large cluster
Full size table
Fig. 7
figure 7

Normalized makespan for the workflows with different sizes on the large cluster

Full size image

5.2 Post-optimality analysis

In the theory of decision-making, although optimizing the objective function is the main issue, it is not necessarily the end of the story: employing a post-analysis can optimize other parameters. In this section, we present two interesting cases of post-optimality analysis.

5.2.1 Choosing a preferred solution among the set of alternative optimal solutions

As a post-optimality analysis, choosing a preferred solution among the set of alternative optimal solutions referred to as the preferred optimal solution is important from the decision-maker’s perspective.

In our case, this can be done in the form of Phase 2 optimization. After solving Model MILP in the first phase and calculating the optimal value of makespan (denoted by \(t^*\)), in phase 2 we optimize the objective function expressing the secondary preferences on the set of alternative optimal phase solutions of Phase 1.

Phase 1: Solving the MILP model as follows:

$$\begin{aligned}&t^{*}=\min MS_n \\&\quad \text {subject to:} ~~~~~~~ Eqs.~ (2) - (31) \end{aligned}$$

One of these secondary preferences (which can be important here) is to choose a type of assignment in which the least possible number of nodes are used while getting the best makespan. In a cluster environment that includes a limited number of computing nodes, the fewer nodes we utilize to run applications, the less energy will be consumed, and the more users can start running their applications. For this purpose, for each node \(CN_k\), we define a binary variable \(\eta _{k}\) as follows:

$$\begin{aligned}&\eta _{k}={\left\{ \begin{array}{ll} 1 & \quad {} if~~ \sum _{i}{\sum _{j}{x_{ijk}}}>0\\ 0 & \quad {} O.W \\ \end{array}\right. } \end{aligned}$$
(36)

According to the definition of decision variables in Phase 1, we want to hold the following proposition for each index k:

$$\begin{aligned} \sum _{i}{\sum _{j}{x_{ijk}}}>0 \Longleftrightarrow \eta _{k}=1 ~~~~~~~\forall k\in \{1,2,...,m\} \end{aligned}$$
(37)

It can be shown that in optimality (in optimal solutions) of the following model the above-mentioned proposition holds:

Phase 2: Solving the MILP-ON model

$$\begin{aligned}&\text {(MILP-ON model)}~~~~ \min \sum _{k}{\eta _k} \end{aligned}$$
(38)
$$\begin{aligned}&\text {subject to:} ~~~~~~~Eqs.~ (2) - (31) \nonumber \\&MS_n\leqslant t^{*} +\epsilon \end{aligned}$$
(39)
$$\begin{aligned}&\sum _{i}{\sum _{j}{x_{ijk}}} \le M \cdot \eta _k ~~~~~~~\forall k\in \{1,2,...,m\} \end{aligned}$$
(40)
$$\begin{aligned}&\eta _k \in \{0,1\} ~~~~~~~~~~~~~~~~~~~~~\forall k\in \{1,2,...,m\} , \end{aligned}$$
(41)

where M is a large enough positive number that its value can be any number greater than or equal to the number of bags of the workflow multiplied by the number of tasks. We define binary quantity \(\eta _{ik}\) in the sense that \(\eta _{ik}=1\) if only if at least one task of \(B_i\) is assigned to the \(CN_k\) equivalently to Eq. 42. Also, we define positive integer quantity \(NN_i\) as Eq. 43 that calculates the number of used nodes of the cluster for each \(B_i\).

$$\begin{aligned}{} & {} {\sum _{j}{x_{ijk}}}>0 \Longleftrightarrow \eta _{ik}=1 ~~~~~~~\forall i\in \{1,2,...,n\}, \forall k\in \{1,2,...,m\} \end{aligned}$$
(42)
$$\begin{aligned}{} & {} NN_i =\sum _k {\eta _{ik}} ~~~~~~~\forall i\in \{1,2,...,n\} \end{aligned}$$
(43)

We conducted an experiment for the workflow of Fig. 8 which has four bags (\(B_1,..., B_4\)). The simulated cluster environment consists of 8 computing nodes (\(k=8\)). Parameters of the DAW and computing nodes are as the following:

  • \(P[CN_k]=\{100,80,60,80,40,100,200,190\}\)

  • \(C[CN_k]=1\)

  • \(BW[CN_k]=1000\)

  • \(mem[CN_k]=\{1000,1050,5000,2000,4000,8000,6000,3000\}\)

  • \(W[T_i]=\{1000,500,500,500,500,400,400,400,400,800\}\)

  • \(Mem[T_i]=\{5000,1000,1000,1000,1000,1000,1000,1000,1000,4000\}\)

  • \(IDS[T_i]=\{0,10,10,10,10,20,20,20,20,20\}\)

  • \(ODS[T_i]=\{10,20,20,20,20,20,20,20,20,0\}\)

Solving the MILP model in Phase 1, the optimal makespan is 18.05. In the obtained optimal solution, assignments are as depicted in Fig. 9a. Solving the MILP-ON model in Phase 2, assignments of the optimal solution are as depicted in Fig. 9b with the same makespan. In the second alternative optimal solution, the number of consumed nodes for \(B_2\) and \(B_3\) is three which is less than that of the first optimal solution(four nodes). In general, not all the optimal solutions of phase 1 might be obtained, and indeed, it is not necessary to do that. However, in the second phase, the most preferred optimal solution can be found.

Fig. 8
figure 8

A workflow with 10 tasks and four bag-of-tasks

Full size image
Fig. 9
figure 9

Two different optimal assignments with the same makespan

Full size image

5.2.2 Relaxation of the makespan in the hope of significantly reducing the number of consumed nodes

Sometimes in decision-making, slight appeasement in one goal (even if it is our main goal) may lead to a significant improvement in other goals or preferences. In such cases, by relaxing(increasing here) the mentioned objective function at different levels, various values are obtained for other goals and preferences. These results show a kind of trade-off between considered goals. The results of this trade-off are provided for the decision-maker in the form of a table called the trade-off table for making a preferred decision. There are two main motivations for relaxing the makespan:

  1. 1.

    As makespan increases, the number of occupied nodes decreases; consequently, the amount of energy consumption decreases.

  2. 2.

    Increasing the makespan reduces the number of nodes occupied, so more users can run their programs.

We conducted experiments on the Epigenome, LIGO, Montage, and CyberShake workflows with 100 tasks. The simulated cluster environment consists of sixteen compute nodes with the following parameters:

  • \(P[CN_k]=\{15,10,20,5,10,20,30,25,18,26,17,25,30,21,10,30\}\)

  • \(C[CN_k]=\{20,32,28,16,10,30,32,8,12,28,24,12,18,6,8,16\}\)

  • \(mem[CN_k]=\{50,100,200,850,150,100,250,300,50,100,200,850,150, 100,250,300\}\)

  • \(BW[CN_k]=1000\)

The numerical results are provided in Tables 5, 6, 7, 8. \(t^{*}\) denotes the optimal makespan obtained by solving the MILP model, \(\theta\) is the percentage of reduction in the number of nodes consumed, \(\eta\) is the percentage of increase in the makespan and \(\Delta\) is the amount of relaxing the makespan. From the numerical results reported in Tables 5, 6, 7, 8, the following points can be highlighted:

  • A very small relaxation in makespan leads to a considerable reduction in the number of consumed nodes. For example in Table 5b just relaxing 0.05 percent in makespan leads to a 28.57 percent reduction in the number of consumed nodes. This fact is depicted in Fig 10. Thus, the ratio of gain (saved nodes) to loss (increasing makespan) is 559.14.

  • As shown in Tables 5, 6, 7, 8, as the amount of relaxation in the makespan increases, the rate of improvement in the number of nodes consumed decreases so that a more value of gain-to-loss ratio occurs near the optimal value of makespan.

Table 5 Makespan relaxation for Epigenome workflow (\(t^*= 97.85\))
Full size table
Table 6 Makespan relaxation for LIGO workflow (\(t^*= 59.98\))
Full size table
Table 7 Makespan relaxation for Cybershake workflow (\(t^*= 49.50\))
Full size table
Table 8 Makespan relaxation for Montage workflow (\(t^*= 0.46\))
Full size table
Fig. 10
figure 10

The effect of makespan relaxation on the total number of consumed nodes

Full size image

5.3 Running time

In this subsection, we express the running time of the MILP, HEFT, CPOP, RBCA, DBCA and TDCA approaches. Table 9 shows the running time of the approaches for the Epigenome, Montage, Cybershake and LIGO workflows for a different number of tasks. As can be seen, in most cases, the running time of the TDCA is better than the other ones. Moreover, the running time of the MILP approach is about a second in most cases while the running time of heuristic approaches is less than one second in all cases. Nevertheless, the running time of MILP is negligible compared with the workflow execution time.

Table 9 Running time of the approaches for the workflows in seconds with different sizes
Full size table

6 Conclusion and future works

We proposed a mathematical model (MILP model) for BoT scientific workflow scheduling in heterogeneous cluster environments which minimizes the makespan. The problem was formulated as an MILP model and solved by the CPLEX solver in a reasonable time. In a mathematical model, the objective function and the problem’s constraints are expressed using some explicit mathematical expressions of decision variables.

This provides a useful insight into the structure of the problem. Some critical information, such as post-optimality analysis or trade-offs, can be derived explicitly. We compared our approach against related approaches. In our proposed approach, it is assumed that the workflows are in the form of BoT; however, there is no such assumption in comparative heuristic methods and they can be used in the most general form of workflows. Therefore, heuristic approaches are expected to give a lower makespan than that of our proposed approach, but since they give sub-optimal solutions, this does not happen in most cases, so that our approach outperforms other approaches in 75% of the cases. It should be noted that in almost all other cases (except one), our approach is ranked second in terms of makespan.

We also investigated choosing a preferred solution among the set of (possible) alternative optimal solutions as a part of the post-optimality analysis. As another part of the post-optimality analysis, relaxation of the makespan is explored in the hope of significantly reducing the number of consumed nodes.

The proposed mathematical model also provides an explicit framework for imposing any possible secondary preferences which have not been considered here and may be needed in the future. In the future, we intend to extend our proposed approach to take into account communication congestion and study its effect on the scheduling of a workflow in heterogeneous cluster environments.