1 Introduction

Over the past years, convolutional neural networks (CNNs) have demonstrated excellent accuracy beyond their traditional application niches in computer vision and signal processing [1, 2]. This is in part due to the regularisation mechanism implicit in CNNs, which takes advantage of the hierarchical structure of the data to (1) avoid overfitting via the application of convolution operators as well as (2) reduce the arithmetic cost. This type of operator, though, is responsible for a major fraction of the computational cost required for CNN training and inference [2]. It is therefore natural that a significant effort has been dedicated to develop and optimise efficient algorithms for this particular computational kernel on almost all current processor architectures, from FPGAs (field-programmable gate arrays) to GPUs (graphics processing units) and multi-core processors.

Among the different methods for the convolution operator, we can list (1) the direct algorithm, usually implemented as six nested loops around a multiply-and-add instruction [3]; (2) the lowering (or im2col/im2row-based) approach, which augments the activation inputs into a matrix in order to cast the operator in terms of a compute-intensive, cache-friendly general matrix-matrix (gemm) multiplication [4, 5]; (3) the FFT-based algorithm, which shifts the computation into the frequency domain in order to reduce the arithmetic requirements [6,7,8]; and (4) the Winograd-based convolution, which leverages the Winograd minimal filtering algorithm to decrease the arithmetic cost of the convolution [6, 9]. The general view of these methods and some of their corresponding high-performance implementations in libraries such as, for example, NVIDIA cuDNN and Intel oneAPI, is that the best option from the viewpoints of performance and accuracy largely depends on the parameters that define the convolution, given by the dimensions of the filter and image, and the number of input images (or batch size).

In this paper, we address the efficient implementation of the Winograd-based convolutionFootnote 1, using vector intrinsics, on current general-purpose processors equipped with SIMD FPUs (single-instruction multiple-data floating-point units). The use of vector intrinsics for this purpose, instead of “hand-coded” low-level assembly kernels (with vector instructions), in principle sacrifices some performance. However, as we demonstrate in this work, it also augments the portability of the solution thanks to the support offered by current C compilers. In addition, the use of “high-level” codes with vector intrinsics ease the development of customised deep learning (DL) solutions via layer fusion. In more detail, in this paper, we make the following major contributions:

  • We describe the implementation of the Winograd-based convolution enhanced with vector intrinsics for three types of processor architectures, Intel, ARMv8-A and ARMv8.2-SVE, using 128-bit, 256-bit, 512-bit and Vector-Length Agnostic (VLA) intrinsics, respectively defined in the Intel SSE/AVX2/AVX512 and ARM NEON/SVE. Our overview of these implementations highlights the similarities and differences between the different architecture-specific vector extensions. Furthermore, it also exposes how current compilers, in combination with a certain convergence in the vector intrinsics, help to overcome part of the portability challenges.

  • We present a “macro-tiling” technique that unrolls loops and fuses individual tiles of the Winograd algorithm to improve the utilisation of long vector registers as those present in Intel AVX2 or AVX512 or ARM SVE intrinsics.

  • We perform a complete evaluation of the implementations based on Intel SSE/AVX2/AVX512 and ARM NEON/SVE on three platforms equipped with Intel Xeon Gold, ARM Cortex-A57 and Fujitsu A64FX multi-core processors. This experimental analysis includes the baseline and our vectorised/parallel Winograd-based convolutions, an alternative lowering-based convolution algorithm, and two storage layouts, using two representative CNNs.

This paper extends the work in [10] with (1) the vectorisation of the Winograd algorithm using Intel AVX2/AVX512 and ARM SVE intrinsics; (2) the design of a “macro-tiling” technique to fully exploit long vector registers; and (3) the evaluation of the ARM SVE implementations on a Fujitsu A64FX processor and the evaluation on other popular CNNs.

The rest of the paper is structured as follows: In Sect. 2, we briefly review the foundations of the Winograd-based method for the convolution. Next, in Sect. 3, we describe our “multi-platform” realisation of these algorithms with vector intrinsics and OpenMP, highlighting the similarities and differences when the target architecture is an Intel processor, an ARM A57 server or a Fujitsu processor A64FX with SVE architecture. In Sect. 4, we evaluate the performance of the implementations on the former three types of architectures, and finally, in Sect. 5, we close the paper with a few remarks and a brief discussion of future work.

2 Convolution operators via the Winograd minimal filtering algorithm

The Winograd (minimal filtering) algorithm provides a method to obtain an efficient realisation of a convolution operator [11]. Concretely, given a convolution layer that applies a filter f to an input image d, consisting of c input channels, in order to produce an output y, with k channels, the Winograd-based convolution can be expressed as

$$\begin{aligned} \begin{array}{l} y_{i_k} = A^T\left( \sum \limits _{i_c=1}^{c} \left( G f_{i_k,i_c} G^T\right) \odot \left( B^T d_{i_c} B\right) \right) A,\quad i_k=1,2,\ldots ,k, \end{array} \end{aligned}$$
(1)

where G, B, respectively, denote the transformation matrices for the filter and input matrices; A is the inverse transformation matrix; \(f_{i_k,i_c}\) is the \(i_c\)-th channel of the \(i_k\)-th filter; \(d_{i_c}\) is the \(i_c\)-th channel of the input image; \(y_{i_k}\) is the \(i_k\)-th channel of the output; and \(\odot\) denotes the Hadamard (or element-wise) multiplication [9].

From a practical point of view, the 2D Winograd-based convolution applies an \(r \times r\) filter to a \(t\times t\) input tile in order to produce an \(m \times m\) output tile, with \(t = m+r-1\). An \(h_i \times w_i\) image is processed by partitioning it into \(t \times t\) tiles, with an overlapping factor of \(r-1\) elements between neighbouring tiles, yielding \(\lceil h_i /m\rceil \lceil w_i/m\rceil\) tiles per channel. In this algorithm, choosing a larger value for m thus reduces the number of arithmetic operations, unfortunately at the cost of introducing numerical instability in the computation [12]. For that reason, m is usually set to be small, with two popular cases being \(F(m \times m, r \times r) = F(4 \times 4, 3 \times 3)\) and \(F(2 \times 2, 3 \times 3)\).

According to Winograd’s formula (1), the intermediate Hadamard products are summed over all c channels to produce the \(i_k\)-th output channel. However, by properly scattering each transformed tile of the filter and input along the \(t \times t\) dimensions, on respective intermediate workspaces U and V, of sizes \(t\times t \times k \times c\) and \(t \times t \times c \times (\lceil h_i/m\rceil \lceil w_i/m\rceil )\), both the Hadamard products and the element-wise summations can be collapsed into \(t \times t\) independent matrix-matrix multiplications (also known as a “batched” gemm). Finally, the same coordinates of the resulting \(t\times t\) matrices are gathered to form a new \(t\times t\) tile which is next used to compute the inverse transform as a \(m\times m\) tile on the output tensor.

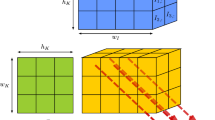
Figure 1 depicts the general workflow of the “batched” gemm variant of the Winograd algorithm, exposing the four major phases: (1) filter transform; (2) input transform; (3) “batched” gemm; and (4) output inverse transform. In the example, the algorithm receives input and filter tensors, respectively, of size \(c \times h_i \times w_i\) and \(k \times c \times r \times r\), to produce an output tensor of size \(k \times h_o \times w_o = k \times (h_i-r+1) \times (w_i-r+1)\).

Fig. 1
figure 1

Workflow for the Winograd algorithm

Full size image

In DL applications, the aforementioned 3D input/output tensors are extended with a batch dimension n, for the number of independent images to process. Such tensors are usually arranged in memory using either the NCHW layout or the NHWC layout; here, N corresponds to the batch dimension n; HW refers to the input image height and width (\(h_i \times w_i)\); C corresponds to the input channels (c); and the physical layout in the computer memory is a multi-dimensional generalisation of the standard “row-major” order.

3 High-performance realisation of the Winograd algorithm using vector intrinsics and OpenMP

In this section, we discuss several high-performance implementations of the Winograd algorithm, vectorised using Intel SSE/AVX2/AVX-512 and ARM NEON/SVE intrinsics, and parallelised using OpenMP. The vectorisation efforts for the Winograd algorithm have been applied to phases 1, 2, and 4 from Fig. 1. For brevity, we describe only the work on phases 1 and 2, corresponding to the filter and input transforms. Phase 3 can be seamlessly vectorised using a high-performance implementation of gemm, for example, as that available in libraries such as Intel MKL, Intel oneAPI, BLIS or OpenBLAS, depending on the target architecture. Finally, we target single-precision floating-point (FP32) arithmetic.

3.1 Intel SSE intrinsics

Listing 1 shows a fragment of code that implements the filter transform (phase 1) for \(F(2\times 2, 3\times 3)\) using Intel SSE intrinsics (128-bit vector registers). Concretely the code computes the collection of products in Eq. (1), \(G \ f_{i_k,i_c}\ G^T\), for \(i_k=1,2,\ldots ,k\), \(i_c=1,2,\ldots ,c\), as follows:

  • The “base vector datatype” is Intel SSE __m128. Arrays of this type (Line 1) abstract the 128-bit XMM vector registers with capacity for four FP32 numbers. The high-level operations with this type of variables (Lines 20–23 and 29–32) thus involve four FP32 values per array entry.

  • The filter matrix is accessed via the C macro FROW, whose implementation is dependent on the type of storage layout being NCHW or NHWC. (For brevity, not shown.)

  • Loading the entries of the filter (Lines 11–13) is carried out via “scalar” operations. For the NCHW layout though, this can be modified to take advantage of vector loads (using Intel SSE instruction _mm_loadu_ps, as in Lines 15–17). Since the filter matrix has 3 (valid) elements per row, but we load 128 bits (i.e. 4 FP32 numbers) with a single SSE instruction, for NCHW the filter array has to be padded to prevent a potential illegal memory access.

  • This solution incurs extra arithmetic operations in the computation of \(W_{i_k,i_c} = G \ f_{i_k,i_c}\) for updating WX[0]–WX[3] (Lines 20–23), as each row has only 3 valid elements but we use SSE instructions operating on four values. For each row/vector register, the last entry contains “garbage”. Therefore, it will not be used in the subsequent multiplication \(U_{i_k,i_c} = G \ W_{i_k,i_c}^T\).

  • The transposition of the matrix stored in WX[0]–WX[3] (Line 26) is done via the C macro _MM_TRANSPOSE4_PS; see Listing 2. After that operation, WX[0]–WX[3] contain the columns of the input. Therefore, WX[3] does not store any valid data.

  • The rows of transformed filter tile \(U_{i_k,i_c}\), stored in UX[0]–UX[3] (Lines 29–32), are accordingly scattered, via the C macro UROW, across the first two dimensions of U (Lines 35–37).

figure a
figure b

The vectorisation of the input and output inverse transforms (phases 2 and 4) of the Winograd algorithm using SSE intrinsics can follow a similar approach to that presented for the filter transform in Listing 1. For variant \(F(2\times 2, 3\times 3)\), the input and output tiles of size \(t\times t\) (with \(t=m+r-1 = 2+3-1 = 4\)) fit on the 128-bit vector. However, this strategy will not apply to those variants of the Winograd algorithm with \(t>4\), such as \(F(2\times 2, 5\times 5)\). In these cases, we need either (1) to individually process the elements that are left out of the 128-bit vector register; or (2) to leverage Intel AVX2/AVX-512 intrinsics, with registers that can accommodate more than four FP32 elements, as described in the next section. At this point, it is worth noting that the filter transform only needs to be computed once, independently of the number of images to process, and for inference, this can be done offline.

3.2 Intel AVX2/AVX-512 intrinsics

The vectorisation of phases 1, 2 and 4 of the Winograd algorithm using Intel AVX2/AVX-512 intrinsics entails re-implementing the codes for each pair (m, r). This is due to the distinct dimensions and sparsity patterns of the transformation matrices G, A and B on the \(m+r-2\) polynomial interpolation points [9]. These re-implementations comprise, among other details, replacing the original SSE data types __m128, with Intel AVX2 __m256 or AVX-512 __m512.

Given that the Winograd algorithm should leverage small values of m and r, such as \(F(2\times 2, 3\times 3)\), \(F(4\times 4, 3\times 3)\), vectorising these phases for 256- or 512-bit vector registers requires unrolling (up to some degree) the loops iterating over the input tiles in order to fully exploit such long vector registers. By doing so, this “macro-tiling” technique can then process a horizontal (and optionally vertical) block of consecutive tiles of the input/output images (or a subset of filters) in a single iteration so that the macro-tile columns, stored in vector registers, exploit their full length. Depending on the Winograd variant and phase, the macro-tile can thus accommodate a different number of tiles in both the horizontal and vertical axes.

Fig. 2
figure 2

Example of the Winograd macro-tiling technique for the input transform \(V_{i} = B^T D_{i} B\) via the variant \(F(2\times 2, 3\times 3)\) and using Intel AVX2 256-bit registers

Full size image

Figure 2 illustrates the macro-tiling technique for the input transform and the variant \(F(2\times 2, 3\times 3)\). For simplicity, we target Intel AVX2 256-bit SIMD units, able to operate with up to 8 FP32 numbers. In this code, the application of the input transform to a macro-tile is split into two sub-operations. The first performs the multiplication \(D'_{i} = B^T\ D_{i}\), where \(D_{i}\) is a macro-tile of size \(h_t \times w_t = 6\times 8\), aggregating a \(2\times 3\) \(d_{i,j}\) input tiles of size \(t \times t = 4\times 4\) overlapping each other \(r-1\) rows and columns. By overlapping \(r-1\) columns between neighbouring tiles, the number of arithmetic operations is reduced by a factor of \(1 - \frac{t\times w_t}{t + s \times (w_t - 1)}\), given that these can then be re-utilised for the tiles that are immediately on the right. Unfortunately, the results related to the \(r-1\) overlapping rows in \(D_i\) cannot be re-utilised for the tiles that are immediately below. In this case though, the aggregation of two rows of tiles in \(D_i\) yields a square \(8\times 8\) matrix that is easy to transpose. The second multiplication \(V^T_{i} = B^T \ {D'_{i}}^T\) uses the previously transposed macro-tile \(D_{i}^T\) and is computed similarly, with the exception that there are no overlapped columns in the transposed resulting matrix \(V^T_{i}\). This macro-tiling technique can be generalised for any other values of (m, r) while taking advantage of long vector registers. However, an implementation using Intel AVX2/AVX-512 has to be manually customised to operate with the appropriate number of elements, which is contrary to the focus on code portability of this work.

figure c

Listing 3 shows a excerpt of code for the Winograd variant \(F(2\times 2, 3\times 3)\) for the input transform, implementing the macro-tiling technique using Intel AVX-512 intrinsics. In that code, the macro-tile of size \(10\times 16\) aggregates \(4\times 7\) input tiles of size \(4\times 4\). Furthermore:

  • The “base vector datatype” corresponds to Intel AVX-512 __m512. The arrays of this type (Line 1) target the 512-bit ZMM vector registers with capacity for 16 FP32 numbers. The high-level operations with this type of variables (Lines 36–39 and 53–56) thus involve 16 FP32 values per array entry.

  • The input matrix is accessed via the C macro DROW, whose implementation is dependent on the type of storage layout being NCHW or NHWC. The loops indexed by i and j iterating over the macro-tile only access “valid” image entries, thus avoiding the need for explicitly padding the input images with zeros.

  • Loading the entries of the macro-tile (Line 32) is carried out via “scalar” operations. For the NCHW layout, this can be modified to take advantage of vector loads (using the Intel AVX-512 instruction _mm512_loadu_ps).

  • The loop in lines 35–40 performs the multiplication \(D'_{i} = H^T\ D_{i}\). For that purpose, it iterates over the vertical axis to uncollapse the \(r-1\) overlapped rows in the resulting vectors WX, containing the macro-tile \(D'_{i}\) of size \(16\times 16\).

  • The transposition of the matrix stored in the array WX (Line 43) is done via the C macro _MM_TRANSPOSE16_PS. (Omitted for brevity).

  • The nested loops in Lines 52–65 perform the multiplication \(V^T_{i} = B^T \ {D'_{i}}^T\). After processing a row of tiles within the macro-tile, the result stored in the four entries of the array UX is accordingly scattered across the entries of the workspace U.

As part of this work, we also vectorised the output transform using the macro-tiling technique. However, due to the more complex access pattern for the result tensor, this technique did not render any performance improvement. In consequence, our Intel AVX2- and AVX-512-based implementations only leverage the macro-tiling technique for the filter and input transform phases.

3.3 ARM NEON intrinsics

The code for the application of the filters vectorised using Intel SSE intrinsics can be easily modified to utilise ARM NEON intrinsics instead. Concretely, the following minor changes have to be added:

  • The base vector datatype for ARM NEON is float32x4_t.

  • The vector loads and stores are, respectively, done via the NEON intrinsics vld1q_f32 and vst1q_f32.

  • The transposition macro in the ARM case is an inlined function, given in Listing 4, that uses the instructions vtrn2q_f64 and vtrnq_f32 to transpose the contents of W[0]–W[3].

figure d

3.4 ARM SVE intrinsics

The migration of the ARM NEON code to employ ARM SVE VLA intrinsics is not straightforward and requires rewriting the codes with some aspects in mind:

  • It is not possible to declare SVE arrays with the vector datatype svfloat32_t, since their size is not known at compile time. This forces to rewrite and unroll some loops of the algorithm in order to mimic the behaviour of the NEON codes, resulting in more verbose implementations.

  • The basic arithmetic operators are not overloaded by default, since the intrinsics require the use of masks (predicates), which have to be declared and initialised in advance. This further increases the code verbosity and diminishes interpretability.

figure e
figure f

Listing 5 shows an excerpt of code for the filter transform phase using ARM SVE intrinsics. Compared with its ARM NEON counterpart, the code presents the following differences:

  • The filter load has is performed in a temporary variable (F_tmp) as the subscripting operator ([]) is also not overloaded by default (Lines 15–17). This modification is required for the NHWC layout, as in that case the filter rows are not contiguous in memory. Afterwards, the filter is loaded into the SVE registers via the intrinsic svld1 with the predicate pred3 (Lines 19–21), which was previously initialised via svwhilelt_v32_u32 to operate only with the first 3 elements.

  • The multiplication \(W_{i_k} = G\ f_{i_k,i_c}\) is performed by steps, as the basic operators are not available for svefloat32_t (Lines 29–36). The same occurs for the multiplication \(U_{i_k} = G\ W_{i_k}\) (Lines 42–49).

  • The transposition of the matrix stored in W0–W3 in Line 29 is performed using a specialised in-house C macro; see Listing 6.

  • The contents of registers U0–U3 are stored via svst1_f32, with the pred4 predicate, into the temporary matrix U_tmp (Lines 52–55). Finally, this matrix is copied to the corresponding entries of U (Lines 58–60).

In general, programming with SVE intrinsics has the advantage of generating a VLA code which does not need to be rewritten for other SVE architectures of different vector length. For the case of the Winograd algorithm, however, this does not bring major advantages as the vector length code strictly depends on the Winograd variant.

3.5 Exploiting thread-level parallelism using OpenMP

In addition to the introduction of vector intrinsics, the four phases of the algorithm can be also parallelised using OpenMP, as the individual kernels involved by the transform matrices for the filter/input/output tiles, as well as the \(t\times t\) gemm, present no data dependencies between them. To augment the degree of thread-level parallelism, we use the OpenMP collapse(2) clause to fuse the first two loops in each phase: across the k and c-dimensions in phase 1; the n and c-dimensions in phase 2; the two loops iterating over t in phase 3; and the n and k- dimensions in phase 4. This is shown, for example, in Listing 1 (Lines 6–7) for the first phase. Also, the \(t\times t\) gemm kernels in phase 3 (see Fig. 1) are executed serially.Footnote 2 Finally, we added the OpenMP clause if to extract thread-level parallelism only when the number of “collapsed” iterations is larger than 1.

4 Experimental results

In this section, we evaluate the performance of our implementations of the Winograd-based convolution on three different platforms, using two well-known DL models, for both the NCHW and NHWC data layouts. For comparison purposes, we also include the Lowering method (also referred to as im2col/im2row + gemm) [4, 13] in the evaluation. All experiments are performed using FP32 arithmetic.

4.1 Hardware setup

For the experimental analysis, we employ the following computer platforms:

  • Sky: This server comprises two Intel Xeon Gold (Skylake) 6126 processors (24 cores in total) running at 2.6 GHz and sharing 64 GiB of DDR4 RAM.

  • Nano: This corresponds to a low-power NVIDIA Jetson Nano board, equipped with a quad-core ARMv8-A Cortex-A57 processor running at 1.5 GHz and 4 GiB of RAM.

  • A64FX: This is a Fujitsu PRIMEHPC FX1000 node equipped with a 48+4-core Fujitsu A64FX processor (ARMv8.2-SVE) running at 2.2 GHz. The cores of the node are grouped into four Core Memory Groups (CMGs), each with 12 compute cores plus an additional assistant core for the operating system. This machine contains 32 GiB of HBM2 memory.

In the experiments, we set the largest number of OpenMP threads to match the number of cores for Nano (4), the cores of a single socket for Sky (12), and the cores of a single CMG for A64FX (12 as well).

4.2 DL framework, libraries, compilation flags, and parallelisation

To evaluate our routines for the Winograd-based convolution, we bundled them into a dynamic C library and integrated the result with PyDTNN, a lightweight framework implemented in Python for DL training and inference [14, 15]. For this purpose, we developed a binding module that internally calls the Winograd functions via the ctypes v1.1.0 Python library. This module interacts with the PyDTNN layer class Conv2D and allows selecting the Winograd variant according to the filter size requested by the convolutional layer encountered in a given neural network model.

The compilation of the Winograd library is carried out using gcc v10.2.0 with the optimisation flags -O3 -fopenmp for all three platforms in addition to -mavx -mfma for Sky. The \(t\times t\) gemm kernels in phase 3 are computed via Intel MKL v2022.1.0 (for Sky) and BLIS v0.8.1 (for Nano and A64FX).

Alternatively, the Conv2D layers in PyDTNN can be also processed via the variant im2col transform + gemm of Lowering for the NCHW layout, or the variant im2row + gemm of Lowering for NHWC. The im2col/im2row transforms are implemented in PyDTNN using Cython v0.29.24, and parallelised using OpenMP. The implementation of gemm is provided by Numpy v1.23.0rc1, linked against Intel MKL for the Sky or BLIS for Nano.

4.3 Testbed

For the evaluation, we measure the inference time spent by PyDTNN on the convolutional layers present in two popular DL models: VGG16 [16] and ResNet-50 (v1.5) [2] for the ImageNet dataset in both cases [17]. In our analysis, we only evaluate the convolutional layers using filters of size \(3\times 3\) with the Winograd variant \(F(2\times 2,3\times 3)\). For comparison purposes, we also measure the execution time of the Lowering approach using the same convolutional layers. The number of images/batch size was set to \(n=1\) in order to reflect the single-stream scenario of the ML Commons benchmark for inference on the edge.

4.4 SIMD vectorisation and parallel scalability

In this section, we individually assess the benefits of the SIMD vectorisation and OpenMP loop parallelisation for the Winograd algorithms on the three selected multi-core platforms and the two CNNs using both data layouts.

Figure 3 shows the speedup obtained when vectorising the Winograd algorithms via SIMD intrinsics with respect to a baseline routine that performs the same operations with no vector instructions. For this initial experiment, all codes run on a single core. Also, for brevity, we only use the AVX-512 intrinsics for Sky. As shown in the figure, the acceleration gained for Sky ranges between 1 and 1.2; while for Nano and A64FX, the highest speedup factors are 1.15 and 1.3, respectively. These gains are modest given mainly to the fact that we are vectorising only phase 1 of the algorithm. For instance, the speedup for layer #63 of ResNet-50 on Sky using the NCHW layout is 1.2, but phase 1 represents 41.04%. Therefore, we could have expected a maximum speedup of \(\frac{1.2\ \cdot \ 0.4104}{1 - 1.2\cdot (1 - 0.4104)} \approx 1.68\) for this phase, according to Amdahl’s law.

Fig. 3
figure 3

Baseline versus vectorised Winograd algorithm speedups for the aggregated inference time of the VGG16 (left) and ResNet-50 (right) convolution layers on the Sky (top), A64FX (middle) and Nano (bottom) platforms

Full size image

Figure 4 reports the parallel speedup of the vectorised Winograd variants when setting the number of OpenMP threads to 4, 12 for Sky/A64FX, and 2, 4 for Nano. With regards to Sky, the speedup achieved using 4 threads is, on average, close to 3.5 for VGG16 and about 3 for ResNet-50; when using 12 threads the speedup remains below 7. Focusing on Nano, the speedup for 2 threads is close to its maximum efficiency, while for 4 threads is below 3.5 in most cases. The scaling for A64FX is slightly higher than for Sky, with speedups for 4 threads close to the theoretical peak, and in the range 7–10 for 12 threads. All in all, the observed speedups are humble when the number of threads is high. However, this is due to the limited dimension of the problem (strong scaling).

Fig. 4
figure 4

Winograd and Lowering algorithms OpenMP speedups for the aggregated inference time of the VGG16 (left) and ResNet-50 (right) convolution layers on the Sky (top), A64FX (middle) and A64FX (bottom) platforms with respect to the sequential algorithm

Full size image

In a separate experiment on Sky, we also analysed the scalability of the Winograd algorithm leveraging the cblas_dgemm_batch routine from Intel MKL to perform the \(t\times t\) independent matrix multiplications of phase 3. The results using 12 threads revealed speedups between 1.40 and 2.30 for VGG16 versus speedups between 3.5 and 5.6 for ResNet-50 in favour of the version that uses the OpenMP pragma (with the collapse(2) clause) to parallelise the two for nested loops of such phase 3.

Fig. 5
figure 5

Winograd versus Lowering execution time of the VGG16 (top) and ResNet-50 (bottom) convolution layers on the Sky platform using 12 threads

Full size image

4.5 Performance evaluation and comparison analysis

4.5.1 Results on the Intel Skylake

Figure 5 reports the inference execution time of the convolutional layers using the Lowering method and the Winograd algorithm vectorised using SSE, AVX2 and AVX-512 intrinsics for both data layouts on the Sky platform.

The experiments show that, for VGG16, almost all convolutional operators appearing in the last layers of VGG16 (3–29), using either NCHW or NHWC and SSE, AVX2 or AVX-512 deliver higher performance than the Lowering approach. This is due to the reduction of the arithmetic cost implicit in the Winograd algorithm (potentially at the expense of less accurate results). Concerning the data layout we observe that, in general, NCHW offers higher performance than NHWC. This is due to the algorithm design, which first processes individual tiles for specific channels, accessing data contiguously according to NCHW. Regarding the use of SSE, AVX2 and AVX-512, we detect slight smaller execution times for AVX2 and AVX-512, with no clear winner between them.

Focusing on ResNet-50, we can highlight similar results: the Winograd algorithm provides, for almost convolutional layers (53–167), higher performance figures than the Lowering method. For the first layers (9–31), however, the Winograd algorithm using the NHWC format provides slightly less competitive results. This is due to the less efficient memory accesses performed by this algorithm for the NHWC data layout plus the convolutional parameters of these layers. We can also observe that, for the rest of the layers, the AVX2 and AVX-512 Winograd implementations deliver superior performance than SSE, with AVX2 providing slightly lower execution times than AVX-512.

Fig. 6
figure 6

Winograd versus Lowering execution time of the VGG16 (top) and ResNet-50 (bottom) convolution layers on the Nano platform using 4 threads

Full size image

4.5.2 Results on the ARM Cortex A57

Figure 6 reports the inference execution time of the convolutional layers using the Lowering method and the Winograd algorithm vectorised using ARM NEON intrinsics for both data layouts on the Nano platform.

The experiments with the VGG16 convolutional layers show that the Lowering approach outperforms Winograd for layers 1–6, while for layers 8–11 the execution time is on pair. For the rest of the layers, from 13 on, the Lowering approach is slower than the Winograd algorithm. We attribute these time differences to the parameters of the convolutional layers k and c, which in some cases favour the Lowering versus the Winograd approach. For this reason, there is no clear winner algorithm for all layers and the selection should be made carefully according to the convolution parameters (see [18]). In contrast with the experiments with the Sky platform, for Nano there are very small differences between the NCHW and NHWC data layouts.

Concerning the convolutional layers of ResNet-50, we observe that the Winograd algorithm outperforms the Lowering approach for all layers (possibly, at the expense of less accurate results). In this case, however, the NCHW format provides slightly lower execution times than NHWC. For the Lowering approach, the performance difference between these two data layouts is more dependent on the convolution parameters.

Fig. 7
figure 7

Winograd versus Lowering execution time of the VGG16 (top) and ResNet-50 (bottom) convolution layers on the A64FX platform using 12 threads

Full size image

4.5.3 Results on the Fujitsu A64FX

Figure 7 reports the inference execution time of the convolutional layers using the Lowering method and the Winograd algorithm vectorised using ARM SVE intrinsics for both data layouts on the A64FX processor.

For VGG16, we observe that the Lowering method offers a significant advantage for the first three convolution layers of VGG16; however, for the remaining layers, the Winograd algorithm is a better option. For ResNet-50, the Winograd-based convolution is always the best option for both data layouts. In any case, the improvements of this algorithm mainly depend on the input and filter sizes.

We also detect differences between the two data layouts, with NCHW being more competitive than NHWC. These differences are due to the design of the Winograd algorithm, which first processes the individual tiles. A more efficient version of this algorithm would require a complete reformulation of the implementation to process first the tiles on the channel dimension, according to the storage of data in the NHWC layout.

5 Concluding remarks

We have presented a collection of multi-threaded and vectorised implementations of the convolution operator, via the Winograd minimal filtering algorithm, that are portable across modern target architectures from Intel, ARM and Fujitsu. This is attained via the use of (1) the OpenMP standard for the multi-threaded parallelisation; (2) a reduced set of architecture-specific vector intrinsics (SSE/AVX2/AVX-512 for Intel and NEON/SVE for ARM) that hint the prelude towards a future common interface; and (3) compiler support for high-level arithmetic operations involving vector registers. In addition, throughout the work, we have discussed thread-level and vectorisation considerations and opportunities for the different phases of the Winograd algorithm.

The experimental results for three state-of-the-art platforms, equipped with SIMD-enabled Intel, ARM and Fujitsu multi-core processors, show that our parallel and vectorised Winograd-based implementations moderately improve the performance with respect to the baseline versions. Also, they deliver competitive performance compared with the Lowering approach on the three platforms.

As future work, we plan to extend our study of vector intrinsics to other DL kernels, including the FFT convolution, as well as to target layer fusion and automatic generation of vectorised code to gain a more complete understanding of this procedure.