Certificateless network coding scheme from certificateless public auditing protocol

Abstract

In recent years, network coding has received extensive attention and has been applied to various computer network systems, since it has been mathematically proven to enhance the network robustness and maximize the network throughput. However, it is well-known that network coding is extremely vulnerable to pollution attacks. Certificateless network coding scheme (CLNS) is a recently proposed mechanism to defend against pollution attacks for network coding, which avoids tedious management of certificates and key-escrow attack. Until now, only a few constructions were presented, and more ones should be given so as to enrich this field. In this paper, for the first time, we study the general construction of CLNS from certificateless public auditing protocol (CL-PAP), although the two areas seem to be quite different in their nature and are studied independently. Since there are many candidates of CL-PAPs, we can naturally obtain abundant constructions of CLNSs according to our systematic way. In addition, in order to show the power of the general construction, we also present a concrete implementation given a specific CL-PAP. The performance analysis and experimental results show that the implemented CLNS is competitive in the existing network coding schemes.

1 Introduction

The traditional way of data transmission is based on a storing-and-forwarding routing mechanism. For a long time, it has been generally believed that processing the transmitted data on the intermediate node would not produce any benefits. Until network coding was first proposed by Ahlswede et al. [1] in 2000, which completely overturned the traditional view and established its important position in modern network communication research. Network coding (NC) is an information exchange mechanism that combines routing and coding, and its advantages are throughput optimization, stronger robustness and lower power consumption. Therefore, it has been widely applied to networks, such as Internet of Things (IoT) networks and wireless sensor networks. However, it is highly vulnerable to pollution attacks, because intermediate nodes may combine polluted packets with other honest packets during the transmission, causing the polluted ones spread rapidly to the entire network. As a result, even if the destination node obtains enough packets, it not only cannot restore the original data, but also wastes network sources.

Linearly homomorphic signature (LHS), as a public-key method, can effectively resist pollution attacks, allowing intermediate nodes to verify packets and discard invalid ones during transmission [2]. In this mechanism, all nodes only need to obtain the public key of the source node S, instead of sharing the same secret key (with S). Boneh et al. [3] first applied a homomorphic signature scheme in network coding, which was based on complexity assumption, random oracle model and bilinear map. In traditional certificate-based network coding, in order to correspond the user’s public key with his identity, the most popular method is to create a user’s digital certificate by a certificate authority (CA). If other nodes intend to confirm the relationship between the public key and the identity of S, they must verify the validity of the corresponding certificate before using this public key.

At present, public key infrastructure (PKI) is the core and foundation of network security construction, which uses digital certificates to manage public keys and binds user’s public keys to their identities through CA. Because generating and managing a large number of certificates is time-consuming, PKI is costly to deploy and cumbersome to utilize in practice. In a network coding system, utilizing CA and PKI for additional validation of each certificate will significantly degrade the performance.

To address the certificate management problem, Shamir [4] introduced identity-based cryptography in 1984, of which method is utilizing user’s information such as email or ID number, etc., as his public key, thereby eliminating the need for the public key certificate. Furthermore, the private key of user is generated from key generation center (KGC) by combining the user’s public key with KGC’s master key. The novel mechanism mitigates the burden of using certificates and can be applied to identity-based network coding [5].

However, KGC possesses the private keys of all users, which brings an inherent problem to identity-based network coding, namely key-escrow attack. In other words, KGC can literally forge any user’s signature, which is insecure for any user. To solve this problem, Al-Riyami et al. [6] proposed the theory of certificateless public key cryptography in 2003, and introduced certificateless signature (CLS). Then, for the first time, Chang et al. [7] proposed the notion of certificateless network coding in 2020, which is a compromise solution between certificate-based network coding and identity-based network coding. So far, there are only a few concrete certificateless network coding schemes (CLNSs) in current literature. As network coding applications expand, it is imperative to design more efficient and secure CLNSs.

In the field of cloud storage, the concept of cloud auditing was put forward by Juels et al. [8] and Ateniese et al. [9] at the same time. They, respectively, proposed proof of retrievability (POR) protocol and provable data possession (PDP) protocol, in which the POR protocol can verify whether a cloud service provider (CSP) owns users’ complete outsourced data. For a data owner, he can leverage the POR protocol to verify the integrity of the data, but traditional implementations such as hash function, digital signature and message authentication code (MAC) require him to preserve the outsourced data locally. Subsequently, Shacham et al. [10] came up with an improved public auditing mechanism on the basis of BLS (Boneh–Lynn–Shacham) signature. The public auditing indicates the data owner can entrust a third-party auditor (TPA) to perform the data integrity auditing on his behalf, without retrieving all outsourced data. Currently, certificateless public auditing protocol (CL-PAP) is a popular method in cloud storage, which avoids the use of certificates and solves the problem of key-escrow attack. Therefore, there are many specific CL-PAPs that can provide cryptographic primitives for CLNSs.

Although network coding and cloud storage are two different fields of networking, both are inherently concerned with data integrity checking. And the connection between them has been revealed by some researchers. In 2015, Chen et al. [11] proposed a cloud storage protocol based on a secure network coding scheme, and enhanced it to support public auditing. In 2021, Chang et al. [12] presented a general transformation from an admissible POR protocol to secure network coding scheme, and described some specific instantiations. Nevertheless, none of their work deals with the certificateless public key cryptography. Intuitively, the relationship between the two research areas can be extended into certificateless public key cryptosystem, which implies that CLNSs can be constructed from existing secure CL-PAPs.

Related Works: The conception of network coding was first introduced by Ahlswede et al. [1] to improve the throughput of the multicast network. Since then, researchers focused on the issue of pollution attacks [13, 14], because pollution attacks affect the practical application of network coding. To resist pollution attacks, most existing schemes can be divided into two solutions: information-theoretic approaches [15,16,17] and cryptographic approaches [18,19,20]. In particular, information-theoretic approaches introduce redundancy in original packets to recover the original file from malicious faults, but they can only passively tolerate pollution attacks at the destination. By comparison, cryptographic approaches enable intermediate nodes to detect and filter polluted packets in transmission, which can alleviate pollution attacks from the origin. In recent years, cryptographic approaches have attracted the attention of researchers, which can be further separated into symmetric-key methods (e.g., homomorphic MAC) [21,22,23] and public-key methods (e.g., homomorphic signature) [2, 3, 24]. Homomorphic signature was firstly introduced by Johnson et al. [2], and Boneh et al. [3] provided a landmark framework for such schemes. Next, Attrapadung [24] et al. proved that the first homomorphic signature scheme was secure in the standard model. Li et al. [25] presented a multi-source network coding scheme that can be applied to the IoT, but their works did not refer to the certificate management problem. To mitigate the burden of using certificates, Lin et al. [5] and Chang et al. [26] introduced different identity-based linearly homomorphic signature schemes, the former one is based on the CDH assumption and the latter one is resistant to the related-key attack. In addition, Fan et al. [27] and Liu et al. [28], respectively, proposed privacy-preserving signature schemes for network coding, which can defend against eavesdropping attacks. However, their works did not take into account the key-escrow attack. To solve the problem, certificateless linearly homomorphic signature has been applied to network coding. Chang et al. [7] introduced a first concrete CLNS based on the CDH assumption and the CLS, however, their scheme did not involve practical application. Lately, Wu et al. [29] came up with a similar scheme for the IoT, but the signing procedure of the scheme is cumbersome.

For the field of cloud storage, Juels et al. [8] and Ateniese et al. [9] described two classic models POR and PDP, respectively. Indeed, POR underlines the retrievability of outsourced data, while PDP achieves cloud auditing by generating some data-related authentication information. Later, Shacham et al. [10] devised two public auditing protocols based on digital signature and MAC. To support dynamic data operations, Wang et al. [30] considered a public auditing protocol with Merkle hash tree (MHT). Zhu et al. [31] and Erway et al. [32] also designed similar protocols by using index hash table and rank-based authenticated dictionary. Shen et al. [33] designed a novel dynamic structure in their protocol, which consists of a doubly linked information table and a location array. To improve security and performance, Wang et al. successively proposed a privacy-preserving public auditing protocol for shared cloud data [34] and an efficient user revocation protocol [35]. For certificate management issues, Wang et al. [36] proposed an identity-based public auditing protocol for multi-cloud storage. Recently, Wang et al. [37] designed a protocol that can tolerance small data errors. After the emergence of the certificateless public key cryptography, many CL-PAPs have been proposed. Wang et al. [38] firstly build an entire certificateless public auditing mechanism in the untrusted cloud. Then, He et al. [39] introduced a CL-PAP for cloud-assisted wireless body area networks. Lately, Li et al. [40] designed a protocol to implement integrity checking of data shared within a group, and Zhou et al. [41] proposed a privacy-preserving protocol.

Our Contributions: In this paper, we first introduce a secure certificateless public auditing protocol and impose some constraints on the protocol to be an admissible CL-PAP. Then, from any admissible CL-PAP, we propose a general construction of CLNS whose security depends on the underlying CL-PAP. The general construction provides an approach for designing more CLNSs from CL-PAPs. Afterward, to show the power of the general construction, we design a concrete admissible CL-PAP and transform it into a CLNS, and then give a security proof. Finally, we evaluate the performance of the transformed CLNS with other related schemes in terms of communication overhead and computation cost. Simulation results demonstrate that the transformed CLNS is efficient and competitive, and can be applied in IoT environment.

Organizations: This article is structured as follows. In Sect. 2, we first introduce some basic notions and preliminaries including bilinear map, linear network coding and complexity assumptions. Next, in Sect. 3, several different network coding system models are described, especially the CLNS. Later, the admissible CL-PAP is defined in Sect. 4. Then, in Sect. 5, a general construction for transforming an admissible CL-PAP into a CLNS is proposed. Additionally, Sect. 6 describes a concrete instantiation for the IoT environment. Last, performance analysis and conclusion are presented in Sects. 7 and 8.

2 Notions and preliminaries

This section presents some basic notations and basic cryptographic tools, including bilinear map, linear network coding and complexity assumptions.

Basic Notations: Primarily, k represents a security parameter. For a given prime number p, $Z_{p}$ and $Z_{p}^{*}$ denote finite fields $\left[ 0,1,\cdots ,p-1 \right]$ and $\left[ 1,2,\cdots ,p-1 \right]$, respectively. Next, PPT means probabilistic polynomial time. Besides, v denotes a vector and $v_i$ represents its i-th element.

2.1 Bilinear map

Suppose $G_1$ and $G_2$ are two multiplicative groups that have the same prime order p, and g is a generator of $G_1$. $e:G_1\times G_1 \rightarrow G_2$ is a bilinear map if it satisfies the following properties:

• 1. Computability: for any $u,v\in G_1$, e(u, v) is efficiently computable.

• 2. Non-degeneracy: there exist two elements $u,v\in G_1$ such that $e(u,v)\ne 1$.

• 3. Bilinearity: for any $a,b\in Z_p^*$ and $u,v\in G_1$, $e(u^{a},v^{b})=e(u,v)^{ab}$.

2.2 Linear network coding

There are three steps to complete the file transmission in a linear network coding scheme:

• A file to be transmitted can be treated as a sequence of n-dimensional vectors $\bar{{{\textbf {v}}}}_{1},\cdots , \bar{{{\textbf {v}}}}_{m} \in Z_{p}^{n}$. Before transmission starts, each vector can be augmented to ${{\textbf {v}}}_1, \dots ,{{\textbf {v}}}_m$ as

  $$\begin{aligned} {{\textbf {v}}}_i=\left( \overbrace{\underbrace{0,\cdots ,0,1}_{i},0,\cdots ,0}^{m},\bar{{{\textbf {v}}}}_{i} \right) \in Z_{p}^{m+n}. \end{aligned}$$

  In this way, ${{\textbf {v}}}_1, \cdots ,{{\textbf {v}}}_m$ form an augmented basis of a subspace V, and the augmented vectors can be transmitted as packets by some senders.

• Once receiving packets (i.e., vectors) ${{\textbf {w}}}_1,\cdots ,{{\textbf {w}}}_l\in Z_{p}^{m+n}$ on its l incoming edges, the router computes the packet (i.e., a linear combination) ${{\textbf {w}}}=\sum _{i}^{l}c_i{{\textbf {w}}}_i$, where $c_i$ is randomly selected from $Z_p$. Then, each router sends the combined vector ${{\textbf {w}}}$ on its outgoing edges.

• For a receiver who wants to recover the original file, he has to receive m linearly independent vectors ${{\textbf {w}}}_1,\dots ,{{\textbf {w}}}_m$. Suppose ${{\textbf {w}}}_i^R({{\textbf {w}}}_i^L)$ denotes the right-most n (left-most m) positions of the vector ${{\textbf {w}}}_i$. Then the receiver computes a $m\times m$ matrix Q such that

  $$\begin{aligned} Q= \left( \begin{array}{ccc} {{\textbf {w}}}_1^L\\ \vdots \\ {{\textbf {w}}}_m^L\\ \end{array}\right) ^{-1}. \end{aligned}$$

  Finally, the receiver is able to recover original file by computing

  $$\begin{aligned} \left( \begin{array}{ccc} \bar{{{\textbf {v}}}}_1\\ \vdots \\ \bar{{{\textbf {v}}}}_m\\ \end{array}\right) = Q \cdot \left( \begin{array}{ccc} {{\textbf {w}}}_1^R\\ \vdots \\ {{\textbf {w}}}_m^R\\ \end{array}\right) . \end{aligned}$$

2.3 Complexity assumptions

Definition 1

(Computational Diffie–Hellman Problem) $e:G_1\times G_1 \rightarrow G_2$ is a bilinear map and g is a generator of $G_1$. Given the tuple $(g,g^x,g^y)$, where x, y are chosen randomly from $Z_p$. For any PPT algorithm, the Computational Diffie–Hellman (CDH) problem is to compute and output $g^{xy}$.

Definition 2

(Computational Diffie–Hellman Assumption) If for any PPT algorithm ${\mathcal {A}}$, the advantage of solving the CDH problem is negligible, then the Computational Diffie–Hellman (CDH) assumption holds. The advantage can be defined as:

$$\begin{aligned} Adv_{G_1, {\mathcal {A}}}^{CDH} =Pr\left[ {\mathcal {A}}(g,g^a,g^b):a,b \xleftarrow {R}Z_p^* \right] \approx 0. \end{aligned}$$

Definition 3

(Discrete Logarithm Assumption) Suppose $\alpha \in Z_p^*$ and g is a generator of $G_1$. Given g and $g^\alpha$ as input, if for any PPT algorithm ${\mathcal {A}}$, it is computational infeasible to output $\alpha$, then the Discrete Logarithm (DL) assumption holds. The advantage can be expressed as:

$$\begin{aligned} Adv_{G_1, {\mathcal {A}}}^{DL} =Pr\left[ {\mathcal {A}}(g,g^{\alpha }):\alpha \xleftarrow {R}Z_p^* \right] \approx 0. \end{aligned}$$

3 Certificateless network coding

This section briefly introduces different network coding mechanisms as well as system models. Next, a secure certificateless network coding scheme CLNS with a security model is proposed.

Fig. 1

System model of certificateless network coding

3.1 System model

• 1) Secure Network Coding: According to the linearly homomorphic signature scheme, three types of nodes should be considered in secure network coding: source node (S), intermediate node (N) and destination node (R).

  • A source node S chooses or generates a key pair containing a private key and a public key (SK, PK) for signing. The data packets can be regarded as a set of vectors ${{\textbf {v}}}_1, \dots ,{{\textbf {v}}}_m$, and S calculates these vectors’ corresponding signatures $\sigma _1,\cdots ,\sigma _m$ for authentication. Then, S transmits each tuple $({{\textbf {v}}}_i,\sigma _i) \left( 1\leqslant i \leqslant m\right)$ to next intermediate nodes Ns.

  • Upon receiving some $({{\textbf {v}}}_1,\sigma _1),({{\textbf {v}}}_2,\sigma _2),\cdots ,({{\textbf {v}}}_l,\sigma _l)$ as vector-signature pairs, an intermediate node N$_i$ first checks the validity of all pairs and discards the “polluted” ones. For the “unpolluted” pairs, N$_i$ randomly chooses l coefficients $c_1,c_2,\dots ,c_l \in Z_p$ to compute the “combined” vector ${{\textbf {v}}}'$ and its signature $\sigma '$ to form a new pair $({{\textbf {v}}}',\sigma ')$, then transmits the new pair to adjacent nodes.

  • After the destination node R$_j$ collects enough pairs $({{\textbf {v}}}'_1,\sigma '_1),({{\textbf {v}}}'_2,\sigma '_2),\dots ,({{\textbf {v}}}'_m,\sigma '_m)$, R$_j$ also checks the validity of the pairs and discard “polluted” ones. Finally, R$_j$ can recover the original vectors ${{\textbf {v}}}_1, \cdots ,{{\textbf {v}}}_m$.

• 2) Identity-Based Network Coding: In PKI, CA issues certificate for public key authentication and binds the user’s public key to corresponding identity. However, the heavy reliance on the PKI introduces the certificate management problem, such as certificate distribution, revocation, storage, and validation. Hence, Shamir [4] introduced an identity-based homomorphic signature scheme that can be used in network coding mechanisms. In identity-based network coding, in addition to the three kinds of nodes mentioned above, there is also a KGC for generating the user’s private key and the public key. Specifically, for any source node S$_i$, it sends an identity $ID_i$ to KGC. Then KGC returns a private key $SK_{ID_i}$ for signing. Additionally, the public key certificate of each source node is not used due to the unique public key PK generated by KGC is universal. For nodes Ns and Rs in different process, they only need the common public key PK of KGC to verify the validity of signatures.

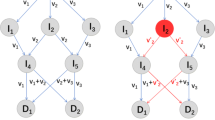
• 3) Certificateless Network Coding: As we described in Introduction, identity-based network coding suffers from the problem of key-escrow attack. Therefore, Al-Riyami et al. [6] proposed the concept of certificateless signature (CLS). In CLS scheme, the user’s private key is a combination of the partial private key and the secret value, where the partial private key is generated from KGC by using the master key and the user’s identity. Subsequently, Chang et al. [7] came up with the notion of certificateless network coding. Concretely, in certificateless network coding, after S sends its identity ID to KGC, KGC only returns the partial private key $PP_{ID}$ of node S. For node S, it selects a secret value $s_{ID}$, and then combines $s_{ID}$ and $PP_{ID}$ to generate the full private key $SK_{ID}$ for signing. Concurrently, the public key $PK_{ID}$ of S is also generated by $s_{ID}$. Then, nodes Ns and Rs are able to use the obtained $PK_{ID}$ to verify the vector-signature pairs. In this mechanism, KGC only provides the partial private key instead of real signing key $SK_{ID}$. Even if KGC is malicious, it cannot forge any signatures for S. Fig. 1 illustrates the process of communication among KGC and the nodes, and note that Ns are undertaking the verify-and-forward tasks in the system.

3.2 Certificateless network coding scheme

A certificateless network coding scheme (CLNS) consists of the following PPT algorithms: Setup, Extract, SetSecretValue, SetPrivateKey, SetPublicKey, Sign, Combine and Verify.

• Setup$\left( k \right)$ $\rightarrow$ $( msk,params)$: KGC runs this algorithm. After inputting a security parameter k, KGC outputs a master key msk known only to itself. The system parameter params consists of some public parameters.

• Extract$\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$: This algorithm is also performed by KGC to create a partial private key. It takes msk and user’s identity ID, and outputs a partial private key $PP_{ID}$.

• SetSecretValue$\left( ID \right)$ $\rightarrow$ $s_{ID}$: The source node S executes this algorithm to generate a secret value. For a node S with the identity ID, the algorithm inputs ID and outputs a secret value $s_{ID}$ on ID.

• SetPrivateKey$\left( s_{ID},PP_{ID} \right)$ $\rightarrow$ $SK_{ID}$: This algorithm is run by node S to generate a full private key. Particularly, it takes user’s secret value $s_{ID}$ and partial private key $PP_{ID}$, and outputs a full private key $SK_{ID}$.

• SetPublicKey$\left( s_{ID} \right)$ $\rightarrow$ $PK_{ID}$: The source node S performs this algorithm to generate a public key. Precisely, it takes user’s secret value $s_{ID}$ and outputs a public key $PK_{ID}$.

• Sign$\left( ID,SK_{ID},PK_{ID},id,V \right)$ $\rightarrow$ $T$: This algorithm is used to sign for node S. For the user’s identity ID, private key $SK_{ID}$, public key $PK_{ID}$, file identifier id and a vector set V as input, the algorithm outputs a signature set T. Concretely, for a set V has m pieces of vectors $\bar{{{\textbf {v}}}}_{1},\cdots , \bar{{{\textbf {v}}}}_{m} \in Z_{p}^{n}$, the algorithm computes the signature $\sigma _{i}$ for each augmented vector

  $$\begin{aligned} {{\textbf {v}}}_i=({{{\textbf {v}}}}_{i,1},\dots ,{{{\textbf {v}}}}_{i,m+n})\in Z_{p}^{m+n}, \end{aligned}$$

  and outputs T with the form $\{\sigma _1,\sigma _2,\cdots ,\sigma _m\}$.

• Combine$\left( ID,PK_{ID},id,\{c_i,{{\textbf {v}}}_{i},\sigma _{i}\}_{i=1}^{l} \right)$ $\rightarrow$ $({{\textbf {v}}},\sigma )$: Intermediate nodes Ns perform this algorithm to process received vector-signature pairs. After receiving l vector-signature pairs with the same identifier id, N randomly selects l coefficients and outputs a combined vector ${{\textbf {v}}}=\sum _{i=1}^{l}c_i{{\textbf {v}}}_{i}$ with the combined signature $\sigma$.

• Verify$\left( ID,PK_{ID},id,{{\textbf {y}}},\sigma \right)$ $\rightarrow$ $1/0$: This algorithm is executed by nodes Rs or Ns to check the validity of received vector-signature pairs, which inputs a tuple $(ID,PK_{ID},id,{{\textbf {y}}},\sigma )$ and outputs 0 (reject) or 1 (accept).

Correctness: The correctness of CLNS requires each key pair $(SK_{ID},PK_{ID})$ generated by Setup, Extract, SetSecretValue, SetPrivateKey and SetPublicKey, it holds that:

• 1) if T $\leftarrow$Sign$\left( ID,SK_{ID},PK_{ID},id,V\right)$, then for all id and ${{\textbf {v}}}_i\in Z_{p}^{m+n}$, 1$\leftarrow$Verify$\left( ID,PK_{ID},id,{{\textbf {v}}_i},\sigma_i \right)$; and

• 2) if for all id and for $1\leqslant i \leqslant l$,

  $$\begin{aligned} 1\leftarrow {\textbf {Verify}}\left( ID,PK_{ID},id,{{\textbf {v}}}_i,\sigma _i\right) , \end{aligned}$$

  then

  $$\begin{aligned}&1\leftarrow {\textbf {Verify}}\left( ID,PK_{ID},id,\sum c_i{{\textbf {v}}}_i,\quad \right. \\&\quad \left. {\textbf {Combine}}\left( ID,PK_{ID},id,\{c_i,\sigma _{i},{{\textbf {v}}}_{i}\}_{i=1}^{l}\right) \right) . \end{aligned}$$

3.3 Security model

In a CLNS, there are two types of adversaries to be considered, and note that the combination algorithm Combine doesn’t need to input the private key. In addition, we need to focus on the valid forgery, because the adversaries can use several vector-signature pairs to generate a new pair by Combine. According to our analysis, we consider two adversaries ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$. The former one ${\mathcal {A}}_{I}$ is a usual adversary who cannot access the system’s master key but can replace the public key with a value. The latter one ${\mathcal {A}}_{II}$ can access the master key but cannot replace the public key, and can be considered as a malicious KGC.

The security of CLNS can be characterized by two games Game-1 and Game-2, where ${\mathcal {A}}_{I}$ interacts with its challenger $CH _{I}$ and ${\mathcal {A}}_{II}$ interacts with its challenger $CH _{II}$, respectively. These games are based on the difficulty of the CDH problem. For the adversary ${\mathcal {A}}_{I}$ in Game-1, we give it some following restrictions. The challenge identity $ID^*$ has not been replaced by a public key and the partial private key has not been extracted, which implies that the adversary ${\mathcal {A}}_{I}$ cannot access the full private key.

Game-1: ${\mathcal {A}}_{I}$ is a usual adversary, it interacts with the challenger in this game.

• Setup-1: $CH _{I}$ runs Setup$\left( k \right)$ $\rightarrow$ $( msk,params)$, it keeps msk secret and gives params to ${\mathcal {A}}_{I}$.

• Queries-1: ${\mathcal {A}}_{I}$ can adaptively perform the following queries, and subject to the above restrictions.

  • Partial-Private-Key-Extract: Given user’s ID, $CH _{I}$ runs Extract$\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$ and returns $PP_{ID}$ to ${\mathcal {A}}_{I}$.

  • Private-Key-Extract: The challenger $CH _{I}$ uses ID to run SetSecretValue$\left( ID \right)$ $\rightarrow$ $s_{ID}$ and outputs secret value $s_{ID}$. Then, $CH _{I}$ continues to run

    $$\begin{aligned} {\textbf {SetPrivateKey}} \left( s_{ID},PP_{ID} \right) \rightarrow SK_{ID} \end{aligned}$$

    and outputs $SK_{ID}$, then returns $SK_{ID}$ to ${\mathcal {A}}_{I}$.

  • Public-Key-Query: Upon receiving a query with an identity ID, the challenger $CH _{I}$ runs SetPublicKey$\left( s_{ID}\right)$ $\rightarrow$ $PK_{ID}$ and returns $PK_{ID}$ to ${\mathcal {A}}_{I}$.

  • Public-Key-Replace: ${\mathcal {A}}_{I}$ can replace the public key $PK_{ID}$ with another value $PK_{ID}^{'}$, and note that ${\mathcal {A}}_{I}$ does not need to provide the secret value corresponding to $PK_{ID}^{'}$.

  • Signing-Query: When ${\mathcal {A}}_{I}$ queries a vector ${{\textbf {v}}}_i\in Z_{p}^{n}$, the challenger $CH _{I}$ chooses a file identifier id and returns id to ${\mathcal {A}}_{I}$. Then, $CH _{I}$ runs

    $$\begin{aligned} {\textbf {Sign}} \left( ID,SK_{ID},PK_{ID},id,V \right) \rightarrow T, \end{aligned}$$

    and returns T to ${\mathcal {A}}_{I}$.

• Output-1: The adversary ${\mathcal {A}}_{I}$ outputs a file identifier $id^{*}$, a nonzero vector ${{\textbf {v}}}^{*}$ with signature $\sigma ^{*}$ corresponding to $ID^{*}$ and $PK_{ID^{*}}$. In this case, ${\mathcal {A}}_{I}$ wins the Game-1 if Verify$\left( ID^{*},PK_{ID^{*}},id^{*},{{\textbf {v}}}^{*},\sigma ^{*} \right)$ $\rightarrow$ $1$ and one of the following two conditions holds:

  • 1) When ${{\textbf {v}}}^{*}\ne 0$ and $id^{*}\ne id_i$ to any $id_i$ appeared in signing queries. (Type-1 forgery)

  • 2) Suppose $id^{*}= id_i$ for some i and ${{\textbf {v}}}^{*}\notin S_i$, where $S_i$ is a subspace spanned by vectors corresponding to $id_i$. (Type-2 forgery)

Denote the advantage or probability of ${\mathcal {A}}_{I}$ winning the Game-1 by $Adv_{{\mathcal {A}}_{I}}^{\text {CLNS}}(k)$.

Game-2: ${\mathcal {A}}_{II}$ is a malicious KGC that interacts with the challenger in this game.

• Setup-2: $CH _{II}$ also runs Setup$\left( k \right)$ $\rightarrow$ $( msk,params)$, then gives msk and params to ${\mathcal {A}}_{II}$.

• Queries-2: ${\mathcal {A}}_{II}$ can adaptively make queries including Private-Key-Extract, Public-Key-Query and Signing-Query, which are the same as those in Game-1.

• Output-2: ${\mathcal {A}}_{II}$ outputs a file identifier $id^{*}$, a nonzero vector ${{\textbf {v}}}^{*}$ with its signature $\sigma ^{*}$ corresponding to $ID^{*}$ and $PK_{ID^{*}}$, here $ID^{*}$ has not been issued as a Private-Key-Extract query. In this case, the adversary ${\mathcal {A}}_{II}$ wins the Game-2 if Verify$\left( ID^{*},PK_{ID^{*}},id^{*},{{\textbf {v}}}^{*},\sigma ^{*} \right)$ $\rightarrow$ $1$ and one of the following two conditions holds:

  • 1) When ${{\textbf {v}}}^{*}\ne 0$ and $id^{*}\ne id_i$ to any $id_i$ appeared in signing queries. (Type-1 forgery)

  • 2) Suppose $id^{*}= id_i$ for some i and ${{\textbf {v}}}^{*}\notin S_i$, where $S_i$ is a subspace spanned by vectors corresponding to $id_i$. (Type-2 forgery)

Denote the advantage or probability of ${\mathcal {A}}_{II}$ winning the Game-2 by $Adv_{{\mathcal {A}}_{II}}^{\text {CLNS}}(k)$.

If for any PPT adversaries ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$, their advantages $Adv_{{\mathcal {A}}_{I}}^{\text {CLNS}}(k)$ and $Adv_{{\mathcal {A}}_{II}}^{\text {CLNS}}(k)$ of winning above games are negligible, then the CLNS is secure under the adaptive chosen message attack.

Fig. 2

System model of certificateless public auditing

4 Certificateless public auditing

In this section, we introduce a secure certificateless public auditing protocol CL-PAP, including system model and security model. Then, in order to transform the CL-PAP into a CLNS, some constraints are imposed on the protocol to make it an admissible certificateless public auditing protocol.

4.1 System model

In the system, there are four different entities including KGC, CSP, data owner and public verifier. The main functions of each entity are described as follows:

• KGC generates master key, public parameters and data owner’s partial private key based on data owner’s identity (i.e., email and name).

• CSP provides sufficient storage space, efficient computing power and retrieval ability. However, CSP is malicious and may modify or delete user’s storage files for various motives.

• Data owner owns data files and outsources the data to cloud servers. In general, he is able to divide a data file into several blocks to process the data blocks efficiently.

• Public verifier is responsible for checking the integrity of cloud data belonging to the data owner, and he cannot access any specific data information during the auditing process. In particular, he doesn’t need to manage certificates.

A typical certificateless public auditing system model is shown in Fig. 2. First, a data owner wants to store a file F to any CSP, and he is able to divide the file into m blocks as ${{\textbf {v}}}_1,{{\textbf {v}}}_2,\dots ,{{\textbf {v}}}_m\in Z_{p}^{n}$. In order to audit the cloud data, the data owner can use the private key to generate an authenticated signature $\sigma _i$ corresponding to the block ${{\textbf {v}}}_i$ $\left( 1\leqslant i\leqslant m\right)$. Then, the data file F and its authenticated signature set T will be stored together in the cloud. During the auditing process, a public verifier first launches a challenge chal to a CSP, and then the CSP returns a proof $\Gamma$ based on the challenge and the user’s cloud data. Finally, the public verifier checks the validity of the proof. In particular, the data owner’s private key consists of two parts, one part is generated by the owner himself, and the other part is generated by KGC. Simultaneously, the public key is provided by the data owner. In essence, the auditing process is a “challenge and response” protocol between the data owner and the CSP. Hence, the data owner himself can also perform the auditing.

4.2 Certificateless public auditing protocol

A secure certificateless public auditing protocol (CL-PAP) needs to meet requirements of public auditability, correctness and unforgeability, and consists of seven PPT algorithms: Setup$^{\prime }$, Extract$^{\prime }$, KeyGen$^{\prime }$, Outsource$^{\prime }$, Chal$^{\prime }$, ProofGen$^{\prime }$ and Verify$^{\prime }$.

• Setup$^{\prime }$ $\left( k \right)$ $\rightarrow$ $(msk,params)$: This algorithm is executed by KGC. After inputting a security parameter k, the algorithm outputs system parameters params and a master key msk. Note that params are public and KGC keeps msk secret.

• Extract$^{\prime }$ $\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$: KGC runs this algorithm to create data owner’s partial private key. Concretely, given a data owner’s identity ID and a master key msk, the algorithm outputs a partial private key $PP_{ID}$. Then, KGC sends $PP_{ID}$ to the data owner through a secure channel.

• KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$ $\rightarrow$ $(s_{ID},SK_{ID},PK_{ID})$: This is a key generation algorithm that is performed by data owner. Precisely, the algorithm takes ID and $PP_{ID}$ as input, and outputs user’s corresponding secret value $s_{ID}$, full private key $SK_{ID}$ and public key $PK_{ID}$.

• Outsource$^{\prime }$ $\left( SK_{ID},PK_{ID},F,id \right)$ $\rightarrow$ $F^{\prime }$: This algorithm is performed by the data owner to create authenticated data files that will be stored in the cloud. After inputting the data file F, private key $SK_{ID}$ and public key $PK_{ID}$, the algorithm first divides F into m blocks, where each block ${{\textbf {v}}}_i$ has the form of a $(m+n)$-dimensional vector over $Z_{p}$. Then, the algorithm generates the signature for each block. Finally, the algorithm randomly selects a file identifier id and outputs an authenticated file $F^{\prime }$. In detail, the file $F^{\prime }$ contains an identifier id, an original file F and a signature set T, that is $F^{\prime }=\{id,F,T\}$.

• Chal$^{\prime }(l)$ $\rightarrow$ $chal$: The data owner or public verifier executes this algorithm. The algorithm generates a challenge message denoted by chal with l elements, and submits the challenge chal to CSP.

• ProofGen$^{\prime }(chal,F^{\prime })$ $\rightarrow$ $\Gamma$: This algorithm is executed by CSP, which inputs a received challenge message chal and an authenticated data file $F^{\prime }$, and outputs an integrity proof $\Gamma$ that will be returned to data owner or public verifier.

• Verify$^{\prime }(ID,PK_{ID},id,chal,\Gamma )$ $\rightarrow$ $1/0$: The data owner or public verifier performs this algorithm. After receiving a proof $\Gamma$ from CSP, the public verifier checks its validity. In particular, the algorithm takes the public key $PK_{ID}$, data owner’s identity ID, file identifier id, challenge message chal and proof $\Gamma$ as input, and outputs 1 or 0 (accept or reject).

Correctness: The correctness of CL-PAP requires that for all $(SK_{ID},PK_{ID})$ generated by Setup$^{\prime }$, Extract$^{\prime }$ and KeyGen$^{\prime }$, any $F^{\prime }$ $\leftarrow$Outsource$^{\prime }$ $\left( SK_{ID},PK_{ID},F,id \right)$, any $chal$ $\leftarrow$Chal$^{\prime }(l)$, and an honest proof $\Gamma$ generated by ProofGen$^{\prime }(chal,F^{\prime })$, it holds that

$$\begin{aligned} 1\leftarrow {\textbf {Verify}}^{\prime }(PK_{ID},ID,id,chal,\Gamma ). \end{aligned}$$

4.3 Security model

There are three types of adversaries ${\mathcal {A}}_{I}^{\prime }$, ${\mathcal {A}}_{II}^{\prime }$ and ${\mathcal {A}}_{III}^{\prime }$ in standard CL-PAP. Specifically, ${\mathcal {A}}_{I}^{\prime }$ and ${\mathcal {A}}_{II}^{\prime }$ have the same abilities as ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$. For the adversary ${\mathcal {A}}_{III}^{\prime }$, he can be viewed as a malicious CSP that can forge the integrity proof without actual data. The advantages of three adversaries are denoted by $Adv_{{\mathcal {A}}_{I}^{\prime }}^{\text {CL-PAP}}(k)$, $Adv_{{\mathcal {A}}_{II}^{\prime }}^{\text {CL-PAP}}(k)$ and $Adv_{{\mathcal {A}}_{III}^{\prime }}^{\text {CL-PAP}}(k)$. To demonstrate security, the following three games Game-1$^{\prime }$, Game-2$^{\prime }$ and Game-3$^{\prime }$ are designed to be played by defined adversaries with their challengers $CH _{I}^{\prime }$, $CH _{II}^{\prime }$ and $CH _{III}^{\prime }$. The simulation process of Game-1$^{\prime }$ and Game-2$^{\prime }$ is, respectively, similar with Game-1 and Game-2, and hence is omitted here. Then, the process of Game-3$^{\prime }$ is described as follows.

Game-3$^{\prime }$: ${\mathcal {A}}_{III}^{\prime }$ is a malicious CSP that can forge the proof without actual data.

• Setup-3$^{\prime }$: $CH _{III}^{\prime }$ runs Setup$^{\prime }\left( k \right)$ $\rightarrow$ $(msk,params)$ and

  $$\begin{aligned} {\textbf {KeyGen}}^{\prime } \left( ID,PP_{ID} \right) \rightarrow (s_{ID},SK_{ID},PK_{ID}). \end{aligned}$$

  Then $CH _{III}^{\prime }$ keeps msk, $SK_{ID}$ secret and gives params to ${\mathcal {A}}_{III}^{\prime }$.

• Queries-3$^{\prime }$: ${\mathcal {A}}_{III}^{\prime }$ can adaptively perform queries including Secret-Value-Extract$^{\prime }$, Public-Key-Query$^{\prime }$ and Signing-Query$^{\prime }$, which are the same as those in Game-1$^{\prime }$.

• Output-3$^{\prime }$: $CH _{III}^{\prime }$ randomly sends a challenge message chal to ${\mathcal {A}}_{III}^{\prime }$, and ${\mathcal {A}}_{III}^{\prime }$ returns a forgery of proof $\Gamma ^{*}$ as respond. The adversary ${\mathcal {A}}_{III}^{\prime }$ wins the game if chal contains the index that has been queried in Signing-Query$^{\prime }$ and 1$\leftarrow$Verify$^{\prime }(PK_{ID},ID,id,chal,\Gamma ^*)$ holds.

If for ${\mathcal {A}}_{I}^{\prime }$ and ${\mathcal {A}}_{II}^{\prime }$, their advantages $Adv_{{\mathcal {A}}_{I}^{\prime }}^{\text {CL-PAP}}(k)$ and $Adv_{{\mathcal {A}}_{II}^{\prime }}^{\text {CL-PAP}}(k)$ of winning Game-1$^{\prime }$ and Game-2$^{\prime }$ are negligible, then the CL-PAP is secure under the adaptive chosen message attack. In addition, if for the PPT adversary ${\mathcal {A}}_{III}^{\prime }$, its advantage $Adv_{{\mathcal {A}}_{III}^{\prime }}^{\text {CL-PAP}}(k)$ of winning Game-3$^{\prime }$ is negligible, then the CL-PAP is secure against the malicious CSP attack.

4.4 Admissible CL-PAP

In this subsection, some slight modifications are made to the standard CL-PAP in order to transform it into a CLNS, so the following definition is given.

Definition 4

(Admissible CL-PAP). A secure certificateless public auditing protocol is called an admissible CL-PAP if it has the following properties.

• 1) The key generation algorithm KeyGen$^{\prime }$ can be decomposed. In CL-PAPs, data owner’s secret value, private key and public key are generated in the same algorithm. To transform the CL-PAP to a CLNS, we restrict that the algorithm KeyGen$^{\prime }$ can be split into algorithms including SetSecretValue, SetPrivateKey and SetPublicKey.

• 2) The challenge message chal has the form of index and coefficient. That is, the j-th element of chal has the form of $(\mu _j,\nu _j)$, where $\mu _j$ is the index of challenge block position and $\nu _j$ is the random coefficient on $Z_{p}$. In most existing CL-PAPs, this kind of challenge message is suitable for instantiating CLNSs.

• 3) The proof $\Gamma$ has the form of a linear combination. In other words, a proof $\Gamma$ generated by ProofGen$^{\prime }$ should have the form $({{\textbf {u}}},\sigma )$, where ${{\textbf {u}}}$ is a linear combination of packets with index and coefficient in chal, and $\sigma$ is the signature of ${{\textbf {u}}}$. Since the pair transmitted in CLNS has the form (packet, tag), for CSP it should return the proof $\Gamma$ like this.

• 4) The Proof $\Gamma$ can be aggregated. There exists an algorithm ${\textbf {Aggr}}^{\prime }$ can aggregate some proofs with the same id into a new proof $\Gamma$. Concretely, input s proof-coefficient pairs $(\Gamma _1,c_1),\cdots ,(\Gamma _s,c_s)$ and id, the algorithm ${\textbf {Aggr}}^{\prime }$ outputs a new combined proof $\Gamma =({{\textbf {w}}},\sigma )$, where ${{\textbf {w}}}$ is a linear combination of vectors with coefficient $c_1,\cdots ,c_s$, and $\sigma$ is the signature of ${{\textbf {w}}}$. This property is designed to describe the Combine algorithm in the CLNS.

• 5) For the malicious CSP, it is computationally infeasible to generate a forgery of auditing proof. More precisely, original CL-PAPs must prove that the malicious CSP cannot generate valid signatures for polluted data packets, otherwise the network would be flooded with spurious packets. This condition ensures that the constructed CLNS is secure against the adversary ${\mathcal {A}}_{III}^{\prime }$.

5 Construct CLNS from admissible CL-PAP

This section begins by describing the basic idea of transformation. Next, we show a general construction of the secure certificateless network coding scheme CLNS from the admissible CL-PAP. Then, we formally present security analysis of the transformed CLNS.

5.1 Basic idea of transformation

As a transformed paradigm, the constructed CLNS can be applied in IoT environment to improve network transmission throughput and defend against pollution attacks. In this case, a data owner (e.g., smart terminal) can be viewed as a source node S and tends to send the data to a destination node R (e.g., cloud server). Since the process of data validation is essentially conducted by the data owner and the server, there is no necessity to consider public verifiers. Intermediate nodes Ns consist of network operators on the Internet. Figure 3 shows the system model for using the CLNS in IoT. Each terminal uses the private key to sign the initial file, and transmits vector-signature pairs and the public key to the server. Then, the cloud server can recover the original data and perform further processing.

Another instance of the CLNS is used for authentication computing. Assuming that there are some untrusted cloud servers, the application of the CLNS ensures data can be “correctly processed,” and “correct results” can be obtained in the system. In this case, the cloud server plays the role of an intermediate node N, which may cause data pollution. By checking the validity of the received packets, the data owner can know which servers are honest. When the server returns a linearly combined vector and corresponding signature, the data owner also can be treated as a next-hop node N or R.

Fig. 3

System model of the CLNS in IoT environment

The basic idea of the general construction is intuitive. In IoT, most source nodes limited by storage capacity, communication bandwidth and battery power, and need to apply more efficient CLNSs for data transmission to reduce communication overhead and computation cost. Apparently, an efficient CLNS is also beneficial to intermediate nodes and destination nodes. Generally, building a CLNS from an admissible CL-PAP is a reasonable and practical approach.

5.2 General construction

According to the introduced admissible CL-PAP =$\left( {\textbf {Setup}}^{\prime },\right.$

$\left. {\textbf {Extract}}^{\prime },{\textbf {KeyGen}}^{\prime },{\textbf {Outsource}}^{\prime },{\textbf {Chal}}^{\prime },{\textbf {ProofGen}}^{\prime },{\textbf {Verify}}^{\prime },\right.$

$\left. {\textbf {Aggr}}^{\prime }\right)$, a CLNS = $\left( {\textbf {Setup}},{\textbf {Extract}},{\textbf {SetSecretValue}},{\textbf {SetPri-}}\right.$

$\left. {\textbf {vateKey}},{\textbf {SetPublicKey}},{\textbf {Sign}},{\textbf {Combine}},{\textbf {Verify}}\right)$ can be constructed as follows.

• Setup$\left( k \right)$ $\rightarrow$ $( msk,params)$: For the security parameter k, this algorithm runs Setup$^{\prime }$ $\left( k \right)$ $\rightarrow$ $(msk,params)$, and outputs params and msk.

• Extract$\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$: For the inputs msk and ID, this algorithm performs Extract$^{\prime }$ $\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$, and outputs the partial private key $PP_{ID}$.

• SetSecretValue$\left( ID \right)$ $\rightarrow$ $s_{ID}$: For the input ID, this algorithm executes KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$, and outputs the secret value $s_{ID}$.

• SetPrivateKey$\left( s_{ID},PP_{ID}\right)$ $\rightarrow$ $SK_{ID}$: This algorithm executes KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$. It first inputs $s_{ID}$ and $PP_{ID}$, and outputs the full private key $SK_{ID}$.

• SetPublicKey$\left( s_{ID} \right)$ $\rightarrow$ $PK_{ID}$: This algorithm also performs KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$, and outputs the public key $PK_{ID}$.

• Sign$\left( ID,SK_{ID},PK_{ID},id,V \right)$ $\rightarrow$ $T$: For the inputs ID, $SK_{ID}$, $PK_{ID}$, id and a set V has m pieces of vectors $\bar{{{\textbf {v}}}}_{1},\cdots ,\bar{{{\textbf {v}}}}_{m} \in Z_{p}^{n}$, this algorithm first augments each vector as ${{\textbf {v}}}_i=({v}_{i,1},\cdots ,{v}_{i,m+n})\in Z_{p}^{m+n}$ and defines $F=({{\textbf {v}}}_1,{{\textbf {v}}}_2,\cdots ,{{\textbf {v}}}_m)\in Z_{p}^{m\times (m+n)}$. Then, it runs

  $$\begin{aligned} {\textbf {Outsource}}^{\prime } \left( SK_{ID},PK_{ID},F,id \right) \rightarrow F^{\prime }. \end{aligned}$$

  Finally, the algorithm splits $F^{\prime }=\{id,F,T\}$ and outputs $T=\{\sigma _1,\sigma _2,\cdots ,\sigma _m\}$.

• Combine$\left( ID,PK_{ID},id,\{c_i,\sigma _{i},{{\textbf {v}}}_{i}\}_{i=1}^{l} \right)$ $\rightarrow$ $({{\textbf {v}}},\sigma )$: For the inputs ID, $PK_{ID}$ and id, upon receiving several tuples $(c_1,{{\textbf {v}}}_1,\sigma _1),\cdots ,(c_l,{{\textbf {v}}}_l,\sigma _l)$ with the same file identifier id, this algorithm defines each $\Gamma _i=({{\textbf {v}}}_i,\sigma _{i})$ according to the condition “The proof $\Gamma$ has the form of linear combination,” where $1\leqslant i \leqslant l$. Then, it aggregates $\Gamma _1,\cdots ,\Gamma _l$ into a new $\Gamma$ based on the condition “The Proof $\Gamma$ can be aggregated,” that is

  $$\begin{aligned} {\textbf {Aggr}}^{\prime }(id,(\Gamma _i,c_i)_{i=1}^l)\rightarrow \Gamma =({{\textbf {v}}},\sigma ). \end{aligned}$$

  Finally, the algorithm outputs the proof $\Gamma$.

• Verify$\left( ID,PK_{ID},id,{{\textbf {y}}},\sigma \right)$ $\rightarrow$ $1/0$: For the inputs ID, $PK_{ID}$, id, a vector ${{\textbf {y}}}\in Z_{p}^{m+n}$ and a signature $\sigma$, this algorithm first divides ${{\textbf {y}}}=(y_1,y_2,\cdots ,y_{m+n})$, and sets the challenge message $chal=\{(i,y_i)_{i=1}^m\}$ according to the condition “The challenge message chal has the form of index and coefficient,” and then sets $\Gamma =({{\textbf {y}}},\sigma )$. Finally, it runs Verify$^{\prime }(ID,PK_{ID},id,chal,\Gamma )$ and outputs 0 (reject) or 1 (accept).

5.3 Security analysis

Due to the ability of the malicious CSP is restricted in the admissible CL-PAP, two types of adversaries ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$ need to be considered. The security of the transformed CLNS can be depicted as follows.

Theorem 1

If the admissible CL-PAP is secure, then the transformed CLNS is secure.

Concretely, suppose there exist two adversaries ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$ attack on the transformed CLNS. Meanwhile, there are other two adversaries ${\mathcal {B}}_{I}$ and ${\mathcal {B}}_{II}$ attack the admissible CL-PAP, regarding ${\mathcal {A}}_{I}$ and ${\mathcal {A}}_{II}$ as a subroutine, respectively. Thereupon, we divide the security proof of the construction into two parts: Proof 1 and Proof 2.

Proof 1: ${\mathcal {A}}_{I}$ attacks the CLNS and ${\mathcal {B}}_{I}$ simulates environment for ${\mathcal {A}}_{I}$ as following steps.

Setup: ${\mathcal {B}}_{I}$ obtains (msk, params) first, then gives params to ${\mathcal {A}}_{I}$.

Queries: ${\mathcal {A}}_{I}$ can adaptively perform the following queries and ${\mathcal {B}}_{I}$ answers these queries.

• Private-Key-Extract: Firstly, ${\mathcal {B}}_{I}$ uses ID to choose a secret value $s_{ID}$. Then, ${\mathcal {B}}_{I}$ continues to perform KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$ and outputs $SK_{ID}$, then returns $SK_{ID}$ to ${\mathcal {A}}_{I}$.

• Public-Key-Query: ${\mathcal {B}}_{I}$ also runs KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$ and returns $PK_{ID}$ to ${\mathcal {A}}_{I}$.

• Public-Key-Replace: ${\mathcal {A}}_{I}$ replaces the public key $PK_{ID}$ with another value $PK_{ID^*}$, but ${\mathcal {A}}_{I}$ does not need to provide the secret value corresponding to $PK_{ID^*}$.

• Signing-Query: For the file $V\subset Z_{p}^{m\times n}$ will be queried, it can be split into n-dimensional vectors $\bar{{{\textbf {v}}}}_{1},\dots , \bar{{{\textbf {v}}}}_{m} \in Z_{p}^{n}$. ${\mathcal {B}}_{I}$ first augments them to ${{\textbf {v}}}_1, \dots ,{{\textbf {v}}}_m\in Z_{p}^{m+n}$ and defines $F=\{{{\textbf {v}}}_1, \cdots ,{{\textbf {v}}}_m\}$. Then, ${\mathcal {B}}_{I}$ runs Outsource$^{\prime }$ algorithm and obtains $F^{\prime }$. Afterward, ${\mathcal {B}}_{I}$ parses $F^{\prime }=\{id,F,T\}$ and returns (id, T) to ${\mathcal {A}}_{I}$.

• Combining-Queries: For the tuples $( id,\{c_i,\sigma _{i},{{\textbf {v}}}_{i}\}_{i=1}^{l})$ will be queried, ${\mathcal {B}}_{I}$ defines each $\Gamma _i=({{\textbf {v}}}_i,\sigma _{i})$, and aggregates $\Gamma _1,\cdots ,\Gamma _l$ into a new $\Gamma =({{\textbf {v}}},\sigma )$ according to the condition “The Proof $\Gamma$ can be aggregated.” Finally, ${\mathcal {B}}_{I}$ returns $\Gamma$ to ${\mathcal {A}}_{I}$.

Output: First, ${\mathcal {A}}_{I}$ outputs a file identifier $id^{*}$, a nonzero vector ${{\textbf {y}}}^{*}$ and a signature $\sigma ^{*}$, which all correspond to $ID^{*}$ and $PK_{ID^{*}}$. Next, ${\mathcal {B}}_{I}$ parses ${{\textbf {y}}}^*=(y_1^*,y_2^*,\cdots ,y_{m+n}^*)$ and sets $chal^{*}=\{(i,y_i^*)_{i=1}^m\}$, $\Gamma =({{\textbf {y}}}^*,\sigma ^*)$. Then, ${\mathcal {A}}_{I}$ outputs $(ID^*,PK_{ID^*},id^*,chal^*,\Gamma ^*)$ as a forgery.

In this case, if

$$\begin{aligned} {\textbf {Verify}}^{\prime }(ID^*,PK_{ID^*},id^*,chal^*,\Gamma ^*)\rightarrow 1, \end{aligned}$$

and it satisfies one of the following conditions:

• 1) ${{\textbf {v}}}^{*}\ne 0$ and $id^{*}\ne id_i$ to any $id_i$ appeared in Signing-Query.

• 2) $id^*$ equals some queried file $V_i$’s identifier $id_i$ but $y^* \notin S_i$.

Then, ${\mathcal {A}}_{I}$ can use $(ID^*,PK_{ID^*},id^*,\Gamma ^*$) to forge the corresponding chal successfully. Proof 1 ends.

Proof 2: ${\mathcal {A}}_{II}$ attacks the CLNS and ${\mathcal {B}}_{II}$ simulates the environment for ${\mathcal {A}}_{II}$ as follows.

Setup: ${\mathcal {B}}_{II}$ obtains (msk, params) first, then gives msk and params to ${\mathcal {A}}_{II}$.

Queries: ${\mathcal {A}}_{II}$ can adaptively perform the following queries and ${\mathcal {B}}_{II}$ answers corresponding queries.

• Private-Key-Extract: ${\mathcal {B}}_{II}$ picks a secret value $s_{ID}$ based on an ID, and executes KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$. Next, ${\mathcal {B}}_{II}$ outputs $SK_{ID}$ and returns $SK_{ID}$ to ${\mathcal {A}}_{II}$.

• Public-Key-Query: ${\mathcal {B}}_{II}$ performs KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$, and returns $PK_{ID}$ to ${\mathcal {A}}_{II}$.

• Signing-Query: Given the queried file $V\subset Z_{p}^{m\times n}$, ${\mathcal {B}}_{II}$ first augments the file as vectors to ${{\textbf {v}}}_1, \cdots ,{{\textbf {v}}}_m\in Z_{p}^{m+n}$ and defines $F=\{{{\textbf {v}}}_1, \cdots ,{{\textbf {v}}}_m\}$. Then, ${\mathcal {B}}_{II}$ performs Outsource$^{\prime }$ algorithm and obtains $F^{\prime }$. In the end, ${\mathcal {B}}_{II}$ parses $F^{\prime }=\{id,F,T\}$ and returns (id, T) to ${\mathcal {A}}_{II}$.

• Combining-Queries: Given the tuples $( id,\{c_i,\sigma _{i},{{\textbf {v}}}_{i}\}_{i=1}^{l})$ will be queried, ${\mathcal {B}}_{II}$ defines each $\Gamma _i=({{\textbf {v}}}_i,\sigma _{i})$ and aggregates $\Gamma _1,\cdots ,\Gamma _l$ into a new $\Gamma =({{\textbf {v}}},\sigma )$ by the algorithm ${\textbf {Aggr}}^{\prime }(id,(\Gamma _i,c_i)_{i=1}^l)$. Finally, ${\mathcal {B}}_{II}$ returns $\Gamma$ to ${\mathcal {A}}_{II}$.

Output: ${\mathcal {A}}_{II}$ first outputs a file identifier $id^{*}$, a nonzero vector ${{\textbf {y}}}^{*}$ and a signature $\sigma ^{*}$, which all correspond to $ID^{*}$ and $PK_{ID^{*}}$. Then ${\mathcal {B}}_{II}$ parses ${{\textbf {y}}}^*=(y_1^*,y_2^*,\cdots ,y_{m+n}^*)$ and sets $chal^{*}=\{(i,y_i^*)_{i=1}^m\}$, $\Gamma =({{\textbf {y}}}^*,\sigma ^*)$. Later, ${\mathcal {A}}_{II}$ outputs $(ID^*,PK_{ID^*},id^*,chal^*,\Gamma ^*)$ as a forgery.

In this situation, if

$$\begin{aligned} {\textbf {Verify}}^{\prime }(ID^*,PK_{ID^*},id^*,chal^*,\Gamma ^*)\rightarrow 1, \end{aligned}$$

and one of the following conditions holds:

• 1) ${{\textbf {v}}}^{*}\ne 0$ and $id^{*}\ne id_i$ to any $id_i$ appeared in Signing-Query.

• 2) $id^*$ equals some queried file $V_i$’s identifier $id_i$ but $y^* \notin S_i$.

In this way, ${\mathcal {A}}_{II}$ utilizes msk and $(ID^*,PK_{ID^*},id^*,\Gamma ^*)$ forges the chal successfully. Proof 2 ends.

Combining Proof 1 and Proof 2, we can conclude that the general construction of the CLNS is secure if the secure admissible CL-PAP is adopted. The proof of Theorem 1 ends.

6 A concrete instantiation

In this section, to demonstrate the power of the general construction in practice, a concrete certificateless network coding scheme based on a secure certificateless public auditing protocol is constructed. Then, the security proof of the transformed scheme is given.

6.1 Scheme details

We note that the certificateless public auditing protocol in [38] satisfies all conditions in Definition 4. Accordingly, we modify it and design a concrete admissible CL-PAP = $\left( {\textbf {Setup}}^{\prime },{\textbf {Extract}}^{\prime },{\textbf {KeyGen}}^{\prime },{\textbf {Outsource}}^{\prime },{\textbf {Chal}}^{\prime },{\textbf {ProofGen}}^{\prime },\right. \left. {\textbf {Verify}}^{\prime },{\textbf {Aggr}}^{\prime }\right)$ as follows.

• Setup$^{\prime }$ $\left( k \right)$ $\rightarrow$ $(msk,params)$: Firstly, given a security parameter k, KGC chooses two cyclic groups $G_1$, $G_2$ with same order p and a bilinear map $e:G_1\times G_1\rightarrow G_2$, then sets g is the generator of $G_1$. Then, KGC randomly picks $\uplambda \in Z_p^*$ as a master key and defines $h=g^{\uplambda }$. Later, KGC selects $m+n$ random elements $(g_1,g_2,\cdots , g_{m+n})\in G_1$, and defines two hash functions $H_1:\{0,1\}^*\rightarrow G_1$ and $H_2:\{0,1\}^*\rightarrow G_1$. As a result, KGC outputs public system parameters $params=$ $(G_1,G_2,e,p,g,h,H_1,H_2,g_1,g_2,\cdots , g_{m+n})$.

• Extract$^{\prime }$ $\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$: Given an identity ID of the data owner, KGC computes partial private key $PP_{ID}=H_1(ID)^{\uplambda }\in G_1$ and returns $PP_{ID}$ to the data owner.

• KeyGen$^{\prime }$ $\left( ID,PP_{ID} \right)$ $\rightarrow$ $(s_{ID},SK_{ID},PK_{ID})$: The data owner randomly selects $s_{ID}\in Z_p^*$ as a secret value, and he generates the full private key $SK_{ID}=(PP_{ID},s_{ID})$ and public key $PK_{ID}=g^{s_{ID}}$.

• Outsource$^{\prime }$ $\left( SK_{ID},PK_{ID},F,id \right)$ $\rightarrow$ $F^{\prime }$: The data owner chooses a random $id\in \{0,1\}^k$ and splits the data file F into m blocks ${{\textbf {v}}}_1, {{\textbf {v}}}_2,\cdots ,{{\textbf {v}}}_m$, each block is in the form of ${{\textbf {v}}}_i=({v}_{i,1},{v}_{i,2},\cdots ,{v}_{i,m+n})\in Z_p^{m+n}$. Next, the data owner computes each signature as

  $$\begin{aligned} \sigma _{i}^{\prime }=&H_1(ID)^{\uplambda }\times \\&\left( H_2(ID||PK_{ID}||id||i)\cdot \prod _{j=1}^{m+n}g_j^{{v}_{i,j}}\right) ^{s_{ID}}. \end{aligned}$$

  Then, it defines ${{\textbf {g}}}=\{g_1,g_2,\cdots ,g_{m+n}\}$, $\sigma _{i}=\left( {{\textbf {g}}},\sigma _{i}^{\prime }\right)$ and $T=\{\sigma _1,\sigma _2,\cdots ,\sigma _m\}$, where $1\leqslant i\leqslant m$. Finally, the algorithm outputs $F^{\prime }=\{id,F,T\}$.

• Chal$^{\prime }(l)$ $\rightarrow$ $chal$: Given an input l, this algorithm picks random $1\leqslant \mu _1<\mu _2<\cdots <\mu _l\leqslant m$ and l elements $\nu _1,\nu _2,\cdots ,\nu _l\in Z_p$, and outputs $chal=\{\left( \mu _j,\nu _j\right) _{j=1}^l\}$.

• ProofGen$^{\prime }(chal,F^{\prime })$ $\rightarrow$ $\Gamma$: For the inputs chal and an authenticated date file $F^{\prime }$, this algorithm first parses $chal=\{\left( \mu _j,\nu _j\right) _{j=1}^l\}$ and $F^{\prime }=\{id,F,T\}=\{id,({{\textbf {v}}}_1,{{\textbf {v}}}_2,\cdots ,{{\textbf {v}}}_m),(\sigma _1,\sigma _2,\cdots ,\sigma _m)\}$, where $\sigma _{i}=({{\textbf {g}}},\sigma _{i}^{\prime })$. Then, for $1\leqslant i\leqslant m$ and $1\leqslant j\leqslant m+n$, the algorithm computes

  $$\begin{aligned} M_j=\sum _{i=1}^{l}\nu _iv_{\mu _i,j}\in Z_p,\text { and } \sigma ^{\prime }=\prod _{i=1}^{l}\left( \sigma _{\mu _i}^{\prime }\right) ^{\nu _i}, \end{aligned}$$

  and defines $\Gamma =\left( M,\sigma \right) =\left( (M_1,\cdots ,M_{m+n}),({{\textbf {g}}},\sigma ^{\prime })\right)$. In particular, M can be regarded as a vector, denoted by ${{\textbf {y}}}=\left( y_1,\cdots ,y_{m+n }\right)$. Last, it outputs the proof $\Gamma$.

• Verify$^{\prime }(ID,PK_{ID},id,chal,\Gamma )$ $\rightarrow$ $1/0$: For the inputs data owner’s ID, public key $PK_{ID}$, file identifier id, challenge message chal and returned proof $\Gamma =({{\textbf {y}}},\sigma )$, this algorithm parses $\sigma =({{\textbf {g}}},\sigma ^{\prime })$ and checks whether

  $$\begin{aligned} e&(\sigma ^{\prime },g)=e\left( \prod _{i=1}^{l}H_1(ID)^{\nu _i},h\right) \\&\cdot e\left( \prod _{i=1}^{l}H_2(ID||PK_{ID}||id||\mu _i)^{\nu _i}\cdot \prod _{j=1}^{m+n}g_j^{y_j},PK_{ID}\right) . \end{aligned}$$

  If it equals, then output 1. If not, output 0.

In detail, the conditions “The challenge message chal has the form of index and coefficient” and “The proof $\Gamma$ has the form of linear combination” are obvious. Moreover, this protocol satisfies the conditions “The algorithm KeyGen$^\prime$ can be decomposed” and “The malicious CSP cannot forge the auditing proof.” As for the condition “The Proof $\Gamma$ can be aggregated,” we design an aggregation algorithm Aggr$^{\prime }$ as follows.

• Aggr$^{\prime }(id,\{c_i,\Gamma _i\}_{i=1}^s)$ $\rightarrow$ $\Gamma$: Given a file identifier id and s proof-coefficient tuples $(c_1,\Gamma _1,),\cdots ,(c_s,\Gamma _s)$, where $1\leqslant i\leqslant s$. This algorithm parses $\Gamma _i=({{\textbf {v}}}_i,\sigma _{i})=({{\textbf {v}}}_i,({{\textbf {g}}},\sigma _{i}^{\prime }))$ and computes,

  $$\begin{aligned} {{\textbf {v}}}=\sum _{i=1}^{s}c_i{{\textbf {v}}}_{i}, \text { and } \sigma ^{\prime }=\prod _{i=1}^{s}\left( \sigma _i^{\prime }\right) ^{c_i}. \end{aligned}$$

  Finally, the aggregated proof $\Gamma =({{\textbf {v}}},\sigma )=({{\textbf {v}}},({{\textbf {g}}},\sigma ^{\prime }))$ is output.

Then, based on the general construction, the transformed CLNS from the above admissible CL-PAP can be depicted as follows, and the algorithm flow also presented in Table 1.

Table 1 The algorithms of the transformed CLNS

• Setup$\left( k \right)$ $\rightarrow$ $( msk,params)$: For the security parameter k as input, this algorithm performs

  $$\begin{aligned} {\textbf {Setup}}^{\prime }\left( k\right) \rightarrow (msk,params) \end{aligned}$$

  and KGC publishes params and keeps msk secret.

• Extract$\left( msk,ID \right)$ $\rightarrow$ $PP_{ID}$: For the inputs msk and ID, this algorithm runs

  $$\begin{aligned} {\textbf {Extract}}^{\prime }\left( msk,ID \right) \rightarrow PP_{ID} \end{aligned}$$

  to generate the partial private key $PP_{ID}=H_1(ID)^{\uplambda }$.

• SetSecretValue$\left( ID \right)$ $\rightarrow$ $s_{ID}$: Given the identity ID, this algorithm executes

  $$\begin{aligned} {\textbf {KeyGen}}^{\prime }\left( ID,PP_{ID} \right) \rightarrow s_{ID} \end{aligned}$$

  and outputs $s_{ID}$ as the secret value.

• SetPrivateKey$\left( s_{ID},PP_{ID} \right)$ $\rightarrow$ $SK_{ID}$: For the inputs $s_{ID}$ and ID, this algorithm performs

  $$\begin{aligned} {\textbf {KeyGen}}^{\prime }\left( ID,PP_{ID} \right) \rightarrow SK_{ID} \end{aligned}$$

  and outputs $SK_{ID}=(PP_{ID},s_{ID})$ as the full private key.

• SetPublicKey$\left( s_{ID} \right)$ $\rightarrow$ $PK_{ID}$: For the input $s_{ID}$, this algorithm also runs

  $$\begin{aligned} {\textbf {KeyGen}}^{\prime }\left( ID,PP_{ID} \right) \rightarrow PK_{ID} \end{aligned}$$

  and outputs $PK_{ID}=g^{s_{ID}}$ as the public key.

• Sign$\left( ID,SK_{ID},PK_{ID},id,V \right)$ $\rightarrow$ $T$: For the inputs ID, $SK_{ID}$, $PK_{ID}$, id and a set V has m pieces of vectors $\bar{{{\textbf {v}}}}_{1},\cdots ,\bar{{{\textbf {v}}}}_{m} \in Z_{p}^{n}$, this algorithm first augments these vectors as ${{\textbf {v}}}_i\in Z_{p}^{m+n}$, where $1\leqslant i\leqslant m$. Then, it sets $F=({{\textbf {v}}}_1,{{\textbf {v}}}_2,\cdots ,{{\textbf {v}}}_m)\in Z_{p}^{m\times (m+n)}$ and runs

  $$\begin{aligned} {\textbf {Outsource}}^{\prime }\left( SK_{ID},PK_{ID},F,id \right) \rightarrow F^{\prime }. \end{aligned}$$

  In particular, the algorithm picks a random id from $\{0,1\}^k$. For each vector ${{\textbf {v}}}_i$, it computes

  $$\begin{aligned} \sigma _{i}^{\prime }=&H_1\left( ID\right) ^{\uplambda }\times \\&\left( H_2\left( ID||PK_{ID}||id||i\right) \cdot \prod _{j=1}^{m+n}g_j^{{v}_{i,j}}\right) ^{s_{ID}}\in G_1. \end{aligned}$$

  Finally, it defines ${{\textbf {g}}}=\{g_1,g_2,\cdots ,g_{m+n}\}$, $\sigma _{i}=\left( {{\textbf {g}}},\sigma _{i}^{\prime }\right)$ and $T=\{\sigma _1,\sigma _2,\cdots ,\sigma _m\}$, then outputs T.

• Combine$\left( ID,PK_{ID},id,\{c_i,{{\textbf {v}}}_{i},\sigma _{i}\}_{i=1}^{l} \right)$ $\rightarrow$ $({{\textbf {v}}},\sigma )$: For the inputs ID, $PK_{ID}$ and id, upon receiving tuples $(c_1,{{\textbf {v}}}_1,\sigma _1),\cdots ,(c_l,{{\textbf {v}}}_l,\sigma _l)$ with the file identifier id, it defines each $\Gamma _i=({{\textbf {v}}}_i,\sigma _{i})$, where $1\leqslant i \leqslant l$. Then, the algorithm runs

  $$\begin{aligned} {\textbf {Aggr}}^{\prime }(id,(\Gamma _i,c_i)_{i=1}^l)\rightarrow \Gamma =({{\textbf {v}}},\sigma ), \end{aligned}$$

  and outputs the aggregated proof $\Gamma$.

• Verify$\left( ID,PK_{ID},id,{{\textbf {y}}},\sigma \right)$ $\rightarrow$ $1/0$: For the inputs ID, $PK_{ID}$, id, a vector ${{\textbf {y}}}\in Z_{p}^{m+n}$ and a signature $\sigma$, this algorithm first divides ${{\textbf {y}}}=(y_1,y_2,\cdots ,y_{m+n})$ and sets the challenge message $chal=\{(i,y_i)_{i=1}^m\}$. Next, the algorithm runs

  $$\begin{aligned} {\textbf {Verify}}^{\prime }(ID,PK_{ID},id,chal,\Gamma ) \rightarrow 1/0. \end{aligned}$$

  That is to check whether

  $$\begin{aligned}&e(\sigma ^{\prime },g)=e\left( \prod _{i=1}^{m}H_1(ID)^{y_i},h\right) \\&\cdot e\left( \prod _{i=1}^{m}H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{j=1}^{m+n}g_j^{y_j},PK_{ID}\right) . \end{aligned}$$

  If it equals, then output 1, and 0 otherwise.

Correctness: Given a data owner’s identity ID, a full private key $SK_{ID}$, a public key $PK_{ID}$, a file identifier id, a set $V=(\bar{{{\textbf {v}}}}_{1},\cdots ,\bar{{{\textbf {v}}}}_{m})\in Z_{p}^{n}$ and a signature set $T\leftarrow$Sign$\left( ID,SK_{ID},PK_{ID},id,V \right)$, the correctness of verification equation for the transformed CLNS can be checked as follows.

$$\begin{aligned}&e(\sigma ^{\prime },g)=e\left( \prod _{i=1}^{m}\left( \sigma _{i}^{\prime }\right) ^{y_i},g\right) \\&=e\left( \prod _{i=1}^{m}\left( H_1(ID)^{\uplambda {y_i}}\right. \right. \\&\quad \left. \cdot \prod _{i=1}^{m}\left( H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{j=1}^{m+n}g_j^{{y_i}{v}_{i,j}}\right) ^{s_{ID}},g\right) \\&=e\left( \prod _{i=1}^{m}H_1(ID)^{\uplambda {y_i}}\right. \\&\quad \left. \cdot \left( \prod _{i=1}^{m}H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{i=1}^{m}\prod _{j=1}^{m+n}g_j^{{y_i}{v}_{i,j}}\right) ^{s_{ID}},g\right) \\&=e\left( \prod _{i=1}^{m}H_1(ID)^{{\uplambda }y_i}\right. \\&\quad \left. \cdot \left( \prod _{i=1}^{m}H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{j=1}^{m+n}g_j^{\sum _{i=1}^{m}{y_i}{v}_{i,j}}\right) ^{s_{ID}},g\right) \\&=e\left( \prod _{i=1}^{m}H_1(ID)^{{y_i}},h\right) \\&\quad \cdot e\left( \prod _{i=1}^{m}H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{j=1}^{m+n}g_j^{y_j},PK_{ID}\right) . \end{aligned}$$

6.2 Security proof

For the security of the transformed CLNS, we prove that if ${\mathcal {A}}_{I}$ or ${\mathcal {A}}_{II}$ can generate a forgery of signature, then there exists an algorithm ${\mathcal {B}}$ is able to solve the CDH problem on $G_1$ (given g, $g^a$ and $g^b$, output $g^{ab}$), which will contradict the CDH assumption. The proof consists of two parts Proof 1 and Proof 2.

Proof 1: This proof is derived from Game-1. ${\mathcal {B}}$ simulates the security game, and ${\mathcal {A}}_{I}$ can replace the public key. Meanwhile, hash function $H_1$ is viewed as a random oracle, and $\perp$ denotes the termination symbol. Given g, $g^a$ and $g^b$, ${\mathcal {B}}$ performs the game as follows.

Setup: ${\mathcal {A}}_{I}$ requests to begin. ${\mathcal {B}}$ sets $h=g^a$, computes and returns system parameters $(G_1,G_2,e,p,g,h,H_1,H_2,g_j)$ to ${\mathcal {A}}_{I}$.

Queries: ${\mathcal {A}}_{I}$ can adaptively perform the following queries and ${\mathcal {B}}$ answers corresponding queries.

• $H_1$-Query: ${\mathcal {A}}_{I}$ sends a hash-I query on identity ID of a node S. ${\mathcal {B}}$ chooses a random $r\in Z_p^*$ and tosses a coin. The probability equals to $p_c$ when the coin shows 1, and 0 otherwise. If the result of tossing is 1, ${\mathcal {B}}$ sets $H_1\left( ID\right) =g^r\in G_1$; if the result is 0, ${\mathcal {B}}$ sets $H_1\left( ID\right) =(g^b)^r\in G_1$. Then, ${\mathcal {B}}$ returns the $H_1\left( ID\right)$ to ${\mathcal {A}}_{I}$. Since $G_1$ is a cyclic group, r is randomly selected from $Z_p^*$, g and $g^b$ are elements of $G_1$, $g^r$ and $(g^b)^r$ have the same distribution on $G_1$, ${\mathcal {A}}_{I}$ cannot distinguish the result of the toss coin according to returned $H_1\left( ID\right)$.

• Private-Key-Extract: ${\mathcal {A}}_{I}$ asks for the partial private key on ID. If the last result of toss coin in hash-I query was 1, ${\mathcal {B}}$ outputs the $PP_{ID}=(g^a)^r$, where r is randomly chosen in the corresponding hash-I query. If not, ${\mathcal {B}}$ outputs $\perp$.

• Public-Key-Replace: ${\mathcal {A}}_{I}$ has the ability to replace the public key. More precisely, ${\mathcal {A}}_{I}$ randomly picks $s_{ID}$ and sets the public key $PK_{ID}=g^{x_{ID}}$. Then, ${\mathcal {A}}_{I}$ sends $\left( ID,s_{ID},PK_{ID}\right)$ to ${\mathcal {B}}$. ${\mathcal {B}}$ records this key replacement process.

• $H_2$-Query: ${\mathcal {A}}_{I}$ sends a hash-II query on identity ID, public key $PK_{ID}$, packet $m_i$ and file identifier id. ${\mathcal {B}}$ computes $V=H_2\left( ID||PK_{ID}||id||i\right) \cdot g_j^{m_i}$ and returns V to ${\mathcal {A}}_{I}$.

• Signing-Query: ${\mathcal {A}}_{I}$ requests a signature of packet $m_i$ and a file identifier id from the former hash-II query. If the output of the corresponding coin toss was 1 in previous hash-I query, then ${\mathcal {B}}$ outputs the signature $\sigma =V^{s_{ID}}(g^a)^r$, where r was randomly chosen in hash-I query. If not, ${\mathcal {B}}$ outputs $\perp$.

Output: Finally, ${\mathcal {A}}_{I}$ outputs a forgery of signature $\sigma$ on $\left( ID,m_i,id\right)$. Then, ${\mathcal {B}}$ grasps the forgery was $H_1\left( ID\right) =(g^b)^r$ from the hash-I query, and the forged signature $\sigma =V^{s_{ID}}(g^{ab})^r$. Accordingly, ${\mathcal {B}}$ can output $g^{ab}$ by computing

$$\begin{aligned} g^{ab}={\left( \sigma /V^{s_{ID}}\right) ^{r^{-1}}}, \end{aligned}$$

because ${\mathcal {B}}$ knows $\left( \sigma ,V^{s_{ID}},r\right)$ according to queries in the game. It indicates if ${\mathcal {A}}_{I}$ generates a forged signature successfully, then ${\mathcal {B}}$ can solve the CDH problem.

Proof 2: This proof is derived from Game-2. Now, we consider another type of adversary ${\mathcal {A}}_{II}$. In this case, ${\mathcal {B}}$ should give the master key to ${\mathcal {A}}_{II}$, but ${\mathcal {A}}_{II}$ cannot replace the public key. In this case, hash function $H_2$ is regarded as a random oracle. Given g, $g^a$ and $g^b$, ${\mathcal {B}}$ performs the game as follows.

Setup: ${\mathcal {A}}_{II}$ requests to start. ${\mathcal {B}}$ randomly chooses a $\uplambda \in Z_p^*$ as the master key. Then, ${\mathcal {B}}$ returns $\uplambda$ and system parameters $(G_1,G_2,e,p,g,h,H_1,H_2,g_j)$ to ${\mathcal {A}}_{II}$.

Queries: ${\mathcal {A}}_{II}$ can adaptively perform the following queries and ${\mathcal {B}}$ answers corresponding queries.

• $H_1$-Query: ${\mathcal {A}}_{II}$ sends a hash-I query on identity ID of a node S. ${\mathcal {B}}$ sets $Q_{ID}=H_1\left( ID\right) \in G_1$ and returns $Q_{ID}$ to ${\mathcal {A}}_{II}$.

• Private-Key-Extract: ${\mathcal {A}}_{II}$ asks for the partial private key on ID. ${\mathcal {B}}$ computes the partial private key $PP_{ID}=Q_{ID}^{\uplambda }$. Then, ${\mathcal {B}}$ returns $PP_{ID}$ to ${\mathcal {A}}_{II}$ and computes $g^a$ as the public key of the S.

• $H_2$-Query: ${\mathcal {A}}_{II}$ sends a hash-II query on identity ID, public key $PP_{ID}$, packet $m_i$ and file identifier id. ${\mathcal {B}}$ selects a random $r\in Z_p^*$ and performs coin toss. If the result is 1, ${\mathcal {B}}$ sets $H_2\left( ID||PK_{ID}||id||i\right) \cdot {g_j^{m_i}}=g^r$; if the result is 0, ${\mathcal {B}}$ sets $H_2\left( ID||PK_{ID}||id||i\right) \cdot {g_j^{m_i}}=(g^b)^r$. Then, ${\mathcal {B}}$ returns the $H_2\left( ID||PK_{ID}||id||i\right) \cdot {g_j^{m_i}}$ to ${\mathcal {A}}_{II}$. Likewise, ${\mathcal {A}}_{II}$ cannot distinguish the result of the toss coin according to returned content from ${\mathcal {B}}$.

• Signing-Query: ${\mathcal {A}}_{II}$ requests a signature of packet $m_i$ and a file identifier id. If the output of the corresponding coin toss was 1 in former hash-II query, then ${\mathcal {B}}$ outputs the signature $\sigma =(g^a)^rPP_{ID}$, because

  $$\begin{aligned} \sigma =\left( g^r\right) ^aPP_{ID}=\left( g^a\right) ^rPP_{ID}, \end{aligned}$$

  where r was randomly picked in hash-II query. If not, ${\mathcal {B}}$ outputs $\perp$.

Output: In the end, ${\mathcal {A}}_{II}$ outputs a forged signature $\sigma$ on $\left( ID,m_i,id\right)$. Then, ${\mathcal {B}}$ grasps the forgery was $H_2\left( ID||PP_{ID}||id||i\right) \cdot g_j^{m_i}=(g^b)^r$ from the hash-II query, and the forgery is $\sigma =(g^{ab})^rPP_{ID}$. Thus, ${\mathcal {B}}$ can output $g^{ab}$ by computing

$$\begin{aligned} g^{ab}={\left( \sigma /PP_{ID}\right) ^{r^{-1}}}, \end{aligned}$$

because ${\mathcal {B}}$ knows $\left( \sigma ,PP_{ID},r\right)$ according to queries in the game. It implies if ${\mathcal {A}}_{II}$ generates a forged signature successfully, then ${\mathcal {B}}$ can solve the CDH problem.

Combining Proof 1 and Proof 2, the transformed CLNS can be proven secure. This ends the security proof.

7 Performance analysis

This section analyzes the performance of the transformed CLNS in Section VI. Specifically, we first compare the CLNS with other classic network coding schemes in [5, 7] and [29] in terms of communication overhead and computation cost. Then, we evaluate their performance by experimental analysis.

7.1 Communication overhead

In this subsection, we consider the communication overhead including the size of $PP_{ID}$ from KGC to node S and signature size from S to other nodes, because the size of private (partial) key affects the storage capability of the node S and the signature size affects the communication overhead of all nodes. Note that Lin et al.’s scheme in [5] is based on identity-based cryptosystem, so $PP_{ID}$ does not exist. KGC generates the whole private key for S, thus the overhead from KGC to S equals the size of $SK_{ID}$. To fairly express a comparison, we use the size of $SK_{ID}$ in Lin et al.’s scheme [5] to represent “the size of $PP_{ID}$.” Here, the lengths of $G_1$ and $Z_p$ are denoted by $\left| G_1 \right|$ and $\left| Z_p \right|$.

Firstly, we consider the overhead from KGC to S (denoted by $PP_{ID}$-Size). In the proposed CLNS, a source node sends its ID to KGC and KGC returns a partial private key $PP_{ID}$. Hence, the communication overhead for KGC to node S is $\left| G_1 \right|$. Similarly, we can obtain the overhead of $PP_{ID}$-Size in [5, 7] and [29] are $2\left| G_1\right| +\left| Z_p\right|$, $2\left| G_1\right|$ and $\left| G_1\right|$.

Secondly, we compute the overhead for node S to other nodes (Sig-Size). Assuming that node S sends all vector-signature pairs to others, for convenience, it is only necessary to calculate the signature size for a single vector ${{\textbf {v}}}_i$. In the transformed CLNS, the signature of a single vector is

$$\begin{aligned} \sigma _{i}=\left( {{\textbf {g}}},\sigma _{i}^{\prime }\right) \in G_1\times \left( G_1\times G_1\right) =G_1^3. \end{aligned}$$

Thus, the Sig-Size equals to $3\left| G_1\right|$. Similarly, it can be computed that Sig-Size in [5, 7] and [29] are $4\left| G_1\right| +2\left| Z_p\right|$, $4\left| G_1\right| +\left| Z_p\right|$ and $4\left| G_1\right|$, respectively.

A detailed comparison of communication overhead is listed in Table 2. Obviously, the transformed certificateless network coding scheme CLNS has minimal communication overhead in terms of Sig-Size, which can help nodes save space for storing signatures and improve transmission efficiency. Besides, $PP_{ID}$-Size also has competitiveness, it enables the node S to store the private (partial) key with less cost.

Table 2 A comparison of communication overhead

7.2 Computation cost

This subsection evaluates the computation cost through theoretical analysis, including the data signing process performed by node S, the combination executed by node N and the verification performed by node N or R, since they are key factors to measure the computing power of nodes. Here, use $T_{bp}$, $T_{exp}$, $T_{mul}$, $T_{lc}$ to represent the execution time of a bilinear pairing operation, a modular exponentiation operation on $G_1$, a multiplication operation on $G_1$ and a linear combination of l vectors ${{\textbf {v}}}_1, {{\textbf {v}}}_2,\dots ,{{\textbf {v}}}_l$. For convenience, we omit the computation like pseudorandom permutation, hash operation, addition on $Z_p$, multiplication on $Z_p$, etc., as their computation cost is negligible.

To begin with, we consider the data signing process (denoted by Sig-Generation). Suppose there is a node S that will transmit a file in the network, which is equivalent to sending a set of vectors $\bar{{{\textbf {v}}}}_{1},\cdots , \bar{{{\textbf {v}}}}_{m}$ with corresponding signatures. Particularly, for a single augmented vector ${{\textbf {v}}}_i$, its generated signature is

$$\begin{aligned} \sigma _{i}^{\prime }=&H_1(ID)^{\uplambda }\times \\&\left( H_2(ID||PK_{ID}||id||i)\cdot \prod _{j=1}^{m+n}g_j^{{v}_{i,j}}\right) ^{s_{ID}}. \end{aligned}$$

Therefore, the computation cost of generating a signature $\sigma _{i}^{\prime }$ equals to $(m+n+2)\cdot T_{exp}+(m+n+1)\cdot T_{mul}$.

Next, we focus on the computation cost of the verification (Sig-Verification). In the CLNS, the node N or R verifies each vector-signature pair $({{\textbf {y}}},\sigma ^{\prime })$ by checking whether

$$\begin{aligned}&e(\sigma ^{\prime },g)=e\left( \prod _{i=1}^{m}H_1(ID)^{y_i},h\right) \\&\cdot e\left( \prod _{i=1}^{m}H_2(ID||PK_{ID}||id||i)^{y_i}\cdot \prod _{j=1}^{m+n}g_j^{y_j},PK_{ID}\right) , \end{aligned}$$

which takes the time of $3\cdot T_{bp}+(2m+n+1)\cdot T_{exp}+(2m+n)\cdot T_{mul}$.

Moreover, we consider the computation cost of the combination (Combination). In particular, given l vector-signature pairs $\{{{\textbf {v}}}_{i},\sigma _{i}\}_{i=1}^{l}$, the node N computes

$$\begin{aligned} {{\textbf {v}}}=\sum _{i=1}^{l}c_i{{\textbf {v}}}_{i}, \text { and } \sigma ^{\prime }=\prod _{i=1}^{l}\left( \sigma _i^{\prime }\right) ^{c_i}, \end{aligned}$$

and outputs a combined pair $({{\textbf {v}}},\sigma ^{\prime })$. Hence, the time consumption of the combination equals to $T_{lc}+l\cdot T_{exp}+(l-1)\cdot T_{mul}$.

In the same way, we can obtain the computation cost of schemes in [5, 7] and [29]. A detailed comparison of computation cost is shown in Table 3. Theoretically, the CLNS spends the shortest time in terms of Sig-Generation, which indicates that the node S can efficiently sign data packets. Then, the computation cost of Sig-Verification is better than the scheme in [29] and worse than the scheme in [7]. Compared to the scheme in [5], the CLNS addresses the problem of key-escrow attack and provides higher security. As for the computation cost of Combination, they are identical to the related schemes.

Table 3 A comparison of computation cost

Fig. 4

Time consumption of Sig-Generation

Fig. 5

Time consumption of Sig-Verification

7.3 Experiments

This subsection mainly evaluates the computation cost by experiments. Concretely, we focus on the time consumption of the private (partial) key generation, signing process and verification process. According to the “Charm” [42] framework, we choose the 512-bit SS elliptic curve as the basis from the PBC library [43]. The experiments are performed on a Lenovo laptop with Intel Core i5-8300H CPU @2.30GHz, 8GB RAM, Ubuntu 20.04 LTS 64-bit and Python 3.8. Besides, each instance is performed 50 times, and the average time is taken.

In the CLNS, the generation of the full private key includes the generation of partial private key and secret value. For the identity-based scheme in [5], the running time of the private key generation can be calculated from KGC. After running 50 times experiments with different user’s identities, we acquire the time consumption to generate the private key (denoted by SK-Generation) in [5, 7, 29] and the CLNS is 20.45, 10.81, 9.78 and 9.63 ms.

For the time consumption time of signing and verification, we select a 512 KB data file and divide it into m vectors, the dimension of each initial vector is n, then simulate the experiment with the change parameter m (or n) from 10 to 50. To facilitate the simulation, we set the parameter $m=n$. In the end, the results for the four proposed schemes are listed in Figs. 4 and 5. From the experimental results, it can be observed that the CLNS performs best in the signing process, and the running time of the signing process remains the fastest as the dimension changes. Additionally, the time consumption of the verification process is not optimal, which may affect the network traffic throughput. For this problem, the node S should avoid transmitting huge files at one time, and set the vector dimension reasonably. Table 4 lists a time-consuming comparison of SK-Generation, Sig-Generation and Sig-Verification in the above schemes (when $m=50$), showing that the CLNS performs better overall.

Table 4 A time-consuming comparison of different processes ($m=50$)

From the above comparison, the constructed CLNS has the following advantages. First, based on the certificateless public key cryptosystem, it can not only avoid tedious certificate management, but also solve the problem of key-escrow attack. Second, it has lower communication overhead in terms of private key size and signature size, which is beneficial for limited source nodes such as smart terminals and IoT devices. Due to the shorter signature size, intermediate nodes and destination nodes can increase the communication capability and the storage capacity, which is lucrative for both network operators and cloud servers. Finally, theoretical and experimental analyses show that the CLNS is efficient and thus can be applied in IoT environment.

8 Conclusion

In this paper, for the first time, we consider how to build more concrete certificateless network coding schemes from existing certificateless public auditing protocols. Unlike other network coding schemes, we emphasize that CLNSs can be constructed from existing secure CL-PAPs. By imposing some constraint conditions on the standard CL-PAP (i.e., admissible CL-PAP), we design a general construction of CLNS from the admissible CL-PAP. Next, we give a concrete implementation to show the power of the general construction. Then, we compare the performance of the transformed CLNS with other related schemes in terms of communication overhead and computation cost. Furthermore, experimental results demonstrate the transformed CLNS is efficient and can be used in IoT. Our future work is to construct new CL-PAPs from existing CLNSs.