Parallel signal detection for generalized spatial modulation MIMO systems

Abstract

Generalized Spatial Modulation is a recently developed technique that is designed to enhance the efficiency of transmissions in MIMO Systems. However, the procedure for correctly retrieving the sent signal at the receiving end is quite demanding. Specifically, the computation of the maximum likelihood solution is computationally very expensive. In this paper, we propose a parallel method for the computation of the maximum likelihood solution using the parallel computing library OpenMP. The proposed parallel algorithm computes the maximum likelihood solution faster than the sequential version, and substantially reduces the worst-case computing times.

1 Introduction

Multiple Input Multiple Output (MIMO) wireless communication systems are becoming the standard communication mode in most currently existing and future systems. Ranging from small systems (routers, cell phones) with a small number of antennas to systems with hundreds of antennas, MIMO systems offer additional performance compared with traditional single-antenna equipment [1, 2]. However, the additional performance of MIMO systems comes at the price of additional complexity in the detection. The correct detection at the receiving end of the signal sent involves finding the solution (exact or approximated) of a discrete minimization problem. There are many methods proposed, with the usual trade-off between complexity and accuracy [3,4,5,6,7].

The most accurate solution, the so-called Maximum Likelihood (ML) solution is obtained by solving the discrete minimization problem exactly. This amounts to finding the solution with the smallest error (in a least squares sense) among all of the possible solutions. The best methods for this problem belong to the family of sphere decoders (SD). These methods can be described as tree search (or branch and bound) methods that are adapted to the MIMO detection problem. The best SD implementations [3, 8,9,10] feature an adjustable radius (equal to the error of the best solution found), which is used to prune whole branches of possible solutions. The complexity of the sphere decoder (although relatively efficient compared with other methods) grows exponentially with the number of antennas and with the cardinality of the constellation used for the digital transmission.

A recent development in MIMO wireless transmission is the Generalized Spatial Modulation (GSM) technique (not to be mistaken with the old GSM cell-phone technology “Global System for Mobile”) [11,12,13]. GSM-MIMO has been developed for systems with many transmit antennas. The idea behind GSM is to use only a subset of the antennas for each transmission, which are called the “active” antennas. The subsets of antennas (i.e., configurations) that can be used to transmit are fixed, numbered, and known in advance by the receiver. As a consequence, the configuration of active antennas in each transmission is used to convey extra bits. Since the ML detection for GSM-MIMO transmission involves solving several (possibly many) standard MIMO subproblems, it has a high degree of complexity. In fact, the complexity of ML detection is too high to be used in actual transmissions. Nevertheless, ML detection provides an important benchmark for research. Therefore, it is important for researchers to be able to compute the ML solution in large GSM-MIMO setups as a necessary resource for the design and development of MIMO GSM communication systems.

Different techniques have been proposed to reduce the cost. A procedure based on a sequential detection and adjustable radius was proposed in [14]. The main idea is the use of an adjustable radius that is similar to the one used in standard MIMO sphere decoders, with a previous ordering of the subproblems. In this work we propose a modification of the method described in [14] that is designed to take advantage of the available cores, using the parallel computing library OpenMP [15]. The proposed method sorts the subproblems similarly to what is described in [14]. Then, the subproblems are distributed among the threads. The main contribution is that a single radius is used for all of the subproblems, which is updated whenever any thread finds a better solution.

We show through simulations that the parallel method greatly reduces the computational cost of the sequential SD, having more influence in the high noise regime.

Section 2 of this work describes the state of the art, including the MIMO problem, the Sphere Decoder, the GSM problem, and the sequential detector described in [14]. Section 3 is devoted to the proposed parallelization, and Sect. 4 describes the experiments. Finally, our conclusions are presented in Sect. 5.

2 Problem description and related work

2.1 The Standard MIMO detection problem

The transmission and reception of a signal through a wireless MIMO system is usually modeled as:

$$\begin{aligned} \begin{aligned} \mathbf {y}&= \mathbf {H} \cdot \mathbf {s}+\mathbf {v}, \\ \mathbf {s}&\in \Omega ^{n_T} \subset \mathbb {C}^{n_T} \end{aligned} \end{aligned}$$

(1)

where

• $\mathbf {s} \in \Omega ^{n_T}$ is the sent signal; $n_T$ is the number of transmit antennas.

• $\Omega \subset \mathbb {C}$ is a finite constellation or alphabet, with cardinality L. The cardinality of the constellation L is usually an even power of 2. Typical values of L are 4, 16, 64 or 256.

• $\mathbf {y} \in \mathbb {C}^{n_R}$ is the received signal, $n_R$ is the number of receive antennas. In standard MIMO systems, $n_R \ge n_T$.

• $\mathbf {H} \in \mathbb {C}^{n_R,n_T}$ is the matrix modelling the transmission, known as channel matrix.

• $\mathbf {v}$ denotes a white-Gaussian noise (AWGN) complex vector. $\mathbf {v}$ is unknown, but the statistical properties of the noise are usually known.

Then, the ML MIMO detection problem is modeled as a minimization problem, trying to recover the sent signal $\mathbf {s}_{opt}$ when $\mathbf {H}$ and $\mathbf {y}$ are known:

$$\begin{aligned} \hat{\mathbf {s}}=\mathop {\arg \min }\limits _{\mathbf {s} \in \Omega ^{n_T} \subset \mathbb {C}^{n_T}} \left\| {\mathbf {H}\cdot \mathbf {s} - \mathbf {y}} \right\| ^2 \;, \end{aligned}$$

(2)

It is known that the MIMO minimization problem (2) is NP-Hard for arbitrary $\mathbf {H}$ and $\mathbf {y}$ [8, 10]. However, in MIMO problems the received signal is not completely arbitrary, because it is obtained perturbing the received signal with noise [16]. This has been used to propose some complexity estimates for SD algorithms, for certain limited cases [3]. However, it is generally acknowledged that to obtain complexity estimates for SD algorithms is intractable [16]. The performance of SD algorithms is usually studied through Monte-Carlo simulations.

There are several suboptimal algorithms for solving (2), with smaller accuracy but also with smaller computational complexity. The simplest suboptimal algorithm to solve (2) starts by removing the constraint on the components of $\mathbf {s}$ (they must belong to $\Omega$ a finite subset of $\mathbb {C}$) and solving the continuous least squares problem:

$$\begin{aligned} \mathbf {u}=\mathop {\arg \min }\limits _{\mathbf {s} \in \mathbb {C}^{n_T} } \left\| {\mathbf {H} \cdot \mathbf {s} - \mathbf {y}} \right\| ^2 \;. \end{aligned}$$

(3)

However, the obtained vector $\mathbf {u}$ is not a feasible solution because (in the presence of noise) its components $\mathbf {u_i}$ will not belong to $\Omega$. In order to obtain a feasible solution, all of the components of $\mathbf {u}$ must be rounded to the nearest element of the constellation $\Omega$ (this process is called quantization). We denote the vector obtained after this process as $\hat{\mathbf {zf}}$. This vector is a feasible solution which is known as the Zero-Forcing (ZF) estimator. This estimator may be a good approximation to the ML solution $\hat{\mathbf {s}}$ when the noise of the transmission is low, but it is known to give bad results if the noise increases. The computation of the $\mathbf {u}$ vector requires the QR decomposition of the channel matrix as $\mathbf {H}=\mathbf {Q} \cdot \mathbf {R}$, where $\mathbf {Q}$ is orthogonal and $\mathbf {R}$ is upper triangular. Then, $\mathbf {u}$ is computed through premultiplication of the received signal $\mathbf {y}$ by the matrix $\mathbf {Q}^T$ and resolution of the triangular system of equations $\mathbf {R} \cdot \mathbf {u}= \mathbf {Q}^T \cdot \mathbf {y}$.

There are many more methods for approximately solving the problem (2): MMSE, Nulling and cancelling [17], K-Best [6], or Fixed Complexity Sphere Decoding [18]. In this work, we are only concerned with ML detection and SD methods. To apply the SD algorithm, it is necessary to transform problem (2) into an equivalent problem using the QR decomposition of the channel matrix:

$$\begin{aligned} \hat{\mathbf {s}}=\mathop {\arg \min }\limits _{\mathbf {s} \in \Omega ^{n_T} \subset \mathbb {C}^{n_T}} \left\| {\mathbf {R} \cdot \mathbf {s} - \mathbf {z}} \right\| ^2 \;, \end{aligned}$$

(4)

where $\mathbf {H}=\mathbf {Q} \cdot \mathbf {R}$, $\mathbf {R}$ is upper triangular and $\mathbf {z}=\mathbf {Q}^T \cdot \mathbf {y}$. The solution $\hat{\mathbf {s}}$ is obtained by traversing a tree of partial solutions, where the maximum depth of the tree is $n_T$ and each leaf can have at most L descendants (recall that L is the cardinality of the constellation $\Omega$). A full search of the tree would generate all of the $L^{n_T}$ possible signals, which would be very inefficient.

The number of solutions to be visited in the tree can be reduced by selecting a radius d so that the solutions $\mathbf {s}$ that do not fulfill the condition:

$$\begin{aligned} \left\| {\mathbf {R} \cdot \mathbf {s} - \mathbf {z}} \right\| ^2 \le d \end{aligned}$$

(5)

are discarded. In order to have a starting realistic radius for the search, sometimes the ZF solution is computed first and its squared distance $\left( d=\left\| {\mathbf {R} \cdot \hat{\mathbf {zf}} - \mathbf {z}} \right\| ^2 \right)$ is used as the starting radius. A simplified version of this algorithm is given as Algorithm 1.

SD algorithms have been described in many papers, with many possible implementations. Algorithm 1 shows a simplified iterative implementation, which is included for the sake of completeness and to illustrate the use of the radius. Algorithm 1 looks for solutions in the form of vectors with $n_T$ components, $(s_1,s_2,...,s_{n_T})$, where $s_i \in \Omega$. As mentioned above, Algorithm 1 implements a depth-first tree search using the best distance obtained (lines 21 to 23 of Algorithm 1.) to prune branches of the tree (line 26). The variable Level indicates the depth of the present partial solution in the tree. The starting level is $Level=n_T$ and the possible solutions (“leaves”) are located at $Level=1$. The $\mathbf {Elem}$ vector (along with the Level variable) is used to keep track of the position of the present partial solution in the tree. At any given moment during the execution of Algorithm 1, if $\mathbf {Elem} =(...,i_{Level}, i_{Level+1},..., i_{n_T})$, it means that the actual partial solution considered is the vector $(...,s_{i_{Level}}, s_{i_{Level+1}},..., s_{i_{n_T}})$ .

The performance of SD algorithms can improve through different types of optimizations. The most well-known is the ordering of the symbols of the constellation (known as Schnorr-Euchner ordering) [9]. In its simplest form, the Schnorr-Euchner ordering computes previously the estimator $\mathbf {u}$ solving problem (3), and sorts the elements of the constellation $\Omega$ differently for each antenna: for the i-th antenna, the elements of the constellation are sorted by increasing distance of the elements to the i-th component of the estimator $\mathbf {u}$. The Schnorr-Euchner ordering has been used in the experiments in this work.

The complexity of Algorithm 1 (and nearly all SD versions) worsens notably when the noise increases. There are sophisticated bounds that reduce the dependence on noise [19], but these algorithms have a significant computational cost and are usually worthwhile mainly for large MIMO problems.

2.2 GSM-MIMO detection problem

GSM-MIMO is a transmission scheme that is designed to obtain high throughput communications in systems with many transmit antennas. Given a system with $n_T$ transmit antennas and $n_R$ receive antennas, with $n_{T}>> n_R$, the distinguishing feature of GSM-MIMO systems is that each transmission will use only $n_A$ transmit antennas, which are selected among the $n_T$ transmit antennas. Of course, $n_{A} < n_T$.

Given that $n_{A}$ is the number of antennas that can be activated in each transmission, then the total number of possible subsets of active antennas is $n_T \atopwithdelims ()n_A$. Usually, not all of the possible configurations are considered as valid configurations (i.e., not all possible configurations are used for transmission). The number of valid configurations $n_c$ is usually chosen as $2^{n_{A}}$. Typical values of $n_{A}$ are 4, 6, 8. Therefore, realistic values of $n_c$ are 16, 64, 256. Each configuration can be described as a set of antenna indexes, $\{i_{k_1}, i_{k_2}, \ldots ,i_{k_{n_A}} \}, 1 \le i_{k_j} \le n_T, j=1, \cdots ,n_A$. These sets are known in advance by the receiver.

Let ${\Omega }$ be the constellation of complex symbols of size $|{\Omega }|= L$. In each transmission, a symbol vector $\mathbf {s}=(s_1,...,s_{n_A})$ is sent (as in standard MIMO transmission). However, in GSM-MIMO additional bits are implicitly sent through the selected configuration, achieving a higher throughput. This also means that the detection process must include the determination of the configuration (the set of active antennas used for the transmission) .

Let $\mathbf {H}\in \mathbb {C}^{n_R \times n_T}$ be the MIMO overall channel matrix, with independent elements $h_{ij}\sim \mathcal {N}(\mathbf{0},\mathbf{1})$. The k-th antenna configuration (with antennas $\{i_{k_1}, i_{k_2}, \cdots ,i_{k_{n_A}} \}$) defines its corresponding channel submatrix $\mathbf {H_k}$, which is formed by the columns $\{i_{k_1}, i_{k_2}, \cdots ,i_{k_{n_A}} \}$ of the overall channel matrix $\mathbf {H}$. If the transmission is carried out through the k-th configuration, the received vector can be written as

$$\begin{aligned} \mathbf {y} = \mathbf {H_k} \cdot \mathbf {s}+\mathbf {v}, \end{aligned}$$

(6)

where $\mathbf {v}$ denotes a white-Gaussian noise (AWGN) complex vector. Thus, the ML detector for the GSM problem can be described as:

$$\begin{aligned} \{\hat{k}, \hat{s} \}= \mathop {\arg \min }\limits _{k \in \{1,...,n_c\}, \mathbf {s}\in \Omega ^{n_{A}}} \Vert \mathbf {y}-{\mathbf {H_k \cdot s}}\Vert ^{2}. \end{aligned}$$

(7)

Therefore, the solution is formed jointly by the signal sent and the index of the configuration used for the transmission.

2.3 GSM-ML detection

Standard ML MIMO detection methods cannot be applied directly to GSM problems when $n_{T} > n_{R}$ because it is not possible to obtain the required triangular factorization of the channel matrix. In such cases, to the best of our knowledge, the only way available for computing the ML GSM-MIMO solution is to decouple the problem in $n_c$ ML standard MIMO detection subproblems, one for each antenna configuration:

$$\begin{aligned} \hat{s}_k =\mathop {\arg \min }\limits _{\mathbf {s} \in \Omega ^{n_{A}} } \Vert \mathbf {y} -{\mathbf {H_k \cdot s}}\Vert ^{2}. \end{aligned}$$

(8)

Equation (8) defines the ML estimator for the k-th antenna configuration. A trivial approach to GSM-ML detection would be to use a standard ML MIMO SD like the one described in Algorithm 1 to solve subproblems (8) for all k. By comparing the optimal Euclidean distances $d_k= \Vert \mathbf {y}-{\mathbf {H_k \cdot \hat{s}_k}}\Vert ^{2}$ for $k=1,...,n_c$, we can obtain the minimal distance, which will indicate the optimal configuration and thus the ML solution. However, the cost of this procedure is very high because $n_c$ different standard ML MIMO subproblems must be solved.

Fig. 1

GSM-ML basic detection procedure

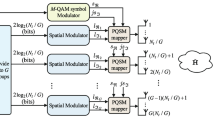
Figure 1 illustrates the procedure. Each box represents the resolution of a MIMO subproblem (8), returning its ML solution and the associated distance. The GSM-ML solution is the ML solution of the subproblem with the smallest associated distance.

2.4 Sequential detection with adjustable radius and ordering of subproblems

The main goal of the idea proposed in [14] is to decrease the computational cost of GSM-ML detection through sequential detection and the use of an adjustable radius across all of the subproblems (8). The idea of the adjustable radius in GSM-ML detection comes from a similar technique that is used in most standard MIMO SD detectors.

In MIMO SD detectors, the initial value of the radius is chosen as the squared Euclidean distance of the best feasible solution obtained so far. MIMO SD detectors search among the possible solutions, looking for the one with the smallest Euclidean distance. When a partial solution has a larger distance than the actual radius, this partial solution is discarded. When a solution is found with a distance that is smaller than the radius, the radius is updated as the squared Euclidean distance of the new solution. [3, 8,9,10].

The selection of the initial radius has a strong impact in the performance of SD MIMO detectors. When the initial radius is too large, too many partial solutions are examined, with a high computational cost; when the initial radius is smaller than the distances of all of the possible solutions, the detection ends very fast and no solution is returned [3, 8,9,10].

Fig. 2

Procedure of sequential detection with adjustable radius

The technique of the adjustable radius was extended to GSM problems in [14], combined with sequential detection. An initial radius d is considered, which is initially chosen as $+ \infty$. Then, the subproblems (8) are solved in order, using a MIMO SD detector with adjustable radius. After the k-th subproblem is solved (returning $d_k$ and $\hat{s}_k$), the radius d is compared with the radius $d_k$. If $d_k < d$, the radius is updated as $d_k$ and the best solution obtained is updated as $\hat{s}_k$. The new best radius d is then used as the initial radius for the next configuration.

Figure 2 describes the procedure. Let us assume that the solution of the $k_{opt}$-th configuration is the actual GSM-ML solution and has radius $d_{k_{opt}}$. Then, the distances of all of the possible solutions in subproblems $k_{opt}+1,...,n_c$ are larger than $d_{k_{opt}}$. Therefore, the SD detector applied to subproblems $k_{opt}+1,...,n_c$ will not return a new solution (which is correct because the GSM ML solution has already been found) and will end very fast.

If the correct configuration (the configuration whose ML solution is the overall GSM-ML solution) is among the first positions on the list of configurations (i.e., $k_{opt}$ is close to 1), then only a few MIMO ML subproblems must be solved, and the process will be quite efficient. On the other hand, if $k_{opt}$ is close to $n_c$, then many subproblems must be solved and the process will be slow. Therefore, for the sake of efficiency, the configurations must be reordered so that the most likely configurations have a high probability of being located among the first positions.

We have used the ordering method proposed in [20], which was proposed as the basis of a suboptimal, non-ML GSM detection method. This method consists of obtaining the ZF estimator of each subproblem, as outlined in sect. 2.1. i.e., solving the continuous subproblems, analogous to problem (3):

$$\begin{aligned} \mathbf {u_k}=\mathop {\arg \min }\limits _{\mathbf {s} \in \mathbb {C}^{n_T} } \left\| {\mathbf {H_k} \cdot \mathbf {s} - \mathbf {y}} \right\| ^2 \;. \end{aligned}$$

(9)

Then, all of the components of $\mathbf {u_k}$ are rounded to the nearest element of the constellation $\Omega$. We denote the vectors obtained after this process as $\hat{\mathbf {zf_k}}$. Then, the squared Euclidean distances of these estimators are computed: $dz_{k}=\Vert \mathbf {y} -{\mathbf {H_k} \cdot \hat{\mathbf {zf}_k}}\Vert ^{2}$. The configurations are then sorted according to the distances $dz_{k}$, from smallest to largest. This method has worked quite well in all of the tested cases.

The sequential algorithm with ordering of subproblems and adjustable radius is described as pseudocode in Algorithm 2.

3 Proposed parallel algorithm

The MIMO subproblems arising in the ML GSM-MIMO problem can be solved independently from each other. Therefore, the ML GSM-MIMO problem allows a completely straightforward parallelization by solving several MIMO subproblems at the same time, or, if there were more cores available than subproblems, all of the subproblems could be solved at the same time. Once the solution of all of the subproblems has been computed, it would be enough to compare the best distances of each subproblem and to select the configuration with the minimal distance. This would be equivalent to parallelizing the process described graphically in Fig. 1.

However, it will be shown experimentally in Sect. 4 that this approach is not competitive compared with the sequential detection described in Algorithm 2. The ordering of subproblems combined with the adjustable radius is relatively quite fast. Therefore, any attempt at parallelizing should keep both of these features.

The preprocessing operations in lines 8 to 10 in Algorithm 2 can be easily parallelized. However, for realistic situations, its computational cost is negligible compared with the cost of the main loop (starting in line 14); therefore, we must pay attention to the main loop. The main loop can be parallelized using the standard OpenMP [15] construct for parallel loops: “#pragma omp parallel for”. However, several refinements would be needed so that the the sequential adjustment of the radius would work correctly. Specifically, the update of the best distance in line 17 in Algorithm would need to be in a “critical” sect. [15] in order to avoid race conditions.

This suggests a more powerful idea for successful parallelization of Algorithm 2: to use a single variable $best\_distance$ that is shared across all of the subproblems. The variable $best\_distance$ is defined as a “local” variable in Algorithm 1. Here, we propose changing the definition of this variable to “global” so that it can be shared by all of the subproblems, or equivalently, by all of the threads that are solving subproblems. Then, when one of the threads finds a better solution (when the condition in line 21 in Algorithm 1 becomes true), the $best\_distance$ variable is updated for all of the threads. Then all of the other threads can use this new value for a tighter (faster) pruning.

In order to avoid race conditions, lines 21 to 23 of Algorithm 1 must be modified so that the updating of the radius is made within an OpenMP “critical section”. This is so that two threads cannot update the $best\_distance$ variable at the same time. This has been implemented using the “critical” OpenMP pragma.

Another detail is that another shared variable $best\_configuration$ is required in order to correctly identify the configuration with the minimal distance. This variable must also be updated when the $best\_distance$ variable is updated (in the critical section). Each thread must be capable of identifying the subproblem being solved; therefore, the configuration index must be passed as a new input argument to Algorithm 1.

A last detail is that it seems possible (although unlikely) that two different threads can execute the “if” instruction in line 21 of Algorithm 1 at the same time. If that were the case, it might be possible that two threads can enter the critical section consecutively, but the second thread could update the $best\_distance$ variable with a value larger than the set by the first thread. In order to avoid this possibility, the “if” instruction in line 21 of Algorithm 1 is replicated inside the critical region.

The modifications to Algorithms 1 and 2 to obtain the parallel algorithm can then be summarized as follows:

• 1. Define $best\_distance$ and $best\_configuration$ as global, shared variables.

• 2. Modify the header of Algorithm 1 to pass as a new input parameter the configuration index ind.

• 3. Modify lines 21 to 23 of Algorithm 1 to embed them in a critical section, as described above:

• 4. Parallelize the main loop in Algorithm 2 (line 14) by inserting the OpenMP pragma : “#pragma omp parallel for” just above line 14.

• 5. Use the new, corrected header for Algorithm 1 in Algorithm 2 (line 16), so that the configuration index ind is passed to Algorithm  1.

• 6. Finally, the lines from 17 to 21 in Algorithm 2 are no longer needed. When the parallel loop ends, the variable $best\_distance$ holds the minimal distance, $best\_configuration$ holds the index of the configuration where the minimal distance has appeared, and $sol\_opt$ holds the ML solution of the GSM problem.

Please note that any adjustable radius implementation of Sphere Decoder can be used, not just the one given as Algorithm 1.

4 Experimental evaluation

The computational cost of computing the ML solution of a MIMO (or GSM-MIMO) detection problem usually increases with noise. Furthermore, even for noise with fixed mean and fixed variance, the cost may vary enormously for two different received signals. This is why the evaluation of detection algorithms is usually made through Monte Carlo simulation, which is the technique used in this work.

All of the algorithms considered return the ML solution of the detection problem. Therefore, there is no difference in accuracy among the methods considered, and we only show results in terms of computing times. However, it must be stressed that, in situations with a low SNR (signal-to-noise ratio) i.e, large noise respect to signal, the ML solution may not coincide with the signal sent.

The experiments were carried out varying the SNR between 5 and 40 dB in increments of 5 dB. These SNR values were achieved by modifying the variance of the noise vectors in Eq (1). We generated 5000 complex Gaussian channel matrices for each value of the SNR. Each matrix was used for 5 GSM-MIMO signals sent(this is similar to what is done in real transmissions), and the computing times that were needed to detect each ML solution were recorded. The tests were carried out on a computer with 2 Intel Xeon E5-2697 processors (12 cores each) and 128 GB of main memory. The operating system was Ubuntu 14.04.3 LTS x86_64, and the experiments were run using MATLAB R2018 [21]. Both the sequential and the parallel SD were implemented as MATLAB MEX files and were compiled using the gcc compiler version 6.5.0. The basic sphere decoder that was used to solve the subproblems was very similar to Algorithm 1, but using the Schnorr-Euchnerr ordering of the symbols of the constellation [9].

The results are usually presented in terms of the average time needed to detect a signal for each SNR. However, as mentioned above, the computing times for some signals may be very large, while, for most signals, the detection time is small. Occasionally huge detection times are the main reason that ML detection cannot yet be used in real transmissions. In order to examine these large cases, we have also recorded the maximum detection times for a single signal for each SNR.

For this work, we have chosen a single, relatively large, GSM-MIMO configuration as our base problem, characterized by the following set of parameters: $n_T=32$ total transmit antennas, $n_A=6$ active antennas in each transmission, $n_R=6$ receive antennas, $L=64$ cardinal of constellation/alphabet, and $n_c=64$ configurations/subproblems. The experiments described below have been designed to evaluate the effect of the parallelization. Other similar experiments varying the parameters of the GSM-MIMO system have given similar results.

The first experiment is designed to demonstrate the need for the ordering of subproblems. To this end, four algorithms were tested: sequential and parallel algorithms without ordering, and sequential and parallel algorithms using the ordering. The technique of adjustable radius was implemented in the four algorithms. Four cores were used for the parallel algorithms. The average computing times are shown in Table 1.

Table 1 Average computing times (seconds) for Experiment 1

The results in Table 1 clearly show the effect of the ordering of subproblems. In several SNRs the sequential algorithm using ordering is better than the parallel algorithm without ordering. Furthermore, the sequential algorithm without ordering performs much worse than the others. It is clear that ordering of subproblems is needed and all of the experiments described below are carried out using the ordered versions.

The next experiment was designed to highlight the effect of increases in the number of cores, although it also provides valuable insight on how the parallelism helps to shorten the computing times. We have solved the same sequence of GSM problems (generated with the base configuration) using 1, 2, 4, 8, 16 and 24 cores. A first experiment was carried out using static scheduling in the “parallel for”; this is the default scheduling for the “parallel for” construct, and it means that the iterations (subproblems) are distributed to the cores at the beginning of the loop in a fixed and deterministic manner. The average times are shown in Fig. 3, the speedups are shown in Fig.  4, and the maximum detection times are shown in Table 2.

Fig. 3

Average computing times increasing the number of cores, with static scheduling

Fig. 4

Speedups for 2, 4, 8, 16 and 24 cores, static scheduling

Table 2 Maximum computing times (seconds) with 1,2,4,8,16,24 cores, with static scheduling

An initial observation is that the results in Table 2 clearly show why this technique cannot yet be used for actual transmissions. Even though most of the signals are detected very fast, some can take unpredictably long times, up to 580 seconds in this experiment (in our experiment the worst cases appear with $SNR=10dB$).

It can also be observed that the speedups show a strange form, with a peak in $SNR=10 dB$. It must be remembered that the evaluation of this problem uses random generation of matrices and signals. The generated cases occasionally have huge detection times. In our simulation, the $SNR=10 dB$ case has worse maximum detection times than the $SNR=5 dB$ case. However, examining the maximum detection times for $SNR=10 dB$ it can be seen that the maximum times decrease much more (when increasing the number of cores) than for other SNR values. Therefore, it seems clear that that these long cases obtain a greater benefit from parallelization. This seems to be the cause of the peak of the speedups at $SNR=10 dB$.

The results show that the extra cores help to decrease the computing times, although the maximum speedups are limited to $2-4$ (apart from the peak). The reasons for this limitation are the nature of the problem solved and the effectiveness of the ordering of the subproblems. If the optimal solution is found in the first subproblem studied, the rest of the subproblems will finish very quickly, regardless of the number of threads used. Therefore, in such cases the parallel times will be close to the sequential time and the speedup will necessarily be low.

It is also observed in Table 2 that most of the signals were detected very fast, while other signals (especially those with low SNR) would take a very long time. Nevertheless, the results show that using more processors helps to shorten the computing times. Consider the situation where a thread finds a subproblem that takes a long time. At the same time, other threads will be solving other subproblems of the same GSM-MIMO problem, and, quite possibly, obtaining a better radius. This better radius will help the thread that is solving the difficult problem, by allowing more partial solutions to be pruned, and, therefore, will end faster.

These observations led us to change the schedule in the parallel loop from “static” to “dynamic” with default behavior, which means that each iteration is dynamically assigned to a core. When the core ends this iteration gets another iteration. This schedule is recommended in situations where some iterations may take much longer than others. In this case, it is even more appropriate because, if a thread has to solve such a long, difficult problem, all of the other subproblems of the configuration may be solved by the other threads, helping to lower the radius. The average times obtained with dynamic scheduling are shown in Fig.  5, the speedups are shown in Fig.  6, and the maximum detection times are shown in Table 3.

Table 3 Maximum computing times (seconds) with 1,2,4,8, 16, and 24 cores, with dynamic scheduling

Fig. 5

Average computing times increasing the number of cores, with dynamic scheduling

Fig. 6

Speedups for 2, 4, 8, 16, and 24 cores, with dynamic scheduling

For visual comparison, Fig. 7 shows the maximum sequential times, the maximum times with 4 cores and static scheduling, and 4 cores with dynamic scheduling.

Fig. 7

Comparison of maximum computing times to detect a single signal

The effect of dynamic scheduling is clearly seen by comparing Tables 2 and 3. The maximum computing times are strongly reduced for all SNR values by using dynamic scheduling. Dynamic scheduling also has a positive effect on the average computing times (and, hence, on the speedups) for all SNR values. However, the speedups remain limited (as mentioned above, the ordering of the subproblems causes that the speedups remain low). In this experiment the speedups have values around 4 except at $SNR=10 dB$, where the speedups are significantly higher. The high speedup at the peak is a consequence of one or several difficult GSM-MIMO problems appearing at $SNR=10 dB$ in this experiment. It seems clear that, when a difficult MIMO subproblem appears, the other cores help to solve it by solving their subproblems, thereby reducing the radius.

The maximum times obtained are still very far from the possibility of practical implementation. However, the time reduction obtained with the parallel algorithm using dynamic scheduling shows that this is an interesting possibility in the way toward practical implementation of ML GSM-MIMO detection

5 Conclusion

The results show that the proposed parallel technique obtains an important reduction in computing time when compared with sequential detection. The proposed method combines techniques used in sequential detection (the ordering of subproblems and the adaptive radius), with parallel solving of the subproblems and dynamic scheduling. The ordering of the subproblems is useful for reduction of the sequential and parallel computing times, although it causes (as a side effect) the limitation of the speedups. The resulting algorithm is especially useful for reduction of the worst-case computing times, which is a very relevant feature for actual transmissions.

The maximum computing times are still far too high to be used in actual transmissions. However, the proposed technique allows larger simulations, which is very useful for researchers in communications. Furthermore, the use of other techniques for faster pruning, combined with the parallel process described, may allow enough complexity reduction so that ML detection in GSM-MIMO systems can become a realistic option.