Abstract
The tsunami disasters that occurred in Indonesia, Chile, and Japan have inflicted serious casualties and damaged social infrastructures. Tsunami forecasting systems are thus urgently required worldwide. We have developed a real-time tsunami inundation forecast system that can complete a tsunami inundation and damage forecast for coastal cities at the level of 10-m grid size in less than 20 min. As the tsunami inundation and damage simulation is a vectorizable memory-intensive program, we incorporate NEC’s vector supercomputer SX-ACE. In this paper, we present an overview of our system. In addition, we describe an implementation of the program on SX-ACE and evaluate its performance of SX-ACE in comparison with the cases using an Intel Xeon-based system and the K computer. Then, we clarify that the fulfillment of a real-time tsunami inundation forecast system requires a system with high-performance cores connected to the memory subsystem at a high memory bandwidth such as SX-ACE.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
On March 11, 2011, the 2011 Great East Japan Earthquake occurred off the coast of east Japan with a magnitude of 9.0, and a devastating tsunami subsequently struck the northeastern part of the Pacific coast of Japan. The impact of the tsunami damaged many buildings and infrastructures in a large area of over 500 km\(^2\), and the number of fatalities reached 19,000 [9]. However, neither the national Japanese government nor the various local governments were able to grasp the whole context of the damage immediately after the tsunami, and they were thus unable to provide prompt responses to the tsunami disasters [12].
Recently, computer simulations have been developed to replicate damage situations resulting from tsunami inundations [3, 8]. We have been developing a real-time tsunami inundation forecast system that can provide an early understanding of damage situations following a tsunami disaster. This system solves nonlinear shallow water equations and estimates information about maximum inundation depths, starting time of inundation, damage of buildings in coastal land areas, etc., with a high resolution of 10-m grid size. In the case of the 2011 Great East Japan Earthquake, the sea level elevation due to the tsunami started to exceed 1 m within 25 min, and therefore, the tsunami inundation and damage forecast should be completed within, at most, 20 min after the occurrence of an earthquake. The total calculation amount also reaches about peta floating-point operations in the cases of predicted earthquakes in Japan such as the Nankai Trough earthquake. Therefore, to achieve the target time, our real-time tsunami inundation forecast system requires high-performance computing (HPC), and we utilize the vector supercomputer SX-ACE, which is developed and manufactured by NEC Corporation, for the real-time tsunami inundation forecast system.
Modern HPC systems employ multi-core processors, and their aggregated peak performances per processor become significantly higher. However, increasing the number of cores and the peak performances of processors often increases the memory loads, and these create a bottleneck. In this paper, we discuss the performance of the tsunami inundation and damage simulation (hereinafter, “tsunami simulation”) on SX-ACE in comparison with a case using an Intel Xeon-based system named LX 406Re-2 and the K computer. We use LX 406Re-2 and the K computer for comparison, because the peak performance of a processor on the Xeon processor of LX 406Re-2 is equal to that of SX-ACE, and the K computer is the flagship supercomputer in Japan. Then, we clarify that the fulfillment of a real-time tsunami inundation forecast system requires a system with high-performance cores connected to the memory subsystem at a high memory bandwidth such as SX-ACE.
This paper is organized as follows: Sect. 2 presents related work on performance evaluations of tsunami simulations using HPC systems. Section 3 presents an overview of our real-time tsunami inundation forecast system, particularly the way in which the HPC system is incorporated. Section 4 explains the tsunami simulation and the program implementation for SX-ACE. Section 5 describes the performance evaluation of the tsunami simulation on SX-ACE, LX 406Re-2 and the K computer. We conclude in Sect. 6 with a brief summary and future work.
2 Related work
A real-time forecast system for disaster prevention requires a reduction in the processing time. The finite difference computation of shallow water equations has been studied with the aim of reducing processing times using high-performance computing technology. Gidra et al. [6] and Amouzgar et al. [2] implemented the TUNAMI N1 and TUNAMI N2 models [10], which were shallow water models, for parallelized computing on a single GPU. Gidra et al. showed that a data parallel programming model, i.e., a model where each thread handles a particular spatial area, was able to achieve high performance on the GPU. Amouzgar et al. evaluated the performance for the Japan coastal region (\(1350~\times ~1822\) km) with a resolution of 450 m. Their GPU system used a single GPU (NVIDIA Tesla M2075) and the execution time was 45 min. Acuña et al. evaluated the performance of a shallow water model that utilized the CIP Conservative Semi-Lagrangian IDO method by using a multi-node GPU cluster system [1]. The nodes included a SUN Fire X4600 and two NVIDIA Tesla S1070s. Their parallel method was the data parallel programming model. They found that the performance with 16 GPUs was similar to that with 1024 CPUs (AMD Opteron Dual Core model 880) and that the execution time was within 30 s when using 32 GPUs for the Japan coastal region (\(370~\times ~735\) km) with a 90-m resolution. However, their model did not handle sea bottom friction, so they were not able to simulate tsunami inundation behavior with sufficient accuracy. In general, calculation amounts related to sea bottom friction become too big for tsunami inundation simulations. Moreover, Nagasu et al. [17] developed an hardware architecture for FPGA-based custom computing of tsunami simulation with the method of splitting tsunami (MOST). The machines contained ALTERA Arria10 with 1518 floating-point DSP blocks and two DDR3 PC12800 SDRAMs, where each of the SDRAMs had a bandwidth of 12.8 GB/s. They achieved the sustained performance of 383.0 Gflop/s and the performance per power of 8.41 Gflop/s/Watts. The performance and performance per power were 1.7 and 7.1 times higher than those of AMD Radeon R9 280X GPU. However, their model did not simulate tsunami inundation behavior. Oishi et al. evaluated the performance of a tsunami inundation simulation on the K computer [24]. Their simulation was based on the TUNAMI N2 model [10] and parallelized using a two-dimensional domain decomposition method [19]. They evaluated the performance for 2 h of tsunami on the Japan coastal region (\(840~\times ~1237\) km) with a 5-m resolution. The execution time was 93 s using 13,498 cores (1688 nodes). These results demonstrated the feasibility of a real-time tsunami inundation forecast. However, they did not deal with fault estimation in real time.
3 A real-time tsunami inundation forecast system
3.1 System configuration
The real-time tsunami inundation forecast system consists of a tsunami source modeling system, a simulation system, and a delivery/mapping server, as shown in Fig. 1. The tsunami source modeling system and delivery/mapping server are active at all times in preparation for earthquake occurrence. The simulation system, which is usually used for academic research, is immediately incorporated into the system only when a tsunamigenic earthquake occurs, and the tsunami simulation job is submitted at top priority using the unique urgency function. The tsunami simulation job is executed on the simulation system, and the simulation results are sent to the delivery/mapping server. Finally, the simulation results are mapped and made available on the Web to Japanese local governments by the delivery/mapping server. The real-time tsunami inundation forecast system is installed at Tohoku University and Osaka University in Japan.
3.2 Tsunami source modeling system
The tsunami source modeling system is implemented on an Intel Xeon-based server. This system receives three types of observation data as listed in Table 1: earthquake early warning (EEW) issued by the Japan Meteorological Agency [14], rapid moment tensor solution (GRiD-MT) using seismic wavefields by the Earthquake Research Institute, the University of Tokyo [22], and finite fault model (RAPiD/REGARD) based on real-time global navigation satellite system (GNSS) data operated by the Geospatial Information Authority of Japan [18]. When the system detects the occurrence of a tsunamigenic earthquake using EEW data, it determines the fault model (size, orientation, and slip amount) of the coseismic fault and submits a tsunami simulation request to the simulation system. Here, the EEW and GRiD-MT data are translated into finite rectangular fault models. The size and slip amounts are derived using empirical relations [23] from the given earthquake magnitudes. The fault orientation of the model using EEW is defined on the basis of its epicenter location. Thrust faulting is assumed when the epicenter is located on the landward side of the trench, whereas the normal faulting type is assumed for the outer rise event. The RAPiD/REGARD system directly estimates the rectangular fault model using the coseismic displacement at each GNSS site.
3.3 Simulation system
We use a vector supercomputer SX-ACE system, which is a multi-node system to simulate tsunami inundation phenomena and estimate damage situations in 10 min. The SX-ACE system is not actually a dedicated system for the real-time tsunami inundation forecast system, but an HPC infrastructure for academic and industry researchers. When a tsunamigenic earthquake occurs, a subset of the SX-ACE system is immediately turned to the real-time tsunami inundation forecast system. This function is performed by a job management system, called NQS II, a batch system that achieves optimal allocation of jobs between nodes. NQS II supports an urgent job function. When NQS II accepts an urgent job, the function allocates the urgent job in nodes that belong to the same innermost network tier of the hierarchical network. The function then immediately suspends other active jobs on the nodes, and the urgent job is executed at higher priority. The suspended jobs automatically resume as soon as the urgent job is completed.
In the nodes that are utilized in the real-time tsunami inundation forecast system, each node memory has a reserved space for an urgent job as shown in Fig. 2. Each node has 64 GB of memory: Nearly 1 GB is reserved for the OS, nearly 3 GB is reserved for the urgent job execution, and the remaining 60 GB is available for normal job executions. The tsunami source modeling system submits the tsunami simulation as an urgent job to the simulation system. As soon as NQS II accepts the job, the urgency function of NQS II issues a process suspend command to the already active running jobs on the nodes utilized in the simulation system. The tsunami simulation is immediately executed at top priority using the reserved memory space. Then, the simulation results are sent to the delivery/mapping server.
3.4 Delivery/mapping server
The delivery/mapping server is an Intel Xeon-based server. It creates maps and a graph of the simulation results using the Geospatial Data Abstraction Library [5]. Figure 3a–e shows the maps of the maximum tsunami inundation depth, the starting time of inundation, the maximum tsunami water level, the structural damage, and the graph of the water level represented as time series in the city of Kochi and its surrounding coast. The maps and graph are sent to the Japanese local governments within 4 min, and the local governments are able to view the maps and graph through a Web interface. Figure 3a–d can be zoomed in and out on a one-to-nine scale. The results of the tsunami simulation can provide clear pictures of imminent disasters (and hazards), enabling Japanese local governments to take the appropriate actions for evacuation and relief. It is important that the forecasts be effectively utilized for making appropriate advance preparations, alerting the public, and preparing for relief activities.
4 Tsunami simulation
4.1 Tsunami simulation model
Our tsunami simulation is based on the TUNAMI model, which solves nonlinear shallow water equations and uses the staggered leap-frog finite difference method as the numerical scheme [11]. This method is adopted as a standard method for the prediction of tsunami inundations by the United Nations Educational, Scientific and Cultural Organization (UNESCO) [7]. The governing equations are
where \(\eta \) is the vertical displacement of the water surface, \(D\) is the total water depth, \(g\) is the gravitational acceleration, \(n\) is Manning’s roughness coefficient, \(P\) is the hydrostatic pressure, \(\rho \) is water density, \(x\) and \(y\) are horizontal directions, and \(z\) is the vertical direction. \(M\) and \(N\) are the discharge fluxes in the x- and y-directions, respectively, which are given by
where h is the still water depth; \(u\) and \(v\) are the water velocities in the \(x\)- and \(y\)-directions, respectively; and \(\bar{u}\) and \(\bar{v}\) are the average water velocities in the \(x\)- and \(y\)-directions, respectively. Regarding the boundary conditions at the run-up front, a wave front condition is judged as follows.
The calculation of the tsunami source utilizes Okada’s equation [20], and the damage estimation is based on the study of Koshimura et. al. [11]
4.2 Computational domain
The tsunami simulation utilizes a nested grid system to deal with the multi-scale nature of tsunamis. The characteristics of the tsunami are of a long wavelength in oceanic regions and of a short wavelength near shores. In the tsunami simulation, the coastal region should be resolved with a 10-m grid size. For example, in the case of Kochi city with the Nankai Trough earthquake, the resolution ratio from an outer domain to the next inner domain is fixed to one-third and the area of the outer domain is determined by water depths. We utilize five different resolution levels, as shown in Table 2 and Fig. 4.
In the nested grid system, discharge fluxes and water levels are continuous between computational domains as a boundary condition [7]. The interpolated discharge fluxes in a computational domain of a large grid size are sent to a computational domain of a small grid size at the boundary. The averaged water levels in a computational domain of a small grid size are sent to a computational domain of a large grid size at the boundary.
4.3 Implementation of the TUNAMI model on SX-ACE
SX-ACE is a vector supercomputer, and achieving high sustained performance generally requires effective utilization of its units. Thus, the tsunami simulation program, which was developed on a Xeon server, needs to be vectorized. Here, Eq. (7) is a difference formula of Eq. (1):
where i and j are the horizontal directions and k is time. The i and j directions of Eq. (7) have no loop-carried dependencies such as control-flow and data dependencies. Similarly, Eqs. (2) and (3) also have no such dependencies. Therefore, the simulation program is a vectorizable program. However, the simulation program has some unvectorized loops, since it makes breaches in the programming manners of vectorization. Figure 5 shows the source code of Eq. (2). The loop in subroutine nlmnt2 is not vectorized because of containing a call statement in the loop. In this case, the loop can be vectorized by inlined subroutine xmmt in subroutine nlmnt2. After we similarly remove other breaches (write, read, and stop statements) in loops, the vector operation ratio achieves 99.6%. Moreover, sustained performance depends on loop length, which is the number of iterations in loops. Specifically, the longer the loop length, the greater the sustained performance on SX-ACE. Since the loop length of the x-direction is longer than that of the y-direction in Table 2, loops of the x-direction are vectorized: The inner loop, index i, is a vectorized loop in Fig. 5.
Source code of Eq. (2)
Also, the simulation program is a parallelizable program due to the same reason for the vectorization. We parallelize the simulation program using the MPI Library for the multi-node system of SX-ACE and using OpenMP for a single node of SX-ACE. In the parallelization using the MPI Library, the simulation program is parallelized by the domain decomposition method. Each computational domain in the nested grid system is divided by any number of processes \(P_d\), and the total number of parallelization P is
where d indicates the dth computational domain. The simulation program has doubly nested loops in the x- and y-directions. We chose one-dimensional domain decomposition instead of two-dimensional one. Generally, the two-dimensional domain decomposition can decrease the amount of communication per process when the number of processes is increased, and the MPI communication time decreases; the sustained performance increases. In contrast, the two-dimensional domain decomposition reduces the loop length of vectorized loops when the number of processes is increased, and the sustained performance of vector processing decreases. Then, the reducing loop length has a greater impact on the total processing time than the decreasing communication volumes in our target simulation size. Therefore, the loops of the x-direction are vectorized and the loops of the y-direction are parallelized. In Fig. 5, the outer loop, index j, is parallelized. Moreover, the load of each process needs to be made as equal as possible for achieving effective parallelization. In the simulation program, calculation amounts in land areas are different from those in sea areas. Hence, we adjust the number of grid points of each process to coincide with roughly the same calculation amount. First, the calculation amounts of each process are measured with the same number of grid points per process, and then the number of grid points on each process is adjusted to coincide with the nearly equal calculation amount by using the previous measurement. Also, to reduce MPI communication time, several items of array data, which are transferred at the same time, are packed as one array.
For a single node of SX-ACE, the simulation program is parallelized by OpenMP. This is because the simulation program parallelized by the MPI Library requires five or more processes from Eq. (8) and the single node of SX-ACE, which has four cores, cannot execute it. We parallelize the loops of the y-direction using OpenMP directives. However, some loops of the simulation program are not parallelized, since the loops have small granularity and the effects of the parallelization are not obtained.
5 Performance evaluation
5.1 Experimental setup
5.1.1 SX-ACE
The SX-ACE system consists of one processor with the total peak performance of 256 Gflop/s and a 64 GB main memory with 256 GB/s memory bandwidth [13]. The processor has four vector architecture cores, where each core is equipped with a large vector on-chip cache composed of an Assignable Data Buffer (ADB) and Miss Status Handling Register (MSHR), as shown in Fig. 6. The ratio of a memory bandwidth to the floating-point operation per second (B/F) of a processor is 1.0. The capacity of ADB is 1 MB in each core, and the data rate between ADB and the vector processing unit is 256 GB/s; its B/F reaches 4.0. Therefore, the computational performance of SX-ACE can be extracted more efficiently by effective utilization of ADB [15, 21], especially for memory-intensive applications. MSHR withholds identical load requests with in-flight load requests on ADB misses and ignores redundant memory requests if the subsequent memory requests that cause ADB misses can be solved by the in-flight load requests. Ignoring these redundant load requests allows the memory bandwidth to be utilized efficiently [16]. With regard to a multi-node system, the SX-ACE is composed of up to 512 nodes connected via a custom interconnect network (called IXS) by an 8 GB/s bandwidth. The memory space (Global Memory) that can be shared among MPI processes is offered in a multi-node SX-ACE system with IXS. Global Memory provides zero-copy MPI communications.
The operating system of the SX-ACE is SUPER-UX, a production-proven environment based on the UNIX System V with a lot of extensions for performance and functionality. The FORTRAN compiler for SX-ACE, FORTRAN90/SX, has advanced functions of automatic vectorization, automatic parallelization, and OpenMP. The MPI Library, MPI2/SX, implements the Message Passing Interface specifications MPI-1.3 and MPI-2.1.
5.1.2 LX 406Re-2
LX 406Re-2 is a Xeon-based system. A single node of LX 406Re-2 consists of two Intel Xeon E5-2695 v2 processors (Ivy Bridge) and 128 GB main memory with 2 \(\times \) 59.7 GB/s memory bandwidth. The processor contains twelve cores and a shared last-level cache of 30 MB. The peak performance of the core ranges from 19.2 to 25.6 Gflop/s due to the Xeon’s turbo function. When full cores operate, the peak performance of the core is usually 19.2 Gflop/s and that of a processor becomes 230.4 Gflop/s. The B/F of a processor is 0.26. Each node is connected with InfiniBand FDR (56 Gbps).
The operating system of LX 406Re-2 is Red Hat Enterprise Linux, and the programming environment is Intel Fortran Composer XE and Intel MPI Library. The Fortran compiler has the function of automatic vectorization, automatic parallelization, and OpenMP.
Table 3 lists the hardware configurations of both evaluated systems.
5.1.3 Evaluated model
We evaluate the performance of three city modes: Kochi, Shizuoka, and Ishinomaki. Kochi and Shizuoka cities are expected to experience a huge tsunami within the next 30 years according to a recent government report in Japan [4]. Ishinomaki city was struck by the huge tsunami at the 2011 Great East Japan Earthquake. The model sizes for these three cities are given in Table 4. Here, the time interval is determined by the Courant–Friedrichs–Lewy condition. In the case of Shizuoka, the water depth is significantly large near the coastal area. Hence, the time interval for the tsunami simulation needs to be smaller than the other cities in order to achieve numerical stability. Period indicates the time since a tsunami phenomenon occurs. Flop count shows the number of floating-point operations.
Table 5 shows the Fortran compiler’s options. The options are high-level optimizations and inlining subroutines. The simulation program is automatically vectorized by the compilers. In the Intel compiler, some loops are not vectorized because the compiler estimates the low efficiency of vector operations. As this is an underestimation, we use a compiler directive, vector always, on LX 406Re-2 for enforcing the vectorization of the loops.
Here, we use a metric of necessary memory performance: code B/F. It indicates the necessary data in bytes per floating-point operation. The number of memory operations and floating-point operations are counted from the code; the code B/F of the simulation program is about 1.85. This shows that the memory bandwidths of a processor on SX-ACE and LX 406Re-2 become short due to the memory bandwidth required by the simulation program, and the sustained performances of SX-ACE and LX 406Re-2 are limited by the memory bandwidth, since the B/Fs of SX-ACE and LX 406Re-2 are 1.0 and 0.26, respectively.
5.2 Overall performance
Figure 7 shows the execution time on the real-time tsunami inundation forecast system. The first major phase (coseismic fault estimation) has a time constraint of 7 min. This is because the phenomena of a fault rupture continue for several minutes in the case of large tsunamigenic earthquakes such as the 2011 Great East Japan Earthquake. Thus, observations during a set time period (here, 7 min) are required for more precise estimation of a fault model. In this time period, three different estimations of the earthquake fault are simultaneously performed several times using three types of observation data. Then, the best result is selected for the tsunami simulation and urgent jobs are submitted to SX-ACE. The tsunami simulation is executed within 5 min by using 512 cores of SX-ACE on each city model, as shown in Table 6. The time for transmission of the results to the delivery/mapping server and visualization on maps is approximately 4 min.
5.3 Processor performance
5.3.1 Single-core performance
In the case of a single core, the Xeon processor of LX 406Re-2 operates at 3.2 GHz of the frequency and the core performance becomes 25.6 Gflop/s. The memory bandwidth of a single core of SX-ACE can use the full memory bandwidth: 256 GB/s, and its B/F is 4.0. The memory bandwidth of LX 406Re-2 is not open to the public. Figure 8 depicts the execution times of a single core of SX-ACE and LX 406Re-2. The memory time indicates the stall time of the CPU due to data loads from the memory. The CPU time is the running time of the CPU. Here, we use the Kochi city model for the evaluation, and the number of floating-point operations (Flop count) is \(0.63\times 10^{15}\).
The code B/F of the simulation program is 1.85, and the B/F of SX-ACE is 4.0. Therefore, SX-ACE has the enough memory bandwidth for the tsunami simulation and the memory time on SX-ACE is 1.8 h. Meanwhile, the memory time on LX 406Re-2 is 6.4 time longer than that on SX-ACE; however, the ratio of SX-ACE to LX 406Re-2 in the memory bandwidth per processor is 4.3. This means that the single core of LX 406Re-2 cannot use the full memory bandwidth 59.7 GB/s. From the ratio of 6.4, the sustained memory bandwidth of the core on LX 406Re-2 is probably 40 GB/s and the B/F of the core is 1.6. The simulation program is thus a memory-limited program for LX 406Re-2, and LX 406Re-2 cannot reduce the memory time. In addition, the CPU time on LX 406Re-2 is 2.9 times longer than that on SX-ACE. As the ratio of SX-ACE to LX 406Re-2 in the peak performance per core is 2.5, the computation efficiency of SX-ACE is 1.15 times higher than that of LX 406Re-2. Therefore, the vector architecture core of SX-ACE is an efficient core for the simulation program. Here, computation efficiency is defined as
The execution time of SX-ACE is 13 h, which is less than 30% of that of LX 406Re-2. This is because the core on SX-ACE has a higher peak performance and efficiency than LX 406Re-2. Moreover, SX-ACE has a higher memory bandwidth than LX 406Re-2 and its performance of SX-ACE is 6.4 times higher than that of LX 406Re-2.
5.3.2 Single-processor performance
The processors of SX-ACE and LX 406Re-2 contain four and twelve cores, respectively. The peak performance of the SX-ACE processor is roughly the same as that of the LX 406Re-2 processor. The memory bandwidth of SX-ACE is 4.3 times higher than that of LX 406Re-2. Figures 9 and 10 show the execution times of the processors of SX-ACE and LX 406Re-2. Here, we use the simulation program parallelized by OpenMP.
As shown in Fig. 9, the memory times of six and twelve cores are nearly the same, and in both cases, the memory time is saturated. Similarly, the memory time on SX-ACE is saturated as shown in Fig. 10. This means that the memory bandwidths of LX 406Re-2 and SX-ACE are insufficient compared to the memory bandwidth required by the simulation program, since the B/Fs of LX 406Re-2 and SX-ACE are smaller than the code B/F. Moreover, the residence times of memory loads on LX 406Re-2 become longer than that of SX-ACE, because the memory bandwidth of LX 406Re-2 is smaller than that of SX-ACE. As a result, the memory time of twelve cores on LX 406Re-2 is ten times longer than that of four cores on SX-ACE, and the memory time of LX 406Re-2 accounts for half of the execution time on the twelve cores. Thus, the execution time of the simulation program depends strongly on the memory bandwidth, and the higher memory bandwidth can reduce the memory time.
The CPU time of the twelve cores is one-fifth of that of the single core on LX 406Re-2 (Fig. 9), and the CPU time of the four cores is two-fifths of that of the single core on SX-ACE (Fig. 10). These results indicate that the effect of parallelization is low. This is because the granularities of some loops in the simulation program are small, and these loops are not parallelized. Moreover, the CPU time of the twelve cores on LX 406Re-2 is 1.4 times longer than that of four cores on SX-ACE. The computation efficiency of SX-ACE is 1.3 times higher than that of LX 406Re-2. As discussed in Sect. 5.3.2, the vector architecture core of SX-ACE is an efficient core for the simulation program.
Figure 11 shows the performance gain by using ADB and MSHR on the four-core case of SX-ACE. When ADB and MSHR are disabled, the memory time is 2.3 times longer than that of the ADB- and MSHR-enabled case, since ADB and MSHR can reduce redundant memory load requests and recover the lack of the memory bandwidth. Moreover, the disabled case increases the CPU time by 0.9 h. This means that the rate of overlapping among calculation operations on vector pipelines is changed due to the increasing memory loads. In this evaluation, the difference in performance between LX 406Re-2 and SX-ACE is caused by the memory system with the high memory bandwidth on SX-ACE.
5.4 Multi-node performance
Our target execution time with this tsunami simulation is less than 10 min for the forecasting. We discuss the parallel performance on SX-ACE and LX 406Re-2, and we also compare the performances of SX-ACE with the K computer. Here, the K computer consists of 82,944 CPUs of SPARC64 VIIIfx with the peak performance 10.62 Pflop/s and 1.26 PB main memory. Table 7 lists the processor configuration of the K computer. The peak performance of a core on SX-ACE is four times higher than that on the K computer, and SX-ACE has four times higher memory bandwidth than the K computer. The result of the K computer by Oishi et al. [19] is used. Their simulation model was the same model as our simulation program, but their simulation program was optimized and parallelized for the K computer. They simulated a tsunami inundation for 2 h for the city of Sendai, which is in the same region and fault model as our Ishinomaki city. Their resolution is 5 m, the number of grid points is \(1.48\times 10^{7}\), and time interval is 0.1 s. Therefore, the total calculation amount of the K computer is nearly equal to that of SX-ACE for 2 h of our tsunami simulation.
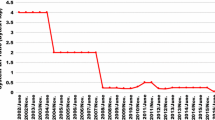
In Sect. 4.3, we put forth that each MPI process should handle the number of grid points that is adjusted to coincide with the nearly equal calculation amounts per process for load balancing, rather than handling the same number of grid points per process. Figure 12 shows the execution times of each MPI process in the case of a 1-h simulation. Case (a) is where each MPI process handles the same number of grid points, and Case (b) is where each MPI process handles the nearly equal calculation amounts. The load balance of Case (b) is better than that of Case (a). Figure 13 shows the execution times of Cases (a) and (b) on SX-ACE and LX 406Re-2. On both SX-ACE and LX 406Re-2, the execution times of Case (b) are shorter than those of Case (a). In the case of 512 cores, the execution time of Case (b) on SX-ACE can decrease by 13%. The reduced time is only 36 s, which is not large, but any reductions in execution time are important for a disaster system. Figure 13 also indicates that SX-ACE can achieve the target time, 10 min, by using 128 cores, i.e., only 32 nodes, with a time of just 9.88 min. The execution time of 512 cores is 4.0 min. Meanwhile, LX 406Re-2 cannot achieve the target time even using 512 cores. The execution time of LX 406Re-2 is 4.1 times longer than that of SX-ACE.
Figure 14 shows the execution times on SX-ACE and the K computer in the case of a 2-h simulation. The execution time of 512 cores on SX-ACE is 80 s. The 16,398 cores (1800 nodes) of the K computer cannot achieve this time; the execution time is 93 s. The K computer has the feasibility of a real-time tsunami inundation forecast; however, a large-scale computer system with 16,398 cores is required. The results of SX-ACE, LX 406Re-2, and the K computer show that a system that has high-performance cores with high memory bandwidth (such as SX-ACE) can deliver a superior performance even with a lower parallel number. This demonstrates that the real-time tsunami inundation forecast system can efficiently be realized by SX-ACE.
6 Summary
A quick and accurate understanding of tsunami disaster situations enables prompt responses to the disaster. Tsunami forecasting systems require increased accuracy and reduced processing time. Therefore, we have developed a real-time tsunami inundation forecast system using an HPC system that can achieve tsunami inundation forecasting within 20 min. We have demonstrated the effectiveness of using an HPC system as a social infrastructure for disaster prevention and mitigation as well as a research infrastructure.
In this study, we implemented the tsunami simulation on a vector supercomputer SX-ACE system. The simulation program is vectorized, and the vectorization ratio of the tsunami simulation is 99.6%. The tsunami simulation was parallelized by using MPI, and we adjusted the load balance among the MPI processes using the pre-estimation of the amount of their computations. Then, the execution of the tsunami simulation for 6 h of tsunami and inundation behaviors was completed within 4 min using 512 cores (128 nodes). We have also developed an urgency function for the SX-ACE job management system that enables SX-ACE to be incorporated into the tsunami forecasting system temporarily when a large earthquake occurs off coasts in Japan.
We evaluated the performance of the tsunami simulation using SX-ACE, LX 406Re-2, and the K computer and found that the execution time depends strongly on their memory bandwidths. We also clarified that a system with high-performance cores connected to the memory subsystem at a high memory bandwidth (such as SX-ACE) can deliver a superior performance even with a lower number of cores. This demonstrates that the real-time tsunami inundation forecast system can be realized by SX-ACE.
In future work, we plan to enhance the performance of the tsunami simulation by improving its MPI performance and to expand the areas covered by our system in Japan. The results will be shared with the public.
References
Acuña MA, Aoki T (2009) Real-time tsunami simulation on multi-node GPU cluster. In: Proceedings of the ACM/IEEE International Conference on High Performance Computing, Networking, Storage and Analysis (SC09) [poster]. Portland, Oregon
Amouzgar R, Liang Q, Clarke PJ, Yasuda T, Mase H (2016) Computationally efficient tsunami modelling on graphics processing units (GPU). Int J Offshore Polar Eng 26(2):154–160
Arikawa T, Tomita T (2016) Development of high precision tsunami runup calculation method based on a hierarchical simulation. J Disaster Res 11(4):639–646
Cabin Office of Japan (2015) Chiyoda-ku Tokyo. Disaster management in Japan, Japan. http://www.bousai.go.jp/1info/pdf/saigaipamphlet_je.pdf. Accessed Mar 2017
The open source geospatial fundation, Geospatial data abstraction library. http://www.gdal.org. Accessed Feb 2018
Gidra H, Israrul H, Nitin PK, Dargurunathan M, Gaur MS, Laxmi V, Zwolinski M, Singh V (2011) Parallelizing TUNAMI-N1 using GPGPU. In: 2011 IEEE International Conference on High Performance Computing and Communications. Banff, Canada
Goto C, Ogawa Y, Shuto N, Imamura F (1997) Numerical method of tsunami simulation with the leap-frog scheme. Technical report, UNESCO. http://unesdoc.unesco.org/images/0012/001223/122367eb.pdf. Accessed Mar 2017
Goto K, Fujima K, Sugawara D, Fujino S, Imai K, Tsudaka R, Abe T, Haraguchi T (2012) Filed measurements and numerical modeling for the run-up heights and inundation distances of the 2011 Tohoku-oki tsunami at Sendai Plain, Japan. Earth Planets Space 64:1247–1257
Imamura F, Anawat S (2012) Damage due to the 2011 Tohoku earthquake tsunami and its lessons for future mitigation. In: Proceedings of the International Symposium on Engineering Lessons Learned from the 2011 Great East Japan Earthquake. Tokyo, Japan
Imamura F, Yalciner AC, Ozyurt G (2006) Tsunami modeling manual (TUNAMI model). Tohoku University, Sendai, Japan. http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf. Accessed Mar 2017
Koshimura S, Oie T, Yanagisawa H, Imamura F (2009) Developing fragility functions for tsunami damage estimation using numerical model and post-tsunami data from Banda Aceh, Indonesia. Coast Eng J JSCE 51(3):243–273
Koshiyama K (2014) Characteristics of emergency responcy at the Great East Japan Earthquake. In: 5th International Disaster and Risk Conference Davos 2014 [poster]. Davos, Switzerland. https://idrc.info/fileadmin/user_upload/idrc/documents/IDRC14_PosterCollection.pdf. Accessed Feb 2018
Momose S (2014) SX-ACE, brand-new vector supercomputer for higher sustained performance I. In: Resch M et al (eds) Sustained simulation performance 2014. Springer, Cham, pp 57–67
Musa A, Kuba H, Kamoshida O (2012) Earthquake and tsunami warning system for natural disaster prevention. In: Resch M et al (eds) Sustained simulation performance 2012. Springer, Cham, pp 81–91
Musa A, Sato Y, Egawa R, Takizawa H, Okabe K, Kobayashi H (2009) Characteristics of an on-chip cache on NEC vector architecture. Interdiscip Inf Sci 15(1):51–66. https://doi.org/10.4036/iis.2009.51
Musa A, Sato Y, Soga T, Okabe K, Egawa R, Takizawa H, Kobayashi, H (2008) Effects of MSHR and prefetch mechanisms on an on-chip cache of the vector architecture. In: Proceedings of the 6th International Symposium on Parallel and Distributed Processing and Application (ISPA08)
Nagasu K, Sane K, Kono F, Nakasato N (2016) FPGA-based tsunami simulation: performance comparison with GPUs, and roofline model for scalability analysis. J Parallel Distrib Comput 106:153–169. https://doi.org/10.1016/j.jpdc.2016.12.015
Ohta Y, Kobayashi T, Tsushima H, Miura S, Hino R, Takasu T, Fujimoto H, Iinuma T, Tachibana K, Demachi T, Sato T, Ohzono M, Umino N (2012) Quasi real-time fault model estimation for near-field tsunami forecasting based on RTK-GPS analysis: application to the 2011 Tohoku-Oki earthquake (Mw 9.0). J Geophys Res 117:B02311. https://doi.org/10.1029/2011JB008750
Oishi Y, Imamura F, Sugawara D (2015) Near-field tsunami inundation forecast using the parallel TUNAMI-N2 model: application to the 2011 Tohoku-Oki earthquake combined with source inversions. Geophys Res Lett 42(4):1083–1091. https://doi.org/10.1002/2014GL062577
Okada Y (1992) Internal deformation due to shear and tensile faults in a half-space. Bull Seismol Soc Am 82(2):1018–1040
Soga T, Musa A, Shimomura Y, Egawa R, Itakura K, Takizawa H, Okabe K, Kobayashi H (2009) Performance evaluation NEC SX-9 using real science and engineering applications. In: Proceedings of the ACM/IEEE International Conference on High Performance Computing, Networking, Storage and Analysis (SC09). Portland, Oregon
Tsuruoka H, Kawakatsu H, Urabe T (2009) GRiD MT (grid-based real-time determination of moment tensors) monitoring the long-period seismic wavefield. Phys Earth Planet Inter 175:8–16
Wells DL, Coppersmith KJ (1994) New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull Seismol Soc Am 84(4):974–1002
Yokokawa M (2012) The K computer and its application. In: 2012 Third International Conference on Networking and Computing (ICNC), pp 21–22. https://doi.org/10.1109/ICNC.2012.13
Acknowledgements
The authors thank Mr. Takayuki Suzuki of Kokusai Kogyo Co., Mr. Masaaki Kachi, Mr. Tsubasa Kawano of A2 Co., Mr. Yoshihiko Sato, and Mr. Takashi Abe of NEC Solution Innovators, Ltd. for developing the system. We appreciate the support from Mr. Raghunandan Mathur. This study was supported in part by the G-spatial City Construction Project from the Ministry of Internal Affairs and Communications and by a CREST grant from JST.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Musa, A., Watanabe, O., Matsuoka, H. et al. Real-time tsunami inundation forecast system for tsunami disaster prevention and mitigation. J Supercomput 74, 3093–3113 (2018). https://doi.org/10.1007/s11227-018-2363-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-018-2363-0