Abstract
Many entrepreneurship applications use data as the core concept of their business to better understand the needs of their customers. However, as the size of databases used by these entrepreneurship applications grows and as more users access data through various interactive interfaces, obtaining the result for a top-k query may take long time if the query matches millions of the tuples in the database. Traditionally, layer-based indexing methods are representative for processing top-k queries efficiently. These methods form tuples into a list of layers where the ith layer holds the tuples that can be the top-i answer. Layer-based indexing methods enable us to obtain top-k answers by accessing at most k layers. Most of these methods achieve high accuracy of query answer at the expense of enlarged index construction time. However, we can adjust between accuracy and index construction time to achieve an optimal performance. Thus in this paper, we propose a method, called the adaptive convex skyline (AdaptCS) for efficient-processing top-k queries in entrepreneurship applications. AdaptCS first prunes the data with a virtual threshold point and finds skyline points over the pruned data. Here, by adjusting virtual threshold we are able to achieve optimal performance. Then, AdaptCS divides the skyline into m subregions with projection partitioning method and constructs the convex hull m times for each subregion with virtual objects. Lastly, AdaptCS combines the objects obtained by computing the convex hull. The experimental results show that the proposed method outperforms the existing methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Entrepreneurship is considered to be an ability to establish new companies using new concepts. Recently, many entrepreneurship applications use data as the core concept of their business to better understand the requirements of their customers. Thus, it has become a fundamental economic value of the many companies behind the service they provide. However, as the size of databases used by these companies grows and as more users access data through various interactive interfaces, managing and performing operations on data has become a challenging issue. For example, one of the well-known entrepreneurship applications, the healthcare field, generates the huge amounts of data, which often comes from electronic health records (EHRs) in the form of medical history, laboratory test results and general information like age and weight. When this data is large and high-dimensional, obtaining the result for a query may take long time if the query matches millions of the tuples in the database. On the other hand, we can get a few top results immediately after the query was issued using the top-k query technique. A top-k query returns k tuples with the highest or the lowest scores from a relation [4, 5, 8, 9]. The following is an example of top-k query in healthcare application.
Example 1
Consider a doctor “Alice” who wants to retrieve information from EHRs about patients with diabetes disease. She wants to find patients with older age, high BMI (body mass index) value and high cholesterol. To find the patients satisfying her preference with a weight (0.3, 0.3, 0.4), she makes the following scoring function f as \(f(t) = 0.3\times \mathrm{age} + 0.3\times \mathrm{bmi} + 0.4 \times \mathrm{chol}\) and issues a query shown below.
-
SELECT *
-
FROM Patient
-
ORDER BY f(t)
-
STOP AT 5
Table 1 demonstrates five patients’ information obtained as the answer to Alice’s query. Here, patient C is top-1 answer, patient E is top-2 answer, patient D is top-3, patient A is top-4 answer, and patient B is top-5 answer
For efficient top-k query processing, constructing indices is important. There have been a number of approaches that constructs an index by making layers over the entire set of tuples. These approaches find the top-k answers by accessing just the first few layers. ONION [3], HL-index [4, 5], AppRI [14], DG [15], PL-index [6] and AppCSE [12] are well-known methods of this approach. ONION and HL-index use convex hull [1] to construct layers. However, these methods have a poor index construction time due to high time complexity of the convex hull computation. In order to avoid this pitfall, AppRI and DG constructs skyline [2] as layers. Skyline layers are calculated faster than convex hull layers. However, in high-dimensional databases, these methods also suffer from bad index construction time because most tuples can become the skyline points. PL-index and AppCSE use convex skyline [6] to construct layers. That is, convex skyline is constructed by computing the convex hull over the skyline. Thus, the layer size of the convex skyline is smaller than those of the skyline, and the index construction time is shorter than those of the convex hull [12]. PL-index and AppCSE achieve high accuracy of query answer at the expense of enlarged index construction time. In this paper, we argue that we can adjust between accuracy and index construction time to achieve an optimal performance.
More precisely, we make the following contributions in this paper:
-
We propose a method, called the adaptive convex skyline (AdaptCS) for efficient-processing top-k queries in entrepreneurship applications. AdaptCS first prunes data with a virtual threshold point and finds skyline points over the pruned data. Then, AdaptCS divides the skyline into m subregions with projection partitioning method and constructs the convex hull m times for each subregion with virtual objects. Lastly, AdaptCS combines the objects obtained by computing the convex hull.
-
We propose a method to regulate the index construction phase. Here, we define a virtual threshold point vTHRES, defined as Definition 3.1, that, according to query, is able to increase accuracy of the query answer or increase the speed of index construction time.
-
We show the performance advantages of AdaptCS through various experiments. We compare the index construction time, and precision of AdaptCS with the existing methods that use approximate convex skyline, convex skyline and skyline.
The rest of this paper is organized as follows. Section 2 describes the existing work related to this paper. Section 3 explains the proposed method. Section 4 demonstrates experiment results. Section 5 summarizes and concludes the paper.
2 Related work
The existing methods use convex hull [1], skyline [2] and convex skyline [6] to construct layers. We briefly review each of these methods in this section.
ONION [3] uses convex hull to construct layers over the set of tuples where outer layers geometrically enclose inner layers. Specifically, it first constructs the convex hull over the entire set of tuples in database, and then proceeds iteratively constructing a new convex hull over the set of remaining tuples. This iteration continues until no tuples remain. The hybrid-layer index (HL-index) [4, 5] is hybrid method of the layer-based and list-based [7] approaches. It first constructs layers with convex hull vertices as ONION does, and then constructs d sorted lists within each layer. Since ONION and HL-index use convex hull to construct layers, these methods have a poor index construction time due to high time complexity of the convex hull computation.
AppRI [14] use skyline to construct layers by exploiting the dominant relationships between tuples in the database. The dominant graph (DG) [15] constructs layers using skylines as well. That is, it constructs the first layer with skyline over the entire set of tuples in database, and then, constructs the second layer with a new skyline over the set of remaining tuples, and so on. In DG, the tuples of adjacent layers are linked together based on dominance relationships which enables selective access to layers [8, 9]. Although, AppRI and DG can decrease index construction time compared to the methods that use convex hull, however, index construction time in high-dimensional databases still remains poor. Specifically, in high-dimensional databases, most objects can become skyline points which results in skyline reading more objects than those of using convex hull.
The partitioned-layer index (PL-index) [6] use convex skyline to construct layers. It consists of two main steps, such as partitioning and layering steps. In partitioning step, PL-index partitions the entire set of tuples into subregions, and in layering step, it constructs layers in each subregion using convex hull over the skyline. As a result, PL-index has a relatively smaller layer size compared to those that use skyline, and the index construction time is relatively shorter than those that use convex hull. The approximate convex skyline enhanced (AppCSE) [12] was proposed to further improve the performance of PL-index. Unlike PL-index, it first constructs skyline over the entire set of tuples in database, and partitions the resulting skyline into subregions. The convex hull is then constructed with vREF and vBASE virtual objects of each subregion. Here, vREF and vBASE are virtual objects with minimum entropy value and minimum coordinate value, respectively. In addition, AppCSE is enhanced to extend to all origins which enable to process various user-defined scoring functions. PL-index and AppCSE demonstrate high accuracy of query answer. In this paper, we argue that index construction time can be further reduced while adjusting accuracy.
The dual-resolution (DL) [8, 9] layer method can reduce the number of tuples accessed in each layer. DL-layer method constructs coarse-level layer using skyline and divides each coarse-level layer into multiple sublayers using convex skyline. In addition, the authors also presented optimization methods for index construction, disk-based storage scheme, the design of the virtual layer, and index maintenance for tuple updates. However, as it can be seen from experiment results, DL-layer method is designed for the databases with small dimensions (i.e., two to five dimensions). The index construction time exponentially increases as the number of dimensions increase, because a large number of calculations are needed to construct a layer list. In this paper, we deal with database that exceeds five dimensions.
3 Proposed method
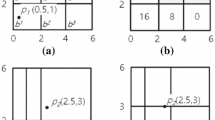
In this section, we describe the proposed method. AdaptCS is constructed of three steps as shown in Fig. 1: (a) skyline step, (b) partition step and (c) combine step. In skyline step, we first prune data using virtual threshold object and construct skyline index over the pruned data. Figure 1a demonstrates threshold-based skyline step. Here, vTHRES is virtual threshold object that prunes data by discovering intersection of minimum values in each axis. In Fig. 1a, line composed of black data points represents the skyline. In partition step, we divide database into m subregions using projection partitioning method. This process is depicted in Fig. 1b. In combine step, we compute convex skyline m times in each partitioned region and merge results. Figure 1c demonstrates the combine step.
3.1 Skyline step
In skyline step, we first prune data using virtual threshold object. The main idea of this method is to find an intersection area (vTHRES) of minimum values in each axis and prune out data objects that are not included within this area. We define vTHRES as in Definition 3.1.
Definition 3.1
(vTHRES): A virtual object is the maximum intersection coordinate value over MinT1, MinT2 ... MinTd. We define MinTi \((0<i\le d)\) as a data object which has a minimum coordinate value in ith axis over entire data objects.
This pre-processing step enables to eliminate unnecessary data objects and reduces skyline construction time. In addition, by adjusting vTHRES, we can obtain various performance advantages. For example, as intersection area of vTHRES decreases, the construction of skyline is accelerated at the expense of accuracy. This occurs due to inclusion of less skyline points in a smaller area of vTHRES. On the other hand, we can adjust vTHRES to obtain a higher accuracy at the expense of index construction time. This gives users flexibility to decide whether to choose accuracy over index construction time. After pruning step, we construct skyline over pruned data objects. Here, we use Sort-Filter-Skyline (SFS) [2] algorithm to construct skyline.
Figure 2 shows the ThresholdSkyline algorithm for constructing the skyline layer using virtual threshold. The input to the ThresholdSkyline algorithm is S which is the set of the d-dimensional objects and a number of axis d. The output from ThresholdSkyline algorithm is the skyline layer. In line 1, the algorithm initializes a remaining set P and starts executing if the input set S is not empty. The algorithm first discovers the object which has a minimum value in ith axis in line 3 to 4. The intersection of minimum values in ith axis is defined as a virtual threshold object and is used for pruning data that falls outside its boundaries. This process is shown in line 5 to 6. Lastly, in line 7 to 8, the algorithm discovers skyline points over the pruned data using SFS algorithm and returns the skyline layer as a result.
3.2 Partition step
In partition step, we can further reduce the number of data points for constructing convex hull by dividing skyline constructed in previous step into m subregions. Unlike AppCSE [12] that uses k-means method to partition the skyline, we use projection partitioning method. The main problem with k-means method is that it consumes much time when database is high-dimensional which enlarges the convex hull construction time. Moreover, as k-means method groups data points that are closely located to each other, it is not appropriate for calculating convex hull as more calculations are needed. Figure 3a demonstrates this notion. In projection-based portioning method, on the other hand, we can reduce the number of calculations in convex hull by dividing skyline points in diagonal manner. Figure 3b depicts data points in universe divided by projection partitioning method.
3.3 Combine step
In combine step, we compute the AdaptCS for the subregions obtained in the partitioning step. AdaptCS performs m computations of the convex skyline as defined in Definition 3.2.
Definition 3.2
(AdaptCS): We define Sky(S) as the set of objects in the skyline constructed with vTHRES over a set S of objects in the universe. We define Skyi(S) \((0\le i<m)\) as the partitioned skyline of the subregion i, as the \(i\hbox {th}\) subregion. We then define CH(T) as the set of objects in the convex hull vertices over target objects \(T = Skyi(S) \cup \{vMAX+, vREF, vBASE\}\). We define CH(T) – {vMAX+, vREF, vBASE} as the AdaptCSi(S) which is AdaptCS in the subregion i \((0\le i<m)\).
Figure 4 shows the algorithm ConstructingAdaptCS for constructing AdaptCS the layer over a given set S of the d-dimensional objects. The input to ConstructingAdaptCS is S as the set of the d-dimensional of objects, the number of subregions m and the number of axis d. The output from ConstructingAdaptCS is the AdaptCS layer. In line 1, the algorithm initializes a skyline layer Sky and starts executing if the input set S is not empty. The algorithm first sorts S through the entropy value in line 3, and then finds skyline using ThresholdSkyline algorithm in line 4. Next, in line 5, we project skyline onto hyperplanes, and then, in line 6, we partition the skyline into m subregions via hyperplanes. In lines 7–13, the algorithm computes convex hull while skyline layer is not empty. We first find virtual objects such as vBASE, vREF and vMAX+ in line 9, and compute the convex hull over target objects that include these virtual objects in line 10. In line 11, we construct AdaptCS in subregion 0, and then recursively perform this step in each subregion. Finally, in line 14, we combine the AdaptCS in each subregion, and return the AdaptCS as the result.
Example 2
Figure 5 shows an example of constructing AdaptCS in the two-dimensional universe. Here, we first find a vTHRES for pruning unnecessary objects as shown in Fig. 5a, where dotted object are pruned objects. Figure 5b shows the skyline over the set of remained objects P. We assume that the sequence of the entropy values of the tuples are g, f, a, e, c, b, d in the ascending order. We project objects onto hyperplane as shown in Fig. 5c, and partition objects into m subregions as shown in Fig. 5d. Figure 5e shows how vBASE and vREF virtual objects are selected from the skyline. Figure 5f–h shows how AdaptCS is constructed in each subregion. When computing the convex hull in subregion0, vREF is e, g, so that the target objects T become a union of {a, b} that are the objects in subregion0 and \(\{e.g., vMAX^{+}\}\) that are the virtual objects shown in Fig. 5f. Thus, the convex hull over T becomes \(CH(T) = a,\,\, e, g,\,\,vMAX^{+}\}\) as shown in Fig. 5f. Here, \(vMAX^{+},vREF\), and vBASE are the virtual objects that should be discarded from the result so that AdaptCS in subregion 0 becomes a as shown in Fig. 5f. AdaptCS is computed in the same process of subregion0 in subregion1 and subregion2 as shown in Fig. 5g, h, respectively. As a result, AdaptCS finds the convex hull objects {a, c, g, f} as shown in Fig. 5i.
4 Experimental result
In this section, we present an experimental result of AdaptCS. We first explain the experimental environment used in the experiments in Sect. 4.1, and we show the superiority of the proposed methods through the results of the experiments in Sect. 4.2.
4.1 Experimental environment
In this section, we explain the experimental environment used in the experiments. We compare the index construction time and precision of AdaptCS with the existing methods like convex skyline [5] (simply, CS), approximate convex skyline [7] (simply, AppCSE). For AdaptCS, we use the ConstructingAdaptCS algorithm presented in Sect. 3.
We use the wall clock time as the measure of the computing time. For the precision, we compare the number of objects contained in a layer of AdaptCS, AppCSE and those of the CS, because the CS calculates the exact convex hull vertices. We perform experiments using synthetic and real dataset. For the synthetic dataset, we generate uniform dataset using the generator mentioned in Borzsonyi et al. [4]. The dataset consists of from two- to eight-dimensional dataset of 10K objects. For the real dataset, we use the diabetes dataset which consists of patients who were interviewed in a study to understand the prevalence of obesity, and diabetes in central Virginia for African Americans [13]. We construct AppCSE and AdaptCS to retrieve patients who have high risk of diabetes. For the experiment, we combine some attributes of the dataset and generate new attributes. Specifically, we calculated BMI from weight and height attributes. We also calculated waist-to-hip ratio from size of waist and hip. The diabetes dataset consists of 394 objects with six attributes: cholesterol, stabilized glucose, glycosylated hemoglobin, age, BMI and waist-to-hip ratio.
For the experiments, we have implemented the AdaptCS, the convex skyline and the approximate convex skyline using C++. To compute the convex hulls for the experiments, we used Qhull library [3]. To compute skylines, we used the SFS algorithm [4]. We conducted all the experiments on an Intel i5-760 quad core processor running at 2.80 GHz Linux PC with 16GB of main memory.
4.2 Experimental results
In this section, we compare the index construction time and precision of the AdaptCS with the existing methods. Experiments 1–4 demonstrate results over syntactic dataset and Experiment 5 demonstrates results over real dataset.
Experiment 1
Comparison of the index building time as dimension d is varied.
Figure 6a, b shows the index construction time of AdaptCS, CS and AppCSE as d is varied. In Fig. 6a, dimension d is varied from 2 to 8 in log scale and in Fig. 6b, dimension d is varied from 2 to 5. AdaptCS improves 0.96–1.84 times over the index construction time of the CS and AppCSE. As it will be presented in Experiment 3, AdaptCS has lower accuracy in comparison to AppCSE. On the other hand, this gives benefit to adjust the index construction time of AdaptCS. That is AdaptCS has shorter index construction time at the expense of the lower accuracy of query answer. In Fig. 6a, AdaptCS has higher index construction time than AppCSE, because vTHRES does not dominate enough objects and generate some overhead. However, as it will be presented in Experiment 4, AdaptCS has shorter index building time by adjusting threshold level.
Experiment 2
Comparison of the partitioning time as dimension d is varied.
Figure 7 presents a comparison of the partitioning time of AdaptCS and AppCSE as dimension d is varied from 2 to 8. AdaptCS improves 1–300 times over the partitioning time of the AppCSE. This occurs because unlike AppCSE that uses k-means method, AdaptCS uses projection partitioning method. Recall from Sect. 3.2 that projection partitioning method divides skyline in diagonal partitioning manner that suits the characteristics of constructing convex hull and thus, enables us to reduce the overall construction time.
Experiment 3
Comparison of the precision as dimension d is varied.
Figure 8 shows the precision of the proposed method AdaptCS, AppCSE and CS as d is varied from 2 to 8. Similar to AppCSE, AdaptCS includes data of CS layer. AdaptCS reaches precision of 87 % and outperforms AppCSE by 1.1 times on average.
Experiment 4
Comparison of the index building time and precision as threshold level is varied.
Figure 9a, b shows the index building time and precision of the proposed method AdaptCS and CS as threshold level is varied. Here, we compared AdaptCS with CS where we can reach high accuracy or fast index construction time by changing threshold value. As can be seen from Fig. 9, we can achieve up to 2 times faster index construction time with decreased threshold level. Even when threshold level is 4 and 5, we can observe that accuracy of AdaptCS is 90 and 98 %, respectively, while maintaining 1.5 times faster index instruction time compared to CS.
Experiment 5
Comparison of the index building time as dimension d is varied when using real dataset.
Figure 10 shows the index construction time of AdaptCS and AppCSE as d is varied when using diabetes dataset. In Fig. 10, dimension d is varied from 2 to 6. AdaptCS improves 1.71–3 times over the index construction time of AppCSE.
5 Conclusion
In this paper, we have proposed AdaptCS, a threshold-based project partitioned layer-based index for efficient-processing top-k queries. The strength of the proposed method compared to other existing methods is twofold. First, we have proposed a new virtual threshold notion that discovers the object which has a minimum value in ith axis. The intersection of minimum values in ith axis is defined as virtual threshold object and is used for pruning data that falls outside its boundaries. In addition, we have used projection-based partitioning method to divide skyline index in diagonal partitioning manner that suits the characteristics of constructing convex hull and thus, enables us to reduce the overall index construction time. Limitation of the proposed method is that it does not reach high accuracy. However, from experiments with syntactic and real dataset in healthcare field, we can observe that AdaptCS reaches up to 90 % accuracy while maintaining 1.5 times faster index construction time compared to existing methods. In future work, we are planning to propose an adaptive algorithm that automatically adjusts its performance according to the type of the dataset.
References
Barber B, Dobkin DP, Huhdanpaa H (1996) The quickhull algorithm for convex hulls. ACM Trans Math Softw (TOMS) 22(4):469–483
Borzsonyi S, Kossmann D, Stocker K (2011) The skyline operator. In: Proceedings of the 17th International Conference on Data Engineering (ICDE), pp 421–430
Chang YC, Bergman L, Castelli V, Li CS, Lo ML, Smith JR (2000) The onion technique: indexing for linear optimization queries. In: Proceedings of the International Conference on Management of Data (SIGMOD), pp 391–402
Heo JS, Cho J, Whang KY (2010) The hybrid-layer index: a synergic approach to answering top-k queries in arbitrary subspaces. In: Proceedings of the 26th International Conference on Data Engineering (ICDE), pp 445–448
Heo JS, Cho J, Whang KY (2013) Subspace top-k query processing using the hybrid-layer index with a tight bound. Data Knowled Eng 83:1–19
Heo JS, Whang KY, Kim MS, Kim YR, Song IY (2009) The partitioned-layer index: answering monotone top-k queries using the convex skyline and partitioning-merging technique. Inf Sci 179(19):3286–3308
Fagin R, Lotem A, Naor M (2001) Optimal aggregation algorithms for middleware. In: Proceedings of the twentieth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS), pp 102–113
Lee J, Cho H, Hwang SW (2012) Efficient dual-resolution layer indexing for top-k queries. In: Proceedings of the 2012 IEEE 28th International Conference on Data Engineering (ICDE), pp 1085–1095
Lee J, Cho H, Lee S, Hwang SW (2014) Toward scalable indexing for top-k queries. IEEE Trans Knowl Data Eng (TKDE) 26(12):3103–3116
Li C, Chang KCC, Ilyas IF (2006) Supporting ad-hoc ranking aggregates. In: Proceedings of the 2006 ACM SIGMOD International Conference on Management of Data (SIGMOD), pp 61–72
Li C, Chang KCC, Ilyas IF, Song S (2005) RankSQL: query algebra and optimization for relational top-k queries. In: Proceedings of the 2005 ACM SIGMOD International Conference on Management of data (SIGMOD), pp 131–142
Ihm SY, Lee KE, Nasridinov A, Heo JS, Park YH (2015) Approximate convex skyline: a partitioned layer-based index for efficient processing top-k queries. Knowl Based Syst 61:13–28
Willem JP, Saunders JT, Hunt DE, Schorling JB (1997) Prevalence of coronary heart disease risk factors among rural blacks: a community-based study. South Med J 90:814–820
Xin D, Chen C, Han J (2006) Towards robust indexing for ranked queries. In: Proceedings of the 32nd International Conference on Very Large Data Bases (VLDB), pp 235–246
Zou L, Chen L (2011) Pareto-based dominant graph: an efficient indexing structure to answer top-K queries. IEEE Trans Knowl Data Eng (TKDE) 23(5):727–741
Acknowledgments
This research was supported by Entrepreneurship Research Program through the Sookmyung Women’s University Entrepreneurship Center (SEC) funded by the Small and Medium Business Administration University Entrepreneurial Center.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Son, Y., Ihm, SY., Nasridinov, A. et al. Adaptive convex skyline: a threshold-based project partitioned layer-based index for efficient-processing top-k queries in entrepreneurship applications. J Supercomput 72, 4262–4275 (2016). https://doi.org/10.1007/s11227-016-1826-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-016-1826-4