1 Introduction

Forest fires are natural disasters that cause significant losses around the world every year. Several risk indexes are used by the authorities to determine the potential damage caused by a fire in a particular region. In this context, several actions are taken to prevent forest fire occurrences, but, unfortunately, in spite of the preventive actions taken, every year many forest fires are declared. When a forest fire has started, it is necessary to provide the extinction services with the best possible prediction of the forest fire propagation so that they can use the available means in the best way possible to mitigate the effects of such hazards. Several models have been developed and integrated into computer simulators (FARSITE [2], FireStation [5] or Wildfireanalyst [6] to estimate forest fire propagation and to provide the control centres with useful information to help them in their decisions.

These propagation models, and the consequent simulators, need a large set of input parameters describing the actual scenario in which the fire is taking place. These parameters include a terrain elevation map, a vegetation map and the features of said vegetation, an initial fire perimeter and meteorological conditions. Concerning meteorological conditions, wind speed and direction are the parameters that most significantly affect fire behaviour. The meteorological winds that can be measured in a meteorological station or can be provided by a meteorological model, such as WRF, are measured or estimated in discrete points with one measure every few kilometres. However, the meteorological wind is modified by terrain topography, generating a wind field that must be estimated every few metres. Therefore, it is necessary to couple a wind field model that provides a particular value of wind speed and direction for each point on the terrain surface.

In this work, the forest fire simulator selected is FARSITE [2] because it is widely used throughout the firefighting community and has been extensively validated, and the wind field simulator chosen is WindNinja [3] because it accepts the same input files as FARSITE and can generate wind field files that can be directly used by FARSITE.

Coupling a wind field model with a forest fire propagation simulator improves the accuracy of the propagation predictions, but it requires longer execution times that in some cases are not affordable in a real operation. Therefore, it is necessary to reduce the execution time of both components to make the coupled approach feasible. This work focuses on accelerating wind field calculation to reduce execution time and make the approach feasible.

The rest of this paper is organised as follows: Sect. 2 presents the main features of WindNinja, the sparse matrix storage method used in WindNinja and the most costly operations involved in wind field calculation. Section 3 presents a new storage system based on the vectorization of subdiagonals to reduce memory requirements. Section 4 presents the sparse matrix-vector multiplication method implemented using the data format proposed. Then, Sect. 5 briefly describes the parallel implementations carried out using MPI, OpenMP and CUDA and shows the results obtained with these parallelisations, and, finally, Sect. 6 summarizes the main contribution of this work.

2 WindNinja

WindNinja [3] is a wind field simulator that requires an elevation map and the meteorological wind speed and direction to determine the wind parameters at each cell of the terrain. The number of the cells of the terrain actually depends on the map size and on the map resolution. The internal functioning of WindNinja can be summarized as follows:

  1. 1.

    WindNinja takes the digital elevation map and the meteorological wind parameters, generates the mesh and applies the mass conservation equations at each point of the mesh to generate the linear system \(Ax=b\).

  2. 2.

    In the linear system \(Ax=b\), Matrix A is a symmetric positive definite sparse matrix which is stored in CSR format. The matrix A has a low density and a diagonal pattern.

  3. 3.

    Once the linear system has been stored, WindNinja applies the preconditioned conjugate gradient (PCG) [7] solver to solve the system of equations. The PCG is an iterative method that uses a matrix M as a preconditioner and iteratively approaches the solution. The original WindNinja includes SSOR and Jacobian preconditioners. By default, SSOR preconditioner is used because it converges faster than Jacobian. However, Jacobian can be parallelised more efficiently, and, therefore, in this work, we use the Jacobian preconditioner.

  4. 4.

    The solution of the PCG is used to build the solution of the wind field.

2.1 Preconditioned conjugate gradient (PCG)

The purpose of including the PCG as a solver is to provide a good solution to the system of equations expressed by \(Ax=b\) in a computational feasible time and faster than without using a Preconditioner. The algorithm that describes how to find the vector x applying the PCG is shown in Algorithm 1.

figure a
Fig. 1
figure 1

Representation of the preconditioned conjugate gradient evolution

Full size image

The x vector, which is the solution to be reached, lies at the intersection point of all the hyperplanes created by the quadratic form of each equation of the equations system. To reach this value, x is initialized at \(x_{0}\) and, at each iteration, it is modified to approach the real solution. The way x is modified is explained by following Algorithm 1. However, it can also be described in a more intuitive way, as shown in Fig. 1. In this figure, it can be observed that an orthogonal vector g at the surface in x is obtained and then an orthogonal vector to g, q, is obtained. These two orthogonal vectors provide the transformation p that must be applied to x. This process is repeated iteratively until the difference is small enough.

Table 1 WindNinja matrices features and memory requirements
Full size table

2.2 Limitations of WindNinja

When the map size is limited, WindNinja is a very stable wind field simulator that generates wind field very fast and does not present memory limitations. However, when the map size increases, the execution time and memory requirements become prohibitive. It must be taken into account that the number of variables to be solved can vary from \(10^{5}\) for small maps to \(10^{8}\) for large maps. So, WindNinja presents three main limitations:

  1. 1.

    Memory requirements WindNinja matrices have particular features. These matrices are symmetric and only include the main diagonal and 13 subdiagonals in the upper part. So, the non-zero elements are very few and the matrices are extremely sparse giving a very low density. These features are shown in Table 1. In this table NE indicates the number of non-zero elements and density indicates the density of the sparse matrix. This table also shows the amount of memory (memory) required to store matrices corresponding to different map sizes. The memory required by WindNinja to store and solve the linear system depends on the map size [11]. Actually, the amount of memory required to solve a map of \(N \times M\) cells can be expressed as shown in Eq. 1, where N and M are the numbers of rows and columns of the map, respectively.

    $$\begin{aligned} \mathrm{Mem} \,(\mathrm{bytes}) = 20{,}480 + 15{,}360*N + 15{,}360*N + 11{,}520*N*M \end{aligned}$$
    (1)
  2. 2.

    Execution time The execution time of the PCG solver depends on the problem size (in this case, on the map size) and on the computing power of the underlying architecture. A wide experimentation was carried out, and it was concluded that the execution time equation depends linearly on the number of cells (NCells \( = N \times M\)), as well as on the features of the underlying hardware architecture. This dependence is shown in Equation 2, where a and b are parameters describing the architecture.

    $$\begin{aligned} t=a \mathrm{NCells}+ b \end{aligned}$$
    (2)
  3. 3.

    Scalability WindNinja incorporates OpenMP parallelisation, but it presents a very bad scalability. Actually, the maximum speed-up that can be achieved by increasing the number of cores is just 1.5, which is not very significant.

Tables 2 and 3 summarize some results for different map sizes, showing the execution times with different numbers of cores and the speedup obtained on 16 cores AMD Opteron (tm) processor 6376.

Table 2 WindNinja execution times on a 16 cores AMD Opteron (tm) processor 6376
Full size table
Table 3 WindNinja SpeedUp on a 16 cores AMD Opteron (tm) processor 6376
Full size table

2.3 WindNinja performance analysis and sparse matrix storage

In a preliminary analysis of WindNinja, it was observed that 80 % of the execution time is taken up by the solver and that 60 % of this time is spent carrying out the well-known matrix–vector multiplication. Therefore, a deep analysis was carried out to determine the causes of such behaviour and how to improve it.

WindNinja stores the matrix using compressed row storage (CRS) [10], also called compressed sparse row (CSR). Using this storage method, the memory savings are really significant, but accessing a particular element in the matrix requires an indirect access, and this fact complicates the algorithms using these CRS matrices and degrades memory performance.

Fig. 2
figure 2

Sparse matrix–vector multiplication considering CRS storage format step by step

Full size image

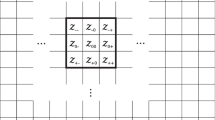
In the Matrix–Vector multiplication, each term in a row is multiplied by the terms in the column vector and the partial results are aggregated to obtain a particular element of the resulting vector, as shown in Eq. 3. The scheme of this multiplication in CRS format is shown in Fig. 2. This irregular memory pattern access provokes a large number of cache misses and, therefore, the performance is significantly degraded.

$$\begin{aligned} c_{0}= & {} a_{00}b_{0}+a_{01}b_{1}+\cdots +a_{(n-1)0}b_{(n-1)}\nonumber \\&\cdots&\nonumber \\ c_{(n-1)}= & {} a_{0(n-1)}b_{0}+a_{1(n-1)}b_{1}+\cdots +a_{(n-1)(n-1)}b_{(n-1)}\\ c_{j}= & {} \sum \limits _{i=0}^{n-1}a_{ij}b_{j}\nonumber \end{aligned}$$
(3)

A simplified piece of code is shown in Fig. 3. In this code it can be observed that in the first loop accesses to vector b components and accesses to vector c in the second loop are not linear, provoking cache misses and increasing execution time. This piece of code assumes that the elements of each row are sorted by columns and that only the upper part of the matrix is stored.

To try to solve this problem different mathematical libraries including Preconditioned Conjugate Gradient solvers were tested. So, Intel MKL [4], ViennaCL [9] and cuSparse [8] were introduced and the implementations of PCG using a Jacobian preconditioner were executed on a 16-core AMD Opteron (tm) processor 6376 with a Nvidia GTX Titan GK 110 for a 800 \( \times \) 800 cell map.

The results in Fig. 4 show that the execution time is not significantly reduced, and it does not present a significant scalability. The main point is the matrices generated by WindNinja have an extremely large number of zero elements and only the non-zero elements must be multiplied by the corresponding elements in the vector. So, WindNinja matrices are extremely sparse and these libraries do not perform very well for these matrices. CuSparse reaches the best execution time, but it does not introduce a significant improvement.

The matrix–vector multiplication can be represented in a schematic way as shown in Fig. 5. In this figure, the elements of matrix subdiagonals are multiplied by the corresponding element of Vector b to obtain a partial term of the corresponding element of vector c. So, it is possible to take advantage of this fact to define a new storage method that avoids irregular memory accesses.

Fig. 3
figure 3

Code showing the matrix–vector multiplication considering CRS format

Full size image
Fig. 4
figure 4

Execution time of an \(800 \times 800\) cell map considering different mathematical libraries

Full size image
Fig. 5
figure 5

Scheme of matrix-vector multiplication

Full size image

3 Vectorization of diagonal sparse matrices

As mentioned above, the matrices generated by WindNinja are extremely sparse. Moreover, the non-zero elements are organised in subdiagonals, and the number of subdiagonals including non-zero elements is just 13 in the lower part, considering that the matrix is symmetric.

Another way of representing sparse matrices that can be found in the literature is the compressed diagonal storage (CDS) [1]. This storage scheme is particularly useful if the matrix arises from a finite element or finite difference discretisation on a tensor product grid. In this scheme, the subdiagonals of the matrix are stored as rows of a matrix, and an additional element indicates the relative position of each subdiagonal to the main diagonal. This format is used when the matrix is banded, that is, the non-zeros elements are within a diagonal band. However, this format is highly unsuitable for general matrices since there are few rows that exceed the diagonal band, resulting in the storage of a large number of zero values. So, this matrix format representation is not suitable for WindNinja matrices.

To tackle this problem and avoid unnecessary memory allocation, a storage scheme has been designed. This storage scheme, called vectorization of diagonal sparse matrix (VDSpM), stores the subdiagonals in a set of vectors (unidimensional arrays) of the exact size to include the elements of the subdiagonal and an index indicating the position of the subdiagonal in the matrix. In this way, the elements of each subdiagonal are stored in consecutive memory positions. This storage scheme allows for a minimum of cache misses since the accesses to the elements of the matrix can be organised in consecutive positions. This storage scheme is illustrated in Fig. 6. In this figure, it can be observed that an array of pointers is used to access each array storing one subdiagonal. Actually, this array of pointers has only 14 elements, and each array storing one subdiagonal has the exact length to store that particular subdiagonal.

Fig. 6
figure 6

Scheme of vectorization of diagonal sparse matrix VDSpM

Full size image

It is necessary to do a pre-analysis of the CRS matrix to express it in the VDSpM storage format. In this analysis, it is necessary to determine the position of each subdiagonal and the values of its elements. It must be pointed out that the number of elements of each subdiagonal and the amount of memory required to store each diagonal are determined from the position of the subdiagonal. So, if a matrix has n rows and n columns (\(n \times n\)), the main diagonal has n elements and the subdiagonal in position i has \(n - i\) elements. In this way, it is possible to determine the array size for each subdiagonal. It must be considered that, in WindNinja, the resulting matrices are symmetric. In this case, the requirements in memory space are reduced by half.

Table 4 VDSpM memory requirements and matrix construction time on a 16 cores AMD Opteron (tm) processor 6376
Full size table
Fig. 7
figure 7

VDSpM matrix construction time on a 16-core AMD Opteron (tm) processor 6376

Full size image

The pre-analysis, the vectorization of the sparse matrix and the construction of the VDSpM matrix involve a certain amount of time. Several measures have been carried out on different matrix sizes and the results show that the time required to carry out these steps depends exponentially on the matrix size. The results are shown in Table 4 and presented in Fig. 7. In this table, \(N \times M\) represents the number of rows and columns of the original matrix and NE is the number of non-zero elements in the matrix, Density is the percentage of non-zero elements in the matrix, MemCRS is the amount of memory required to store the matrix in CRS format, MemVDSpM is the amount of memory required to store the matrix in VDSpM format and t is the time required to build the matrix in VDSpM format. It can be observed that for maps smaller than \(600 \times 600\) cell, the time to build the matrix is very low, and, for larger maps, this time presents a linear behaviour. This is due to the fact that, for small maps, the matrices are stored in the cache memory, and the execution time is not penalized by cache misses. However, when the maps are larger, the number of misses is larger, and the execution time presents a linear dependency on the number of non-zero elements of the matrix. From these data, it is possible to determine the time required to build the VDSpM matrix, as shown in Eq. 4.

$$\begin{aligned} t = 3.32 \cdot 10^{-8}NE-4.96 . \end{aligned}$$
(4)

4 Vectorized diagonal sparse matrix vector multiplication VDSpMV

Using the Vectorized Diagonal Sparse Matrix (VDSpM) storage format, it is possible to implement the matrix–vector multiplication. The main advantage of this storage format is that the subdiagonals of the diagonal sparse matrix are stored as sequential vectors. Each subdiagonal vector term must be multiplied by the corresponding terms of the multiplying vector and the partial results must be added to create the terms of the resulting vector. This scheme is represented in Fig. 8. This method has been parallelised using three different approaches: OpenMP, MPI and CUDA.

Fig. 8
figure 8

Scheme of sparse matrix-vector multiplication considering VDSpM storage format step by step

Full size image

This parallel process is also shown in a simplified way in Fig. 9. This figure shows a piece of parallel code where it can be observed that the vectors (diagonals) and vector p are accessed linearly, avoiding cache misses.

Fig. 9
figure 9

Code showing the matrix-vector multiplication considering VDSpM format

Full size image

5 Experimental results

Concerning the OpenMP and the MPI experiments, a cluster based on 16-core AMD Opteron (tm) processor 6376 with 10GB ethernet has been used to run the experiments. To test the GPUs performance, a Nvidia GTX Titan GK 110 with 2688 CUDA cores and 6GBytes of memory has been used.

A large set of experiments has been carried out considering different maps. In the following subsections, some results are summarized.

5.1 OpenMP parallelisation

The operations corresponding to the elements of the main diagonal and the elements of the subdiagonals are mapped to the threads. The vector and the resulting vector components are kept in shared memory and, therefore, can be accessed by all the threads. Each thread calculates the terms corresponding to some elements of the main diagonal and the subdiagonals. This scheme is shown in Fig. 10.

Fig. 10
figure 10

Scheme of VDSpMV OpenMP parallelisation

Full size image

The results for different matrix sizes and different numbers of cores are shown in Figs. 11 and 12. It can be observed that the speedup with 2 cores is about 1.8; with 4 cores, about 2.6; and with 8 cores, up to 2.9. But the most significant point is that an execution of a \(900 \times 900\) cell that takes 2268 s in one core is executed in just 920 s using 4 cores. This means a reduction in the execution time from more than 37 min to less than 16 min, and this can make the use of a wind field simulator feasible.

Fig. 11
figure 11

Execution time of WindNinja OpenMP parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image
Fig. 12
figure 12

Speedup of WindNinja OpenMP parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image

5.2 MPI parallelisation

In this case, a Master–Worker structure has been implemented. In this approach, the Master process distributes the rows of the matrix to the worker processes. The workers start working and calculate their elements. They do not return the values to the Master, but they just exchange some few data with other workers to execute the next step in the PCG. The Master only receives all the elements at the end of the process. It is not a dynamic Master–Worker structure, but there is a Master that distributes the data and gather the results at the end. This implementation is shown in Fig. 13.

Fig. 13
figure 13

Scheme of VDSpMV MPI parallelisation

Full size image

The execution time and the speedup are shown in Figs. 14 and 15. In this case, the results are not as good as the OpenMP parallelisation. With 2 workers, the speedup obtained is around 1.7; with 4 workers, is around 2.4; and with 8 processors, it is just 2.3. In the case of small maps (\(500 \times 500\) and \(600 \times 600\) cell maps) the results are particularly bad, because, in these cases, the communication is more significant compared with the computation itself.

Fig. 14
figure 14

Execution time of WindNinja MPI parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image
Fig. 15
figure 15

Speedup of WindNinja MPI parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image

5.3 CUDA parallelisation

To execute WindNinja considering VDSpM, the first step is to reserve memory in the GPU and then store the matrix and the vectors involved in that GPU memory. To calculate the matrix–vector multiplication, a CUDA kernel is created. In this CUDA kernel, the total computation is divided into blocks of 1024 threads so that each thread computes an element. This structure is shown in Fig. 16. Once all the blocks have been computed, the next two kernels compute a reduction operation to aggregate the previously obtained values. This structure is repeated to carry out the complete PCG, alternating operation and reduction kernels. The complete structure is represented in Fig. 17.

Fig. 16
figure 16

Scheme of VDSpMV CUDA parallelisation

Full size image
Fig. 17
figure 17

PCG CUDA implementation

Full size image

The GPU used has 2688 CUDA cores, and all of these cores are devoted to executing the application. The execution time and the speedup are shown in Figs. 18 and 19. The execution time is reduced to 451 s (less than 8 min) for a map of \(800 \times 800\), which is a very significant reduction, and the speedup for each case is a little bit over 3. However, in this case, there is a significant drawback: the maps larger than \(800 \times 800\) cell cannot be executed because such maps do not fit into the 6GBs of GPU memory.

Fig. 18
figure 18

Execution time of WindNinja CUDA parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image
Fig. 19
figure 19

Speedup of WindNinja CUDA parallelisation on a 16 cores AMD Opteron (tm) processor 6376

Full size image

5.4 Comparison

Figure 20 summarizes the results obtained for the three parallel implementations in a single figure. In this case it can be observed that, for an \(800 \times 800\) cell map, which is the largest map that can be executed in the GPU, the CUDA implementation reaches 450 s, the OpenMP implementation with 8 cores reaches 641 s and the MPI implementation is clearly the one that provides the poorest results with 774 s.

Fig. 20
figure 20

Comparison of WindNinja Execution time for a map of \(800 \times 800\) on a cluster of 16 cores AMD Opteron (tm) processor 6376 with a Nvidia GTX Titan GK 110

Full size image

6 Conclusions

Wind field calculation is a critical issue for the accuracy of forest fire propagation prediction. However, wind field calculation becomes prohibitive for real-time operation due to memory and time requirements. A wind field simulator WindNinja has been analysed to improve execution time and memory requirements by applying parallelisation techniques. This wind field simulator represents the problem with a very sparse symmetric diagonal matrix with just the main diagonal and 13 subdiagonals. A new storage method has been designed and the sparse matrix–vector SpMV multiplication operation has been developed exploiting the features of this new storage method. Three different implementations (OpenMP, MPI and CUDA) have been developed. Results show that all three implementations reduce execution time, but the CUDA parallelisation reaches the most significant execution time reduction and provides the best speedup, although the size of the map is limited by the GPU memory.