Introduction

Ammonia is a low-cost chemical, which is widely available commercially. However, its high volatility is a major concern when aqueous ammonia liquors are used in many industrial process settings e.g. ammonia based air-conditioning [1] and CO2 scrubbing from gas streams [2]. Inexpensive approaches to controlling ammonia vapour pressure could have many potential benefits, including reducing pollution/emissions and process costs. The amount of free ammonia in the gas phase above ammonia-containing liquors is a function of temperature, pressure and other thermodynamic parameters. In the aqueous phase, the dissociation constant Kb for the reaction: NH3 + H2O → NH4 + + OH− is 1.774 × 10−5 at 25 °C i.e. ammonia is a weak base, pKb 4.76 [3]. Due to this small value, it can be assumed that [NH4 +(aq)] ≪ [NH3(aq)] and ammonia vapour losses will be significant except at the lowest pH values. Typical engineering solutions to suppress ammonia vapourisation at high pH involve cooling or pressurisation. However, this often has an unsatisfactory effect on operating costs, especially if refrigeration is needed in warmer climatic zones.

In this report, we explore reducing ammonia volatility via low cost alkali salt additives as an alternative to refrigeration/pressurisation. We focus on the alkali metal ion series Li+–Cs+ for two main reasons: (i) the metal ion/ammonia coordination number is expected to increase with increasing ion radius (from Li+ → Cs+), and (ii) the uni-directionality of the (mostly) electrostatic M+ ↔ NH3 interaction is likely to be lost (and less likely to inhibit important ammonia lone-pair chemistry) as the ion radius (M+···NH3 separation) and solvent coordination number increase. These arguments suggest Cs+ will perform better in this role than, say Na+, because less salt will be needed to achieve the same volatility reduction. A central goal of this study is the computational prediction of differences in the vapour–liquid equilibrium (VLE) of ammonia–water and ammonia–water–salt mixtures with the accuracy needed to assess process performance.

In the first instance, the Gibbs ensemble Monte Carlo (GEMC) method was used to investigate VLE properties of various water–ammonia–MCl mixtures, M = Na, Cs. The GEMC method has previously been used for the direct determination of the phase coexistence of microfluids by Panagiotopoulos [4, 5]. This technique makes use of distinct vapour and liquid phases. No interface between the two regions exists in the simulation and the conditions of phase coexistence are satisfied in a statistical sense.

We also aim to gain an understanding of the thermodynamics of the “salting-in” effect which could prevent ammonia escape from aqueous liquors. To the best of our knowledge, this is the first computational study of ammonia–water systems that attempts to verify this phenomenon. From the GEMC simulations, liquid and vapour densities, compositions and radial distribution functions (RDFs) for molecules in the liquid phase are generated. Radial distribution functions are used to gain insight into the bulk solution structure and the effect of ionic additives on intermolecular order. Experimental results for the hydration structures of alkali-metals in pure water show a decrease in the strength of the ion–water interaction with increasing ion size, together with a small increase in coordination number [6], consistent with our earlier points. Water shows a characteristic orientational ordering of hydrogen-bonded (H-bonded) molecules [7]. This structure is disrupted by pressure changes and chemical additives, as demonstrated by neutron scattering via changes in water–water H–H RDFs [8]; in this context, HCl was found to be less effective than other solutes (e.g. NaOH) at the same concentration [9–11]. The increase of ammonia solubility in alkali-metal water solutions is also related to the nature of the interaction—chiefly electrostatic—between the ammonia molecules and alkali cations. For this reason, we have also investigated the binding free energies of M+–X, M = Li–Cs, X = NH3 or H2O, using ab-initio methods, in both the gas- and aqueous-phases.

Methods

Simulations

Thermodynamic properties of salt–ammonia–water systems were derived using the GEMC technique [12, 13]. For the two component ammonia–water system, aggregated volume bias (AVB) steps were used [14, 15].

Pseudo-random numbers for the Monte Carlo (MC) steps were generated using DX-1597-2-7 [16]. The extended simple point-charge (SPC/E) interaction potential, which includes corrections for self-polarisation, was chosen to simulate water [17, 18]. This model comprises three electrostatic interaction sites with an OH distance of 1 Å and HOH angle of 109.471°. Atomic charges were set to +0.433e for hydrogen atoms and −0.848e for oxygen atoms [18]. For the computation of van der Waals forces between water molecules, we used a Lennard–Jones (LJ) interaction potential centred on the oxygen atom (see Eq. 1).

Interactions within, and between, ammonia molecules are described by the optimised potential for liquid simulation—all atoms (OPLS-AA) force field with a charge of −1.02e for nitrogen, and charges of 0.34e for hydrogen [19]. This force field has also been shown to work well within the SPC/E model [20]. For cations and anions, the Aqvist and LGM force fields were used, respectively [21, 22].

Non-bonded interactions are represented by an LJ plus Coulomb term as shown in Eq. 1:

$$E = \sum\limits_{i} {\sum\limits_{j > i} {\left\{ {\frac{{q_{i} q_{j} }}{{4\pi \varepsilon_{0} r_{ij} }} + 4\varepsilon_{ij} \left[ {\left( {\frac{{\sigma_{ij} }}{{r_{ij} }}} \right)^{12} - \left( {\frac{{\sigma_{ij} }}{{r_{ij} }}} \right)^{6} } \right]} \right\}} } $$
(1)

where q is the charge of the atom, r is the distance between the interaction centres, \(\varepsilon\) the depth of the potential well and σ the distance at which the potential reduces to zero. i and j define different interaction centres. Geometrical mixing rules were applied throughout this study for the determination of LJ parameters for different atoms as shown in Eqs. 2 and 3:

$$\sigma_{ij} = \sqrt {\sigma_{ii} \sigma_{jj} } $$
(2)
$$\varepsilon_{ij} = \sqrt {\varepsilon_{ii} \varepsilon_{jj} } $$
(3)

An 11 Å cut-off with analytical tail correction was applied throughout [23]. Coulombic interactions were determined using the Ewald sum method with a cut-off radius adjusted to half the box length [23, 24].

Cubic boxes with periodic boundary conditions were used for the liquid and vapour phases. Molecules were partitioned such that approximately two thirds were placed in the liquid box and the remainder in the vapour box. The total number of particles in the simulations was 404, consisting of 360 water-, 40 ammonia-, two cations and two anions. The simulations were performed at a constant pressure of 101.3 kPa over the temperature range 273–400 K. All simulations were run until quasi-equilibrium was achieved (between 100,000 and 300,000 MC cycles). Each MC cycle involves N steps, N = total number of molecules. Values were recorded during the production period of 50,000–100,000 cycles. The standard deviations for all results were calculated by breaking the production period into five blocks.

To sample phase space, four different kinds of MC steps have been assigned: constant pressure volume steps [25], inter-box and intra-box swap steps [12, 13], translations of the centre-of-mass of the molecules and rotation around the centre-of-mass. The corresponding probabilities were 1, 14, 15, 37 and 33 %, respectively. The mole fraction of salt in the vapour phase was fixed at zero. In the ammonia–water two-component system, an additional aggregated volume bias step [14, 15] has been assigned with a probability of 3 % on cost of the translation of the centre-of-mass. The maximum displacement of molecules during rotational and translational steps was adjusted to yield acceptance rates of 50 % in all simulations.

Version 7.0.2 of the MCCCS Towhee source code was used throughout this study [26]. Calculations with Towhee were performed on an IBM System x iDataplex dx360 M3 cluster system running Linux. The cluster consists of 146 compute nodes, each with dual 6-core Intel Xeon Westmere cores with 12 MB cache—a total of 1,752 cores. The node interconnect is quad data rate (QDR) Infiniband. The system is housed at CSIRO Advanced Scientific Computing in Docklands, Melbourne, Australia.

Ab-initio calculations

For a systematic study of the influence of cation-size on the strength of the M+–NH3 interactions, ΔG 298 (M+ − NH3 → M+ + NH3) for M = Li–Cs has been calculated. The composite G4 method was used to determine the strength of interaction for M = Li–K [27, 28]. These calculations were performed with the G09 software suite [29]. For Li–Cs, interaction free energies were calculated with GAMESS software [30] using a hybrid-meta density functional and an effective core potential—triple zeta basis set combination: M06-2X/RECP-TZVPPD [31]. This approach explicitly includes the outer nine valence electrons of Cs+ and Rb+ via the augmented triple-zeta basis set [30, 32]. The Li+–NH3, Na+–NH3 and K+–NH3 system binding energies were evaluated using both the composite G4 and M06-2X methods to compare the accuracy of the density functional theory (DFT) values: excellent agreement (|ΔG G4−ΔG M06-2X| <2 %) was found (see Table 1). The electronic energies in solution were calculated at the SM6 + M06-2X/TZVPPD level, using redistributed Löwdin population analysis (RLPA) charges [33] and the following Bondii radii [34]: K = 2.75 Å, Na = 2.27 Å, Li = 1.82 Å [35]. State corrections for the free energy change of 1 mol of an ideal gas from 1 atm (24.4 L mol−1) to 1 mol L−1 \(\Updelta G^{0 \to *}\) were calculated with Eq. 4 [35, 36].

$$\Updelta G^{0 \to *} = RTln(24.4). $$
(4)
Table 1 Results from ab-initio calculations using M06-2X/TZVPPD, M06-2X/RECP-TZVPPD and the composite G4 method (values in brackets): The self consistent field (SCF) energies, bonding length, Gibbs free energy for the dissociation reaction at 298 K (ΔG 298), M+–X → M+ + X (M+ = Li+ to Cs+, X = NH3 or H2O) and the total electronic energy including the zero-point energy (V(0 K))
Full size table

with R being the ideal gas constant and T = 298 K. Solvation free energies were calculated using the GAMESSPLUS software [37] and—in the case of hydrated cations—were also adjusted for the change in water concentration, RTln(55.34), as described by Goddard [38]. Ab-initio calculations were performed on the sun constellation cluster ‘vayu’ housed at the NCI National Facility at ANU, Canberra, Australia. This system consists of 1,492 nodes in Sun X6275 blades, each containing two quad-core 2.93 GHz Intel Nehalem cpus with 6.4GTs QPI bus and a total of 37 TB of RAM on the computer nodes.

Experiments

Methods

Density measurements were performed using an Anton Paar DMA 38 digital benchtop density meter. The accuracy for density measurements with this device is 0.001 g/ml over the temperature range 288–313 K. For concentration measurements of ammonia in the liquid phase, calibration curves were recorded. Five different ammonia concentrations between 0 and 10 % were measured, and linear regression was used to correlate the liquid density to the ammonia concentration in the ammonia–water and NaCl–ammonia–water systems. The concentration of NaCl was 0.5 mol% which yields a mole ratio of NaCl:NH3 of ~1:20. For the experimental study of ammonia evaporation, 20 mL of each solution was heated to 323 K in water bath. At defined time-steps, 1 mL samples were taken with a syringe and immediately injected into the sample cell of the density meter. The density value was recorded after the temperature of the sample equilibrated within the cell (to 293 K).

Materials

Ammonium hydroxide solution ACS reagent, 28–30 % NH3 base was purchased from Sigma-Aldrich. The salts used in this study were CsCl, 99.9 %, and NaCl (BioXtra, ≥99.5 %) from Sigma-Aldrich. Milli-Q water (R > 18 MΩ) was used throughout.

Results

Calculated density values from GEMC simulations are presented in Fig. 1 for the liquid (Fig. 1a) and vapour phase (Fig. 1b). Experimentally measured density values for the liquid phase from 293 to 313 K are also presented. Over this temperature range, simulated values are in excellent agreement with the experimental values. In addition, the ammonia–water system exhibits a maximum in density around 290 K and both the NaCl and CsCl containing systems exhibit maximum vapour densities around 300 K. At higher temperatures (up to 400 K), the densities of all systems are reduced.

Fig. 1
figure 1

Densities as a function of temperature of 10 mol% ammonia–water system and the same system containing 0.5 mol% CsCl in the liquid (a) and vapour phase (b) at 101.3 kPa. Open triangles and full black line represent the ammonia–water system and points and dashed red line the CsCl–ammonia–water system. Full symbols represent experimentally measured values at the same composition. The connecting lines have been plotted as a guide for the eye

Full size image

The liquid-phase concentration of ammonia derived from GEMC simulations is presented in Fig. 2. In the presence of NaCl and CsCl, an increase in the concentration of ammonia (ammonia:water molar ratio) is evident. No difference between the two salts could be observed within the accuracy of the method.

Fig. 2
figure 2

Concentration of ammonia in the liquid phase depending on temperature at 101.3 kPa from GEMC simulations. Black points represent the 10 mol% ammonia–water system. Red squares and green diamonds show the 10 mol% ammonia–water system containing 0.5 mol% CsCl and NaCl, respectively. The lines are a guide for the eye obtained by fitting exponential decays to the data points

Full size image

The experimental Gibbs free energy of solvation of ammonia is the difference between the free energy of formation in the aqueous phase and in the gas phase: ΔG s = ΔG 0f,aq −ΔG 0f  = −10.1 kJ mol−1 at 298.15 K and 100 kPa [3]. The value obtained from the GEMC simulations is −10.8 kJ mol−1 at 295 K and 101.3 kPa, which is in good agreement with the literature value. The Gibbs free energy of transfer from the gas to the liquid phase was calculated from GEMC simulations at several different temperatures and is presented in Fig. 3. Lower Gibbs free energies were observed in the salt containing system.

Fig. 3
figure 3

Temperature dependence of the Gibbs free energy of transfer from the gas to the liquid phase (ΔG transfer) from GEMC simulations of 10 % ammonia in water (black circles) and 10 % ammonia in water containing 0.5 mol% NaCl–water (green squares) at 101.3 kPa. The lines are linear fits to the simulated data points and should be a guide for the eye

Full size image

To validate the GEMC findings of ammonia vapour suppression, measurements of ammonia concentration as a function of time in an open vessel (T = 323 K) were performed. The results are presented in Fig. 4. The curves reveal a relative decrease in ammonia concentration in the liquid phase in the presence of 0.5 mol% NaCl.

Fig. 4
figure 4

Experimental measurements of the liquid phase ammonia concentration during evaporation of ammonia from a 10 mol% ammonia in water sample with time at 50 °C and 101.3 kPa. The full black points and full black line represent the ammonia–water system and the green squares and the green line the NaCl–ammonia–water system. The lines are linear fits to the data-points to guide the reader

Full size image

The influence of ions on the H-bonding network in the ammonia–water system has been investigated by calculating the RDFs for H–H interactions in water for the liquid box at 293.15 K. The RDF for ammonia–water presented in Fig. 5a exhibits three peaks near 2.4, 3.9 and 4.7 Å. The peak positions for the RDFs are consistent with those extracted from neutron scattering curves for pure water [7] (plotted in the same graph) and represent the strong orientational ordering within the H-bonded water network. After addition of 0.5 mol% NaCl or CsCl, the height of the first and second peaks increases by about 10 % and the third peak at 4.7 Å diminishes. This indicates that the number of water molecules in the first and second solvation shell of water increases in the presence of ions; yet, the average distance of the orientational interactions in the H-bonded network decreases, and this is evident by the loss of the third order peak.

Fig. 5
figure 5

a Water–water H–H RDFs: The scatters are experimental data from neutron scattering experiments on water taken from [7], the full black line is derived from the GEMC simulations of 10 mol% ammonia in water, 0.5 mol% NaCl in ammonia–water (dashed green line) and 0.5 mol% CsCl in ammonia–water system (dashed red line). The curves have been shifted by constant values for better visibility. b Comparison between the radial distribution functions (RDF) for Na+ and oxygen atoms in water (black line) and Na+ and nitrogen atoms in ammonia (red line) for 10 mol% ammonia in water containing 0.5 mol% NaCl at 293.15 K and 101.3 kPa

Full size image

A plot of the RDFs for (water) oxygen-atoms surrounding Na+ and (ammonia) nitrogen-atoms surrounding Na+ is presented in Fig. 5b. Both water and ammonia are present in the first solvation shell of Na+. The extent of the first solvation shell for both O and N is 2.49 Å. This value is in good agreement with the optimised bond lengths from ab-initio calculations shown in Table 1 and also consistent with experimental data for (water) oxygen-atoms around Na+ derived from X-ray and neutron scattering [39, 40].

Representative snapshots of the liquid- and vapour box for ammonia–water and NaCl–ammonia–water at 293.15 K and 101.3 kPa are presented in Fig. 6. For the salt-containing systems, there is a clear reduction in the number of vapour phase ammonia molecules. The distribution diagram of ammonia molecules within the liquid simulation box of the NaCl–ammonia–water system at two temperatures (293.15 and 370 K) is presented in Fig. 7. The box-dimensions have been normalised to simplify comparison. Fig. 7a shows that ammonia prefers to be self-solvated, or surrounded by other ammonia molecules; the extent of self-solvation decreases at higher temperatures (e.g. 370 K in Fig. 7b). From these distributions, it is also clear that ammonia molecules do not necessarily accumulate near Na+ or Cl− ions (located in the corners of the liquid box) but are almost evenly distributed throughout the (x,y) area.

Fig. 6
figure 6

Representative snapshots from the GEMC simulation at 293.15 K and 101.3 kPa for the vapour- (a) and liquid phase (b) at 10 mol% aqueous ammonia, and the vapour- (c) and liquid phase (d) at 0.5 mol% NaCl in 10 mol% aqueous ammonia. Oxygen atoms are in red, hydrogen in gray, nitrogen in violet, sodium in blue and chloride in green

Full size image
Fig. 7
figure 7

Distribution density of the ammonia–nitrogen atom at 101.3 kPa and T = 293.15 (a) and 370.00 K (b) in the horizontal xy plane of the liquid simulation box. The box dimensions x and y are normalised to one. The probability of finding ammonia at a certain position is represented by colours from black (0) to yellow (maximum)

Full size image

The values for the binding energies of M+–X, M = Li–Cs X = NH3 or H2O, are presented in Table 1 alongside the M+–NH3/H2O optimised bond lengths (M06-2X/(RECP)-TZVPPD calculations; values obtained using the composite G4 method for M+ = Li–K are given in brackets. Optimisations in the dielectric continuum (SM6 + M06-2X/TZVPPD, M+ = Li–K) were used to generate the corresponding aqueous values. The equilibrium constants for the dissociation reaction M+–X → M+ + X (Table 2) from the standard Gibbs thermodynamic relation:

$$K_{\text{eq}} = e^{{ - \frac{{\Updelta G_{\text{R}} }}{RT}}} $$
(5)

show that equilibrium clearly lies towards the M+–X complex and M+–NH3 is preferred to M+–H2O in the gas- and aqueous phase.

Table 2 Equilibrium constants for the reaction M+–X → M+ + X calculated from the reaction free energy presented in Table 1 at T = 298 K
Full size table

The binding energy differences between ammonia and water complexes for a specific cation: ΔΔG(M+–X → M+ + X) in both the gas- and aqueous phases are plotted in Fig. 8a. The ion-ammonia binding energies are consistently larger than corresponding ion-water values.

Fig. 8
figure 8

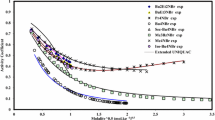
a Log–log plot of the binding energy (V [kJ/mol]) versus the M+–NH3 bond length (r [Å]) for M+ = Li+ to Cs+ to a single ammonia molecule at 298 K. The full line is a linear fit to the data with a slope of −3. b Difference in the Gibbs free energy (ΔΔG 298) for the reactions M+–NH3 → M+ + NH3 and M+–H2O → M+ + H2O at T = 298 K of (M+ = Li+ to Cs+). The values obtained from calculations in the gas-phase are represented by gray—and the aqueous phase by semitransparent red bars

Full size image

A log–log plot of the gas-phase binding free energy of M+–NH3 versus \( {\text{r}}_{\text{M} - \text{NH}_3}\) derived from DFT calculations is presented in Fig. 8b. The linearity of the graph demonstrates an approximate third order distance-dependence for the M+–NH3 interaction potential.

Discussion

Gibbs ensemble Monte Carlo simulations have been used to gain insight into intermolecular interactions between alkali metal ions and ammonia in aqueous solutions. The quality of simulated densities of ammonia–water and salt–ammonia–water liquid phases was the basis for force-field selection. Densities were remeasured experimentally and show quantitative agreement with the simulation results. In general, all systems demonstrate a decrease in density with increasing temperature. The change of density with temperature is predominantly due to the following effects: (i) increased molecular motions which weaken the H-bonding network → density decrease, and (ii) evaporative ammonia losses → density increase. All systems (with or without added cations) exhibit decreasing density with increasing temperature, indicating that thermal effects are dominant. However, the simulations also show that in solution, density decreases more slowly with increasing temperature in the presence of salt cations. This suggests that less ammonia will evaporate when salts are present and thus the ammonia solubility in the liquid phase is higher at higher temperatures, albeit only slightly. Similarly, the mole ratio of ammonia in water as a function of temperature also indicates higher ammonia solubility in the aqueous phase resulting from a ‘salting-in’ effect. This trend could also be confirmed experimentally through measurements of lower ammonia evaporation rates in the presence of NaCl. To further investigate the effect of alkali-metal salts on the vapour liquid equilibrium, the Gibbs free energy of transfer from the gas to the liquid phase was calculated from GEMC simulations at several different temperatures. Lower Gibbs free energies of solvation were derived from GEMC simulations at several different temperatures. Lower solvation free energies were observed in the salt containing system, which implies a higher solubility of ammonia in the aqueous phase and consequently a lower ammonia vapour pressure.

From an intermolecular point of view, addition of NaCl and CsCl alters the structure of the solvent H-bond network. Ammonia is displaced from the water–water H-bonded network towards the aqueous Na+ and Cs+ ions. An increase in the water–water coordination number and a denser H-bonding network between water molecules is a direct consequence. No increase in the ammonia molecule density around the Cl− counterions was evident. Electrostrictive effects influence the coordination of water molecules which could possibly decrease the length-scale of interactions within the hydrogen-bonded network.

The preferential solvation of Na+ and Cs+ by ammonia is supported by the strength of the electrostatic interactions between alkali-metals and ammonia, as determined using ab-initio calculations: The M+–NH3 complex is preferred over M+–H2O for M = Li–Cs. This is evident from the binding energies given in Table 1 as well as the corresponding reaction equilibrium constants presented in Table 2. Systematic investigation of the interactions between alkali-metal cations and both ammonia and water showed a decrease in the potential with increasing cation size from Li+ to Cs+ in the gas- and aqueous phase. The decrease is more pronounced in the M+–NH3 system due to a stronger Li+/NH3 interaction. For instance, the Gibbs free energy of the dissociation reaction for gas-phase ammonia complexes decreases from 136 to 37 kJ mol−1, whereas the values for water decrease from 117 to 34 kJ mol−1. A possible explanation for this might be the molecular polarisability of ammonia (2.21 Å3), which is higher than that of water (1.43 Å3). The ion dipole potential can be written as [41, 42]:

$$V_{\text{id}} \cong - \frac{{\alpha q^{2} }}{{2r^{4} }} - \frac{{\mu_{\text{D}} q}}{{r^{2} }} $$
(6)

where r, radial distance of the solvent molecule from the point-positive charge, α, solvent polarisability, μ D, solvent dipole moment and q, electron charge. The variation of the ion–dipole potential with distance separation is most favourable for ammonia up to around 2.1 Å. At larger separations, the second term of Eq. 6 begins to dominate. Since the dipole moment of water is larger than the dipole moment of ammonia, the potential of interaction becomes more favourable for water beyond 2.1 Å. Note that Eq. 6 assumes dipole ‘locking’ parallel to the M+–NH3 bond (cos 0° = 1). The DFT binding energies (which capture higher order attractive terms) are plotted in a log–log plot and exhibit a distance dependence of r −3, an order of magnitude smaller than a pure ion–dipole interaction, but larger than the ion-polarisability interaction in Eq. 6.

The decrease in binding energy with increasing cation radius which is predicted by the DFT calculations is not apparent in the VLE data simulations. Both Na+ and Cs+ have a comparable effect on the increase in ammonia solubility—within the accuracy of our simulations. This suggests that: (i) the effect is too small to be observed with sub-molar additive concentrations, or (ii) there is an alteration of the local water structure that causes stronger ammonia–water interactions down the group. It is presumed throughout that the M+–NH3 versus M+–H2O binding free energies will predict favourable solute–solute interactions via a preference for ammonia solvation rather than water; expanding the solvation shell and treating more solvating molecules explicitly at the quantum level is necessary for the most accurate picture.

Distribution densities of ammonia within the liquid GEMC simulation box suggest micro-aggregation of ammonia molecules. This means that ammonia molecules tend to self-solvate whereas water forms tetrahedral aggregates which can exclude ammonia. At higher temperatures, mixed ammonia–water clusters predominate. A similar behaviour has been found for alcohol–water mixtures [43]. As suggested by the results presented here, some of the ammonia will preferentially solvate the cations in the aqueous phase.

Conclusion

Suppressing ammonia vapourisation from aqueous ammonia solutions is important for many processes e.g. refrigeration or ammonia based CO2 capture processes. A possible approach to vapour suppression is via the addition of small amounts of alkali metal salts. Gibbs ensemble Monte Carlosimulations were used to study the effect of 0.5 mol% NaCl and CsCl on the VLE of 10 mol% aqueous ammonia solutions. Sodium chloride and CsCl have been selected as two strategic representatives of the alkali metal series to demonstrate favourable interactions between cations and ammonia in aqueous solutions. The results of this study shed light on the influence of salts on thermodynamic properties as well as any solution structures that result from strong intermolecular interactions. Ions interact with ammonia molecules in the liquid phase through complex electrostatic interactions depending on species and composition. The simulations indicate that ammonia is preferentially located near Na+ and Cs+. This is supported by the binding energies computed with G4 and M06-2X/RECP-TZVPPD, which predict binding energies ΔG bind(M+–NH3) > ΔG bind (M+–H2O) for M = Li–Cs in the gas-phase and M = Li–K in the aqueous phase. These results also showed a decrease in the potential with increasing cation size from Li+ to Cs+ in the gas- and aqueous phase.

Gibbs ensemble Monte Carloalso shows that NaCl and CsCl have comparable effects on the solubility of ammonia, suggesting only a small dependence on the cation size. The results for densities obtained from the vapour liquid equilibrium are well reproduced by experiments within the temperature range approached by the experimental set-up used. In addition, the water–water H–H RDF and the free energy of solvation of ammonia in the ammonia–water mixture are within the range of tabulated literature data.