Skip to main content
SpringerLink
Log in

Computational Investigation of the Effect of Reinforcement Schemes and Angles on the Stress-Strain State and Strength of Composite Cylinders Under Axisymmetric Internal Explosion. Part 1. Effect of the Discretization Spacings of the Computational Domain on the Accuracy of Determination of Stress-Strain State and Strength

  • SCIENTIFIC AND TECHNICAL SECTION
  • Published:
Strength of Materials Aims and scope

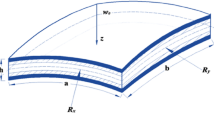
The effect of two-dimensional regular finite-difference mesh spacings on the accuracy of calculation of the dynamic axisymmetric stress-strain state and strength of hollow composite cylinders of finite length, fixed overall dimensions and thickness has been numerically determined by the Wilkins method modified for helical orthotropy and implemented in an application package, created earlier by the authors. The cylinders were made by a ribbon consisting of VMPS glass fibers, impregnated with an ÉDT-10 epoxy binder, on a technological mandrel. Loading is done by exploding a spherical explosive charge in the center of symmetry of a cylinder in an air atmosphere. The obtained results allow one to choose mesh spacings along the radial and axial coordinates, which ensure an acceptable accuracy of determination of the maximum values of hoop stresses and strains, as well as strength functions by maximum stress and strain criteria and by the generalized von Mises criterion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. P. Lepikhin and V. A. Romashchenko, Strength of Inhomogeneous Anisotropic Hollow Cylinders under Impulsive Loading [in Russian], Naukova Dumka, Kiev (2014).

    Google Scholar 

  2. N. A. Abrosimov and A. V. Elesin, “Mathematical modeling of the progressive fracture of cylindrical composite shells under multiple impulsive loading,” in: Proc. of the XI Int. Conf. on Nonequilibrium Processes in Nozzles and Jets (NPNJ’2016) (May 25–31, 2016, Alushta) [in Russian], MAI, Moscow (2016), pp. 287–289.

  3. N. A. Abrosimov and N. A. Novosel’tseva, “Numerical analysis of the progressive fracture process in cylindrical metal-filled plastic shells under impulsive loading,” in: Proc. of the XI Int. Conf. on Nonequilibrium Processes in Nozzles and Jets (NPNJ’ 2016) (May 25–31, 2016, Alushta) [in Russian], MAI, Moscow (20016), pp 289–291.

  4. A. I. Abakumov, P. N. Nizovtsev, V. P. Solov’ev, et al., “A computational-experimental study of the stress-strain state of composite shells of revolution under dynamic loading with allowance for large strains,” Mekh. Kompoz. Mater., 34, No. 1, 28–37 (1998).

    Google Scholar 

  5. N. A. Abrosimov and A. V. Elesin, “Numerical analysis of the effect of reinforcement structure on the dynamic behavior of cylindrical composite shells under explosive loading,” Probl. Prochn. Plastichn., Issue 74, 78–83 (2012).

  6. N. A. Abrosimov, A. V. Elesin, and N. A. Novosel’tseva, “Numerical analysis of the effect of reinforcement structure on the dynamic behavior and ultimate deformability of composite shells of revolution,” Mekh. Kompoz. Mater., 50, No. 2, 313–326 (2014).

    Google Scholar 

  7. N. A. Abrosimov, A. V. Elesin, and S. A. Pirogov, “Numerical analysis of the non-axisymmetric deformation and progressive fracture of cylindrical laminated composite shells under impulsive loading,” Probl. Prochn. Plastichn., 77, No. 1, 23–32 (2015).

    Google Scholar 

  8. N. A. Abrosimov and N. A. Novosel’tseva, “Numerical simulation of the process of layer-by-layer failure of cylindrical shells under explosive loading,” Mekh. Kompoz. Mater., 51, No. 4, 579–594 (2015).

    Google Scholar 

  9. P. P. Lepikhin, V. A. Romashchenko, O. S. Beiner, et al., “A program for numerical calculation of dynamic stress-strain state and strength of hollow multilayer anisotropic cylinders and spheres. Part 2. Comparison of numerical results with experimental and theoretical for cylinders,” Strength Mater., 47, No. 3, 406–414 (2015).

    Article  Google Scholar 

  10. P. P. Lepikhin, V. A. Romashchenko, and O. S. Beiner, “Theoretical investigation of fracture in stress waves of anisotropic cylinder under internal explosion,” Strength Mater., 48, No. 5, 615–631 (2016).

    Article  Google Scholar 

  11. V. A. Romashchenko and O. S. Beiner, “Numeric simulation of three-dimensional dynamics and strength of multilayered spirally orthotropic cylinders,” Strength Mater., 44, No. 2, 187–195 (2012).

    Article  Google Scholar 

  12. V. A. Romashchenko, Yu. N. Babich, and E. V. Bakhtina, “Strength assessment for composite and metal-composite cylinders under pulse loading. Part 2. Numerical evaluation of strength for multilayer cylinders of finite length under internal explosion,” Strength Mater., 44, No. 5, 502–511 (2012).

    Article  Google Scholar 

  13. S. Nelson, B. O’Toole, and J. Thota, “Explosive testing of open cylinders for verification of composite properties used in computational analysis,” in: ASME 2012 Verification and Validation Symposium (May 2–4, 2012, Las Vegas, NV) (2012).

  14. P. P. Lepikhin, V. A. Romashchenko, and O. S. Beiner, “A numerical study of 3D dynamics and strength of metal-composite cylinders under internal explosion loading,” Strength Mater., 49, No. 6, 796–808 (2017).

    Article  Google Scholar 

  15. V. V. Adishchev, V. M. Kornev, and L. A. Talzi, Evaluation of Maximum Stresses in Closed Cylindrical Vessels under Axisymmetric Explosive Loading [in Russian], Deposited in VINITI, No. 6588-83, Novosibirsk (1983).

  16. G. Randers-Pehrson and K. A. Bannister, Airblast Loading Model for DYNA2D and DYNA3D, Technical report ARL-TR-1310, Army Research Laboratory (1997).

  17. P. P. Lepikhin, V. A. Romashchenko, O. S. Beiner, et al., “A program for numerical calculation of dynamic stress-strain state and strength of hollow multilayer anisotropic cylinders and spheres. Part 1. Program description,” Strength Mater., 47, No. 2, 249–256 (2017).

    Article  Google Scholar 

  18. A. G. Fedorenko, M. A. Syrunin, and A. G. Ivanov, “Dynamic strength of shells made of oriented fibrous composites under explosive loading (review),” Prikl. Mekh. Tekhn. Fiz., No. 1, 126–132 (1993).

  19. A. G. Ivanov (Ed.), Fracture of Multi-Scale Objects in the Explosion [in Russian], RFYaTs-VNIIÉF, Sarov (2001).

  20. A. G. Fedorenko, M. A. Syrunin, and A. G. Ivanov, “Criteria for the choice of composite materials for shell structures localizing explosion (review),” Fiz. Goren. Vzryv., No. 5, 3–11 (2005).

Download references

Author information

Authors and Affiliations

  1. Pisarenko Institute of Problems of Strength, National Academy of Sciences of Ukraine, Kiev, Ukraine

    P. P. Lepikhin, V. A. Romashchenko, O. S. Beiner & S. A. Tarasovskaya

Authors
  1. P. P. Lepikhin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. A. Romashchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. O. S. Beiner
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. A. Tarasovskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Problemy Prochnosti, No. 6, pp. 5 – 14, November – December, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lepikhin, P.P., Romashchenko, V.A., Beiner, O.S. et al. Computational Investigation of the Effect of Reinforcement Schemes and Angles on the Stress-Strain State and Strength of Composite Cylinders Under Axisymmetric Internal Explosion. Part 1. Effect of the Discretization Spacings of the Computational Domain on the Accuracy of Determination of Stress-Strain State and Strength. Strength Mater 50, 833–840 (2018). https://doi.org/10.1007/s11223-019-00029-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11223-019-00029-0

Keywords

Search

Navigation