SB-ETAS: using simulation based inference for scalable, likelihood-free inference for the ETAS model of earthquake occurrences

Abstract

The rapid growth of earthquake catalogs, driven by machine learning-based phase picking and denser seismic networks, calls for the application of a broader range of models to determine whether the new data enhances earthquake forecasting capabilities. Additionally, this growth demands that existing forecasting models efficiently scale to handle the increased data volume. Approximate inference methods such as inlabru, which is based on the Integrated nested Laplace approximation, offer improved computational efficiencies and the ability to perform inference on more complex point-process models compared to traditional MCMC approaches. We present SB-ETAS: a simulation based inference procedure for the epidemic-type aftershock sequence (ETAS) model. This approximate Bayesian method uses sequential neural posterior estimation (SNPE) to learn posterior distributions from simulations, rather than typical MCMC sampling using the likelihood. On synthetic earthquake catalogs, SB-ETAS provides better coverage of ETAS posterior distributions compared with inlabru. Furthermore, we demonstrate that using a simulation based procedure for inference improves the scalability from $\mathcal {O}(n^2)$ to $\mathcal {O}(n\log n)$. This makes it feasible to fit to very large earthquake catalogs, such as one for Southern California dating back to 1981. SB-ETAS can find Bayesian estimates of ETAS parameters for this catalog in less than 10 h on a standard laptop, a task that would have taken over 2 weeks using MCMC. Beyond the standard ETAS model, this simulation based framework allows earthquake modellers to define and infer parameters for much more complex models by removing the need to define a likelihood function.

1 Introduction

In recent years, an accelerated growth in the number of seismic sensors and machine learning algorithms for detecting the arrival times of earthquake phases (e.g. Zhu and Beroza 2019), has meant that the size earthquake catalogs have grown by several orders of magnitude Kong et al. (2019). In California, a deployment of a dense network of seismic sensors over the last century combined with an active tectonic regime has resulted in a comprehensive dataset of earthquakes in the region (Hutton et al. 2010). Furthermore, in more specific areas of California, through machine learning based seismic phase picking and template matching, enhanced earthquake catalogs have been created which contain many small previously undetected earthquakes (White et al. 2019; Ross et al. 2019). It is fair to assume that these datasets will only continue to grow in the future as past continuous data is reprocessed and future earthquakes are recorded. Determining whether increased data size leads to improved earthquake forecasts is a crucial question for the seismological community. The growing volume of data requires an expansion of modeling capabilities within the field. This not only necessitates that existing models can scale with the increasing datasets but also calls for a broader range of models to be fit to the data.

In this work we propose using Simulation Based Inference (SBI) to address this modeling expansion. We present SB-ETAS: a simulation based estimation procedure for the Epidemic Type Aftershock Sequence (ETAS) model, the most widely used earthquake model among seismologists. SBI is a family of approximate procedures which infer posterior distributions for parameters using simulations in place of the likelihood (Beaumont et al. 2002; Cranmer et al. 2020). By specifying a model through simulation rather than the likelihood, SBI broadens the scope of available models to encompass greater complexity. This study also demonstrates that for the ETAS model, SBI improves the scalability from $\mathcal {O}(n^2)$ to $\mathcal {O}(n \log n)$.

While there is extensive literature on SBI, its application to Hawkes process models (Hawkes 1971), of which ETAS is a member, is limited. This work builds upon earlier studies by Ertekin et al. (2015) and Deutsch and Ross (2021), which applied SBI to 1-dimensional Hawkes processes with exponential kernels. We expand upon their choice of summary statistics to fit the more complex ETAS model, which includes a magnitude (mark) domain and power law kernels. We add that since both simulation and summary statistic computation can be performed with time complexity $\mathcal {O}(n \log n)$, then SBI offers the additional benefit of scalability. Additionally, we enhance inference performance by using sequential neural posterior estimation (SNPE). SNPE trains a neural density estimator to approximate the posterior distribution from pairs of simulations and parameters. Section 3 provides an overview of SNPE and other SBI methods.

The Epidemic Type Aftershock Sequence (ETAS) model (Ogata 1988) has been the most dominant way of modeling seismicity in both retrospective and fully prospective forecasting experiments (e.g. Woessner et al. 2011; Rhoades et al. 2018; Taroni et al. 2018; Cattania et al. 2018; Mancini et al. 2019, 2020; Iturrieta et al. 2024) as well as in operational earthquake forecasting (Marzocchi et al. 2014; Rhoades et al. 2016; Field et al. 2017; Omi et al. 2019). The model characterises the successive triggering of earthquakes, making it effective for forecasting aftershock sequences. The parameters of the model are also used by seismologists to characterise physical phenomena of different tectonic regions such as structural heterogeneity, stress, and temperature (e.g. Utsu et al. 1995) or relative plate velocity (e.g. Ide 2013).

Most commonly, point estimates of ETAS parameters are found through maximum likelihood estimation (MLE). From these point estimates, forecasts can be issued by simulating multiple catalogs over the forecasting horizon. Forecast uncertainty is quantified by the distribution of simulations from MLE parameter values, however, this approach fails to quantify uncertainty contained in estimating the parameters themselves. Parameter uncertainty for MLE can be estimated using the Hessian of the likelihood (Ogata 1978; Rathbun 1996; Wang et al. 2010), which requires a very large sample size to be effective, and is only asymptotically unbiased (i.e. when the time horizon is infinite). Multiple runs of the MLE procedure with different initial conditions (Lombardi 2015) can also be used to express parameter uncertainty.

Full characterisation of the parameter uncertainty is achieved with Bayesian inference, a procedure which returns the entire probability distribution over parameters conditioned on the observed data and updated from prior knowledge. This distribution over parameters, known as the posterior, does not have a closed form expression for the temporal and spatio-temporal ETAS model and so several approaches have used Markov Chain Monte Carlo (MCMC) to obtain samples from this distribution (Vargas and Gneiting 2012; Omi et al. 2015; Shcherbakov et al. 2019; Shcherbakov 2021; Ross 2021; Molkenthin et al. 2022). These approaches evaluate the likelihood of the ETAS model during the procedure, which is a an operation with quadratic complexity $\mathcal {O}(n^2)$, and therefore are only suitable for catalogs up to 10,000 events. In fact, the GP-ETAS model by Molkenthin et al. (2022) has cubic complexity $\mathcal {O}(n^3)$, since their spatially varying background rate uses a Gaussian-Process (GP) prior. Modern earthquake catalogs, now comprising up to $10^6$ events, have outgrown the computational capacity of these traditional methods for fitting ETAS models. While larger datasets often reduce uncertainty, Bayesian inference enables seismologists to rigorously quantify and express model uncertainty, particularly when dealing with non-stationary data observed within finite time windows.

An alternative to MCMC is based on the Integrated Nested Laplace Approximation (INLA) method (Rue et al. 2017), which approximates the posterior distributions using latent Gaussian models. The implementation of INLA for the ETAS model, named inlabru, by Serafini et al. (2023) also seeks to broaden the modeling complexity and scalability of Hawkes process models such as ETAS. While inlabru demonstrated a factor 10 speed-up over MCMC for a catalog of 3500 events, they do not provide scaling results on larger catalogs. In this work we seek to directly compare the approximation ability of both SB-ETAS and inlabru through performing Bayesian inference for the temporal ETAS model. To evaluate the immediate speed benefits these methods provide, we investigate how they scale with the size of earthquake catalogs.

In SBI, models are defined through a simulator, eliminating the need to specify a likelihood function for inference. This approach has been adopted in other scientific fields where the likelihood is intractable, such as when it involves integrating over numerous unobserved latent variables. Seismology already encounters such intractable likelihoods. For instance, models that account for triggering from undetected earthquakes (Sornette and Werner 2005b) and those that incorporate geological features (Field et al. 2017) present estimation challenges. By linking earthquake modeling with SBI, this study introduces a framework for fitting these complex models while also providing an immediate scalability benefit for simpler models.

The remainder of this paper is structured as follows: In Sect. 2 we give an overview of the ETAS model along with existing procedures for performing Bayesian inference; Sect. 3 gives an overview of SBI, following which we describe the details of SB-ETAS in Sect. 4. We present empirical results based on synthetic earthquake catalogs in Sect. 5 and observational earthquake data from Southern California in Sect. 6, before finishing with a discussion in Sect. 7.

2 The ETAS model

The temporal Epidemic Type Aftershock Sequence (ETAS) model (Ogata 1988) is a marked Hawkes process (Hawkes 1971) that describes the random times of earthquakes $t_i$ along with their magnitudes $m_i$ in the sequence ${{\textbf {x}}} = \{(t_1,m_1),(t_2,m_2),\ldots ,(t_n,m_n) \} \in [0,T]^n \times \mathcal {M}^n \subset \mathbb {R}_+^n \times \mathcal {M}^n$. A quantity $\mathcal {H}_t$, known as the history of the process, denotes all events up to time t. Marked Hawkes processes are usually specified by their conditional intensity function (Rasmussen 2018),

$$\begin{aligned}&\lambda (t,m|\mathcal {H}_t) \nonumber \\&\quad =\lim _{\Delta t, \Delta m \rightarrow 0} \frac{\mathbb {E}\left[ N([t,t+\Delta t) \times B(m,\Delta m)|\mathcal {H}_t\right] }{\Delta t |B(m,\Delta m)|}. \end{aligned}$$

(1)

where N(A) counts the events in the set $A \subset \mathbb {R}_+ \times \mathcal {M}$ and $|B(m,\Delta m)|$ is the area of the ball $B(m,\Delta m)$ with radius $\Delta m$.

The ETAS model typically has the form,

$$\begin{aligned} \lambda (t,m|\mathcal {H}_t) = \left( \mu + \sum _{i:t_i<t} g(t-t_i,m_i) \right) f_{GR}(m), \end{aligned}$$

(2)

where $\mu$ is a constant background rate of events, g(t, m) is a non-negative excitation kernel which describes how past events contribute to the likelihood of future events and $f_{GR}(m)$ is the probability density of observing magnitude m. For the ETAS model this triggering kernel factorises the contribution from the magnitude and the time,

$$\begin{aligned}&g(t,m) = k(m; K, \alpha ) h(t;c,p) \end{aligned}$$

(3)

$$\begin{aligned}&k(m; K, \alpha ) = Ke^{\alpha (m-M_0)}\ :\ m \ge M_0 \end{aligned}$$

(4)

$$\begin{aligned}&h(t;c,p) = c^{p-1}(p-1)(t+c)^{-p}:\ t \ge 0 \end{aligned}$$

(5)

where the $k(m; K, \alpha )$ is known as the Utsu law of productivity (Utsu 1970) and h(t; c, p) is a power law known as the Omori-Utsu decay (Utsu et al. 1995). The model comprises the five parameters ${\mu , K, \alpha , c, p}$. The magnitudes are said to be “unpredictable” since they do not depend on previous events and are distributed according to the Gutenberg-Richter law for magnitudes (Gutenberg and Richter 1936) with probability density $f_{GR}(m) = \beta e^{\beta (m-M_0)}$ on the support ${m: m \ge M_0}$.

2.1 Branching process formulation

An alternative way of formulating the ETAS model is as a Poisson cluster process (Rasmussen 2013). In this formulation a set of immigrants I are realisations of a Poisson process with rate $\mu$. Each immigrant $t_i \in I$ has a magnitude $m_i$ with probability density $f_{GR}$ and generates offspring $S_i$ from an independent non-homogeneous Poisson process, with rate $g(t-t_i,m_i)$. Each offspring $t_j \in S_i$ also has magnitude $m_j$ with probability density $f_{GR}$ and generate offspring $S_j$ of their own. This process is repeated over generations until a generation with no offspring in time interval [0, T] is produced. If the average number of offspring for a given event; $\frac{K\beta }{\beta -\alpha }$, is greater than one, the process is called super-critical and there is a non-zero probability that is continues infinitely. Although it is not observed in the data, this process is accompanied by latent branching variables $B = \{B_1, \ldots , B_n \}$ which define the branching structure of the process,

$$\begin{aligned}&B_i = {\left\{ \begin{array}{ll} 0\text { if } t_i \in I\ (\text {i.e. } i \text { is a background event})\\ j\text { if } t_i \in S_j\ (\text {i.e. } i \text { is an offspring of } j) \end{array}\right. } \end{aligned}$$

(6)

Both the intensity function formulation as well as the branching formulation define different methods for simulating as well as inferring parameters for the Hawkes process. We now give a brief overview of some of these methods, and we direct the reader to Reinhart (2018) for a more detailed review.

2.2 Simulation

A simulation algorithm based on the conditional intensity function was proposed by Ogata (1998). This algorithm requires generating events sequentially using a thinning procedure. Simulating forward from an event $t_i$, the time to the next event $\tau$ is proposed from a Poisson process with rate $\lambda (t_i|\mathcal {H}_{t_i})$. The proposed event $t_{i+1} = t_i + \tau$ is then rejected with probability $1- \frac{\lambda (t_i+\tau |\mathcal {H}_{t_i})}{\lambda (t_i|\mathcal {H}_{t_i})}$. This procedure is then repeated from the newest simulated event until a proposed event falls outside a predetermined time window [0, T].

This procedure requires evaluating the intensity function $\lambda (t|\mathcal {H}(t))$ at least once for each one of n events that are simulated. Evaluating the intensity function requires a summation over all events before time t, thus giving this simulation procedure time complexity $\mathcal {O}(n^2)$.

Algorithm 1, which instead simulates using the branching process formulation of the ETAS model was proposed by Zhuang et al. (2004). This algorithm simulates events over generations $G^{(i)}, i=0,\ldots ,$ until no more events fall within the interval [0, T].

Algorithm 1

Hawkes Branching Process Simulation in the interval [0, T]

This procedure has time complexity $\mathcal {O}(n)$ for steps 1–5, since there is only a single pass over all events. An additional time constraint is added in step 6, where the whole set of events are sorted chronologically, which is at best $\mathcal {O}(n\log n)$.

2.3 Bayesian inference

Given we observe the sequence ${{\textbf {x}}}_{\text {obs}} = \{(t_1,m_1),(t_2,m_2),\ldots ,(t_n,m_n) \}$ in the interval [0, T], we are interested in the posterior probability $p(\theta |{{\textbf {x}}}_{\text {obs}})$ for the parameters $\theta = (\mu , K, \alpha ,c,p)$ of the ETAS model defined in (2)–(5), updated from some prior probability $p(\theta )$. The posterior distribution, expressed in Bayes’ rule,

$$\begin{aligned} p(\theta |{{\textbf {x}}}_{\text {obs}}) \propto p({{\textbf {x}}}_{\text {obs}}|\theta )p(\theta ), \end{aligned}$$

(7)

is known up to a constant of proportionality through the product of the prior $p(\theta )$ and the likelihood $p({{\textbf {x}}}_{\text {obs}}|\theta )$, where,

$$\begin{aligned} \log p({{\textbf {x}}}_{\text {obs}}|\theta )&= \sum _{i=1}^n \log \left[ \mu + \sum _{j=1}^{i-1} h(t;c,p) k(m; K, \alpha ) \right] \nonumber \\&\quad - \mu T - \sum _{i=1}^nk(m; K, \alpha )H(T-t_i; c, p). \end{aligned}$$

(8)

Here, $H(t; c,p) = \int _0^t h(s;c,p)ds$, denotes the integral of the Omori decay kernel.

Vargas and Gneiting (2012) draw samples from the posterior $p(\theta |{{\textbf {x}}}_{\text {obs}})$ through independent random walk Markov Chain Monte Carlo (MCMC) with Metropolis-Hastings rejection of proposed samples. This approach, however, can suffer from slow convergence due to parameters of the ETAS model having high correlation (Ross 2021).

Ross (2021) developed an MCMC sampling scheme, bayesianETAS, which conditions on the latent branching variables $B = \{B_1, \ldots , B_n \}$. The scheme iteratively estimates the branching structure,

$$\begin{aligned}&\mathbb {P}(B_i^{(k)} = j| {{\textbf {x}}}_{\text {obs}} , \theta ^{(k-1)}) \nonumber \\&\quad = {\left\{ \begin{array}{ll} \frac{\mu ^{(k-1)}}{\mu ^{(k-1)} + \sum _{{l}=1}^{i-1}k(m_{{l}})h(t_i-t_{{l}})} \ : j=0\\ \frac{k(m_j)h(t_i-t_j)}{\mu ^{(k-1)} + \sum _{{l}=1}^{i-1}k(m_{{l}})h(t_i-t_{{l}})}\ : j = 1,2,\ldots ,i-1 \end{array}\right. } \end{aligned}$$

(9)

and then samples parameters, $\theta ^{(k)} = (\mu ^{(k)},K^{(k)}, \alpha ^{(k)},c^{(k)},p^{(k)})$, from the conditional likelihood,

$$\begin{aligned}&\log p({{\textbf {x}}}_{\text {obs}}|\theta , B^{(k)}) \nonumber \\&\quad =\! |S_0^{(k)}|\log \!\mu \!-\! \mu T \!+\! \sum _{j=1}^n \Biggl (-k(m_j;K,\alpha )H(T-t_j;c,p) \nonumber \\&\qquad + |S_j^{(k)}| \log k(m_j;K,\alpha ) + \sum _{t_i \in S_j^{(k)}} \log h(t_i-t_j; c,p) \Biggr ), \end{aligned}$$

(10)

where $|S_j|$ denotes the number of events that were triggered by the event at $t_j$.

By conditioning on the branching structure, the dependence between parameters $(K,\alpha )$ and (c, p) is reduced, decreasing the time it takes for the sampling scheme to converge. We can see from Eq. (9) that estimating the branching structure from the data is a procedure that is $\mathcal {O}(n^2)$. Since for every event $i = 1,\ldots ,n$, to estimate its parent we must sum over $j = 1,\ldots ,i-1$. For truncated version of the time kernel h(t), this operation can be streamlined to $\mathcal {O}(n)$. However, due to the heavy-tailed power-law kernel typically used, the complexity scaling remains high as significant truncation of the kernel is unfeasible.

More recently Serafini et al. (2023) have constructed an approximate method of Bayesian inference for the ETAS model based on an Integrated Nested Laplace Approximation (INLA) implemented in the R-package inlabru as well as a linear approximation of the likelihood. This approach expresses the log-likelihood as 3 terms,

$$\begin{aligned}&\log p({{\textbf {x}}}_o | \theta ) \nonumber \\&\quad = -\Lambda _0({{\textbf {x}}}_{\text {obs}},\theta ) - \sum _{i=1}^n \Lambda _i({{\textbf {x}}}_{\text {obs}},\theta ) + \sum _{i=1}^n \log \lambda (t_i|\mathcal {H}_{t_i}), \end{aligned}$$

(11)

where,

$$\begin{aligned} \Lambda _0({{\textbf {x}}}_{\text {obs}},\theta )&= \int _0^T\mu dt, \\ \Lambda _i({{\textbf {x}}}_{\text {obs}},\theta )&= \sum _{h=1}^{C_i}\int _{b_{h,i}} g(t-t_i,m_i)dt\\ &= \sum _{h=1}^{C_i}\Lambda _i({{\textbf {x}}}_{\text {obs}},\theta ,b_{h,i}). \end{aligned}$$

where $b_{1,i},\ldots ,b_{C_i,i}$ are chosen to partition the interval $[t_{i-1},t_i]$. The log-likelihood is then linearly approximated with a first order Taylor expansion with respect to the posterior mode $\theta ^*$,

$$\begin{aligned}&\widehat{\log p}({{\textbf {x}}}_{\text {obs}}|\theta ; \theta ^*) = -{\widehat{\Lambda }}_0({{\textbf {x}}}_{\text {obs}},\theta ,\theta ^*) \\&\qquad - \sum _{i=1}^n\sum _{h=1}^{C_i}{\widehat{\Lambda }}_i({{\textbf {x}}}_{\text {obs}},\theta ,b_{h,i}; \theta ^*) + \sum _{i=1}^n \widehat{\log \lambda }({{\textbf {x}}}_{\text {obs}},\theta ;\theta ^*) \\&\quad = -\exp \{\overline{\log {\Lambda }_0}({{\textbf {x}}}_{\text {obs}},\theta ,\theta ^*)\} \\ &\qquad - \sum _{i=1}^n\sum _{h=1}^{C_i}\exp \{\overline{\log \Lambda }_i({{\textbf {x}}}_{\text {obs}},\theta ,b_{h,i}; \theta ^*)\}\\&\qquad + \sum _{i=1}^n \overline{\log \lambda }({{\textbf {x}}}_{\text {obs}},\theta ;\theta ^*), \end{aligned}$$

where the notation, ${\widehat{\Lambda }}$, denotes the approximation of $\Lambda$ and $\overline{\log \Lambda ( \;\theta ^*)}$ denotes the first order Taylor expansion of $\log \Lambda$ about the point $\theta ^*$.

The posterior mode $\theta ^*$ is found through a Quasi-Newton optimisation method and the final posterior densities are found using INLA, which approximates the marginal posteriors $p(\theta _i|{{\textbf {x}}}_{\text {obs}})$ using a latent Gaussian model.

This approach speeds up computation of the posterior densities, since it only requires evaluation of the likelihood function during the search for the posterior mode. However, the approximation of the likelihood requires partitioning the space into a number of bins, which the authors recommend choosing as greater than 3 per observation. This results in the approximate likelihood having complexity $\mathcal {O}(n^2).$

3 Simulation based inference

A family of Bayesian inference methods have evolved from application settings in science, economics or engineering where stochastic models are used to describe complex phenomena. In this setting, the model may simulate data from a given set of input parameters, however, the likelihood of observing data given parameters is intractable. The task in this setting is to approximate the posterior $p(\theta |{{\textbf {x}}}_{\text {obs}}) \propto p({{\textbf {x}}}_{\text {obs}}|\theta )p(\theta )$, with the restriction that we cannot evaluate $p({{\textbf {x}}}|\theta )$ but we have access to the likelihood implicitly through samples ${{\textbf {x}}}_r \sim p({{\textbf {x}}}|\theta _r)$ from a simulator, for $r = 1,\ldots ,R$ and where $\theta _r \sim p(\theta )$. This approach is commonly referred to as Simulation Based Inference (SBI) or likelihood-free inference.

Until recently, the predominant approach for SBI was Approximate Bayesian Computation (ABC) (Beaumont et al. 2002). In its simplest form, parameters are chosen from the prior $\theta _r \sim p(\theta ),\ r=1,\ldots ,R$, the simulator then generates samples ${{\textbf {x}}}_r \sim p({{\textbf {x}}}|\theta _r),\ r=1,\ldots ,R$, and each sample is kept if it is within some tolerance $\epsilon$ of the observed data, i.e. $d({{\textbf {x}}}_r,{{\textbf {x}}}_{\text {obs}}) < \epsilon$ for a given distance function $d(\cdot ,\cdot )$.

This approach, although exact when $\epsilon \rightarrow 0$, is inefficient with the use of simulations. Sufficiently small $\epsilon$ requires simulating an impractical number of times, and this issue scales poorly with the dimension of ${{\textbf {x}}}$. In light of this an MCMC approach to ABC makes proposals for new simulator parameters $\theta _r \sim q(\cdot |\theta _{r-1})$ using a Metropolis-Hastings kernel (Beaumont et al. 2002; Marjoram et al. 2003). This leads to a far higher acceptance of proposed simulator parameters but still scales poorly with the dimension of ${{\textbf {x}}}$.

In order to cope with high dimensional simulator outputs ${{\textbf {x}}} \in \mathbb {R}^n$, summary statistics $S({{\textbf {x}}})\in \mathbb {R}^d$ are chosen to reduce the dimension of the sample whilst still retaining as much information as possible. These are often chosen from domain knowledge or can be learnt as part of the inference procedure (Prangle et al. 2014). Summary statistics $S({{\textbf {x}}})$ are then used in place of ${{\textbf {x}}}$ in any of the described methods for SBI.

3.1 Neural density estimation

Recently, SBI has seen more rapid development as a result of neural network based density estimators (Papamakarios and Murray 2016; Papamakarios et al. 2017; Lueckmann et al. 2017), which seek to approximate the density p(x) given samples of points $x \sim p(x)$. A popular method for neural density estimation is normalising flows (Rezende and Mohamed 2015), in which a neural network parameterizes an invertible transformation $x = g_\phi (u)$, of a variable u from a simple base distribution p(u) into the target distribution of interest. In practice, the transformation is typically composed of a stack of invertible transformations, which allows it to learn the complex target density. The parameters of the transformation are trained through maximising the likelihood of observing $p_g(x)$, which is given by the change of variables formula. Since x is expressed as a transformation of a simple distribution $u \sim p(u)$, samples from the learnt distribution $p_g(x)$ can be generated by sampling from p(u) and passing the samples through the transformation. Neural density estimators may also be generalised to learn conditional densities $p({{\textbf {x}}}|{{\textbf {y}}})$ by conditioning the transformation $g_\phi$ on the variable y (Papamakarios et al. 2017).

In the task of SBI, a neural density estimator can be trained on pairs of samples $\theta _r \sim p(\theta ), {{\textbf {x}}}_r \sim p({{\textbf {x}}}|\theta _r)$ to approximate either the likelihood $p({{\textbf {x}}}_{\text {obs}}|\theta )$ or the posterior density $p(\theta |{{\textbf {x}}}_{\text {obs}})$, from which posterior samples can be obtained. If the posterior density is estimated, in a procedure known as Neural Posterior Estimation (NPE) (Lueckmann et al. 2017), then samples can be drawn from the normalising flow. If the likelihood is estimated, known as Neural Likelihood Estimation (NLE) (Papamakarios et al. 2019), then the approximate likelihood can be used in place of the true likelihood in a MCMC sampling algorithm to obtain posterior samples. Other neural network methods exist for SBI such as ratio estimation (Izbicki et al. 2014) or score matching (Geffner et al. 2022; Sharrock et al. 2022), however, we direct the reader to (Cranmer et al. 2020) for a more comprehensive review of modern SBI.

Neural density estimation techniques consistently outperform ABC-based methods in benchmarking experiments, since they can efficiently interpolate between different simulations (Cranmer et al. 2020; Lueckmann et al. 2021). We confirm this in Fig. 1, where we apply Sequential Neural Posterior Estimation (SNPE) to a 3 parameter Hawkes experiment from (Deutsch and Ross 2021). SNPE provides a better approximation of the posterior than ABC-MCMC and requires fewer simulations.

Fig. 1

Posterior densities for a univariate Hawkes process with exponential kernel. The ‘observed’ data contains 4806 events and was simulated from parameters indicated in red on the diagonal plots. In green are posterior samples found using the ABC-MCMC method for SBI using 300,000 simulations. In blue are posterior samples from SNPE using the same summary statistics as ABC-MCMC but only 10,000 simulations. In orange are posterior samples found using MCMC sampling with likelihood function. A $\text {Uniform}([0.05, 0,0],[0.85, 0.9,3])$ prior was used for all three methods

4 SB-ETAS

Fig. 2

An outline of the SB-ETAS inference procedure. Samples from the prior distribution are used to simulate many ETAS sequences. A neural density estimator is then trained on the parameters and simulator outputs to approximate the posterior distribution. Samples from the posterior given the observed earthquake sequence can then be used to improve the estimate over rounds or are returned as the final posterior samples

We now present SB-ETAS, our simulation based inference method for the ETAS model. The method avoids computing the likelihood function and instead leverages fast simulation from the ETAS branching process. The inference method uses Sequential Neural Posterior Estimation (SNPE) (Papamakarios and Murray 2016; Lueckmann et al. 2017), a modified version of NPE which performs inference over rounds. Each round, an estimate of the posterior proposes new samples for the simulator, a neural density estimator is trained on those samples and the estimated posterior is updated (Fig. 2, Algorithm 2). SNPE was chosen over other methods of Neural-SBI, as it avoids the need to perform MCMC sampling, a slow procedure. Instead, sampling from the posterior is fast since the approximate posterior is a normalising flow.

Algorithm 2

SB-ETAS

4.1 Summary statistics

What differentiates Hawkes process models from other simulator models used in Neural-SBI is that the output of the simulator ${{\textbf {x}}} = (t_1,m_1),\ldots ,(t_n,m_n)$ itself has random dimension. For a specified time interval over which to simulate earthquakes [0, T], one particular parameter $\theta _1$ will generate different numbers of events if simulated repeatedly. This is problematic for neural density estimators since even though they are successful over high dimensional data, they require a fixed dimensional input. For this reason, we fix the dimension of simulator output through calculating summary statistics of the data $S({{\textbf {x}}})$.

Works to perform ABC on the univariate Hawkes process with exponential decay kernel have found summary statistics that perform well in that setting. Ertekin et al. (2015) use the histogram of inter-event times as summary statistics as well as the number of events. Deutsch and Ross (2021) extend these summary statistics by adding Ripley’s K statistic (Ripley 1977), which is a popular choice of summary statistic in spatial point processes (Møller and Waagepetersen 2003). Figure 1 shows the performance of the ABC-MCMC method developed by Deutsch and Ross (2021), using the aforementioned summary statistics. Using SNPE on the same summary statistics yields a more confident estimation of the “true” posterior than ABC-MCMC and requires far fewer simulations (10,000 versus 300,000).

The ETAS model is more complex than a univariate Hawkes process since it is both marked (i.e. it contains earthquake magnitudes) and contains a power law decay kernel which decays much more slowly than exponential, making it harder to estimate (Bacry et al. 2016). For SB-ETAS we borrow similar summary statistics to Ertekin et al. (2015), namely $S_1({{\textbf {x}}}) = \log ( \# \text { events})$, $S_2,\ldots ,S_4({{\textbf {x}}}) =$20th, 50th and 90th quantiles of the inter-event time histogram. Similar to Deutsch and Ross (2021), we use another statistic $S_5({{\textbf {x}}})$, which is the ratio of the mean and median of the inter-event time histogram.

4.1.1 Ripley’s K statistic

For the remaining summary statistics, we develop upon the introduction of Ripley’s K statistic by (Deutsch and Ross 2021). For a univariate point process ${{\textbf {x}}} = (t_1,\ldots ,t_n)$, Ripley’s K statistic is (Dixon 2013),

$$\begin{aligned}&K({{\textbf {x}}},w) \nonumber \\&\quad = \frac{1}{\lambda }\mathbb {E}(\# \text { of events within }w\text { of a random event} ). \end{aligned}$$

(12)

Here, $\lambda$ is the unconditional rate of events in the time window [0, T]. An estimator for the K-statistic is derived by Diggle (1985),

$$\begin{aligned} {\hat{K}}({{\textbf {x}}},w) = \frac{T}{n^2}\sum _{i=1}^n \sum _{j\ne i}\mathbb {I}(0< t_j-t_i \le w). \end{aligned}$$

(13)

Despite containing a double-sum, computation of this estimator has complexity $\mathcal {O}(n)$ since $\{t_i\}_{i=1}^n$ is an ordered sequence, i.e. $(t_3 - t_1< w) \Rightarrow (t_3 - t_2 < w)$. Calculation of Ripley K-statistic therefore satisfies the complexity requirement of our procedure if the number of windows w for which we evaluate ${\hat{K}}({{\textbf {x}}},w)$ is less than $\log n$. In fact, our results suggest that less than 20 are required.

The use of Ripley’s K-statistic for non-marked Hawkes data is motivated by Bacry and Muzy (2014), who show that second-order properties fully characterise a Hawkes process and can be used to estimate a non-parametric triggering kernel. Bacry et al. (2016) go on to give a recommendation for a binning strategy to estimate slow decay kernels such as a power law, using a combination of linear and log-scaling. It therefore seems reasonable to define $S_6({{\textbf {x}}})\ldots S_{23}({{\textbf {x}}})= {\hat{K}}({{\textbf {x}}},w)$, where w scales logarithmically between [0, 1] and linearly above 1.

We modify Ripley’s K-statistic to account for the particular interaction between marks and points in the ETAS model. Namely, the magnitude of an earthquake directly affects the clustering that occurs following it, expressed in the productivity relationship (4). In light of this, we define a magnitude thresholded Ripley K-statistic,

$$\begin{aligned}&K_T({{\textbf {x}}},w,M_T) \nonumber \\&\quad = \frac{1}{\lambda _{T}}\mathbb {E}(\# \text { events within }w\text { of an event }m_i\ge M_T), \end{aligned}$$

(14)

where $\lambda _T$ is the unconditional rate of events above $M_T$. One can see that $K_T({{\textbf {x}}},w,M_0) = K({{\textbf {x}}},w)$. We estimate $K_T$ with

$$\begin{aligned} {\hat{K}}_T({{\textbf {x}}},w,M_T) = \frac{T}{\nu ^2}\sum _{i:m_i\ge M_T} \sum _{j\ne i}\mathbb {I}(0< t_i-t_j \le w), \end{aligned}$$

(15)

where $\nu$ is the number of events above magnitude threshold $M_T$. For general $M_T$, we lose the $\mathcal {O}(n)$ complexity that the previous statistic has, instead it is $\mathcal {O}(\nu n)$. However, if the threshold is chosen to be large enough, evaluation of this estimator is fast. In our experiments, $M_T$ is chosen to be (4.5, 5, 5.5, 6), with $w = (0.2,0.5,1,3)$. This defines the remaining statistics $S_{24}({{\textbf {x}}}),\ldots ,S_{39}({{\textbf {x}}})$.

5 Experiments and results

To evaluate the performance of SB-ETAS, we conduct inference experiments on a series of synthetic ETAS catalogs. On each simulated catalog we seek to obtain 5000 samples from the posterior distribution of ETAS parameters. The latent variable MCMC inference procedure, bayesianETAS, will be used as a reference model in our experiments since it uses the ETAS likelihood without making any approximations. We compare samples from this exact method with samples from approximate methods, inlabru and SB-ETAS.

We begin with an experiment to test the scalability of all 3 methods. Following that we evaluate the performance of SB-ETAS on parameter sets estimated from real earthquake catalogs.

5.1 Scalability

Multiple catalogs are simulated from a fixed set of ETAS parameters, $(\mu ,k,\alpha ,c,p) = (0.2,0.2,1.5,0.5,2)$ with magnitude of completeness $M_0 = 3$ and Gutenberg-Richter distribution parameter $\beta = 2.4$. Each new catalog is simulated in a time window [0, T], where $T \in (10,20,30,40,50,60,70,80,90,100,250,500,1000) \times 10^3$.

Fig. 3

The runtime for parameter inference versus the catalog size for SB-ETAS, inlabru and bayesianETAS. Separate ETAS catalogs were generated with the same intensity function parameters but for varying size time-windows. The runtime in hours and the number of events are plotted in log-log space

Fig. 4

Maximum Mean Discrepancy for samples from each round of simulations in SB-ETAS. Each plot corresponds to a different simulated ETAS catalog simulated with identical model parameters but over a different length time-window (MaxT). In red is the performance metric evaluated for samples from inlabru. 95% confidence intervals are plotted for SB-ETAS across 10 different initial seeds

Fig. 5

Classifier Two-Sample Test scores for samples from each round of simulations in SB-ETAS. Each plot corresponds to a different simulated ETAS catalog simulated with identical model parameters but over a different length time-window (MaxT). In red is the performance metric evaluated for samples from inlabru. 95% confidence intervals are plotted for SB-ETAS across 10 different initial seeds

Figure 3 shows the runtime of each inference method as a function of the number of events in each catalog. Each method was run on a high-performance computing node with eight 2.4 GHz Intel E5-2680 v4 (Broadwell) CPUs, which is equivalent to what is commonly available on a standard laptop. On the catalogs with up to 100,000 events, inlabru is the fastest inference method, around ten times quicker on a catalog of 20,000 events. However, the superior scaling of SB-ETAS allows it to be run on the catalog of $\sim 500,000$ events, which was unfeasible for inlabru given the same computational resources i.e. it exceeded a two week time limit. The gradient of 2 for both bayesianETAS and inlabru in log-log space confirm the $\mathcal {O}(n^2)$ time complexity of both inference methods. SB-ETAS, on the other hand, has gradient $\frac{2}{3}$ which suggests that the theoretical $\mathcal {O}(n\log n)$ time complexity is a conservative upper-bound.

The prior distributions for each implementation are not identical since each has its own requirements. Priors are chosen to replicate the fixed implementation in the bayesianETAS package,

$$\begin{aligned}&\mu \sim \text {Gamma}(0.1,0.1) \end{aligned}$$

(16)

$$\begin{aligned}&K,\alpha ,c \sim \text {Unif}(0,10) \end{aligned}$$

(17)

$$\begin{aligned}&p \sim \text {Unif}(1,10). \end{aligned}$$

(18)

The implementation of inlabru uses a transformation $K_b = \frac{K(p-1)}{c}$, with prior $K_b \sim \text {Log-Normal}(-1,2.03)$ chosen by matching $1\%$ and $99\%$ quantiles with the bayesianETAS prior for K. SB-ETAS uses a $\mu \sim \text {Unif}(0.05,0.3)$ prior in place of the gamma prior as well as enforcing a sub-critical parameter region $K\beta < \beta -\alpha$ (Zhuang et al. 2012). Both the uniform prior and the restriction on K and $\alpha$ stop unnecessarily long or infinite simulations.

Once samples are obtained from SB-ETAS and inlabru, we measure their (dis)similarity with samples from the exact method bayesianETAS using the Maximum Mean Discrepancy (MMD) (Gretton et al. 2012) and the Classifier Two-Sample Test (C2ST) (Lehmann and Romano 2005; Lopez-Paz and Oquab 2016). Figures 4 and 5 show the values of these performance metrics for samples from each of 15 rounds of simulations in SB-ETAS compared with the performance of inlabru. Since SB-ETAS involves random sampling in the procedure, we repeat it across 10 different seeds and plot a 95% confidence intervals. In general across the 10 synthetic catalogs, SB-ETAS and inlabru are comparable in terms of MMD (Fig. 4) and inlabru performs best in terms of C2ST (Fig. 5). Figure 6 shows samples from the $T=60,000$. Samples from inlabru are overconfident with respect to the bayesianETAS samples, whereas SB-ETAS samples are more conservative. This phenomenon is shared across the samples from all the simulated catalogs and we speculate that it accounts for the difference between the two metrics.

A common measure for the appropriateness of a prediction’s uncertainty is the coverage property (Prangle et al. 2014; Xing et al. 2019). The coverage of an approximate posterior assesses the quality of its credible regions ${\hat{C}}_{{{\textbf {x}}}_{obs}}$ which satisfy,

$$\begin{aligned} \gamma = \mathbb {E}_{{\hat{p}}(\theta |{{\textbf {x}}}_{obs})}\left( \mathbb {I}\{{\hat{\theta }}\in {\hat{C}}_{{{\textbf {x}}}_{obs}}\}\right) \end{aligned}$$

(19)

An approximate posterior has perfect coverage if its operational coverage,

$$\begin{aligned} b({{\textbf {x}}}_{obs}) = \mathbb {E}_{p(\theta |{{\textbf {x}}}_{obs})}\left( \mathbb {I}\{{\hat{\theta }}\in {\hat{C}}_{{{\textbf {x}}}_{obs}}\}\right) \end{aligned}$$

(20)

is equal to the credibility level $\gamma$. The approximation is conservative if it has operational coverage $b({{\textbf {x}}}_{obs}) > \gamma$ and is overconfident if $b({{\textbf {x}}}_{obs}) < \gamma$ (Hermans et al. 2021). Expectations in Eqs. (19)–(20) cannot be computed exactly and so are replaced with Monte Carlo averages, resulting in empirical coverage $c({{\textbf {x}}}_{obs})$. Figure 7 shows the empirical coverage for both SB-ETAS, averaged across the 10 initial seeds, along with inlabru on the 10 synthetic catalogs. inlabru consistently gives overconfident approximations, as the empirical coverage lies well below the credibility level. SB-ETAS has empirical coverage that indicates conservative estimates, but that is generally closer to the credibility level.

Fig. 6

Samples from the posterior distribution of ETAS parameters for the simulated catalog with $T=60,000$, for bayesianETAS, inlabru and SB-ETAS. The data generating parameters are marked in red in the diagonal plots

5.2 Synthetic catalogs

We now perform further tests to evaluate the performance of SB-ETAS on parameter sets estimated from real earthquake catalogs (Table 1). We consider MLE estimates of ETAS for the Amatrice earthquake sequence, taken from Stockman et al. (2023), for both Landers and Ridgecrest earthquakes, taken from Hainzl (2022) and finally for the Kumamoto earthquake, taken from Zhuang et al. (2017). From each of these parameter sets, we simulate an earthquake catalog of around 6000 events and compare posterior samples using bayesianETAS with both SB-ETAS and inlabru.

Figure 8 displays the MMD and C2ST scores for samples from each of 15 rounds of simulations in SB-ETAS compared with the performance of inlabru. SB-ETAS outperforms inlabru on the synthetic Amatrice, Landers and Ridgecrest catalogs across both metrics. This superior performance is attributed to the posterior distributions from SB-ETAS exhibiting less bias and providing better coverage of the “ground truth” MCMC posteriors (Figs. 12, 13, 14, 15, 16 and 17). While inlabru provides the closest approximation for the synthetic Kumamoto catalog (Fig. 15), its posteriors are generally overconfident, leading to a lack of coverage for the MCMC posteriors whenever there is bias. Furthermore, the posterior distribution for the synthetic Landers catalog exhibits weak identifiability between parameters (c, p). While SB-ETAS expresses this in the posterior (Fig. 16), inlabru is unable to (Fig. 17).

Fig. 7

Empirical estimates of the coverage of both SB-ETAS and inlabru. Coverage below the black line $y=x$ indicates an overconfident approximation, whereas coverage below $y=x$ indicates a conservative approximation

Table 1 Parameter values used to generate the synthetic earthquake catalogs. Amatrice parameters were taken from Stockman et al. (2023), Landers and Ridgecrest parameters were taken from Hainzl (2022) and Kumamoto parameters were taken from Zhuang et al. (2017). The parameter K has been transformed for Landers, Ridgecrest and Kumamoto to account for the unnormalised Omori-Utsu law

Fig. 8

a Maximum mean discrepancy (MMD) and b Classifier two-sample test (C2ST) scores for samples from each round of simulations in SB-ETAS. Each plot corresponds to a different synthetic ETAS catalog simulated using MLE parameters taken from the Amatrice, Kumamoto, Landers and Ridgecrest earthquake sequences. In red is the performance metric evaluated for samples from inlabru. 95% confidence intervals are plotted for SB-ETAS across 10 different initial seeds

6 SCEDC catalog

We now evaluate SB-ETAS on some observational data from Southern California. The Southern California Seismic Network has produced an earthquake catalog for Southern California going back to 1932 (Hutton et al. 2010). This catalog contains many infamous large earthquakes such as the 1992 $M_W$ 7.3 Landers, 1999 $M_W$ 7.1 Hector Mine and $M_W$7.1 Ridgecrest sequences. We use $N=43,537$ events from 01/01/1981 to 31/12/2021 with earthquake magnitudes $\ge M_W\ 2.5$ since this assures the most data completeness (Hutton et al. 2010). The catalog can be downloaded from the Southern California Earthquake Data Center https://service.scedc.caltech.edu/ftp/catalogs/SCSN/.

This size of catalog contains too many events to find ETAS posteriors using bayesianETAS (i.e. it would take longer than 2 weeks). Therefore we run only SB-ETAS and inlabru on the entire catalog and validate their performance by comparing the compensator, $\Lambda ^*(t;\theta ) = \int _0^t \lambda ^*(s;\theta )ds$, with the observed cumulative number of events in the catalog N(t). $\Lambda ^*(t;\theta )$ gives the expected number of events at time t, and therefore a model and its parameters are consistent with the observed data if $\Lambda ^*(t;\theta ) = N(t)$.

We generate 5000 samples using SB-ETAS and inlabru and use each sample to generate a compensator curve $\Lambda ^*(t;\theta )$. We display $95\%$ confidence intervals of these curves in Fig. 9, along with a curve for the Maximum Likelihood Estimate (MLE). Consistent with the synthetic experiments, we find that SB-ETAS gives a conservative estimate of the cumulative number of events across the catalog, whereas inlabru is overconfident and does not contain the observed number of events within its very narrow confidence interval. Both inlabru and the MLE match the total observed number of events in the catalog, since this value, $\Lambda ^*(T)$, is a dominant term in each of their loss functions (the likelihood) during estimation.

For both the MLE and SB-ETAS, we fix the $\alpha$ parameter equal to the $\beta$ parameter of the Gutenberg-Richter law $f_{GR(m)}$, a result that is consistent with other temporal only studies of Southern California (Felzer et al. 2004; Helmstetter et al. 2005), and which reproduces Båth’s law for aftershocks (Felzer et al. 2002). Fixing $\alpha$ has also shown to result in sub-critical parameters, compared with a free $\alpha$ (Seif et al. 2017; van der Elst 2017); a requirement for both our simulation based procedure as well as for simulating forecasts. We were unable to successfully fix $\alpha$ for inlabru and therefore use the 5 parameter implementation of ETAS.

Posterior distributions are displayed in Figs. 10 and 11 including $\alpha = \beta$ and free $\alpha$ implementations of the MLE. Although the modes of the marginal distributions do not match the MLE, the SB-ETAS posteriors contain the MLE parameters within their wider confidence ranges. Since inlabru has much narrower confidence, although the distributions are relatively close to the MLE, the confidence ranges do not contain MLE parameters.

Fig. 9

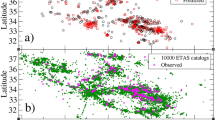
The compensator $\Lambda ^*(t)$ found from estimating the ETAS posterior distribution on the SCEDC catalog (events displayed in background). 5000 Samples from the posterior using both SB-ETAS and inlabru were used to generate a mean and 95% confidence interval. The compensator is compared against the observed cumulative number of events in the catalog along with the MLE

Fig. 10

The posterior distribution of ETAS parameters found on the SCEDC catalog using SB-ETAS. This implementation of ETAS fixes $\alpha = \beta$. MLE parameters are plotted for comparison

Fig. 11

The posterior distribution of ETAS parameters found on the SCEDC catalog using inlabru. This implementation of ETAS has a free $\alpha$ parameter. MLE parameters are plotted for comparison

7 Discussion and conclusion

The growing size of earthquake catalogs generated through machine learning based phase picking and an increased density of seismic networks, calls for the application of a broader range of models to assess whether the new data enhances forecasting capabilities. Furthermore, this growth demands that our existing models scale effectively to handle the new volume of data. We propose using a simulation-based approach, where models are defined by a simulator without the need for a likelihood function, thereby alleviating some modeling constraints. Simulation based inference (SBI) performs Bayesian inference for such models using outputs of the simulator in place of the likelihood. SB-ETAS: our simulation based estimation procedure for the Epidemic Type Aftershock Sequence (ETAS) model, establishes an initial connection between earthquake modeling and simulation based inference, demonstrating improved scalability over previous methods.

In our study, using SB-ETAS we generate samples of the ETAS posterior distribution for a series of synthetic catalogs as well as a real earthquake catalog from southern California. Additionally, we generate samples using another approximate inference method: inlabru. Our general finding is that inlabru produces overconfident and sometimes biased posterior estimates, while SB-ETAS provides more conservative and less biased estimates. Although it might seem reasonable to judge an approximate posterior by its closeness to the exact posterior, for practical use, overconfident estimates should be penalised more than under-confident ones. Bayesian inference seeks to identify a range of parameter values which are then used to give confidence over a range of earthquake forecasts. However, failure to identify regions of the parameter space that give likely parameters, would result in omission of a range of likely forecasts.

Although improvements have been made to reduce the computational time of performing Bayesian inference for the ETAS model, first with bayesianETAS followed by inlabru, neither of these approaches improve upon the scalability of inference. Therefore as catalogs continue to grow in size, these methods become less feasible to use. On experiments where we give SB-ETAS, bayesianETAS and inlabru access to the same 8 CPUs, only SB-ETAS could be used to fit a catalog of 500,000 events and was the fastest method for catalogs above 100,000 events. Both inlabru and SB-ETAS are parallelized methods and would therefore see a reduction in runtime if given access to more CPUs. This is unlike bayesianETAS which is not parrallelized in its current implementation. It is also worth noting that although SB-ETAS and inlabru were given the same CPUs, inlabru required over 4 times the amount of memory than SB-ETAS with catalogs over 100,000 events, (Fig. 18). This additional memory demand far exceeds the capacity typically available on standard laptops.

A clear limitation of this inference procedure is that the posterior distribution must lie in the sub-critical region of the parameter space. Super-critical parameters, which lie outside this region, result in simulations that explode with non-zero probability. That is, infinitely many earthquakes would be simulated within the finite time window. In our experiments, to avoid this we enforce a sub-critical parameter region using the prior. There is however, the possibility that the “true” posterior lies outside of the prior. While this may an immediate problem for SB-ETAS, MCMC or inlabru do not circumvent the problem when forecasts are made. Generating forecasts requires simulating multiple earthquake catalogs, and therefore super-critical parameters will result in explosive forecasts. The practical solution is to discard such forecasts, however this ignores the fact that the model is unable to successfully recreate real earthquake sequences over extended time periods: we do not observe infinitely many earthquakes occurring in nature.

An inability to replicate nature indicates a poorly fit or misspecified model. Restricted by our need for non-critical simulations we wish to advocate for models which are sub-critical. Developing models in a simulation based way could ensure that fitted models better resemble nature. Using a truncated magnitude distribution (Sornette and Werner 2005a), which expands the size of the sub-critical region, or by fixing the alpha parameter, provide small model alterations which reduce criticality. For the SCEDC catalog the branching ratio of the 5 parameter MLE was $\eta = 2.033$, compared with $\eta = 0.699$ for the 4 parameter implementation. More significant alterations such as considering a spatially varying background rate (Nandan et al. 2021, 2022) have led to sub-critical models, compared with super-critical one that use a uniform background rate. Furthermore, time-varying parameters may account for the “intermittent” criticality of the system (Bowman and Sammis 2004; Harte 2014).

Equally, improperly considering boundary effects, in space, time and magnitude can lead to poor estimation of a model’s criticality (Sornette and Werner 2005b; Wang et al. 2010; Seif et al. 2017). Models that consider events outside of the observed space-time-magnitude region, may better replicate nature. This could include simulating additional observed events (e.g. Shcherbakov et al. 2019; Shcherbakov 2021), or unobserved events (e.g. Deutsch and Ross 2021) that both have triggering capabilities.

SB-ETAS is particularly well aligned for modeling such contributions from unobserved events. For example, consider the same ETAS branching process used in this study, but instead events are deleted with a time varying probability h(t). The induced likelihood of this process,

$$\begin{aligned} p({{\textbf {x}}}|\theta ) \propto \int p({{\textbf {x}}},{{\textbf {x}}}_u|\theta ) \prod _{t_i \in {{\textbf {x}}}}h(t_i)\prod _{t_j \in {{\textbf {x}}}_u}(1-h(t_j))d{{\textbf {x}}}_u, \end{aligned}$$

(21)

is intractable since it involves integrating over the set of unobserved events ${{\textbf {x}}}_u$ (Deutsch and Ross 2021). Current methods to deal missing data estimate the true earthquake rate from the apparent earthquake rate assuming no contribution from undetected events (Hainzl 2016). A likelihood-free method of inference such as SB-ETAS could avoid the biases from ignoring such triggering (Sornette and Werner 2005b).

There is a natural extension to SB-ETAS for the spatio-temporal form of the ETAS model. The spatio-temporal ETAS extends the temporal model used in the study by modeling earthquake spatial interactions with an isotropic Gaussian spatial triggering kernel (Ogata 1998). It is also defined as a branching process and so retains the $\mathcal {O}(n\log n)$ complexity of simulation. This study has illustrated that the Ripley K-statistic is an informative summary statistic for the triggering parameters of the temporal ETAS model. It seems fair to assume that the spatio-temporal Ripley K-statistic,

$$\begin{aligned}&{\hat{K}}({{\textbf {x}}},w_t,w_s) \\&\quad = \frac{A T}{n^2}\sum _{i=1}^n \sum _{j\ne i}\mathbb {I}(0< t_j-t_i \le w_t)\mathbb {I}(||s_j-s_i||_2 \le w_s). \end{aligned}$$

where A is the area of the study region, would be a reasonable choice for the spatio-temporal form of SB-ETAS. This statistic loses the $\mathcal {O}(n)$ efficiency that the purely temporal one benefits from. Instead Wang et al. (2020) have developed a distributed procedure for calculating this statistic with $\mathcal {O}(n\log n)$ complexity that would retain the overall time complexity that SB-ETAS has.

Ideally, the value of the Ripley K-statistic ${\hat{K}}({{\textbf {x}}},w)$ for all $w \in \mathbb {R}_+$ would be used as the summary statistic for the observed data ${{\textbf {x}}}$. However, since the neural density estimator requires a fixed length vector as input, we have to sample this function at pre-specified intervals. Increasing the number of samples would increase the dimension of this fixed length vector, making the density estimation task more challenging. On the other hand, using fewer samples w, would make the density estimation task easier but would reduce the information contained in the summary statistic. Future work, should address how to balance the number of samples of the Ripley K-statistic as well as moving beyond the hand chosen values used in this study. We speculate that the loss of information from under-sampling the K-statistic, weakens the generalisation of the method in its current form, e.g. the MMD for the MaxT=30000 experiment does not decrease over the simulation rounds (Fig. 4).

Further model expansion using this simulation based framework could help estimate earthquake branching models that include complex physical dependencies. One possible example would be to calibrate the Third Uniform California Earthquake Rupture Forecast ETAS Model (UCERF3-ETAS), a unified model for fault rupture and ETAS earthquake clustering (Field et al. 2017). This model extends the standard ETAS model by explicitly modeling fault ruptures in California and includes a variable magnitude distribution which significantly affects the triggering probabilities of large earthquakes. This model is only defined as a simulator and uses ETAS parameters found independently to the joint ETAS and fault model. In fact, Page and van der Elst (2018) validate the models performance through a comparison of summary statistics from the outputs of the model. This validation could be extended to comprise part of the inference procedure for model parameters using the same simulation based framework as SB-ETAS.

Appendices

Posterior distributions

See Figs. 12, 13, 14, 15, 16 and 17.

Fig. 12

Samples from the posterior distribution of ETAS parameters for the synthetic Ridgecrest catalog (5528 events, $M_0=2.0$), using bayesianETAS and SB-ETAS. The data generating parameters are marked in red in the diagonal plots

Fig. 13

Samples from the posterior distribution of ETAS parameters for the synthetic Ridgecrest catalog (5528 events, $M_0=2.0$), using bayesianETAS and inlabru. The data generating parameters are marked in red in the diagonal plots

Fig. 14

Samples from the posterior distribution of ETAS parameters for the synthetic Amatrice catalog (6673 events, $M_0=3.0$), using bayesianETAS, inlabru and SB-ETAS. The data generating parameters are marked in red in the diagonal plots

Fig. 15

Samples from the posterior distribution of ETAS parameters for the synthetic Kumamoto catalog (5340 events, $M_0=3.5$), using bayesianETAS, inlabru and SB-ETAS. The data generating parameters are marked in red in the diagonal plots

Fig. 16

Samples from the posterior distribution of ETAS parameters for the synthetic Landers catalog (6538 events, $M_0=2.0$), using bayesianETAS and SB-ETAS. The data generating parameters are marked in red in the diagonal plots

Fig. 17

Samples from the posterior distribution of ETAS parameters for the synthetic Landers catalog (6538 events, $M_0=2.0$), using bayesianETAS and inlabru. The data generating parameters are marked in red in the diagonal plots

Memory

See Fig. 18.

Fig. 18

The memory usage for parameter inference versus the catalog size for SB-ETAS, inlabru and bayesianETAS. Separate ETAS catalogs were generated with the same intensity function parameters but for varying size time-windows. The memory usage and the number of events are plotted in log–log space